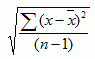Internet Publikation für Allgemeine und Integrative Psychotherapie
(ISSN 1430-6972)
IP-GIPT DAS=08.09.2003 Internet-Erstausgabe, letzte Änderung:  15.06.24
Impressum: Diplom-Psychologe Dr. phil. Rudolf Sponsel  Stubenlohstr. 20   D-91052 Erlangen
Mail: sekretariat@sgipt.org_Zitierung  &  Copyright


---

Anfang _Beweise in der Statistik_Datenschutz_Überblick_Rel. Aktuelles  _Rel. Beständiges  _Titelblatt_ Konzept_ Archiv_ Region_Service_iec-verlag__Wichtiger Hinweis zu Links und zu Empfehlungen

---

Willkommen in unserer Abteilung Abstrakte Grundbegriffe aus den Wissenschaften (Analogien, Modelle und Metaphern für die allgemeine und integrative Psychologie und Psychotherapie sowie Grundkategorien zur Denk- und Entwicklungspsychologie), hier speziell zum Thema:

Beweis und beweisen in der Statistik
„Je planmäßiger die Menschen vorgehen, desto wirksamer trifft sie der Zufall“
Friedrich Dürrenmatt, hierzu passend Brecht in seiner Ballade von der Unzulänglichkeit menschlichen Planens (1928):
"Ja mach nur einen Plan! Sei nur ein großes Licht! Und mach dann noch 'nen zweiten Plan. Gehn tun sie beide nicht."

Blicke über den Zaun zum Auftakt für eine integrative psychologisch-psychotherapeutische Beweislehre
aus allgemein integrativer psychologisch-psychotherapeutischer und einheitswissenschaftlicher Sicht

Einführung, Überblick, Verteilerseite Beweis und beweisen

von Rudolf Sponsel, Erlangen

Hinweis: Wenn nicht ersichtlich werden (Externe Links) in runden und [interne IP-GIPT Links] in eckige Klammern gesetzt, direkte Links im Text auf derselben Seite sind direkt gekennzeichnet. In dieser Übersichtsarbeit wird das Thema im Überblick gesamtheitlich aus einheitswissenschaftlicher Perspektive dargestellt. Im Laufe der Zeit folgen weitere Ausarbeitungen.

---


Inhaltsübersicht
• Einstieg Beweis und beweisen in der Statistik.
• Beispiele für praktisch-statistische Fragestellungen.
• Praktisch wichtige Grundfragen an die statistische Wissenschaft.
• Genauere Operationalisierungen (Auswahl).
• Repräsentativität, Transparenz und Kontinuität statistischer Zeitreihen.
• Tradition mehrdeutiger und daher unsinniger Auszeichnungen in der bayerischen Statistik.
• Missing Data (MD) Unterscheidungen.
• Beispiel MD3b: Schätzung des Gesamtschuldenstandes Nürnbergs am 31.3.1929 in Reichsmark.
• Veränderungen der Erhebung statistischer Kenngrößen 1973 und 1978 am Beispiel Verschuldung der Gemeinden.
• Was "beweist" nun dieser wenig erfreuliche Sachverhalt?
• Probleme.
• Grundannahme-Paradoxie: Konstanz des Zufalls?.
• Mathematik und Statistik.
• [Der Signifikanztest in der Wissenschaft, Psychologie, klinischen und Psychotherapieforschung. Szientismus zwischen numerologischer Esoterik, Gaukeln und Betrug?]
• Statistische Paradoxien und Dilemmas nach Stegmüller
• Die Paradoxie des statistischen Syllogismus (nach Stegmüller).
• Simpson's Paradox.
• Die Korrelations-Paradoxien.
• [Partielle Korrelationen]
• Multivariate Fallstricke.
• [Kollinearität und numerisch instabile Matrizen in der Psychologie]
• [Einführung und Überblick. Kritik der Handhabung der Faktorenanalyse]
• Fehler
• Ungenaue Angaben und Beschreibungen (Voraussetzungen, Hypothesen, Methoden, Ergebnisse, Geltungsbereiche, Aussagekraft/Bedeutung, Verständlichkeit, Nachvollziehbarkeit, ...).
• Übertragung von Gruppenkennwerten auf die Individuen der Gruppe.
• Grundlagen der Interpretation statistischer Daten und Modelle.
• Manipulation, tricksen, frisieren, täuschen, verdrehen, lügen, ausblenden, weglassen.
• Glossar: Wahrscheinlichkeit und Statistik (Stichwortsammlung).
• Literatur * Links * Allgemeine Querverweise.




---

Einstieg Beweis und beweisen in der Statistik
In memoriam: Trau keiner Statistik, die Du nicht selbst gefälscht hast * Man kann mit Statistik alles beweisen

Diese beiden bösen geflügelten Worte aus Volk und Bildungswelt sagen eigentlich schon alles über den Zustand dieser Wissenschaft, ihrer Vermittelbarkeit und allgemeinen Anerkennung. Das ist sehr schade, weil ich denke, daß Wahrscheinlichkeit und Statistik unverzichtbare und bedeutende Errungenschaften für die Wissenschaft und Gesellschaft sind. Ohne zuverlässige Statistiken, insbesondere langer Zeitreihen über Jahrzehnte und Jahrhunderte kann es keine zuverlässige und vernünftige Analyse, Planung, Erklärung und Prognose geben. Die Amerikaner wissen und können das, Deutschland und Europa können und wissen es leider anscheinend nicht (> Repräsentativität, Transparenz und Kontinuität statistischer Zeitreihen).

Beispiele für praktisch-statistische Fragestellungen:

1. Wie viele Menschen umfaßt das deutsche Volk zum Zeitpunkt TT.MM.JJ?
2. Wie gut wirkt das Medikament M bei Kranken mit der Krankheit K?
3. Ist das Symptom S1 typisch für Störungen vom Typ T?
4. Wie gut und treffsicher ist der Test T für die Erkennung von Störungen vom Typ X?
5. Wie wahrscheinlich ein Sechser im Lotto?
6. Wie hoch ist das Bruttoinlandsprodukt?
7. Ist Elektrosmog schädlich?
8. Wer gewinnt die deutsche Fußballmeisterschaft?
9. Warum sinkt die [Mordstatistik] gegenüber Ausländern, obwohl mehr gewaltpolitisch motiviert umgebracht werden?
10. Wie entwickelt sich die Bevölkerungszahl?
11. Jemand hat fünf mal nacheinander eine zwei gewürfelt. Wie wahrscheinlich ist es, daß auch der sechste Wurf eine zwei ergibt?
12. Wie hoch ist das Erkrankungsrisiko für tbc, wenn man schon röntgenpositiv ist [Bayes]?
13. Wie sehr wachsen die Arbeitslosen?
14. Wie hoch ist das Risiko an AIDS zu erkranken? Wie hoch ist das Wachstum von an AIDS-Erkankten?
15. Wie wahrscheinlich ist es, daß die Therapie T erfolgreich wird?
16. Wie wahrscheinlich ist es, daß Fritz seine Schuhe aufräumt, wenn er nach Hause kommt, wenn seine bisherige Aufräumungszahl a und seine Nichtaufräumungszahl u ist (alle=n=a+u)?
17. Wie oft verschlafen Menschen Prüfungstermine?
18. Wie sicher sind Atomkraftwerke?
19. Wie kann man verstehen, daß die Arbeitslosenstatistik fällt, obwohl immer weniger Menschen Arbeit haben?
20. Wie wahrscheinlich ist es, daß man im Skat vier Buben auf eine Hand bekommt?
21. Weshalb nimmt die [Arztdichte] ständig zu?
22. Wie sicher sind die Renten?
_
Wie man sieht ist das statistische Feld weit und wir tun gut daran, eine Grundordnung entlang am Thema Beweis und beweisen in der Statistik zu entwickeln.

1. Wichtige Grundbegriffe und Größen (Parameter) zur Charakterisierung zufälliger oder vom Zufall beeinflußter Prozesse (z.B. Merkmal, Klassenbildung, relative Häufigkeit, Verteilung).
2. Wahrscheinlichkeiten von Ereignissen: Wie wahrscheinlich ist ein Ereignis, Merkmal oder Geschehen? Nach Pearson und Neyman wird Wahrscheinlichkeit hier als Grenzwert relativer Häufigkeiten gedeutet.
3. Wahrscheinlichkeiten von Hypothesen ([Bayes; Entscheidungstheorie, Justiz]): Wie wahrscheinlich sind die Hypothesen H₀, H₁, H₂, ... ?
4. Welche Repräsentationsverfahren gibt es? Wie stellt man fest, ob und wie das Repräsentationsverfahren (z.B. Zufallsauswahl) gültig ist? Wie repräsentativ ist eine Stichprobe für die betreffende Population?
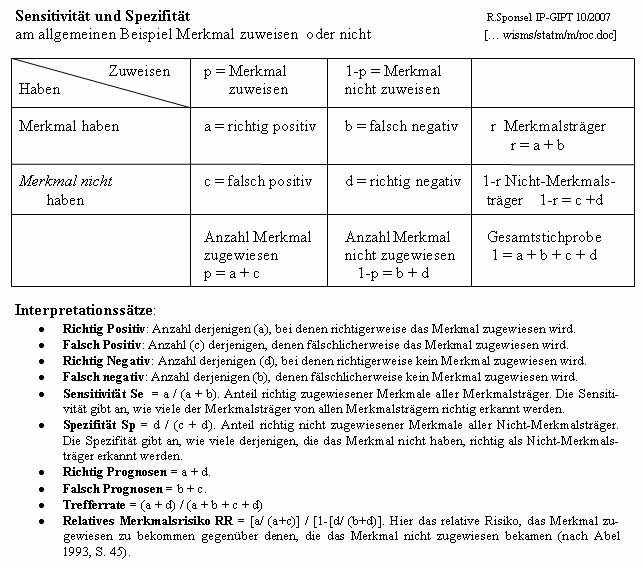
5. Wahrscheinlichkeiten von Fehlern: Wie genau gilt eine statistische Aussage? Im statistischen Grundmodell gibt es immer drei Fehler- von den [vier Grundmöglichkeiten]: richtig positiv, falsch positiv, richtig negativ, falsch negativ.
6. Wahrscheinlichkeiten von Gültigkeiten: wie sicher gelten unter welchen Bedingungen für wie lange statistische Aussagen? Welche Bedingungen und Voraussetzungen sind für die Gültigkeit einer statistischen Aussage wichtig? [Grundannahme-Paradoxie: Konstanz des Zufalls?]
7. [Entscheidungs- und Risikomodelle]. Man entscheidet immer, ob man will oder nicht, weil auch Nichtstun oder warten als eine Entscheidung anzusehen ist. Auch das kann falsch und folgenreich sein. Bei statistischen Entscheidungen sollten deshalb die wichtigsten Sachverhalte und ihre jeweiligen Folgen berücksichtigt werden.
8. Deskriptive Statistik und Einzelfallbewertung. Beispiel: Speckgürtel-Hypothesen-Untersuchung am Einzelfallbeispiel Mittelfranken 2009.
9. Interpretation, empirische und praktische Bedeutung der statistischen Kennwerte. Methoden und Prüfverfahren. Dieses Feld ist das am meisten und sträflich vernachlässigte Feld.


Genauere Operationalisierungen (Auswahl):

Klassenbildung nach Merkmalen
Statistiken werden meist über Gruppen gemacht. Eine Gruppe wird nach einem oder mehreren Merkmalen (z.B. Alter, Geschlecht, Bildung, ...) gebildet. Man erhält eine Gruppe also über Abstraktion durch Merkmalsklassifikation.

Grundgesamtheiten
Die betrachtete statistische Grundgesamtheit (Masse, Kollektiv) nennt man auch Population. Populationen können potentiell unendlich (alle Menschen, Münzwürfe) oder endlich (alle Magenkrebskranken der Uniklinik U im Zeitraum t) und mehr oder minder genauer bestimmt oder allgemein sein. Es ist meist sehr wichtig, sich genau darüber klar zu werden, über welche Population Aussagen getroffen werden sollen.

Häufigkeiten
Wie oft (h) ereignet sich E (z.B. Vulkanausbrüche, Stürme, Hitze-/ Trockenperioden/ HIV, Magenkrebs, arbeitslos, Sterbealter usw.) in einem Zeitraum t und in der soziokulturellen Umgebung u:  h(E | t, u)?
" | t, u" bedeute unter den Bedingungen t und u. Die Beweismethode ist die Zählung. Nachdem das Zählen sehr aufwendig in Mühe, Zeit und Kosten werden kann, ergibt sich sofort die nächste Beweisfrage:

Stichproben
Welche Stichprobe ist wie aussagekräftig für eine Schätzung h_s(E | t, u) für He | t, u) in der Population? Darin steckt auch: Welche repräsentativen Stichprobenziehungen gibt es?

Verteilungen
Je nach der Anzahl und Ausprägung der in eine Verteilung eingehenden Größen ergeben sich unterschiedliche Verteilungsdarstellungen und daher unterschiedliche Modelle für Verteilungen. Modell d-t-a(m) für t Meßzeitpunkte und a Ausprägungsgrade, z.B. 1=wenig, 2=mittel, 3=viel eines Merkmals m. Würde z.B. einmal in der Woche gemessen, wie viel es geregnet (m) hat, so ergäben sich für ein Jahr Vv=3^52 theoretische Verteilungsmöglichkeiten.

Charakteristische Größen (Parameter)
Im obigen Beispiel wären charakteristische Parameter z.B. die Anzahl der 1, 2 und 3 und der Perioden, wenn eine Periode z.B. aus einer gleichen Anzahl besteht. Führte man einen solchen Versuch über mehrere Jahre durch, könnte man feststellen, ob es - bezüglich zu nennender Kriterien - Veränderungen gibt, vielleicht oder auch nicht.

Fehlerschätzungen
Es gilt als fundamentaler Erfahrungssatz, dass alle empirischen Feststellungen mit Fehlern behaftet sind, die sich aus vielerlei Quellen zusammensetzen, ausgleichen, mindern oder verstärken (potenzieren) können. Zu einer guten empirischen Theorie und Beobachtung, gehört daher auch die Einbeziehung von Fehlern.

Zur Genauigkeit der amtlichen Daten zum Wirtschaftswachstum
Pressemitteilung des Statistischen Bundesamtes Nr. 307 vom 3. August 2007
"WIESBADEN - Wie genau sind die Daten der deutschen amtlichen Statistik, speziell die der Volkswirtschaftlichen Gesamtrechnungen (VGR) zum Wirtschaftswachstum? Eine Frage, die immer wieder von Wirtschaftsforschern, Analysten und Journalisten gestellt wird.
    Berechnungen zeigen: Die laufenden Revisionen des Bruttoinlandsprodukts (BIP) liegen in einem der hohen Aktualität angemessenen und vertretbaren Rahmen. Im internationalen Vergleich gehören die vierteljährlichen deutschen BIP-Berechnungen sogar zu den besten: Nach einer Untersuchung der OECD sind die frühen Quartals-BIP-Schätzungen der Statistikämter aus Deutschland, Frankreich und Großbritannien die zuverlässigsten und genauesten, dicht gefolgt von denen für die USA, Kanada und die Niederlande.
    Dies ist umso bemerkenswerter, da Deutschland mit seiner Schnellmeldung zum vierteljährlichen Bruttoinlandsprodukt (BIP) nach nur 45 Tagen auch in punkto Aktualität zu den Spitzenreitern in Europa zählt. Seit dem Jahr 2000 hat sich die erste Veröffentlichung des BIP, unter anderem auf Drängen der Finanzwelt und des Bedarfs der EZB nach aktuelleren Daten für die Eurozone, von 65 auf nur noch 45 Tage nach Abschluss des Berichtsquartals beschleunigt.
    Mit der Veröffentlichung der von den Nutzern geforderten hochaktuellen Konjunkturdaten befindet sich die amtliche Statistik immer im Spannungsfeld zwischen Aktualität und Genauigkeit. Um möglichst frühzeitig aktuelle Zahlen veröffentlichen zu können, werden die
Ergebnisse auf unvollständiger Datengrundlage berechnet und zum Teil geschätzt. Diese vorläufigen Ergebnisse werden kontinuierlich
aktualisiert, wenn neue statistische Ausgangsdaten verfügbar sind. Darauf wird in einem eigenen Qualitätsbericht ausdrücklich hingewiesen."

Aussagen und Extrapolationen


---


Repräsentativität, Transparenz und Kontinuität statistischer Zeitreihen.
Zeitreihen sind von großer Bedeutung für die Planung, Analyse, Prognose und Beeinflussung von sozio-ökonomischen Prozessen, z.B. die Erfassung der Verschuldung von Gebietskörperschaften. Voraussetzung für die angemessene Verarbeitung, Bewertung (Evaluation) der Schuldenentwicklung ist, dass die Definition der Schulden in der Zeitreihe gleich oder wenigstens vergleichbar bleibt. Falls unterschiedliche Schuldenwerte erfasst und mitgeteilt werden, ist es zwingend erforderlich, dass die Repräsentativität, Transparenz und Kontinuität der Daten gewährleistet wird. Dies ist in Deutschland seit 1995 nicht mehr der Fall, wobei sich natürlich die Frage stellt, warum die statistischen Ämter nicht für Repräsentativität, Transparenz und Kontinuität sorgen können oder wollen? Nun, es fällt auf, dass die zunehmende Intransparenz und fragliche Repräsentativität der mitgeteilten Schuldendaten durch die statistischen Landesämter einhergeht mit einer aus dem Ruder laufenden exponentiellen, zunehmend bedrohlich erscheinenden Schuldenentwicklung auf allen Ebenen der Gebietskörperschaften, besonders auch der größeren Gemeinden (Städte und Großstädte). In Bayern beispielsweise führte das zu unklaren und unzulänglichen Veröffentlichungen [71327-001r]. Dort verwendet man z.B. Spiegelstriche " - " sowohl für "0" als auch für keine Angabe oder unbekannt ("Missing Data"); weder Definition - auch nicht deren Rechtsgrundlage - noch Repräsentativität und Kontinuität werden ausgewiesen, so dass man hier die Frage stellen muss, ob dieses verwirrende Desinformation politisch gewollt ist? [L1; L2].

Tradition mehrdeutiger und daher unsinniger Auszeichnungen in der bayerischen Statistik
Anmerkung: Der Unsinn der Vieldeutigkeit von Zeichen könnte - auf jeden Fall in der bayerischen - Statistik sogar Tradition haben. So wird z.B. im Statistischen Jahrbuch der Stadt Nürnberg von 1930 unten beim Inhaltsverzeichnis ausgeführt:



Ein solches Vorgehen ist wissenschaftlich und praktisch vollkommen abzulehnen. "Nicht vorhanden"  ist etwas ganz anders als die Zahl 0 und gehört infolgedessen auch mit einem eigenen Zeichen versehen, und zwar zwingend eineindeutig und nicht "verodert" (wie z.B. in der Zeugenbefragung geboten). Die Zahl 0 ist natürlich kein fehlendes Datum, insbesondere nicht bei den Schulden, und gehört selbstverständlich zwingend als 0 ausgewiesen, wenn der Schuldenstand eben Null ist (das war in Bayern erfreulicherweise im Jahre 2004 bei 76 Gemeinden der Fall). Folgende Fallunterscheidungen könnten hierbei sinnvoll sein:

Missing Data (MD) Unterscheidungen
• MD1: Zahl liegt grundsätzlich vor, ist aber noch nicht eingetroffen; mit ihr zu rechnen ist bis TT.MM.JJJJ.
• MD2: Zahl liegt hier nicht vor, kann aber wahrscheinlich bei ... erkundet werden.
• MD3: Zahl liegt nicht vor und ist auch nicht beschaffbar.
• MD3a: Schätzmethoden sind derzeit nicht bekannt....
• MD3b: Als Schätzmethode eignet sich ...


Beispiel MD3b: Schätzung des Gesamtschuldenstandes Nürnbergs am 31.3.1929 in Reichsmark
Im folgenden wird dargelegt, wie man den Gesamtschuldenstand - aus Mark ("Papiermark") und Reichsmark - für 1928/29 schätzen kann, wenn die einzubeziehenden Geldgrößen klar ausgewiesen oder Umrechnungsformeln angegeben würden. Zunächst der Sachverhalt, wie ihn das Statistische Jahrbuch der Stadt Nürnberg 1930 ausweist:



Man sieht hier zwei Werte in der Rubrik "Schuldenstand am Schlusse des Jahres", einmal in "M" ("Papiermark") und der andere in "RM" (Reichsmark), ohne dass erklärt würde, wie nun der Gesamtschuldenstand zu bilden ist. Das ist wenig verständlich, wenn man sich vergegenwärtigt, dass es sich um das Jahrbuch von 1930 handelt, also 6 Jahre nach der Hyperinflation und die tatsächlichen Verrechnungsdaten ja auf jeden Fall in der Kämmerei vorliegen müssen.

Für das Haushaltsjahr 1928/29 wird im Verwaltungsbericht der Stadt Nürnberg, bearbeitet im Statistischen Amt und herausgegeben vom Stadtrat 1929, S. 434 ausgeführt:



Nach diesen Mitteilungen, sollten sich Schätzungen und Umrechnungen durchführen lassen - wenn man wüsste, wie sich die einzelnen Finanzgrößen (Rückkauf 339949 RM; Umtausch mit Auslosungsrechten mit 16916156 RM und Umtausch ohne Auslösungsrechte mit 104375 RM) zu einander verhalten. Das wird aber leider nicht mitgeteilt, so dass der Gesamtschuldenstand natürlich davon abhängt, welche Größen in die Umrechnung "Papiermark" und Reichsmark eingehen. Man kann also rätseln, welcher drei hier möglich erscheinenden Gesamtschuldenstände der richtige ist:
    (1) Spielten die Umtauschgrößen keine Rolle. ergäbe sich für die Gesamtschuld am 31.3.1929 folgender Schätzungsansatz: 140092500 / 336949 = 415.7676681, also ein Verhältnis von 1 Reichsmark zu gerundet 416 Mark ("Papiermark").
    (2) Rechnet man die Umtauschgrößen mit ein, ergibt sich folgende Umrechnung: 140092500 / (336949 + 16916156 + 104375)  =  140092500 / (17357480) = 8.071016069, also ein Verhältnis von 1 Reichsmark zu gerundet 8 Mark ("Papiermark").
    (3) Es zählt nur die Gesamtschuld in Reichsmark, weil die Ablösen schon in die Summe eingerechnet wurden.
Dies ergibt die möglichen Gesamtschuldenbeträge:
Rechnung (1), die 140 Mill. Papiermark sind 336949 RM wert, ergäbe 88,676999 Millionen RM Gesamtschuld.
Rechnung (2), die 140 Mill. Papiermark sind 17,357480 Mill. Reichsmark wert, ergäbe 105,697530 Millionen RM Gesamtschuld.
Rechnung (3), es zählt nur der mitgeteilte Schuldenstand in Reichsmark, es bliebe wie mitgeteilt, 88,340050 Millionen RM Gesamtschuld.

Veränderungen der Erhebung statistischer Kenngrößen 1973 und 1978 am Beispiel Verschuldung der Gemeinden
Den folgenden Ausführungen aus "Statistisches Jahrbuch Deutscher Gemeinden", 66. Jahrgang, 1979, S. 438 kann man entnehmen, dass die Erfassungsmerkmale der Schulden "eine Anknüpfung an die Berichterstattung bis einschließlich 1973 (61. Jahrgang) nicht mehr zu" lassen. "Im Unterschied zu 1977 sind die Krankenhäuser nicht mehr in den Gesamtschuldenstandsbeträgen enthalten. Sie werden wie die Eigenbetriebe nachrichtlich aufgeführt."



Was "beweist" nun dieser wenig erfreuliche Sachverhalt ?
Nun, anscheinend ist die deutsche Statistik nicht in der Lage oder motiviert, Sinn und Notwendigkeit vergleichbarer wichtiger sozioökonomischer Daten, wie z.B. die Verschuldung einer Gemeinde, so zu begreifen, dass sie die Kontinuität der Daten auch tatsächlich sicher stellen würden. Das mag auch politisch gewollt sein, um Zusammenhänge zu verschleiern und Transparenz und Kontinuität zu behindern.
_


---


Probleme

Grundannahme-Paradoxie: Konstanz des Zufalls ?
Hier gibt es zwei Aspekte: 1) daß es so etwas wie Zufallsgesetze überhaupt gibt; 2) inwiefern diese über die Zeit und Bedingungen hinweg gelten ("sollen").
    In der schließenden und sog. Inferenzstatistik möchten wir nicht nur Aussagen für den Augenblick treffen, sondern auch über statistische Regelhaftighaften von Dauer etwas erfahren, wobei unklar ist, ob oder inwieweit "Zufall", Dauer und Konstanz einander nicht ausschließen. Wie wollen wir Regelhaftigkeiten von Dauer erkennen, wenn schon das einzelne Ereignis sehr unsicher ist und eine große statistische Ereignis-Bandbreite hat?

Mathematik und Statistik
Das Wesen mathematischer Statistik besteht auf der Basis einen strengen Theoriegebäudes vielfach darin, die Wahrscheinlichkeit für ein Modell M1 gegenüber einem Vergleichs- oder Kriteriums-Modell M2 oder für Annahmen A1 gegenüber anderen Annahmen A2 zu bestimmen. Das ist einerseits sinnvoll und ergiebig, etwa bei der Frage, ob ein empirischer Datensatz als normalverteilt angesehen werden darf oder nicht, andererseits sehr merkwürdig, wenn die Empirie aus einem Vergleich herausfliegt und nur noch zwei theoretische Modelle oder hypothetische Annahmen [verglichen] werden: Beispiel: der unselige [Signifikanztest], der ja, kurz und bündig formuliert, nur eine statistische Aussage unter der Annahme zuläßt, daß die Nullhypothese richtig ist. Wir testen mit dem Signifikanztest also ein virtuelles Ergebnis.
 

Denn die gewöhnliche EmpirikerIn wird meist nicht wissen wollen, was ist, wenn die Nullhypothese richtig wäre?, sondern: ist sie anzunehmen oder nicht? Welche Hypothese ist vorzuziehen, falls eine Entscheidung möglich ist ?

Eine EmpirikerIn interessiert sich also meist nicht dafür, ob ein Ergebnis angenommen oder verworfen werden darf, wenn die Nullhypothese richtig ist, sondern ob sie sie annehmen oder verwerfen soll. Die Gretchenfrage der empirischen Statistik lautet: Welche Hypothese ist anzunehmen, die Null- oder die Alternativhypothese. Weiß man nichts, können im Falle zweiwertiger Logik, beide Hypothesen richtig oder falsch sein, so daß vier Fälle zu unterscheiden wären. Das aber macht der Signifikanztest gerade nicht. Signifikanztesten scheint also ein gigantisches Schautheater und numerologisches Zahlenspiel zu sein, das nicht nur kaum einen Erkenntniswert hat, sondern vor allem Verwirrung stiftet. Dafür ist die mathematische Statistik anscheinend bestens gerüstet. Wissenschaft? Oder Wirrenschaft?
 

Die großen Probleme in der Wahrscheinlichkeitsrechnung und Statistik liegen weniger in der Theorie als in der Anwendung. Es scheint so, als hätte die mathematische Statistik sich wenig um die sozialwissenschaftlichen Gegebenheiten gekümmert. Die meisten AnwenderInnen können die mathematische Statistik nicht richtig verstehen und die meisten mathematischen StatistikerInnen sind nicht in der Lage, ihre Theorien praktisch sinnvoll zu vermitteln. Theorie und Praxis driften extrem auseinander. Über weite Strecken entsteht der Eindruck, als ob nur theoretische Modell-1/ Annahme-1 gegen theoretisches Modell-2/ Annahme-2 getestet würde, wodurch wir aber nichts über die Wirklichkeit erfahren und wie wir zwischen Hypothesen entscheiden sollten.

---

Statistische Paradoxien und Dilemmas nach Stegmüller

Im großen wissenschaftstheoretischen Werk Stegmüllers finden sich mehrere Kapitel oder Abschnitte, die Wahrscheinlichkeit und Statistik

Stegmüller (1973, Teil E), nennt Elf Paradoxien und Dilemmas im Inhaltsverzeichnis:
 

1. (1) Die Paradoxie der Erklärung des Unwahrscheinlichen (S. 281-285), z.B. 7 mal nacheinander eine 6 zu würfeln.
2. (2) Das Paradoxon der irrelevanten Gesetzesspezialisierung (S. 285-286), z.B. das Problem von Scheinerklärungen zufälliger Koinzidenzen, die falsch interpretiert werden (der Mond erscheint nach einer Finsternis wieder aufgrund des großen Spektakels, das man veranstaltete).
3. (3)  Das Informationsdilemma. (S. 286-287), fehlende oder widersprüchliche Information mit unterschiedlichen Wahrscheinlichkeiten je nachdem, welche Merkmalskombination zugrunde gelegt wird [Partielle Korrelation]
4. (4) Das Erklärungs-Bestätigungs-Dilemma  (S. 287-289),
5. (5) Das Paradoxon der reinen ex post facto Kausalerklärung (S. 289-291), Bestätigung und Erklärungen scheinen zirkulär und austauschbar verwendet werden können.
6. (6) Das Verzahnungsparadoxon. (S. 291-295)
7. (7) Das Erklärungs-Begründungs-Dilemma. (S. 295-298)
8. (8) Das Dilemma der nomologischen Implikation (S. 298-299)
9. (9) Das Weltanschauungsdilemma (S. 299-301)
10. (10) Das Argumentationsdilemma (S. 301-303)
11. (11) Das Gesetzesparadoxon. (S. 303) [analog Goodman-Paradoxon]




---


Die Paradoxie des statistischen Syllogismus (nach Stegmüller)



Ein schönes Beispiel und ein Fall für eine Plausibilitätsanalyse. Hier liegen zwei ganz unterschiedliche Populationen vor: In (9) die Population der Schweden und die Teilpopulationen der römisch-katholoischen Schweden und damit auch der nicht römisch-katholoischen Schweden; in (10) die Population der Lourdes Pilger und die Teilpopulation der Lourdespilger, die nicht römisch-katholischen Lourdespilger. Für eine genauere statistische Analyse wären wahrscheinlich die tatsächlichen Häufigkeitswerte interessant. Der Focus berichtet in (7) 2008 von ca. 6 Millionen jährlich. Nehmen wir an, davon sind 30.000 Schweden. Damit wären in einem Jahr (30.000/6.000.000)*100 =  0.50% Schweden dabei. Bei einem Anteil von 25% Männern bei den Besuchern wäre es dann noch 0.125%, ein Viertel von 0.50%, womit die Wahrscheinlichkeit für Petersen Lourdes Besuch bestimmt. Wenn weniger als 2% der Schweden römisch-katholisch sind

Können die beiden statistischen Schlussfolgerungen gewichtet werden?
 

---


Simpson's Paradox
Simpson fand bei bedingten Wahrscheinlichkeiten in Vierfeldertafeln einen Widerspruch dergestalt, dass bedingte Wahrscheinlichkeitsaussagen je nachdem, ob eine Gesamtbetrachtung gegenüber einer - vollständigen und disjunkten - Aufspaltung erfolgt, zu widerspruchsvollen Aussagen führen können. Solche Phänomene darf man nicht einfach nur als "Paradoxon" euphemistisch herunterspielen, sondern hier liegen tiefe und ernste Probleme in der Mathematik der Verhältnisrelationen vor, die weite Teile der angewandten Statistik-Interpretation grundsätzlich in Frage stellen, weil je nach Auswahl nicht nur unterschiedliche, sondern sogar widersprüchliche Aussagen resultieren können, wobei meist verdeckte Abhängigkeiten eine Rolle spielen, wie Székely (1990, S. 63f) ausführte, die bei der Rechnung und Interpretation nicht angemessen berücksichtigt und dargestellt werden. Das grundlegende Problem wurde von  Hain & Sponsel (1994)  mit dem Begriff der Relationentreue  benannt, womit sich auch das Simpson'sche Paradoxon gut charakterisieren lässt, weil hier gerade eine Verletzung der Relationentreue vorliegt: Die Verhältnisrelationen von Teilen eines Ganzen sind bezüglich des Ganzen nicht relationstreu, sondern können sich sogar umkehren. Bei genauer Betrachtung stellt sich allerdings die Frage, ob in der Darstellung der sechs-Felder Tafel nicht schon im Ansatz der Fehler steckt, wenn unterschiedliche - nicht voneinander unabhängige - Teile und Ganze zu einander in Beziehung gesetzt werden, weshalb dann natürlich eine Verletzung der Relationentreue auch nicht wirklich überraschen kann. Die zahlreichen Widersprüche, Paradoxien, Absurditäten und Unverständlichkeiten in der Statistik (> Beck-Bornholdt, Székely) zeigen, dass eine gründliche Analyse, Umsicht und Skepsis gute Helfer sein können, um den zahlreichen Fallstricken und Tücken zu entgehen.



Literatur und Links zu Simpson's Paradox (Auswahl): Linksammlungen: 1, 2, 3,

• Beck-Bornholdt, Hans Peter & Dubben, Hans-Hermann (1997). Der Hund, der Eier legt. Erkennen von Fehlinformationen durch Querdenken. Reinbek: Rowohlt.
• Beck-Bornholdt, Hans Peter (2005). Mit an Wahrscheinlichkeit grenzender Sicherheit : logisches Denken und Zufall. Reinbek: Rowohlt.
• Bishop, Y. M. M.; Fienberg, S. E. & Holland, P. W. (1975). Discrete Multivariate Analysis. Cambridge, Mass.: MIT Press.
• Blyth, Colin R. (1972). On Simpson's Paradox and the Sure-Thing Principle. In: Journal of the American Statistical Association. 67, Nr. 338, 1972, p. 364–366.
• Dawid, A. P. (1979). Conditional Independence in Statistical Theory Journal of the Royal Statistical Society A41(1):1-31
• Fleiss, Joseph L. (2003). Statistical methods for rates and proportions. Hoboken, NJ: Wiley.
• Grams, Timm (Denkfallen und Paradoxa): Simpson's Paradoxon.
• Pearl, Judea  (1999). Simpsons's Paradox: An Anatomy. University of California, 1999, p. 1–11. [PDF]
• Pearson K, Lee A, Bramley-Moore L. (1899). Mathematical contributions to the theory of evolution: VI – Genetic (reproductive) selection: Inheritance of fertility in man, and of fecundity in thoroughbred racehorses. Philos Trans R Soc Lond A. 1899;192: 257–330.
• Simpson, E. H.  (1951). The Interpretation of Interaction in Contingency Tables. In: Journal of the Royal Statistical Society. Series B (Methodological) 13 (1951), Nr. 2, p. 238–241.
• Stanford Encyclopedia of Philosophy:  Simpson's Paradoxon (2004).
• Stevens, S. S. (1946). On the Theory of Scales of Measurement. Science Vol. 103, No. 2684, 677-680.
• Tu, Yu-Kang ; Gunnell, David  &  Gilthorpe, Mark S. (2008). Simpson's Paradox, Lord's Paradox, and Suppression Effects are the same phenomenon – the reversal paradox. Emerg Themes Epidemiol. 2008; 5: 2. [Online]
• Wagner, C. H. (1982). Simpson's Paradox in Real Life. In: The American Statistician, 36 (1982), Nr. 1, p. 46–48.
• Wikipedia: W.de, W.en. [Die Literaturangabe zu Pearson (1899) in W.de und W.en 16.4.9 ist falsch und unzulänglich]
• Yule, G. U. (1903). Notes on the theory of association of attribution in statistics. Biometrika, 2, 121-134.




---

Die Korrelations-Paradoxien

Was bedeutet ein korrelativer Zusammenhang?
Was eine Korrelation bedeutet, weiß man nicht genau ['Schein'korrelation], es ist ein rein statistisch-artifizielles ('künstliches') Zusammenhangsmaß, das von Erhebung zu Erhebung, und sogar innerhalb einer einzigen Erhebung von Merkmalsraum zu Merkmalsraum sowohl ganz unterschiedliche Zahlenwerte als auch Bedeutungen annehmen kann. Empirisch gilt meist der Satz: je nachdem welche Variablen in die Berechnung einbezogen oder nicht einbezogen werden, ändern sich die Korrelationskoeffizienten, und zwar möglicherweise sehr erheblich. Beweis: [Partielle Korrelationen].

---


Fehler
Stelzl, Ingeborg (1982). Fehler und Fallen der Statistik. Für Psychologen, Pädagogen und Sozialwissenschaftler. Bern: Huber.

Ungenaue Angaben und Beschreibungen (Voraussetzungen, Hypothesen, Methoden, Ergebnisse, Geltungsbereiche, Aussagekraft/Bedeutung, Verständlichkeit, Nachvollziehbarkeit, ...).

Übertragung von Gruppenkennwerten auf die Individuen der Gruppe.
Alexandra Hake hat diesem Fehlschluss zwei Bände gewidmet.
 

---


Grundlagen der Interpretation statistischer Daten und Modelle
Fragen: durch die verschiedenen "Paradoxa" (Simpson, Grundannahme: Konstanz des Zufalls, Stegmüller, Korrelation) stellt sich die Frage der Bedeutung statistischer Daten verschärft. Viele Paradoxien und Widersprüche verlören an Schärfe oder lösten sich auf, wenn man folgendes Hauptprinzip anerkennt und streng beachtet:

Hauptprinzip statistischer Interpretation
 

Werden bei einem statistischen Sachverhalt neue Information hinzugenommen oder vorhandene vernachlässigt, können sich die statistischen Sachverhalte verändern und ihre Relationentreue verlieren. Diese Grundidee wird auch benutzt für die Interpretation der statistischen Un/Abhängigkeit: Spielt ein statistischer Sachverhalt B für einen statistischen Sachverhalt A keine Rolle, verändert sich mit anderen Worten die Wahrscheinlichkeit für ein Ereignis A nicht, wenn man B mit hinzu nimmt, so spricht man im Hinblick von A und B von unabhängigen Ereignissen.  Diese Überlegung kann man auch für die Definition statistischer Relevanz heranziehen. Eine Sachverhalt B ist für einen Sachverhalt A relevant in dem Maße, wie er A beeinflusst, d.h. durch seine An-, Abwesenheit oder so-oder-so-Beschaffenheit (Ausprägung) zu verändern in der Lage ist.  Aus unterschiedlichen Voraussetzungen oder Basen, können sich unterschiedliche Folgerungen oder Wirkungen ergeben. So erscheint z.B. die Erwartung, dass sich relative Häufigkeiten additiv wie die zugrunde liegenden absoluten Zahlen verhalten irrational, wenn die Bezugsgrößen nicht gleich sind, was folgende Vierfeldertafel illustriert:        A   a  A+a  Rel% für a bezügl. Z  Rel% A bezügl. Z3  Rel% a bezügl. A+a  Z1  10   4  14   4/10 = 0.40           10/30= 1/3        4/14 = 2/7  = 0.286   Z2  20   5  25   5/20 = 0.25           20/30= 2/3        5/25 = 1/5  = 0.200  Z3  30   9  39   9/30 = 0.33           30/30= 1.00       9/39 = 3/13 = 0.231

---


Manipulation, tricksen, frisieren, täuschen, verdrehen, lügen, ausblenden, weglassen.
> Repräsentativität, Transparenz und Kontinuität statistischer Zeitreihen.

Ursula von der Leyen, die Bundesagentur und die verdreht-falsche Kinder Hartz-IV Statistik [> Politiker]
DER SPIEGEL berichtet in Nr.5, 2012, S. 14 [Online]: "15,1 Prozent aller Kinder unter 15 Jahren in Deutschland leben von Hartz IV. Das sind nur 1,5 Prozentpunkte weniger als noch vor fünf Jahren. Damals wie heute lebt etwa jedes sechste Kind am Rande des Existenzminimums. Vergangene Woche jedoch freute sich Bundes-arbeitsministerin Ursula von der Leyen (CDU) über Zahlen der Bundesagentur für Arbeit, nach denen im Jahr 2011 rund 257000 Kinder weniger von Sozialleistungen lebten als noch 2006 - ein Rückgang um 13,5 Prozent. Von der Leyen sprach triumphierend von „sinkender Kinderarmut" und der „Ernte dessen, was wir in den letzten Jahren an Kraftanstrengungen unternommen haben". Die Statistik trügt allerdings, denn seit 2006 ist auch die Gesamtzahl der unter 15-Jährigen um 750000 gesunken. Wenn es insgesamt weniger Kinder gibt, ist es kein Wunder, dass in absoluten Zahlen auch weniger Kinder auf Hartz IV angewiesen sind. Der Rückgang ist in großen Teilen ein demografischer Effekt."
    Die Bundesagentur ist offenbar daran interessiert, bewusst unzulänglich bis falsche Zahlen mitzuteilen, um einen Erfolg zu suggerieren, der sich bei genauer Analyse so gar nicht ergibt. Wie viel tückische Absicht dahintersteckt, mag man daran ermessen, wie einfach es doch gewesen wäre, die vier Zahlen - Anzahl Jugendliche unter 15 im Jahre 2006 und 2011, Anzahl Jugendliche, die Hartz IV 2006 und 2011 bekamen, mitzuteilen. Diese Datenmanipulationspraxis knüpft offenbar nahtlos an die - von Erwin Bixler aufgedeckte - Fälschungstradition der Bundesanstalt für Arbeit an. Euphemistisches Stroh dreschen durch tricksen, verdrehen und frisieren von Daten scheint inzwischen auch eine besondere Spezialität der Arbeitsministerin Ursula von der Leyen zu sein.

Weitere Quellen:
SZ: http://www.news4teachers.de/2012/01/kinderarmut-geht-zuruck-aber/
Spiegel: http://www.spiegel.de/wirtschaft/soziales/0,1518,811455,00.html
Reuters: http://de.reuters.com/article/worldNews/idDEBEE80P07W20120126
destatis [404]: Bevölkerung nach Altersgruppen seit 1950. (Klassen: unter 20, 20 - 40; 40 - 60; 60 - 80; 80 und mehr)
bpb: http://www.bpb.de/wissen/X39RH6,0,0,Bev%F6lkerung_nach_Altersgruppen_und_Geschlecht.html
bpb: http://www.bpb.de/wissen/RCQ36N,0,Familienhaushalte_nach_Zahl_der_Kinder.html

Ich wollte die Sache aufklären und habe das Statistische Bundesamt, die Bundesagentur für Arbeit, das Familienministerium und das Bundesministerium für Arbeit und Soziales angeschrieben. Die Bundesagentur für Arbeit hat bis heute nicht geantwortet. Alle anderen haben schnell und informativ reagiert. Im folgenden die

Doku Kommunikation mit dem BMAS  [> Ergebnis]

(1) Von: kontaktformular@bmas.de [mailto:kontaktformular@bmas.de] Gesendet: Montag, 6. Februar 2012 21:17. An: info@bmas.bund.de.
Cc: Rudolf-Sponsel@sgipt.org Betreff: KAV Kontakt-Email.
Betreff: Anzahl Kinder unter 15 im Jahre 2006 und 2011
Nachricht: Sehr geehrte Damen und Herren,
ich suche die Zeitreihe der Anzahlen von Kindern unter jeweils x Jahren, im vorliegenden Fall die Zahlen von 2006 und 2011 für Kinder unter 15. Ich habe auf Ihrer Seite hierzu nichts gefunden. Vielen Dank für Ihre Bearbeitung.
Mit freundlichen Grüßen: Rudolf Sponsel (Psychologe)
https://www.sgipt.org/lit/toman/famstat.htm (ISSN 1430-6972)

(2) Auf diese Anfrage erhielt ich am 7.2. folgende Antwort:
Am 07.02.2012 08:23, schrieb info@bmas.bund.de:
Sehr geehrter Herr Sponsel,
vielen Dank für Ihre E-Mail.
Das Bundesministerium für Arbeit und Soziales ist nicht der richtige Ansprechpartner für Ihr Anliegen.
Wir schlagen Ihnen vor, sich an das Statistische Bundesamt zu wenden.

(3) Ich schrieb daraufhin am 7.2. zurück:
Hallo Kommunikationscenter, vielen Dank für Ihre Anregung. Ich hatte schon vorher beim Statistischen Bundesamt angefragt. Die haben aber nur die Zahlen bis 2010. Da die Bundesarbeitsministerin die Zahlen aber bei einer Pressekonferenz* verwendet hat, muss sie ja wohl über die Zahlen verfügen. Also sollte Ihr Haus diese Zahlen auch haben. Daher möchte ich Sie noch einmal eindringlich bitten, sich der Sache anzunehmen. Ich habe die Zahlen* von einem Mathematiker mehrfach nachrechnen lassen immer mit dem Ergebnis einer Inkonsistenz.
Mit freundlichen Grüßen: Rudolf Sponsel (Psychologe)
https://www.sgipt.org/lit/toman/famstat.htm (ISSN 1430-6972)
*DER SPIEGEL berichtet in Nr. 5, 2012, S. 14 [Online*]: "15,1 Prozent aller Kinder unter 15 Jahren in Deutschland leben von Hartz IV. Das sind nur 1,5 Prozentpunkte weniger als noch vor fünf Jahren. Damals wie heute lebt etwa jedes sechste Kind am Rande des Existenzminimums. Vergangene Woche jedoch freute sich Bundesarbeitsministerin Ursula von der Leyen (CDU) über Zahlen der Bundesagentur für Arbeit, nach denen im Jahr 2011 rund 257000 Kinder weniger von Sozialleistungen lebten als noch 2006 - ein Rückgang um 13,5 Prozent. Von der Leyen sprach triumphierend von „sinkender Kinderarmut" und der „Ernte dessen, was wir in den letzten Jahren an Kraftanstrengungen unternommen haben". Die Statistik trügt allerdings, denn seit 2006 ist auch die Gesamtzahl der unter 15-Jährigen um 750000 gesunken. Wenn es insgesamt weniger Kinder gibt, ist es kein Wunder, dass in absoluten Zahlen auch weniger Kinder auf Hartz IV angewiesen sind. Der Rückgang ist in großen Teilen ein demografischer Effekt."

(4) Am 8.2. erhielt ich die Mitteilung: Sehr geehrter Herr Sponsel, vielen Dank für Ihre E-Mail. Ihre Zuschrift wurde zur Bearbeitung und Beantwortung an ein Fachreferat weitergeleitet. Mit freundlichem Gruß

(5) Am 22.2. erhielt dann folgendes Schreiben (Name entfernt):



Ergebnis: Offenbar hält das Referat an der Aussage fest, dass es zwischen September 2006 und September 2011 einen Rückgang um 13.5% gab, ohne zu berücksichtigen, dass die Bezugspopulationsgröße der unter 15jährigen in der Größenordnung von ca. einer halben Million geschrumpft ist. Die Größen der Bezugspopulation im September 2006 und 2011 werden leider nicht mitgeteilt. Vergleicht man die mitgeteilten Hilfequoten von 2006 (16.5%) und von 2010 (15.9%) wird ersichtlich, dass bei dem angemessenen Vergleichsmaßstab der Quoten lediglich eine Verbesserung um 16.5 - 15.9 = 0.6% erreicht wurde.
 

Thatchers Arbeitslosenstatistik Tricks. Aus Claus Peter Ortlieb: Die Zahlen als Medium und Fetisch [PDF]
"Als Anfang des Jahres 2005 die Anzahl der Arbeitslosen in Deutschland die Marke von fünf Millionen überschritt, war die Aufregung groß, und die Stimmung verdüsterte sich. Der Kanzler nannte diese Zahl „bedrückend“, obwohl er doch wie alle wusste, dass sie nur einer neuen Zählweise geschuldet war. Offenbar war es hier die Zahl selbst und nicht die dahinter liegende gesellschaftliche Realität, die die öffentliche Wahrnehmung auf sich zog und ihrerseits beeinflusste. Die Bundesregierung hätte vielleicht besser daran getan, sich ein Beispiel an der früheren britischen
Regierung Thatcher zu nehmen, die in ihrer Regierungszeit die Arbeitslosigkeit dadurch bekämpfte, dass sie sie in dreizehn aufeinander folgenden gesetzlichen Vorschriften immer weiter herunter rechnete. Wenn nur die Zahlen sinken, ist alles in Ordnung. ..."

Reallohn-Entwicklung schaltet auf negativ, doch eine Verdummungskampagne hält dagegen. "Da meldet das Statistische Bundesamt heute vollmundig die angeblich frohe Botschaft, die deutschen Reallöhne seien im vergangenen Jahr um 1 % gestiegen. Und selbst die Seriosität vorspielende ZEIT titelt: "Reallöhne im Jahr 2011 gestiegen - Trotz hoher Inflationsrate konnten die Deutschen 2011 über mehr Geld verfügen. Experten erwarten für das Jahr 2012 einen weiteren Zuwachs der Reallöhne." Nichts kann mehr in die Irre führen. Denn erstens werden hier nur die Löhne vollzeitbeschäftigter Arbeitnehmer erfaßt, womit ein großer Teil des wuchernden Niedriglohnsektors mit Teilzeitarbeit und besonders negativer Lohnentwicklung unter den Tisch fällt. Der Anteil der ausschließlich geringfügig Beschäftigten liegt derzeit besonders hoch (Abb. 17072, 17712).  ... " [jj 7.2.12]

Internationale Ausbeutung und Verletzung elementarer Menschenrechte (gestützt von Ursula von der Leyen) [> Politiker]
Monitor beschäftigte sich in der Sendung vom 2.2.12 mit dem Thema "Ihre Armut, unsere Hemden. Wie die Bundesregierung die Billigmode verteidigt."  Hierbei ging es um die Mindeststandards, die Unternehmen kontrollierbar abverlangt werden sollten, etwa hinsichtlich Kinderarbeit oder Löhnen unter jedem Existenzminimum ohne jede soziale Absicherung. Dass selbst eine Verdoppelung der Löhne nur einen geringfügigen Mehrpreis des Endproduktes nach sich zöge, wurde an einem Beispiel aus Bangladesch verdeutlicht: "'Bei der Verdopplung der Löhne in Bangladesch würde sich der Einkaufspreis eines T-Shirts ungefähr um 15 bis 20 Cent erhöhen.', so Prof. Herbert Loock, Akademie für Mode und Design, Düsseldorf . Um dem kritischen und solidarischen Verbraucher Möglichkeiten bei der Auswahl zu geben, beabsichtigt nun die EU-Kommission "Eine Rechtsvorschrift über die Transparenz der sozialen und ökologischen Informationen“ zu erlassen. "Im Klartext: Unternehmen müssen ihre Produktions- und Lieferketten offenlegen. Dazu beabsichtigt die Kommission: Zitat: "zu überprüfen, ob Unternehmen den von ihnen eingegangenen Verpflichtungen nachgekommen sind." Doch ausgerechnet die Bundesregierung lehnt die EU-Initiative rigoros ab. Richard Howitt ist Berichterstatter des EU-Parlamentes für die soziale Verantwortung von Unternehmen. Wie bewertet er die Ablehnung der Deutschen? Richard Howitt, EU-Parlament Berichterstatter für soziale Standards (Übersetzung MONITOR): "Ich bin sehr enttäuscht über die deutsche Haltung. Kaum war die neue Strategie veröffentlicht, kam die Ablehnung. Vor allem gegen unsere zentralen Vorschläge zur Modernisierung und Veränderung der Standards unternehmerischer Verantwortung." Zuständig für die soziale Verantwortung von Unternehmen ist Arbeitsministerin Ursula von der Leyen. Wir fragen nach. Reporterin: "Warum blockieren Sie und Ihr Ministerium denn hier die EU-Strategie, die eben nicht nur auf Freiwilligkeit basieren soll?"
    Ursula von der Leyen: "Ich finde, dass es ganz wichtig ist, die soziale Verantwortung von Unternehmen zu diskutieren. Insofern sind wir im Augenblick mit der EU-Kommission in Diskussionen darüber, für welche Bereiche es Berichtspflichten geben soll oder auch nicht. Die Diskussion ist noch offen."
    Offen? In einem Schreiben an die EU Kommission, das MONITOR vorliegt, spricht sich die Bundesregierung ausdrücklich Zitat: "Gegen neue gesetzliche Berichtspflichten aus."  Und weiter unten heißt es unmissverständlich Zitat: "Das Prinzip der Freiwilligkeit muss gewahrt bleiben."
    Reporterin: "Aber in Ihrem Positionspapier haben Sie sich doch ganz stark gegen eine gesetzliche Berichtspflichten ausgesprochen?"
Ursula von der Leyen: "Wir sind mit der EU-Kommission genau darüber in Diskussion. Also ich sage Ihnen hier als Ministerin, dass ich offen bin für den Dialog."
    Die Recherche und Dokumentation von Monitor zeigt klar und unmissverständlich auf, dass Arbeitsministerin Ursula von der Leyen schriftliche und überprüfbare Tatsachen einfach wegleugnet. Das ist eine weitverbreitete und beliebte Methode in der Politik.
_


---


Glossar: Wahrscheinlichkeit und Statistik: Messen, Schätzen, Testen, Schliessen.  (Stichwortsammlung)
Querverweis: Elemente wissenschaftlicher und sachlicher Texte. Kleines Wissenschaftsvokabular und  -Glossar mit Signierungsvorschlägen.
__
Abduktion * Abhängigkeit * Abweichung * Additiv-verbundene Messung * Alpha-Fehler * Alternativhypothese(n) * Antinomie * ANOVA * A posteriori Wahrscheinlichkeit * a priori - a posterori - Ding an sich * A priori Wahrscheinlichkeit * AR *  ARCH *  ARIMA-Prozess * ARMA *  AUC * Ausgleichsrechnung * Ausschließen * Auswahl, Auswahlverfahren * Autokorrelation * Bayes Theorem * Bayesianer * Bedeutungsamkeitsproblem * Bedingungen * Bedingte Wahrscheinlichkeit * Bestimmtheitsmaß > Determinationskoeffizient. * Beta-Fehler * Binominalverteilung * Biplot*Conjoint measurement * cum hoc ergo propter hoc * cut off Werte * Darstellung statistischer Ergebnisse * Daten * Datentheorie * Datentyp * Datenverarbeitung *   Determinationskoeffizient * Deutung statistischer Werte  *  Diagnostik *  Diagnostische Fehlerarten * Dichte, Dichtefunktion * Differentialdiagnostik *  Diskret * Diskriminanzanalyse *  DNA-Test * Durchschnitt * Eindeutigkeitsproblem * Einschlusschance * Einzelfall * Entropie * Entscheidbarkeit *  Entscheidung  *  Entscheidungstheorie * Epidemiologie *  Ereignis *  Ereignisalgebra (Mengenlehre) * Ergodisch, Ergodizität, Ergodensätze  * Erhebungszeitraum *  erklären und verstehen * Erwartungswert *  Erwartungstreu(e Schätzung) *  Evaluation * Evidenz * Evidenz-basierte-Medizin  *  Exzess *  Faktorenanalyse *  f *  Falsch negativ *  Falsch positiv *  Fehler * Fehlerarten *  Fiduzialkonzept * Fourier-Analyse * GARCH * Größe * Gruppenkennwert * Gültigkeitszeitraum *  Häufigkeit *  Heteroskedastizität * Histogramm * Homoskedastizität  * Hypothese * Hypothesendiskussion * Hypothesenraum * Identifikationsanalyse *  Indifferenzprinzip * Inferenz, Inferenzstatistik * Integratives Testprinzip * Interpretation statischer Größen und Ergebnisse * Intra * Inter * Inzidenz  * Inzidenzenrate *  IQ *  Kappa * Kausalität * Kennwerte (Größen, Parameter) * Kohärenzprinzip * Kohorte *  Kolmogoroff-Axiome * Kollinearität * Konnektivität, Konnexität * Konfundiert, Konfundierung * Kontingenz, kontingent *  Kontinuität * Korrelation * Kovarianz * Kurtosis * Laborwertnormen *  Lag * Längsschnitt-Statistik (Longitudinal) * Laplace-Experiment * Letalität * Likelihood, Likelihood Ratio, negative, positive *  Logik * Longitudinal > Längsschnitt. * MA *  Markovkette * Maßtheorie * Maximale Clique  * Maximum-Likelihood-Methode * Median * Mengenlehre * Merkmalsraum, relevanter * Messen, Messung * Metatheorie (psychologische) * Messungen per fiat  * Messfehler * Messwert, Zahlenwert * Methode * Minimum. *  Mikrozensus * Missing Data * Mittel * Mittelwert ohne nähere Angabe * Mittelwert, arithmetischer * Mittelwert, geometrischer * Mittelwert, harmonischer. * Mittelwerte und Durchschnitte * Modalwert * Modell * Moderatorvariable * Moment * Morbidität * Mortalität * Multidimensionale Skalierung  * Multikollinearität * Non-parametrische Statistik * Norm * Normbedingung * Normalbedingung * Normalverteilung  *  Normwerte *  Nullhypothese *  Numerologie * Nutzen  *  Objektivität *  Objektivität, spezifische *  Odds-Ratio * Ökonomie * Operationalisierung * Operationscharakteristik * Panelstudien * Parameter * Parameter-Konstanz  *  parametrische Verfahren. *  Paranormale Fähigkeiten testen * Pfadanalyse * Plausibel/Plausibilität * Poissonverteilung * Polung. *  Population. *  Power, negativ prädiktive, positiv prädiktive * Prävalenz. * Praxeologie * Produkt-Moment * Prozentrang * Prüfstatistik * Quantile * Quartile  *   Querschnitts-Statistik * Rang, Rangzahl, Rangtests * RCT * Referenzwert * Regression, Regressionsanalyse  *  Relation (Beziehung) * Relationentreue * Reliabilität  *  Repräsentation. *  Repräsentationsproblem * Risiko: * Risikokompetenz * Risikowahrscheinlichkeiten * ROC *  Rohwert * Sachverhalt * Scheidewert * Schiefe  *  Schließende Statistik * Score *  Sensitivität. *  Signifikanz. *  Simpson's Paradoxon * Skalierung. Messverfahren, Messmethode *  Skalierungsproblem * Spannweite * Spezifität * Spiel *  Spieltheorie * Spurenhypothesen * Stabil, Stabilität [numerische] *  Standardabweichung * Standardbedingung * Standardnormalverteilung * Standardwert * Stanine * Statistik * Statistik, deskripve * Statistik, mathematische * Statistikpakete/ Statistikprogramme * Statistik, schließende *  Statistische Hypothesen * Statistische Kennwerte * Statistisches Paradigma * Statistische Schlussweisen * Stichprobe * Stichprobenauswahlverfahren * Stichproben-Kennwerte *  Stichprobenumfang * Stationär, Stationarität *   Stetig  *  Stichprobe *  Stochastik. *  subjektive Wahrscheinlichkeitstheorie *  Summen-Score-Funktion* Surveillance * Syllogismus, statistischer. *  Telepathische Fähigkeiten * Test *  Testen  * Testgütekriterien. *  Teststärke (Power). *  Testtheorie: *  Theorie * Transformation.  *  Transparenz. *  Trennschärfe * T-Werte * unabhängig * Unsicherheit. *  Unterscheiden. *  Unzureichender Grund > Indifferenzprinzip * Überdiagnose-Fehler * Utilität  *  Validität, inkrementelle * Varianz. * Varianzanalyse *  Vergleichen *  verstehen * Verteilung. *  Verteilungsannahmen. * Verteilungsfreie statistische Verfahren * Verteilungsfunktionen * Verteilungskennwerte *  Vertrauensintervall * Vieldeutigskeitssatz. * Vorlauf-Zeit-Fehler * Voraussetzungen. *  w *  Wahrscheinlich, Wahrscheinlichkeit. *  Wahrscheinlichkeit 1 und 2 nach Carnap * Wahrscheinlichkeit, bedingte * Wahrscheinlichkeitsbegriff Stegmüllers *  Wahrscheinlichkeitsmodell. *  Wahrscheinlichkeit, objektive. * Wahrscheinlichkeit, subjektive. * Wahrscheinlichkeit, totale * Welten * Wert * Wert, richtiger * Wert, wahrer *  Wertzuweisung *  Wette *  Wissenschaftliches Arbeiten *  Würfelspielparadoxon *  x *  Zahlen * Zeit * Zeitpunkt. *  Zeitreihenanalyse * Zensus (Census) * Zentraler Grenzwertsatz * Ziel und Ziele *  Zipf'sches Gesetz * Zufall * Zufallsgröße * Zureichender Grund * Zuverlässigkeit* z-Werte *
__
Abduktion Peirce (): "Abduktion ist der Vorgang, in dem eine erklärende Hypothese gebildet wird."
__
Abhaengig, Abhaengigkeit
Wichtiger und häufiger allgemeiner, wissenschaftlicher und besonders statistischer Grundbegriff. Was wie von wem abhängt ist eine der wichtigsten Fragen in der Wissenschaft. Hierzu haben die verschiedenen Wissenschaftszweige z.T. ihre eigenen Methoden entwickelt, z.T. greifen sie auf allgemeine Methoden, die von der Wissenschaftstheorie und Statistik entwickelt wurden, zurück, z.B. Datenanalyse, bedingte Wahrscheinlichkeiten, Regression, Korrelation, kanonische, partielle Korrelation. Sich ausschließende Ereignisse in der Wahrscheinlichkeitsrechnung sind abhängige Ereignisse (Rumsey 2007, S. 57).
__
Abweichung. ... von einem Bezugs-, Norm- oder Referenzwert, z. B. die  Standardabweichung  als Abweichungsgröße vom  arithmetischen Mittelwert.
__
Additiv-verbundene Messung
__
Alpha-Fehler (Fehler erster Art). Die 0-Hypothese - z. B. A und B sind gleich -  wird verworfen, obwohl sie wahr ist.
__
Alternativhypothese(n): H1, (H2, ...)  Im Allgemeinen die von einer ForscherIn inhaltlich vertretene Hypothese, z.B. Lernmethode A ist für den Zweck Z "besser" als Lernmethode B. Die einseitige Nullhypothese (H0) würde dann so formuliert: A ist nicht besser, höchstens genau so gut wie B. Zweiseitig ungerichtet: A und B unterscheiden sich nicht.
    Bortz (1985, S. 143) führt aus: "Grundsätzlich sollte die statistische H1 so formuliert werden, daß sie die inhaltliche Hypothese so präzise wie möglich wiedergibt. In Abhängigkeit von der Art der statistischen Hypothese ist dann ein statistisches Verfahren auszuwählen, das eine möglichst „strenge" Überprüfung des hypothetisch behaupteten Sachverhaltes gewährleistet. Wir werden diese Forderung im Zusammenhang mit den einzelnen in diesem Text behandelten statistischen Verfahren erneut aufgreifen. (Ausführlicher wird das Problem des Umsetzens wissenschaftlicher Hypothesen in statistische Hypothesen bei Hager u. Westermann, 1983 diskutiert.)"
__
Antinomie.
__
ANOVA Analysis of Variance - Varianzanalyse
__
A posteriori Wahrscheinlichkeit Wahrscheinlichkeit für einen Zustand unter der Voraussetzung schon bekannter Größen und ihren Wahrscheinlichkeiten. > Bayes.
__
A priori Wahrscheinlichkeit Wahrscheinlichkeit aufgrund von Vorwissen oder per Annahme, z.V. Beispiel Gleichverteilung (fairer Würfel,. Münze), Normalverteilung, Poissonverteilung (Warteschlange), ...
__
a priori - a posterori - Ding an sich.
__
AR  Autoregressives Modell. > Zeitreihenanalyse.
Springer-Gabler definieren [A141113]: "autoregressiver Prozess p-ter Ordnung. Ein stochastischer Prozess heißt AR(p), wenn seine Realisation im Zeitpunkt t linear nur von seinen p gewichteten Vergangenheitswerten und einem weißen Rauschen abhängt."
    Mehr: [1, Matlab, 3,]
__
ARCH  ARCH Autoregressives Conditionales Heteroscedastic Modell. > Zeitreihenanalyse.
__
ARIMA-Prozess Autoregressives Integrated Moving Average Modell. [ ,Matlab, ] > Zeitreihenanalyse.
__
ARMA Auto Regressive-Moving-Average.  > Zeitreihenanalyse. "In der ARMA-Modellierung werden zeitliche Abhängigkeiten aufeinanderfolgender Beobachtungen analysiert." S. 16: Stroe-Kunold, Esther (2005) Multivariate Analyse instationärer Zeitreihen: Integration und Kointegration in Theorie und Simulation. Diplom-Arbeit Psychologisches Institut Heidelberg. [PDF]
    [, Matlab, ]
__
AUC area under curve (Fläche unter der ROC-Kurve). Enthält auf der Ordinate (Y-Achse) die Sensitivität und auf der Abszisse (X-Achse) 1-Spezifität. Sie gibt die Trefferrate über das Verhältnis der richtig positiv vorhergesagten zu falschen falsch positiv Vorhergesagten ("falsche Alarme) an. Es gibt Werte zwischen 0 und 1. Werte um 0.5 bedeuten, es gibt so viele richtige wie falsch Vorhersagen: man könnte auch eine Münze werfen. [W]
__
Ausgleichsrechnung.
__
Ausschliessen, ausschliessbar [können, nicht]
Wichtiger und häufiger allgemeiner, wissenschaftlicher und besonders statistischer Grundbegriff.
__
Autokorrelation.
__
Auswahl, Auswahlverfahren. Vielfach können ganze Populationen nicht vermessen werden, so dass Stichprobenauswahlen erfolgen müssen. Die meisten statistischen Verfahren setzen eine Zufallsausfall voraus, wobei eine solche in den meisten Fällen nicht durchgeführt wird.
__
Bayes Theorem  ...kann man auch anwenden, ohne "Bayesianer" zu sein. Grundmodell: E => H, Schluss von den Ereignissen auf die Hypothese (Frequentisten: H => E, Schluss von der Hypothese auf die Ereignisse)
__
Bayesianer  Mit dieser unglücklichen Wortschöpfung -  weil sie Assoziationen zum Bayes-Theorem erweckt und dieses zu diskreditieren vermag - werden die Vertreter (z.B. Keynes, Jeffrey, de Finetti, Savages)  der subjektiven - im Gegensatz zur frequentistischen - Wahrscheinlichkeitsinterpretation bezeichnet. Bayesianer sollen in der deutschen Mathematik nicht gern gesehen sein. Im Gegensatz zum Bayes-Theorem, das die Wahrscheinlichkeit einer Hypothese für ein Ereignis berechnet, wenn die Ereignisse schon eingetreten sind (E => H), geht es bei den "Bayesianern" um die grundsätzliche Auffassung und Interpretation der Wahrscheinlichkeit.
Fischer, Hans (Eichstätt: 404) Vortrag: Über die richtige Art statistischen Schließens: Frequentisten gegen Bayesianer, Planetarium Nürnberg, 8.10.2013: "Soll man statistischen Schlussfolgerungen Erwartungen über zukünftige Ereignisse zugrunde legen, die man dann an den tatsächlichen Beobachtungen misst oder soll man besser ausgehend von angestellten Beobachtungen stochastische Betrachtungen vornehmen? Ein Gutteil der frühen Entwicklung der mathematischen Statistik stand unter dem Leitbild der zweitgenannten, sogenannten aposteriorischen Methoden, die von Bayes begründet wurden. Laplaces einschlägige Arbeiten bildeten zugleich einen ersten Höhepunkt dieser Entwicklung, andererseits leiteten sie aber auch einen Paradigmenwechsel hin zu apriorischen Betrachtungen ein.
    Die endgültige Trendwende hin zu dem heute dominierenden, sogenannten "frequentistischen" Standpunkt wurde von R. A. Fisher und weiteren Statistikern zwischen ca. 1920 und 1935 vollzogen. Die ursprünglichen "Bayesschen" Methoden verschwanden dennoch nie vollständig und erfreuen sich heute wieder zunehmenden Interesses. Am elementaren Beispiel der "verfälschten Münzen" sollen die beiden Arten stochastischen Schließens beleuchtet, allfällige Begriffe geklärt und ein Überblick über die historische Entwicklung gegeben werden."
__
Beta-Fehler (Fehler zweiter Art). Die 0-Hypothese wird angenommen - z. B. A und B sind gleich - obwohl sie falsch ist.
__
Bedeutungsamkeitsproblem
Ausdruck der psychologischen Messtheorie. Coombs et al, S. 22: "(3) Das Bedeutsamkeitsproblem: Welche Folgerungen können aus einer bestimmten, gegebenen Meßskala gezogen werden? Welche Aussagen können aufgrund einer numerischen Meßskala sinnvollerweise gemacht werden?"
__
Bedingungen. Überhaupt, aber besonders im statistischen Bereich, elementarer Grundbegriff, der eine Erhebungssituation charakterisiert. Z.B. wird ein Lungentumor nur dann operiert, wenn er noch keine Metastasen gebildet hat. Bestimmte Test sind nur dann durchführbar, wenn eine Normalverteilung vorliegt. Andere Verfahren erfordern ein bestimmtes Skalierungsniveau oder eine Zufallsauswahl. Man spricht auch von Rand- oder Nebenbedingungen, worauf man gut verzichten kann.
__
Bedingte Wahrscheinlichkeit. Wahrscheinlichkeit für ein Ereignis E unter der Bedingung B: p(E|B).
__
Bestaetigung > Wichtiger wissenschaftlicher Grundbegriff.
__
Bestaetigungsgrad
__
Bestimmtheitsmass > Determinationskoeffizient.
__
Binominalverteilung. Wahrscheinlichkeitmodell für die zwei Ergebnismöglichkeiten in n Versuchen: Ereignis tritt für jeden Versuch mit der festen Wahrscheinlichkeit p ein ("Erfolg"), Ereignis tritt für jeden Versuch mit der festen Wahrscheinlichkeit q=1-p nicht ein ("Misserfolg"), wobei Vorgänger-  und Nachfolger- Wahrscheinlichkeit voneinander unabhängig sind. Typisches Beispiel: Münzwurf mit dem Ereignis "Zahl" und "Wappen".
__
Biplot  Krusche 1999, S. 34. "Biplots sind graphische Darstellungen von Datenmatrizen, die gleichzeitig Objekte und Variablen in einer Graphik abbilden (daher auch 'Bi'plots). Biplots stellen demnach nicht eine eigene Analysemethode dar, sondern bieten die Möglichkeit der Visualisierung der Zeilen und Spalten einer Datenmatrix, aufbauend auf verschiedenen dimensionserniedrigenden Verfahren (zum Beispiel der Hauptkomponentenanalyse, der mehrdimensionalen Skalierung und der Korrespondenzanalyse)." Lit:
• Gabriel, K. R. (1971). "The biplot graphic display of matrices with application to principal component analysis". Biometrika 58 (3): 453–467.
• Gower, J. C. ad Hand, D. J (1996). Biplots. London: Chapman & Hall.
• Krusche, Stefan (1999). Visualisierung und Analyse multivariater Daten in der gartenbaulichen Beratung -  Methodik, Einsatz und Vergleich datenanalytischer Verfahren. DISSERTATION zur Erlangung des akademischen Grades doctor rerum horticultorum (Dr. rer. hort.) Landwirtschaftlich-Gärtnerische Fakultät der Humboldt Universität zu Berlin.
• [W.eng]
__
Conjoint measurement  verbundene Messung
Der Wert einer Variablen A wird durch den Wert der "Untervariablen" a₁, a₂, ... a_i ...a_n zustande gebracht gedacht. A = f(a₁, a₂, ... a_i ...a_n), im einfachsten Fall A =  a₁+  a₂+ ... + a_i + ... + a_n. Ich habe dieses Modell mit dem ZUF13-Versuch  untersucht und weitgehend bestätigen können. Die Attraktivität (A) einer Wohnung mag abhängen von a₁=Lage),  a₂=Größe), a₃=Preis), a₄=Ausstattung, a₅= Stockwerk u.a.m., so dass sich A=f(a₁=Lage),  a₂=Größe), a₃=Preis), a₄=Ausstattung, a₅= Stockwerk).
    Spektrum Lexikon der Psychologie führt aus: "verbundene Messung, conjoint measurement, die Messung von Variablen, die keine einfache Meßstruktur haben, sondern sich nur durch das additive, multiplikative oder polynomiale Zusammenwirken zweier oder mehrerer (einfach meßbarer) Einflußgrößen erklären lassen"
    Quelle (Abruf 12.08.2020): https://www.spektrum.de/lexikon/psychologie/verbundene-messung/16217
__
cum hoc ergo propter hoc lat.: danach, also deshalb.
Folgt B auf A, kann A als Ursache von B angesehen werden, was falsch sein kann: dann bezeichnet der lateinische Spruch einen kausalen Fehlschluss.
__
cut off Werte.  "ACOMED statistik" führt aus (071025): "Der Cut-Off-Wert ist der Wert in einem quantitativen diagnostischen Test, der zwischen zwei Testergebnissen (positiv, negativ) unterscheidet und damit einen Patienten einem der zwei untersuchten Krankheitszustände (z. B. krank vs. nicht krank oder Erkrankung 1 vs. Erkrankung 2) zuordnet. Dabei gibt immer einen Überlappungsbereich, in dem je nach Lage des Cut-Off-Punktes Patienten testpositiv oder testnegativ eingeordnet werden. Deshalb ist die Auswahl des Cut-Off-Punktes sorgfältig vorzunehmen. ..."
__
Darstellung statistischer Ergebnisse > Deutung ..., Interpretation..., Signifikanz ...,
Verständliche, in klaren deutschen Worten formulierte. inhaltliche Darstellungen sind in der Statistik - wie auch Mathematik - nicht üblich. So wirken die meisten statistischen Untersuchungsergebnisse nichtssagend und im wahrsten Sinne des Wortes bedeutungslos.
__
Daten
Unklarer und vieldeutiger wissenschaftlicher und statistischer Grundbegriff. Unterscheidbarer Sachverhalt, den man erfassen oder auch zählen und somit weiterverarbeiten kann. Werden Sachverhalte in einer Reihe (Zeitreihe) gezählt, so sollten sie gleichartig sein.
    Alltägliches Datum: So ist z.B. der Sachverhalt A öffnet das Fenster gleichartig zu B öffnet das Fenster, so dass man verallgemeinernd fragen kann: wie oft, wurde an dem und dem Tag das Fenster geöffnet? Hierbei bleibt unberücksichtigt, wer es geöffnet hat, wie lange es geöffnet war, zu welchem Zeitpunkt es geöffnet und geschlossen wurde und wie lange es jeweils geöffnet war u.a.m..
    Astronomisches Datum: "Alle 5000 bis 7000 Jahre kommt der Komet Neowise der Erde so nah, dass er mit bloßem Auge zu sehen ist - derzeit ist es wieder soweit. «Am 23. Juli steht er der Erde am nächsten», sagt die Wissenschaftlerin Carolin Liefke vom Haus der Astronomie in Heidelberg. Dann beträgt seine Entfernung nur noch 103 Millionen Kilometer ..."
    [Quelle und Abruf 12.08.2020: https://der-farang.com/de/pages/so-nah-wie-selten-komet-neowise-derzeit-mit-blossem-auge-zu-sehen]
    Sprachliches Datum: "Der, die, das" sind in der deutschen Sprache
    Mathematisches Datum: Kronecker soll den Ausspruch getan haben: Die Natürlichen Zahlen sind von Gott gemacht, alles andere ist Menschenwerk" (Ein anderes Datum hierzu Popper widerspricht in dem Band Alles Leben ist Problemlösen, S. 98).
    Psychologisches Datum: Am Nachmittag des 12.08.2020 beschäftigte ich mich mit allgemeiner Datentheorie.
    Christlich-religiöses Datum: Ob  Jesus Christus im Jahr 0 unserer Zeitrechnung geboren wurden, ist strittig.
    Kalendarisches Datum: Wenn es heißt 2020 n.Chr. und damit das Jahr jetzt (12.08.2020) gemeint ist, dann wurde Jesus Christus im Jahre 2020-2020 = 0 geboren.
    Physikalisches Datum: Wirft man auf der Erde einen Körper in die Luft, fällt er nach einiger Zeit zu Boden.
    Informatik Datum: In der Informatik bedeutet Datum das kleinste unteilbare Element des Wertebereichs eines Datentyps. (Informatik Duden 1993, S. 188).
__
Datentheorie:
Offensichtlich gibt es eine große Mengen unterschiedlicher und unterschiedlich komplexer Daten. Die Erfassung, Klassifikation und Durchdringung der Datenvielfalt ist Aufgabe der allgemeinen Datentheorie, die derzeit immer noch nicht richtig entwickelt ist. Technisch am weitesten scheint hier die Informatik.
__
Datentyp
Nachdem es sehr viele verschiedenen Daten gibt, erscheint es sinnvoll, Datentypen zu unterscheiden. Dies sollte von einer allgemeinen Datentheorie geleistet werden, was aber noch nicht so weit ist. Von der Informatik (abstrakte, konkrete; integer [natürliche Zahl], real [rationale Zahl], boolean [wahr, falsch], char [Textzeichen]) und Psychologie (Erleben, Verhalten; beobachtbar, nicht beobachtbar) sind mir Ausarbeitungen bekannt, z.B.:
    Roskam, Edward E. (1983). Allgemeine Datentheorie. In: Feger, Hubert & Bredenkamp, Jürgen (1983, Hrsg.). Messen und Testen, 1-135. Enzyklopädie der Psychologie, Themenbereich B Methodologie und Methoden, Serie I Forschungsmethoden der Psychologie, Bd. 3. Göttingen: Hogrefe.
__
Datenverarbeitung
Allgemein wissenschaftlicher, informatischer und statistischer Grundbegriff. Eine wirklich allgemeine Datenverarbeitungstheorie ist mir nicht bekannt.
__
Determinationskoeffizient. Dt. auch Bestimmtheitsmaß. Der Determinationskoeffizient ist das Quadrat des Korrelationskoeffizienten. Er gibt an, welcher Varianzanteil von den korrelierten Variablen erfasst ist ("erklärt" wird). Spielt auch eine wichtige Rolle beim Kurvenfitten und dient hier zur Prüfung der Stärke oder Güte der Anpassung. Beispiel: Es steht zur Beurteilung an, ob die 7-Tage-Mittelwerte der Corona-Neuinfektionen durch eine Exponentialverteilung beschreibbar sind. So sucht man gewöhnlich mit der Methode der kleinsten Quadrate diejenige Fitkurve, die die tatsächlichen Daten mit kleinster Abweichung erfassen. Als Maß für die Güte der Anpassung wird meist der Determinationskoeffizient R^2 (rsquare) herangezogen. Welche Grenze man für die "erklärte" Varianz wählt, z.B. 0.90, 0.95, 0.98, 0.99 ist in gewisser Weise willkürlich und kann letztlich jeder für sich selbst entscheiden. Die strenge Definition (jeder Zuwachs eines Nachfolgers muss größer als der Zuwachs des Vorgängers sein) ist bei dem Fit meist nicht eingehalten, er soll ja gerade die normalen oder üblichen Abweichungen neutralisieren. Exponentiell heißt hier also "tolerant" exponentiell, indem man schaut, wie gut (rsquare) sich die 7TM-Kurve durch eine exponentielle Gleichung anpassen lässt. Ausführliches Beispiel hier.
__
Deutung statistischer Werte und Ergebnisse > Interpretation..., Darstellung..., Signifikanz ...,
Deutungen statistischer Werte und Ergebnisse, insbesondere solche in klaren deutschen Worten, sind der Statistik - und Mathematik - nicht üblich.
__
Diagnostik := Liegt ein Merkmal in dieser oder jener Ausprägung vor? Hier gibt es immer zwei Fehlerarten.
__
Diagnostische Fehlerarten: 1) Ein Merkmal wird zugeschrieben, obwohl es nicht zutrifft (falsch positiv). 2) Ein Merkmal wird nicht erkannt, obwohl es zutrifft (falsch negativ). Man erkennt auf eine Diagnose, obwohl sie nicht vorliegt (falsch positiv) oder man erkennt eine Diagnose nicht, obwohl sie vorliegt (falsch negativ). Dieser Fehlertyp ist universell, so z. B. auch für die Rechtsprechung: jemand wird für eine Tat verurteilt, obwohl er sie nicht begangen hat (falsch positiv) oder er wird frei gesprochen, obwohl er die Tat begangen hat (falsch negativ). Nachdem das Recht idealistisch orientiert ist und vor allem Falsch-Positiv minimieren möchte, ergibt sich zwangsläufig,  dass Falsch-Negativ maximiert wird, d. h. immer mehr intelligente und skrupellose TäterInnen kommen straffrei davon und durchsetzen die Gesellschaft.
__
Dichte, Dichtefunktion. Die Dichtefunktion bezieht sich auf stetige oder kontinuierliche Zufallsvariable. Sie ordnet dem Intervall, in dem sich der Wert der Zufallsvariable befindet, eine Wahrscheinlichkeit zu. Die Dichtefunktion entspricht bei diskreten Zufallsvariablen die Wahrscheinlichkeitsfunktion, die jedem der diskreten Werte, eine Wahrscheinlichkeit zuordnet. [B: 404]
__
Differentialdiagnostik := was ist es hier genau, und was nicht?
__
Diskret. Mathematischer Grundbegriff unterbrochener ("diskontinuierlicher", "unstetiger") Meßpunkte. Die 10 Millimeterstriche auf dem Metermaß sind diskret, die Strecken zwischen 1 cm und 2 cm auf dem Metermaß kontinuierlich.
__
Dimension
Wichtiger wissenschaftlicher Grundbegriff für Einteilungen und Zugehörigkeiten. Will man ordnen, stellt sich als erstes die Frage: in oder nach welcher Dimension (z.B. Zeit, Raum, Ausprägung).
__
Diskriminanzanalyse. Mathematisch-statistische Methode, ob und wie gut sich aufgrund gegebener Messwerte unterschiedliche Gruppen von einander trennen bzw. zuordnen oder klassifizieren lassen.
__
DNA-Test (auch genetischer Fingerabdruck)  > Spurenhypothesen.
Er dient der Identitätsfeststellung und hat eine sehr hohe Wahrscheinlichkeit, aber er ist nicht absolut eindeutig und es gibt auch falsch positive und falsch negativ Fehler, was von manchen unkritischen forensischen Sachverständigen ausgeblendet oder gar bestritten wird.
__
Durchschnitt > Mittelwerte und Durchschnitte.
Die allgemeine Idee des Durchschnitts sind Ausprägungen in einem mittleren Bereich (> Beispiel Normalverteilung). In der Statistik und in den Sozialwissenschaften ist der "Durchschnitt" ein viel gebrauchter Begriff mit unterschiedlichen Bedeutungen. Man kann den Durchschnitt auf einen Punktwert (z.B. Mittelwert) reduzieren oder auf einen "mittleren" Wertebereich (z.B. mittlere 50% einer Verteilung zwischen 1. und 4. Quartil).  Das kommt der allgemeinen Bedeutung von "mittlerer Bereich"
    Die formalen Ableitungen sind gewöhnlich nicht das Problem, aber die Interpretation(en), wovor sich StatistikerInnen und MathematikerInnen erfahrungsgemäß gerne drücken. Ich habe in kaum einer Arbeit inhaltliche Aussagen in einfachen, klaren deutschen Worten zur Bedeutung der statistischen fiktiven Größen oder zu den statistischen Ergebnissen gefunden. Mittelwerte ohne Streuungsangaben und Verteilungsparameter sind problematisch. Fast immer sinnvoll ist eine graphische Darstellung der Verteilung der Zahlenwerte. Welchen Durchschnitt man nimmt, wird im allgemeinen von Zielen und Zwecken abhängen, die man mit seinem Durchschnittsanliegen verfolgt.
Verschiedene Mittelwertskonstruktionen
• Arithmetisches Mittel (Summe der Werte durch Anzahl der Werte)
• Geometrisches Mittel (n-te Wurzel des Produkts der n Zahlen; Anwendung Wachstumsraten. Mathebibel: "Das geometrische Mittel (im Gegensatz zum arithmetischen Mittel) dient zur Messung des Durchschnitts einer prozentualen Veränderung. Aus diesem Grund sagt man zum geometrischen Mittel auch durchschnittliche Veränderungsrate.")
• Gewogenes Mittel (die einzelnen Werte werden gewichtet)
• Harmonisches Mittel (Anzahl der Werte durch die Summe der Kehrwerte der Werte; Anwendung Geschwindigkeiten. Mathebibel: "Das harmonische Mittel kommt meist dann zum Einsatz, wenn der Mittelwert von Verhältniszahlen gesucht ist. Eine Verhältniszahl ist als Quotient zweier statistischer Größen definiert.")
• Hölder-Mittel (verallgemeinerter Mittelwert)
• Kubisches Mittel (3. Wurzel aus der Summe der n-Zahlenwerte dividiert durch n)
• Lehmer-Mittel (verallgemeinerter Mittelwert)
• Logarithmisches Mittel ()
• Median (Wert, der eine Zahlenreihe in zwei Hälften teilt)
• Modalwert (der Wert, der in einer Zahlenreihe am häufigsten vorkommt)
• Quadratisches Mittel  (Quadratwurzel aus Summe der n quadrierten Zahlenwerte durch n)
• Stolarsky-Mittel (verallgemeinerter logarithmischer Mittelwert)
__
Eindeutigkeitsproblem
Ausdruck der psychologischen Messtheorie. Coombs et al, S. 21: (2) Das Eindeutigkeitsproblem: Wieviel Freiheit besteht für ein bestimmtes, gegebenes Meßverfahren in der Zuordnung von Zahlen zu Objekten? Sind die Zahlen durch den Meßvorgang eindeutig bestimmt oder sind sie willkürlich gewählt?
__
Einschlusschance
"3. Einschluss- / Ausschluss-Kriterien 3.1 Einschluss Wenn in Mischspuren alle DNA-Merkmale der fraglichen Person durchgängig nachweisbar sind, dann kommt diese Person als Spurenmitverursacher in Betracht. 3.2 Ausschluss Wenn in Mischspuren DNA-Merkmale der fraglichen Person nicht nachweisbar sind, kommt diese Person als Spurenmitverursacher nicht in Betracht" [Q]
__
Einzelfall. Recht, Kriminologie, Medizin, Psychologie sind auch angewandte idiographische Wissenschaften, d. h. sie machen Aussagen über ein Individuum. Hierbei ist ein großes und bislang ungelöstes Problem, wie man Erkenntnisse, die für Gruppen (Aggregate) gelten, auf den Einzelfall anwenden kann > Grundzüge einer idiographischen Wissenschaftstheorie. Man bedenke, dass in unseren Praxen, Büros, Kanzleien und Gerichten keine Stichproben und Populationen Platz nehmen, sondern individuelle Menschen.> Praxeologie, > evidenzbasierte Medizin.
Querverweise:
• Hake: Statistische Falschschlüsse Gruppe/Einzelfall.
• Nedopil: Prognosen in der Forensischen Psychiatrie.
__
Entropie > Information, > Redundanz.
Allgemein (Maß für "Unordnung" bzw. umgepolt der "Ordnung", Ungewißheit oder Gewissheit, Gleichverteilung oder Ungleichverteilung) wichtiger wissenschaftlicher Grundbegriff aus der Physik und Thermodynamik (Energieumwandlungen  vergrößern die Entropie des Universums; Wärmetod des Universums: Clausius 1867), Biologie (Streben nach Ordnung), Wahrscheinlichkeitstheorie und Statistik (Maß für die Stabilität eines Zustands; Boltzmann 1880), Informationstheorie (Informationsdichte) und Sozialwissenschaften (Informationsmangel), in der Psychologie ("Entropie, Grad der Zufälligkeit, der in einem bestimmten System vorhanden ist; Maß für den Grad der Ungewißheit über den Ausgang eines Versuchs (Informationstheorie)" nach Spektrum Lexikon der Psychologie.)
 

Quelle: https://de.wikipedia.org/wiki/Entropie_(Informationstheorie)#/media/Datei:Entropy_max.png

Der Informationsbegriff der Informations- theorie Shannons, der Nachrichtentechnik und Kybernetik ist beschränkt weil syntaktisch; er entspricht nicht dem gewöhnlichen Informationsbegriffs, der semantisch ist auf den sachlichen und inhaltlichen Gehalt der Information abzielt. Wie inhaltliche und sachliche Informationsgehalte gemessen werden können, ist bislang nicht gelöst.  Einige Sätze aus der Informationstheorie:  Der Informationsgehalt einer Nachricht ist umso größer, je unwahrscheinlicher ihr Eintreffen ist. Eine Nachricht, die nichts Neues enthält, hat die Wahrscheinlichkeit 1. Die Entropie ist hier dann 0.

__
Entscheidbarkeit. Wichtiger mathematischer Begriff aus der Beweistheorie (Turing, Halteproblem > W).
__
Entscheidung. Grundlegender Begriff für alle Systeme mit Wahlmöglichkeiten. Watzlawick postulierte für den zwischenmenschlichen Bereich, dass man nicht nicht-kommunizieren könne. Übertragen kann man sagen, dass man nicht nicht-entscheiden kann, denn nichts tun, warten, nicht-entscheiden ist paradoxerweise auch eine Entscheidung.
__
Entscheidungstheorie.  [1 (Bamberg), ]
__
Epidemiologie. Inzidenz, Letalität, Morbidität, Mortalität, Prävalenz. > Grundbegriffe.
__
Ereignis. bestimmt durch Ort und Zeit (Grundbegriff).
Zu unabhängigen und sich ausschließenden Ereignissen schreibt Rumsey (2007), S.57: "Einander ausschließende Ereignisse können nicht unabhängig sein, und unabhängige Ereignisse können einander nicht ausschließen, außer mindestens eins der beiden Ereignisse ist die leere Menge."
__
Ereignisalgebra (Mengenlehre):
__
Ergodisch, Ergodizität, Ergodensätze
1931: Birkhoff: Allgemeiner Ergodensatz. Schlitthen & Streitberg (1984), S. 147:
__
Erhebungszeitraum. Zeitraum (Anfang - Ende) in dem eine Erhebung erfolgte.
__
erklären und verstehen [Quelle]
Verstehen ist wie die meisten Worte ein vielfältiges Homonym und hat mehrere Grundbedeutungen:
    1) kommunikativ: die Worte und Aussage sprachlich verstehen;
    2) verstehen der Bedeutung der Aussage: geistig nachvollziehen, begreifen;
    3) emotionales verstehen: einfühlen, nacherleben können;
    4) verstehen eines Zusammenhanges.
    5) billigen, gut heißen.
    6) verstehen als geistes- und sozialwissenschaftliche Methode
        6b) im Unterschied zum naturwissenschaftlichen erklären.
Erklären hat ebenfalls unterschiedliche Bedeutungen:
    1) Einen Zusammenhang erklären: was hängt wie mit wem zusammen?
    2) Gründe G für einen Sachverhalt S angeben: S wird durch G erklärt.
    3) Ursachen U für einen Sachverhalt S angeben: S wird durch U erklärt.
Anmerkung: Gründe und Ursachen bedeuten im sachlichen, logischen Kern das Gleiche. Im sozial- und geisteswissenschaftlichen Bereich bevorzugt man den Ausdruck "Gründe", im Naturwissenschaftlichen Bereich den Ausdruck Ursache.
    Von Windelband (1894) wurde der wenig hilfreiche und scheinbare Gegensatz zwischen der nomothetischen, Gesetze und Regel suchenden, und der idiographischen, den konkreten Einzelfall verstehenden, Wissenschaft geschaffen. Dilthey (1900) stiftete den scheinbaren Gegensatz zwischen naturwissenschaftlichem Erklären und geisteswissenschaftlichem Verstehen.
    In der Psychologie, Psychopathologie und Psychotherapie haben wir es in der Praxis immer mit dem Einzelfall oder einem individuellen Einzelfall-System (z.B. Familie) zu tun. Gesetzesartiges oder Regelhaftes gibt es aber nicht nur im Längsschnitt, in Entwicklung und Verlauf, sondern auch im Einzelfall. Einen prinzipiellen Gegensatz zwischen erklären und verstehen vermag ich nicht zu erkennen. Wenn jemand einen Pullover anzieht, weil ihm zu kalt ist, so können wir sinnvoll und verständlich sagen, wir erklären das Pullover anziehen mit unangenehm erlebtem Kälteempfinden, das den Grund liefert. Sagen wir, wir verstehen, dass er einen Pullover anzieht, weil ihm kalt ist, schwingt hier mit, dass wir uns einfühlen können, dass wir selbst Ähnliches schon erlebt haben. Diese Bedeutung hat sich seit Windelband und Dilthey in den Geisteswissenschaften - und seit Jaspers (1913) in der Psychopathologie - eingebürgert, so mag man sie denn so belassen; hier aber mit der Erweiterung, dass in den Sozial- und Geisteswissenschaften erklären und Erklärung sowohl erwünscht als auch möglich und zulässig sind. Die meisten dürften nicht verstehen, wie jemand auf Befehl von Stimmen einen Angehörigen umbringt, weil die allermeisten das selbst noch nie erlebt haben, aber dieser Sachverhalt taugt durchaus als Erklärung für einen Mord durch einen schizophrenen Schub. Ich werde in meinen forensischen Arbeiten diesen künstlichen und falschen Gegensatz nicht übernehmen und nicht weiter pflegen. Den Grundfragen des Verstehens gehe ich in einer anderen Arbeit nach.
    Das Thema erklären und verstehen spielt auch in der Psychiatrie eine historische Rolle (Jaspers, Kehrer, Gruhle, Straus). Besonders aber in der forensischen Psychiatrie (> Beweisfragen-Fehler), wenn es z.B. darum geht, festzustellen, inwieweit die psychopathologischen Entsprechungen ("Voraussetzungen") für Einsichts-_§ und Steuerungsfähigkeit_§, Schuldfähigkeit_§, Gefährlichkeit_§ oder Wiederholungsrisiko_§ vorliegen. [teilweise aus der Quelle 2.1.4] oder nicht bzw. mangels Informationen oder Daten nicht feststellbar sind.
__
Erwartungswert. Theoretisch der - immer unbekannte - wahre Mittelwert, praktisch oft der arithmetische Mittelwert als beste empirische Näherung ("richtiger Wert") für den gedachten wahren Wert.
__
Erwartungstreu(e Schätzung). Eine Schätzfunktion heißt erwartungstreu, wenn sie im Durchschnitt den richtigen Wert als besten Schätzer für den unbekannten "wahren" Wert liefert.
__
Evaluation. Den Wert einer Methode untersuchen und erweisen.
__
Evidenz. Offenkundig, offensichtlich, klar, banal, trivial, selbstverständlich.
__
Evidenz-basierte Medizin. Neuere Evaluations-Methode in der Heilkunde, die versucht, Entscheidungen durch wissenschaftliche Forschungsergebnisse zu stützen, also eine Verbindung zwischen der idiographischen (einzelfallorientierten, intra-individuellen) und nomothetischen (inter-individuell gültige empirische Gesetze und Regelhaftigkeiten) Betrachtungs- und Herangehensweise einzugehen. Anmerkung: Evidenz ist hier in der anglo-amerikanischen Bedeutung  (Beweis, belegt) gemeint. Die deutsche Übersetzung suggeriert eine falsche Bedeutung.
__
Exzess (Kurtosis) := das 4. Moment, Abweichung von der Normalverteilung.
__
Faktorenanalyse.
__
f := Hier Zeichen für Fehler. In der psychologischen Testtheorie meist mit "e" (error) bezeichnet.
__
Falsch negativ := ein Merkmalsträger wird nicht erkannt.
__
Falsch positiv =: ein Nicht-Merkmalsträger wird fälschlich als Merkmalsträger identifiziert.
__
Fast sicher
Wenig überzeugender Ausdruck der mathematischen Wahrscheinlichkeitslehre für die Wahrscheinlichkeit 1 eines Ereignisses. Intuitiv und nach dem gesunden Menschenverstand würde man ein Ereignis mit Wahrscheinlichkeit 1 nicht "fast sicher", sondern sicher nennen.
__
Fast unmöglich
Wenig überzeugender Ausdruck der mathematischen Wahrscheinlichkeitslehre für die Wahrscheinlichkeit 0 eines Ereignisses. Intuitiv und nach dem gesunden Menschenverstand würde man ein Ereignis mit Wahrscheinlichkeit 0 nicht "fast unmöglich", sondern vollständig unwahrscheinlich nennen.
__
Fehler. Alles menschliche Feststellen und jede Messung ist mit einem Fehler behaftet, mag er auch noch so klein sein. Allgemein bedeutet Fehler eine Abweichung vom Zutreffenden oder für richtig Erachteten, wodurch eine subjektive Komponente entsteht, weil, z.B. in der  Welt der Werte  es keine Objektivität oder Intersubjektivität gibt.
 

Entscheidung / Sachverhalt	Sachverhalt = wahr, richtig	Sachverhalt = falsch, unrichtig
Entscheidung für wahr, richtig	Entscheidung = wahr, richtig	Entscheidung = falsch, unrichtig
Entscheidung für falsch, unrichtig	Entscheidung = falsch, unrichtig	Entscheidung = wahr, richtig

In der Statistik werden unter bestimmten - meist problematischen, unbekannten oder nicht erfüllten - Annahmen, die Annahmen richtig oder falsch geschätzt. Über die Wirklichkeit selbst erfährt dabei gewöhnlich nichts. Aber man bewegt sich in scheinbar exakten, wenn auch virtuellen Räumen.
__
Fehlerarten: Fehler können durch systematische oder zufällige Störquellen, durch die Messmethode, das Messgerät, die Eichung, Anzeige, Ablesung, Irrtümer oder bewusste Fälschung zustande kommen.

• Fehler, absoluter. f = x - r.   [> Messfehler]
• Fehler, relativer. f / Mittelwert
• Fehler, systematischer. Fehlerhafte Messmethode, fehlerhaftes Gerät, fehlerhaftes Ablesen; mangelnde Kontrolle anderer Einflüsse oder Störvariablen, z. B. leichtfertiges ungeprüftes oder ungesichertes Glauben von Angaben in sehr, sehr interessegeleiteten Situationen (Prüfungen, Bewerbungen, Aufträge erringen, Aussagen vor Gericht oder der MPU).

Fehler, zufälliger. Schwieriger statistischer Begriff, meist negativ definiert als nicht-systematisch; klein; durch viele Faktoren bedingt und Abweichungen nach beiden Richtungen, so dass ein gewisser Ausgleich bei der Mittelwertsbildung erfolgt. [> Zufall]
    > Fehler (Genauigkeit, Reliabilität, Zuverlässigkeit)
__
Fehler, statistische.   > W; Interaktive Bestimmung Fehler 1. und 2. Art Uni-Konstanz.
__
Fiduzialkonzept. Konzept von Fisher, wonach aus den Realisationen der Zufallsvariablen Schlüsse auf die theoretische Verteilung und Ihre Parameter ohne a-priori Kenntnisse gezogen werden. Voraussetzungen: kontinuierliche Zufallsvariable, suffiziente Schätzung. Nach Dieter Rasch (1978, S. 202) hätten James (1954) und Stewart (1959) gezeigt, dass die Fiduzialfunktion nicht immer auf 1 normiert sei und daher nicht immer eine Dichtefunktion der Wahrscheinlichkeitsrechnung entspreche.
__
Fourier-Analyse Eine mathematische Wunderwaffe zur Analyse, Erzeugung und Zerlegung aus Komponenten von (Mess-) Daten (Reihen). Es gilt, dass jede beliebige Verlaufsform aus Sinuskurven konstruiert werden kann.
__
Frequentisten Name für die VertreterInnen eines Wahrscheinlichkeitsbegriff, der die relativen Häufigkeit von Ereignissen zum Dreh- und Angelpunkt der Statistik macht, z.B. Fisher, Pearson, Neyman, von Mises. Grundmodell direkter Schluss: H => E.  Inverser Schluss: E => H Bayes Theorem).  Grundsätzliche Gegenposition "Bayesianer",
__
GARCH Generalized ARCH > Zeitreihenanalyse.
__
Gesetz der großen Zahlen
Oskar Anderson (1954), S. 105: "4. Das Prinzip· oder Gesetz der großen Zahlen. Der Begriff des “Gesetzes der großen Zahlen” hat im Laufe der 120 Jahre, die nunmehr seit dem Erscheinen von Poissons “Recherches” (1837) verflossen sind, bedeutende Wandlungen durchgemacht, und wenn in der Fachliteratur bis heute noch keine vollständige Einmütigkeit über seinen Inhalt herrscht, so geht die allgemeine Entwicklung doch zweifellos dahin, im Anschluß an Poissons Einleitung (aber in einem gewissen Gegensatz zum weiteren Text seines Werkes) unter diesem “Gesetz” (oder, wie es richtiger wäre zu sagen, unter diesem “Prinzip”) die ganz generelle Tatsache zu verstehen, daß bei Einhaltung gewisser allgemeiner Bedingungen sehr viele statistische Kollektivmaßzahlen, die für eine Beobachtungsserie berechnet werden, im allgemeinen desto weniger von gewissen konstanten '‘Grenzwerten” abweichen werden, je größer der Umfang n der Serie genommen wird 11). So verstanden, ist das Prinzip der großen Zahlen jedenfalls kein Theorem der reinen Mathematik, die an und für sich keine Möglichkeit bietet, allein aus ihrem theoretischen Inhalt heraus irgendwelche Aussagen über die konkrete Tatsachenwelt bloß durch tautologische Umformungen abzuleiten. Es wäre z.B. undenkbar, nur aus den Lehrsätzen der Geometrie eine zwingende Schlußfolgerung darüber zu gewinnen, ob der tatsächliche Raum, in dem wir uns befinden, derjenige von Euklid,, Riemann oder etwa von Lobatschewskij ist l2.
    Hieraus folgt aber andererseits durchaus nicht, daß das Prinzip der großen Zahlen ganz ohne Anwendung eines mathematischen Apparats begründet werden könne. Die Versuche, die in dieser Hinsicht von einer Anzahl “antimathematischer” (insbesondere deutscher) Statistiker gemacht worden sind, haben zu keinen wissenschaftlich verwertbaren Ergebnissen geführt: der Sinn des meistens recht wortreichen Rerumredens um dieses Prinzip bleibt dunkel und nebelhaft.
    M. E. bestehen nur zwei Möglichkeiten dafür, das Prinzip der großen Zahlen logisch sauber zu begründen: entweder man nimmt — wie es etwa v. Mises getan hat — gewisse Beobachtungen des täglichen Geschehens in die Zahl der Axiome und Definitionen der Wahrscheinlichkeitstheorie mit hinein und leitet dann dieses Prinzip aus ihnen durch tautologische Umformungen ab, oder aber man sagt sich in der Wahrscheinlichkeitsrech-[>106]nung von jeglicher Bezugnahme auf die Tatsachenwelt von Anfang an los und üherläßt diese jenen Disziplinen, die die betreffenden Lehren praktisch anzuwenden und auszuwerten haben. Im ersten Falle gehört die Wahrscheinlichkeitstheorie zum Gebiet der angewandten Mathematik, im letzteren bleibt sie als Teil der reinen Mathematik bestehen. Die moderne Richtung in der Wahrscheinlichkeitstheorie neigt sich immer mehr zur zweiten Alternative hin. Dies bedeutet, daß man anstelle des v. Misesschen jenen Weg betreten sollte, den uns A. Coumot (1843) bereits vor 114 Jahren gewiesen hat. Dieselbe Idee wurde später von P. Mansion (1903) wieder aufgegriffen und durch das klassische Buch von A. A. Tschuprow (1910) (welches leider seinerzeit nicht ins Deutsche übersetzt worden war) im Bereiche der die russische Sprache verstehenden Welt im weitesten Maße popularisiert. In der französischen wissenschaftlichen Literatur wird derselbe Standpunkt z. B. von Frackel vertreten."

Größe. Grundlegender wissenschaftlicher Begriff, der im allgemeinen eine quantitative (messbare) Qualität beschreibt und mit anderen Größen in Zusammenhängen steht, deren Erforschung Aufgabe der Wissenschaft ist. Im Umfeld der Statistik und Wahrscheinlichkeit werden Größen vorschnell und leichtfertig als ausschließliche Zufallsgrößen (Zufallsvariablen) aufgefasst, was sie natürlich nicht sind. Der Zufall ist nur ein Aspekt. Für Größen gilt daher G = f(F₁, F₂, ..., F_i, ...  F_n), f(Z₁, Z₂, ..., Z_i, ...  Z_n), wobei F hier kausale, korrelative und Z "zufällige" Einflüsse bedeuten sollen.
__
Gruppenkennwert > Zur Problematik Übertragung auf den Einzelfall.
Kennwerte oder Merkmale, die für eine Gruppe (Menge) gelten, gelten in der Regel nicht für ihre Elemente. Und Merkmale oder Kennwerte, die für ein Element gelten, gelten in der Regel nicht für die Gruppe (Menge). Sind 7 SchülerInnen in einer Klasse von 28 SchülerInnen an Grippe erkrankt, so gilt für eine zufällig herausgegriffene SchülerIn nicht, dass sie mit einer Wahrscheinlichkeit von p=0.25 oder mit 25% Grippe hat. Denn jedes Element SchülerIn hat entweder Grippe oder hat keine Grippe. Die Übertragung von Gruppenkennwerten auf den Einzelfall ist unzulässig, wenngleich ein häufiger Fehler mit hoher suggestiver Kraft und Ausstrahlung.
__
Gueltigkeitszeitraum
Aussagen gelten in der Regeln nicht absolut (wie z.B. die Lichtgeschwindigkeit), sondern nur unter bestimmten Bedingungen (Normalbedingungen, Normbedingung, Standardbedingung, Validität). Für Statistiken ist das natürliche Referenzdatum das Erhebungsdatum. Hier stellt sich dann die Frage: wie lange und unter welchen Bedingungen gelten gelten die Werte zum Zeitpunkt der Erhebung?
__
Häufigkeit := Anzahl von Ereignissen für einen bestimmten Zeitraum.
__
Heteroskedastizität: ungleiche, veränderliche Varianz, Inkonstanz der Varianz.
__
Histogramm. Grafische Darstellung von Häufigkeiten. [W]
__
Homoskedastizität: gleiche Varianz, Varianz Konstanz
__
Homogenität  Allgemein Gleichartigkeit, rein
Für psychologische Tests erklären  Bortz & Döring  (1995), S. 201f: "Homogenität: Die Items eines eindimensionalen = Instruments stellen Operationalisierungen desselben Konstrukts dar. Entsprechend ist zu fordern, daß die Items untereinander [RS: positiv] korrelieren. Die Höhe dieser wechselseitigen Korrelationen nennt  man Homogenität. (Die Auswahl des geeigneten; Korrelationskoeffizienten hängt auch hier wiederum vom Skalenniveau der Items ab.). Korreliert man alle k Testitems paarweise miteinander, ergeben sich k*(k-i)/2 Korrelationskoeffizienten (r_ii) deren Durchschnitt (r-quer_ii) die Homogenität des Tests quantifiziert (zur Berechnung einer durchschnittlichen Korrelation vgl. Bortz, 1993, S. 201). Mittelt man dagegen nur die Korrelationen eines Items mit allen anderen Items, erhält man die itemspezifische Homogenität. Bei der Homogenitätsberechnung werden die Autokorrelationen (Korrelation eines Items mit sich selbst) außer acht gelassen."
    Die Homogenitätsforderung ist z.B. im CST-Charakter-Struktur-Test von Sponsel erfüllt (siehe bitte hier): Alle Z, H, S und D-Items korrelieren positiv untereinander.
__
Hypothese. Wissenschaftlicher Grundbegriff. Verwerfungsregel: Eine Hypothese für ein Ergebnis wird verworfen, wenn bezüglich der Voraussetzungen und Annahmen die Wahrscheinlichkeit für das Ergebnis kleiner-gleich einer gewählten Schranke (Irrtumswahrscheinlichkeit, Signifikanzniveau) ist. Das Ergebnis gilt bezüglich der gewählten Schranke als unwahrscheinlich. Die meisten Hypothesenprüfungen in der angewandten Statistik prüfen nur virtuelle Möglichkeiten mit virtuellen Annahmen gegen andere virtuelle Annahmen. Das Zusammenwirkungen kausaler Faktoren, korrelativer Faktoren und "des Zufalls" ist weitgehend ungeklärt und wird gewöhnlich nicht erörtert. Die Lehrbücher sind leer davon.
__
Hypothesendiskussion. Zu ihr gehören die Erörterung der Hypothesen, ihre Entwicklung und Begründung, die Prüfmethoden, Voraussetzungen und Annahmen, Formulierung der Ergebnisse in deutschen Worten, Erörterung der Fehlerarten und die Möglichkeiten ihrer Abschätzung. Sehr oft kommen inhaltliche Erörterungen viel zu kurz.
___
Hypothesenraum. > Integratives Testprinzip, relevanter Merkmalsraum. Gesamtheit der potentiell relevanten Hypothesen. Eine vernünftige und realitätsorientierte Statistik muss den gesamten relevanten Hypothesenraum erfassen und die Hypothesendiskussion realitätsbezogen darin führen.
__
IMA Integrated Moving Average Modell. > Zeitreihenanalyse.
__
Indifferenzprinzip „Wenn keine Gründe dafür bekannt sind, um eines von verschiedenen möglichen Ereignissen zu begünstigen, dann sind die Ereignisse als gleich wahrscheinlich anzusehen.“ (Carnap & Stegmüller, 1958, S. 3). In der Philosophie und Wissenschaft auch: Prinzip vom unzureichenden Grund.
__
Identifikationsanalyse
Ein Merkmalsträger soll mit einem Kriteriumsmerkmalsträger verglichen werden und mit Hilfe eines Vergleichs der Kriteriumsmekrmalsträgergruppe zugeordnet werden können oder nicht. Im Prinzip das Kernproblem der Diskriminanzanalyse. Der Ausdruck wird verwendet von Flury, Bernhard & Riedwyl, Hans (1983) Identifikationsanalyse. In (99-111): Angewandte multivariate Statistik. Computergestützte Analyse mehrdimensionaler Daten. Stuttgart: Gustav Fischer.

• Identifikationsanalyse  99
• Einleitung  99
• Identifikation als Spezialfall der Diskrimination  100
• Die verallgemeinerte Distanzfunktion; Mahalanobis-Distanz  100
• Zusammenhänge zwischen Mahalanobis-Distanz, Identifikationsanalyse, Diskriminanzanalyse und Normalverteilungstheorie  103
• Identifikation einer Banknote  104
• Analyse von Ausreißern und Extremwerten  106
__
Inferenz, Inferenzstatistik.  > statistische Schlussweisen, > schließende Statistik. Schließende, schlußfolgernde Statistik (ergänzend zur deskriptiven, beschreibenden). Zentrale Grundidee und ein Paradigma wahrscheinlichkeitstheoretischer und statistischer Problemlösungen und Aufgaben. Beispiele: Man zieht eine Stichprobe und möchte wissen, wie repräsentativ ist diese Stichprobe für die Grundgesamtheit (Population). Man berechnet einen Wert und möchte wissen, wie gut dieser Wert den unbekannten Parameter schätzt, mit welchen Abweichungen unter diesen oder jenen Annahmen zu rechnen ist? Im Grunde genommen, haben sich Wahrscheinlichkeitstheorie und Statistik in einer eigenen unlösbaren Aufgabe (Aporie) verfangen: Wie gewinnt man Sicherheit (Wissen), wo es keine(s) gibt? Damit ist eine unendliche "Spielwiese" für die mathematische Statistik eröffnet, indem unter "bestimmten" - in Wirklichkeit unbekannten - Annahmen gewisse Annahmen gegenüber anderen Annahmen untersucht und getestet werden. Man bewegt sich weitgehend in virtuellen, fiktiven Welten, obwohl man doch etwas über die Wirklichkeit erfahren möchte. Einen hohen Wert hat allerdings die Mathematik gegenüber allen anderen Wissenschaften: sie zwingt zur Klärung der Voraussetzungen und Annahmen, die ansonsten oft oft leichtfertig und wenig (problem-) bewusst einfach unausgewiesen angenommen werden.
__
Information (Nachricht)
Wissenschaftlicher Grundbegriff. "Energie, Materie und Information stellen die drei wichtigsten Grundbegriffe der Natur- und Ingenieurwissenschaften dar." (Duden Informatik 1993, S. 315)
• Attneave, Fred (dt. 1965, engl. 1959) Informationstheorie in der Psychologie. Grundbegriffe, Techniken, Ergebnisse. 2. d. A. Bern: Huber.
• Haken, Hermann & Haken-Krell, Maria (1989) Entstehung von biologischer Information und Ordnung. Darmstadt: WBG. [Information 37-54]
• Jaglom, A. M. & Jaglom, I. M. (dt. 1967, russ. 1960) Wahrscheinlichkeit und Information. 3. ber. A. Berlin: VEB d Wiss. [Informationsbegriff S. 85-107.
• Seiffert, Helmut (1968) Information über die Information. München: C.H. Beck.
__
Informationstheorie (Nachrichtentheorie)
1948 von Shannon begründet, die sich mit der strukturellen und quantitativen Erfassung von Information, ihrer Speicherung und Übertragung befasst. Werden k Abfragen benötigt, um eine Information zu finden, wird der Informationswert k zugeordnet.
__
Integratives Testprinzip. > Hypothesenraum. Es geht von der Annahme aus, das ein empirisch erhaltener Datensatz mehr oder minder repräsentativ für die Population ist. Für eine Gesamtbeurteilung sind mehrere hypothetische Betrachtungen sinnvoll und notwendig. Das bloße Testen gegen eine Hypothese, gewöhnlich Nullhypothese genannt, Stichprobenwert = Populationswert, erscheint viel zu einseitig, virtuell und viel zu wenig informativ.
__
Inter := zwischen verschiedenen Systemen (inter-individuell).
__
Interpretation statistischer Größen und Ergebnisse  > Deutung..., Darstellung..., Signifikanz ...,
Statistische Größen und Ergebnisse werden sehr selten inhaltlich in klaren deutschen Worten interpretiert. Das ist schon Tradition in den Lehrbüchern, die man so gesehen besser Leerbücher nennen sollte.
__
Intra := innerhalb eines Systems (intra-individuell).
__
Inzidenz. Medizinstatistischer, epidemiologischer Begriff. Nach ²⁵⁷Pschyrembel: Anzahl der Neuerkrankungsfälle in einem bestimmten Zeitraum.
__
Inzidenzenrate. Medizinstatistischer, epidemiologischer Begriff. Nach ²⁵⁷Pschyrembel: Anzahl der Neuerkrankungsfälle in einem bestimmten Zeitraum im Verhältnis zur Anzahl der exponierten Personen. Das Psychometrische Wörterbuch (Rasch  et al. 1987) führt aus: "I, Zugangs- oder Neuerkrankungsrate heißt die relative Häufigkeit bzw. Wahrscheinlichkeit des Neuauftretens einer bestimmten Krankheit in einem bestimmten Zeitraum bezogen auf den Umfang der Population, aus der die Erkrankungen hervorgingen. Die I. kann man kumulativ, d.h. auf dem ganzen Untersuchungszeitraum bezogen, oder in Form der Inzidenzdichte für einen (kurzen) bestimmten Teilzeitraum betrachten. Die Inzidenzdichte dient zum Studium der Veränderung der I. mit der Zeit, z. B. in Abhängigkeit vom Alter. Die I. wird in > Längsschnittstudien analysiert.
__
IQ. Normierungseinheit der Intelligenzschätzung.
__
Kappa  > W.  Übereinstimmungsmaß verschiedener Beurteiler oder eines Beurteilers zu verschiedenen Zeiten (Reliabilität), das eine zufällige Übereinstimmung berücksichtigt.
__
Kausalität

• Allgemeines Grundmodell Kausalität ohne Wechselwirkungen.
• Das Ursachenproblem: Kausalität, Verantwortung, Vernetzung.
Kausalität im Psychischen: Ist jemand kalt, dann kann dies der Grund sein, sich einen Pullover anzuziehen. So gesehen gibt es Kausalität natürlich auch im Psychischen. > erklären und verstehen.
__
Kennwerte (Größen, Parameter)
Liegen viele Werte zu einer Fragestellung und Erhebung vor, entsteht das Bedürfnis, die Information dieser vielen, oft unübersichtlichen Werte auf wenige Größer oder Werte zu verdichten oder zu konzentrieren, z.B. durch Mittelwert und Streuung. Haben wir z.B. 100 Werte, so lassen sich diese 100 Werte durch zwei charakterisieren, z.B. durch Mittelwert und Streuung.

Kohärenzprinzip. Begriff der subjektiven Wahrscheinlichkeitstheorie, wonach in einem Wettsystem sichere Verluste ausgeschlossen werden. [1,2,3,]
__
Kohorte.
Die  Internetseite  von de statis definiert (Abruf 1.8.18): "Kohorte Eine Gruppe von Personen die ein gleiches Ereignis zur gleichen Zeit erfahren hat. Eine Geburtskohorte entspricht z.B. einer Gruppe von Personen die im gleichen Kalenderjahr geboren wurden (auch Geburtsjahrgang)."
__
Kolmogoroff-Axiome.


Quelle Kolmogoroff, A. (1933; Nachdruck 1973, S. 2).
__
Kollinearität: [Kollinearitätsanalyse in Korrelationsmatrizen]
__
Konnektivitaet, Konnexität
Ausdruck der psychologischen Messtheorie: a >= b oder b >= a.
__
Konfundiert, Konfundierung. untrennbar zusammenhängend; miterfasst. Sind zwei Merkmale M1 und M2 untrennbar miteinander verbunden, z.B. Alter und Geschlecht, so kann sich die Frage stellen, ob ein Effekt E durch das Alter, das Geschlecht, durch beides oder durch keines von beidem bestimmt ist. Die Kontrolle von miteinander konfundierten Variablen spielt in Experimenten eine wichtige Rolle. Eine Möglichkeit konfundierte Effekte im wahrsten Sinne des Wortes herauszurechnen besteht in der Nutzung partieller Korrelationsanalyse.
__
Kontingenz - kontingent
Allgemein Zusammenhang, in der Statistik Zusammenhangsmaß. Übersicht bei Wikipedia [Abruf 16.05.18].
In der Lerntheorie meist der Zusammenhang zwischen Reiz und Reaktion. Ein Kontingenzschema der verschiedenen Reiz- und Reaktionsvarianten finden Sie bei Wikipedia [Abruf 16.05.18]
__
Kontinuität. relativ dauerhaft, nachhaltig, stetig, konstant zu einem Bezugsverlauf. > Stationarität.
__
Korrelation. Zusammenhang. Es gibt viele Zusammenhangsmaße und damit unterschiedliche Korrelationsbegriffe, so dass immer dazu gesagt werden sollte, um welche Korrelation es sich handelt. [partielle Korrelation]. > Regression.
__
Kovarianz. Ko = mit. Varianz = Streuung. Mit- oder gemeinsame Streuung von zwei Datensätzen: S_xy = 1/n [Summe(x_i - m_x) (y_i - m_y), wobei hier m der arithmetische Mittelwert sei. Beispiel: X=1,2,3. Y=2,3,4. m_x=2;   m_y=3. n = 3:

 

xi	yi	xi - mx	yi - my	(xi - mx) (yi - my)
1	2	1-2 = -1	2-3= -1	(-1 * -1) = 1
2	3	2-2 = 0	3-3= 0	(0 * 0 ) = 0
3	4	3-2 = 1	4-3= 1	(1 * 1) = 1
Sum=1+2+3=6	Sum=2+3+4=9			Sum=1+0+1=2
mx=6/3 = 2	my=9/3=3			Sxy = 2/3 = 0.667

Besonderheiten und Zusammenhänge: Kovarianzen sind nicht standardisiert (nicht normiert auf die Standardabweichung). Wird mit standardisierten Werten gerechnet, ist die Kovarianzmatrix mit der Korrelationsmatrix identisch. In der schließenden (Inferenz-) Statistik wird wegen der Erwartungstreue nicht durch n, sondern durch 1/(n-1) dividiert. Die Kovarianz steht in der Korrelationsformel nach Bravais-Pearson im Zähler.
__
Kovarianzanalyse
Im  Dorsch  wird ausgeführt: "Kovarianzanalyse (= K.) [engl. analysis of covariance], [FSE], Erweiterung des varianzanalytischen Verfahrens, um (1) den Versuchsfehler zu verringern, indem verzerrende Einflüsse möglicherweise konfundierter Drittvariablen (Konfundierung) kontrolliert werden, oder (2) die Wirkung von unabhängigen Variablen auf die Kovarianz zweier abhängiger Variablen zu analysieren. Die Anwendung einer K. ist z. B. erforderlich, wenn die Wirkung zweier Lernmethoden auf die Behaltensleistung an zwei Gruppen untersucht werden soll, die sich in ihrer Intelligenz (konfundierte Variable) unterscheiden, da angenommen werden kann, dass Intelligenz und Behaltensleistung nicht unabhängig voneinander sind. Kovariate, Varianzanalyse, Propensity score."
    In einem Vergleich Varianz- und Kovarianzanalyse stellen Röhr et al. (1983), S. 299 fest: "Durch beide Untersuchungen wird belegt, daß mittels Kovarianzanalyse Fehlentscheidungen (möglicherweise schwerwiegender Art) vermeidbar sind. Da es in Pädagogik und Psychologie sicher ist, daß Effektvariablen durch zahlreiche Kovariablen beeinflußt werden könnten oder tatsächlich beeinflußt werden, erweist sich die Kovarianzanalyse in vielen Fällen als geeignetere Analysetechnik. Es soll nicht unerwähnt bleiben, daß man beispielsweise mit der Homogenisierung von Gruppen ein Mittel in der Hand hat, um Unterschiede in Kovariablen auszugleichen. ..."
    Röhr et al. (1983), S. 305 zählen folgende Voraussetzungen auf: "Voraussetzungen und deren Überprüfung
Die Voraussetzungen für die einfache Kovarianzanalyse müssen naturgemäß mit denen der einfachen Varianzanalyse zusammenfallen, sofern sie allein die Effektvariable Y betreffen. Da zusätzlich zu Y die Kovariable X₁ betrachtet wird, kommen jedoch weitere Voraussetzungen hinzu, die die Regression von X₁ auf Y betreffen. Zusammengefaßt heißen die Voraussetzungen für eine kovarianzanalytische Auswertung:
I  Für X1 und Y liegen Meßwerte vor.
II  Aus jeder der p Grundgesamtheiten wurde eine Zufallsstichprobe vom Umfang n_i (i = 1,... , p) entnommen. Die Stichproben sind voneinander unabhängig.
III  Die Effektvariable Y ist in jeder der p Grundgesamtheiten normalverteilt.
IV  Die Varianzen Sig² für F sind in allen p Grundgesamtheiten gleich (Homogenität der Varianzen).
V   In jeder der p Grundgesamtheiten existiert eine lineare Regression von X₁ auf Y.
VI  Die Regressionskoeffizienten ß_i sind in allen p Grundgesamtheiten gleich (Homogenität der Regressionen).
Die Erfüllung von I und II muß vom Experimentator durch eine geeignete Versuchsplanung von vornherein gesichert werden, da eine mathematisch-statistische Überprüfung nicht möglich ist. Für III ist es erforderlich, mittels geeigneter Verfahren die Anpassung der p empirischen Verteilungen von Y an die zugehörigen Normalverteilungen zu ermitteln.
    Verwendet man das chi²-Verfahren, ist es ratsam, dies in eine Voruntersuchung zu verlagern, da die Stichprobengrößen n_i bei einer Kovarianzanalyse oft nicht die für den Test nötigen Größenordnungen (etwa n_i > 60) besitzen."
__
Kurtosis  Das 4. Moment. Maß oder Kennwert für die Wölbung, Steil- oder Flachheit einer eingipfligen Verteilung.
__
Laborwertnormen.
__
Längsschnitt-Statistik (Longitudinal). Erhebung von Werten über verschiedene Zeit- bzw. Messzeitpunkte hinweg, z. B. alle zwei Monate Bestimmung der Leberwerte für die Dauer eines Jahres. > Querschnitt.
__
Lag Lücke zwischen zwei Markierungen, in der Zeitreihenanalyse der Wert für die Verschiebung, z.B. 1, 2, 3, ...
__
Laplace-Experiment. "Ein stochastisches Experiment heißt Laplace-Experiment, wenn die zugehörige Wahrscheinlichkeitsverteilung gleichmäßig ist."  Die Wahrscheinlichkeit bei einem Laplace-Experiment ergibt sich dann mit p = günstige Fälle/ mögliche Fälle. (Beispiele: Urne, Würfel, Münze)
    Quelle: Barth,F. & Haller, R.  (1984a). Stochastik Leistungskurs. München: Ehrenwirt.
__
Letalität. Sterblichkeit.
__
Likelihood. Engl.: Mutmaßlichkeit, Wahrscheinlichkeit. Manchmal auch das Verhältnis von (relativen) Häufigkeiten, wodurch sich Werte größer 1 ergeben können. Das Prinzip besteht in der Überlegung bei einer erhaltenen Wahrscheinlichkeit diesen für den wahrscheinlichsten zu halten. Nimmt man eine Verteilung an, so kann man ausrechnen, welcher Parameter, z.B. die relative Häufigkeit - die ein Maximum Likelihood Schätzer für den Mittelwert ist - am besten zu dem gegebenen Wert passt > Maximum Likelihood Methode.
__
Likelihood-Quotient  L = p(S|B) / p(S|-B). Allgemein in Worten: Das Verhältnis der Wahrscheinlichkeit für einen Sachverhalt S unter der Bedingung B gegenüber der Nichtgegebenheit der Bedingung B, also -B. Für L =1 spielt B oder -B keine Rolle. Je mehr L > 1 desto stärker wirkt B für S, je mehr L < 1, desto geringer wirkt B für S.
    Likelihood-Überlegungen spielen auch in der juristischen Indizienbewertung eine wichtige Rolle. Bender & Nack (1995) Tatsachenfeststellung vor Gericht. Bd. 1 Glaubwürdigkeits- und Beweislehre. München: Beck gehen im 2. Teil, Beweislehre, ausführlich mit Beispielen darauf ein (Rn 403-485 oder S. 226-275). Bsp. S. 228:  Angenommen 30% aller betrunkenen Mofafahrer (B) fahren ohne Licht (S), während das bei den nüchternen Mofafahrern (-B) nur in 5% der Fall ist, so ergibt sich ein L = 0.30 / 0.05 = 6. Das heißt, die Wahrscheinlichkeit ohne Licht zu fahren, ist unter Trunkenheit 6x größer als bei Nüchternen.

Likelihood-Quotienten-Test. Vergleicht die Wahrscheinlichkeiten für die Null- und Alternativhypothese unter den Annahmen, dass sie richtig sind. Diese Idee erscheint gegenüber dem Signifikanztest, der mit Annahme A1 eine Annahme A2 mit einer anderen Annahme A3 vergleicht, und keinerlei Aussage über die Wirklichkeit erlaubt, etwas informativer. Nachteil: parametrische Voraussetzungen. Anwendung Forensik [z.B. Q].
__
Likelihood Ratio
__
Likelihood Ratio, negative
__
Likelihood Ratio, positive
__
Logik  Lehre vom richtigen Schließen aufgrund der Form. Wenn zu jedem S ein P gehört und M ein S ist, dann gehört zu M auch ein P. Die Inhalte von S, P, M spielen hier keine Rolle. Der Schluss ist logisch immer richtig, unabhängig davon, was man für S, P und M einsetzen mag. Ein logisches Urteil ergibt sich oder gilt aus "rein" logischen Gründen.
__
Longitudinal > Längsschnitt.
__
Masstheorie  mathematische Theorie des Messens
__
MA Moving Average Modell. > Zeitreihenanalyse. [, Matlab, ]
__
Markovkette
__
Maximale Clique (auch: Maximaler vollständiger Untergraph). Ausdruck der Graphentheorie und Klassifikation. Eine maximale Clique ist eine Clique, die durch das Umfassen eines mehr angrenzenden Scheitelpunkts, d. h. eine Clique nicht erweitert werden kann, die exklusiv innerhalb des Scheitelpunkt-Satzes einer größeren Clique nicht besteht.
    Eine Clique in einem ungerichteten Graphen G = (V, E) ist eine Teilmenge des Scheitelpunkt-Satz-C  V, solch, dass für alle zwei Scheitelpunkte in C, dort ein Rand besteht, der die zwei verbindet (anschließt). Das ist äquivalent, dass der durch C veranlasste Subgraph abgeschlossen ist (in einigen Fällen, kann sich der Begriff (Frist) Clique auch auf den Subgraphen beziehen).
__
Maximaler vollständiger Untergraph > maximale Clique.
__
Maximum-Likelihood-Methode. Von R. A. Fisher 1921 entwickeltes Verfahren zur Schätzung von Wahrscheinlichkeiten. Es wählt diejenige aus, die unter bestimmten Annahmen die größte Wahrscheinlichkeit für ein vorliegendes Resultat hat.
    Wallis  & Roberts (dt. 1969), S. 371:

"14.2.1.2 Maximale Mutmaßlichkeit. Das Prinzip, unter dem Punkt-Schätzfunktionen im allgemeinen ausgewählt werden, wird als das Prinzip der maximalen Mutmaßlichkeit {maximum likelihood) bezeichnet. Es handelt sich dabei um einen Gedanken, den Sir Ronald Fisher erstmalig im Jahre 1921 behandelte (vgl. Abschn. 1.4.2). Man betrachtet jeden möglichen Wert, den der Parameter haben könnte, und errechnet für jeden Wert die Wahrscheinlichkeit, daß die jeweilige spezifische Stichprobe eingetreten wäre, wenn dies der richtige Wert des Parameters wäre. Von allen möglichen Werten des Parameters wird dann derjenige als Schätzung ausgewählt, für den die Wahrscheinlichkeit der tatsächlichen Beobachtungen die größte ist. Formeln, die solche Schätzungen angeben, werden als Schätzfunktionen der maximalen Mutmaßlichkeit {maximum likelihood estimators) bezeichnet. ... .... ...
.    Eine Warnung: Der Grund für die Schätzung von P als 0,65 ist nicht die Tatsache, daß, wenn P = 0,65, das wahrscheinlichste Stichproben-Resultat p =0,65 wäre; in der Tat ist p — 0,65 das wahrscheinlichste Ergebnis in einer Stichprobe von 20 für jedes P zwischen 0,619 und 0,667. Der Grund für die Schätzung von P als 0,65 ist der, daß eine Stichprobe mit p = 0,65 wahrscheinlicher ist, wenn P = 0,65, als wenn P irgendeinen anderen Wert hat."

__
Median. Der Wert, der eine Messwert-Reihe in zwei Hälften teilt, z. B. 3 in:  1, 1, 2, 2, 3,  3,  3, 3, 4, 5, 5.
__
Mengenlehre. Nach der Mengenlehre besteht die Messwert-Reihe  "1, 1, 2, 2, 3,  3,  3, 3, 4, 5, 5"  aus 5 Elementen.
__
Merkmalsraum, relevanter. [1,]
__
Messen, Messung. Genau beschriebenes und damit prinzipiell wiederholbares und überprüfbares Verfahren zur Feststellung einer Ausprägung. Eine Messung ist lehr- und lernbar. Es ist sehr zweifelhaft, ob in der Erlebnis-Psychologie echte Messungen möglich sind.
__
Messfehler. Als allgemeiner Erfahrungssatz gilt: jede Messung ist mit einem Fehler behaftet, so das für den Messwert x, den gedachten wahren Wert w und den Messfehler f gilt: x = w + f.  Da der wahre Wert eine gedachte Konstruktion und nie bekannt ist, muss er in praxi geschätzt werden. Diesen Näherungswert nennt man auch den "richtigen" Wert r und damit gilt dann: x = r + f. Man nimmt hierfür oft den arithmetischen Mittelwert.  [> Fehlerarten.]
__
Messtheorie
Bezeichnung für die psychologische Messtheorie. Sie erforscht die Grundlagen des Messens in der Psychologie. Die "Messtheorie" der  Mathematik heißt Maßtheorie. In der Naturwissenschaft und Technik gilt die Norm DIN 1319 [W].
    Orth (1974) führt S. 9 aus:

"Das Messen ist sowohl historisch als auch methodisch gesehen eine der Grundlagen der Wissenschaft. Ohne die Durchführung exakter Messungen läßt sich die Entwicklung der empirischen Wissenschaften, insbesondere der Naturwissenschaften, nicht vorstellen. Seit sich die Psychologie, wie auch andere Sozialwissenschaften, mehr und mehr als empirische Wissenschaft versteht, stellt sich auch hier die Frage der Entwicklung geeigneter Meßmethoden. Es erwies sich jedoch sehr bald, daß die Messung psychischer Eigenschaften, wie z. B. Empfindungen, Einstellungen, Intelligenz oder Angst, zumindest schwieriger ist als die physikalischer Eigenschaften, wie z. B. Länge, Zeit, Gewicht oder elektrischer Widerstand. Es wurde sogar die Auffassung vertreten, daß das Messen in der Psychologie prinzipiell nicht möglich sei, zumindest nicht in dem Sinne wie beispielsweise in der Physik.
Vor diesem Hintergrund zeichneten sich zwei Fragen von grundlegender Bedeutung für die Psychologie ab:
1. Ist die Messung psychischer Eigenschaften prinzipiell möglich, und zwar in einem mit dem Messen in den Naturwissenschaften zu vereinbarenden Sinne?
2. Falls dies der Fall ist, wie können psychische Eigenschaften gemessen werden?
Der Klärung dieser sowie weiterer, hiermit zusammenhängender Fragen widmeten sich — in verstärktem Maße etwa seit den fünfziger Jahren — vor allem Wissenschaftstheoretiker, Logiker, Mathematiker, Wirtschaftswissenschaftler und Psychologen. Das Forschungsgebiet, das sich aus den Bemühungen um eine Antwort auf diese Fragen entwickelte, bezeichnen wir heute als Theorie des Messens oder als Meßtheorie.
Die Meßtheorie erforscht mit mathematischen Methoden die Grundlagen des Messens und gibt so die Voraussetzungen für die Meßbarkeit von Eigenschaften an. Ihre Ergebnisse zeigen, daß auch psychische Eigenschaften grundsätzlich meßbar sind, und zwar in demselben Sinne, wie es physikalische sind. Die theoretischen Untersuchungen der Meßtheorie führten darüber hinaus zur Entwicklung praktischer Meßverfahren, die in den Sozialwissenschaften neben die länger bekannten Skalierungsverfahren und Tests treten und neue Möglichkeiten der Messung insbesondere auch psychischer Eigenschaften bieten."

Die Grundprobleme des psychologischen Messens werden in vier Bereichen erörtert: Bedeutsamkeitsproblem, Eindeutigkeitsproblem, Repräsentationsproblem, Skalierungsproblem. Trotz eines gewaltigen formalen Apparates:

Krantz, D. H., Luce, R. D., Suppes, P. & Tversky, A. (1971). Foundations of measurement. Vol. 1 New York: Academic Press. [Taschenbuch 2006]

Suppes, Patrick, Krantz, David H., Luce, Duncan R. & Tversky, Amos (1989) Foundations of Measurement, Vol. 2 Geometrical, Threshold, and Probabilistic Representations. New York: Academic Press. [Taschenbuch 2006]

Luce, Duncan R.; Krantz, David H.; Suppes, Patrick & Tversky, Amos (1990) Foundations of Measurement, Vol. 3 Representation, Axiomatization and Invariance. New York: Academic Press. [Taschenbuch 2006]

sieht es mit der psychologischen Mess-Praxis immer noch sehr düster aus (August 2018). Die  grundlegenden Probleme der Psychologie  scheinen nicht begriffen. Vgl. hierzu auch die Kritik von Jaenecke, Peter  (10.12.07/28.12.07/04.08.14) Einführung in die Messtheorie. PDF Online.
__
Messwert. Zahlenwert.
__
Messungen per fiat  Orth, B. (1974, S. 41). Einführung in die Theorie des Messens. Stuttgart. Kohlhammer: "Das über die Skalierungsverfahren Gesagte gilt sinngemäß auch für psychologische Tests. Diese sind auch 'Meßverfahren per fiat' genannt worden (Torgerson, 1958; Pfanzagl, 1968; Fischer, 1970), da sie auf dem Glauben beruhen, daß die jeweilige Eigenschaft meßbar sei, und daß Tests zur Messung auf Intervallskalenniveau führten. Ein weiterer Unterschied zwischen Meßstrukturen und Tests besteht darin, daß bei letzteren nicht ein empirisches Relativ in ein numerisches, sondern ein numerisches Relativ in ein anderes numerisches Relativ abgebildet wird. Es werden (numerische) Testrohwerte in numerische Testwerte abgebildet bzw. transformiert. Für eine Messung mit Hilfe von Tests auf Intervallskalenniveau sind die meßtheoretischen Grundlagen erst noch zu entwickeln. ..."
__
Methode Methodisch vorgehen heißt, Schritt für Schritt, von Anfang bis Ende, Wege und Mittel zum (Erkenntnis-) Ziel angeben. Zum allgemeinen Methodenbegriff gehört wenigstens ein Ziel, ein Mittel, um dieses Ziel zu erreichen und ein Weg bzw. eine Anwendungsregel für die Mittel. In der Psychopathologie und Psychotherapie gibt es zwei Hauptziele: Erkenntnis-Ziele (Diagnostik), Veränderungs-Ziele (Behandlung).
__
Metrik  > W: Metrischer Raum.
Eine Metrik definiert Abstandsmaße, wovon es verschiedene geben kann (euklidische, nicht-euklidische, ...)
__
Minimum. Der kleinste Wert in einer Reihe, z. B. 1 in: 1, 1, 2, 2, 3,  3,  3, 3, 4, 5, 5.
__
Mikrozensus. Stichprobenauswahlverfahren.  [W]
__
Missing Data (fehlende Daten bei Erhebungen)
Bei multivariaten Verarbeitung kann es zu erheblichen Störungen kommen, wenn Missing Data und keine angemessenen Lösungen vorliegen. Werden unvollständige Datensätze paarweise aus der Korrelationsberechnung ausgeschlossen, kommt es zu einer Verzerrung der Winkel aufgrund verschieden grožer Stichumfänge. Formal äquivalent und daher ebenso problematisch sind Metaanalytische Stichproben-Mischungen mit unterschiedlichen Umfängen N. Sponsel & Hain (1994, Kap. 3.2.4, Hain 6.5.4) haben den Auswirkungen von Missing Data Arbeiten vorgelegt. Sponsel hat an zahlreichen Matrizenanalysen gezeigt, welche Entgleisungen auftreten können, wenn mit falschen Missing Data Lösungen gearbeitet wird. Viele Statistikprogrammpakete bieten seit Jahrzehnten Missing-Data-Problemlösungen an (z.B. BMDP 1983: SAS 1983; SPSS 1975; SPSS 9 1983), aktuell Holm/ALMO 2020 "plausible values".
    Aktuell kann man bei Coronazahlen der epidemiologischen Statistiker täglich viele ungelöste und nicht einmal ordentlich dokumentierte Missing Data beobachten.

Lit-MisDat (Auswahl):
Dodge,Y. (1985) Analysis of experiments with missing data. Wiley.
Enders, Craig K. (2010) Applied Missing Data Analysis.  Guilford Press
Graham, John W. (2012)  Missing Data. Springer
Little, Roderick J. A.; Rubin, Donald B. (2002), Statistical Analysis with Missing Data (2nd ed.). Wiley.
Lösel,F.,  Wüstendörfer, W. (1974)  Zum Problem unvollständiger Datenmatrizen in der empirischen Sozialforschung, Kölner Zeitschrift für Soziologie und  Sozialpsychologie 26, 1974, 342-357
Mirkes, E.M.; Coats, T.J.; Levesley, J.; Gorban, A.N. (2016). Handling missing data in large healthcare dataset: A case study of unknown trauma outcomes. Computers in Biology and Medicine. 75: 203–216. arXiv:1604.00627.
Raghunathan, Trivellore (2016) Missing Data Analysis in Practice. Chapman & Hall

__
Mittel  um Ziele zu erreichen. Wichtiger allgemeiner und wissenschaftlicher Grundbegriff, der zum Methodenbegriff gehört. Die sprachliche Wendung Mittel zum Zweck bringt es ganz gut auf den Punkt.
__
Mittelwerte
 

Mittelwert ohne nähere Angabe. Meist ist der arithmetische gemeint und oft auch so erkennbar. Sicher wäre es, genau zu anzugeben, von welchem man spricht. Most (1955, S. 8, § 12: S. 57-65) führt folgende Mittelwerte an: "I. Errechnete Mittelwerte: 1. und 2. Arithmetische Mittel. 3. und 4. Geometrische Mittel. 5. Harmonisches Mittel. 6. Quadratisches Mittel. 7. Antiharmonisches Mittel. II. Mittelwerte der Lage: 1. Zentralwert. 2. Häufigster Wert. 3. Schwerster Wert. 4. Scheidewert." Lit: > Jecklin; [W]
__
Mittelwerte und Durchschnitte
Informations- und Lernseite des statistischen Bundesamtes zum Thema "Mittelwerte und Durchschnitte".

Mittelwert, arithmetischer. Summe aller Werte dividiert durch die Anzahl. [W]
__
Mittelwert, geometrischer.
Geometrisches Mittel (n-te Wurzel des Produkts der n Zahlen; Anwendung Wachstumsraten, durchschnittliche Verzinsung bei jährlich unterschiedlichen Zinssätzen. Mathebibel: "Das geometrische Mittel (im Gegensatz zum arithmetischen Mittel) dient zur Messung des Durchschnitts einer prozentualen Veränderung. Aus diesem Grund sagt man zum geometrischen Mittel auch durchschnittliche Veränderungsrate.")
__
Mittelwert, harmonischer. [W]
Besonders geeignet für Mittelwerte bei Verhältniszahlen (z.B. von Geschwindigkeiten: v = s/t). [W]
Harmonisches Mittel (Anzahl der Werte durch die Summe der Kehrwerte der Werte; Anwendung Geschwindigkeiten. Mathebibel: "Das harmonische Mittel kommt meist dann zum Einsatz, wenn der Mittelwert von Verhältniszahlen gesucht ist. Eine Verhältniszahl ist als Quotient zweier statistischer Größen definiert.")

__
Modalwert Der häufigste Wert in einer Reihe, z. B. 3 in:  1, 1, 2, 2, 3, 3, 3, 3, 4, 5, 5.
__
Modell  Wichtiger, nützlicher aber vieldeutiger wissenschaftlicher Grundbegriff. 1) Nachbildung, künstliche Kopie von etwas Bestehendem, z.B. Modellauto, Eiffelturm, Gehirn, Landkarte. 2) Konstruktion für einen Sachverhalt zu seinem besseren Verständnis, zur Erklärung und Vorhersage, Theorie, z.B. Urnenmodell der Wahrscheinlichkeit, Messmodelle. 3a) Isomorphie zwischen zwei Repräsentationen. 3b) In der Mathematik auch die konkrete Realisation einer abstrakten Theorie. Die Vorstellung, im Ganzen oder in Teilen, von Bild (Original) und Abbild (Modell) trifft es ganz allgemein. Zusammenhänge zwischen Begriffen können graphisch dargestellt werden: Modell des Zusammenhanges. Skizzen, Graphiken, Fotos oder 3D Darstellungen können als Modelle aufgefasst werden. Ein Modell der Denkprozesse bildet nach, wie Denken psychologisch tatsächlich abläuft. Ein Handlungs-Modell erklärt Entwicklung, Entscheidung, Entschluss und Ausführung einer Handlung. Modelle stehen oft auch am Anfang der Theorienbildung als heuristische Konstruktionen. Besonders wertvoll kann an Modellen sein, dass sie zu Präzisierungen zwingen, Stärken und Schwächen treten klarer und fassbarer hervor.
__
Moderatorvariable
Eine Variable V, die über eine andere Variable und mit ihr verbundene A auf eine Variable B wirkt, z.B. auch im klassischen Fall einer Scheinkorrelation (Geburtenrate und Anzahl der Storchennester)
__
möglich, Möglichkeit  > Gegensatz  unmöglich.
Wichtiger allgemeiner und wissenschaftlicher Grundbegriff, dass sich ein  Sachverhalt  ereignen kann, aber nicht ereignen muss. Nicht alles  Denkbare ist auch möglich. Denken kann man alles, auch sein Gegenteil. Ontologisch gilt im allgemeinen die Stugfenfolge: Denkbar > möglich > wirklich.
__
Moment. Sammelbezeichnung oder Klassenbegriff für die verschiedenen statistischen Kennwerte oder Parameter einer Verteilung:  [W]. 1. Moment Erwartungwert (Mittelwert), 2. Moment Varianz, 3. Moment Schiefe, 4, Moment Kurtosis (Exzess).
__
Morbidität. Unklarer medizinstatistischer, epidemiologischer Begriff. 1) Gesundheitsbrockhaus 1990: Gibt die Häufigkeit einer Erkrankung pro 1000 oder 10.000 für ein Jahr oder einen anderen Zeitraum an. 2) Grundmann, E. (1994, Hrsg.; S.4-5): „Die M. ist die Zahl einer bestimmten Erkrankung in einer bestimmten Bevölkerungsgruppe in einem bestimmten Zeitraum (meist einem Jahr). Sie berechnet sich nach der Formel: M_z = (Erkrankungszahl x 10 000) / Bevölkerungszahl“. In dieser Formel fehlen die Einheiten der Zeit und die soziologische Spezifikation. 3) Nach Renner, D. (6.A. 1990, S. 24): „M. - Anzahl an einer bestimmten Krankheit leidender Personen per Gesamtbevölkerung in einem bestimmten Beobachtungszeitraum.“ Nach diesem Autor wird M. auch synonym mit Neuerkrankungsrate (> Inzidenz) verwendet. Die Inzidenz wird von Schaefer & Blohmke (1978, S.111) wiederum der > Prävalenz gleichgesetzt.
__
Mortalität. Medizinstatistischer, epidemiologischer Begriff, der die Sterblichkeit einer Krankheit bezogen auf die Gesamtzahl der Lebenden eines Jahrganges pro 10.000 oder 100.000 angibt im Unterschied zur > Letalität, die das Verhältnis der an einer Krankheit Gestorbenen in Beziehung zur Anzahl der Erkrankten angibt.
__
Multidimensionale Skalierung
"Multidimensionale Skalierung (MDS) umfasst eine Gruppe von  Skalierungsmethoden, die Messungen von Ähnlichkeiten bzw. Unähnlichkeiten zwischen Paaren von Objekten als Distanzen zwischen Punkten in einem niedrigen multidimensionalen Raum wiedergibt (Borgi Groenen 2005, S. 3)." Quelle S. 153: Rohrlack, Christian () Multidimensionale Skalierung. In (153-173) Albers, Sönke; Klapper, Daniel ; Konradt, Udo; Walter , Achim & Wolf, Joachim (2009,  Hrsg.)  Methodik der empirischen Forschung 3.,  überarbeitete und erweiterte Auflage. Wiesbaden: Gabler.
__
Multikollinearität. In einer Tabelle (Matrix) gibt es mindestens 2 Kollinearitäten (vergleichbarer Datensätze, also aus der gleichen Stichprobe oder Population mit jeweils gleicher Anzahl n).
__
Nebenbedingung >  > Bedingung.
__
Non-parametrische Statistik. Nicht-parametrische ist im Gegensatz zur parametrischen Statistik voraussetzungsarm und mehr datenangemessen.  Altmeister Siegel schreibt (dt. 1976, S. 2f): "Im Lauf der Entwicklung der modernen statistischen Methoden konstruierte man zunächst Verfahren des statistischen Schließens, die sehr viele Annahmen über die Art der Population machten, aus der die Stichprobe gezogen wurde. Da die Populationswerte "Parameter" sind, nennt man diese statistischen Verfahren parametrisch. Eine Technik des Schließens kann z.B. auf der Annahme beruhen, daß die Daten aus einer normalverteilten Population stammen. Oder sie kann auf der Annahme beruhen, daß zwei Datenbündel aus Populationen erhoben wurden, die dieselbe Varianz (a2) oder Streuung der Daten aufweisen. Diese Verfahren führen zu eingeschränkten Schlußfolgerungen, z.B. 'Wenn die Annahmen über die Art der Verteilung der Population(en) gültig sind, läßt sich daraus schließen, daß... '.
    Inzwischen sind eine große Anzahl von Verfahren des statistischen Schließens entwickelt worden, die ohne die zahlreichen oder strengen Annahmen über Parameter auskommen. Diese neueren "verteilungsfreien1 oder nicht-parametrischen Verfahren führen zu Schlüssen, die mit weniger Einschränkungen verbunden sind. Wenn wir eines davon anwenden, so können wir etwa sagen: "Ungeachtet der Verteilungsform der Population(en) können wir folgern, daß...". In diesem Buch werden wir uns mit diesen neueren Verfahren beschäftigen.
    Einige nicht-parametrische Verfahren werden oft "Rang-Tests" oder "Ordinal-Tests" genannt, und diese Bezeichnungen lassen noch andere Unterschiede zu parametrischen Tests erkennen. Bei der Berechnung parametrischer Tests addieren, multiplizieren, und dividieren wir die Werte aus den einzelnen Stichproben, Führt man diese Rechenarten auch mit Daten durch, die eigentlich nicht numerisch sind, so werden diese verzerrt, und die aus dem Test gezogenen Schlußfolgerungen sind nicht mehr zulässig. Man ist also in der Anwendung parametrischer Verfahren auf Daten beschränkt, die in numerischer Form vorliegen. Dagegen gehen viele nicht-parametrische Tests von der Rangordnung der Daten und nicht von deren 'numerischem' Wert aus, und einige Tests lassen sich sogar auf Daten anwenden, die nicht einmal eine Rangordnung zulassen, d.h. die lediglich klassifiziert sind. Während der parametrische Test etwa die Differenz der arithmetischen Mittel zweier Datenreihen untersucht, geht es im äquivalenten nicht-parametrischen Test um den Unterschied zwischen den Medianwerten. Die Berechnung des arithmetischen Mittelwertes erfolgt über arithmetische Operationen (Addition und anschließend Division), die Bestimmung des Medians geschieht durch Zählen. Die Vorteile von Rangstatistiken für Daten aus den Verhaltenswissenschaften (deren Daten nur scheinbar 'numerisch' im strengen Sinne sind) liegen auf der Hand. Wir werden diesen Punkt in Kap. 3 ausführlicher behandeln, wo parametrische und nicht-parametrische Tests miteinander verglichen werden."
__
Norm. Bezugs- oder Vergleichgröße. Vieldeutiger Begriff in Wissenschaft und Leben.
__
Normalverteilung. Gaußsche Glockenkurve [1, 2, W, ]. Wichtigste Verteilung der mathematischen Statistik. Häufung der Werte in der Mitte und von da aus in der Häufigkeit abnehmend zu den Rändern hin.

Grimms Behauptung scheint überzogen.
__
Normalbedingungen > Normbedingungen, > Standardbedingungen.
Viele Aussagen gelten nur relativ zu bestimmten Bedingungen. Mit Normalbedingungen sind durchschnittliche, übliche oder gewöhnlich Bedingungen gemeint, wobei diese Begriff selbst auch erklärungsbedürftig sind. Liegen genaue und klar Bedingungen vor, für die eine Aussage gelten soll, kann man auch von  Normbedingung  oder  Standardbedingung  sprechen.
__
Normbedingung  > Normalbedingungen > Standardbedingungen.
Hier werden genaue und klar Bedingungen formuliert, unter denen eine Aussage gelten soll. Es ist eine Regel des  wissenschaftlich gesunden Menschenverstandes, dass Aussagen nur relativ zu bestimmten und auszuweisenden Bedingungen gelten. Während Mathematik, Naturwissenschaft und Technik hier ein hohes Niveau erreicht haben, sieht es in den Sozial-, Psycho- und Geisteswissenschaften unverantwortlich schlecht aus (Stand 25.07.2018).
__
Normalwert. > Referenzwert.
__
Normwerte. Werte, die nach einem bestimmten, nachvollzieh- und prüfbaren Verfahren, gewonnen und berechnet werden. In Straube (1988, Hrsg.), S.9 heißt es: "Der Ausdruck „Normwert" steht hier synonym für Normal-, Richt- oder Referenzwert, wobei sich letztere Bezeichnung durchzusetzen scheint. Es wird nachdrücklich darauf hingewiesen, daß alle Normwertangaben die intraindividuelle Situation des Gesunden und des Kranken nicht berücksichtigen können. Weiterhin muß der Arzt auf tages-, monats- und jahreszeitliche Schwankungen Rücksicht nehmen."
    Hier noch eine Tabelle aus Lienert (1969, 3. A.), S. 337:
_

__
Nullhypothese [1, ] Streng formal besagt die Nullhypothese Kennwert-1  = Kennwert-2 oder x = y, wenn die Irrtumswahrscheinlichkeit einen Wert < Signifikanzniveau alpha hat unter der Voraussetzung, dass x = y gilt. Die häufigste und übliche, aber keineswegs zwingende Deutung ist: Es gibt keinen Unterschied zwischen den Kennwerten. Tatsächlich kann jede spezifizierte Hypothese zur Nullhypothese gemacht werden. Die Alternativhypothese, sofern sie spezifiziert ist, lässt sich natürlich auch berechnen. Vom praktischen Standpunkt wählt man die Hypothese zur Nullhypothese, deren Verwerfung besonders interessiert. Grundsätzlich ist zu fordern, dass alle relevanten Annahmen und Voraussetzungen, die in die Prüfung eingehen mitgeteilt und in einer Hypothesendiskussion kritisch erörtert werden.
    Bortz (1985, S. 144) führt aus: "Die statistische Nullhypothese (H₀) folgt ebenfalls zwingend aus der statistischen Alternativhypothese (H₁). Bezogen auf den Vergleich zweier Mittelwerte sind die folgenden drei Hypothesenpaare denkbar: H₁:  µ₀ > µ₁ H₀: µ₀ <= µ₁
 H₁:  µ₀ < µ₁ H₀: µ₀ >= µ₁
H₁:  µ₀ =|= µ₁ H₀: µ₀ = µ₁

In ähnlicher Weise formuliert man statistische Nullhypothesen zu statistischen Alternativhypothesen, die sich auf Zusammenhänge beziehen (z.B. H₁: rho > 0, H₀:  rho <= 0).
    Die Nullhypothese stellt in der klassischen Prüfstatistik die Basis dar, von der aus entschieden wird, ob die Alternativhypothese akzeptiert werden kann oder nicht. Nur wenn die Realität „praktisch" nicht mit der Nullhypothese zu erklären ist, darf sie zugunsten der neuen Alternativhypothese verworfen werden."
__
Numerologie. Nicht prüf- oder wiederholbare Methode, spezielle Bedeutungen von Zahlen zu erkennen. Auch in der modernen Wissenschaft sehr verbreitet, z. B. in der Faktorenanalyse oder Signifikanzstatistik.
__
Nutzen: mehr oder - meist - minder intersubjektive Wertzuweisung über den Gebrauchswert von Sachverhalten. Der Nutzen spielt eine große Rolle für die meisten Menschen in fast allen Lebensbereichen, aber auch in der Wissenschaft, besonders in der Ökonomie (Grenznutzentheorie) und Psychologie: Nützlich erscheint, was Bedürfnisse, Wünsche und Interessen befriedigt.
__
Objektivität := die Messung soll nicht davon abhängen, wer mißt. Allgemeiner: eine Feststellung über einen Sachverhalt heißt objektiv, wenn sie unabhängig vom Feststeller ist, also andere das Gleiche feststellen.
__
Objektivität, spezifische := Begriff des Rasch-Modells, wonach die Messergebnisse (Relationen der Messobjekte) nicht vom Messinstrument (Test, Skalierungsverfahren) abhängen darf (>Relationentreue).
__
Odds-Ratio. Das Odds Ratio gibt, um wieviel größer die Chance zu erkranken in der Gruppe mit Risikofaktor ist (verglichen mit der Gruppe ohne Risikofaktor). Das Odds Ratio nimmt Werte zwischen 0 und Unendlich an. Ein Wert von 1 bedeutet ein gleiches Chancenverhältnis. [W]
__
Ökonomie (Nutzen, Utilität). Kosten, Aufwand, Nutzen, Preis-Leistungs-Verhältnis.
__
Operationalisierung
__
Operationscharakteristik (OCR). [W]
__
Ordnung
Wichtiger allgemeiner, wissenschaftlicher und mathematischer Grundbegriff, allerdings mit unterschiedlichen Bedeutungen (Homonym). Als erste Grundunterscheidung bietet sich gewöhnlich an: in welcher Dimensionen, wobei auch dimensionslose Ordnungen möglich sind, also Ordnungen, die auf keine Dimension Bezug nehmen: Alpha, Beta, Gamma, ...; 4, 2, 9, 29, ... Ordnung heißt in den zwei vorangehenden Beispielen Anordnung, Reihenfolge. Man kann aber auch die Ordnung selbst als Dimension auffassen. Grundlegende Ordnungskriterien sind Anfang, Ende, Verlauf, Vorgänger, Nachfolger, Anzahl der Sachverhalte, Stelle (Platz, Position).
__
Orthosprache  Methodisch aufgebaute Wissenschaftssprache.
__
Panelstudien

Demoskopischer und soziologischer Begriff für wiederholte Erhebungen mit dem gleichen Variablensatz an gleichen Stichproben. Arminger, Gerhard (1976). Anlage und Auswertung von Paneluntersuchungen. In (134-235) Holm, Kurt (1976) Die Befragung 4. München: Francke.

__
Paradigma. Charakteristische, typische und grundlegende Situation. Zweiwertiges Aussageparadima: eine Aussage ist wahr oder falsch. Dreiwertiges Aussageparadigma: Eine Aussage ist wahr, falsch oder nicht bestimmbar. > Statistisches Paradigma.
__
Parameter: kennzeichnende, charakteristische Größe, z.B. Mittelwert, Varianz, Minimum, Maximum, Spanne, Verteilung.
__
Parameter-Konstanz: kennzeichnende Größe, die für bestimmte Bedingungen gleich bleibt, z.B. Mittelwert, Varianz.
__
parametrische Verfahren. Sie gehen von bestimmten Modellannahmen, z. B. Normalverteilung oder Parameterkonstanz, aus.
__
Paranormale Fähigkeiten testen. [PDF, S. 376] [GWUP] [Randi]
__
Pfadanalyse
__
Plausibel, Plausibiliät
Ein Sachverhalt₁ ist in dem Maße plausibel₂ (pl), je stärker gewichtete₂ Gründe₁ G₊  für und je schwächer gewichtete₂ Gründe₁G_- gegen ihn angegeben werden können (Quelle). Plausibilitätsformel:
 

pl+  =  (G+)  /  (G+ +  G- ) pl-  =  1 - pl+

__
Poissonverteilung
"Diese Verteilung wird dann angewendet, wenn ein Ereignis sehr selten eintritt. Man erhält die Poisson-Verteilung durch
einen Grenzübergang aus der Binomialverteilung. Ein klassisches Beispiel für eine Poisson-Verteilung (von S. D. Poisson
1837 eingeführt) ist der Tod von Soldaten durch Pferdehufschlag." Hirz, Helmut (2008), S. 42.
__
Polung. negative oder positive Wertzuweisung zu einem Bearbeitungssachverhalt.
Population: Gesamtheit, Ganzes.
__
Population. Grundgesamtheit, die betrachtet wird.
__
posteriori
__
Power. Auch Macht, Teststärke oder Gütefunktion genannt: Wahrscheinlichkeit dafür, dass die Nullhypothese abgelehnt wird, wenn die Alternativhypothese richtig ist. Power = 1 - b mit b als Fehler 2. Art. [W]. Programm der Uni-Düsseldorf zur Berechnung der Power. Lit: Cohen (1969).
__
Power, positiv prädiktive
__
Power, negativ prädiktive
__
Prävalenz. Epidemiologisch-statistischer Begriff, der das Verhältnis aus Anzahl der Kranken zu einem Stichtag gegenüber den Personen mit Merkmal an diesem Stichtag angibt. Anwendung: an X Erkrankte : Medikamentenanwender.  Beaglehole et al. (1997, S. 30): "Die Prävalenz einer Krankheit ist die Anzahl der Krankheitsfälle in einer definierten Population zu einem bestimmten Zeitpunkt."
___
Praxeologie. Ein Name für lehr- und lernbares, begründetes praktisches Vorgehen nach Wissenschaft, Erfahrungswissen und individuell situativen Gegebenheiten. In den stark idiographisch geprägten Berufen der JuristInnen, Heilfachkundigen und PsychologInnen  müssen wissenschaftliche Ergebnisse auf einen Einzelfall angewendet werden. Das ist ein bislang von den Universitäten sehr stark vernachlässigtes Gebiet, so gibt es m. W. auch keinen Lehrstuhl für idiographische Wissenschaftstheorie und Praxeologie. Hier spielen auch der berüchtigte sog. "gesunde Menschenverstand" und alltägliches Regelwissen wie praktische Vernunft eine große Rolle. > evidenzbasierte Medizin.
Querverweise:

Hake: Statistische Falschschlüsse Gruppe/Einzelfall.

Nedopil: Prognosen in der Forensischen Psychiatrie.

__
Produkt-Moment (kleines, großes). Ausdruck aus der Matrixalgebra (z.B. Horst 1963, p. 166-171) im Umfeld multivariater Datenanalyse (z.B. Revenstorf 1980, S.28, 53, 85 ). Sei X eine Matrix, dann wird X'X das kleine (Minor) und XX' gelegentlich das große (Major) Produktmoment genannt. Die Bravais-Pearson Korrelation wird auch als Produkt-Moment-Korrelation bezeichnet. Die Encyclopedia of Statistical Science, 1986, Vol. 7, p. 292 führt aus:

__
Prognose.  Wichtiger allgemeiner und wissenschaftlicher Grundbegriff, der bei seriöser Betrachtung eine Theorie voraussetzt, wobei meist Erklären und Vorhersagen zusammenhängt.
__
Prozentrang. Prozentsatz derjenigen, die einen so oder so großen Wert erreichen.
__
Prüfstatistik. > Signifikanztest. Clauss & Ebner (1970, S. 170) schreiben: "Der gesamten Prüfstatistik liegt demnach folgender Gedanke zugrunde: Dann und nur dann, wenn die Stichproben Ergebnisse liefern, die bei Gültigkeit der Ausgangshypothese unwahrscheinlich sind, verwerfen wir die Hypothese."
__
Quantile. Vielheiten, meist in gleiche Klassen zusammengefasst. Quartile und Prozentränge sind Quantile.  (Beispiele hier)
__
Quartile. 1. Quartil := erstes Viertel der Stichprobe. 2. Quartil:  Zweites Viertel der Stichprobe. Median := halbiert die Stichprobe, 3. Quartil =: drittes Viertel der Stichprobe.  4. Quartil = letztes Viertel der Stichprobe. Seien 100 Messwerte von 1,2,3, ..., 100 gegeben, dann gehören 1-25 zum ersten Quartil, 26-50 zum zweiten Quartil, 51-75 zum dritten und 76 bis 100 zum vierten Quartil.
__
Querschnitts-Statistik, eine Statistik, die über verschiedene Objekte im gleichen Zeitraum erhoben wird, z. B. der arithmetische Mittelwert für den durchschnittlichen Alkoholkonsum junger Frauen zwischen 21 und 25 Jahren in Bayern. > Längsschnitt.
__
Randbedingung  > Bedingung.
__
Rang, Rangzahlen, Rangtests. Ränge haben nach traditioneller Auffassung nur sog. Ordinalniveau. Mit solchen Größen sind numerische Rechnungen bis auf monotone Transformationen nicht zulässig.  Das wird aber von vielen sog. Rangtests missachtet. Die mathematische Statistik ist hier falsch und unsauber, wenn sie unzulässig addiert, subtrahiert, dividiert, multipliziert, ohne im Einzelfall gezeigt zu haben, dass die metrisch-numerische Handhabung zu den zulässigen ordinalen Operationen äquivalente Ergebnisse liefert.
__
RCT randomized controlled trial. Randomisierte kontrollierte Studie. Hier werden die ProbandInnen per Zufall einer Bedingung zugeordnet, um die Fehler zu minimieren. Die Untersuchungsgruppen sollten hierbei "groß" genug sein.
__
Referenzwert > wörtlich Bezugswert bzw. Bezugswertbereich,  Normwert, Normalbereichswert in der Medizin  (im Laborbereich gewöhnlich unzulänglich ausgewiesen). In der Psychologie werden z. B. sog. "Normen" bei Intelligenztests meist für Geschlecht, Alters- und Bildungsklassen bestimmt. In der Medizin sind naturgemäß besonders wichtige Kriterien spezielle Erkrankungen und Risiko-, aber auch ökologische Faktoren (wie z. B. Stadt, Land, Abgasbelastung, Sendemasten, Strahlungsbelastung [Elektrosmog], Chemie- oder Atomkraftwerke in der Nähe, oder Berufe, die mit bestimmten Risiken einhergehen, können sehr wichtig sein. Beispielrechnung. Setzt man bei parametrischen statistischen Verfahren eine Mindeststichprobengröße von N=30 an und geht man aus von 2 Geschlechtern, 5 Altersklassen, 3 Schulbildungsgraden, 6 ökologischen Klassen, 27 Gesundheitsfaktoren (3 Bewegungsgrade, 3 Ernährungsgrade, 3 Körperindexgrade), 100 Krankheitsklassen und 10 Risikofaktoren ergibt sich folgende Rechnung: STC [Stichprobencharakteristiken] = 30 * 2 * 5 * 3 * 6 * 27 * 100 * 10 = 48.600.000, d. h. 48,6 Millionen Laborbefunde. Das wären die theoretischen Erfordernisse, wenn jede Stichprobenkombination vertreten sein soll. Es kann natürlich durchaus vorkommen, dass nicht jede Kombination mit 30 Fällen besetzt werden kann, weil sie zu selten vorkommt.
__
Regression, Regressionsanalyse. Einfaches lineares Modell nach y = a + b*x. Ein Wert y wird auf einen Wert x zurückgeführt, z.B. das Gewicht auf die Körpergröße. Das geht auch umgekehrt, indem man die Körpergröße auf das Gewicht zurückführt. Als Maß für den Zusammenhang beider Regressionen dient der Korrelationskoeffzient, der sich auch aus der Wurzel des Produktes beider Regressionskoeffzienten (geometrisches Mittel) errechnen lässt. b ist die Steigung und heißt auch beta-Gewicht. Inhaltlich interpretiert gibt b an, in welchem Verhältnis y steigt (fällt), wenn x um eine Einheit steigt (fällt). Im Prinzip gibt es beliebige Regressionsmodelle, letztlich so viele, wie Datenmodelle und Funktionsverläufe, die sie charakterisieren. Das einfache lineare Modell ist also nur eines, wenn auch das wohl meist angewendete. Regressionen bei Wachstumsprozessen werden "linearisiert" durch logarithmieren (Bsp.). Rinne (1995), S. 415f f gibt 7 Voraussetzungen an.
__
Relation (Beziehung). Beispiele: größer, kleiner, gleich, auf, unter, gleich alt wie, besser. Grundlegender, aber wegen seiner Abstraktion schwieriger mathematischer Grundbegriff, der seit der Durchsetzung der Mengenlehre auch über diese definiert wird: Eine Relation ist eine Teilmenge der Kreuzmenge (kartesisches Produkt, Paarmenge). Sei A = {Main, Passau, Frankfurt, Donau}, so ist die Kreuzmenge, AxA, numeriert: 1. (Main, Main), 2. (Main, Passau), 3. (Main, Frankfurt), 4. (Main, Donau), 5. (Passau, Main), 6. (Passau, Passau), 7. (Passau, Frankfurt), 8. (Passau, Donau), 9. (Frankfurt, Main), 10. (Frankfurt, Passau), 11. (Frankfurt, Frankfurt), 12. (Frankfurt, Donau), 13. (Donau, Main),  14. (Donau, Passau), 15. (Donau, Frankfurt) und 16. (Donau, Donau). Relationen können hier sein: I. Fluß und Stadt gehören zusammen: 3 und 8. II. Fluß und Stadt gehören nicht zusammen: 2 und 7. III. identische Flüsse: 1 und 16. IV. Identische Städte: 6 und 11. V. Flüsse: 1, 4, 13 und 16. VI. Städte: 1, 3, 5, 6, 7, 9, 10., 11. VII. Identische Namen: 1, 6, 11, 16. VIII. schwebt über: wird von keinem der Paare erfüllt.
__
Relationentreue.
__
Reliabilität. Messgenauigkeit. In der Psychologie meist - und nicht unproblematisch - über die Korrelation geschätzt.
__
Repräsentation. Grundlegender Begriff für die Stichprobenstatistik, schließende Statistik und für die allgemeine, auch alltägliche "Testtheorie". Erheben wir Werte, so sollen diese repräsentativ für ... sein. Bei Laborwerten kann es sehr darauf ankommen, wie die Randbedingungen der Erhebung sind (z. B. Tageszeit, nüchtern). Ist ein Laborwert, z. B. Gamma-GT pathologisch erhöht, so wird man das im allgemeinen beobachten und Messwiederholungen ansetzen. Ein Gamma-GT-Wert ist sozusagen nur eine einzige Stichprobenziehung aus den praktisch unendlich viel anmutenden Möglichkeiten. Eine besondere Bedeutung hat der Begriff noch in der Messtheorie. Das Repräsentationstheorem dort besagt, dass es eine homomorphe Abbildung von einem empirischen Relativ, z. B. drei Hölzchen, in ein numerisches Relativ mit z. B. drei Zahlen so gibt, dass die Beziehungen zwischen den Hölzchen durch die Zahlen repräsentiert werden.
__
Repraesentationsproblem
Ausdruck der psychologischen Messtheorie. Coombs et al, S. 21: "(1) Das Repräsentationsproblem: Können alle Eigenschaften gemessen werden? Wenn nicht, was sind die Bedingungen dafür, daß Meßskalen eingeführt werden können? Was sind die notwendigen (oder hinreichenden) Bedingungen für die Konstruktion zum Beispiel einer Gewicht- oder Nutzenskala?"
__
Risiko: Viele Entscheidungen bergen ein Risiko, das oft unbekannt oder nur sehr ungenau zu bestimmen sind. Umso mehr werden dann Vermutungen oder Vorurteile bemüht. Durch die oft sensationsorientierten Medien wird hier viel Schaden angerichtet (> Risikowahrscheinlichkeiten). So beklagt Gigerenzer in seinen Büchern Das Einmaleins der Skepsis(2002) und Risiko (2013) fehlende Risikokompetenz - nicht nur der BürgerInnen.

Risikokompetenz
Wichtigerer neuerer Begriff, für den sich Gigerenzer in seinen Büchern Das Einmaleins der Skepsis (2002) und Risiko (2013) sehr einsetzt und dafür plädiert, Risikokompetenz bereits in der Schule zu lehren. Besonders die drei Themen Gesundheitskompetenz, Finanzkompetenz und Digitale Risikokompetenz hält er mit den drei zu vermittelnden Fertigkeiten Statistisches Denken, Faustregeln, Die Psychologie des Risikos für wichtig.

Risikowahrscheinlichkeiten - immer die absoluten Häufigkeiten einbeziehen
Gigerenzer warnt in seinen Büchern Das Einmaleins der Skepsis (2002) und Risiko (2013) eindringlich und überzeugend belegt davor, sich von Wahrscheinlichkeiten lenken zu lassen, weil sich viele Menschen schwer tun, verschiedene Wahrscheinlichkeiten gegeneinander angemessen und vernünftig in Beziehung zu setzen. Insbesondere warnt er vor der Angabe relativer Risikowahrscheinlichkeiten und empfiehlt stattdessen, absolute Zahlen zu verwenden. In mehr oder minder regelmäßigen Abständen werden die Frauen aufgeschreckt, wonach das Thromboserisiko durch Einnahmen von Antibabypillen wieder einmal "erschreckend" gestiegen sei. So meldete man in Großbritannien: "Die Antibabypillen der dritten Generation verdoppeln das Thromboserisiko - das heißt, sie erhöhen es um 100 Prozent". Man verschwieg, dass das Thromboserisiko der Vorgängerpille bei 1 : 7000 lag. In der neuen Generation der Antibabypille sei das Risiko auf 2 : 7000 gestiegen. Tatsächlich erhöhte sich rein rechnerisch das relative Risiko um 100% - aber bei welchen Grundraten! Die Folgen dieser "Warnung" waren verheerend (S. 17): "Diese eine Warnung führte im folgenden Jahr in England und Wales zu geschätzten 13000 (!) zusätzlichen Abtreibungen. Doch das Unheil währte länger als ein Jahr. Vor der Meldung gingen die Abtreibungsraten stetig zurück, aber danach kehrte sich dieser Trend um, und die Abtreibungshäufigkeit stieg in den folgenden Jahren wieder an. Die Frauen hatten das Vertrauen in orale Kontrazeptiva verloren, und die Pillenverkäufe gingen stark zurück."
__
ROC. Diagramm bei dem auf der Ordinate die Sensitivität und auf der Abszisse 1-Spezifität eingetragen wird. Daraus lässt sich das Verhältnis aller richtig positiven und falsch positiven Zuweisungen ersehen. [W]
__
Rohwert := scorierter Bearbeitungswert, dem Bearbeitungswert wird ein Zahlenwert zugeordnet. Wichtiger Grundbegriff für sozialwissenschaftliche Fragestellungen.
__
Sachverhalt
Allgemeiner und wissenschaftlicher Grundbegriff mit folgenden Eigenschaften:

seine Existenz kann in Bezug auf eine Welt wahr, falsch, unentscheidbar sein. Wahre und falsche Sachverhalte nennt man auch Tatsachen.

er kann mit einer Ausprägungsmöglichkeit (Quantität) ausgestattet sein.

die Feststellung seiner Existenz, Dauer oder Ausprägung gilt mit einer gewissen Sicherheit (Fehler).

__
Scheidewert. Der Median der Momentverteilung heißt Scheidewert (oder auch Medial) [PDF]
__
Schiefe := Abweichungsmaß von der Symmetrie einer Verteilung; rechtsschief, linksschief.
__
Schließende Statistik (Inferenz-Statistik).
__
Schwerster Wert. Ausdruck der älteren deutschen Statistik: mit der Häufigkeit gewichteter Modalwert. Nach Most ein Mittelwert der Lage.
__
Score :=  Zahlenwert, Ausdruck in der Testpsychologie. Bekommt eine ProbandIn auf die Frage, wie der Bundeskanzler der BRD heißt, z. B. einen "Wertpunkt" für die richtige Antwort, so ist dieser Wertpunkt der Rohwert-Score. > Summenscorefunktion.
__
Sensitivität. Ein Maß für die Richtig-Positiv-Zuweisungen.
Kurz und bündig: sensitiv=richtig positiv erkennt, spezisch=richtig falsch erkannt.

__
Sicherheit  wichtiger allgemeiner, wissenschaftlicher und statistischer Begriff, der mehrere Aspekte betreffen kann: Genauigkeit, Gültigkeit für einen Zeitraum,  einer Feststellung, Sicherheit und Güte einer Feststellung. Dahinter steckt die allgemeine und wissenschaftliche Erfahrung, dass unser Handeln fehlerträchtig und nicht immer zuverlässig ist.
__
Signifikanz. > Prüfstatistik. Zufallskritische Beurteilung von Annahmen. Der Signifikanztest errechnet, ob unter der Voraussetzung der Richtigkeit der 0-Hypothese (H0: es besteht kein statistischer Unterschied) zwischen beobachteten Werten, die 0-Hypothese bei Zugrundelegung dieser oder jener Irrtumswahrscheinlichkeit (Signifikanzniveau, oft 5%) beibehalten oder zu Gunsten der Alternativhypothese (H1) verworfen werden muss. Es wird also nicht die Wirklichkeit geprüft, sondern unter bestimmten Annahmen wird eine Annahme einer anderen Annahme gegenübergestellt, so dass nicht selten der Eindruck einer virtuellen Scheinwissenschaft entsteht. Sog. "signifikante" Ergebnisse werden auch selten in klaren - hierzulande deutschen - Sätzen interpretiert, woran man schon erkennt, wie schwach und unbedeutend (nicht signifikant ;-) solche Erkenntnisse sind. Der "Signifikanz-Popanz" ist vermutlich eine Folge der - oft genug sehr problematischen - Mathematisierung der Sozialwissenschaften. Viele denken zu Unrecht, dass nur, wo Zahlen und Formeln verwendet werden, schon Wissenschaft vorliegt; nicht selten ist es blosse moderne Numerologie und das Gegenteil von Wissenschaft. Signifikanztest.
__
Simpson's Paradoxon
__
Skalierung. Messverfahren, Messmethode für Ausprägungen von Merkmalen.
Man unterscheidet seit  Stevens 1946  vier Skalenniveaus, wobei der Sprung von Ordinal- zu Intervallniveau viel zu groß und der sozialwissenschaftlichen und psychologischen Realität nicht angemessen ist. Es fehlt so etwas wie ein Quasi-Intervallniveau, wofür das Fuzzy-Konzept geeignet erscheint. Das Messproblem ist für die Sozialwissenschaften und Psychologie grundsätzlich nicht gelöst > Messen per fiat.
__
Skalierungsproblem
Ausdruck der psychologischen Messtheorie. Coombs et al, S. 22: "(4) Das Skalierungsproblem: Wie gehen wir bei der eigentlichen Konstruktion von numerischen Skalen vor? Wie verwandeln wir ordinale Information in Aussagen über Zahlen? Und schließlich, wie werden wir mit Meßfehlern fertig, die durch die Ungenauigkeit der Waage oder die Inkonsistenz der Bevorzugungsurteile auf treten können?"
__
Spannweite = Maximum - Minimum. Ist die zahlenmäßig kleinste Note in einem Zeugnis 1 und die größte Note eine 4, dann beträgt die Spannweite 4 - 1 = 3. Mit Spannweite kann auch ein Streuungsbereich gemeint sein, z. B. der 1 Sigma Bereich bei der Standard-Normalverteilung umfasst die mittleren 68%, der 2 Sigma-Bereich die mittleren 95,5% und der 3-Sigmabereich 99,7%, also fast die gesamte Verteilung.
__
Spezifität. Ein Maß für die Richtig-Negativ-Zuweisungen > Sensitivität. (Richtig-Positive-Zuweisung).
__
Spiel.
__
Spieltheorie.
__
Spurenhypothesen in der Kriminalistik, Kriminologie, Rechtsmedizin und Wissenschaft

Gigerenzer beschreibt die Fehlermöglichkeiten in der Spurenschlusskette sehr ausführlich. (226-229) am Beispiel des genetischen Fingerabdrucks. Die wichtigen zu berücksichtigenden Begriffe lassen sich der Graphik sehr schön entnehmen.
Der Urheberfehlschluss setzt falsch gleich: p(nicht Urheber | Übereinstimmung) = p (Übereinstimmung).
Der Anklägerfehlschluss setzt falsch gleich: p(unschuldig | Übereinstimmung) = p(Übereinstimmung).

__
Stabil, Stabilität [numerische]
__
Standardabweichung (Symbol: Sigma) . Wichtiges Streuungsmaß. Wurzel aus der Summe der quadrierten Abweichungen der Rohwerte vom Mittelwert durch n-1 dividiert. Ohne die Wurzel ergibt sich die Varianz = quadrierte Standardabweichung.

__
Standardbedingungen > Normbedingung  > Normalbedingungen.
Damit sind der Regel Bedingungen gemeint, auf die "man" (Fachausschüsse, Verordnung, Gesetz) sich geeinigt hat, z.B. DIN-Normen. "Geregelt werden die Normalbedingungen in Deutschland in DIN 1343 „Referenzzustand, Normzustand, Normvolumen; Begriffe, Werte“ ...  Standardbedingungen Heute sind neue Normalbedingungen als SATP für „Standard Ambient Temperature and Pressure“ üblich:
    Standardtemperatur T = 298,15 K entsprechend 25 °C (analog zu STP)
    Standarddruck p = 101.300 Pa = 1013 hPa = 101,3 kPa = 1,013 bar. " (Quelle: Chemie.de).
Eine Übersicht findet man bei Wikipedia unter dem Stichwort "Standardbedingungen".
__
Standardnormalverteilung.
__
Standardwert. > z-Wert.
__
Stanine. Aus standard und nine gebildete Verdichtung an den Rändern der 13 Centil-Normen auf 9 Werte: [> Normwerte]

__
Stationär, Stationarität (> Ergodizität) Parameter-Konstanz über die Zeit. Meist selbstverständlich vorausgesetzte, tatsächlich aber eine nicht unproblematische - und meist ungültige - Annahme.
    Gruber (2011), S. 59f: "Unter einem stationären Prozess versteht man einen Prozess, dessen Erwartungswert und Varianz unabhängig von der Zeit, also konstant sind. Die Verteilung ist somit zu jedem (Mess-) Zeitpunkt gleich. Man könnte sagen, dass der Prozess sein Verhalten über die Zeit nicht verändert, sondern zufällig um den wahren Wert des Merkmals schwankt.
    Der einfachste stationäre Prozess ist normalverteiltes Weißes Rauschen. Hier ist die zufällige [<59] Abweichung von Mittelwert normalverteilt mit Varianz Sigma². Meist nimmt man sogar eine Standardnormalverteilung mit Erwartungswert Null und Varianz Eins an und schreibt dafür epsilon_t ~ W N (0;Sigma²) (Fan & Yao, 2003)."
    Man differenziert auch eine sog. schwache Stationarität neben einer strikten, drei Bedingungen bei Vermerk S. 283f [Teil PDF]
    Im Lexikon der Geographie von Spektrum [O] wird ausgeführt: "Stationarität, statistische Eigenschaft von zeit-varianten, raum-varianten bzw. raum-zeit-varianten Prozessen (Variablen). Eine zeit-variante Variable X(t) ist stationär, wenn ihre Verteilung zu jedem Zeitpunkt t invariant ist gegenüber t, andernfalls nennt man den Prozess nichtstationär bzw. instationär ( Abb. ). Sind nur die beiden ersten Potenzmomente (arithmetischer Mittelwert und Varianz) invariant gegenüber t, so nennt man die Variable schwach stationär. In ähnlicher Weise kann für raum- bzw. raum-zeit-variante Variablen Stationarität definiert werden. Stationäre Variablen weisen insbesondere keine Trends auf (Trendanalyse). Stationarität ist Voraussetzung zur Messung der Autokorrelation von Variablen und zur Modellierung eines Prozesses durch ein Autoregressivmodell. ..."
    Kiencke, Uwe & Eger, Ralf  (2008) Messtechnik. Systemtheorie für Elektrotechniker. Berlin: Springer. [3., 6.4.4, 6.1.5]
__
Statistik. Erfassen und Verarbeitung von Zählungen von bestimmten Merkmalen an bestimmten Merkmalsträgern an bestimmten Orten zu bestimmten Zeiten unter bestimmten Bedingungen. > Deskriptive S., > schließende S.. > Querschnitts-S., > Längsschnitts-S..
__
Statistik, deskriptive. Sie beschränkt sich auf die Erfassung und Beschreibung statistischer Kennwerte; nicht selten die ehrlichste und letztlich oft aussagestärkste Form der Statistik.
__
Statistik, mathematische. Hochentwickelte, komplizierte, umfangreiche und spezialisierte mathematische Fundierung der Statistik. Für mathematische Laien teilweise sehr schwer bis gar nicht verständlich, besonders was die Anwendung und auch den wirklichen Nutzen bezüglich vieler Annahmen betrifft. Teilweise kann man den Eindruck gewinnen, dass sich die Aussagen nur in virtuellen Welten jenseits unserer Wirklichkeit bewegen. Viele ausgearbeitete Modelle beruhen auf Voraussetzungen, die - besonders in der sozialwissenschaftlichen Forschungspraxis - nicht erfüllt werden (Intervallniveau der Daten, Normalverteilung, Zufallsauswahl, Parameterkonstanz). Eine wirklich konsequente Anwendung der Mathematik würde wahrscheinlich mehr als 90% der Veröffentlichungen gar nicht zulassen.
__
Statistikpakete/ Statistikprogramme.
__
Statistik, schließende. > Inferenzstatistik. Die schließende Statistik macht Aussagen - teilweise auch sehr fragwürdige oder nichtssagende wie z. B. "signifikant" - über die Bedeutung der deskriptiv erhaltenen Kennwerte mit Hilfe statistischer Modellannahmen.
__
Statistische Hypothesen
Stegmüller (1973), S. 85, behauptet: "Statistische Hypothesen sind, wie bereits früher erwähnt, stets Verteilungshypothesen." Dagegen sprechen die zahlreichen verteilungsfreien statistischen Verfahren. > Statistische Schlussweisen.
__
Statistische Kennwerte sind z. B. Median, Quartile, Minimum, Maximum, Spanne; Mittelwert (Typ), Standardabweichung; relative Häufigkeiten, Quantile, Prozentränge, Verteilung und Verteilungskennwerte (z. B. Schiefe, Exzess, Gipfel); Stichprobe, Stichprobenumfang; Population; Erhebungszeitraum; Reliabilität und Validität, Sensitivität und Spezifität; cut-off Werte mit  Erläuterungen und Begründungen. Hinzu kommen besonders bei psychologischen Tests auch abgeleitete Normen wie z. B. z-Werte = (Rohwert - Mittelwert) / Standardabweichung, Stanine oder T-Werte.
__
Statistisches Paradigma. In der üblichen, an mathematischer Wahrscheinlichkeitstheorie und Statistik orientierter Einstellung geht man oft  - Ausnahme z.B. voraussetzungsreiche Varianzanalyse - von einem Wahrscheinlichkeitsraum- und Modell aus, in dem die Parameter zufällige Prozesse festgelegt werden. In den empirischen Wissenschaften geht es aber gewöhnlich um systematische Einflüsse, bei denen der Zufalls zwar auch eine Rolle spielt, aber eben nur eine Rolle. Ein empirisch orientiertes statistisches Paradigma muss also von einem grundlegende anderen Ansatz ausgehen, nämlich von der paradigmatischen Grundgleichung E = f( S, Z). Ergebnisse (E) von Beobachtungen oder Experimenten führen zu Hypothesen, wie diese Ergebnisse erklärt werden können. Das grundlegende statistische Paradigma sieht vor, dass es systematische (S) und zufällige (Z) Einflüsse gibt. Es stellt sich für den Statistiker daher immer das Problem, zu entscheiden, welcher Anteil der Ergebnisse auf systematische Einflussgrößen (S) und welcher Anteil auf zufällige Einflüsse (Z) in welchem Wirkungszusammenhang (f)  zurückgehen, also erklärt werden können.
___
Statistische Schlussweisen.
Dieter Rasch (1978, S. 193-243) beschreibt im 7. Kapitel  "Statistische Schlußweisen" seines Buch folgende:

7.1  Grundgesamtheit und Stichprobe  (S. 193).
7.2. Formen des induktiven Schließens (S. 198).
7.2.1.  Bayessches Vorgehen  (S. 199)
7.2.2.  Empirisches Bayessches Vorgehen  (S. 201)
7.2.3.  Fiduzialkonzept (S. 202)
7.2.4.  Klassisches Vorgehen (Häufigkeitsvorgehen) (S. 203)
7.3.   Parameterschätzung  (S. 206)
7.3.1.   Wünschenswerte Eigenschaften von Schätzfunktionen (S. 206)
7.3.2.   Maximum-Likelihood-Methode  (S. 217)
7.3.3.   Methode der kleinsten Quadrate   (S. 219)
7.3.4.   Minimums-Methode  (S. 222)
7.4.  Konfidenzbereiche  (S. 224)
7.5.  Statistische Tests  (S.228 )
7.6.  Beziehungen der Statistik zur Spiel- und Entscheidungstheorie  (S. 238)
7.6.1.   Spieltheorie  (S. 239)
7.6.2.   Statistische Entscheidungstheorie (S. 241)

__
Stetig. Grundlegender mathematischer Begriff mit der alltagssprachlichen Bedeutung einen fortgesetzten Ununterbrochenen, ohne Lücke. Gegensatz diskret.
__
Stichprobe. Teil eines Ganzen. Meist ist angestrebt, dass der Teil das Ganze repräsentieren soll und der Teil fürs Ganze stehen kann (pars pro toto). Hierbei entsteht gewöhnlich ein Stichprobenfehler.
__
Stichprobenauswahlverfahren. Der Sinn einer Stichprobe ist die Repräsentativität für eine Gesamtheit.
__
Stichproben-Kennwerte. Auch Stichprobencharakteristik. Zu jeder wissenschaftlichen statistischen Normwert-Angabe gehören ihre Bedeutung und die charakteristischen Kennwerte, sowie die Bezugsgruppe, d. h. die Stichprobe, Zusammensetzung der Stichprobe, das Auswahlverfahren und die Population, der Zeitraum der Erhebung, die Größe der Stichprobe und der Population. Genau diese Angaben werden von der Labormedizin so gut wie nie ausgewiesen (Stand 10/ 2007).
__
Stichprobenumfang. Anzahl der Messobjekte in der Stichprobe.
__
Stochastik. Lehre von den Zufallserscheinungen und ihrer mathematisch-statistischen Behandlung.
__
subjektive Wahrscheinlichkeitstheorie. Eine gewisse Nähe gibt es zur Nutzen- und Entscheidungstheorie.
Vertreter (Auswahl): Bayes, de Finetti, Fishburn, Kleiter, Ramsey, Savage, Wieckmann.
__
Summen-Score-Funktion. Die blosse Anzahl im Sinne des positiven Kriteriums bearbeiteter (meist "gelöster") Aufgaben dient als (Ausgangs-) Maß für eine Ausprägung.
__
Surveillance (Beobachtung, Überwachung), Ausdruck der Gesundheitsberichterstattung.
__
Syllogismus, statistischer. Wenn a aus A mit p₁ m zeigt, dann sagt man, a habe mit der Wahrscheinlichkeit p₁ das Merkmal m.
Wenn a aus A mit p₁ m zeigt und und a aus B mit p₂ m zeigt und p₁ ungleich p₂ ist, dann gibt zwei unterschiedliche Wahrscheinlichkeitsaussagen bezüglich der Merkmalszuordnung m. Viele WissenschaftstheortietikerInnen sehen hier einen Widerspruch. Ich kann hier aber keinen sehen. Nicht, wenn  A und B verschiedene Stichproben oder schon gar nicht, wenn A und B aus verschiedenen Populationen stammen.
___
Test: Kontrolliertes und fundiertes Prüfverfahren mittels einer Stichprobe und Kennwerten. Stichprobe zur - meist quantitativen - Schätzung eines Sachverhaltes. Ein Fahrtest ist eine Stichprobe aus dem Fahrverhalten einer Person. Aus der Fahrprobe schließt man auf die technische Kraftfahreignung.
__
Testen: Kontrolliertes und fundiertes Prüfen mittels einer Stichprobe und Kennwerten
__
Testgütekriterien. > Objektivität, > Reliabilität, > Validität, > Utilität, > Ökonomie.
__
Teststärke (Power). "Die Teststärke gibt an, mit welcher Wahrscheinlichkeit ein Signifikanztest zugunsten einer spezifischen Alternativhypothese H1 (z. B. „Es gibt einen Unterschied“) entscheidet, falls diese richtig ist. (Die abzulehnende Hypothese wird H0, die Nullhypothese genannt.). Die Teststärke hat den Wert 1-?, wobei ? die Wahrscheinlichkeit bezeichnet, einen Fehler 2. Art zu begehen." [W071027]
__
Testtheorie: Theorie zur Konstruktion, Auswertung und Beurteilung von Tests.
__
Theorie  allgemeines oder wissenschaftliches sprachliches Modell der Wirklichkeit, das besagt, wie sich die Wirklichkeit unter diesen oder jenen Bedingungen verhält, wie sie funktioniert.
__
Transformation. Umwandlung von Werten, z. B. y = ax + b. Hierbei kann es sehr wichtig sein, die Relationentreue zu wahren. Achtung: In der Psychologie gibt es sehr merkwürdige Transformationen, die, bei Lichte betrachtet, Datenfälschungen sind, wenn z. B. nicht normalverteilte Rohwertdaten in Quantile gewandelt und dann so zurückgerechnet werden, als ob sie normalverteilt wären (z. B. fragwürdiges McGall-Verfahren). Das gilt auch für die meisten Faktorenanalysen, weil die Kommunalitätsmatrizen den ursprünglichen Korrelationsmatrizen nicht mehr ähnlich sind.
__
Transparenz. Klarheit, Durchsichtigkeit, Verständlichkeit, Nachvollziehbarkeit.
__
Trennschärfe  wie gut trennt eine Methode zwischen Merkmalsträgern.
__
T-Werte.

T-Wert-Formel 112 nach Lienert (1969, S. 331)

Lienert verweist in seinem Werk Testaufbau und Testanalyse (1969) mehrfach auf McCall, so auf S. 331 (Fußnote 10):


Die T-Werte werden zur "Normalisierung" nicht normalverteilter Daten nach einem dubiosen Verfahren von McCall verwendet: erst werden von der nicht-normalen Verteilung Prozentränge berechnet, also eine Flächentransformationswerte vorgenommen, sodann werden diese in Standard-Äquivalente umgewandelt (Darstellung aus Lienert 1969, S. 341):



Das Wesentliche und Problematische der "Normalisierung" bei anormalen Verteilungen wird von Lienert offenbar erkannt, aber gleichzeitig in den Fußnotenbereich (S. 331) verbannt. Das Entscheidende ist hier natürlich, dass durch diese Transformation alle nicht-normalverteilten Rohwerte verändert werden, manche werden mehr oder minder stark größer, andere kleiner. Begründet wird dieses Vorgehen so gut wie nie. Implizit ist indessen klar, man unterstellt eine Daten-Theorie der Normalverteilung und "korrigiert" die empirischen Daten daraufhin. Es handelt sich hierbei meist um eine willkürliche Datenmanipulation vom Typ Neu-Skalierung.

___
Ueberdiagnose-Fehler
Gigerenzer (2013), Risiko, S. 245: "Eine Überdiagnose liegt vor, wenn Ärzte Abnormalitäten entdecken, die weder Symptome noch frühen Tod verursachen. Dies ist etwa der Fall, wenn bei einem Patienten zwar richtigerweise eine Krebserkrankung diagnostiziert wird, diese sich jedoch so langsam entwickelt, dass der Patient sie nie bemerken würde."
__
unabhaengig - Unabhaengigkeit  grundlegender Begriff für Beziehungen und Zusammenhänge, z.B. von Ereignissen E₁, E₂, ..., E_i, ... E_n.  In der Praxis oft schwierig zu bestimmen, weil anscheinend statistisch unabhängige Beziehungen bei Auspartialisierungen ihre Unabhängigkeit einbüßen, so dass immer das Problem auftritt, was denn nun der relevante Merkmalsraum, der als Basis dienen kann, ist. Sind zwei Größen von einander unabhängig, ist die Korrelation 0, aber die Umkehrung gilt nicht. Aus einer Korrelation = 0 darf man nicht auf Unabhängigkeit schließen, man sagt, die beiden Größen seien unkorreliert.
    Zu unabhängigen und sich ausschließenden Ereignissen schreibt Rumsey (2007), S.57: "Einander ausschließende Ereignisse können nicht unabhängig sein, und unabhängige Ereignisse können einander nicht ausschließen, außer mindestens eins der beiden Ereignisse ist die leere Menge."
__
unmöglich, Unmöglichkeit > Gegensatz  möglich.
Wichtiger allgemeiner und wissenschaftlicher Grundbegriff, dass sich ein  Sachverhalt  nicht ereignen (existieren) kann. Aber das Unmögliche ist gewöhnlich  denkbar. Denken kann man alles, auch sein Gegenteil. Ontologisch gilt im allgemeinen die Stufenfolge: Denkbar > unmöglich > nicht wirklich/existent.
__
Unsicherheit. Das Leben und die meisten Entscheidungen, die es abverlangt, sind mit Unsicherheit verbunden. Diese  Unsicherheiten ab- und einschätzen können, ist ein vielfaches und bedeutsames Anliegen von Wissenschaft und alltäglicher Praxeologie.
__
Unterscheiden. Grundlegende kognitive Funktion. Eng verbunden mit vergleichen.
__
Unzureichender Grund > Indifferenzprinzip.
__
Utilität. Nutzen, Wert eines Tuns. Aufwands-Ergebnis-Verhältnis. [> Ökonomie.]
__
Validität. Gültigkeit. Typischer Ausdruck, der in der psychologischen Testtheorie eine große Rolle spielt. Man spricht dort davon, dass die Validität eines Verfahrens angibt, in welchem Maße festgestellt wird, was festgestellt werden soll. Das ist eine merkwürdige Bestimmung. Denn wie stellt man denn fest, ob festgestellt wurde, was festgestellt werden soll? Meist ist damit das Problem zwischen Begriff und seiner  Operationalisierung  angesprochen, was man auch Konstruktvalidität nennt. Also z.B. die Beziehung zwischen den Ergebnissen eines Intelligenztests (Operationalisierung) und dem Begriff der Intelligenz. Anders gesagt: misst der Intelligenztest tatsächlich das, was mit Intelligenz gemeint ist. > erklären und verstehen. Genau betrachtet ist hier das Verhältnis zwischen einem operationalen Erhebung- (Intelligenztestergebnis) und einem abstrakt-allgemeinen Zielbegriff (Intelligenz) angesprochen. Um herauszufinden zu können, wie gut der operatioanle Erhebungs- den abstrakt-allgemeinen Zielbegriff repräsentiert, in diesem Sinne also "valide" wäre, müsste der abstrakt-allgemeine Zielbegriff vollständig operationalisiert sein, was nicht möglich ist. Im übrigen wäre damit nur ein theoretisches Interesse befriedigt. Eine solch allgemeine Validitätsdiskussion ist nicht sinnvoll. In der Praxis sollte man sich damit begnügen, konkrete Prediktorvaliditäten anzugeben. Diese Validität nennen man in der psychologischen Testtheorie Kriteriumsvalidität. Von inhaltlicher oder logischer Validität wird gesprochen, wenn in den Testaufgaben der Begriff enthalten ist. Diese Auffassung ist ebenfalls eine merkwürdige Konstruktion. Denn sie lässt zu, dass Aufgaben, die anscheinend mit dem Zielbegriff inhaltlich nichts zu tun haben, trotzdem Aussagen über den Zielbegriff zulassen, z.B. wenn Bildungs- oder Wissensfragen (Wie heißt der Bundespräsident?), die keinerlei Intelligenz erfassen, in einem Intelligenztest genutzt werden. Das könnte im Grunde nur dadurch gerechtfertigt werden, wenn gezeigt werden kann, dass Bildung und Wissen mit Intelligenz hoch korrelieren. Solche Tests sind allesamt gegenüber bestimmten Gruppen unfair (Zuwanderern; andere Kulturen). Dass das nicht so gut ist hat man wohl erkannt, sonst hätte man nicht "kulturfreie" Intelligenztests zu konstruieren versucht.
__
Validität, inkrementelle Der Zuwachs an Validität, den die Hinzunahme eines weiteren Kriteriums erbringt. Bei Vorhersagen spricht man auch von Prädiktorvalidität einer Variablen (Kriteriums). In operationalem Verständnis: ein Begriff wird noch mehr in seinem inhaltlichen Bedeutungsumfang ausgeschöpft, wenn ein weiteres Kriterium hinzugenommen wird. Geht es z.B. um die Prognose eines Rückfalls, so ist die inkrementelle Validität 0, wenn die Hinzunahme dieses Kriteriums die Prognose nicht verbessert. Verbessert sich die Prognose z.B. von 15% auf 18%, so hat die Prediktorvalidität um 20% zugenommen oder das Inkrement (Zuwachs) beträgt absolut 3% oder relativ 20% bezogen auf die Basis 15%.
__
Varianz. Streuungsmaß. Quadrat der Standardabweichung.
__
Varianzanalyse. Untersuchungsverfahren, das die Einflüsse von Bedingungen auf statistische Kennwerte durch Analyse der Mittelwerte und Varianzen erforscht. [W]
__
Variation. Variante, andere Realisation. Wertneutraler Begriff im Unterschied zur Abweichung. Statistisch meist mit der Varianz, Standardabweichung oder einem anderen Streuungsmaß erfasst. > sexuelle Variationen.
__
Vergleichen := elementares geistiges Handeln, Grundprinzip jeder Messung. Eng verbunden mit unterscheiden.
__
verstehen  > erklären und verstehen.
__
Verteilung. Häufigkeit oder Ausprägung von Werten nach geordneten Kriterien. Meist wird die Häufigkeit an der Ordinate und an der Abszisse die  Zeit  aufgetragen.
__
Verteilungsfunktionen. [W, Liste] Sie geben die Summe von Wahrscheinlichkeiten bis zu einer Grenze k an. Bei diskreten Verteilungen z.B. der ProzentRANG, bei stetigen oder kontinuierlichen Verteilungen wie z.B. der Normalverteilung ist es die Ogive.
• Merz: Zusammenstellung wichtiger Dichte- und Verteilungsfunktionen: * Binomialverteilung * Exponentialverteilung * Erlangverteilung  * Normalverteilung *  Hjorthverteilung * Weibullverteilung *
__
Verteilungsannahmen. Es gibt beliebige Verteilungen. Die meisten parametrischen Tests setzen aber bestimmte Verteilungsannahmen, z. B. normalverteilte Daten voraus. Dort, wo mit Verteilungsannahmen gerechnet wird, müssen diese natürlich angegeben werden. Ebenso wichtig ist, die Verteilungsannahmen zu begründen und zu prüfen.
__
Verteilungsfreie statistische Verfahren

__
Verteilungskennwerte (z. B. Median, Mittel, Streuung, Schiefe, Exzess, Gipfel, Verlauf).
__
Vertrauensintervall (Konfidenz). [W]
__
Vieldeutigskeitssatz.

• Für Korrelationskoeffizienten (Sponsel 1984, S. 213)
• Das Simpsonsche "Paradoxon" zeigt auch die Gültigkeit für bedingte Wahrscheinlichkeiten.
Vermutlich gilt allgemein: Ein Zusammenhang zwischen Variablen a und b, bedeutet den Zusammenhang zwischen a und und b und der mit a und b verbundenen Variablen, d.h. spaltet man die Einflußvariablen auf - etwa durch auspartialisieren - , ergeben sich womöglich ganz andere - und auch widerspruchsvolle - Zusammenhänge. Damit stellt sich natürlich die Frage, was statistische Zusammenhänge überhaupt bedeuten. Das Problem ist derzeit (2009) nicht nur nicht geklärt, sondern bei nicht wenigen Statistiker- und MethodologInnen noch gar nicht angekommen.
__
Voraussetzungen. Bestimmte Verfahren erfordern bestimmte Voraussetzungen, die oftmals nicht ausdrücklich genannt werden, z. B. Normalverteilung, Intervallskalenniveau, Zufallsauswahl, Parameterkonstanz über die Zeit, Raum und Bedingungen hinweg. So sind z. B. die Schulnoten auf Ordinalniveau und damit ist die arithmetische Mittelwertsbildung unzulässig, weil hierfür mindestens Intervallskalenniveau erforderlich ist.
__
Vorlauf-Zeit-Fehler  (lead time bias)
Gigerenzer (2013) in Risiko, S. 245: "In der britischen Gruppe wird Prostatakrebs durch Symptome entdeckt, nehmen wir an, im Alter von 67 Jahren (Abbildung 10.1, oben). Alle diese Männer sterben mit 70. Jeder überlebte nur drei Jahre, daher beträgt die 5-Jahres-Überlebensrate 0 Prozent. In der US-amerikanischen Gruppe wird Prostatakrebs durch PSA-Tests früh entdeckt, sagen wir mit 60 Jahren, aber auch dort sterben die Patienten mit 70 (Abbildung 10.1, unten). Laut Statistik überlebte jeder in der Gruppe zehn Jahre, und damit ist die 5-Jahres-Überlebensrate 100 Prozent. Die Überlebensrate hat sich spektakulär verbessert, obwohl sich am Todeszeitpunkt nichts geändert hat: Egal, ob die Patienten ihre Diagnose mit 67 oder mit 60 erhielten, alle starben sie mit 70. Durch Vorverlegung der Diagnose wird die Überlebensrate aufgebläht. Kein Leben wird verlängert oder gerettet."
__
w := Hier Zeichen für gedachten wahren Wert bei einem Messvorgang. Der wahre Wert ist grundsätzlich unbekannt und muss geschätzt werden, hier durch r := Näherungswert für w.
__
Wahrscheinlich, Wahrscheinlichkeit. Mehrdeutiger Grundbegriff der Wahrscheinlichkeitstheorie (z.B. subjektiver und  objektiver Wahrscheinlichkeitsbegriff).  Die Kern- und Grundbedeutung der Wahrscheinlichkeit ist der Grad mit dem ein Sachverhalt mehr oder weniger zutrifft. Hierfür sind verschiedenen Modelle entwickelt worden:
• Laplace-Modell der günstigen zu den möglichen Fällen. Eine Spezifikation davon ist das sog. Urnenmodell.
• Häufigkeitstheorie nach Mises
• Induktive Wahrscheinlichkeit nach Carnap
• Logische Wahrscheinlichkeit nach Keynes
• Axiomatische Wahrscheinlichkeit nach Kolmogoroff
• Informations- und Indizmodell (Sponsel 2022): je mehr Informationen/ Indizien vorliegen, desto größer wird die Wahrscheinlichkeit, den Sachverhalt richtig zu erkennen.


Ähnlich wie der wahre Wert einer Messung ist die Wahrscheinlichkeit eines Ereignisses letztlich unbekannt.
Als eine beste Näherungsschätzung wird in der Statistik meist die relative Häufigkeit eines Ereignisses für den Wahrscheinlichkeitsparameter genommen, wobei sich gewöhnlich für den Fall unendlich vieler Realisationen - die in praxi natürlich nicht möglich sind - die Identität von Näherungs- und wahrem Wahrscheinlichkeits-Wert ergibt. Praktisch heisst das: je größer der Stichprobenumfang oder je mehr Messungen vorliegen, desto mehr nähert sich der empirische Wert dem wahren Wert an. In der Mathematik gilt dieser Grundbegriff seit der Axiomatisierung 1933 durch Kolmogoroff geklärt. Überblick zu den verschiedenen Wahrscheinlichkeitsbegriffen nach Steinbring (1980), S. 115:

"Es gibt wohl kaum einen mathematischen Begriff, der eine ähnliche Vielfalt verschiedenartiger Definitionen und gegensätzlicher Interpretationen aufweist, wie der Begriff der Wahrscheinlichkeit: Da sind z.B. die Gleichwahrscheinlichkeit und die klassische Laplacesche Definition von Wahrscheinlichkeit, die Häufigkeitstheorie von Richard von Mises, die logische Wahrscheinlichkeit  (etwa von Keynes) und schließlich die axiomatische Begründung der Wahrscheinlichkeit durch Kolmogoroff. Berücksichtigt man zudem die schon lang andauernde heftige Diskussion um die subjektive und objektive Wahrscheinlichkeitsauffassung, so kann man insgesamt Kendall nur zustimmen, der sagt:  "Few branches of scientific method have been subject to so much difference of opinion as the theory of probability."  (Kendall,  1949, S. 101) Dies alles macht den Wahrscheinlichkeitsbegriff zwar zu einem sehr interessanten, aber gleichzeitig wohl auch zu einem der problematischsten mathematischen Begriffe für die Schule überhaupt."
__
Wahrscheinlichkeit 1 und 2 nach Carnap
"Wir haben zwischen zwei Bedeutungen des Wortes Wahrscheinlichkeit unterschieden: die erste (Wahrscheinlichkeit!) bedeutet Gewicht des Datums oder Stärke der Bestätigung, die zweite (Wahrscheinlichkeit bedeutet relative Häufigkeit. Hauptanliegen dieses Buches ist das Problem einer Explikation der Wahrscheinlichkeit!. Wie schon früher dargelegt wurde (Abschn. 3), kann man auf drei verschiedenen Ebenen an dieses Problem herantreten; wir können versuchen, ein Explikat für Wahrscheinlichkeit in einer der drei folgenden Formen zu definieren:
1. als klassifikatorischen Begriff der Bestätigung („die Hypothese h wird durch das Datum e bestätigt");
2. als komparativen Begriff der Bestätigung („h wird durch e mindestens ebensosehr bestätigt wie h' durch e'");
3. als quantitativen Begriff der Bestätigung, als Begriff des Bestätigungsgrades („h wird durch e im Grad r bestätigt").
Wäre ein zureichendes Explikat von der Form 3 zu finden, so wäre dies offenbar die wünschenswerteste Lösung unseres Problems. Eine Theorie des Begriffes des Bestätigungsgrades, gegründet auf einer genauen Definition dieses Begriffes, würde eine quantitative induktive Logik ergeben. Wenn ein befriedigendes quantitatives Explikat nicht gefunden wird oder — wie einige Autoren glauben — niemals zu finden ist, dann bliebe uns die bescheidenere Aufgabe, ein komparatives Explikat zu definieren. Dies würde zu einer komparativen induktiven Logik führen." Quelle: Carnap, Rudolf (1958), S. 40.
__
Wahrscheinlichkeit, bedingte. p(A|B), d.h. die Wahrscheinlichkeit für das Ereignis A unter der Bedingung B. Wichtiger Grundbegriff. Genau betrachtet kann es gar keine "unbedingte" Wahrscheinlichkeit geben. Wenn daher allgemein von "unbedingter" Wahrscheinlichkeit gesprochen wird, so heißt das meist nur, dass nicht angegeben oder gewusst wird, unter welchen Bedingungen eine Wahrscheinlichkeitsaussage gilt.
__
Wahrscheinlichkeitsbegriff Stegmüllers (1973), Teil A., S. 107:
"Der Begriff der Wahrscheinlichkeit wird als Undefinierter Grundbegriff eingeführt und nur axiomatisch charakterisiert. Dies bedeutet: Die möglichen Deutungen von „Wahrscheinlichkeit“ werden nur einer formalen Einschränkung unterworfen, und zwar durch die Forderung, daß bestimmte Axiome von diesem Begriff gelten sollen. Diese Axiome werden nach dem russischen Wahrscheinlichkeitstheoretiker KOLMOGOROFF, der diese Axiome erstmals präzise formulierte, auch die Kolmogoroff-Axiome genannt. Den Wahrscheinlichkeitsbegriff, der allein durch diese Axiome festgelegt ist, nennen wir den formalen oder mathematischen Wahrscheinlichkeitsbegriff."
__
Wahrscheinlichkeitsfunktion. Ordnet dem Wert eine diskreten Zufallsvariable eine Wahrscheinlichkeit zu. Bei stetigen oder kontinuierlichen Werten von Zufallsvariablen spricht man von Dichtefunktion, die einem Intervall eine Wahrscheinlichkeit zuordnet..
__
Wahrscheinlichkeitsmodell. Z. B. Urnenmodell mit oder ohne Zurücklegen.

Wahrscheinlichkeitsmodell-Information

__
Wahrscheinlichkeit, objektive. [ > relative Häufigkeit]
Die "objektive" Wahrscheinlichkeitstheorie sucht unter bestimmten Annahmen (Modellen), andere Annahmen auf ihre statistische Schlüssigkeit hin zu überprüfen, was sich nicht selten in völlig nichtssagenden Signifikanzaussagen erschöpft. Grundlage ist die Laplace Definition der Wahrscheinlichkeit als Bruch aus der Anzahl der günstigen Fälle durch alle möglichen Fälle. Eine Axiomatisierung gelang 1933 Kolmogoroff.
__
Wahrscheinlichkeit, subjektive. [> Bayes]
__
Wahrscheinlichkeit, totale.
__
Welten.
__
Wert. > Größe, Zufallsgröße. 1) Zahlenwert im Rahmen einer Messung. W = f(F₁, F₂, ..., F_i, ...  F_n), f(Z₁, Z₂, ..., Z_i, ...  Z_n), wobei F hier kausale, korrelative und Z "zufällige" Einflüsse bedeuten sollen. 2) anderer Wert, den ein Sachverhalt relativ für einen Bewertenden hat (z. B. Wind für einen Segler, Regen für einen Bauern, Musik und Alkohol für einen Feiernden). [> werten]
__
Wert, richtiger. Beste bekannte empirische Näherung an den gedachten wahren Messwert.
__
Wert, wahrer. Idee, dass ein Zustand oder Merkmal zum Zeitpunkt der Messung einen wahren Messwert hat, den es "bestmöglich" zu schätzen gilt. Fiktive Größe und nicht immer hinreichend klare Vorstellung, repräsentier- oder schätzbar. Beispiel: Zu messen sei das Volumen einer Streichholzschachtel. Hierbei wird man mehrfache Messfehler begehen. Einmal weil die Ausdehnungen (Länge, Breite, Höhe) nicht streng starr geradlinig sind. Zum andern weil man in aller Regel bei jeder Messung auch Messfehler macht. Trotzdem ist hier die Idee, dass die Streichholzschachtel zu einem bestimmten "Zeitpunkt" - einen fiktive und genau betrachtet unklare Vorstellung - einen wohlbestimmten Volumenwert hat, plausibel und intuitiv unmittelbar einsichtig.
__
Wertzuweisung. Bestimmten Sachverhalten können Werte zugewiesen werden, z. B. "nützlich für ...", "gesund", "krank", "Symptom für x". Die Wertzuweisung kann mehr oder minder begründet und methodisch ausgewiesen sein oder willkürlich, "per fiat" nach gutem Glauben oder Fachkompetenz erfolgen.
__
Wette.
__
Wissenschaftliches Arbeiten.
__
Würfelspielparadoxon. Székely (1990, S. 12)
__
x := Hier Zeichen für einen empirischen Messwert.
__
Zahlen.
__
Zeit. Wichtiger, doch letztlich bezüglich seiner Bedeutung oft sehr unklarer Grundbegriff in der Statistik. > Die Zeit als Variable.
__
Zeitpunkt. Fiktive und - genau betrachtet mitunter - problematische Vorstellung einer "Momentaufnahme". Tatsächlich dürfte in den meisten Fällen der "Moment" nur ein ungefähres Zeit-Intervall bzw. einen "Zeitraum" bedeuten. Beispiel: "Tages-Temperatur". Ein "Tag" besteht aus 8-24 Stunden (Arbeitstag, astronomischer Tag einschließlich der Nacht), 1440 Minuten oder 86400 Sekunden. Die Temperatur dürfte im Regelfall über die Zeiten schwanken; zudem hängt sie auch vom Ort der Messungen ab.
__
Zeitreihe  Anordnung der Daten nach der Zeit, allgemeiner Ordnungsreihe
__
Zeitreihenanalyse. Sie wird meist verkürzt auf Autokorrelation reduziert dargestellt, nicht selten auch unkritisch. Dabei handelt es sich schlicht und einfach um Daten oder Werte, die zeitlich geordnet auf einer Zeitachse nur dargestellt werden. Die Zeit selbst ist ja in der allermeisten Fällen keine Variable (> Die Zeit als Variable).
    Es werden eine ganze Reihe von Modellen unterschieden:

• AR Autoregressives Modell.
• ARMA Autoregressives Moving Average Modell.
• ARIMA Autoregressives Integrated Moving Average Modell.
• ARCH Autoregressives Conditionales Heteroscedastic Modell.
• GARCH Generalized ARCH
• IMA Integrated Moving Average Modell.
• MA Moving Average Modell.
__
Zeitreihenanalyse Psychologie, Psychopathologie und Psychotherapie
Verlaufsdaten, meist auf der Zeitachse angeordnet, spielen in der gesamten Psychologie, Psychopathologie und Psychotherapie eine große Rolle. Man darf sich aber hier nicht auf mathematisch-technische Autokorrelation beschränken. >
    Gruber (2011), S. 15: "Mit der Veröffentlichung von Box und Jenkins (1976) hatte die Zeitreihenanalyse ihren Durchbruch in den Wirtschaftswissenschaften. Kurze Zeit später erfolgte durch die Einführung von vektoriell autoregressiven Prozessen die Erweiterung in den multivariaten Bereich (Sims, 1980). Mittlerweile findet man zunehmend Verwendungen in den Sozialwissenschaften wie der Psychologie. So nicht nur in den Neurowissenschaften (z.B. Mezer, Yovel, Pasternak, Gorfine & Assaf, 2009), sondern auch zur Dokumentation eines Therapieverlaufs (z.B. J. D. Smith, Handler & Nash, 2010; Kupfer, Brosig & Brähler, 2005)."
__
Zeitreihenanalyse Wirtschaft Grundmodell: X = Trend+Zyklus+Saison+Zufall. [O]
__
Zensus (Census). Bevölkerungsdaten.
__
Zentraler Grenzwertsatz. (ZGWS) Günter Menges (1972, S. 249) teilt hierzu mit: "1. Das Modell
Wie erklärt es sich, daß immerhin doch viele vom Zufall beeinflußte Phänomene der unbelebten Natur der Normalverteilung gehorchen? Die Antwort auf diese Frage, die überhaupt erst die Normalverteilung aus dem Kreis ihrer Schwestern (§ 51) heraushebt, wurde erst im Jahre 1901 gefunden, obwohl sie Laplace schon vermutet hatte. Die Antwort ist der zentrale Grenzwertsatz; er wurde von Ljapunoff gefunden und bewiesen, seitdem von zahlreichen Autoren verallgemeinert und modifiziert.
Das Modell, das diesen Satz so eminent wichtig für die Praxis werden läßt, ist das folgende :
1.  Gegeben ist eine Erscheinung, die von einem Komplex zahlreicher Faktoren beeinflußt, beherrscht, determiniert wird.
2.  Jeder einzelne Faktor des Komplexes übt nur eine sehr kleine Wirkung aus ; für sich allein genommen ist seine Rolle praktisch vernachlässigbar.
3.  Jedem einzelnen Faktor wird eine Zufallsvariable Xi (i = l, 2, ..., n) zugeordnet.
4.  Es ist nicht bekannt, wieviel Zufallsvariablen (und damit Faktoren) beteiligt sind.
5.  Es ist nicht bekannt, wie die einzelnen Xi verteilt sind.
6.  Man weiß indessen (oder nimmt an), daß die Xi (und damit die Faktoren) sich gegenseitig nicht beeinflussen."
Es ist sehr fraglich, ob die Bedingungen 2 und 6 in der Forschungs-Realität erfüllt sind. Jedenfalls wäre überall dort, wo der ZGWS angewendet oder benutzt wird, zu begründen, warum und wie genau die Bedingungen 2 und 6 erfüllt sein sollten. Eine solche Diskussion findet gewöhnlich in der Statistikanwendung und -ausbildung nicht statt.
__
Ziel und Ziele
Wichtiger allgemeiner und wissenschaftlicher Begriff, der u.a. zum Methodenbegriff gehört. Ziele können in unterschiedlichen Beziehungen stehen:
• unabhängig voneinander
• abhängig voneinander
• Zielen können logisch verknüpft werden
• Ziele können Rangfolgen bilden, so kann man erst Syndrome bilden, wenn man Symptome hat und diese setzen Daten des Erlebens und Verhaltens voraus wie die Diagnose den Befund.
• Ziele können in Hierarchien angeordnet werden: Oberziele, Unterziele, Nebenziele ...
• Ziele können sich fördern, hemmen oder behindern und miteinander unverträglich sein.
__
Zipf'sches Gesetz
Ein merkwürdiges Phänomen in "natürlich wachsenden Systemen" (Simon), wonach das häufigste in einer Reihe ungefähr doppelt so oft vorkommt wie das zweithäufigste, 3 mal so häufig wie das Dritthäufigste usw.
__
Zufall (Welt der Möglichkeiten) Sehr schwieriger, mehrdeutiger und möglicherweise widerspruchsvoller Begriff. Subjektive Bedeutungen: (1) Ohne (erkennbaren) Zusammenhang; Ereignis A und Ereignis B haben nichts miteinander zu tun: sie sind in Bezug aufeinander zufällig. (2) Im einzelnen nicht vorhersagbar (Münzwurf- oder Würfelergebnis). (3) Regellos, chaotisch, willkürlich. (4) ein Ereignis geschieht relativ zu einem Betroffenen nicht absichts- oder bedeutungsvoll (beim Wähnen, Eigenbezug und im Wahn gestört: hier hat u. U. alles Absicht oder Bedeutung). Einige Äußerungen:
Laplace (dt. 1896) in Philosophischer Versuch über die Wahrscheinlichkeiten, nach der 6. Auflage, (orig. 1814):
S. 3: "Alle Ereignisse, selbst die, welche wegen ihrer Geringfügigkeit nichts mit den grossen Naturgesetzen zu thun zu haben scheinen, sind eine ebenso nothwendige Folge derselben als die Umläufe der Sonne. Unbekannt mit deren notwendigem Zusammenhang, in welchem sie mit dem ganzen System des Weltalls stehen, hat man sie, je nachdem sie mit Regelmässigkeit oder ohne sichtbare Ordnung eintraten und aufeinanderfolgten, entweder von Zweckursachen oder vom Zufall abhängen lassen; aber diese eingebildeten Ursachen traten in dem Maasse zurück, als die Schranken unserer Kenntniss sich erweiterten und verschwinden vor der gesunden Philosophie, welche in ihnen nichts als den Ausdruck unserer Unwissenheit in Betreff der wahren Ursachen sieht.
    Die gegenwärtigen Ereignisse stehen mit den vergangenen in einer Verbindung, die sich auf das evidente Prinzip gründet, dass ein Ding nicht anfangen kann zu sein ohne Ursache, die es hervorbringt. Dieses Axiom, bekannt unter dem Namen des „zureichenden Grundes", erstreckt sich auch auf Handlungen, die man für indifferent hält. Der freieste Wille kann sie nicht ohne ein bestimmendes Motiv hervorbringen; denn wenn er in dem Falle, dass alle Umstände zweier Lagen gleich wären, das eine Mal handelte und das andere Mal nicht, dann wäre seine Wahl eine Wirkung ohne Ursache; sie wäre dann, sagt Leibnitz, der blinde Zufall der Epikuräer. Die entgegengesetzte Meinung ist eine Täuschung des Geistes, der, indem er die flüchtigen Gründe der Wahl des Willens in indifferenten Dingen aus dem Auge verliert, sich überredet, dass sich der Wille durch sich selbst und ohne Motive bestimmt hat."
S. 6: "Die Theorie des Zufalls (des hasards) besteht darin, alle Ereignisse derselben Art auf eine gewisse Anzahl gleich möglicher Fälle zurückzuführen, d. h. auf solche, über deren Existenz wir in gleicher Weise im Unklaren sind, und dann die Zahl der Fälle zu bestimmen, die dem Ereigniss, dessen Wahrscheinlichkeit man sucht, günstig sind. Das Verhältniss dieser Zahl zu der aller möglichen Fälle ist das Maass dieser Wahrscheinlichkeit, die also nur ein Bruch ist, dessen Zähler die Zahl der günstigen Fälle, und dessen Nenner die Zahl aller möglichen Fälle ist."
Haller-Wedel (1967) in Messen, Zählen, Auswerten und Beurteilen, S. 20: "Definition des Zufalls
Der „Zufall" im strengen Sinne des Wortes findet keinen Platz in unserer ausschließlich auf dem Prinzip von Ursache und Wirkung aufgebauten Welt. Der Zufall kann als der gemeinsame zeitliche Schnittpunkt mehrerer ursächlich ablaufender, voneinander unabhängiger Einzelereignisse aufgefaßt werden.
Wenn beispielsweise ein Verkehrsunfall als „unglücklicher Zufall" bezeichnet wird, dann ergeben sich mehrere voneinander unabhängige und streng kausal ablaufende Ereignisfolgen (z.B. regelwidriges Verhalten eines Verkehrsteilnehmers, nasse Straßen oder abgefahrene Reifen), die sich im Zeitpunkt des „zufälligen" Verkehrsunfalles treffen bzw. überschneiden.
    Im allgemeinen ist die Anzahl der Ursachen für ein „zufälliges" Ereignis so groß, daß dieses Vorkommnis nichtmehr vorherbestimmbar ist. So beeinflussen etwa 45 verschiedene Einflußgrößen — unabhängig vom Können und von der Geschicklichkeit des Arbeiters — den Zeitpunkt, wann ein Drehmeißel unbrauchbar wird. Über die Anzahl der einzelnen Einflußgrößen und über den Zeitpunkt, wann im Einzelfall der Meißel stumpf wird, ist keine verbindliche Vorhersage möglich. Dennoch ist die Standzeit, seine voraussichtliche Lebensdauer, eine brauchbare statistische, d. h. wahrscheinliche Größe.
Vom Zufall spricht man in der Statistik auch dann, wenn für jedes Element eine Gesamtheit (bzw. Grundgesamtheit) die Auswahlchance berechenbar Ist, „Mit-Glied" einer Stichprobe zu sein."
Barth und Haller (1984) in Stochastik Leistungskurs (2.A.) gehen einer Definition des Zufalls aus dem Weg, S. 10f:
"Vernünftige Experimente sind dadurch gekennzeichnet, daß man präzise die Bedingungen festlegt, unter denen das Experiment durchgeführt werden soll. Bei einem echten Experiment steht das Ergebnis nicht schon vorher fest. Trotzdem muß man sich vor der Durchführung einen Überblick über die möglichen Ergebnisse verschafft haben. Nur so kann ein Experiment gezielt eingesetzt werden. Man kann sich in einer derartigen Situation auf den Standpunkt stellen, daß das auftretende Ergebnis vom »Zufall« ausgewählt wird. Dabei wollen wir die Frage nicht diskutieren, ob es wirklichen Zufall gibt (was das auch immer sein soll), oder ob der Zufall nur deshalb als Lückenbüßer eintreten muß, weil wir die Situation nicht völlig durchschauen. In diesem Sinne nennen wir Experimente auch Zufallsexperimente.
Besonders deutlich tritt der Zufallscharakter eines Experiments bei den sogenannten Glücksspielen hervor. Bekannte Beispiele dafür sind:
1. Der Würfelwurf. Üblicherweise läßt man als Ergebnisse nur die Augenzahlen 1, 2, 3, 4, 5 und 6 zu und verzichtet darauf, Situationen wie »Der Würfel steht auf einer Kante« oder »Der Würfel steht auf einer Ecke« als Ergebnisse zu berücksichtigen. Führt man das Experiment mehrfach nacheinander durch, so sieht man das Wirken des Zufalls besonders eindrucksvoll. In Tabelle 10.1 sind die Ergebnisse von 1200 Würfelwürfen zeilenweise aufgezeichnet.
2. Der Münzenwurf. Hier betrachtet man meist nur zwei Ergebnisse, nämlich Adler und Zahl bzw. Kopf und Wappen je nach der Gestaltung der Münze. Neutral kann man die Ergebnisse z.B. auch durch 0 und 1 kennzeichnen. In Tabelle 11.1 sind die Ergebnisse von 800 Münzenwürfen aufgezeichnet."
Mises, Richard (1928 ff) in Wahrscheinlichkeit, Statistik und Wahrheit (hier 4.A. 1970)
geht einer direkten Definition des Zufalls aus dem Weg. Im Abschnitt Zufallsmechanismen diskutiert er den Sachverhalt anhand einer Lottoziehungsmaschine und erörtert die hier zu beachtenden Mechanismen
Klaus Mainzer in Mittelstraß (1996, Hrsg.) Enzyklopädie für Philosophie und Wissenschaftstheorie, Bd. 4, S. 855:
"zufällig/Zufall, in der Alltagssprache Bezeichnung für ein Ereignis, das nicht notwendig (> notwendig/Notwendigkeit) oder ohne erkennbaren Grund oder unbeabsichtigt eintritt. ... R. M. v. Mises schlägt 1919 vor, Zufall  mathematisch durch die Unregelmäßigkeit einer unendlichen 0-l-Folge unabhängig von physikalischen Vorgängen zu definieren. Danach heißt eine unendliche 0-1 -Folge x₁, x₂,... zufällig (oder ein Kollektiv), wenn die relative Häufigkeit



des Auftretens von l (a) gleich 1/2 ist und (b) sich nicht ändert, wenn man vermöge einer Auswahlregel zu einer Teilfolge x_m1, x_m2 ... übergeht, ... " Es wird weiter ausgeführt, dass sich die von Mises Definition als ungeeignet  erwies ( J. Ville 1939). Auch der neue Versuch Kolmogorovs 1965  sei gescheitert. "Daher wird von P. Martin Löf vorgeschlagen, als z. solche unendlichen 0-1-Folgen u bezeichnen, die einen universellen wahrscheinlichkeitstheoretischen Sequentialtest bestehen. Dann lässt sich beweisen, daß so definiert z,e  0-1-Folgen nicht Turing-berechenbar sind.
In den Naturwissenschaften wird Z. im Gegensatz zu kausal determinierten und voraussagbaren bzw. berechenbaren Ereignissen verstanden (>Determinismus, >Kausalität). In der klassischen Physik wird von einem vollständig determinierten Naturgeschehen ausgegangen. Daher sind dort gewisse Z.e ausgeschlossen; nur epistemische Zufälligkeit in Abhängigkeit vom Kenntnisstand eines Beobachters ist zugelassen, So erscheinen z, B. die Bewegungen einzelner Atome in einem Gasgemisch z., sind aber nach klassischer Auffassung vollständig determiniert. Ihre Eigenschaften werden durch Z.svariablen quantifiziert. Eine Z.svariable ist eine numerische Funktion X, die jedem z. gewählten Element w einer Ereignismenge eine Zahl X(w) zuordnet. Dabei kann es sich z. B. um die Augenzahl eines Würfels handeln. Elementen von Ereignismengen können mehrere Z.svariablen zugeordnet werden (z. B. Gewicht, Geschwindigkeit und Rotationsenergie von Gasmolekülen). Ihre Linearkombinationen, Produkte und Verhältnisse ergeben wieder Z.svariablen. ...."

Eislers Wörterbuch der philosophischen Begriffe [Online]
"Zufall (tychê, automaton, casus) ist 1) das Walten unbeabsichtigter, unvorhergesehener Ereignisse, 2) das Zusammentreffen zweier Ereignisse, das einer Berechnung nicht zugänglich ist, so aber, daß sowohl jedes der Vorgänge Wirkung einer Kausalreihe, als auch das Zusammentreffen beider Kausalreihen im Weltzusammenhang an sich begründet sein muß. Das Zufällige (s. Akzidens, Kontingenz) in diesem Sinne ist das für uns nicht gesetzlich Bestimmbare, nicht zur Allgemeinheit und Notwendigkeit des Gesetzes Erhebbare. Eine große Rolle spielt der »Zufall«, bedingt durch das Zusammentreffen von Kausalreihen sowie durch die Individualitäten, in der Geschichte. ..."
Timirjasew, K. A. (1843-1920) in Kurzer Abriß der Theorien Darwins: "„Ein leeres Wort, mit dem Unwissen verschleiert wird, ein Köder für den trägen Verstand. Existiert der Zufall denn wirklich in der Natur? Kann es ihn geben? Ist denn eine Wirkung ohne Ursache überhaupt denkbar?“ Nach Sekundärequelle S.7: Rastrigin, Leonhard A. (1973) Zahl oder Wappen. Ein Buch über den Zufall. Leipzig: Urania.
__
Zufallsgröße, Zufallsvariable. Unklarer Grundbegriff der Wahrscheinlichkeitstheorie. Im engeren Sinne hängt der Wert einer Zufallsvariable ausschließlich von einem Zufallsmodell ab (z.B. Würfel, Urnenmodell). Im weiteren Sinne der empirischen Wissenschaften, gilt für die allermeisten Größen oder Variablen: W = f(F₁, F₂, ..., F_i, ...  F_n), f(Z₁, Z₂, ..., Z_i, ...  Z_n), d.h. sie ergeben sich aus beeinflussenden Faktoren F₁, F₂, ..., F_i, ...  F_n und zufälligen Einflüssen Z₁, Z₂, ..., Z_i, ...  Z_n.
    Meschkowski definiert:


Zum Verständnis braucht man den Begriff der normierten Boolschen Algebra. Zunächst die Boolsche Algebra:

Und schließlich:

__
Zufall und Gesetz bei der Entstehung des Lebens
Eigen, Manfred (1983) Zufall und Gesetz bei der Entstehung des Lebens. Aulavorträge Hochschule St. Gallen, S. 11f:
    "Mit Hilfe von Spielregeln werden Gesetzmässigkeiten festgelegt. Diese Regeln variieren, je nach dem welcher physikalische, chemische oder biologische Vorgang simuliert werden soll. Der Ablauf des Spiels ist durch das Würfeln und die Anwendung der geltenden Spielregeln auf die jeweils getroffene Kugel gekennzeichnet.
    Beginnen wir mit einem ersten Spiel, das in sehr anschaulicher Weise die Natur des statistischen Gleichgewichts in Physik und Chemie beschreibt. Es wird mit zwei verschiedenen Materieteilchen, die durch schwarze und weisse Kugeln repräsentiert werden, gespielt. Wir gehen von einem Spielbrett aus, das mit schwarzen und weissen Kugeln in willkürlicher Mischung komplett besetzt ist. Daneben gibt es noch ein Reservoir, das eine grosse Zahl von schwarzen und weissen Kugeln enthält. Die Spielregel ist sehr einfach und lautet: Die jeweils getroffene Kugel wird durch eine Kugel der anderen Farbe ersetzt. Haben wir zum Beispiel eine schwarze Kugel erwürfelt, so [>12] ausgetauscht. Treffen wir dagegen eine weisse Kugel, so wird daraus eine schwarze. Es ist dabei übrigens völlig gleichgültig, von welcher Kugelverteilung man ausgeht, d.h. ob man ausschliesslich weisse oder nur schwarze oder irgendein Gemisch beider Arten zu Beginn des Spieles auf dem Spielbrett hat. Nach einigen Spielrunden, und zwar schon nach etwa 64 Zügen — wir bezeichnen diesen Zeitabschnitt als eine Generation, da jedes Feld einmal die Chance hat, erwürfelt zu werden — sind immer beide Kugelfarben im zeitlichen Mittel in gleicher Menge auf dem Spielbrett vertreten.
    In einem solchen Spielablauf wird der Vorgang der Gleichgewichtseinstellung demonstriert. Das Ergebnis ist ganz einfach zu verstehen. Sind beispielsweise sehr viel mehr schwarze Kugeln auf dem Spielbrett, so ist auch die Wahrscheinlichkeit sehr viel grösser, dass beim nächsten Wurf eine schwarze Kugel getroffen und in eine weisse umgewandelt wird. Jeder Überschuss der einen Sorte gegenüber der anderen gleicht sich dadurch sehr bald aus. Mit anderen Worten: Jede Abweichung von der Gleichverteilung der Farben ist Ursache für einen Ausgleich. Dem entspricht in der Chemie das Massenwirkungsgesetz für zwei Substanzen, die die gleiche freie Energie besitzen."
    Sekundärquelle: Materialien zur Kausalität in der Naturwissenschaft und Technik.
    Eigen: https://www.youtube.com/watch?v=nFCwr1btiSs
    Eigen: https://www.youtube.com/watch?v=NTVw-ongVyw

__
Zureichender Grund
Grundprinzip, das kurz und bündig verlangt: nichts ohne Begründung. Leibniz: „Im Sinne des zureichenden Grundes finden wir, daß keine Tatsache als wahr oder existierend und keine Aussage als wahr betrachtet werden kann, ohne daß ein zureichender Grund vorhanden wäre, warum es so ist und nicht anders" (G. W. LEIBNIZ, Monadologie, § 33, Nr. 32)."
__
Zuverlässigkeit. > Reliabilität. In der psychologischen Testtheorie meist Messgenauigkeit.
__
z-Werte = (Rohwert - Mittelwert) / Standardabweichung.
__

---


Literatur (Auswahl)
Siehe bitte auch Literaturliste Bayes, Diskriminanzanalyse, Faktorenanalyse, Irrtum, Fehler, Betrug, Kommunalität, Korrelation, Laborwertnormen, Metaanalysen, Numerisch instabile Matrizen und Kollinearität in der Psychologie, ProzentRANG, Signifikanztest, Simpson's Paradox, Statistikpakete, Zeitreihen, ..., ...
 
• Bagdonavicius, V., Kruopis, J., Nikulin, M. S. (2011). Non-parametric tests for complete data.  ISTE & WILEY: London & Hoboken..
• Bamberg, Günter (1972). Statistische Entscheidungstheorie. Würzburg: Physica.
• Barth, Friedrich & Haller, Rudolf  (1984) Stochastik Leistungskurs. 2. A. München: Ehrenwirth.
• Bender & Nack (1995) Tatsachenfeststellung vor Gericht. Bd. 1 Glaubwürdigkeits- und Beweislehre. München: Beck
• Borovcnik, M. (1984). Was bedeuten statistische Aussagen. Schriftenreihe für Didaktik der Mathematik. Wien: Hölder-Pichler-Tempsky.
• Bortz, Jürgen & Döring, Nicola (1995) Forschungsmethoden und Evaluation. 2.A. Berlin: Springer.
• Bullen, P. S. (2003). Handbook of Means and Their Inequalities. O?: Kluwer Acad. Pub.  ISBN 1-402-01522-4.
• Carnap, Rudolf  & Stegmüller, Wolfgang (1958) Induktive Logik und Wahrscheinlichkeit. Berlin: Springer.
• Clauss, Günter & Ebner, Heinz (1970), Grundlagen der Statistik. Für Psychologen, Pädagogen und Soziologen. Frankfurt: Deutsch.
• Cohen, J. (1969 ff). Statistical power analysis for the behavioral sciences. New York, NY: Academic Press.
• Coombs, Clyde H.; Dawes, Robyn M. & Tversky, Amos (dt. 1975, engl. 1970) Mathematische Psychologie. Weinheim: Beltz.
• Corder, G. W. & Foreman, D. I. (2009) Nonparametric Statistics for Non-Statisticians: A Step-by-Step Approach, Wiley.
• Dewdney, Alexander K. (1998).  Alles fauler Zauber ?, Basel: Birkhäuser.
• Eigen, Manfred (1983) Zufall und Gesetz bei der Entstehung des Lebens. Aulavorträge Hochschule St. Gallen.
• Fisher, R. A. (1925). STATISTICAL METHODS FOR RESEARCH WORKERS. Edinburgh: Oliver And Boyd. [Online]
• Flury, Bernhard & Riedwyl, Hans (1983) Lineare Diskriminanzanalyse im Zweigruppenfall. In (72-98): Angewandte multivariate Statistik. Computergestützte Analyse mehrdimensionaler Daten. Stuttgart: Gustav Fischer.
• Garry, R. C. (1947). Testing for normality. Biometrika 34, 209-242.
• Gibbons, Jean Dickinson and Chakraborti, Subhabrata (2003) Nonparametric Statistical Inference.
• Gigerenzer, Gerd  (1981). Messung und Modellbildung in der Psychologie. München: Reinhardt.
• Gigerenzer, Gerd (2002). Das Einmaleins der Skepsis. Über den richtigen Umgang mit Zahlen und Risiken. Berlin: Berlin.
• Gigerenzer, Gerd (2007) Bauchentscheidungen  Die Intelligenz des Unbewussten und die Macht der Intuition. München: Goldmann.
• Gigerenzer, Gerd (2013)  Risiko. Wie man die richtigen Entscheidungen trifft. München: Bertelsmann.
• Grawe, Klaus (1991). Über den Umgang mit Zahlen. In: Grawe et al. (1991, Hrsg.). Über die richtige Art Psychologie zu betreiben. Göttingen: Hogrefe. S. 89-105.
• Grimm, H (1960). Transformation von Zufallszahlen. Biometrische Zeitschrift, Bd. 2, 164-182.
• Gruber, Antje Birgit (2011) Kointegration in Theorie und Praxis: Statistische Analyse gemeinsamer Entwicklungstrends in psychologischen Zeitreihensystemen. Dissertation [PDF]
• Hake, A. (2001). Was sagen gruppenstatistische Kennwerte über den Einzelfall aus? (Materialien für Lehre, Aus- & Weiterbildung 24). Landau: Verlag empirische Pädagogik.
• Hake, Alexandra (2002). Trugschlüsse in der Statistik im Spannungsfeld zwischen Aggregat und Einzelfall. Eine Bestandsaufnahme und kritische Evaluation. Lengerich [u.a.]: Pabst Science Publisher.
• Haller-Wedel, Ernst (1967) Messen, Zählen, Auswerten und Beurteilen. München. Hanser.
• Hettmansperger, T. P.; McKean, J. W. (1998). Robust nonparametric statistical methods. Kendall's Library of Statistics. 5 (First ed.). London: Edward Arnold.
• Hirz, Helmut (2008) Ein Blick in die Historie der Wahrscheinlichkeitsrechnung. Bayern in Zahlen 1|2008 Beiträge aus der Statistik, 32-48.
• Horst, Paul (1963). Matrix Algebra for Social Scientists. New York: Holt, Rinehart and Winston.
• Huff, Darrell (1954, 1973f). How to Lie With Statistics. Penguin.
• Jecklin, H. (1949). Versuch einer Systematik des mathematischen Mittelwertbegriffs. Commentarii Mathematici Helvetici, Vol. 22, 1. Basel: Birkhäuser.
• Juhos, Béla  & Katzenberger, Wolfgang  (1970) Wahrscheinlichkeit als Erkenntnisform. Berlin: Duncker & Humblot. [GB]
• Kiencke, Uwe & Eger, Ralf  (2008) Messtechnik. Systemtheorie für Elektrotechniker. Berlin: Springer.
• Kolmogoroff, A. (1933). Grundbegriffe der Wahrscheinlichkeitsrechnung. Berlin: Springer. Nachdruck 1973.
• Kotz, S. & Johnson, N. (1982-1989, Ed.). Encyclopedia of Statistical Science.  Vol. 1-10. New York: Wiley.
• Krämer, Walter (1991). So lügt man mit Statistik. Frankfurt: Campus.
• Krämer, Walter (1996). Denkste! Trugschlüsse aus der Welt des Zufalls und der Zahlen. Frankfurt: Campus.
• Krauth, J. & Lienert, G.A. (1973) KFA Die Konfigurationsfrequenzanalyse- Freiburg: Alber.
• Kriz, Jürgen (1967) Der Likelihood-Quotient zur Erfassung des subjektiven Signifikanzniveaus. Wien: Forschungsbericht (17 S.)
• Laplace, P. S. de (dt. 1896, orig. 1814)  Philosophischer Versuch über die Wahrscheinlichkeiten. Dt. Übersetzung nach der 6. Auflage. Leipzig: Duncker & Humblot.
• Lienert, G. A. (1973) Verteilungsfreie Methoden in der Biostatistik. Bd. I. Meisenheim/Glan: Hain.
• Lienert, G. A. (1975) Verteilungsfreie Methoden in der Biostatistik. Tafelband. Meisenheim/Glan: Hain.
• Lienert, G. A. (1978) Verteilungsfreie Methoden in der Biostatistik. Bd. II. Meisenheim/Glan: Hain.
• Matlab: Statistics Toolbox.
• Menges, Günter (1972). Statistik 1 Theorie. Opladen: Westdeutscher Verlag.
• Mises, Richard von (196, 4.A. 1972). Wahrscheinlichkeit, Statistik und Wahrheit. Wien: Springer.
• Mittelstraß, Jürgen (1980-1996, Hrsg.). Enzyklopädie Philosophie und Wissenschaftstheorie. 4 Bde. Die ersten beiden Bände erschienen bei BI, Mannheim. Die letzten beiden Bände bei Metzler, Stuttgart.
• Most, Otto (1955). Allgemeine Statistik. Baden-Baden: Lutzeyer.
• Müller, P. H. (1970, Hrsg.) Lexikon Wahrscheinlichkeitsrechnung und mathematische Statistik. Berlin: Akademie.
• Ortlieb, Claus Peter (2005). Die Zahlen als Medium und Fetisch. In: Schröter, J. / Schwering, G. / Stäheli, U.  (2006). Media Marx. Ein Handbuch, 153 - 167.  Bielefeld: transcipt.
• Piattelli-Palmarini, Massimo (dt. 1997, ital. 1993). Die Illusion zu wissen. Was hinter unseren Irrtümern steckt. Reinbek: Rowohlt.
• Quatamber, Andreas (2015) Statistischer Unsinn. Berlin: Springer
• Randow, Gero von (1992). Das Ziegenproblem. Denken in Wahrscheinlichkeiten. Reinbek: Rowohlt.
• Rasch, Dieter (1978). Einführung in die mathematische Statistik. Bd. I. Wahrscheinlichkeitsrechnung und Grundlagen der mathematischen Statistik. Berlin: VEB d Wiss.
• Revenstorf, Dirk (1980). Faktorenanalyse. Stuttgart: Kohlhammer.
• Rosenthal, Jacob (2004) Wahrscheinlichkeiten als Tendenzen. Eine Untersuchung objektiver Wahrscheinlichkeitsbegriffe. Paderborn: Mentis.
• Röhr, Michael; Lohse, H.;  Ludwig, R. (1983). Statistische Verfahren. Thun und Frankfurt a.M.: Harri Deutsch.
• Rößler, Irene & Ungerer, Albrecht (2010). Statistik für Wirtschaftswissenschaftler. Würzburg: Physica-Verlag.  Hierzu als PDF im Netz:  Kommentierte Formelsammlung der deskriptiven und induktiven Statistik für Wirtschaftswissenschaftler.
• Rumsey, Deborah (dt. 2004). Statistik für Dummies. Weinheim: Wiley-VCH.
• Rumsey, Deborah (dt. 2007). Wahrscheinlichkeitsrechnung für Dummies. Weinheim: Wiley-VCH.
• Schneider, Ivo (1988, Hrsg.) Die Entwicklung der Wahrscheinlichkeitstheorie von den Anfängen bis 1933. Einführungen und Texte. Darmstadt: WBG.
• Schnoor, C. P. (1971) Zufälligkeit und Wahrscheinlichkeit. Eine algorithmische Begründung der Wahrscheinlichkeitstheorie. Berlin: Springer
• Schüller, Katharina (2015) Statistik und Intuition. Alltagsbeispiele kritisch hinterfragt. Heidelberg: Springer Spektrum.
• Siegel, Sidney (1956): Nonparametric Statistics FOR THE BEHAVIORAL SCIENCES. New York, Toronto, London: McGraw-Hill. Deutsche Übersetzung 1976 bei der Fachbuchhandlung für Psychologie, Frankfurt am Main.
• Sponsel, R. (1994). Numerisch instabile Matrizen und Kollinearität in der Psychologie. Ill Conditioned Matrices and Collinearity in Psychology. Zweisprachig. Ins Englische übersetzt von Agnes Mehl. Mit einem Beitrag (Kap. 6) von Dr. B. Hain: Bemerkungen über Korrelationsmatrizen. Erlangen: IEC Verlag.
• Sponsel, R. (2005). Fast- Kollinearität in Korrelationsmatrizen mit Eigenwert-Analysen erkennen Ergänzungsband - Band II zu Numerisch instabile Matrizen und Kollinearität in der Psychologie.
• Statistiklabor. Statistikprogramm.
• Stegmüller, Wolfgang (1969). Statistische Erklärungen. Deduktiv-nomologische Erklärungen in präzisen Modellsprachen. Offene Probleme. Studienausgabe Teil 5: Probleme und Resultate der Wissenschaftstheorie und analytischen Philosophie Bd. I. Wissenschaftliche Erklärung und Begründung.
• Stegmüller, Wolfgang (1973). Aufgaben und Ziele der Wissenschaftstheorie. Induktion. Das ABC der modernen Wahrscheinlichkeitstheorie und Statistik.  Probleme und Resultate der Wissenschaftstheorie und analytischen Philosophie  Band IV Personelle und statistische Wahrscheinlichkeit. Studienausgabe Teil A. Berlin: Springer.
• Stegmüller, Wolfgang (1973). Statistische Begründung. Statistische Analyse. Das Repräsentationstheorem von de Finetti. Metrisierung qualitativer Wahrscheinlichkeitsfelder. Studienausgabe Teil E: Probleme und Resultate der Wissenschaftstheorie und analytischen Philosophie Bd. IV. Personelle und Statistische Wahrscheinlichkeit.
• Steinbring, Heinz (1980) Zur Entwicklung des Wahrscheinlichkeitsbegriffs — Bernoullis Theorem aus didaktischer Sicht. Journal für Mathematik-Didaktik.

September 1980, Volume 1, Issue 3, pp 115-141. First online: 20 December 2013.
• Stelzl, Ingeborg (1982). Fehler und Fallen der Statistik. Für Psychologen, Pädagogen und Sozialwissenschaftler. Bern: Huber.
• Sweschnikow, A. A. S. (1970, Hrsg.) Wahrscheinlichkeitsrechnung und Mathematische Statistik in Aufgaben. Leipzig: Teubner.
• Székely, Gábor J. (1990). Paradoxa. Klassische und neue Übersetzungen aus Wahrscheinlichkeitsrechnung und mathematischer Statistik. Frankfurt aM.: Deutsch.
• Wasserman, Larry (2007) All of nonparametric statistics. Springer.
_


---


Links (Auswahl)
 
• Fehlurteile und Missverständnisse: Gerd Gigerenzer und der richtige Umgang mit Zahlen. Für die Interpretation eines Gutachtens ist vor allem die Form, in der es dargestellt wird, von Bedeutung. Daher gilt für Gerd Gigerenzer: Um Fehlschlüsse zu vermeiden, sollten statistische Informationen besser und verständlicher kommuniziert werden. Falsche Auslegung von Statistiken kann fatale Folgen haben: für die eigene Gesundheit, die eigene Freiheit oder auch das Bankkonto. Experten wie Laien sind häufig nicht in der Lage, statistische Informationen richtig zu verstehen.
• Denkfallen und Paradoxa.
• Engineering Statistics Handbook.
• Glossar Biomathe Uni Münster.
• Lügen mit Statistik.
• Statistiklabor der Uni Berlin (Schlittgen)
• Unsinn in den Medien - vom sorglosen Umgang mit Daten.
• Unstatistik des Monats.


IP-GIPT Links:

• [R. Sponsel: Der Signifikanztest in der Wissenschaft, Psychologie, klinischen und Psychotherapieforschung. Szientismus zwischen numerologischer Esoterik, Gaukeln und Betrug?]
• [R. Sponsel: Partielle Korrelationen.]
• [R. Sponsel: Das Bayes'sche Theorem].
• [Reader zu den Grundlagen der Statistik: Günter Bamberg: Verschiedene Auffassungen von Statistik und die Auffassung der statistischen Entscheidungstheorie.]
• [R. Sponsel: Statistik-Pakete - Methodische Anforderungen. Kriterien Checkliste ("TÜV") für Statistik-Pakete.]
• [R. Sponsel: Dynamische Systeme. Ein Buchhinweis (Schiepek & Strunk).]
• [R. Sponsel: Diskriminanzanalyse]
• [R. Sponsel: Meta-Analyse: Was sind und was sagen Meta-Analysen aus?]
• [R. Sponsel: Die grundlegenden Probleme und Aporie jeglicher Einzelfall- und damit Therapieforschung. Grundzüge einer idiographischen Wissenschaftstheorie. ]
• [R. Sponsel: Allgemeine Theorie und Praxis des Vergleichens und der Vergleichbarkeit. Grundlagen einer psychologischen Meßtheorie. ]
• [R. Sponsel: Über den Aufbau einer präzisen Wissenschaftssprache in Psychologie, Psychopathologie, Psychodiagnostik und Psychotherapie aus Allgemeiner und Integrativer Sicht (GIPT).  Operational-Konstruktive Definition psychologischer Termini. Definitionslehre der GIPT.]
• PORTRAITS OF STATISTICIANS. [1,2,3,]
_


---


Glossar, Anmerkungen, Endnoten:  > Eigener wissenschaftlicher Standort.
GIPT= General and Integrative Psychotherapy, internationale Bezeichnung für Allgemeine und Integrative Psychotherapie.
__
Internetseite
Um die häufige und lästige Fehlermeldung 404 zu minimieren, geben wir nur noch Links von Quellen an, die in den letzten Jahrzehnten eine hohe Stabilität ihrer URL-Adressen gezeigt haben (z.B. Wikipedia, DER SPIEGEL). Staatliche Institutionen gehören nicht dazu.
__
Schaefer & Blohmke (1978, S.111): "Die Mortalität ist das Ergebnis zweier voneinander unabhängiger Determinanten: der Häufigkeit einer Erkrankung und ihrer Gefährlichkeit. Das Maß der ersteren nennt man die Morbidität, eine Maßzahl, welche als Morbiditätsziffer auf 1000 Lebende der betrachteten Bevölkerungsgruppe (Altersgruppe, Geschlecht, Stadt, Land etc.) bezogen wird. Sie ist jedoch eine wenig sinnvolle Größe. Die moderne Demographie und Epidemiologie ersetzt sie daher durch die Prävalenz oder Inzidenz einer Krankheit, die ebenfalls unten definiert sind (Abschn. 4.4.5.). Der Ausdruck Morbidität wird nur noch als allgemeines Kennzeichen für Daten benutzt, welche quantitative Angaben über Krankheitshäufigkeiten machen. Je gefährlicher die Krankheit ist, desto mehr Erkrankte sterben an ihr. Die krankheitsspezifische Mortalitätsziffer ist also besonders hoch für häufig vorkommende und zugleich gefährliche Krankheiten."


---

Wird gelegentlich vervollständigt, ergänzt überarbeitet - Anregungen und Kritik erwünscht

---

Querverweise
Standort: Beweis und beweisen in der Statistik.
*
Überblick Statistik in der IP-GIPT.
Einführung, Überblick, Verteilerseite Beweis und beweisen
Wissenschaft in der IP-GIPT
Überblick: Abstrakte Grundbegriffe aus den Wissenschaften
Elemente wissenschaftlicher und sachlicher Texte. Kleines Wissenschaftsvokabular und  Glossar mit Signierungsvorschlägen.




---

Wird gelegentlich vervollständigt, ergänzt überarbeitet - Anregungen und Kritik erwünscht

---

Zitierung
Sponsel, Rudolf  (DAS). Beweis und beweisen in der Statistik. Blicke über den Zaun zum Auftakt für eine integrative psychologisch-psychotherapeutische Beweislehre. Abteilung Abstrakte Grundbegriffe aus den Wissenschaften: Analogien, Modelle und Metaphern für die allgemeine und integrative Psychologie und Psychotherapie sowie Grundkategorien zur Denk- und Entwicklungspsychologie. Internet Publikation - General and Integrative Psychotherapy   IP-GIPT. Erlangen: https://www.sgipt.org/wisms/gb/beweis/b_stat.htm
Copyright & Nutzungsrechte
Diese Seite darf von jeder/m in nicht-kommerziellen Verwertungen frei aber nur original bearbeitet und nicht  inhaltlich verändert und nur bei vollständiger Angabe der Zitierungs-Quelle benutzt werden. Das direkte, zugriffsaneignende Einbinden in fremde Seiten oder Rahmen ist nicht gestattet, Links und Zitate sind natürlich willkommen. Sofern die Rechte anderer berührt sind, sind diese dort zu erkunden. Sollten wir die Rechte anderer unberechtigt genutzt haben, bitten wir um Mitteilung. Soweit es um (längere) Zitate aus  ...  geht, sind die Rechte bei/m ... zu erkunden oder eine Erlaubnis einzuholen.

---

  Ende_Beweise in der Statistik_Datenschutz_Überblick_Rel. Aktuelles  _Rel. Beständiges_Titelblatt_ Konzept_ Archiv_ Region_Service_iec-verlag  Mail:  sekretariat@sgipt.org__Wichtiger Hinweis zu Links und zu Empfehlungen

 irs: 29.08.2021 - 03.09.2021 Rechtschreibprüfung

Änderungen
15.06.24    Rubrik Fehler.
02.04.22    Gesetz der großen Zahlen  (nach Anderson). * Fast sicher. * Fast unmöglich *  möglich, Möglichkeit * unmöglich, Unmöglichkeit * Dimension * Ordnung *
08.09.21    Missing Data.
19.08.21    Eingangszitate (Plan).
06.08.21    Aktualisierung Determinationskoeffizient.
31.01.21    Homogenität, Kovarianzanalyse.
13.08.20    Entropie. * Conjoint measurement *
12.08.20    Neue Stichwörter: Daten * Datentheorie * Datentyp * Datenverarbeitung * Information * Informationstheorie *
11.07.19    Neues Stichwort: Poissonverteilung *
09.07.19    Neue Stichworte:  Statistische Hypothesen * Verteilungsfreie statistische Verfahren * Wahrscheinlichkeitsbegriff Stegmüllers *
19.02.19    Hinweis auf Elemente wissenschaftlicher und sachlicher Texte. Kleines Wissenschaftsvokabular und  -Glossar mit Signierungsvorschlägen.
12.08.18    Neue Glossareinträge (Messtheorien):  Bedeutsamkeitsproblem, Eindeutigkeitsproblem, Konnektivität, Konnexität, Maßtheorie (mathematische), Messtheorie (psychologische), Metrik, Repräsentationsproblem, Skalierungsproblem.
01.08.18    Neue Glossareinträge: Durchschnitt,Deutung..., Darstellung..., Interpretation ..., Mittelwerte und Durchschnitte, Kennwerte (Größen, Parameter),
05.07.18    Neuaufnahmen Glossar: Normbedingung, Normalbedingung, Standardbedingung, Gültigkeitszeitraum.
03.06.18    4 Linkfehler entfernt.
16.05.18    Kontingenz, kontingent
12.05.18    Zufall und Gesetz bei der Entstehung des Lebens (Eigen).
05.09.17    a priori - a posterori - Ding an sich.
28.07.17    Klassenbildung nach Merkmalen.
11.05.17    Logik ins Glossar aufgenommen..
06.12.16    Moderatorvariable.
14.10.16    RCT.
25.07.16    Linkfehler geprüft und korrigiert.
29.02.16    Eintrag: unabhängig - Unabhängigkeit. * Wahrscheinlichkeit 1 und 2 nach Carnap *
27.02.16    Likelihood-Quotient.
13.09.15    Neue Links zu Unsinn in der Statistik, Lit: Quatamber, Zipf'sches Gesetz.
14.08.15    Risiko, Riskokompetenz, Risikowahrschenlichkeit, Überdiagnose-Fehler, Vorlauf-Zeit-Fehler
18.02.15    Linkfehler geprüft und korrigiert.
29.01.15    Zureichender Grund.
21.01.15    AUC.
18.01.15    Messung per fiat.
17.01.15    DNA-Test,Gruppenkennwert, Einschlusschance, Spurenhypothesen (nach Gigerenzer).
13.01.15    Validität, inkrementelle. Überarbeitung Validität.
09.11.14    Ergänzungen u.a. zur Zeitreihenanalyse.
24.06.14    Überarbeitung und Ergänzungen zum Zufallsbegriff.
22.06.14    Methode * Mittel * Nebenbedingung * Operationalisierung * Randbedingung * Theorie * Trennschärfe * Ziel und Ziele *
21.06.14    erklären und verstehen.  * cum hoc ergo propter hoc. * Kausalität.
09.10.13    Ins Glossar aufgenommen: Frequentisten, Modell, Bayesianer.
18.04.13    Kritische Anmerkung zum T-Wert und dem sog. McCall-Verfahren der "Normalisierung".
16.04.13    Ins Glossar aufgenommen: Panelstudien, Pfadanalyse.
25.12.12    Kappa.
04.10.12    Maximale Clique (auch: Maximaler vollständiger Untergraph).
03.10.12    Biplot in das Glossar aufgenommen.
17.09.12    Determinationskoeffizient.
25.02.12    Doku Kommunikation mit dem BMAS.
06.02.12    Die Tricks der Margret Thatcher, die Arbeitslosenzahlen runter zu rechnen.
02.02.12    Manipulation, tricksen, frisieren, täuschen, verdrehen, lügen, ausblenden, weglassen.
19.01.12    Quellenhinweis paranormale Fähigkeiten testen.
05.10.11    Link zur Seite Rangzahl.
10.09.11    Ergänzungen Alternativhypothese, Hypothesendiskussion,  Nullhypothese, Größe.
09.09.11    Integratives Testprinzip * Hypothesenraum * Zentraler Grenzwertsatz.
06.09.11    Paradigma * Stat. Paradigma * Fehler * Non-parametrische Statistik * Rang, Rangzahlen, Rangtests *
04.09.11    Ergänzungen: 1, 2.
29.08.11    Glossar: Fiduzialkonzept, Prüfstatistik, Statistisches Paradigma, statistische Schlussweisen, Lit: Clauss & Ebner, Dieter Rasch.
14.05.11    Überarbeitung Simpson's Paradox.
12.05.11    Kleine Korrekturen und Literaturergänzungen.
23.05.09    Ergänzungen zum Mittelwert.
25.04.09    Würfelspielparadoxon erfasst und Laplace-Experiment.
21.04.09    Grundlagen der Interpretation statistischer Daten und Modelle.
17.04.09    Simpson's Paradoxon mit fehlender Relationstreue identifiziert.
16.04.09    Ergänzung zu Simpsons Paradoxon.
14.04.09    Simpson's Paradoxon. * Vieldeutigkeitssatz.
15.12.07    Produkt-Moment (kleines, großes). * Regression, Regressionsanalyse.
30.11.07    Aufnahme wichtiger stat. Begriff: Erwartungstreu(e Schätzung), Inferenz-Statistik, Kovarianz, Zeitpunkt; Erg. z. Wert, wahrer.
03.08.07    Zur Genauigkeit der amtlichen Daten zum Wirtschaftswachstum.
21.04.07    Veränderungen der Erhebung statistischer Kenngrößen 1973 und 1978 am Beispiel Verschuldung der Gemeinden.
09.04.07    Korrektur zum 30.03.07:
30.03.07    Beispiel MD3b: Schätzung des Gesamtschuldenstandes Nürnbergs am 31.3.1928 in Reichsmark.
17.03.07    Tradition mehrdeutiger und daher unsinniger Auszeichnungen in der bayerischen Statistik.
09.03.07    Repräsentativität, Transparenz und Kontinuität statistischer Zeitreihen.
11.03.06   Linkhinweis: Lügen mit Statistik. Hinweis auf das "Statistiklabor" der Uni-Berlin (Schlittgen).
02.11.03   Einige Ergänzungen, Kurzdefinitionen und Links im Glossar.