Internet Publikation für Allgemeine und Integrative Psychotherapie
    (ISSN 1430-6972)
    IP-GIPTDAS=06.11.2021 Internet Erstausgabe, letzte Änderung: 08.02.22
    Impressum: Diplom-Psychologe Dr. phil. Rudolf Sponsel   Stubenlohstr. 20   D-91052 Erlangen
    Mail:_sekretariat@sgipt.org_ Zitierung  &  Copyright
    Anfang_ Eigene Untersuchung Plausibilität_Datenschutz_Rel. Aktuelles_Überblick_Überblick Wissenschaft _Rel. Beständiges_ Titelblatt_Konzept_Archiv_Region_Service iec-verlag__Wichtige Hinweise zu Links und Empfehlungen
    Willkommen in unserer Internet-Publikation für Allgemeine und Integrative Psychotherapie IP-GIPT1, Abteilung Wissenschaft, Bereich Sprache und Begriffsanalysen und hier speziell zum Thema:

    Eigene Untersuchung zum Plausibilitätsbegriff und einer allgemeinen Plausibilitätstheorie

    Originalarbeit von  Rudolf Sponsel,  Erlangen

    Überblicks- und Verteilerseite Plausibilitätsanalysen_ Gesamtergebnisse Pilotstudie.

    Zusammenfassung - Summary
    Inhaltsübersicht

    Zusammenfassung Abstract Summary:
    __Quellenbasis.
    __Plausibel ein Metasprachlicher Ausdruck 2. Stufe.
    __Gründe ein metasprachlicher Ausdruck 1. Stufe.
    __Gewichte, ein metasprachlicher Ausdruck 3. Stufe, und das Gewichtungsproblem.
    __Definitionsvorschlag Plausibilität von Sachverhalten.
    __Plausibilitätsformel.
    __Das Skalierungsproblem.
    __Plausibilitätsforschung.
    __Ergebnisse meiner nichtrepräsentativen Pilotstudie (n=52).
    __Begriffsbasis für die Definition von plausibel.
    Entwicklung der Plausibilitätsformel.
    Gewichtungsproblem.
    __Argumentationsschemata.
    Skalierungsproblem.
    Systematik der Plausibilitätsgründe.
    Standardmodelle für Plausibilitäten.
    __Standardmodelle Alltag.
    ____Standardmodell Frühstücksaufstrichwahl.
    ____Standardmodell Essen.
    __Standardmodelle Epidemiologie.
    ____Plausibilität der Kritische Masse Hypothese der Omikronvariante.
    __Standardmodelle Ökologie.
    __Standardmodelle Politik.
    __Standardmodelle Staat.
    __Standardmodelle Gesellschaft.
    __Standardmodelle Medien.
    __Standardmodelle soziale Medien & Internet.
    __Standardmodelle Recht.
    __Standardmodelle Wirtschaft.
    __Standardmodelle Finanzen.
    __Standardmodelle Wissenschaft.
    __Standardmodelle in der Psychologie.
    ____Standardmodell Psyche * Was ist die Seele praktisch psychologisch betrachtet?
    Geltungs- oder Gültigkeitsbereiche:
    __Subjektives Plausibilitätsurteil.
    __Gruppensubjektives Plausibilitätsurteil.
    __Intersubjektives Plausibilitätsurteil (sollte von fast allen so gesehen werden).
    __Objektiver Bezug (sollte objektiv gelten, unabhängig vom menschlichen Erkenntnissystem).
    Recherchen zum Gebrauch des Plausibilitätsbegriffs.
    Untersuchungen anderer zur Plausibilität (Auswahl) Teil-Kommentierte Literaturliste. 

    Literatur und Links. 
    Glossar, Anmerkungen und Endnoten:
    Querverweise, Zitierung & Copyright, Änderungen.

    Zusammenfassung
    Zitiervorschlag: Sponsel, Rudolf (6.11.2021) Zusammenfassung Plausibilitätsstudie. Internet-Publikation für Allgemeine und Integrative Psychotherapie (IP-GIPT): https://www.sgipt.org/wisms/sprache/BegrAna/Plausib/RSEUPT.htm.

    Quellenbasis: Aus der Analyse der Forschungsliteratur, insbesondere auch  Rescher 1976, der Analyse der  Gebrauchsbeispiele  und aufgrund der Ergebnisse meiner empirischen  Pilotstudie, bin ich zu folgendem Hauptergebnis gelangt: Plausibel oder Plausibilität wird in sehr vielen Zusammenhängen in Wissenschaft und Leben als undefinierter und allgemeinverständlich gedachter und meist auch funktionierender Grundbegriff mit den Kerncharakterisierungen einleuchtend, nachvollziehbar, glaubhaft, stimmig, richtig, so könnte es sein, wahrscheinlich wahr verwendet. Die meisten Begriffsklärungsversuche laufen aber genau betrachtet ins Leere, weil ein unklarer Begriff wie plausibel auf andere ebenso unklare Begriffe verschoben wird usw. usf.. So entstehen ganze Begriffsverschiebebahnhöfe,  typisch besonders in den Geistes-, Rechts- Sozial- und Kulturwissenschaften.

        Vor der Definition der Plausibilität ist eine genaue begriffliche Analyse sinnvoll. Sie ist zwar schwierig, aber notwendig. Plausibel ist ein metasprachlicher Ausdruck mindestens der 2. Stufe, weil in jede Plausibilitätsbeurteilung Gründe eingehen, die der ersten metasprachlichen Stufe angehören. Die wichtigeren Begriffe werden zur Klarheit und zum einfacheren Verständnis indiziert: Objektsprache0,  Metasprache1, Metasprache2, Metasprache3 ... Eine Metasprache beschreibt nicht Sachverhalte1 in der Welt (Welten), z.B. da steht0 ein Baum (sog. Objektsprache0), sondern beurteilt die Beschreibungen der Sachverhalte1, z.B. es ist richtig1 (falsch1, fraglich1, Unsinn1), dass da ein Baum steht0. Metasprache1 1. Stufe: Es zieht, weil1 Tür und Fenster offen sind0. Metasprache2 2. Stufe: es ist plausibel2, dass es zieht, weil1 Tür und Fenster offen sind. Objektsprache0: es ist0 heiß, Tür und Fenster sind0 offen. Metasprache1 1. Stufe: Tür und Fenster sind0 offen, weil1 es heiß ist0. Metasprache2 2. Stufe: es ist0 plausibel2, dass Tür und Fenster offen sind0, weil1 es heiß ist0. "weil" kann man nicht direkt wahrnehmen, die  Kausalbeziehung  ist eine erkenntnistheoretische Konstruktion. Und weiter Metasprache3 3. Stufe: Ich sehe nicht ein3, weshalb das plausibel2 sein soll. Hier findet also eine Diskussion3 über eine Plausibilitätsbeurteilung2 statt.

        Grundidee: Ob oder wie sehr etwas als plausibel2 beurteilt wird, hängt von den Gründen1 ab, die für oder gegen einen Sachverhalt1 vorgebracht werden. Das wirft zunächst die wichtige Frage auf, was ein Grund1 sein soll.
    Grund1, ein metasprachlicher Begriff 1. Stufe, sind  allej Sachverhalte1, die mehr oder weniger auf andere Sachverhalte1wirken, fördernd oder hemmend. Kausalität1, Wahrscheinlichkeit1, Häufigkeiten1, Regelhaftigkeiten1 und Gesetzesartigkeiten1 spielen bei den Gründen1 eine wichtige Rolle wie auch Erfahrungen0 und schon Erlebtes0. Sämtliche Kriterien für die Wahrheit1 oder Falschheit1 von Sachverhalten1 können auch für die Plausibilität2 eine wichtige Rolle spielen.

        Die erste Basis für Plausibilität2 ist also die die Anzahl der Gründe1, die für oder gegen einen Sachverhalt1 geltend gemacht werden. Obwohl manchmal ein einziger Grund1 genügt, sind in der Regel aber nicht alle Gründe1 gleichwertig, so dass die wichtige Frage beantwortet werden muss, wie die Gründe1 zu gewichten2 sind, genauer: wie man unterschiedliche Gewichte2 begründen kann. Das kann einfach sein, wenn der Grund1 z.B. die Häufigkeit1 ist. Dann kann man Gewicht2 und Häufigkeit1 gleichsetzen. Ähnlich kann man es mit Wahrscheinlichkeiten1 machen. Eine andere Idee ist, den Prognosewert1 zu nehmen, wenn prognostizierbare Sachverhalte1 in Rede stehen: dann wären die Gewichte2 gut, die eine bestmögliche Prognose1 ermöglichen. Eine wichtige Hilfe zur Erfassung und Beurteilung der Gründe können die Arbeiten zu den  Argumentationsschemata  z.B. Walton et al. (2008) geben. Beim derzeitigen Wissensstand, wo noch kaum  Standardmodelle  analysiert und durchgerechnet wurden, wird man sich damit begnügen müssen, Begründungen zu verlangen, damit man sie kritisch prüfen kann.

        Damit komme ich zu meinem Definitions-Vorschlag für Plausibilität2:
     

    D1: Ein Sachverhalt1 ist in dem Maße plausibel2 (pl), je stärker gewichtete2 Gründe1 G+  für und je schwächer gewichtete2 Gründe1G- gegen ihn angegeben werden können. 

        Grundsätzlich können Gründe1 vier Modalitäten1 haben: Sie können eine positive (+), eine (negative (-), eine sowohl positive als auch negative (+-) und eine fragliche, unklare, unbestimmte (?) Wirkung haben. Eine Plausibilitätsgesamtbewertung2 (pl) für einen Sachverhalt1 bestünde damit aus einer vierfachen Angabe: +, -, +-, ?. Praktisch wird man sich wohl oft auf die ersten beiden Modalitäten (Gründe dafür und Gründe dagegen) beschränken können , so dass am Ende eine Plausibilitätsformel  resultiert, weil sich die eine jeweils aus der anderen ergibt:
     

     pl+  =  (G+)  /  (G+ +  G- )
    pl-  =  1 - pl+

    Allgemeines Beispiel: Ergeben die gewichteten2 Gründe1 G+ für einen Sachverhalt1 z.B. G+ = 3 und ergeben die gewichteten2 Gründe1 G-  gegen diesen Sachverhalt1 G- = 1, dann erhält man bei Einsetzen der absoluten Zahlen für pl+=  (3) / (3+1) = 3/4 oder pl+= 0.75 und damit für pl- = 1 - 0.75 = 0.25.
    Konkretes Beispiel (EA31): Angenommen es gilt für die gewichteten2 Gründe1: G+(Straße ist0 nass, weil1 es geregnet hat) = 998, G-(Straße ist0 aus anderen Gründen nass)=27, dann ist die Plausibilität für pl+(Straße ist nass, weil1 es geregnet hat) = (998) / (998 + 27) = 998/1025 = 0.974 und pl-(Straße ist aus anderen Gründen nass) = 1 - 0.974  = 0.026.

    Skalenproblem: Bei Nutzung der mathematischen Grundoperationen (Addition, Subtraktion, Multiplikation, Division) ist vorausgesetzt, dass die Zahlenwerte mindestens auf Intervallskalenniveau vorliegen, was kaum zu leisten ist. Der wichtige Zwischenbereich zwischen Ordinal- und Intervallskala wurde von  Stevens (1946)  weder erkannt noch gelöst. Man kann die Zahlenwerte entsprechend schwächer interpretieren (quasi- oder fuzzy-intervallskaliert) und zur Rechtfertigung pragmatisch ihre Nützlichkeit erweisen.

    Plausibilitätsforschung
    Stichworte zur Plausibilitätsforschung: Plausibilität, Argumentation, Alltagslogik, Evidenztheorie, Glauben, Glaubhaftigkeit, Glaubwürdigkeit.
        Zum Stellenwert der Plausibilität2 in der deutschsprachigen Wissenschaft > Koch,  der allerdings Kienpointners Alltagslogik 1992, den Eintrag Schills im Wörterbuch der Kognitionswissenschaften (1996) und den informativen Eintrag im Historischen Wörterbuch der Rhetorik (HWR) übersah. Meine Analyse  u.a.  in  Logik,  Wissenschaftstheorie  und  Philosophie  zeigt, dass plausibel / Plausibilität zwar oft gebraucht wird, aber so gut wie nie erklärt oder begründet wird (Ausnahme Kienpointner, HWR). Allein das internationale Verlagsprogramm von  DeGruyter  enthält über 10.000 Gebrauchsbeispiele aus allen Gebieten der Wissenschaften, von denen nur einige in meine Untersuchung eingehen.
        Anders sah es in den USA aus. Dort gab es eine reichhaltige Plausibilitätsforschung, wie  Schmidt-Scheeles Literaturverzeichnis  zeigt, wobei ich Reschers  Plausible Reasoning  1976 und Waltons Plausible Argument 1992 besonders hervorheben möchte.
        Viele Sprachgebiete (z.B. Asien, Australien, Ozeanien, Süd- und Mittelamerika, Afrika, Arabische Regionen, Europa) konnte ich mangels Sprachkenntnissen und Wissen nicht berücksichtigen und kann daher darüber auch nichts sagen. Meine Aussagen können daher nur für meine Quellen gelten. Die geistigen Leistungen kleiner Völker und Minderheiten (z.B. Indigene) werden in der Wissenschaft leider oft nicht berücksichtigt.

        Ergebnisse (Auswahl) meiner nichtrepräsentativen empirischenPilotstudie:  Es wurden bei 52 BearbeiterInnen 24 Merkmale mit der Frage untersucht: wie viel des Merkmals steckt in plausibel? Und es wurden 21 Gründe unter Vorgabe einer Regel mit einem erläuternden Beispiel erfragt. An Beurteilungen waren 9 Wahlen 0,1,2,3,4,5,6,7,? bei den 24 Merkmalen und 21 Gründen möglich. Differenziert ausgewertet wurden die Wahlen  der Merkmale und Gründe nach  Alle, Alter, Geschlecht, Schulbildung und Berufsgruppen,  wobei sich sehr bemerkenswert ergab, dass keine großen Unterschiede in den Beurteilungen vorkamen. Ein  Sachverhalt1  erscheint den meisten umso plausibler2, je mehr beleg- und prüfbare Gründe1 für seine Realisierung  vorliegen. Plausibel2 darf nicht zu bewährten Erfahrungen im Widerspruch1 stehen und darf auch selbst keine Widersprüche1 enthalten. Insgesamt liegen 52 außerordentlich wertvolle  denkpsychologische  Dokumente vor, deren vollständige Auswertung noch eine Weile dauern wird. Zudem wurde eine  multivariate Korrelations- und Eigenwertanalyse  durchgeführt, die immerhin 17 Fastlineare Abhängigkeiten  (Fast-Kollinearitäten) erbrachte, am eindruckvollsten beim  Zusammenhang zwischen den Gründen1 35-36.

    Begriffsbasis für die  Definition  von plausibel:  Argument,  Bewertungsklassen, Formel, Funktion, Gesetzesartigkeit, Gewicht, Gewichtungsproblem, Grund, Häufigkeit, Kausalität, Metasprache(n), Möglichkeit, Nützlichkeit, Objektsprache, pragmatisch, Sachverhalt, Plausibilitätsgesamtbewertung, Rahmen, Regelhaftigkeit, Skalierungsproblem, Wahrscheinlichkeit, Wirkung.
        Es ist wichtig, dafür zu sorgen, dass die Begriffe der Begriffsbasis klar definiert sind, um Verschiebebahnhöfe, das unendliche Laster der Geistes-, Rechts- Sozial- und Kulturwissenschaften (>Sprachkritik), nachhaltig zu begrenzen. Sind Definitionen zu schwierig, kann man sich mit typischen Beispielen und Gegenbeispielen behelfen, am besten konkret-operational  mit  Referenzierungen. Viele Probleme lassen sich lösen, sobald man konkret-operational wird und nicht  nur  meint.

    Ende deutsche Zusammenfassung  PDF

    Entwicklung der Plausibilitätsformel
    Verwendete Kürzel: B := Beweis, BL := Logischer Beweis, BM= mathematischer Beweis, BE := empirischer Beweis; Bex:=Existenzbeweis; D := Definition; ES := Erfahrungssatz; f := Funktion; F := Formel; Fr := Frage; g=Gewicht, G=Grund, gG=Gewichteter Grund,  pl := plausibel, p := Wahrscheinlichkeit, S := Sachverhalt, ub := unbegrenzt.

    Schön wäre, wenn man Plausibilität quantifizieren könnte, etwa in oder mit einer Plausibilitätsformel entsprechend der allgemeinen Plausibilitätsfrage:
     

    Fr1: Allgemeine Plausibilitätsfrage: Wie mehr oder minder plausibel ist ein Sachverhalt? Genauer: in welcher Welt, für welchen  Geltungsbereich,  in welcher Situation unter welchen Bedingungen aus welcher Perspektive? 

    Dies wird im Folgenden versucht. Hierbei ist von der Definition der Plausibilität auszugehen:
     

    D1: Ein Sachverhalt ist in dem Maße plausibel (pl), wie sehr positiv gewichtete  Gründe  gG+  für und wie sehr negativ gewichtete Gründe gG-gegen ihn angegeben werden können.

    Entscheidend ist demnach der Begriff der Gründe:
     

    D2: Gründe  sind  allej, die mehr oder weniger wirken, fördernd oder hemmend.

    ES1: Kausalität, Wahrscheinlichkeit, Häufigkeiten, Regelhaftigkeiten und Gesetzesartigkeiten spielen bei den Gründen eine wichtige Rolle wie auch Erfahrungen, schon Erlebtes oder Allgemeinwissen.

    ES2: Möglichkeit ist eine notwendige, aber keine hinreichende Bedingung für Plausibilität. Unmögliches kann nicht plausibel sein. Ob ein Sachverhalt möglich ist, kann u.a. durch ein Beispiel (wahrer Sachverhalt = Tatsache), also durch einen  Existenzbeweis  gezeigt werden.

    D3: Ein Sachverhalt  kann aus unterschiedlichen gewichteten Gründen (gGi) mehr oder minder plausibel (pl) sein. Plausibel ist damit ein quantitativer Begriff, d.h. es gibt ein mehr oder weniger an Plausibilität (pl) wie bei der Wahrscheinlichkeit (p). 

    D4: Gewichtete Gründe können für (Index "+") oder gegen (Index "-") einen Sachverhalt sprechen. Daneben mag  es Gründe geben, die sowohl für als auch gegen einen Sachverhalt sprechen können (Index "+-") und schließlich kann man berücksichtigen, dass es Gründe geben kann, die unklar oder fraglich sind (Index "?"). 

     
    F1:   pl = f  (G1, G2, ... Gi ..., Gn). Plausibilität ist eine Funktion der Gründe, die für, gegen, sowohl als auch für oder gegen einen Sachverhalt sprechen können fraglich oder unklar sind. Indizierung Gründe: G = 1, 2, ...n.  F1 enthält also die bloße Anzahl der Gründe, die in F1 noch nicht qualitativ gekennzeichnet sind.

     
    D5:  Ordnet man die Gründe nach ihrer Qualität, kann dies so dargestellt werden: 
          G+ = f  (G+1, G+2, ... G+i ..., G+n). 
         G- = f  (G-1,  G-2, ...  G-i ...,  G-n).
               G+- = f  (G+-1, G+-2, ... G+-i ..., G+-n).
            G? = f  (G?1,  G?2, ...  G?i ...,  G?n).

    Gründe G sind oft nicht gleichwertig, daher kann es sinnvoll sein, sie unterschiedlich zu gewichten, wobei natürlich die Gewichtungsmethodik darzulegen und zu begründen ist. Hier kommt es meist auf den Einzelfall an. Gründe, die z.B. auf vielen unabhängigen Belegen beruhen, sollten natürlich ein anderes und viel höheres Gewicht haben als eine bloße Plausibilitätsmeinung.  In die Gewichtsbeurteilung können - und sollten  sogar - auch die Qualität und Güte der Quellen nach  Rescher 1976  eingehen.
     

    D6:  Gründe G 1,2, ...i ... , n  können unterschiedliches Gewicht (g)  hinsichtlich der Plausibilität für einen Sachverhalt haben. g = 0 ... ub aus der Menge der rationalen Zahlen. So mag z.B. Das Gewicht g(Grund G37(Sachverhalt oft aufgetreten)) = 10,  g(Grund G36(Sachverhalt mehrfach aufgetreten)) = 4,  g(Grund G35(Sachverhalt schon einmal aufgetreten)) = 1  zugeordnet werden. 

    Berücksichtigt man die Gewichte g, ergibt sich die Darstellung:

       gG+  = f  (g+G1,  g+G2, ...,  g+Gi , ...,  g+Gn), positive Gewichte der Gründe für einen Sachverhalt
       gG-   = f  (g-G1,   g-G2 , ...,  g-Gi , ...,  g-Gn ), negative Gewichte der Gründe gegen einen Sachverhalt
       gG+- = f  (g+-G1,  g+-G2, ..., g+-Gi ,..., g+-Gn ),  Sowohl-als-auch Gewichte der Gründe bei einem Sachverhalt
       gG?  = f  (g?G1,  g?G2, ...,   g?Gi ,...,  gr?Gn),  unklare / fragliche Gewichte der Gründe bei einem Sachverhalt
     

    Anmerkung: Zählt man die Gründe nur und verzichtetet auf ihre Gewichtung, so hat man dennoch gewichtet, nämlich gleich (Gewichtungsparadox). Die Grundsatzfrage beim Gewichten lautet nun, wie man unterschiedliche Gewichte begründen kann. Das ist u.U. einfach, wenn der Grund die Häufigkeit ist. Dann kann man Gewicht und Häufigkeit gleichsetzen. Ähnlich kann man es mit Wahrscheinlichkeiten machen. Eine andere Idee ist, den Prognosewert, wenn prognostizierbare Sachverhalte in Rede stehen: dann wären die Gewichte gut, die eine bestmögliche Prognose ermöglichen. Beim derzeitigen Wissensstand, wo noch kaum  Standardmodelle  analysiert und durchgerechnet wurden, wird man sich damit begnügen müssen, Begründungen zu verlangen, damit man sie kritisch prüfen kann.
     

     D7:  Setzt man für die Funktion f die Addition + , ergibt sich:
       gG+  =  (g+G1 +  g+G2, ...,  + g+Gi , ..., + g+Gn),  Summe gewichtete Gründe 1...n  für den Sachverhalt
       gG-   =  (g-G1  +  g-G2 , ..., +  g-Gi , ..., + g-Gn ), Summe gewichtete Gründe 1...n gegen den Sachverhalt
       gG+- =  (g+-G1 + g+-G2, ..., + g+-Gi ,..., + g+-Gn ), Summe gewichtete Gründe 1...n sowohl für als auch gegen den Sachverhalt
       gG?  =  (g?G1 +  g?G2, ...,   + g?Gi ,...,  + g?Gn),  Summe unklare / fragliche gewichtete Gründe 1...n zu dem Sachverhalt

    Man gewichtet jeden Grund und zählt die gewichteten Gründe nach ihren Qualitäten zusammen, so dass sich z.B. ergibt: 

    gG+= 17;   gG-  =  3;    gG+- = 1;  gG? =  2

    Anmerkung: Das muss nicht so sein, wie Berres (1984) mit seinem, für NichtmathematikerInnen schwer verständlichen, nicht-additiven Modell gezeigt hat.
     

     
    D8:  Als Gesamtformel, die die ersten drei von allen vier Modalitäten berücksichtigt, schlage ich nun für die Plausibilität vor:

    F3                              pl =  (g+  +  1/2 * g+- )  /  (g+ +  g- + 1/2 * g+- )

    Für das Beispiel oben ergäbe sich:  pl = (17+0.5) / (17+3+0.5) = 0.854. 
    Anmerkung:  1 steht für und gegen den Sachverhalt. Dann ist 1/2, also 0.5 bei für zu addieren und  0.5 bei gegen.

    Oft wird man sich hierbei auf die ersten beiden g+ und g- beschränken können, also auf Gründe, die für einen Sachverhalt sprechen gegenüber Gründen, die gegen diesen Sachverhalt sprechen.
     

    F4:       pl+= (g+)  /  (g+ + g- ) für einen Sachverhalt und damit 
    pl- = 1 - pl+

    Allgemeines Beispiel: Gibt es z.B. mit 3 gewichtete positive Gründe und einen mit 1 gewichteten negativen Grund für die Plausibilität eines Sachverhalts, dann erhält man bei Einsetzen der absoluten Zahlen in pl+ = (3) / (3+1) = 3/4 oder pl+ = 0.75 und für pl-  = 1 - pl+  = 0.25.
    Konkretes Beispiel (EA31): Angenommen es gilt pl+(Straße ist nass, weil es geregnet hat)=998, pl- (Straße ist aus anderen Gründen nass)=27, dann ist die Plausibilität für pl+(Straße ist nass, weil es geregnet hat) PL = (998) / (998 + 27) = 998/1025 = 0.974 und pl-(Straße ist aus anderen Gründen nass) = 1- p+ = 0.026.

    Skalenproblem: Bei Nutzung der mathematischen Grundoperationen (Addition, Subtraktion, Multiplikation, Division) ist vorausgesetzt, dass die Zahlenwerte mindestens auf Intervallskalenniveau vorliegen, was kaum zu leisten ist. Der Sprung vom Ordinal- auf Intervallniveau ist für viele praktische Zwecke zu groß. Der wichtige Zwischenbereich zwischen Ordinal- und Intervallskala wurde von  Stevens (1946)  in seiner praktischen Bedeutung weder erkannt noch gelöst. Das gilt bis heute, worunter vor allem die Sozial- und Psychowissenschaften leiden.. Man kann die Zahlenwerte entsprechend schwächer interpretieren (quasi- oder fuzzy-intervallskaliert) und zur Rechtfertigung pragmatisch ihre Nützlichkeit erweisen.

        Anmerkung: Möglichkeit1 ist eine notwendige, aber keine hinreichende Bedingung1 für Plausibilität2. Unmögliches1 kann nicht plausibel2 sein. Ob ein Sachverhalt1 möglich ist, kann u.a. durch ein Beispiel (wahrer Sachverhalt = Tatsache), also durch einen Existenzbeweis gezeigt werden. Ein Sachverhalt  kann mit unterschiedlichen Gründen (Gi) mehr oder minder plausibel (pl) sein. Plausibel2 ist damit ein quantitativer Begriff, d.h. es gibt ein mehr oder weniger an Plausibilität2 (pl) wie bei der Wahrscheinlichkeit1 (p).


    Gewichtungsproblem
    Zählt man die Gründe nur und verzichtetet auf ihre Gewichtung, so hat man dennoch gewichtet, nämlich gleich (Gewichtungsparadox). Die Grundsatzfrage beim Gewichten lautet, wie man unterschiedliche Gewichte begründen kann. Das ist u.U. einfach, wenn der Grund die Häufigkeit ist. Dann kann man Gewicht und Häufigkeit gleichsetzen. Ähnlich kann man es mit Wahrscheinlichkeiten machen. Eine andere Idee ist, den Prognosewert zu bestimmen, wenn prognostizierbare Sachverhalte in Rede stehen: dann wären die Gewichte gut, die eine bestmögliche Prognose ermöglichen. Beim derzeitigen Wissensstand, wo noch kaum  Standardmodelle  analysiert und durchgerechnet wurden, wird man sich damit begnügen müssen, Begründungen zu verlangen, damit man sie kritisch prüfen kann.
        Eng verbunden mit dem Gewichtungsproblem ist das Skalierungsproblem.
    Argumentationsschemata
    Eine wichtige Hilfe zur Erfassung und Beurteilung der Gründe können die Arbeiten zu den Argumentationsschemata geben, z.B. nach Lumer (2011), der ausführt, hier grob übersetzt: "Der Vorfahre der Theorien der Argumentationsschemata sind Aristoteles’ unglaublich reichhaltige und ausgearbeitete „Topics“, die bis ins 20. Jahrhundert die Rhetorik dominierten. Mit der Renaissance der Argumentationstheorie Ende der 1950er Jahre hat die Erforschung von Argumentationsschemata jedoch einen kontinuierlichen Zustrom neuer Ideen und Ansätze erfahren. Wichtige Beiträge haben seitdem geleistet: Perelman & Olbrechts-Tyteca (1958), Hastings (1963), Grennan (1984, 1997), Schellens (1985, 1987), Govier (<1985> 2000, 1987), Kienpointner (1992a, 1992b), Walton (1996), Garssen (1997, 2001, 2002) und Walton & Reed & Macagno (2008). Obwohl Fortschritte gemacht wurden, sind die meisten dieser Ansätze immer noch stark von Aristoteles’ „Topics“1 beeinflusst, und dies könnte problematisch sein. Topics oder „topoi“ auf Griechisch sind Gemeinplätze; und die Hauptidee eines aktuellen Argumentationsansatzes besteht darin, Sammlungen von leistungsfähigen Inhalten zu erstellen. Drei miteinander verbundene argumentationstheoretische Probleme bei diesem Ansatz sind erstens, dass die Listen der resultierenden Schemata lang, oft sehr lang, nie vollständig und immer willkürlich sind. Zweitens sollten heutige Ansätze nicht inhaltlich, sondern formal sein und damit die Inhalte erklären. Drittens gibt es hinter diesen Listen von Schemata keine (allgemeinere) Theorie, die ihre Gültigkeit oder einen anderen Wert erklären und garantieren und uns einer wirklich vollständigen Liste näher bringen könnte."

    Skalierungsproblem
    Bei Nutzung der mathematischen Grundoperationen (Addition, Subtraktion, Multiplikation, Division) ist vorausgesetzt, dass die Zahlenwerte mindestens auf Intervallskalenniveau vorliegen, was kaum zu leisten ist. Der wichtige Zwischenbereich zwischen Ordinal- und Intervallskala wurde von  Stevens (1946)  weder erkannt noch gelöst. Das gilt bis heute, worunter vor allem die Sozial- und Psychowissenschaften leiden. Man kann die Zahlenwerte entsprechend schwächer interpretieren (quasi- oder fuzzy-intervallskaliert) und zur Rechtfertigung pragmatisch ihre Nützlichkeit erweisen.

    Systematik der Plausibilitätsgründe
    Überall wo es Wirkungsbeziehungen gibt, gibt es potentielle Plausibilitätsgründe.

        Metagründe

    1. Grund
    2. Mehrere Gründe
    3. Mehrere unabhängige Gründe


        Allgemeine Gründe

    1. Ähnlichkeit
    2. Allgemeines Wissen
    3. Alltags-Logik
    4. Autorität (Fachautorität)
    5. Bekannt
    6. Erfahrung
    7. Gesunder Menschenverstand (Hausverstand)
    8. Gewohnheiten (Üblichkeiten)
    9. Gruppenmeinung
    10. Häufigkeit
    11. Lebenserfahrung
    12. Logik
    13. Möglichkeit
    14. Motivation
    15. Naturgesetze
    16. Öffentliche Meinung
    17. Quellenanzahl
    18. Quellengüte
    19. Quellenunabhängigkeit
    20. Regelhaftigkeiten (Zusammenhänge)
    21. Schon erlebt (vertraut)
    22. Sitte und Brauch
    23. Stimmig
    24. Vernünftig
    25. Wahrscheinlichkeit
    26. Zweckmäßig
    27. X-Sonstig


        Spezielle Gründe

    1. Gefällt
    2. Ziele verträglich
    Plausibilität im Tun: Verhalten und Handeln
    Gründe wegen der Sitten und Gebräuche
     
     


    Standardmodelle für Plausibilitäten

    Es dürfte in vielen Fällen nützlich sein, auf eine Standard-Gründe-Liste Bezug nehmen zu können. Die folgende Liste ist nicht vollständig, mehr Vorschläge (brain-stormings).


     

    Standardmodelle Alltag
    Anmerkung: Eine praktisch-operationale Theorie für Bedürfnisbefriedigungen hat  Walter Toman  vorgelegt.

    Standardmodell Frühstücksaufstrich

    Aufstrichwahl: welche Wahl ist am plausibelsten?
    A. überlegt was er als Aufstrich für sein Brötchen wählen will: Camembert, Marmelade, Wurst, Butter, Butter mit frischem Schnittlauch, Eiersalat. An potentiellen Gründen für seine Wahl bieten sich an: Verfügbarkeit, Zubereitungsaufwand, Appetit, schmecken, Abstand Verfalldatum, Nährwert, Kalorien, Bekannt, Häufigkeit, Gewohnheit, Preis, Einstellung ("Ess.Ideologie"), Sonstiges.
     
    Wahl-Gründe Verfüg-
    barkeit.    		 Zuberei-
    tungs-
    aufwand    		 Appetit Schmeckt Abstand Verfall Nährwert Kalorien Bekannt Häufig-
    keit/Woche    		 Moti-
    vation    		 Schon
    erlebt    		 Sitte &
    Brauch
    Camembert
    Sum=28-1    		 vorhanden
    möglich=1    		 keiner
    G=1    		 sehr
    G=10    		 sehr 10
    G=10    		 15 Tage
    G=0    		 45% Fett
    Proteine
    G= -1    		 280/100g
    2    		 Ja=1 2 mit Appe- tit erfasst Ja=1 in  Häufig- keit erfasst
    Marmelade
    Sum=12-1    		 vorhanden
    möglich=1    		 keiner
    G=1    		 mäßig
    G=3    		 schon 2
    G=2    		 30 Tage
    G=0    		 viel Zucker
    G= -1    		 50/20g
    1    		 Ja=1 2 mit Appe- tit erfasst Ja=1 in  Häufig- keit erfasst
    Wurst keine da. - - - - - - - - - - -
    Butter 
    Sum=12-1     		 vorhanden
    möglich=1    		 keiner
    G=1    		 mäßig
    G=3    		 schon 2
    G=2    		 20 Tage
    G=0    		 viel Fett
    G= -1    		 143/20g
    2    		 Ja=1 1 mit Appe- tit erfasst Ja=1 in  Häufig- keit erfasst
    Butter mit fr. Schnittlauch
    Sum=16-1    		 vorhanden
    möglich=1    		 schnei-
    den G=1    		 mäßig
    G=3    		 gut 
    G=4    		 2 Tage
    G=2    		 viel Fett
    G= -1    		 143/20g
    2    		 Ja=1 1 mit Appe- tit erfasst Ja=1 in  Häufig- keit erfasst
    Eiersalat
    Sum=21-2    		 ein Rest
    möglich=1    		 keiner
    G=1    		 mäßig
    G=3    		 G=5 1 Tag
    G=5    		 reichlich
    G= -2    		 318/100g
    3    		 Ja=1 1 mit Appe- tit erfasst Ja=1 in  Häufig- keit erfasst

    In dieser Frühstückssituation erhält der Camembert Aufstrich die Gründe-Punkte, nämlich 27, gefolgt vom Eiersalat mit 19 und Butter mit frischem Schnittlauch 17.

    Standardmodell Essen
    Zur Plausibilität für Essen
    Kaum für jemand, der gerade fastet.
    Unterschiedlich für Nichtfaster je nach Situation

    • Kaum während der Nacht.
    • Gering während eines Toilettenganges.
    • Gering während Wege vollbracht werden.
    • Gering während der Arbeit.
    • Hoch während der Pausen und Essenszeiten.


    Zur Ausarbeitung vorgemerkt:

    • Standardmodell Einkaufen
    • Standardmodell Putzen
    • Standardmodell Regenschirm (mitnehmen oder nicht?)
    • Standardmodell Waschen
    • Standardmodell Autowartung.
    • ...
     
    Standardmodelle Epidemiologie
    • Plausibilität der Kritische Masse Hypothese der Omikronvariante.

    StandardmodelleÖkologie
    Wir haben hier drei große Problemkomplexe: 1. Feststellung von Problemen, 2. Erklärungen für die Probleme, 3. Maßnahmen zur Bewältigung der Probleme.

    • CO2 Ausstoß
    • Dürren
    • Erdbeben
    • Hochwasser / Fluten / Überschwemmungen
    • Klimaerwärmung
    • Tsunamis
    • Vermüllung (besonders der Ozeane, Kosmos)
    • Vulkanausbrüche
    • Wetterextreme


    Standardmodelle Politik

    • Wettrüsten
    • Friedensbedingungen
    • Entwicklung Diktatoren
    • Gemeinwohlorientierung


    Standardmodelle Staat

    • Bürokratieproblem
    • Föderalismusproblem
    • Rente
    • Staatsverschuldung
    • Verwaltung
    • Wahlkreise


    Standardmodelle Gesellschaft

    • Chancengleichheit (Teilhabe, Bildungszugänge)
    • Gerechtigkeit
    • Gesundheit
    • Grundversorgung


    Standardmodelle Medien

    • Informationsqualität / Fake news
    • Privatbesitz
    • Wikipedia.


    Standardmodelle soziale Medien & Internet

    • Darknet
    • Facebook / Meta
    • Google
    • Suchmaschinen
    • Twitter
    • Usenet / Foren


    Standardmodelle Recht
    Viele Grundfragen der Rechtswissenschaft sind  hier  gelistet und erforscht.

    Standardmodelle Wirtschaft

    • Logistik / Lieferkettenproblem
    • Ressourcenprobleme
    • Wachstumsproblem


    Standardmodelle Finanzen

    • Geldanlage / Zins, Zinspolitik
    • Geldschöpfung
    • Geldentwertung, Inflation
    • Steuern, Steueroasen, Steuerwettbewerb


    Standardmodelle Wissenschaft

    • Qualität, nichtssagende Publikationsflut
    • Manipulation und Fälschungen
    • Stand der Wissenschaft: was ist Stand der Wissenschaft?


    Standardmodelle in der Psychologie
    Man kann sehr viele und unterschiedliche Standardmodelle entwickeln und formulieren, z.B. Dörners Bauplan für eine Seele.

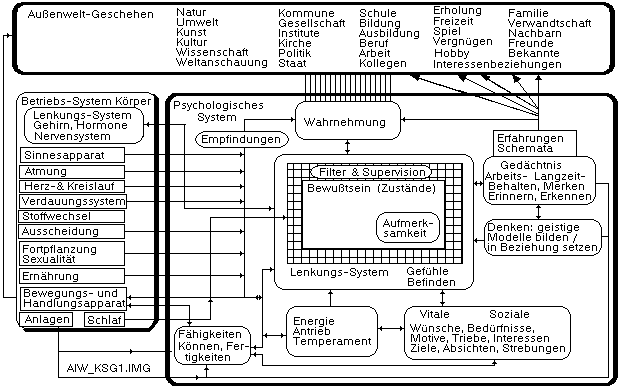
    Standardmodell Psyche (Quelle)
    Ist es plausibel, sich die Psyche, das psychische System wie folgt zu denken? Was spricht dafür, was spricht dagegen, welche Fragen und Klärungsbedürfnisse bringt dieses Modell mit sich?


     

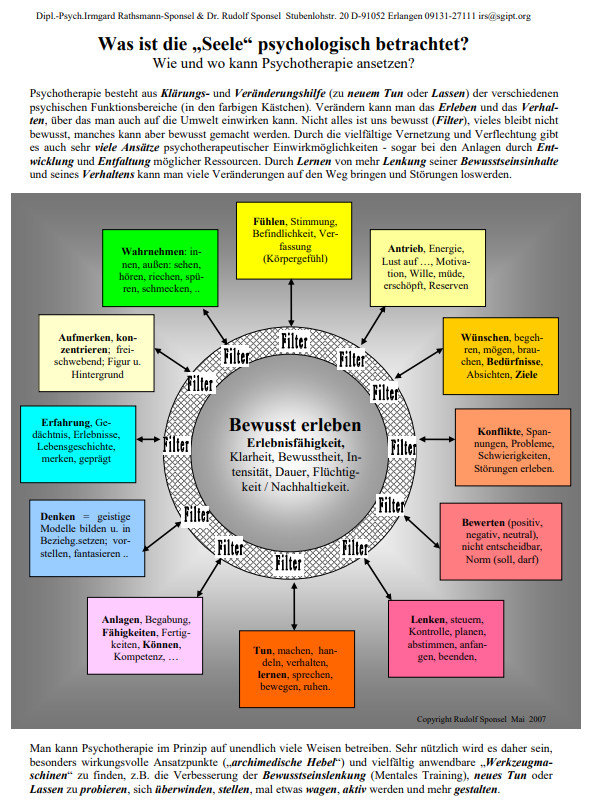
    Was istSeele praktisch psychologisch betrachtet?  (Quelle)
    Ist es plausibel, sich die Seele wie folgt vorzustellen? Welche Gründe sprechen dafür, welche dagegen?


    Geltungs- oder Gültigkeitsbereiche
    Das Plausibilitätsurteil wird meist als subjektives Urteil gesehen, auch wenn falsch objektivistisch gesprochen wird: das ist0 plausibel. Tatsächlich können zu den subjektiven Geltungsansprüchen weitere gedacht werden:

    Subjektives Plausibilitätsurteil

    • so könnte es nach meiner Meinung sein
    • so könnte es nach meiner Meinung tatsächlich sein
    • so könnte es nach meiner Meinung sein, weil das schon so vorgekommen ist
    • so könnte es nach meiner Meinung sein, weil das schon öfter so vorgekommen ist
    • das ist nach meiner Meinung eine realistische Möglichkeit
    • das ist nach meiner Meinung eine wahrscheinliche Möglichkeit


    Gruppensubjektives Plausibilitätsurteil

    • so könnte es nach Meinung der Gruppe ... sein
    • so könnte es nach Meinung der Gruppe ... tatsächlich sein
    • so könnte es nach Meinung der Gruppe ... sein, weil das schon so vorgekommen ist
    • so könnte es nach Meinung der Gruppe ... sein, weil das schon öfter so vorgekommen ist
    • das ist nach Meinung der Gruppe ... eine realistische Möglichkeit
    • das ist nach  Meinung der Gruppe ... eine wahrscheinliche Möglichkeit


    Intersubjektives Plausibilitätsurteil (sollte von fast allen so gesehen werden)

    • stimmt nach allgemeiner Meinung, dass es so ist
    • stimmt nach allgemeiner Meinung, dass es so sein könnte
    • stimmt nach allgemeiner Meinung, dass es tatsächlich so ist
    • stimmt nach allgemeiner Meinung, weil das schon so vorgekommen ist
    • stimmt nach allgemeiner Meinung, weil das schon öfter so vorgekommen ist
    • stimmt nach allgemeiner Meinung, ist eine realistische Möglichkeit
    • stimmt nach allgemeiner Meinung, ist eine wahrscheinliche Möglichkeit


    Objektiver Bezug (sollte objektiv gelten, unabhängig vom menschlichen Erkenntnissystem)

    • Unabhängig von Menschen könnte es so sein
    • Unabhängig von Menschen könnte es tatsächlich so sein
    • Unabhängig von Menschen  könnte es so sein, weil das schon so vorgekommen ist
    • Unabhängig von Menschen könnte es so sein, weil das schon öfter so vorgekommen ist
    • Unabhängig von Menschen ist das eine realistische Möglichkeit
    • Unabhängig von Menschen ist das eine wahrscheinliche Möglichkeit


    Recherchen zum Gebrauch des Plausibilitätsbegriffs
    Schon ins Netz gestellte Erstversionen werden verlinkt (aktuell 15 von 28).

    1. Alltag.
    2. Geschichte, Zeitgeschichte, Kulturgeschichte, Archäologie.
    3. Forensische Psychologie.
    4. Informatik.
    5. Lexika, Wörterbücher, Enzyklopädien.
    6. Kriminalistik und Kriminologie.
    7. Kunst und Musik.
    8. Literatur.
    9. Logik.
    10. Mathematik.
    11. Medien.
    12. Medizin.
    13. Naturwissenschaften: Physik, Chemie, Biologie, ...
    14. Philosophie.
    15. Politik.
    16. Psychiatrie.
    17. Psychoanalyse.
    18. Psychologie.
    19. Psychotherapie.
    20. Recht.
    21. Religion, Theologie, Esoterik.
    22. Soziologie.
    23. Sprachwissenschaft, Linguistik, Journalistik, Kommunikationswissenschaft, Rhetorik.
    24. Technik.
    25. Wirtschaft und Finanzen.
    26. Wissenschaftstheorie.
    27. Wissen und Wissenschaft ohne nähere Spezifikation.
    28. Zukunft, Zukunftsforschung (Futurologie), Prognostik.



    Untersuchungen anderer zur Plausibilität (Auswahl) -Teil-Kommentierte Literaturliste
    Einige wichtiger erscheinende Arbeiten wurden umfangreicher analysiert und deshalb auf ausgelagerten eigenen Seiten dargestellt, was man an der Verlinkung erkennt.

    Barnett, J. A. (1981). Computational methods for a mathematical theory of evidence, Proc. 7th Int. Joint Conf. on Artificial Intelligence (IJCAI-81), Vancouver, pp. 868-875. [Literaturliste Smets]


    Berres, Manfred (1984) Glaubens- und Plausibilitätsgrade : e. Beitr. zur Maß- und Integrationstheorie. UB Erlangen 1 Mikrofiche 24x, Umfang: 85 Bl.
        Kommentar: Die Arbeit ist für Nicht-Mathematiker trotz eines Anwendungsbeispiels aus der Testpsychologie leider nur schwer zu verstehen. [Rescher 1976 nicht im Literaturverzeichnis].


    Böhnert, Martin & Reszke, Paul (2015): „Linguistisch-philosophische Untersuchungen zu Plausibilität: Über kommunikative Grundmuster bei der Entstehung von wissenschaftlichen Tatsachen“ In: Engelschalt, Julia; Maibaum, Arne (Hg.), 2015, Auf der Suche nach den Tatsachen: Proceedings der 1. Tagung des Nachwuchsnetzwerks INSIST, S. 40-67. Permalink: https://www.ssoar.info/ssoar/handle/document/45590
        Kommentar: Noch nicht ausgewertet. [Rescher 1976 und 2003 nicht im Literaturverzeichnis.]

    Bohn, Irina/ Feuerhelm, Wolfgang & Hamburger, Franz (2000): Die Erzeugung von Plausibilität als Konstruktion von Wirklichkeit. Eine Fallrekonstruktion. Zur Berichterstattung über Sinti und Roma, in: Kraimer, Klaus (Hrsg.): Die Fallrekonstruktion. Sinnverstehen in der sozialwissenschaftlichen Forschung. Frankfurt am Main: Suhrkamp, S. 532-560. [Mehr. S.u.R.; Ztg.; Inh.-A.; Inh.; Krim.; Vor.]
        Kommentar: Noch nicht ausgewertet. [Rescher im Literaturverzeichnis noch nicht prüfen können.]

    Bonissone, P. P. (1986). Plausible reasoning: coping with uncertainty in expert systems. Technical Information Series, Report 86CRD053, General Electric. [Literaturliste Smets]
        Kommentar: Noch nicht ausgewertet.

    Cellucci, Carlo  (2014)  Knowledge, Truth and Plausibility. Received: 12 March 2014 / Accepted: 8 May 2014 / Published online: 13 May 2014 [PDF]
    Abstract From antiquiy several philosophers have claimed that the goal of natural science is truth. In particular, this is a basic tenet of contemporary scientific realism. However, all concepts of truth that have been put forward are inadequate to modern science because they do not provide a criterion of truth. This means that we will generally be unable to recognize a scientific truth when we reach it. As an alternative, this paper argues that the goal of natural science is plausibility and considers some characters of plausibility.
        GÜ: "Seit der Antike haben mehrere Philosophen behauptet, das Ziel der Naturwissenschaft sei die Wahrheit. Dies ist insbesondere ein grundlegender Grundsatz der zeitgenössischen wissenschaftlicher Realismus. Alle vorgestellten Wahrheitskonzepte sind jedoch für die moderne Wissenschaft unzureichend, weil sie kein Kriterium für Wahrheit bereitstellen. Das bedeutet, dass wir eine wissenschaftliche Wahrheit in der Regel nicht erkennen können, wenn wir sie erreichen. Als Alternative argumentiert dieser Beitrag, dass das Ziel der natürlichen Wissenschaft Plausibilität ist und berücksichtigt einige Plausibilitätszeichen."
        Kommentar: Noch nicht ausgewertet.


    Connell, Louise & Keane, Mark T.  (?) The Knowledge-Fitting Theory of Plausibility. In (40-45) The 14th Irish Conference on Artificial Intelligence & Cognitive Science AICS 2003  Proceedings  Trinity College Dublin
    17-19 September 2003 [PDF]
        Abstract.  Plausibility is judged on a daily basis in a wide range of cognitive phenomena, yet the study of plausibility in its own right has been long  neglected  in  cognitive  science.  In  this  paper,  we present the Knowledge-Fitting Theory of Plausibility that incorporates  both  concept-coherence (i.e. the conceptual structure and relatedness of a scenario) and word-coherence (i.e.  the distributional properties of the individual words used to describe a scenario) in plausibility judgement. We also present the Plausibility Analysis Model (PAM), which is an implementation of this theory and the first computational mode to specifically address the issue of human plausibility judgements
        GÜ:  Abstrakt. Die Plausibilität wird täglich in einer Vielzahl von kognitiven Phänomene beurteilt, aber das Studium der Plausibilität an sich wurde in der Kognitionswissenschaft lange vernachlässigt. In diesem Papier präsentieren wir die wissensangepasste Plausibilitätstheorie, die beinhaltet sowohl Konzeptkohärenz (d.h. die Konzeptstruktur und Zusammenhang eines Szenarios) und Wortkohärenz (d. h. die Verteilungseigenschaften der einzelnen Wörter zur Beschreibung von einem Szenario) bei der Plausibilitätsbeurteilung. Wir präsentieren auch die Plausibilitätsanalysemodell (PAM), das eine Implementierung dieser Theorie und der erste Rechenmodus ist, der sich speziell mit der Frage der menschlichen Plausibilitätsurteile befasst.
        Kommentar: Noch nicht ausgewertet.
    _
    Connell, Louise  & Keane, Mark T.  (2006) A Model of Plausibility. Cognitive Science 30 (2006) 95–120 [PDF]
    Abstract: Plausibility has been implicated as playing a critical role in many cognitive phenomena from comprehension to problem solving. Yet,  across cognitive science, plausibility is usually treated as an operationalized variable or metric rather than being explained or studied in itself. This article describes a new cognitive model of plausibility, the Plausibility Analysis Model (PAM), which is aimed at modeling human plausibility judgment. This model uses commonsense knowledge of concept–coherence to determine the degree of plausibility of a target scenario. In essence, a highly plausible scenario is one that fits prior knowledge well: with many different sources of corroboration, without complexity of explanation, and with minimal conjecture. A detailed simulation of empirical plausibility findings is reported,which shows a close correspondence between the model and human judgments. In addition, a sensitivity analysis demonstrates that PAM is robust in its operations.
    _ "Abstrakt: Plausibilität spielt bei vielen kognitiven Phänomenen vom Verstehen bis zur Problemlösung eine entscheidende Rolle. In der Kognitionswissenschaft wird Plausibilität jedoch in der Regel als operationalisierte Variable oder Metrik, anstatt für sich selbst erklärt oder untersucht. Dieser Artikel beschreibt ein neues kognitives Plausibilitätsmodell, das Plausibility Analysis Model (PAM), das auf Modellierung des menschliches Plausibilitätsurteils abzielt. Dieses Modell verwendet das Commonsense-Wissen der Konzeptkohärenz, um den Plausibilitätsgrad eines Zielszenarios zu bestimmen. Im Wesentlichen ist ein sehr plausibles Szenario, eines, das gut zum Vorwissen passt: mit vielen verschiedenen Bestätigungsquellen, ohne komplizierte Erklärungen und mit minimaler Vermutung. Über eine detaillierte Simulation empirischer Plausibilitätsbefunde wird berichtet, was eine enge Übereinstimmung zwischen dem Modell und menschlichen Urteilen zeigt. Darüber hinaus zeigt eine Sensitivitätsanalyse, dass PAM in seinen Operationen robust ist.
    Schlüsselwörter: Psychologie; Erkenntnis; Argumentation; Plausibilität; Computersimulation; Symbolisch Berechnungsmodell; Plausibility Analysis Model (PAM).
        Kommentar:


    Dempster-Shafer-Theorie der Glaubensfunktionen
    Muss noch recherchiert werden.

    Dubois, D. and Prade, H. (1985). Theorie des possibilités. Masson, Paris [Literaturliste Smets]
        Kommentar: Noch nicht ausgewertet.


    Eemeren, F. H. van, Garssen, B., Godden, D., and Mitchell, G. (2011, eds.) Proceedings of the 7th International ISSA Conference on Argumentation.
        Kommentar: Noch nicht ausgewertet.


    Fischer, Ernst Peter (2013)  Wie der Mensch seine Welt neu erschaffen hat.  Springer Spektrum.


    Friedman, Charles P.; Gatti, Guido G.; Murphy, Gwendolyn C.; Franz,Timothy M.; Fine, Paul L.; Heckerling, Paul S.; Miller, Thomas M. (2002) Exploring the Boundaries of Plausibility: Empirical Study of a Key Problem in the Design of Computer-Based Clinical Simulations. AMIA 2002 Annual Symposium Proceedings, 275-279. Online.
        Abstract grob übersetzt:: "Alle Designer klinischer Simulationen stehen vor dem Problem, die plausiblen Diagnose- und Managementoptionen zu identifizieren, die in ihre Simulationsmodelle aufgenommen werden sollen. In dieser Studie wird untersucht, wie viele plausible Diagnosen für einen bestimmten Fall vorliegen und wie viele Probanden einen Fall bearbeiten müssen, bevor alle plausiblen Diagnosen identifiziert werden. Die Daten stammen von 144 Assistenzärzten und Fakultätsärzten aus 3 medizinischen Zentren, die jeweils 9 diagnostisch schwierige Fälle bearbeiteten, die aus einer Gruppe von 36 ausgewählt wurden. Jeder Proband generierte für jeden Fall bis zu 6 diagnostische Hypothesen, und jede Hypothese wurde von einem Klinikerpanel auf Plausibilität bewertet. Von den 2091 erstellten Diagnosen wurden 399 (19,1%/), durchschnittlich 11 pro Fall, nach Studienkriterien als plausibel erachtet. Die Verteilung der Plausibilitätsbewertungen erwies sich als statistisch fallabhängig. Im Durchschnitt der Fälle wurde die endgültige plausible Diagnose von dem 28. Arzt (sd = 8) erstellt, der den Fall bearbeitete. Die Ergebnisse veranschaulichen den Reichtum und die Vielfalt der menschlichen Kognition und die Herausforderungen, die diese für die Erstellung realistischer Simulationen in biomedizinischen Bereichen darstellen."
        Kommentar: Der Suchtext "defin" ergab keinen Treffer im Sinne von Definition. Der Suchtext "plausib" ergab 71 Treffer. Ein Treffer p. 275 warf die hoffnungsheischende Frage auf  "Wie also kann ein Simulationsdesigner bestimmen, was plausibel ist?" p.276 "Können sich die Planer von Simulationen auf ihre eigenen Einschätzungen verlassen, was plausibel ist ...?" legt nahe, dass es um Einschätzungen, also Meinungen geht. Das bestätigt auch der Abschnitt "Methods", p.276f. Der Plausibilitätsbegriff wird in dieser Untersuchung unkritisch als valide bei den Ratern angenommen.

    Good, I. J. (1950). Probability and the Weighting of Evidence. Griffin, London. [Literaturliste Smets]
        Kommentar: Noch nicht ausgewertet.


    Handstein, Holger (2016) Plausibilität in Journalistikon [Online, Abruf 16.10.2021]
    "Die Prüfung auf Plausibilität kann anhand verschiedener Einzelkriterien erfolgen – etwa anhand der Übereinstimmung eines von einer Quelle oder in einem journalistischen Beitrag behaupteten Sachverhaltes auf Übereinstimmung mit Naturgesetzen, sozialen Normen oder den Prinzipien der Logik. Erfüllt eine Information eines oder mehrere dieser Kriterien nicht, steigt die Wahrscheinlichkeit, dass es sich um eine Falschaussage handelt.
    Die Prüfung auf Plausibilität kann auf verschiedenen Ebenen stattfinden – zunächst im journalistischen Arbeitsprozess als Teil der Recherche, darüber hinaus aber auch während der Rezeption durch das journalistische Publikum. Insbesondere für dieses ist die Prüfung auf Plausibilität wichtig, da oftmals kein direkter Zugriff auf die Quellen besteht, die einem Beitrag zugrunde liegen. Aufgrund dieses Zusammenhangs ist es für Journalisten wichtig, nicht nur über plausible Informationen zu verfügen, sondern die Plausibilität dieser Informationen in ihren Beiträgen auch überzeugend zu vermitteln – etwa durch einen stringenten inhaltlichen Aufbau von Texten.
        Quelle Handstein, Holger (2016) Journalistikon (letzter Abruf 16.10.2021)
      Kommentar: Eine fundierte Begriffsklärung erfolgt nicht. An Kriterien werden genannt: Übereinstimmung mit Naturgesetzen, sozialen Normen, Prinzipien der Logik. [Kein Hinweis auf Rescher 1976]



    Hannken-Illjes, Kati (2018) Einführung in die Theorie und Analyse der Argumentation. Tübingen:  Narr Francke Attempto.
    [04PA/CC 4700 H245  zur Zeit keine Vormerkung möglich  Handapparat / 04PA/HA Dr. Jungert]
            Kommentar: Noch nicht ausgewertet. [Literaturverzeichnis nach Hinweis auf Rescher noch nicht überprüfen können]

    Josephson, John R. & Josephson, Susan G. (1994, ed.) Abductive inference. Compuation, philosophy, technology. Cambridge University Press.
           Analyse auf einer eigenen Seite.


    Kertész, András ; Egyetem, Debreceni  & Rákosi, Csilla  (2012) Data and Evidence in Linguistics. A Plausible Argumentation Model.
        Kommentar: Noch nicht ausgewertet.


    Kienpointner: Recherche zur wissenschaftlichen Analyse von plausibel, Plausibilität und Plausibilitätskriterien bei Kienpointner 1992.
     


    Klärner, Holger (2003) Der Schluß auf die beste Erklärung. Berlin: de Gruyter.


    Koch: Recherche zur wissenschaftlichen Analyse von plausibel, Plausibilität und Plausibilitätskriterien bei Lutz Koch (2002). Am 16.10.2021 fand ich im Wörterbuch der Kognitionswissenschaften (1996) einen Eintrag Plausibilität (plausibility) von Kerstin Schill. Auch im Historischen Wörterbuch der Rhetorik gibt es einen mehrseitigen Eintrag.


    Kuhn-Rahloff, Clemens (2012) Realitätstreue, Natürlichkeit, Plausibilität: Perzeptive Beurteilungen in der Elektroakustik ; ein Beitrag zum Verständnis der "inneren Referenz" am Beispiel der Plausibilität ausgewählter Wiedergabesysteme [VT]
        Kommentar: Noch nicht ausgewertet. [Rescher nicht im Literaturverzeichnis.]


    Lumer, Christoph (2011) "Argument schemes — an epistemological approach" (2011). OSSA Conference Archive. 17
        Kommentar-Lumer-2011: Informative und wichtige Arbeit zum Stand der argumentativen Schemata.

    Mittelstraß, Jürgen (1980-1996, Hrsg.). Enzyklopädie Philosophie und Wissenschaftstheorie. 4 Bde. Die ersten beiden Bände erschienen bei BI, Mannheim. Die letzten beiden Bände bei Metzler, Stuttgart. 2. Auflage 2005ff.
    In der Enzyklopädie Philosophie und Wissenschaftstheorie, 2.A., O-P, hat Plausibilität keinen eigenen Eintrag. Aber im Artikel Meinung wird Plausibilität erwähnt.


    Müller, Stephan S. W. (2010) Theorien sozialer Evolution : Zur Plausibilität darwinistischer Erklärungen sozialen Wandels [VT]
        Kommentar: Noch nicht ausgewertet. [Rescher nicht im Literaturverzeichnis.]


    Rescher: Plausibilitätstheorie: Einzelanalyse Plausible Reasoning (1976) und Plausibility and Presumption (2003) von Nicholas Rescher.


    Schill, Kerstin (1996) Plausibilität (plausibility) in (S. 509) Stube (1996, Hrsg.) Wörterbuch der Kognitionswissenschaften. Stuttgart: Klett-Cotta.
     
    Der Ansatz, Plausibilität durch Glauben zu fundieren, erscheint grundsätzlich vernünftig. Aber die Plausibilitätsfrage wird auf die Glaubensfrage verschoben und damit ein 
    neuer  Begriffsverschiebebahnhof
    eingerichtet.


    Schmidt-Scheele: Recherche zur wissenschaftlichen Analyse von plausibel, Plausibilität und Plausibilitätskriterien bei Schmidt-Scheele.


    Selin, Cynthia  (2007) Negotiating Plausibility: Intervening in the Future of Nanotechnology. Sci Eng Ethics (2011) 17:723—737 DOI 10.1007/s11948-011-9315-x [PDF]
        Abstract grob übersetzt: Zusammenfassung Das Szenarioprojekt NanoFutures auf nationaler Ebene konzentriert sich auf die sozialen, politischen, wirtschaftlichen und ethischen Implikationen der Nanotechnologie und wird initiiert vom Center for Nanotechnology in Society an der Arizona State University (CNS-ASU). Das Projekt beinhaltet neuartige Methoden zur Entwicklung plausibler Visionen über nanotechnologiefähige Zukünfte, verdeutlicht öffentliche Präferenzen für verschiedene Alternativen und, solche Präferenzen nutzend, Zukunftsvisionen für die Forschung zu verfeinern und die Reichweite zu erhöhen. Dabei zielt das Projekt NanoFutures auf eine zentrale Fragestellung ab: wie man die sozialen Implikationen einer aufstrebenden Technologie abwägt, deren Ergebnisse nicht bekannt sind. Die vom NanoFutures-Projekt verfolgte Lösung ist zweifach. Erstens beschränkt NanoFutures Spekulationen über die Technologie auf plausible Visionen. Dieser Ehrgeiz führt zu einer Reihe von Bedenken hinsichtlich der Grenzen der Vorhersage, der Natur der Plausibilität und wie man Plausibilität herstellt. Zweitens unterwirft es diese Visionen einer demokratischen Bewertung durch eine Reihe von Akteuren, wodurch methodische Fragen aufgeworfen werden, wer relevante Stakeholder sind und wie sich verschiedene Gruppen in der fernen Zukunft engagieren. Dieser Artikel macht die Dilemmata von Entscheidungen über solche methodischen Fragen transparent und artikuliert somit die Rolle der Plausibilität für vorausschauende Steuerungen.
       Kommentar: Im Artikel wird Suchtext "Plausib" 55 mal gefunden, also fast vier mal pro Seite. Aber der Begriff wird, wie meist, nicht definiert. S.4: "Bei der Bewältigung dieser Herausforderungen war die CNS-ASU gezwungen, mit einem Mangel an Klarheit und Wissenschaftlichkeit in Bezug auf das Konzept der Plausibilität zu kämpfen. Während eine vollständige theoretische Darstellung von Plausibilität verfrüht ist, kann Plausibilität in der Praxis operationalisiert werden." Wie genau blieb letztlich offen.


    Shafer, Glenn (1976). A Mathematical Theory of Evidence. Princeton University Press.
    [(THE book on belief functions. Highly readable, a must!)  Literaturliste Smets]
        Kommentar: Noch nicht ausgewertet.

    Shafer, Glenn (2006).  Mathematical Theory of Evidence turns 40.
    gshafer@business.rutgers.edu
    www.glennshafer.com


    Simon, H. A. (2014) On Judging the Plausibility of Theories
    https://doi.org/10.1016/S0049-237X(08)71211-4
    Publisher-Zusammenfassung grob übersetzt: Dieses Kapitel konzentriert sich auf die enge Wechselwirkung zwischen Hypothesen und Daten beim Aufbau und Testen von Theorien. In den meisten formalen Induktionstheorien – insbesondere denen, die zur Gattung „hypothetisch-deduktiv“ (H-D) gehören – entspringen Hypothesen vollständig aus dem Kopf des Zeus und werden dann mit Daten getestet, die zeitlos und ganz unabhängig von den Hypothesen existieren. Theorien, die ansonsten so unterschiedlich sind, wie die von Popper und Carnap, teilen diesen gemeinsamen Rahmen. Es war einer der wichtigen Beiträge von Norwood Hanson, diese Trennung von Hypothesen und Daten in Frage zu stellen und zu zeigen, dass in der Geschichte der Wissenschaft die Rückführung von Verallgemeinerungen und Erklärungen aus Daten einer der zentralen und entscheidenden Prozesse war. In diesem Kapitel wurden auch mehrere Aspekte des Problems des Testens von Theorien untersucht, insbesondere solche wichtigen Theorien, die die Form von Extremhypothesen annehmen.
        Kommentar: Noch nicht ausgewertet.


    Smets, P. (1988). Belief functions. In P. Smets, E. Mamdani, D. Dubois & H. Prade (Hrsg.), Non-standard logic for automated reasoning (S. 253-286). London: Academic Press. [Literaturhinweis von  Schill]
        Kommentar: Noch nicht ausgewertet.


    Stegmüller, Wolfgang  Plausibel und Plausibilität in den wissenschaftstheoretischen Werken Wolfgang Stegmüllers
    • Stegmüller, Wolfgang (1973) 5. Die Likelihood-Regel. In (84-94) und (94-128) 6. Die Leistungsfähigkeit der Likelihood-Regel  und (167-176) Die Likelihood-Testtheorie. Jenseits von Popper und Carnap: Die logischen Grundlagen des statistischen Schließens. Studienausgabe Teil D. Probleme und Resultate der Analytischen Philosophie Band IV Personelle und statistische Wahrscheinlichkeit. 4.c Axiome der Stützungslogik (82-84) a.a.O.
    • Stegmüller, Wolfgang (1983)  Probleme und Resultate der Wissenschaftstheorie und Analytischen Philosophie, Band I Erklärung - Begründung - Kausalität Studienausgabe, Teil A Das dritte Dogma des Empirismus, Das ABC der modernen Logik und Semantik. Der Begriff der Erklärung und seine Spielarten. 2., verb. u. erw. A. Berlin: Springer. [digital] [Chi  im Text x] Zum Begriff der  Likelihood.


    Steudel-Günther, A.  (2006) Plausibilität. In (1282-1285, Spalten) Ueding, Gert  (2003, Hrsg.) Historisches Wörterbuch der Rhetorik. Tübingen: Niemeyer.
        Kommentar: Sehr informative, ausführliche Darstellung zur Geschichte des Plausibilitätsbegriffs.

    Stratt, T. M. (1984). Continuous belief functions for evidential reasoning. Proc. 4th American Association for Artificial Intelligence Conf., Austin, Texas, pp. 308-313. [Literaturliste Smets]
        Kommentar: Noch nicht ausgewertet.


    Tuhrim, Stanley, Reggia, James &  Goodall, Sharon (2007) An experimental study of criteria for hypothesis plausibility. Journal of Experimental & Theoretical Artificial Intelligence Volume 3, 1991 - Issue 2, 129-144. [von Schmidt-Scheele nicht erfasst]
        Grob übersetzt: "Abduktive diagnostische Problemlösungssysteme verwenden kausale Zusammenhänge, um plausible diagnostische Hypothesen abzuleiten. Eine wichtige, aber umstrittene Frage für solche Modelle ist, welche Merkmale die plausibelsten Hypothesen definieren sollten. Zwar gibt es zu diesem Thema relevante theoretische Vorhersagen, aber es gibt fast keine empirischen Daten, auf die rationale Entscheidungen gestützt werden könnten. Dementsprechend untersucht diese Studie vier verschiedene Kriterien der Hypothesen-Plausibilität bei der Diagnose des Ortes der Hirnschädigung bei 100 medizinischen Patienten. Die untersuchten Kriterien sind (1) naive minimale Kardinalität, (2) Irredundanz, (3) höchstwahrscheinlich (Bayesian) und (4) minimale Kardinalität unter Berücksichtigung von Adjazenzbeziehungen. Die Modellleistung, wenn diese verschiedenen Hypothesen-Plausibilitätskriterien verwendet werden, bestätigt die zuvor vorhergesagte Unzulänglichkeit der minimalen Kardinalität. Es weist auch darauf hin, dass Irredundanz („Minimalität“), das in aktuellen KI-Modellen am häufigsten verwendete Kriterium, in diesem Kontext aufgrund der Vielzahl von alternativen, unplausiblen Hypothesen nicht nützlich ist. Das interessanteste Ergebnis ist, dass ein modifiziertes Minimalkardinalitätskriterium die besten Hypothesen liefert, wenn es als Verhältnis der Übereinstimmungen mit menschlichen Experten pro generierter Hypothese gemessen wird. Darüber hinaus zeigt der Vergleich der Ergebnisse dieser Studie mit zwei früheren regelbasierten Systemen für eine ähnliche Anwendung, dass abduktive Diagnosesysteme als Anwendungsprogramme sehr leistungsfähig sein können. Diese an sich nützlichen Ergebnisse unterstreichen die Notwendigkeit systematischer empirischer Studien zu abduktiven Problemlösungsmodellen."
        Kommentar: Eine Plausibilitätsdefinition ist der Zusammenfassung nicht zu entnehmen.


    Walton, D. N. (1992) Plausible Argument in Everyday Conversation nach einer Definition von Plausibilität und Prüfkriterien.
        Analyse auf ausgelagerter, eigener Seite in Arbeit.

    Walton, D. N., Reed, Ch., and Macagno, F. (2008). Argumentation Schemes. Cambridge: Cambridge University Press.


    Weinberger, Ota (1973) Topik und Plausibilitätsargumentation. 17-36.Archiv für Rechts- und Sozialphilosphie, LIX/1


    Weyh, Florian Felix (2021.04.01) Letztgültige Antworten in der Wissenschaft Was wissen wir wirklich? (Abruf 01.07.2021): https://www.deutschlandfunkkultur.de/letztgueltige-antworten-in-der-wissenschaft-was-wissen-wir.976.de.html?dram:article_id=495081
        Zusammenfassung-Weyh:  Der interessante Artikel enthält 48 Fundstellen zum Suchtext "plausib". Eine Klärung oder gar Definition liefert er nicht. Mehr hier.
     


    Literatur (Auswahl)


    Links (Auswahl: beachte)


    Glossar, Anmerkungen und Endnoten  > Eigener wissenschaftlicher Standort.
    1) GIPT= General and Integrative Psychotherapy, internationale Bezeichnung für Allgemeine und Integrative Psychotherapie.
    __
    Abduktion "Abduktion ist ein erkenntnistheoretischer Begriff, der im Wesentlichen von dem US-amerikanischen Philosophen und Logiker Charles Sanders Peirce in die wissenschaftliche Debatte eingeführt wurde. „Abduktion ist der Vorgang, in dem eine erklärende Hypothese gebildet wird“." (Wikipedia Abruf 07.08.2021)
    __

    Quelle K. Schill in Stube (Hrsg. 1996) Wörterbuch der Kognitionswissenschaften. Stuttgart: Klett-Cotta.
    __
    grob übersetzt - mit Hilfe von Internet-Übersetzern.
    __
    Internetseite
    Um die häufige und lästige Fehlermeldung 404 zu minimieren, geben wir nur noch Links von Quellen an, die in den letzten Jahrzehnten eine hohe Stabilität ihrer URL-Adressen gezeigt haben (z.B. Wikipedia, DER SPIEGEL)
     
     
     

    Querverweise
    Standort: Eigene Untersuchung Plausibilität.
    *
    Verteilerseite Plausibilitätsanalysen_ Gesamtergebnisse Pilotstudie.
    Haupt- und Verteilerseite Begriffsanalysen  * Methodik der Begriffsanalysen nach Wittgenstein *
    Überblick Arbeiten zur Theorie, Definitionslehre, Methodologie, Meßproblematik, Statistik und Wissenschaftstheorie besonders in Psychologie, Psychotherapie und Psychotherapieforschung.
    *
    Suchen in der IP-GIPT, z.B. mit Hilfe von "google": <suchbegriff> site: www.sgipt.org
    z.B. Wissenschaft site: www.sgipt.org. 
    *
    Dienstleistungs-Info.
    *
    Zitierung
    Sponsel, Rudolf  (DAS). Eigene Untersuchung zum Plausibilitätsbegriff und einer allgemeinen Plausibilitätstheorie mit einer Gesamtzusammenfassung in 8 Sprachen (germ, engl, franz, span, port, russ, chin, arab). Internet Publikation  für Allgemeine und Integrative Psychotherapie  IP-GIPT. Erlangen:  https://www.sgipt.org/wisms/sprache/BegrAna/Plausib/RSEUPT.htm
    Copyright & Nutzungsrechte
    Diese Seite darf von jeder/m in nicht-kommerziellen Verwertungen frei aber nur original bearbeitet und nicht  inhaltlich verändert und nur bei vollständiger Angabe der Zitierungs-Quelle benutzt werden. Das direkte, zugriffsaneignende Einbinden in fremde Seiten oder Rahmen ist nicht gestattet, Links und Zitate sind natürlich willkommen. Sofern die Rechte anderer berührt sind, sind diese dort zu erkunden. Sollten wir die Rechte anderer unberechtigt genutzt haben, bitten wir um Mitteilung. Soweit es um (längere) Zitate aus  ...  geht, sind die Rechte bei/m ... zu erkunden oder eine Erlaubnis einzuholen.

    Ende_ Eigene Untersuchung Plausibilität__Datenschutz_Rel. Aktuelles _Überblick_Überblick Wissenschaft _Rel. Beständiges_ Titelblatt_ Konzept_ Archiv_ Region_ Service iec-verlag__Wichtige Hinweise zu Links und Empfehlungen_ Mail: sekretariat@sgipt.org_

    korrigiert: irs gelesen 04.11.2021 / Rechtschreibprüfung 01.11.2021 / gelesen 16.10.2021 / Rechtschreibprüfung 14.10.2021


    Änderungen Kleinere Änderungen werden nicht extra ausgewiesen; wird gelegentlich überarbeitet und ergänzt.
    08.02.22   Standardmodelle Epidemiologie. Plausibilität der Kritische Masse Hypothese der Omikronvariante
    05.01.22   Begriffsanalyse plausibel, Plausibilität, Plausibilitätskriterien in der Mathematik.
    20.11.21   Analyse Josephson 1994 ergänzt mit Link zur Auswertung.
    08.11.21   Arabisch korrigierte Fassung.
    07.11.21   Bei den Wahlen fehlte die 2.
    06.11.21   Grundversion ans Netz.
    04.11.21   Standardmodelle der Psychologie (noch nicht Korrektur gelesen).
    01.11.21   Noch nicht freigegebene Testversion im Netz.
    14.10.21   Angelegt.