Die Korrelationsrechnung spielt eine kaum zu überschätzende Rolle in der empirischen Sozialforschung und speziell in der Testpsychologie und wird selten kritisch hinterfragt. Die Mathematik- und Statistikbücher sind, was die Anwendung und Interpretation betrifft, zumeist sehr nachlässig und schlecht geschrieben, dafür werden z.B. die PsychologiestudentInnen umso mehr mit Formeln und Ableitungen gequält, die für die Anwendung ohne jede Bedeutung sind, mehr verwirren und ablenken, statt hilfreich zu sein. Das Wesentliche bleibt meist auf der Strecke. Das ist grob der Stand der Methodenausbildung in der Psychologie wie ich ihn kenne. Inhalte, Anwendung, Interpretation und Bedeutung scheuen die SzientistInnen wie der Teufel das Weihwasser.
Das Grundproblem
in der Psychologie sind das Skalenniveau ihrer Messdaten und ihre unscharfen
Begriffe, die nicht streng normiert sind.
Der extreme Erfolg der Mathematik beruht auf der Schärfe ihrer Begriffe
und ihres unerbitterlichen Beweissystems. Und der von der Mathematik maßgeblich
beeinflusste große Erfolg der Naturwissenschaft und Technik beruht
auf genauen Definitionen, sorgfältiger Beobachtung und Messuung der
Daten, kritischer Kontrolle der Daten, Hypothesen. Modelle und Theorien.
Allerdings haben wir in der Psychologie auch das Problem, dass wir mit
Menschen aus ihrer Lebenswelt arbeiten müssen. Es scheint, als ob
es zwischen exakter Wissenschaft und Wissenschaft in realen menschlichen
Lebenswelten und im Alltag einen kommunikativen Gegensatz gibt: Je
exakter vorgegangen wird, desto alltagsuntauglicher sind die Methoden für
den Alltag und die reale Lebenswelt, in der die Kommunikation durch das
Unscharfe, Ungefähre ("fuzzyhafte") sehr erfolgreich ist.
Entscheidend für jede Wissenschaft ist ihre
Datenbasis. Der Überbau kann nicht stabiler sein als das Fundament.
Noch bewegt sich die Psychologie auf einem sehr schwammigen, schwankenden,
unscharfen und flüchtigen Boden.
Der Produkt-Moment.Korrelationskoeffizient setzt
wie die meisten statistischen Verfahren Interverskalen-Niveau der Daten
voraus, da so gut wie nie gegeben ist. Wir "messen" also per fiat,
also mit ungefähren Näherungswerten, die wir nicht genau einschätzen
können und auf Glaubensniveau beruhen . Die in der Psychologie vorliegenden
Daten müsste man mit unscharfen Zahlen bestimmen lernen für die
eigene Rechengesetze zu entwickeln wären. Ein einfaches Überstülpen
mathematisch-statistischer Methoden kann man nur als szientistische Numerologie
und Esoterik bezeichnen. Ungeachtet dessen ist es wohl hilfreich
und sinnvoll, zu verstehen versuchen, was man da macht und wo die Methoden,
wenn man ihre Anwendungsmöglichkeit voraussetzt und unterstellt, ihre
Schwächen haben oder gar völlig entgleisen können, wenn
etwa negative Eigenwerte - die es bei korrekter Anwendung gar nicht geben
dürfte (numerische Mathematiken kennen diese Phänomene natürlich
zur Genüge) - in Korrelationsmatrizen verborgen sind (was man
einer Korrelationsmatrix nicht ansehen kann: man muss sie
untersuchen).
Der Korrelationskoeffizient
| Korrelationskoeffizienten können Werte zwischen -1 und +1 annehmen: -1 <= r <= +1. Eine negative Korrelation bedeutet einen gegenläufigen Zusammenhang zwischen z.B. a und b: steigt a, fällt b und umgekehrt. Eine positive Korrelation bedeutet einen gleichsinnigen Zusammenhang zwischen a und b. Steigt a, steigt b, fällt a, fällt auch b und umgekehrt. Eine Korrelation um 0 zeigt keinen Zusammenhang zwischen a und b und den mit ihnen verbundenen Variablen. Das kann sich schnell ändern, wenn auspartialisiert wird. Partialisieren ist der korrelationsrechnerische Ausdruck für "Einfluß ausschalten durch konstant halten". Man untersucht also die Zusammenhänge zwischen a und b und hält die bekannten Einflüsse von c,d,e, ... konstant. Partielle Korrelationen werden wie folgt gekennzeichnet und gelesen: rXY.ABC... , d.h. es wird die Korrelation zwischen X und Y betrachtet wobei die Einflüsse von ABC ... ausgeschaltet = konstant gehalten werden. * Info partielle Korrelation * Info Beweis in der Statistik * Info Statistik IP-GIPT * | 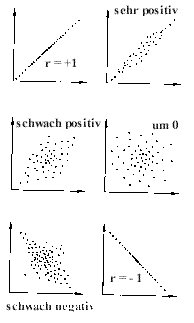 |
 |
Wie man sieht, gibt es auch zahlreiche nicht- lineare Korrelationen. Prüfverfahren und Kriterien, ab wann welches Korrelations- Modell anzuwenden ist, scheinen nicht vorzuliegen und auch nicht gelehrt zu werden. Auch dies trägt mit zum schlechten Ruf der Statistik bei. Wichtig scheint hauptsächlich zu sein, dass man rechnen kann und dass etwas "rauskommt". |
Korrelation(skoeffizient) ist nicht gleich Korrelation(skoeffizient)
Das Wort Korrelation ist ein vielfältiges Homonym [1,
2,
3,
4].,
d.h. das Wort umkleidet sehr verschiedenartige Begriffe und Maße
und wird in der Literatur auch in den unterschiedlichsten Bedeutungen gebraucht.
Dieser Sachverhalt hat mir zu Beginn meiner systematischen
Untersuchung zu "Korrelationsmatrizen" große Schwierigkeiten
bereitet. Es ist daher sehr wichtig, wenn man von "Korrelation" spricht,
genau zu spezifizieren, welche man meint. Für multivariate
statistische Analysen benötigt man gewöhnlich den sog. Maß-,
Produkt-Moment-
oder Bravais-Pearson Korrelationskoeffizienten.
Ganz allgemein kann man Ko-Relation als Zusammenhang
für Merkmale, Ereignisse oder Zustände verstehen, für den
die mathematische Statistik vielfältige Maßzahlen entwickelt
hat. Tatsächlich wird aber gewöhnlich nicht allein
"der" Zusammenhang zwischen X und Y erhoben, sondern der Zusammenhang zwischen
X und Y und der mit X und Y verbundenen Einflüsse.
Sonderformen
der Korrelation
Mit dem Produkt-Moment-Korrelations-Koeffizienten gibt es einige Sonderformen
der Korrelation.
Multiple Korrelation
Bei der multiplen Korrelation wird die Korrelation zwischen den Ausprägungen
einer
und mehreren anderen Variablen bestimmt.
Partielle
Korrelation
Bei der partiellen Korrelation wird die Korrelation zwischen zwei Variablen
unter
Ausschluss einiger oder mehrerer anderer Variablen bestimmt. Man
kann auch sagen, der Einfluss bestimmter, hier der auspartialisierten Variablen
wird eliminiert, wodurch die experimentelle Technik des Konstanthaltens
simuliert werden kann.
Kanonische Korrelation
Mit der kanonischen Korrelation kann man die Korrelation zwischen zwei
Variablenblöcken, also eine Art Verallgemeinerung der multiplen
Korrelation, bestimmen. Das kann sehr hilfreich sein, wenn Merkmale mehrdimensional
sind und auch nur mehrdimensional ausgedrückt werden können,
wie z.B. Farbwerte (Grün, Rot, Blau, Helligkeit, Schärfe, Kontrast).
Eine sehr nützliche Anwendung ergibt sich für
die Testpsychologie, wenn ganze Untertests - also mehrere Variablenblöcke
- auf ihren korrelativen Zusammenhang hin untersucht werden können.
Beispiel:
Kanonische
Korrelation zwischen Verbal- und Handlungsteil beim HAWIE (Hamburg-Wechseler
Intelligenz-Test für Erwachsene). Für die Altersgruppe der 20-34jährigen
ergab sich ein kanonischer Korrelationskoeffizient rk(20-34) = 0.7813
und für die Altersgruppe der 35-49jährigen ein rk(35-49) =0.8339.
D.h. die Intelligenzen des Verbal- und Handlungsteils korrelieren kanonisch
ziemlich hoch,wobei sich durch die Werte entwicklungspsychologisch die
Hypothese ergibt, ob sich Verbal- und Handlungs-Intelligenz mit zunehmendem
Alter annähern? Dieser Befund führte mich zur Frage, ob sich
denn die Intelligenzen des Verbal- und Handlungsteils "wirklich" unterscheiden?
Zu diesem Zweck führte ich eine Eigenwertanalyse
mit einem für mich völlig überraschenden Ergebnis durch:
die Eigenwertstruktur des HAWIE
zeigt ganz klar - im Gegensatz zur faktorenanalytischen Literatur - einen
Generalfaktor an.
_
Kreuzkorrelation > Autokorrelation.
"Die Kreuzkorrelation beschreibt die statistische Ähnlichkeit
zweier Signale, die zeitlich gegeneinander verschoben werden. Die Kreuzkorrelation
ist im Gegensatz zur Autokorrelation nicht symmetrisch zur y-Achse." (DasyLab
11 > Karrenberg) D.h. man
verschiebt unterschiedliche Datenreihen.
_
Auto-Korrelation
(> Kreuzkorrelation)
Korrelation zwischen Vorgängern und Nachfolgern einer Verlaufsdatenreihe
bei Annahme von Stationarität
(meist unrealistisch und daher sehr problematisch in der Psychologie, Psychopathologie
und Psychotherapie).
_
Quantenmechanische Korrelation
Der Ausdruck "Korrelation" ist sehr unglücklich gewählt,
da in der statistischen Bedeutung die quantenmechanische Korrelation 1
beträgt und damit eine funktionale, gesetzmäßige Abhängigkeit
vorliegt. Quantenmechanischer Korrelation kann daher auch als kausale
Bindung zwischen Sachverhalten S1 und S2 interpretiert
werden, wonach eine Änderung in einem Sachverhalt zur Änderung
des anderen Sachverhalts führt, auch wenn die beiden Sachverhalte
sehr weit von einander entfernt sind. Diese Interpretation ist aber falsch,
wenn diese Änderung gleichzeitig erfolgt, weil
Kausalität
ein Nacheinander beinhaltet. Dieser spektakuläre Mechanismus, der
auch mit Verschränkung bezeichnet wird, ist
m.E. noch nicht verstanden.
Im Lexikon der Physik von Spektrum
() wird ausgeführt: "Korrelation Quantenmechanik Mathematische Methoden
und Computereinsatz, 1) allgemein ein durch Wechselwirkung bedingter Zusammenhang
zwischen physikalischen Größen, die getrennt gemessen werden.
Besonders interessant sind quantenmechanische Korrelationen, die durch
die Nichtlokalität in der Quantenmechanik auch dann auftreten, wenn
sie laut klassischer Theorie im Widerspruch mit der Kausalität stünden
(z.B. EPR-Paradoxon). (Meßprozeß in der Quantenmechanik, Quanteninformatik).
2) in der Statistik ... ".
Formel der Produkt-Moment-Korrelationsrechnung nach Bravais-Pearson

Quelle: http://www.uni-essen.de/imibe/download/kapitel22.pdf
Der Ausdruck im Zähler heißt auch Kovarianz. Im Nenner stehen die Standardabweichungen der beiden betrachteten Variablen, hier mit x und y bezeichnet.
Beispiel für eine lineare Korrelation
Gehen wir vom einfachsten Fall zweier Meßwertreihen X (z.B. Gewicht) und Y (z.B. Körpergröße) aus. Dann gibt der Korrelationskoeffizient Auskunft darüber, wie gut sich durch die beiden Meßwertreihen jeweils eine Gerade legen läßt, so dass die Quadrate der Abstände der Meßwerte von der Geraden minimal werden. Beide Geraden gehen einen Winkel ein, der das Maß der Korrelation graphisch veranschaulicht. Es gilt: je kleiner der Winkel, desto größer die Korrelation. Es gilt -1 <= r <= +1. Bei perfekter Korrelation r = |1| (+1, -1) fallen die beiden Geraden zusammen und die Korrelation drückt eine funktionale Abhängigkeit aus. Im folgenden Phantasie- Beispiel ergibt sich zwischen dem Körpergewicht und dem Körpergröße ein Korrelationskoeffizient r = 0,84367.
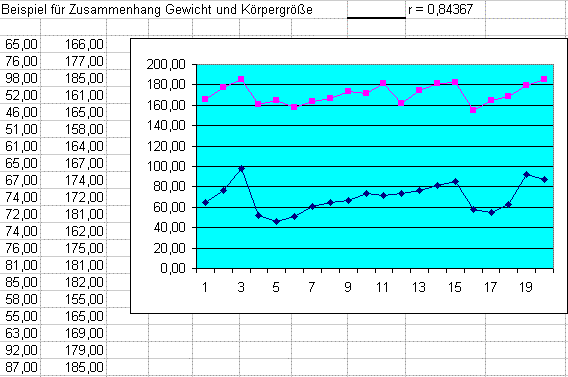
Dieses Beispiel wirkt verständlich und plausibel (aber: siehe Seltsames ...).
Was bedeutet eine Korrelation - Wichtige Korrelationssätze
_
| (1a) Unabhängigkeitssatz: Sind zwei Variablen voneinander (statistisch) unabhängig, so sind sie unkorreliert. Die Umkehrung gilt nicht: |
| (1b) Unkorreliertheitssatz: Sind zwei Variablen unkorreliert, so sind sie nicht unbedingt unabhängig. Das kann so sein, muß aber nicht so sein. |
Anmerkung: In der Encyclopedia of Statistical Sciences, Vol. 2, p. 194: wird 1a und 1b wie folgt formuliert: "If X and Y are independent, then corr(X,Y) = 0, but the converse is not necessarily true."
_
| (1c) Linearitätssatz: Gibt es zwischen zwei Variablen einen linearen Zusammenhang, so zeigt der Korrelationskoeffizient dies entsprechend an. Die Umkehrung gilt nicht zwingend: Aus einem hohen Korrelationskoeffzienten darf nicht notwendig auf einen linearen Zusammenhang geschlossen werden; ein solcher kann, muß aber nicht vorliegen. (Sponsel 1994, Kap. I,. S. 32): Linearitätsparadox. |
| (2)
Vieldeutigkeitssatz:
Mit einem Korrelationskoeffizienten r(ij) wird der lineare Zusammenhang
zwischen den Variablen i und j und der mit i und j verbundenen
Variablen ausgedrückt (Sponsel 1984, S. 213).
(2b). Aus gleichen Eigenwerten können unterschiedlichen Korrelationsmatrizen hervorgehen (3 Beispiele). Diese Korrelationsmatrizen heißen dann ähnlich im mathematischen, linear-algebraischen Sinne. (2c). Unterschiedliche
Rohwerte können zu gleichen Korrelationsmatrizen führen (3
Beispiele).
|
 |
|
|
Satz (1) und (2) sind bekannte Sätze, die in jedem guten Statistikbuch zu finden sind. (3) ist den meisten unbekannt und (4) hört sich für die meisten einigermaßen provokativ an. Seine Richtigkeit möchte ich im folgenden durch einige Beispiele (Beweis durch Modellbildung) begründen.
_
| (4)
Isometriesatz (Hain
1994). "Das Parallelotop der zentralen, normierten Rohwerte ist isometrisch
zu den Spaltenvektoren der oberen Dreiecksmatrix der Cholesky Zerlegung."
Praktisch bedeutet dieser Satz u.a., dass ein Eingriff in die Korrelationsmatrix
einem Eingriff in die normierten Rohwerte gleichkommt, d.h. wer die Korrelationsmatrix
verändert - wie es oft sehr gewaltsam bei Faktorenanalysen
geschieht - verändert zugleich die normierten Rohwerte und landet
meist in dem Widerspruch,
dass Datenreduktionen zwar möglich sind, aber dann nicht mehr die
usprünglichen Daten repräsentieren.
(4b) Partielle Korrelationsmatrix nicht notwendig positiv [semi] definit. |
(5) Bedeutungen nach Hans Bartel (1974, S. 88f):
Die Bedeutungen Bartels sind sämtlich formal-statistischer Natur.

(6)
Speziell zur Deutung führt Baur
1928 (S. 50f) aus:
Baur weist zwar auf die artefiziellen Korrelationsmöglichkeiten
hin, aber auch er liefert keine inhaltliche Korrelationstheorie
| "... das wichtigste bleibt aber immer die Deutung der errechneten Maßzahlen." Im einzelnen: |
"25. DIE DEUTUNG DER KORRELATIONSKOEFFIZIENTEN UND KORRELATIONSVERHÄLTNISSE
In den vorangehenden Kapiteln wurden die Berechnungsweisen und die Bedeutung
des Kkf. und des Kvh. als Maßzahlen der stochastischen Verbundenheit
von zwei zufälligen Veränderlichen besprochen. Es war das Bestreben
des Verfassers, die Darstellung so zu gestalten, daß auch mathematisch
weniger geschulte Leser in den Stand gesetzt werden, die K.-R. in ihrem
Arbeitsgebiet nutzbringend anzuwenden. Damit dieses Ziel auch wirklich
erreicht werde, ist es aber noch nötig, ausdrücklich darauf aufmerksam
zu machen, daß es natürlich nicht damit abgetan ist, Kkfn. und
Kvhe. und ihre Fehler zu berechnen. Zur Gewinnung sicherer Grundlagen
ist es zwar von großer Bedeutung, die Strammheit des stochastischen
Zusammenhanges oder den Grad, in welchem die Schwankungen zweier Erscheinungen
als annähernd proportional angesehen werden können, zahlenmäßig
festzustellen, das wichtigste bleibt aber immer die Deutung
der errechneten Maßzahlen. Hierbei muß vor allem im Auge behalten
werden, daß selbst aus einem ganz nahe an l liegenden Kkf. oder Kvh.
noch nicht auf einen unmittelbaren ursächlichen Zusammenhang
der beiden Erscheinungen in dem Sinne, daß die eine die „Ursache"
der anderen wäre, geschlossen werden darf. Es kann eine hohe K. zwischen
zwei Erscheinungen auch dadurch zustande kommen, daß beide durch
einen übergeordneten Erscheinungskomplex beeinflußt werden.
In diesem Falle nennen wir die K. eine symptomatische. Ein ausgezeichnetes
Beispiel einer symptomatischen K. hat SORER [FN 1):R. SORER, Allgem. statistisches
Archiv 8. Jahrg. 1914, S.193] gegeben. Er fand zwischen der Größe
der Produktion und der Größe des Verkehrs in Österreich
im Zeitraum 1882 bis 1911 den Kkf. + 0.988, zwischen-Produktion [> S. 51]
und Verbrauch im gleichen Zeitraum + 0.975, zwischen Verkehr und Verbrauch
+ 0.994. Diese hohen Kkfn. sind „Symptome" der Steigerung des gesamten
österreichischen Wirtschaftslebens im genannten Zeitraum. Stellt man
den zeitlichen Verlauf der drei Zahlenreihen bildlich dar, so bekommt man
3 steil ansteigende Kurven. Es wäre verfehlt, aus der hohen K. auch
auf einen hohen Grad der Übereinstimmung der 3 Erscheinungen in den
Abweichungen von ihrem Hauptverlauf schließen zu wollen. Will man
den stochastischen Zusammenhang der Schwankungen um den gemeinsamen
Hauptverlauf untersuchen — und das ist in den meisten Fällen das wichtigste
—, so muß man bei der Berechnung der K.-Maße nicht von den
Abweichungen vom arithmetischen Mittel, sondern von den Abweichungen vom
Hauptverlauf ausgehen. Dabei ist jedoch darauf zu achten, daß die
Summe aller Abweichungen einer Veränderlichen stets gleich 0 sein
muß. Nur unter dieser Voraussetzung kann z. B. die Formel (18) auch
auf die Abweichungen vom Hauptverlauf angewandt werden. Der Hauptverlauf
wird in der Naturwissenschaft als „säkulare Schwankung", in der Wirtschaftsstatistik
mit dem englischen Worte „Trend" bezeichnet.
Auf noch wenig durchforschten Gebieten ist es oft
sehr schwierig, zur richtigen Deutung von Kkfn. zu kommen. Durch zielbewußte
Vorbearbeitung des gegebenen Zahlenstoffes, z. B. Ausschaltung säkularer
Schwankungen, Untersuchung vieler verwandter Erscheinungen mit den Mitteln
der K.-R., Betrachtung der Änderungen (oder auch der angenäherten
Konstanz) der Kkfn. und Kvhe. in Zeit und Raum wird man aber schließlich
doch zum gewünschten Ziele gelangen."
(7) Die von Koller
1962 empfohlene Deutungssystematik (S. 74/75)
Auch Koller liefert keine inhaltliche Korrelationstheorie, aber eine
praktisch nützliche Prüfsystematik.

Inhomogenitätskorrelation:
Beschreibung: https://dorsch.hogrefe.com/stichwort/inhomogenitaetskorrelation
Graphik: https://www.io-warnemuende.de/tl_files/scripte/statistikseminar/IOW_Seminar_2012_Statistik6_Korrelation.pdf
(8)
Bedeutungsdiskussion bei R.A.
Fisher gegenüber einer dritten Variable
Auch Fishers Überlegungen sind formal-statistischer Natur und
geben inhaltlich nichts her, Eben das, was er Wirkung nennt, wäre
inhaltlich näher zu bestimmen.

(9) Clauß & Ebner (1982) zur Interpretation von Korrelationskoeffizienten.
"Bei der Interpretation von Korrelatiönskoeffizienten ist man geneigt,
allein aus der Größe des Koeffizienten auf die Stärke des
Zusammenhangs zwischen beiden Variablen zu schließen. Ein r = 0,40
beschreibt einen „schwachen" positiven Zusammenhang, ein r = 0,80 dagegen
ist Ausdruck eines „starken" positiven Zusammenhangs. Eine solche Aussage
ist zwar nicht völlig falsch, aber doch bedenklich und möglicherweise
unberechtigt. „Stark" und „schwach" sind in diesem Falle sehr relative
Begriffe. Ihre konkrete Bedeutung hängt erheblich von dem untersuchten
Problem ab. Sollte sich ein r = 0,40 zwischen Leistungseigenschaften von
Schülern und pädagogischen Eigenschaften ihres Lehrers ergeben,
dann wäre dies Ausdruck einer überraschend „hohen" Korrelation.
Ergäbe sich dagegen r = 0,40 für den Zusammenhang zwischen Erst-
und Zweitleistungen bei derselben Aufgabenart, dann müßte man
dies als verwunderlich „niedrig" betrachten. Um die Größe eines
Koeffizienten zu beurteilen, muß man diesen folglich mit der durchschnittlichen
Höhe entsprechender Kennwerte vergleichen, die bezüglich desselben
Problems sonst gefunden wurden. Außerdem ist die Zahl der zugrunde
liegenden Messungen n zu berücksichtigen. Diese Umstände verbieten
es, verbindliche Hinweise darüber zu geben, welche numerischen Werte
des Korrelationskoeffizienten als Ausdruck eines „starken", „mäßigen"
oder „schwachen" Zusammenhangs aufzufassen sind. Es sei darauf hingewiesen,
daß Korrelationskoeffizienten nicht als Prozentwerte gedeutet werden
dürfen. So bedeutet r = 0,80 keineswegs, daß die Werte beider
Variablen in 80 von 100 Fällen übereinstimmen würden. Eine
solche Deutung verbietet sich für r. Sie kann jedoch für r2
sinnvoll vor- [<122, >124] genommen werden, r2
wird manchmal als „Determinationskoeffizient", oft j als „Bestimmtheitsmaß"
(E.WEBER, 1963; S. 270ff.) bezeichnet. Dieser] Wert gibt an,
in welchem Ausmaß die Varianz der einen Variablen durch die Varianz
der anderen Variablen bestimmt wird. So führt ein r= 0,80 auf] r2
= 0,64, und dies läßt die Aussage zu, daß 64% der Varianz
beider Variablen determiniert sind. Sollen X und Y mindestens 50% ihrer
Varianz bestimmen, muß r >= 0,71 sein, denn dann ist r2
>= 0,50." (S. 122f)
(10)
Korrelation und Kausalität
Dieser Abschnitt hat auf Grund seiner Größe eine eigene
Seite erhalten. Dort finden Sie neben Ausführungen zu kausalen
Grundmodellen
einen Beweis
für die Zulässigkeit der Kausalinterpretation von Korrelationen.
An 20
Beispielen von Korrelationsmatrizen aus den drei Bänden "Korrelation
und Kausalität" wird die Anwendung der Methode der Eigenwert- und
Fast-Kollinearitätsanalyse gezeigt und ihre Leistungsfähigkeit
gezeigt (Ergebnisübersicht).
Abschließend werden einige Orientierungsregeln
für die Kausalinterpretation von Korrelationen vorgeschlagen.
.
(11) Interpretation der Groesse von Korrelationskoeffizienten.
Die Beurteilung der Größe von Korrelationskoeffizienten hängt von verschiedenen Faktoren ab.
- die formale, reine numerische Größe.
- die tatsächliche Bedeutung des korrelativen Zusammenhangs.
- den relevanten Merkmalsraum.
- den beeinflussenden anderen Merkmalen ("Moderatorvariablen" > Storchennester / Geburtenrate)
- zufälligen Einflüssen.
- sonstigen Faktoren.
| Aus einem hohen numerischen Korrelationswert folgt nicht zwingend auch ein tatsächlich hoher Zusammenhang. Und aus einem niedrigen numerischen Korrelationswert folgt nicht zwingend auch ein tatsächlicher geringer Zusammenhang. Was tatsächlich vorliegt, muss in der Regel sorgfältig analysiert werden. |
Verbale Charakterisierungen: Ein
Vorschlag zur sprachlichen Interpretation der formal, rein numerischen
Größen:
- r = 1 => positive lineare Abhängigkeit (Kollinearität): wenn das eine, dann das andere und umgekehrt.
- 0.85 < r < 1 => fast kollinear linear positiver Zusammenhang.
- 0.75 < r <= 0.85 => stark linear positiver Zusammenhang.
- 0.6 < r <= 0.75 => mittelstark linear positiver Zusammenhang.
- 0.4 < r <= 0.6 => deutlicher bis mittlerer linear positiver Zusammenhang.
- 0.2 < r <= 0.4=> schwacher bis deutlicherer linear positiver Zusammenhang.
- 0.0 < r <= 0.2 => keiner bis kaum ein linearer Zusammenhang.
- r um 0 kein linearer Zusammenhang
- 0.0 > r <= -0.2 => keiner bis kaum ein negativer linearer Zusammenhang.
- -0.2 < r <= -0.4 => schwach linear negativer Zusammenhang.
- -0.4 < r <= -0.6 => deutlicher bis mittlerer linear negativer Zusammenhang.
- -0.6 < r <= -0.75 => mittelstark linear negativer Zusammenhang.
- -075 < r <= -0.85 => stark linear negativer Zusammenhang.
- -0.85 < r < -1 => fast kollinear linear negativer Zusammenhang.
- -1 => negative lineare Abhängigkeit (Kollinearität). wenn das eine nicht, dann das andere und umgekehrt.
Man kann die Grenzen natürlich auch anders wählen, dann
sollte man angeben, welche Sprachregelung man gebraucht. Über die
inhaltliche, tatsächliche Bedeutung sagen diese Sprachregelungen aber
nichts aus. Diese müssen im Zusammenhang eigens begründet werden.
Definition Korrelationsmatrix
Nicht alles, was aussieht wie eine Korrelationsmatrix ist auch eine. Jeder der folgenden sechs Bedingungen ist notwendig für eine Korrelationsmatrix und alle sechs sind insgesamt auch notwendig und hinreichend:
- Die Matrix ist quadratisch
- Die Matrix ist symmetrisch.
- Die Matrix enthält in der Hauptdiagonale 1.
- Die Korrelationen sind im Wertebereich +1 und -1.
- Die Matrix ist positiv semidefinit, d.h. sämtliche Eigenwerte sind >= 0.
- Die Eigenwertsumme ist gleich der Ordnung n der Korrelationsmatrix.
Die
kaum zu überschätzende Bedeutung der Eigenwerte einer Korrelationsmatrix.
Die Eigenwerte einer Korrelationsmatrix sind
so etwas wie ihre "Gene", sie sagen der KennerIn sofort, was mit der Korrelationsmatrix
"los" ist, wie es um ihre Beschaffenheit und Eigenart, besonders im Hinblick
auf Fast-Kollinearitäten
(lineare Abhängigkeiten) bestellt ist. Korrelationsmatrizen
gehören zur Gruppe der quadratischen
(Bilinear-) Formen und symmetrischen Matrizen. Notwendiges mathematisches
Charakteristikum einer Korrelationsmatrix ist daher ihre sog. semipositive
Definitheit
oder anders ausgedrückt: alle Eigenwerte >= 0. Sind alle Eigenwerte
> 0, spricht man von positiv definit. Ist mindestens ein
Eigenwert 0 heißt die Korrelationsmatrix semi positiv definit;
auch singulär. Durch falsche Formeln (z.B. "correction
for attenuation", tetrachorische Koeffizienten, Assoziationsmaße
oder vollständige Partialisierungen [zwei gegen alle = den ganzen
Rest] , falsche Missing Data Lösungen und andere unsachgemäße
Manipulationen (z.B. der Hauptdiagonalelemente bei der sog. "Kommunalität"
oder unangemessenen Faktorenreduktionen in der Faktorenanalyse), aber auch
durch Rundungsfehler bei fast-kollinearen
Korrelationsmatrizen können Eigenwerte negativ werden und die
Matrix dadurch entgleisen. Indefinite
Matrizen sind keine Korrelationsmatrizen, auch wenn sie äußerlich
("phänotypische Korrelationsmatrizen") so aussehen.
Zu einer korrekten Diagnose, ob eine phänotypische auch eine genotypische,
echte - mathematisch korrekte - Korrelationsmatrix ist, gehört
daher auch die Bestimmung der Eigenwerte, was mit den heutigen Programmen
zur multivariaten Statistik routinemäßig
ohne großen Aufwand erfolgen kann. Durch Eigenwertanalysen
von Korrelationsmatrizen können manchmal auch schwerwiegende methodische
Fehler oder Datenfälschungen erkannt werden. Es ist auch gut möglich,
dass eine Korrelationsmatrix äußerlich ("phänotypisch")
nicht erkennen lässt, ob und wie viele (Fast-) Kollinearitäten
(Beispiel hier)
sie enthält. Hierzu muss man die Eigenwerte berechnen.
Was besagen nun die Eigenwerte
einer Korrelationsmatrix? Kleine Eigenwerte "nahe 0" sind ein Hinweis
darauf, wie viele fast-kollineare Beziehungen, also Gesetzmäßig-
oder Regelhaftigkeiten in der Korrelationsmatrix enthalten sind. Kleine
Eigenwerte bedeuten also keineswegs, daß die Matrix viel zu vernachlässigende
Information (Redundanz oder Fehler)
enthält; das ist nur eine mögliche Folgerung. Weil
die Faktorenanalytiker darauf fixiert waren, Korrelationsmatrizen in ihrem
Rang zu reduzieren und Eigenwerte < 1 völlig falsch ("Screetest")
als zu vernachlässigende Größen mißdeuteten, erkannten
sie überhaupt nicht, dass Eigenwerte "nahe" 0 die Entdeckung einer
Gesetzmäßigkeit bedeuten kann, die eine besondere Aufmerksamkeit
und Untersuchung geradezu herausfordert. Der Fehler bestand also darin,
die Bedeutung eines Eigenwertes "nahe" 0 (praktisch <= 0,2) nicht
zu erkennen oder zu verkennen, meist durch einseitige faktorenanalytische
Fixierung auf Datenreduktion bedingt.
Wie ich vor einiger Zeit herausfand,
eignen sich Eigenwertanalysen vorzüglich
zur Untersuchung von Generalfaktoren
(ein großer Eigenwert > 50% der Gesamtvarianz, alle anderen in ähnlich
kleiner Größenordnung), z.B. der Interkorrelationsmatrizen
von Intelligenztests (ein anderes Beispiele hier).
Dimension und Eigenwerte.
Besteht eine Korrelationsmatrix aus einem einzigen großen Eigenwert
(Faustregel: ca. 60-80% der Varianz der Eigenwertsumme=Ordnung der Matrix)
und sind alle anderen Eigenwerte relativ klein (Faustregel: nicht größer
als ca. 5% der Varianz), so kann man sagen, dass diese Korrelationsmatrix
Eindimensionalität anzeigt. In der
Sprachstudie-01
hat sich ergeben, dass die drei gewählten Skalierungsvarianten eine
Eindimensionalität repräsentieren, womit bewiesen ist, dass solche
empirisch existieren.
Ganz allgemein ist folgende Faustregel
nützlich, dass Eigenwerte >1 die Anzahl der Dimensionen, 0,2 <
Eigenwerte < 1 spezifische Merkmale ("Faktoren") und Eigenwerte <=
0,2 Fast-Kollienaritäten schätzen.
Zerlegt man eine Korrelationsmatrix
C in ihre Hauptkomponenten (Eigenvektoren) V und ihre Eigenwertdiagonalmatrix
D, so gilt: F = V* SQRT(D). F heißt die Matrix der Faktoren (genauer:
Faktorenladungen). Man sieht dieser Gleichung an, dass die Eigenwerte
nicht negativ werden dürfen, sonst resultieren imaginäre
oder komplexe Faktoren (Beispiel),
die zugleich imaginäre oder komplexe Rohdatensätze implizieren
würden. Hat eine Korrelationsmatrix der Ordnung N einen kleineren
Rang Rg (1 <= Rg <= N, so kann die Korrelationsmatrix aus der
Matrix von Rg Faktoren mathematisch exakt reproduziert werden, denn es
gilt: C = F * F' (Matrix der Faktoren multipliziert mit ihrer Transponierten).
Fazit: Ob eine Korrelationsmatrix
der N auf Faktoren der Ordnung (Fast-) Rg < N zurückgeführt
werden könnte, wenn man sich nicht um die damit entdeckte Gesetzmäßig-
oder Regelhaftigkeit kümmern möchte, hängt genau
davon ab, wie viele Eigenwerte (Fast-) 0 sind. Jede darüber hinausgehende
Manipulation der Korrelationsmatrix führt nach dem Hain'schen
Isometriesatz zu einer Rohdatenveränderung und damit Datenverfälschung.
[Siehe auch: Kommunalität].
Querverweise: Aus
gleichen Eigenwerten unterschiedliche Korrelationsmatrizen erzeugen.*
Zu
gleichen Korrelationsmatrizen unterschiedliche Rohwerte erzeugen. *
Zur
Frage, ob sich zu einer vorgegebenen Eigenwertstruktur mindestens eine
Korrelationsmatrix konstruieren lässt.
Pseudo-Korrelationsmatrizen.
[Beispiele]
(Phänotypische) Pseudo-Korrelationsmatrizen sehen nur aus wie
solche, sind aber keine, wenn man sich die Eigenwerte näher ansieht.
Hier sind sehr merkwürdige und hochpathologische
Konstruktionen möglich, wobei bereits aus einem einzigen Beispiel
folgt: Symmetrische Matrizen mit 1 in der Hauptdiagonale für deren
Einträge r gilt -1 <= r <= 1 sind nicht unbedingt Korrelationsmatrizen
(mehr). Ein sehr krasses Beispiel einer Pseudo-Korrelationsmatrix
aufgrund unterschiedlicher Stichprobenumfänge mit völlig entgleisten
negativen Eigenwerten finden Sie hier.
Der Rang und seine Bedeutung bei Korrelationsmatrizen

Quelle: Sponsel,
R. (1994), Kapitel 2, Abschnitt Rang.
Weitere Querverweise zum Rang: , Kurzbedeutung,
Epsilon-Rang,
Anmerkung: Den Rang kann man auch von Rohdaten bestimmen. Hierbei gilt für den Rang = Min(Zeilen-Rang, Spalten-Rang). Man sagt und es gilt auch, der Zeilen-Rang ist gleich dem Spaltenrang.
Die verschiedenen Korrrelations-Techniken
Matrix,
Zeilen und Spalten, Korrelationen der Spalten und der Zeilen
Eine Matrix ist eine Tabelle aus Zeilen und Spalten.
Sie kann quadratisch sein, wie die Korrelationsmatrix und sie kann rechteckig
sein wie gewöhnlich bei den Rohdatenmatrizen. Für Korrelationen
sollte bei den Rohwerttabellen gelten: Anzahl Zeilen > Anzahl Spalten.
Sind Zeilen und Spalten gleich, gibt es bei der Korrelationsmatrix
einen Rangverlust. Sind es weniger Zeilen z als Spalten s, so gilt, dass
bei der Korrelationsmatrix k=s-(z+1) Eigenwerte = 0 sind, also k
artefizielle Kollinearitäten vorliegen (Zeilenrang = Spaltenrang).
Allgemeine
Regel für den Standardfall Korrelation der Spalten
Die meisten Programme sind standardmäßig
so eingestellt, dass über den Zeilen die Spalten korreliert werden,
d.h. zum Standardfall gehört, dass die den Spalten zugeordneten Merkmale
über den in den Zeilen stehenden Merkmalen korreliert werden. Bei
Excel
(Beispiel) kann man z.B. einstellen,
ob die Spalten oder Zeilen korreliert werden. Um Verwirrungen zu vermeiden,
gibt man im Einzelfall am besten genau an, was man gemacht hat. Noch besser
ist es, die Rohwerttabellen so zu organiseren, dass es mehr Zeilen als
Spalten gibt und die Spalten korreliert werden.
Zeilen
und Spalten zugeordnete Merkmale können typische Untersuchungstypen
repräsentieren
Jenachdem welche Merkmale man Zeilen und Spalten
zuordnet, können sich jeweils typische Untersuchungstypen ergeben.
Besonders in den faktorenanalytischen Tradition haben sich folgende Prototypen
herausgebildet:
R-Technik: s Merkmale in Spalten, z Objekte (Personen) in Zeilen
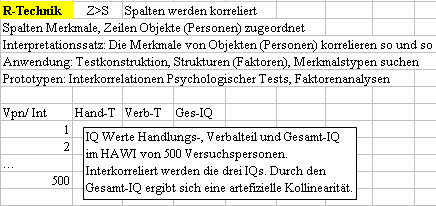
Q-Technik: s Objekte (Personen) in Spalten, z Merkmale in Zeilen
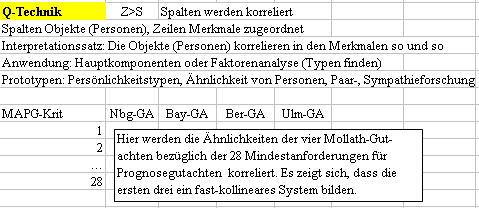
Beispiel: Die vier Mollath-Gutachter
aus Nürnberg, Bayreuth, Berlin und Ulm.
P-Technik: s Merkmale in Spalten, z Zeitkriterien in Zeilen
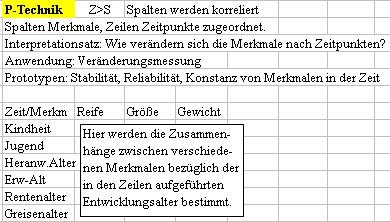
O-Technik. s Zeitcharakteristiken in Spalten, z Merkmale in Zeilen

S-Technik: s Objekte (Personen) in Spalten, z Zeitkriterien in Zeilen
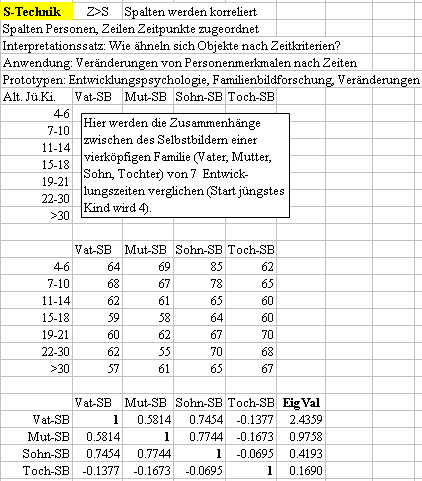
T-Technik: s Zeitkriterien in Zeilen, z Objekte (Personen) in Spalten

Geschichte der Korrelationsrechnung nach Baur (1928)


|
|
|
|
Pearson
|
Yule
|
Spearman
|
|
Gauß wird in der Geschichte der Korrelationsrechnung oft vergessen
zu erwähnen, dabei spielt ja die von ihm entwickelte Methode
der kleinsten Quadrate, die Fehler- und Ausgleichsrechnung
und
die Normalverteilung eine kaum zu überschätzende
und grundlegende Rolle für die Entwicklung der Korrelationsrechnung,
Testtheorie und Statistik.
Argumentationen und Interpretationen
Die Korrelation zwischen Inzidenzen-Impfquoten
Hypothese: Wenn Impfen vor Neu-Infektionen schützt, dann sollten Länder mit hohen Impfquoten geringere Inzidenzen aufweisen.

Gegen diese Hyopthese wurde eingewendet (Twitter 24.11.21): "Glaube ich gerne, frage mich nur wie sinnvoll es ist, Länder zu vergleichen die ggf an unterschiedlichen Punkten der Welle(n) sind." Genau das will man ja mit dem Inzidenz-Impfquotenvergleich untersuchen. Ist die Inzidenz niedrig, dann befindet sich die Welle auf niedrigem Niveau (niedrige Neu-Infektionszahlen), ist die Inzidenz hoch, dann befindet sich die Welle auf hohem Niveau (hohe Neu-Infektionszahlen). Hätten alle Länder das gleiche Wellen-Niveau, dann hätten alle gleiche Neu-Infektionszahlen pro 100.000 Einwohner, also gleiche Inzidenzen.
Seltsames, Merkwürdiges, Paradoxien und Kuriosa um die Korrelation
Spuriose Korrelationen und das Problem der
inhaltlichen Bedeutungsanalyse von Korrelationen
Grundsätzlich sollten Korrelationen hypothesenorientiert und theoriegeleitet
und nicht willkürlich und blind effektheischend sein wie in den meisten
der unten vorgestellten Fälle, die zeigen, dass extrem hohe Korrelationen
nahe 1 sein können, obwohl sie absurd anmuten, d.h. inhaltlich - zumindest
auf den ersten Blick - nichts bedeuten (> Beispiel Wissenschaftsausgaben
und Sucide). Damit stellt sich erneut (>Relevanter
Merkmalsraum) die Frage, wie man inhaltlich bedeutungsvolle bzw. bedeutungslose
Korrelationen finden und feststellen kann. Im allgemeinen haben StatistikerInnen,
WahrscheinlichkeitstheoretikerInnen und MathematikerInnen hierzu nichts
zu sagen und sie äußern sich dazu gewöhnlich auch nicht.
Inzwischen gibt es mehrere Seiten, die inhaltlich absurd erscheinende Korrelationen
zusammengestellt haben, z.B.:
- https://www.tylervigen.com/spurious-correlations
- https://www.tylervigen.com/sources
- https://scheinkorrelation.jimdofree.com/
Vigens "spurious correlations"
Beispiel Wissenschaftsausgaben und Sucide (Vigen) r=0.9979
Tyler Vigen, Jurist, ein höchst erfolgreicher Sammler von scheinbar
absurden (spuriosen = falschen) Korrelationen, teilt u.a. folgende extrem
hohe Korrelation zwischen Wissenschaftsausgaben und Suiziden mit:

Datenquellen: U.S Office of Management
and Budget and Centers for Disease Control & Prevention
Auf den ersten Blick erscheint die extrem hohe Korrelation unverständlich, weil man zwischen Wissenschaftsausgaben und Suiziden keinerlei Zusammenhang erkennen kann. Ein Brainstorming über mögliche Moderatorvariablen zeigt aber, dass es hier einige ernst zu nehmende Kandidaten gibt, nämlich:
- Wachstumszeitreihen (viele Wachstumszeitreihen korrelieren hoch bis extrem hoch)
- Wohlstand als verbindende Variable, er kann über das BIP bzw. das GDP (USA) geschätzt werden.
- Bevölkerungswachstum als gemeinsame Variable
- Mediale Aufbereitung von Wissenschaftsausgaben und Suiziden (Nachahmereffekte)
Es böte sich sich, die Korrelationen mit den hypothetischen Einflussgrößen neu zu rechnen, um die Einflüsse auszupartialisieren. Das würde aber nichts an der extrem hohen Korrelation, die praktisch eine lineare Abhängigkeit bedeutet, zwischen Wissenschaftsausgaben und Suiziden ändern. Auspartialiseren anderer Einflussgrößen kann erstens wegen der fast linearen Abhängigkeit der Ausgangskorrelation misslingen (>Anderson Warnung), indem zusätzlich unsinnige Werte resultieren, und zweitens nach dem Hain'schen Satz, dass die positive Definitheit bei Auspartialisieren alle gegen den Rest entgleisen kann. Wie man es auch dreht und wendet: es führt kein Weg daran vorbei, eine inhaltliche Korrelationstheorie zu entwickeln, damit man die reale Bedeutung einer Korrelation abschätzen kann und der Falle spurioser (falscher) Korrelationseffekte einigermaßen gewappnet gegenübersteht.
Falsche Interpretation des Klassikers
Storchennester und Geburtenraten
Vigens Interpretation, p. xii, des Klassikers
Storchennester
und Geburtenraten ist falsch, wenn erschreibt "Remember the correlation
between babies and storks? It was also coincidence" (Erinnern Sie sich
an die Korrelation zwischen Babys und Störchen? Es war auch Zufall).
Diese Scheinkorrelation war kein "Zufall", sondern durch die ("Moderator")
Variable Industriealisierung vermittelt. Man beachte auch die Anmerkung
Sachs. Kritisch bleibt anzumerken, dass die Quellenangaben eine Zumutung
sind (sowohl im Buch als auch auf der Quellen-Homepage).
Jeder Kenner der Materie weiß im Übrigen, dass Korrelation
und Kausalität zwei paar Stiefel sind, obwohl sie sich natürlich
nicht ausschließen. Trotz der wissenschaftlichen Mängel - auch
bei der Quellen "Dokumentation", ist die Arbeit durch ihre Popularität
dennoch verdienstvoll, weil sie sehr plastisch deutlich macht, dass eine
bloße rechnerische Korrelation inhaltlich
nichts besagen muss, was zweifelllos richtig ist.
Das Scheinkorrelations- und Partialisierungsparadox
Die merkwürdige Beliebigkeit der Korrelationskoeffizienten: Partielle Korrelationen
Ganz allgemein kann hier gesagt werden, dass die Möglichkeit der Partialisierung uns geradezu instand setzt, besondere Abhängigkeiten und Besonderheiten zu erkennen. So gesehen sollten dann aber auch Partialisierungen der wichtigsten Einflussquellen ausdrücklich in die Untersuchungen einbezogen und gerechnet werden.
Mit Nicht- & Linearitäts-Paradox des Korrelationskoeffizienten bezeichne ich einen dem Anschein nach nicht-linearen Zusammenhang im Schaubild oder im Werteverlauf, wobei der Korrelationskoeffizient aber einen sehr hohen bis vollkommen linearen Zusammenhang anzeigt (Beispiel 1a, Variante b), Empirisches Beispiel (Zusammehang Italien Anzahl Infizierter und Anzahl Todesfälle). Andererseits können auch eindeutig nicht lineare Zusammenhänge zu sehr hohen linearen Korrelationskoeffzienten führen (Beispiel 2). Und drittens können der Anschauung nach fast lineare Zusammenhänge zur Fast-Unkorreliertheit führen (Beispiel 3), durch Vertauschen zweier Werte wird die Korrelation +1 (Beispiel 4). Eine andere Doppel-Paradoxie zeigt Beispiel 5.
Beispiel 1 [Werte zum direkten Einlesen und nachrechnen]
Bei folgendem Graphen würde kaum jemand vermuten, daß hier eine lineare Korrelation von 1 vorliegt:
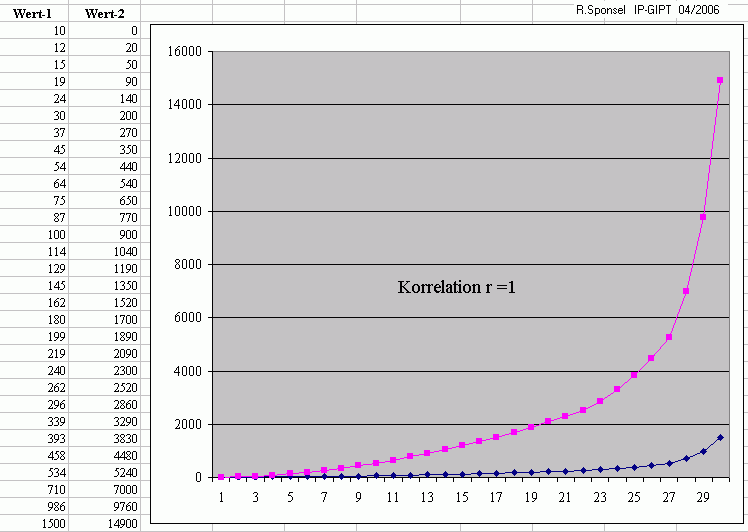
1b) Eine andere Variante aus Sponsel (2005, S. 35) mit r = 0.999999111
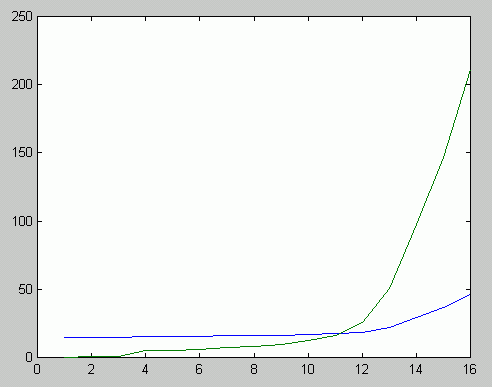 |
14.9138 14.9895 15.5672 15.6475 15.7055 15.8960 16.0851 16.3145 16.6591 17.2783 18.6461 22.3315 29.2784 36.5532 46.0904 |
0.490 1.000 4.890 5.460 5.810 7.120 8.340 9.850 12.190 16.410 25.460 50.400 97.600 146.500 211.010 |
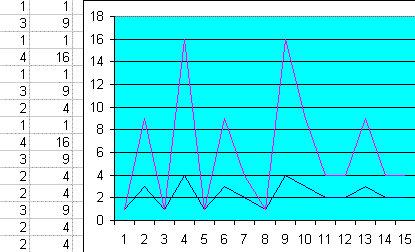
1c) Die Korrelationsmatrix der Partitionen von n=1,2,3, ... liefert ein konkretes Beispiel aus der kombinatorischen Zahlentheorie:
Man kann jede natürliche Zahl n aus Zahlen 1...n zusammengesetzt denken. Beispiel: 4 kann auf folgende Weisen zusammengesetzt werden: 1+1+1+1, 1+1+2, 1+3, 2+2, 4. Das heißt, die Anzahl aller Partitionen von 4 ist 5. Eine Ausarbeitung zur Anzahl aller Partitionen von n= 1,2,3, ... fanden Sie hier (URL geändert). Wir betrachten hier für unser Korreleationsbeispiel nur die Matrix der Anzahlen der Partitionen der natürlichen Zahlen von 1 bis 10:

Lesebeispiele: Die Zahl 3 kann aus 1+1+1, 2+1 und 3 zusammengesetzt werden. Es kommen also 4 Einsen in den Partitionen von 3 vor. In den Partitionen von 1, 2, 3, ...10 gibt es insgesamt 284 Einsen, das ergibt, nach dem insgesamt 538 Zahlen in den Partitionen vorkommen, einen Anteil von 52,79%. Die Zweien bringen es auf 114 mit einem Anteil von 21,19%. Man sieht, wie sich die Graphen exponentiell entwickeln.
Korrelationsmatrix
der Anzahl aller Partitionen n= 1,2,3, ... 10.
Hintergrund: Im September 2008 kam mir bei einem Spaziergang
die Idee, dass die allermeisten Summanden in Partitionen n= 1,2,3, ...
zunehmend aus 1 bestehen. Es sollte sich daher bei einer Faktorenenanalyse,
hier Hauptkomponentenmethode, ein Generalfaktor zeigen. Da ich nicht wusste,
ob und wie sehr das der Fall war, habe ich mir vorgenommen, ein überschaubares
Beispiel mal zu rechnen. Hier ist nun das Ergebnis:

Ergebnis: Die Korrelationsmatrix ist fast durchweg von sehr hohen Korrelationskoeffizienten nahe 1 belegt, was man der Datenmatrix so nicht "ansieht". Die Hauptkomponentenfaktorenanalyse zeigt einen einzigen großen ("übermächtigen") sog. "Generalfaktor", der - entsprechend dem größten Eigenwert - 97,553% der Varianz ausschöpft; ein Generalfaktor, der Spearman sicher begeistert hätte. Die Korrelationsmatrix hat - exakt betrachtet - Rang 9, "praktisch" aber Rang 1. Dass ein Eigenwert 0 ist bedeutet hier nur, dass eine artefizielle Kollinearität vorliegt, weil nämlich in der Korrelationsmatrix nur gleich viele Zeilen wie Spalten und nicht mehr gegeben sind (Faustregel: für empirische Korrelationsanalysen sollten wenigstens drei mal so viele Datensätze wie Variablen gegeben sein). Praktisch bedeutet dieses Generalfaktorergebnis, dass man die 10*10-Korrelationsmatrix ziemlich "gut" aus dem Generalfaktor F1 * F1' gewinnen kann:

Diskussion: Mich hat das Ergebnis in
dieser Ausprägung überrascht. Intuitiv-naiv hatte ich erwartet
für jede der Zahlen 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 einen Faktor zu
finden, und zwar, grob geschätzt, etwa in der Ausprägung wie
die Zahlen nach ihrer Häufigkeit vorkommen. Diese Idee wird durch
diese Auswertung nicht gestützt. Für n=10 kommen insgesamt 538
Summanden vor, davon 284 Einsen, das sind "nur" 52,79%, wie oben
mitgeteilt. Doch der Generalfaktor nimmt einen Anteil von 97,553% ein.
Sollte hier etwa eingehen, dass sich jede natürliche Zahl auf Einsen
zurückführen lässt? Doch woher sollte das die Datenmatrix
"wissen"? Das scheint doch ziemlich abwegig. Was also bedeutet dieser übermächtige
"Generalfaktor"? Ich deute derzeit, er spiegelt gar nicht die Anteile der
"Zahl-Faktoren" 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 wider, sondern die Gesetzmäßigkeit,
hier die lineare Abhängigkeit, die in der ganzen Partitionsmatrix
dieser
natürlichen Zahlenanordnung steckt; genau genommen stecken neben der
einen artefiziellen Kollinearität (nZeilen = mSpalten) noch 8 Fast-Kollinearitäten
in dieser n=10-Partitionsmatrix. Dieser Generalfaktor könnte daher
das Bildungsgesetz der Partitionierung von n = 1,2,3, ... bedeuten.
Beispiel 2
Obwohl hier y = x^2 gilt, y also funktional - genauer quadratisch und nicht linear von x abhängt - ergibt sich folgende merkwürdige sehr hohe "lineare" Korrelation von r = 0,9805.
Rohdaten, Korrelationen,
Matrix-Standard-Analyse und Faktorenanalyse (Generalfaktorbeispiel).
Beispiel 3 [siehe auch Reliabilitätsparadox]
Obwohl fast alle Werte gleich sind und damit ein Höchstmaß an anschaulicher linearer Korrelation enthalten, ist der lineare Korrelationskoeffizient mit r = - 0.034482759 infolge der geringen Streuung fast 0:

Beispiel 4
Vertauscht man die 99 und 100 "synchron", wird die Korrelation 1:

Beispiel 5 Pseudolinearer Anschein und Doppelparadox
Die folgende Matrix ist aus Werten zusammengesetzt, die zwischen 1 und 19 eine Korrelation von r = +1 und zwischen 20 und 159 eine Korrelation von r = -1 haben. Insgesamt ergibt sich eine positive Korrelation von r = 0,401. Obwohl die grobe Anschauung eine hohe positive Korrelation nahelegt, ergibt sich doch bei genauerer Betrachtung eher das Gegenteil. Eigentlich sollte man eine negative Korrelation erwarten, weil von den 160 Werten 141 eine vollkomme negative Korrelation haben (-1) und nur 19 eine vollkommen positive Korrelation (+1). Die negativen Alternationen überwiegen also bei weitem. Man sollte also eher eine negative Korrelation in der Größenordnung von r ~ - 0,40 erwarten, aber das Gegenteil ist der Fall.

Die
Werte aus Beispiel 5 zum Einlesen und nachrechnen.
Beispiel 6: Korrelation zwischen "Ehrenmorden" und medialer Präsentation. [von Quelle]
Auf den ersten Blick erscheint die Korrelation von 0.9528 für den Graph der beiden Kurven ungewöhnlich hoch. [mehr an der Quelle hier]
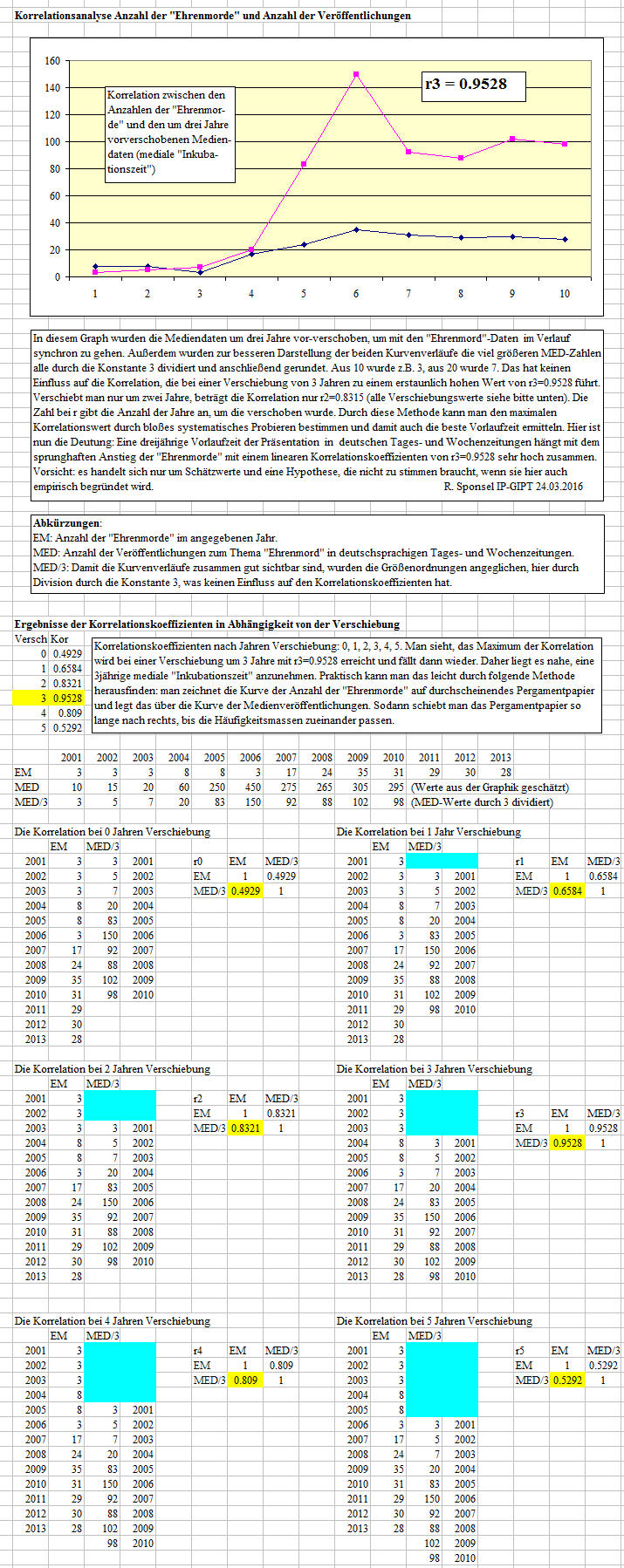
Das Größenordnungsparadoxon
| a
b
c
10.00006 10.00024 10.00095 10.00046 10.00014 10.00065 10.00033 10.00034 10.00035 10.00090 10.00083 10.00040 10.00045 10.00094 10.00080 10.00083 10.00023 10.00090 10.00014 10.00088 10.00005 10.00077 10.00036 10.00069 10.00029 10.00087 10.00052 10.00089 10.00022 10.00028 |
Erläuterung: Die drei Rohdatensätze
a, b. c liegen alle in der gleichen Größenordnung
um 10. Nach intuitiver Anschauung könnte man zwischen den drei Rohdatensätzen einen hohen Zusammenhang vermuten. Aber das Gegenteil ist der Fall. Man könnte sich die drei Rohdatensätze als durch Meßfehler hervorgegangen denken. Dann wären diese Meßfehler hier ein Beispiel für un- bis negativ korrelierte, wie die Korrelationsmatrix zeigt. |
Korrelationsmatrix
a b c a 1.0000 -0.1983 0.0179 b -0.1983 1.0000 -0.3336 c 0.0179 -0.3336 1.0000
|
Das Wachstumsparadox bei Zeitreihen
Das Wachstumsparadox scheint verwandt mit dem hier sog. "Linearitätsparadox". Hier kann man, besonders bei volkswirtschaftlichen Zeitreihen extrem hohe Korrelationen, ja viele (Fast-) Kollinearitäten [W], beobachten, die zumindest der Idee einer linearen Korrelation zuwiderlaufen. Ein vernünftig konstruierter linearer Korrelationskoeffzient sollte eigentlich kleiner werden, wenn die Linearität abnimmt. Da er das nicht tut, muss er also unabhängig von der tatsächlichen Linearität konstruiert sein. Das ist an sich kein grundsätzliches Problem, da man ja verlangen könnte, bevor mit dem Verfahren des linearen Korrelationskoeffizienten gerechnet wird, einen graphischen Test auf Linearität bzw. ganz allgemein auf Daten- Verteilungs- Angemessenheit durchzuführen.
Überhaupt kann an dieser Stelle angemerkt werden, dass es stets sinnvoll und zu empfehlen ist, sich die Daten in ihrem graphischen Verlauf anzuschauen, bevor man ihnen ein Modell unterlegt und rechnet.
Querverweise:
- Zur Multi-Kollinearität in der Ökonomie > Belsley et al.
- Die Zeit als Variable, Zeitdiagramme, Zeitreihenanalysen. Was bedeutet die Zeit als Variable? Was sagen Zeitdiagramme aus - oder sagen sie gar nichts aus? Zum grundlegenden Unterschied und Verständnis von Korrelation und Kausalität.
- Wachstum - Kritische Reflexionen zu einem äußerst fragwürdigen Konzept.
Ein Wachstumsparadox bei derAusbreitung des Corona-Virus [Quelle und hier ausführlich]
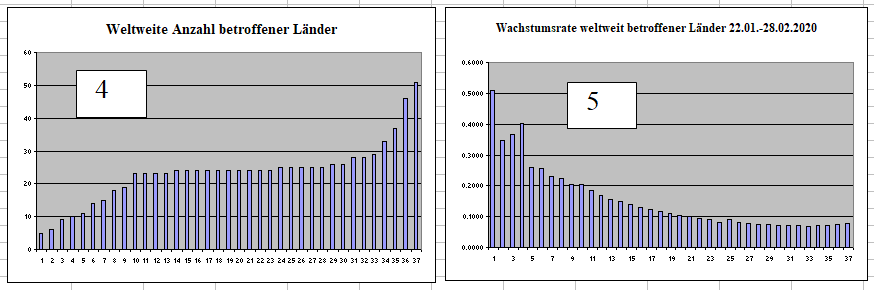
Obwohl die betroffenen Länder weltweit zunehmen (Graph 4), am 28.02.2020 bei 51 standen, nehmen die Wachstumsraten (Graph 5) der weltweit betroffenen Länder ab mit einer leichten Zunahme der letzten Tage. Obwohl also die absoluten Zahlen der betroffenen Länder zunehmen, nehmen die Wachstumsraten des Zuwachses ab. Das mutet paradox an und verlangt nach einer Erklärung. Nun, das ergibt sich schlicht und und einfach aus den Zahlen und der Wachstumsrechnung mit ihren drei Variablen (Endwert, Anfangswert, Anzahl der Zeiteinheiten). Es zeigt, man muss rechnen und grafisch darstellen und nicht meinen und phantasieren, um ein angemessenes Bild der Lage zu gewinnen.
Vergleich Korrelationen und Eigenwerte absoluter und logarithmierter Häufigkeiten am Beispiel Corona-Virus Ergebnis: Die Unterschiede zwischen den Korrelationen- und Eigenwerten ob auf absoluten Häugikeiten oder auf logarithmierten Häufigkeiten beruhend sind sehr gering und fallen praktisch nicht ins Gewicht.
Eine Logarithmus-Paradoxie ? [15.5.8]
Befund * Rechenbeispiel * Ergebnis * Brainstorming: 16.5.8,
Befund: Bei der multivariaten Untersuchung der Zeitreihen von 24 Wirtschaftsvariablen für den Zeitraum 1991-2007 ergab sich als eine Nebenfrage, wie sich die Korrelationskoeffizienten verändern, wenn man die Rohdaten LN-logarithmiert. Zu meiner Überraschung - und auch der zweier Mathematiker, denen ich das Ergebnis vorlegte - unterschieden sich die beiden Korrelationsmatrizen in den mittleren Abweichungsbeträgen nur um 0.02. Meine erste Idee war, dass dieser Befund durch die geringe Anzahl der Zeitreihe mit nur 17 Jahreswerten erklärt werden kann, weil sich der typische exponentielle Wachstumsverlauf erst nach einiger Zeit zeigt und am Anfang doch sehr einer Geraden ähnelt. Beide Kurven zeigen also bei den Anfangswerten einen sehr ähnlichen Verlauf. Dies sei am Beispiel der Staatseinnahmen illustriert:
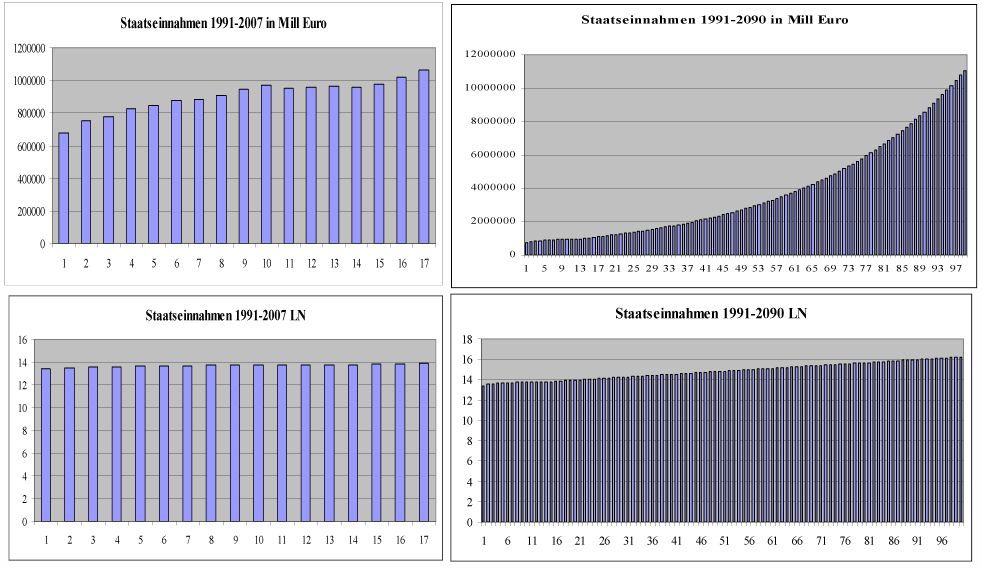
Rechenbeispiel: Die Korrelationskoeffizienten und ihre Abweichungen 1991-2007 bzw. 1991-2090 ergeben sich wie folgt:
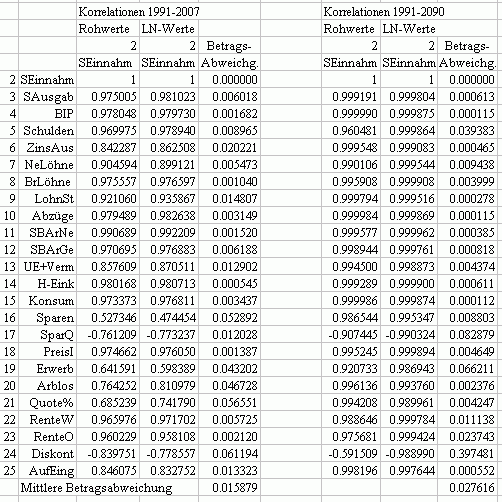
Ergebnis: Vergleicht man die Korrelationskoeffizienten - und ihre Abweichungen - der Rohdaten mit den LN-logarithmierten Rohdaten über eine Zeitreihe von 100 Jahren, hier 1991-2090, so zeigt sich im Schaubild ganz klar einmal der exponentielle Verlauf, wie wir ihn kennen und erwarten und beim Logarithmus eine näherungsweise Gerade. Trotzdem unterscheiden sich die Korrelationskoeffizienten am Beispiel Variable 2 Staatseinnahmen nur um den mittleren Abweichungsbetrag von 0.027616 der Zeitreihe 1991-2090 gegenüber der Zeitreihe 1991-2007 mit dem mittleren Abweichungsbetrag von 0.015879. Das ist für mich ein überraschender Befund mit einer gewissen Anscheinsparadoxie (für aufklärende Hinweise bin ich dankbar).
Brainstorming:
16.5.8: Gilt diese enge Beziehung der Korrelatiion
zwischen Daten und ihren Logarithmen nur bei Daten, die ein Wachstum bergen?
Lässt sich diese Idee sich durch ein einfaches Gegenbeispiel widerlegen,
z.B. indem man die Daten von Größe und Gewicht (oben)
hernimmt, logarithmiert und die Korrelationen vergleicht?
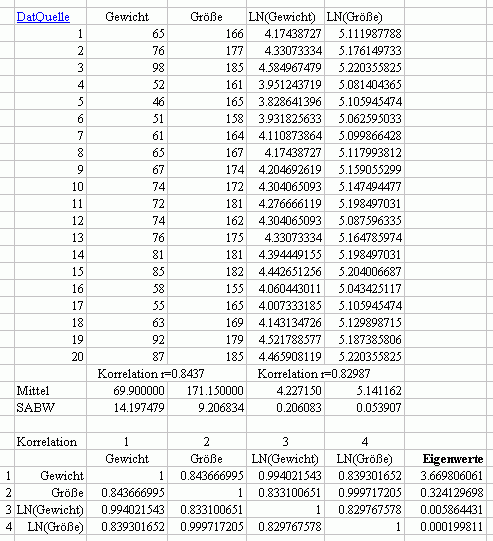
Das Beispiel liefert ein ähnliches Ergebnis wie die Wachstumstumswert-Zeitreihen,
sie könnten also auch als Wachstumszeitreihe interpretiert werden
und wären dann kein geeignetes (Gegen-) Beispiel. Tatsächlich
liefern die meisten Erhebungen von Körpergrößen und Körpergewichten
als Wachstum interpretierbare Daten. Das sieht man sofort, wenn man die
Werte der Größe nach sortiert, z.B. nach dem Gewicht: 46, 51,
52, 55, 58, 61, 63, 65, 65, 67, 72, 74, 74, 76, 76, 81, 85, 87, 92, 98.
Systematische Veränderungs Paradoxie
Alle systematischen Effekte, echte wie auch systematische Fehler [EN], bleiben bei der Korrelation verborgen, je mehr die systematischen Effekte konstant sind. Dies kann z.B. für eine Reliabilitätstheorie wie sie im Rahmen der sog. "klassischen" - besser naiven - psychologischen Testtheorie fatal sein, wie im folgenden Link durch Modellbildung bewiesen wird:
Ein Reliabilitätsparadox der numerologischen Testtheorie
Reliabilität bedeutet in der Testtheorie Zuverlässigkeit und Genauigkeit einer Messung. Man unterscheidet verschiedene Arten von Reliabilitäten, u.a.: Paralleltestreliabilität und Retestreliabilität (Testwiederholung). Nehmen wir an, wir haben einen Test, der 30 Fragen (Items) umfaßt und der bei einer Versuchsperson zu folgendem Ergebnis führt 1= Ja, 0= Nein):
Item: 123456789012345678901234567890
10 20
30
Tag1: 111111111111111111111111111110
Tag2: 111111111111111111111111111101
Wie man ohne besondere psychologische, statistische oder testtheoretische Kenntnisse sehen kann, sind beide Testreihen in 28 Fragen gleich bearbeitet, nur in den letzten beiden unterschiedlich. Man sollte also annehmen, dass die Korrelation zwischen beiden Testreihen sehr hoch ist, aus dem Bauch heraus wünscht man sich intuitiv eine Korrelation in der Größenordnung 28/30 = 0,93. Tatsächlich ergibt jedoch der Produkt- Moment- Korrelationskoeffizient (aufgrund der geringen Streuung, die die Werte zeigen) einen Wert von r = -0,034482759, behauptet also praktisch die Unkorreliertheit der Werte. Verdoppelt man die Testreihe auf 60 Fragen (Items) wird es auch nicht recht viel besser mit r = -0,016949153:
Item: 123456789012345678901234567890123456789012345678901234567890
10 20
30 40
50 60
Tag1: 111111111111111111111111111111111111111111111111111111111101
Tag2: 111111111111111111111111111111111111111111111111111111111110
| Man mag daher mit Fug und Recht bezweifeln, ob der lineare Produkt-Moment-Korrelationskoeffizient geeignet ist, die Reliabilität vernünftig zu schätzen. |
Die sog. "Attenuitäts-Korrektur" - correction of attenuation
Eine falsche "Korrekturformel" für den Korrelationskoeffzienten, 1904, durch Charles Spearman eingeführt, die zu Entgleisungen Kollinearität einer Korrelationsmatrix führen kann, weil sie einen unangemessenen (verzerrenden) Eingriff in die Relationen (> Relationentreue) der Korrelationsmatrix bedeuten kann (die Relationentreue verletzt), ist die "Attenuitäts-Korrektur".
Die Attenuitäts-Korrektur muss schon deshalb mathematisch falsch sein, weil sie Korrelationskoeffzienten außerhalb -1 <= r <= 1 zuläßt, so fand etwa Thorndike (1921, p. 147) einen "korrigierten" Koeffizienten von -2,56.
Das dahintersteckende praktische Motiv war wohl, die Korrelationskoeffizienten zu erhöhen. Das zumindest ist das praktische numerische Ergebnis dieser "Korrektur", die man nicht anwenden sollte.
Formel für die Attenuitäts-Korrektur (attenuation of correction):
r(ab) = r(ab)/ SQR [r(aa) * r(bb)]
mit:
r(ab) =: "wahre" Korrelation zwischen a und b, wenn die Messungen fehlerfrei erfolgen würden
r = Korrelationskoeffzient -1 <= r <= 1
r(aa) =: Reliabilitätskoeffizient von a
r(bb) =: Reliabilitätskoeffizient von b
SQR = Quadratwurzel
Beispiel
Die Korrelation zwischen Gedächtnisleistung G und Intelligenz I sei mit 0,68 angenommen. Die Reliabilität (Zuverlässigkeit, Genauigkeit) mit der die Gedächtnisleistung G gemessen werde, sei 0,91, die Reliabilität (Zuverlässigkeit, Genauigkeit) mit der die Intelligenz I gemessen werde, betrage 0,82. Eingesetzt ergibt sich:
r(ab) = 0,68 / [SQR(0,91 * 0,82)]
= 0,68 / SQR(0,7462)
= 0,68 / 0,86383
= 0,787
=====
Man sieht, dass sich durch die "Attenuitäts-Korrektur" der ursprüngliche Korrelationskoeffizient von "nur" 0,68 auf 0,787 erhöht, das sind relativ zum Ausgangswert immerhin 15,73%.
Ähnliche problematische oder falsche Korrekturkoeffizienten: multivariate correction for attenuation (Bock & Petersen) und Korrektur für kleine Stichproben (Olkin & Pratt 1958).
Spruch zum Thema: Und die Moral von der Geschicht? Korrigiere originale Daten nicht
Literatur zu den dubiosen "Verbesserungs- und Korrekturformeln". Spearman (1904); Thorndike 1921; Olkin, I. & Pratt, J. W. (1958); Cureton (1966); Bock, R. D. & Petersen, A. C. (1975). Kritisch: Sponsel 1994.
Ansätze einer inhaltlichen Korrelationstheorie - Interpretation von Korrelationen
Zusammenhänge können mehr oder minder echt oder unecht sein. Daher braucht man, um ganz allgemein einen Zusammenhang zu verstehen, wozu die Korrelation gehört, eine Theorie, aus der sich der Zusammenhang erklären und begründen lässt. Zur Interpretation von Korrelationen braucht man also zwei Theorien: eine Theorie des korrelativen Zusammenhanges und eine Theorie der korrelativen Echtheit, genauer: Echtsbedeutung, weil, wie Sachs kritisch bemerkt, die Korrelation als solche ja besteht. Ein allgemeines Modell für einen Zusammenhang Z(x,y) zwischen den Variablen x und y kann z.B. wie folgt formuliert werden: Z(x,y) = f (U1, U2, ..., Ui, .... Un), wobei die U hier unterschiedliche Ursachen-Einflussgrößen symbolisieren. Ist der Zusammenhang Z(x,y) eine Korrelation K(x,y), so sind in der Regel Werte zwischen -1 bis +1 möglich. Für ein r(x,y)=0.62 könnte z.B. das lineare Ursachen-Modell gelten U1= 0.26, U2= 0.18, U3=0.12 und U4=0.06. Nimmt man als anschauliches Beispiel einen Quader mit Länge L=4, Breite B=3 und Höhe H=1, kann man die Theorie aufstellen, dass das Volumen zu 4/8 von der Länge, zu 3/8 von der Breite und zu einem 1/8 von Höhe verursacht wird. Eine Hauptkomponenten- oder Faktorenanalyse hilft hier nicht weiter, weil diese nur die inneren Komponenten oder Faktoren erfasst. Hier geht es aber um äußere Ursachen (U).
Zusammenhangsprüfung
Hier ist zu begründen, welcher inhaltliche Zusammenhang zwischen
x und x bestehen. So lässt sich z.B. der inhaltliche Zusammenhang
zwischen Fußgröße und Körpergröße durch
den allgemeinen Satz begründen, dass die Teile größer werden,
wenn das Ganze oder andere Teile größer werden. Infektionszahlen
steigen, wenn die Kontakte nicht verringert werden, weil die Infektion
über Kontakt erfolgt. Wachsende Zeitreihen haben das Wachsen gemeinsam.
Echtheitsprüfung
Ob eine Korrelationsbedeutung "echt" ist oder nicht, kann schwierig
herauszufinden sein (>relevanter
Merkmalsraum). Hilfreich kann hier sein, über einen klaren Zufallsbegriff
zu verfügen. Eine oft anwendbare Methode besteht aber oft in der
partiellen
Korrelationsanalyse. Verändert sich ein korrelativer Zusammenhang
zwischen x und y nicht oder nur unwesentlich, wenn man z auspartialisiert,
kann man sagen, dass z keinen nachweisbaren Einfluss auf die Korrelation
zwischen x und hat. Die Einbeziehung weiterer Variablen ist ein großes
Thema in der Korrelationsstatstik (Lazarsfeld 1955, Die Interpretations
statistischer Beziehungen, übersetzt in (1-15) Hummel & Ziegler
Korrelation
und Kausalität, Bd. 1.
Literatur (Auswahl) > Siehe bitte auch (überlappende) Literaturliste Autokorrelation und Literaturliste Die Zeit als Variable (überlappend).
- Aldrich, John (1995). Correlations Genuine and Spurious in Pearson and Yule. Statistical Science, Vol. 10, No. 4 (Nov., 1995), 364-376. [Abs]
- Anderson, Oskar (1954). Probleme der statistischen Methodenlehre in den Sozialwissenschaften. Würzburg: Physica. [enthält ein ausführliches Kapitel zur Korrelation und geht auf die Tücken und Fallen bei der Partialisierung ein]
- Bartel, Hans (1974). Korrelationen. In: Statistik I, 79-111. Stuttgart: Gustav Fischer.
- Baur, Franz (1928). Korrelationsrechnung. Mathematisch-Physikalische Bibliothek. Leipzig: Teubner. [historisch]
- Belsley, David A.; Kuh, Edwin & Welsch, Roy E. (1980). Regression Diagnostics: Identifying Influential Data and Sources of Collinearity. New York: Wiley. [Den Ökonomen sind die Probleme mit der (Multi-) Kollinearität im Gegensatz zu den meisten PsychologInnen wohlvertraut]
- Betz, W. (1911). Über Korrelation. Methoden der Korrelationsrechnung und kritischer Bericht über Korrelationsuntersuchungen aus dem Gebiete der Intelligenz, der Anlagen und ihrer Beeinflussung durch äußere Umstände. Beihefte zur Zeitschrift für angewandte Psychologie und psychologische Sammelforschung. Leipzig: Barth. [mit umfassenden Literaturverzeichnis, historisch]
- Bock, R. D. & Petersen, A. C. (1975). A multivariate correction for attenuation. Biometrika, 62,3, p. 677. [Anmerkung: die "true correlation matrix" verliert ihre positive Definitheit und produziert einen negativen Eigenwert, dokumentiert in Sponsel 1994, Kap. 9]
- Bravais, A. (1846). Analyse mathématique sur les probabilités des erreurs de situation d`un point. Mém. prés. par divers savants à l`Acad. des sciences de l`Inst. de France, 2. Serie, 9, p. 255-332. [historisch]
- Clauß, G. & Ebner (1982). Statistik. Für Soziologen, Pädagogen, Psychologen und Mediziner. Band 1 Grundlagen. Frankfurt: Deutsch.
- Cureton, Edward E. (1966). Corrected Item-Test Correlations. Psychometrika 31,1,93-96. [mit "Verbesserungs- bzw. Korrekturformeln für die Item-Test-Reliabilität"]
- Cureton, Edward E. (1966). On Correlation Coefficients. Psychometrika 31,4,605-607. [mit "Verbesserungs- bzw. Korrekturformeln"]
- Eisenreich, G. (1991). Korrelationen. In: Lineare Algebra und analytische Geometrie. Berlin: Akademie, S. 286.
- Encyclopedia of Statistical Science (1982). Correlation. Vol. 2, pp. 195-204. New York: Wiley.
- Fisher, Ronald A. (1925). Statistical Methods for Research Workers. Edinburgh: Oliver & Boyd. [Online]
- Fisher, Ronald A. (dt. 1956). Der Korrelationskoeffizient. In: Statistische Methoden für die Wissenschaft. Edinburgh: Oliver and Boyd. Seiten 176-211.
- Galton, Francis (1886). Family likeness in stature. ProcRoSoc 40, p. 42 [historisch]
- Galton, Francis (1888). Head growth in students at the University of Cambridge. In: Nature 38, pp. 14-15 [historisch]
- Galton, Francis (1888). Correlations and their measurement. [historisch]
- Hain, Bernhard (1994). Bemerkungen über Korrelationsmatrizen. Kap. 6 in: Sponsel, Rudolf & Hain, Bernhard (1994). Numerisch instabile Matrizen und Kollinearität in der Psychologie. Diagnose, Relevanz & Utilität, Frequenz, Ätiologie, Therapie. Ill-Conditioned Matrices and Collinearity in Psychology. Deutsch-Englisch. Übersetzt von Agnes Mehl. Erlangen: IEC-Verlag.
- Hummell, Hans J. & Ziegler, Rolf (1976, Hrsg.) Korrelation und Kausalität. 3 Bde. [Reader] Stuttgart: Enke.
- Karrenberg, U. (2012) Signale - Prozesse - Systeme. Eine muldimediale und interaktive Einführung in die Signalverarbeitung. 6. A. Berlin: Springer. Anmerkung: Eingegliedert ist DASYLab 11, eine speziell für den Lernen entwickelte Software der Messdatenerfassung und Messdatenanalyse, so dass viele Beispiele in dem Buch hiermit gerechnet und anschaulich dargestellt werden können.
- Koller, Siegfried. (1962). Typisierung korrelativer Zusammenhänge. Metrika, 65-75. [enthält systematisch hierarchische Abfrage zur Deutungsanalyse] [Digital]
- Koller, Siegfried (1971). Mögliche Aussagen bei Fragen der statistischen Ursachenforschung. Metrika 17, 30-42.
- Münzner, H. (1936). Grundbegriffe und Probleme der Korrelationsrechnung. Deutsche Mathematik, 1, 290-.
- Olkin, I. & Pratt, J.W. (1958). Unbiased Estimation Of Certain Correlations Coefficients. The Annals of Mathematical Statistics, Vol. 39, 201-211. [Studie zu den Folgen in Sponsel 1994, Kap. 7.10. Die num. Stabilität nimmt zu und kein Eigenwert entgleist negativ]
- Quenouille, M.H. (1957). The Analysis of Multiple Time Series. Griffins Statistical Monographs 1.
- Pearson, Karl (1901). On the Correlation of Characters not Quantitatively Measurable. Philosophical Transactions Of The Royal Society Of London. Series A. Vol. 195, I. Mathematical Contributions to the Theory of Evolution - VII, pp. 1-47. [historisch]
- Revenstorf, Dirk (1979) Zeitreihenanalyse für klinische Daten. Methodzik und Anwendungen. Weinheim: Beltz.
- Schlittgen, Rainer & Streitberg, Bernhard H.J. (1984) Zeitreihenanalyse. München: Oldenbourg.
- Schmitz, Bernhard (1987) Zeitreihenanalyse in der Psychologie. Verfahren zur Veränderungsmessung und Prozeßdiagnostik. Weinheim: Beltz.
- Schlosser, Otto (1976). Einführung in die sozialwissenschaftliche Zusammenhangsanalyse. Reinbek: Rowohlt.
- Spearman, Charles (1904). The proof and measurement of association between two things. American Journal of Psychology 15, pp. 88 (formula p.90).
- Sponsel, R. (1984) Lebens- und Selbstzufriedenheit als Psychotherapieerfolgskontrolle. Praktische Systematik psychologischer Behandlungsforschung. Dissertation, Erlangen: IEC-Verlag. [Enthält viele Regressions-, Korrelations- und partielle Korrelationsstudien, sowie Dokkumentation einer indefiniten Entgleisung, Ausgangpunkt für die Eigenwert- und Fast-Kolloinearitätsanalysen]
- Sponsel, R. (1994). Numerisch instabile Matrizen und Kollinearität in der Psychologie. Diagnose, Relevanz & Utilität, Frequenz, Ätiologie, Therapie. Ill-Conditioned Matrices and Collinearity in Psychology. Deutsch-Englisch. Übersetzt von Agnes Mehl. Kapitel 6 von Dr. Bernhard Hain: Bemerkungen über Korrelationsmatrizen. Erlangen: IEC-Verlag [ISSN-0944-5072 ISBN 3-923389-03-5].
- Sponsel, R. (2005). Fast- Kollinearität in Korrelationsmatrizen mit Eigenwertanalysen erkennen. Erlangen: IEC-Verlag.
- Thorndike, E. L. (1921). On The Organization Of Intellect. Psychological Review XXVIII, p. 147. Bemerkung: Die kleine Matrix der Ordnung 7 enthält zwei stark negative Eigenwerte.
- Tschuprow, A.A. (1925). Grundbegriffe und Grundprobleme der Korrelationsrechnung. Leipzig: Teubner. [mit umfassendem und kommentiertem Literaturverzeichnis, historisch]
- Vigen, Tyler (2015) Spurious correlations. Correlation does not equal Causation. New York: Hachette. [Anmerkung: Die Quellenangaben sind eine Zumutung]
- Yule, G.U. (1926). Why do we sometimes get nonsense-correlations between time series? Journal of the Royal Statistical Society, 89, 1-64.
Links (Auswahl)
- Die Erfindung des Galton-Brettes und die Entwicklung des Konzeptes der Korrelation: http://www.galton.de/Kap1_2_4.htm
- Gregor Brand: Gehirngröße und Intelligenz: http://www.loni.ucla.edu/~thompson/MEDIA/NN/gb_nn.htm
- Joachim Funke: Intelligenz: Die psychologische Perspektive: http://www.psychologie.uni-heidelberg.de/ae/allg/mitarb/jf/intelligenz.pdf
Glossar, Anmerkungen und Endnoten
1) GIPT= General and Integrative Psychotherapy, internationale Bezeichnung für Allgemeine und Integrative Psychotherapie.
___
Beispiel excel

__
Definitheit
bei quadratischen Formen. Wir übernehmen von Eisenreich, G. (1991).
Lineare Algebra und analytische Geometrie. Berlin: Akademie, S.258,
folgende Sprachregelung: "Eine quadratische Form ist genau dann positiv
definit, wenn sämtliche Eigemverte positiv sind; sie ist genau dann
positiv semidefinit, wenn sämtliche Eigenwerte >=0 sind; sie ist genau
dann negativ definit, wenn ihre samtlichen Eigenwerte negativ sind; und
sie isl genau dann negativ semidefinit, wenn sämtliche Eigenwerte
<=0 sind. Schließlich ist die Form genau dann indefinit, wenn
sie sowohl positive als auch negative Eigenwerte besitzt."
__
Die Werte
aus Beispiel 5 zum Einlesen und nachrechnen:
1 1 -9 21 0 1 41 0 1 61 0 1
81 0 1 101 0 1 121 0 0 141 0 1
2 2 -8 22 1 0 42 1 0 62 1 0
82 1 0 102 1 0 122 1 0 142 1 0
3 3 -7 23 0 1 43 0 1 63 0 1
83 0 1 103 0 1 123 0 1 143 0 1
4 4 -6 24 1 0 44 1 0 64 1 0
84 1 0 104 1 0 124 1 0 144 1 0
5 5 -5 25 0 1 45 0 1 65 0 1
85 0 1 105 0 1 125 0 1 145 0 1
6 6 -4 26 1 0 46 1 0 66 1 0
86 1 0 106 1 0 126 1 0 146 1 0
7 7 -3 27 0 1 47 0 1 67 0 1
87 0 1 107 0 1 127 0 1 147 0 1
8 8 -2 28 1 0 48 1 0 68 1 0
88 1 0 108 1 0 128 1 0 148 1 0
9 9 -1 29 0 1 49 0 1 69 0 1
89 0 1 109 0 1 129 0 1 149 0 1
10 10 0 30 1 0 50 1 0 70 1 0
90 1 0 110 1 0 130 1 0 150 1 0
11 11 1 31 0 1 51 0 1 71 0 1
91 0 1 111 0 1 131 0 1 151 0 1
12 12 2 32 1 0 52 1 0 72 1 0
92 1 0 112 1 0 132 1 0 152 1 0
13 13 3 33 0 1 53 0 1 73 0 1
93 0 1 113 0 1 133 0 1 153 0 1
14 14 4 34 1 0 54 1 0 74 1 0
94 1 0 114 1 0 134 1 0 154 1 0
15 15 5 35 0 1 55 0 1 75 0 1
95 0 1 115 0 1 135 0 1 155 0 1
16 16 6 36 1 0 56 1 0 76 1 0
96 1 0 116 1 0 136 1 0 156 1 0
17 17 7 37 0 1 57 0 1 77 0 1
97 0 1 117 0 1 137 0 1 157 0 1
18 18 8 38 1 0 58 1 0 78 1 0
98 1 0 118 1 0 138 1 0 158 1 0
19 19 9 39 0 1 59 0 1 79 0 1
99 0 1 119 0 1 139 0 1 159 0 1
20 1 0 40 1 0 60 1 0 80 1 0
100 1 0 120 1 0 140 1 0 160 1 0
__
numerologische Testtheorie.
[Numerologie]
Das Spiel mit Zahlen [1,2,3,4,5,6,7]
und Mathematik ist nirgendwo sachungemäßer und regelrecht falsch
verbreitet als in der sog. psychologischen, zu allem Überfluß
meist auch noch völlig zu Unrecht so genannten "klassischen" Testtheorie,
die an Hollywoodmechanismen, Hochstapler,
Gaukler, Fälscher und Betrüger gemahnt. Seit wann verdienen
Gaukler den Ehrennamen "Klassiker"? So findet der größte Wissenschaftsbetrug
in den Sozialwissenschaften in der Verkleidung angeblicher Exaktheit statt.
Mittlerweile herrschen wohl schlimmere Verhältnisse als im Frankreich
des 19. Jahrhunderts, als der angesehene Mathematiker Joseph Bertrand [W]
gegen das pseudowissenschaftliche Gauklertum in mathematisch- statistischer
Verkleidung erfolgreich zu Felde zog. Das Zentrum der pseudowissenschaftlichen
Scheinmessungen, Irrtümer und Fälschungen, sitzt in den USA und
hier zentral lokalisiert in der Zeitschrift "Psychometrika".
Dunlap sprach zum 25-jährigen Jubiläum mehr ironisierend als
selbstkritisch von "PSYCHOMETRICS - A SPECIAL CASE OF THE BRAHMAN THEORY"
(Psychometrika 26,1,1961, p.65). Er ahnte wohl nicht, wie sehr er damit
ins Schwarze traf. Dort hat man sich entschlossen, wie weiland in der Scholastik
und im Mittelalter, Naturgesetze und wissenschaftliche Erkenntnisse zu
"beschließen", zu "meinen" und mit Veröffentlichungs-Macht eine
falsche Wirklichkeit vorzugaukeln, allen voran die sog. "Elite- Universitäten",
die zu Beginn dieses Jahres (2004) auch hierzulande so falsch als nacheifernswert
dargestellt werden.
__
Eigenwerte
nicht negativ. Das ist bei fast- kollinearen Korrelationsmatrizen im
Zusammenhang mit Rundungsfehlern nicht immer der Fall, daher müssen
dann vor multivariater Weiterverarbeitung solche indefiniten, mathematisch
nicht korrekten ("phänotypischen") Korrelationsmatrizen, erst richtig
eigenwert-"therapiert" werden. Das bedeutet praktisch, daß die negativen
Eigenwerte beseitigt werden müssen. Hierzu gibt es eine ganze Reihe
von Methoden, z.B.: (1) bei sehr kleinen negativen Eigenwerten diese
0 setzten; (2) bei nicht so kleinen negativen Eigenwerten diese 0 setzen
und die Korrelationsmatrix nachskalieren; (3) SVD - Singulärwertzerlegung;
(4) Faktorenanalyse mit der Centroid-Methode durchführen; (5) Eliminationsmethode
Variable (fast- kollineare Vektoren) entfernen; (6) TIKHONOV-Regularisierung
(Ridge-Methode), (7) KNOL & TEN-BERGE Methode. (mehr und Literatur
in Sponsel
1994, Kap. 5).
__
Fehler. In der numerologischen Zauberwelt
der Fehler- und Ausgleichsrechnung scheinen systematische Fehler keine
Rolle zu spielen, wie ihre Grundgleichung EW = T + e oder Empirischer Wert
= Wahrer Wert (T) plus zufälliger Fehler (e) in der verdeckten
Bedeutung von e (zufälliger, normalverteilter Fehler) gewöhnlich
gedeutet wird. Das zumindest ist die häufigste - und meist falsche
- Deutung in der mathematisch- statistischen Testtheorie, wenn das Modell
auch in vielen naturwissenschaftlich- technischen Anwendungen sich bewähren
mag. Tatsächlich kann und muß man auch in den meisten Fällen
e weiter differenzieren, etwa e = f(v, s, z) mit v =: Verfahrensfehler-Meßbereich,
s =: systematische Fehler und z =: zufällige Fehler. Dies würde
allerdings bedeuten, dass man richtig denken, forschen und begründen
muss und nicht mehr so einfach sagen könnte: die Fehler mitteln sich
bei Normalverteilungsannahme heraus und brauchen daher nicht weiter berücksichtigt
zu werden.
__
Kapitel
6, S. 20 ff in: Sponsel, Rudolf & Hain, Bernhard (1994). Numerisch
instabile Matrizen und Kollinearität in der Psychologie. Diagnose,
Relevanz & Utilität, Frequenz, Ätiologie, Therapie.
Ill-Conditioned Matrices and Collinearity in Psychology. Deutsch-Englisch.
Übersetzt von Agnes Mehl. Kapitel 6 von Dr. Bernhard Hain: Bemerkungen
über Korrelationsmatrizen. Erlangen: IEC-Verlag [ISSN-0944-5072
ISBN 3-923389-03-5]. Aktueller Preis:
www.iec-verlag.de. Informativ zum Begriff Kollinearität.
__
Korrelationen
nach Eisenreich.

__
Ökonomische Zeitreihen
Speth, Hans-Theo (2004) Methodenberichte Heft 3. Komponentenzerlegung
und Saisonbereinigung ökonomischer Zeitreihen mit dem Verfahren BV4.1.
Statistisches Bundesamt, Gruppe Mathematisch-statistische Methoden. Wiesbaden.
[PDF]
S.4:

Prüfverfahren, ob ein lineares Korrelationsmodell angemessen ist. In meiner nun einige Jahrzehnte zurückliegenden Statistikausbildung wurde der Frage, wie man denn prüfen kann, ob man das Modell des linearen Korrelationskoeffizienten anwenden darf, keine Aufmerksamkeit gewidmet. Dabei ist diese Frage nicht weniger wichtig wie z.B. die Frage der Prüfung, ob sich Daten normal verteilen als Voraussetzung dafür, einen Test anzuwenden, der eben eine Normalverteilung voraussetzt. Verallgemeinert kann man sagen: Im Prinzip ist immer zu begründen und zu rechtfertigen, ob eine bestimmte Modellwahl die Voraussetzungen erfüllt. Bei der linearen Korrelationskoeffzienten-Rechnung stellt sich daher die Grundfrage: liegt überhaupt Linearität vor, ist das Modell des linearen Korrelationskoeffizienten angemessen? Wie stellt man also fest, ob Linearität vorliegt?
Der einfachste Test ist wie oben schon veranschaulicht die graphische Darstellung der Daten. Gibt es k Regressionsfunktionen, so ist numerisch formal diejenige die Beste, deren Abweichungen (Abweichungsquadrate) am kleinsten sind. Man wird daher sinnvollerweise so vorgehen, dass erst grob eingegrenzt wird, welcher Typus von Regressionsfunktion der Anschauung nach in Frage kommt. So bietet sich etwa im Schaubild d) Abb.5 eine Parabel vom Typ y=ax^2 + b an.
__
quadratische (Bilinear-) Formen und symmetrischen Matrizen:
http://www.mi.informatik.uni-frankfurt.de/teaching/lecture_notes/schnorr.lineareAlgebra.pdf
Quadratische Form: Wikipedia, Definitheit, .
Bilinearform: Bilinearform (Wikipedia), .
Symmetrische Matrizen: Wikipedia, .
Eigenwerte: Wikipedia, .
__
routinemäßig. Zu Thurstones Zeiten mußte man evtl. noch ein 1/4 Jahr - eine beachtliche Leistung - oder länger rechnen, dafür kannten die Pioniere der Faktorenanalyse meist ihre Daten und konnten durch einen kundigen Blick auf die graphische Darstellung die Rotation interpretationsförderlich einrichten.
__
Sponsel 1984, S. 213 (auch CST-System 03-07,8-35-01): "Der Regelfall der Empirie ist, daß viele Zusammenhänge zwischen den Variablen durch einen Verbund, durch Vermittlung mit anderen Variablen zustande kommen. Damit stellt sich das Deutungsproblem verschärft. Im Grunde erhebt man mit einer Korrelation nicht notwendig den Zusammenhang zwischen a und b, sondern den Zusammenhang zwischen a und b und der mit a und b verbundenen Variablen. Will man also die echten Zusammenhänge zwischen a und b kennen, so muß man partialisieren. (Weber 1967, Kapitel 51; Hays 1973, ch. 16.20; Kriz 1978, 9.1; Sachs 1978, Kapitel 58; Guilford 1950, p. 345). "
__
systematischen Untersuchung zu "Korrelationsmatrizen": "1.5.1 Allgemeines. Als ich anfing, "Korrelationsmatrizen zu sammeln", ahnte ich nicht, auf was ich mich da eingelassen habe. Oft war gar nicht angegeben, welcher Koeffizient angewandt wurde. Auch die Mitteilung des Stichprobenumfanges ist meist Glückssache. Missing Data Informationen werden praktisch fast nie mitgeteilt. Die Stellengenauigkeit ist nichtssagend. Mit welcher Eingangsdatengenauigkeit gerechnet wird, erfährt man nie. Auch nicht, wie weitergerechnet und wie gerundet wird. Die Fachzeitschriften werden offensichtlich von Leuten redigiert, die die Zahlen selbst nicht ernst nehmen und wohl mehr den illustrativen Charakter im Sinn haben nach dem Motto, dass zu einer "wissenschaftlichen" Veröffentlichung auch ein paar Zahlen gehören. Selbst die PSYCHOMETRIKA glänzt durch eine Schlampigkeit, dass man sich nur wundern kann. Dazu passt dann auch, dass sich die schlimmsten Korrelations-Matrizen gerade dort finden, wo man es niemals für möglich gehalten hätte: ebenda. Ist "korrigiert" worden, wie, wozu? - Fragen, auf die man so gut wie nie eine Antwort erhält. Druckfehler noch und noch. Ohne jede Vorwarnung oder Erläuterung wird gemittelt. All das hat die richtige Erfassung der Matrizen so erschwert, dass sich die Zusammenstellung einer aussagefähigen Stichprobe und die statistische Analyse der numerischen Kriterien um zwei Monate verzögert hat.
1.5.2 Die verschiedenen Koeffizientenfamilien. Es gibt viele Assoziationsmasse, Korrelationskoeffizienten im weiteren Sinne, die jeweils zu einer Matrix angeordnet werden können. So stellt sich die Frage, wie man diese vielen Koeffizienten ordnen kann oder sollte. Was als Korrelationsmatrix im genuinen, originären Sinne anzusehen ist, wurde in 1.4.1 ausgeführt. Jetzt geht es aber darum, die empirisch vorgefundenen Matrizenrechnungen zu erfassen. Eine gewisse systematische Ordnung wäre die nach dem vorausgesetzten Skalenniveau. Demnach ergäbe sich folgende Einteilung: Ordnung nach [dem meist vorausgesetzten] Skalenniveau der Datenwerte: (1) Masskorrelations-Familie. (2) Rangkorrelations-Familie. (3) Kontingenzkoeffizienten-Familie" (Aus).
Hinweis: Einfache Berechnung der multiplen Korrelationen nach Tucker et. al. Aber Vorsicht: Ist die Matrix nicht semipositiv definit, so enthält die Haupdiagonale negative Einträge und es entgleisen nach der Tucker et al.-Methode die multiplen "Korrelationskoeffizienten" bis in den zweistelligen Bereich hinein.
__
Widerspruch (Antinomie), Aporie, Paradoxie, Pseudo-Paradoxie.
Antinomie. Ein echter Widerspruch (Russellsche Antinomie der Mengen aller Mengen, die sich nicht selbst als Element enthalten; Widerspruch Datenreduktion Faktorenanalyse und Reproduzierbarkeit der Ursprungsmatrix, wenn nicht wenigstens ein Eigenwert nahe 0 ist. Ist das nicht der Fall, kann man mit einer Faktorenanalyse zwar die Daten reduzieren, aber nur um den Preis, dass sie dann nicht mehr die ursprünglichen Daten repräsentieren, man hat durch einen methodologischen Beschluß virtuell neu skaliert, ohne es konsequent und logisch an den Rohdaten zu vollziehen.).
Aporie. Etwas erwiesenermaßen Unlösbares (Quadratur des Kreises, Gödel'sche Sätze; Heilmittelaporie in der Psychotherapie).
Paradoxie. Eine absurd oder widersinnig erscheinende Aussage, gegen die sich der Verstand sträubt, ohne zwingend falsch zu sein (Beispiel: Nach Cantor sind |N und |Q gleichmächtig, obwohl es offensichtlich mehr rationale als natürliche Zahlen gibt; Lit: Basieux (2000). Top Ten, S. 111).
Pseudo-Paradoxie (Sophismen: Zenons Achilles und die Schildkröte, Lügner-Problem).
Siehe bitte auch: [1, 2,]
Lit: Meschkowski, Herbert (1963, 1969, 1979). Paradoxie und Antinomie. Natur und Geist, Frankfurt 1963. Rektoratsrede "Der Monat" 169; 1969. Wissenschaft und Bildung, Weinheim 1969. In: Mathematik und Realität, Mannheim 1979, 9-19.
___
Werte zum direkten Einlesen und nachrechnen:
Wert-1 Wert-2
10 0
12 20
15 50
19 90
24 140
30 200
37 270
45 350
54 440
64 540
75 650
87 770
100 900
114 1040
129 1190
145 1350
162 1520
180 1700
199 1890
219 2090
240 2300
262 2520
296 2860
339 3290
393 3830
458 4480
534 5240
710 7000
986 9760
1500 14900
___
[Besonderheiten:
Tetraedenrelation: http://www2.gsu.edu/~mkteer/relmeth.html]
Standort: Korrelation.
*
| Suchen in der IP-GIPT,
z.B. mit Hilfe von "google": <suchbegriff>
site:www.sgipt.org
z.B. Korrelation site:www.sgipt.org. |
Korrelation und Kausalität - Modelle und Methoden. Ursachen und Wirkungen in Korrelationsmatrizen
mit Eigenwert- und Fast-Kollinearitätsanalysen auf die Spur kommen
Aus gleichen Eigenwerten unterschiedliche Korrelationsmatrizen erzeugen.
Zu gleichen Korrelationsmatrizen unterschiedliche Rohwerte erzeugen.
(Semi) Indefinite Pseudo-Korrelationsmatrizen.
Einfache Berechnung der multiplen Korrelationen nach Tucker et. al.
Überblick Statistik in der IP-GIPT.
Fast- Kollinearität in Korrelationsmatrizen mit Eigenwertanalysen erkennen.
Partielle Korrelationen: Definition und Methode, Tücken und Fallen , Wichtige Anwendungen in der Psychologie, Kombinatorik der Anzahlen. * Standard-Matrix-Analyse (SMA) und Nicht-Linearitäts-Paradox in Korrelationsmatrizen * Systematische Veränderungs-Paradoxie * Vollständige 501 partielle Korrelationsanalysen am Beispiel IST 70 * Wissenschaft in der IP-GIPT * Kritik Handhabung Faktorenanalyse * Numerisch instabile Matrizen und Kollinearität in der Psychologie * Fehlersimulation und Faktorenanalyse * Zahlen * Der Kardinal-Skalenbeweis zur Summen-Score-Funktion * Grundzüge einer ideographischen Wissenschaftstheorie * Welten *
Beweis und beweisen in der Statistik * Signifikanztest *
*
Dienstleistungs-Info.
*
Zitierung
Sponsel, R. (DAS). Korrelation. Was bedeutet der lineare Korrelationskoeffizient? Probleme, Kurioses, Paradoxes, Ungereimtheiten und Widersprüchliches in der Korrelationsrechnung und wie man dem begegnen kann. IP-GIPT. Erlangen: https://www.sgipt.org/wisms/statm/kor/kurkor.htm
Copyright & Nutzungsrechte
Diese Seite darf von jeder/m in nicht-kommerziellen Verwertungen frei aber nur original bearbeitet und nicht inhaltlich verändert und nur bei vollständiger Angabe der Zitierungs-Quelle benutzt werden. Das direkte, zugriffsaneignende Einbinden in fremde Seiten oder Rahmen ist nicht gestattet, Links und Zitate sind natürlich willkommen. Sofern die Rechte anderer berührt sind, sind diese dort zu erkunden. Sollten wir die Rechte anderer unberechtigt genutzt haben, bitten wir um Mitteilung. Soweit es um (längere) Zitate aus ... geht, sind die Rechte bei/m ... zu erkunden oder eine Erlaubnis einzuholen.
Ende Korrelation _Datenschutz__Überblick_ Rel. Aktuelles _Rel. Beständiges_ Titelblatt_ Konzept_Archiv_ Region_Service iec-verlag _Mail: sekretariat@sgipt.org___Wichtiger Hinweis zu Links und Empfehlungen.
korrigiert irs 1.4.6
Änderungen * Kleine Fehler- oder Layoutkorrekturen werden nicht etxra aufgeführt.
16.07.23 Definition Korrelationsmatrix
31.03.22 Vigens falsche Interpretation des Klassikers Strochennester und Geburtenraten.
26.03.22 Ansätze einer inhaltlichen Korrelationstheorie.
24.03.22 Spuriouse Korrelationen und das Problem der inhaltlichen Bedeutungsanalyse von Korrelationen. irs korrigiert.
01.03.20 Ein Wachstumsparadox bei der Ausbreitung des Corona-Virus.
10.02.20 Vergleich Korrelationen und Eigenwerte absoluter und logarithmierter Häufigkeiten am Beispiel Corona-Virus.
30.09.19 (11) Interpretation der Größe von Korrelationskoeffizienten.
04.09.18 Dimension und Eigenwerte.
20.07.18 Quantenmechanische Korrelation.
18.11.16 Link: Konstruktion einer Korrelationmarix aus einer vorgegebenen Eigenwertstruktur.
24.10.16 Link: 12-Variablen-Korrelationsmatrix, der man weder den Generalfaktor noch die (Fast-) Kollinaritäten ansieht
09.10.16 Ergänzung "Wie ich vor einiger Zeit herausfand, ..." Faustregel zur Eigenwertdeutung im Eigenwertabschnitt.
20.07.16 Linkfehler geprüft und korrigiert.
25.03.16 Beispiel 6: Korrelation zwischen "Ehrenmorden" und medialer Präsentation.
09.11.14 Querverweis auf eine neue Arbeit zur Autokorrelation. Hinweis auf völlig entgleiste Matrix durch unterschiedliche Stichprobenumfänge.
25.10.14 Neu in der Einführung: Das Grundproblem in der Psychologie
23.10.14 Interpretationssatz Zeitreihen, Ökonomische Zeitreihen.
23.05.13 Beispiel excel (Zeilen, Spalten Korrelationseinstellungen)
20.05.13 Die verschiedenen Korrrelations-Techniken und ihre Interpretation.
16.04.13 Neuer Abschnitt 10 Korrelation und Kausalität, der auf Grund seiner Größe, ausgelagert wurde.
27.09.12 Das Größenordnungsparadoxon.
24.09.12 Graphik zu Eigenwerten, Korrelationsmatrizen und Rohdaten.
19.09.12 (9) Clauß & Ebner (1982) zur Interpretation von Korrelationskoeffizienten.
25.12.09 Kleine Korrektur der quantitativen kanonischen Korrelationen bei HAWIE: 0.7813 RICHTIG statt 0.796627 UNGENAU und 0.8339 RICHTIG statt 0.851599 UNGENAU.
16.12.09 Beispielwerte für die kanonische Korrelation zwischen Verbal- und Handlungsteil im HAWIE.
05.12.09 Sonderformen der Korrelation angelegt.
05.02.09 Anmerkung: Prüfverfahren, ob ein lineares Korrelationsmodell angemessen ist.
23.12.08 Neues Beispiel: Die Korrelationsmatrix der Partitionen von n = 1, 2, 3, ...
24.05.08 Zwei Ergänzungen zur Ähnlichkeit von Korrelationsmatrizen: 2b, 2c.
16.05.08 Brainstorming zur Frage der Logarithmus-Paradoxie: Widerlegung einer Idee 16.5.8.
15.05.08 Eine Logarithmus-Paradoxie?
30.11.06 (Semi) Indefinite Pseudo-Korrelationsmatrizen.
02.08.06 Der Rang und seine Bedeutung bei Korrelationsmatrizen.
28.06.06 Querverweis (Beweis Dr. Hain): Partielle Korrelationsmatrix nicht notwendig positiv [semi] definit.
21.05.06 Hinweis: Einfache Berechnung der multiplen Korrelationen nach Tucker et. al.
29.04.06 Korrelationen nach Eisenreich; Sprachregelung "Definitheit" bei quadratischen Formen.
27.04.06 Therapiemethoden indefiniter (phänotypischer) Korrelationsmatrizen.
25.04.06 Einfügung: Die kaum zu überschätzende Bedeutung der Eigenwerte einer Korrelationsmatrix. 27.4.6: Kleine Verbesserungen.
02.04.06 Beispiel 4 (= Beispiel drei ein Wert vertauscht und die Korrelation spingt von -0,03 auf 1 glatt) und Beispiel 5: Pseudolinearer Anschein ...
31.03.06 Überarbeitung und Ergänzungen zu den Nicht- & Linearitätsparadoxien.
27.11.05 Aufnahme weiterer Arbeiten zu dubiosen Verbesserungs- und Korrekturformeln (Olkin & Pratt 1958, Cureton 1966, Bock & Petersen 1975)
26.11.05 Ergänzung bei Antinomie (in der Faktorenanalyse). Links, Suchfunktion in der IP-GIPT.
26.02.05 Zitat-Beleg zur Interpretationsproblematik und Bedeutung von Korrelationen nach Sponsel 1984, S. 213.
30.10.04 "Paradoxie" durch Widerspruch ersetzt. Anmerkung hierzu.
12.09.04 Attenuitäts-Korrektur. Ursprünglich eine Textspende an Wikipedia. Dort wurde der Text offenbar von einer DestruktorIn gelöscht. Daher wird er nun auf "sicherem Gelände" präsentiert.
02.04.04 Kleine Korrekturen. Anmerkung: Überhaupt kann an dieser Stelle angemerkt werden, dass es stets sinnvoll und zu empfehlen ist, sich die Daten in ihrem graphischen Verlauf anzuschauen, bevor man ihnen ein Modell unterlegt und rechnet.
02.02.04 Systematische Veränderungs-Paradoxie eingebunden, Ergänzungen Historisches(Bilder), kleine Fehlerkorrekturen
01.02.04 Einbau 1c) Linearitätssatz, Fisher, Link Systematisches Veränderungs Paradox
30.01.04 Zwei Rechtschreibfehler im Linearitätsparadox beseitigt.
29.01.04 Einbindung Deutungssystematik Koller, Fußnote numerologische Testtheorie, Lit-Ergänzung u.a. Kleinigkeiten
28.01.04 Beginn Literaturverzeichnis, erste Links; Ergänzungen [1,2]
25.01.04
- Der Korrelationskoeffizient
- Korrelation(skoeffizient) ist nicht gleich Korrelation(skoeffizient)
- Formel der Produkt-Moment-Korrelationsrechnung nach Bravais-Pearson
- Geschichte der Korrelationsrechnung nach Baur (1928)
- Ein Reliabilitätsparadox der numerologischen Testtheorie.