Internet Publikation für Allgemeine und Integrative Psychotherapie
    IP-GIPT DAS=02.06.2004 Internet-Erstausgabe, letzte Änderung 3.11.11
    Impressum: Diplom-Psychologe Dr. phil. Rudolf Sponsel Stubenlohstr. 20   D-91052 Erlangen
    Mail: sekretariat@sgipt.org_ Zitierung  &  Copyright
    Anfang Wachstums-Schaubilder__Überblick__Rel. Aktuelles __Rel. Beständiges  _Titelblatt__ Konzept__ Archiv__ Region__Service-iec-verlag__Wichtiger Hinweis zu Links und zu Empfehlungen
    Willkommen in unserer Internet Publikation für Allgemeine und Integrative Psychotherapie, Abteilung Wirtschaft und Soziales, Bereich Wachstum, hier speziell zum Thema:

    Wachstums-Tabellen und Schaubilder
    Zur Veranschaulichung des Schuldenproblems
    Das Beispiel von Dirk Müller zum Unterschied zwischen Zins und Zinseszins.

    von Rudolf Sponsel, Erlangen (ohne Gewähr)

    Tabelle Wachstum ("Zinseszins") von 1,2,3,...,10% in 100 Jahren

    Lesebeispiel  Eine jährliche durchschnittliche Verschuldung von 3% führt nach 10 Jahren zum 1,34fachen Schuldenbetrag, nach 25 Jahren zum 2,09fachen, nach 50 Jahren zum 4,38fachen, nach 75 Jahren zum 9,18fachen und nach 100 Jahren zum 18,85fachen des ursprünglichen Betrages. Aus einer Schuld von 1 Milliarde werden also in 10 Jahren 1,34  Milliarden, in 25 Jahren 2,09 Milliarden, in 50 Jahren 4,38 Milliarden, nach 75 Jahren 9,18 Milliarden und nach 100 Jahren 18,85 Milliarden. Entsprechend vervielfacht sich die Zinslast.
        Noch viel schlimmer sieht es aus, wenn die jährliche durchschnittliche Schuldenlast um 5% zunimmt. Dies führt nach 10 Jahren zum 1,63fachen, nach 25 Jahren zum 3,39fachen, nach 50 Jahren zum 11,47fachen, nach 75 Jahren zum 38,83fachen und nach 100 Jahren zum 126,49fachen.
        Ganz schlimm sieht es in den neuen Ländern bis 2002 aus, dort liegen die Schuldenwachstumsraten um die 20% und mehr.

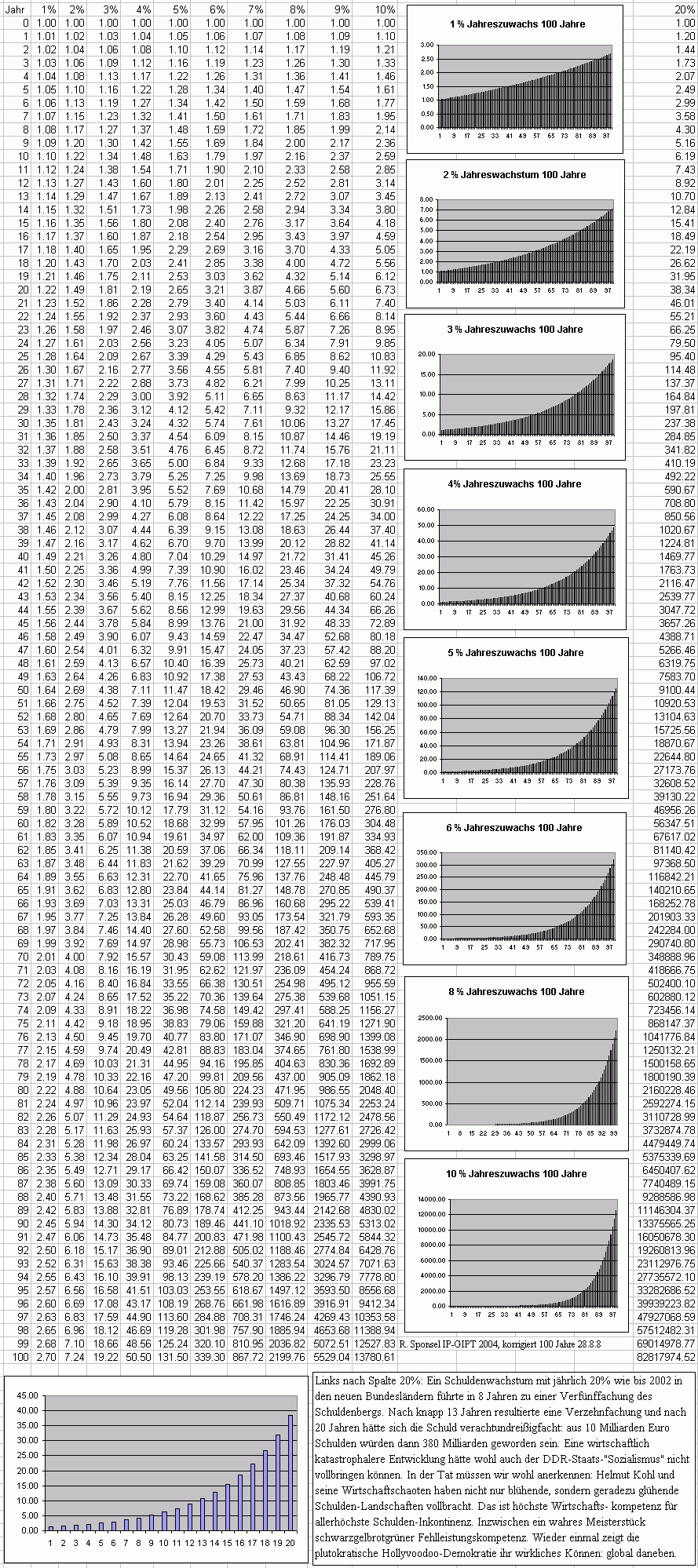
    [Interne Quelle: ...sgipt/wirtsch/wachst/wgraph.xls]

    Dirk Müller zum Unterschied zwischen Zins und Zinseszins.
    In der Sendung "Markus Lanz" (ZDF 24.3.2011, youtube) brachte Dirk Müller ("Mr. DAX", Homepage) ein außerdentlich anschauliches und eindrucksvolles Beispiel - in der Literatur als Josephspfennig bekannt - , um den Unterschied zwischen Zins und Zinseszins zu erläutern. Angenommen Joseph hätte bei Jesus Geburt einen Eurocent mit 5% Verzinsung angelegt . Müllers Ergebnis: "295 Milliarden Weltkugeln aus purem Gold - 88000 Sonne und ein paar Monde, je nach Wechselkurs, wie Sie's gern hätten, das ist der Zinseszinseffekt, der von uns allen unterschätzt wird, weil der Mensch nicht exponentiell denken kann, nicht in Zinseszins denken kann, wir können ja nur linear denken. Und jetzt machen wir die Gegenprobe, jetzt wird es richtig spannend: Nehmen wir an, der Joseph hätte seinem Sohn Jesus die Zinsen jedes Jahr abgeholt, gleiche Verhandlung, er hätte die Zinsen nur nicht stehen lassen, sondern jedesmal abgeholt und unters Kopfkissen gelegt. Und jetzt finden Sie das Sparbuch unter dem Kopfkissen: wie viel steht Ihnen jetzt zur Verfügung? 1 Euro. 1 Euro zu 295 Milliarden Weltkugeln aus Gold. Das ist der Unterschied zwischen Zins und Zinseszins."

    Für die Rechnung benötigen wir folgende Basiskennwerte:

        I. Zinseszinsrechnung:

      Währungseinheit: Eurocent, Euro.
      Anfangswert zur Geburt Jesus (hier mit 0 angesetzt): 1 Eurocent
      Verzinsungs pro Jahr: 5 %
      Anzahl der Jahre: 2000 im Jahr 2000
      Endwerte: 2000 (unter Einbeziehung  2001, ..., 2010 (ergeben sich weitere Rechnungen).
          Endwert Zinseszins (2000) = 1.05^2000 = 1.05^2000 = 2.3911^42, also 2.3911 Septillionen Eurocent,
          durch 100 dividiert ergibt Euro: Endwert Zinseszins (2000) = 2.3911^40 Euro.
      Ergebnis Zinseszins (0-2000): Aus einem Eurocent zur Geburt Christi wird bei 5% jährlicher Verzinsung bis zum Jahre 2000 ein Vermögen von 2.3911 Septillionen Eurocent oder von 2.3911^40 Euro, das ist eine Zahl mit 40 Stellen oder, in einem Wort, 23,9111 Sextilliarden.


        II. Gewicht der Erde in Gold

      Volumen der Erde: 1.083.319.780.000  km^3 (Quelle: Daten der Erde, Abruf 1.11.11)
      Wir bestimmen zunächst das Goldgewicht für einen km^3 Volumen Erde.
          Das spezifische Gewicht von Gold = 19,302 g/cm13 [nach Wikipedia (1.11.11)]
          Ein cm^3 Gold wiegt 19,302 g.
          Ein m^3 (Kubikmeter) wiegt dann 19,302 * 100^3 = 19,302 * 1.000.000  =  19302000 g.
          Ein km^3 (Kubikkilometer) wiegt dann 19302 kg * 1000^3 = 1.9302 * 10^13.
          Die Erde in Gold wöge dann 1.9302 * 10^13 * 1.083.319.780.000 = 2.091 * 10^25 kg


        III. Preis der Erde in Gold im Jahr 2000

      Nach Angaben der Bundesbank war das Goldfixing bei einer Unze in London für das Jahr 2000 für eine Unze = 31,1034768 g bei 302,640  Euro, also pro Gramm 302,64 : 31,1034768 = 9.7301 Euro. 1 Kilo Gold (2000) = 9730.1 Euro
      PEG2000= 2.091 * 10^25 * 9730.1= 2.0346 * 10^29.
       
        IV. Wie viele Erden im Goldwert von 2000 bekäme man für 2.3911^40?
      ZZ2000  = 2.3911 * 10^40 = 2.3911 * 10^40
      PEG2000=2.0346 * 10^29
      NErden = ZZ2000 / PEG2000 = 1.1752 * 10^11 = 117,52  Milliarden Erden.


    Ergebnis: Nach dieser Rechnung könnte man bei einer Anlage von 1 Eurocent zur Zeit Christi Geburt mit einem Zins von 5% nach 2000 Jahren rund 118 Milliarden Erden in Gold des Preises von 2000, nämlich 302,64 Euro pro Unze, erhalten. Hätte man die Zinsen alljährlich abgehoben, wären es nach 2000 Jahren tatsächlich nur 1 Euro gewesen.
     


    Glossar, Anmerkungen und Endnoten:
    1) GIPT= General and Integrative Psychotherapy, internationale Bezeichnung für Allgemeine und Integrative Psychotherapie.
    ___
    Bundesbank zum Goldpreis 1999-2010 (Goldfixing London) mit (Abruf 1.11.11):

    ___
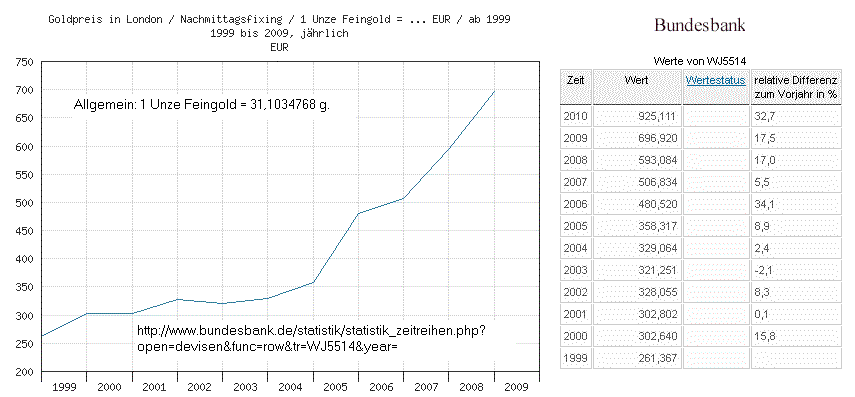
    Erdvolumen.
      Daten der Erde (Abruf 1.11.11): 1.083.319.780.000  km3
          Äquator Radius  6.378.137  m    (WGS84)
          Polradius  6.356.752  m    (WGS84)
          Abplattung der Erde  21.385  m    (WGS84)
          Äquatordurchmesser  12.756.274  m    (WGS84)
          Poldurchmesser  12.713.504  m    (WGS84)
          Äquatorumfang / Äquatorlänge  40.076.592  m
          Nullter Längengrad (über die Pole)  40.009.153  m
          Differenz zum Äquatorumfang  67.439  m kleiner
          Oberfläche  510.100.934  km2
          Festlandfläche (29,3 %)  149.459.574  km2
          Meeresfläche (70,7 %)  360.641.360  km2
          Volumen  1.083.319.780.000  km3
          Umlaufgeschwindigkeit um die Sonne  29,76  km/sec
          mittlere Entfernung zur Sonne  149.597.870  km
          Masse  5,9736  *1021 Tonnen
          Durchschnittstemperatur  13  °C
          Achsneigung  23,45  °
          Mindestalter  4,3  Mrd. Jahre
          Höchster Berg (Mount Everest)  8.844  m
          Größte Tiefe (Witjastief 1/Marianengraben)  11.034  m
      ___
      Erde-Volumen:
      Aus dem Lexikon der Kartographie und Geomatik von Bollmann, Jürgen et al. (2002). Spektrum Akademischer Verlag GmbH, Heidelberg, Berlin
      Erde, ...  Das Volumen der Erde beträgt 1,083 * 10^21 m^3 und die Erdmasse entspricht 5,973 * 10^24 kg (Abb. 1).
    ___
    Josephspfennig. [W] Dirk Müller erzählt die Geschichte in Crashkurs (S. 194) wie folgt: "Sehen wir uns den berühmten »Josefspfennig« an. Hätte Josef vor etwas über 2000 Jahren auch nur einen einzigen Cent fiir seinen Sohn Jesus mit 5 Prozent Zinsen angelegt, was schätzen Sie, wie hoch das Vermögen seiner Nachkommen heute wäre? Nun, es wären sagenhafte 295 Milliarden Weltkugeln aus purem Gold. Wer es gerne wärmer hat, kann alternativ auch 888000 Sonnen aus reinem Gold haben. Einige Monde Abweichung je nach Gold- und Wechselkurs seien mir verziehen. Ich würde gerne das Gesicht Ihres Bankberaters sehen, wenn Sie ihm sagen: »Ich habe da noch ein altes Sparbuch der Volksbank von Judäa auf dem Dachboden gefunden. Könnten Sie mir bitte die Zinsen nachtragen?«
        Sie sehen: In einem begrenzten System, wie unsere Erde es nun einmal ist, kann ein unendliches exponentielles Wachstum wie ein Zinseszinssystem schon rein logisch nicht funktionieren. Unser Wirtschaftssystem wird irgendwann kollabieren. So wie alle Systeme, die auf Zins und Zinseszins beruhen, in den vergangenen Jahrtausenden kollabieren mussten. Das ist mathematisch gar nicht anders möglich. Ein See, in dem sich die Algen ständig vermehren, kippt auch irgendwann um. Mit dem Zinssystem ist es genauso. Denn so wie auf der einen Seite das Vermögen von immer weniger Menschen immer abstrusere Dimensionen annimmt, so muss auf der anderen Seite ja auch die Verschuldung der anderen immer dramatischere Formen annehmen. Denn wer zahlt schließlich Zinsen, wenn nicht ein Schuldner?"
        Wikipedia listet folgende Literatur:
    • Price, Richard (1772). An Appeal to the Public on the Subject of National Debt. London, 1772. Zweite Auflage. S. 18f ". Zitiert nach Marx, Karl &  Engels, Friedrich (1983). Werke, Band 25, "Das Kapital", Bd. III, Fünfter Abschnitt, S. 408. Dietz Verlag, Berlin/DDR 1983:
    • Hudson, Michael (2000). The mathematical economics of compound interest: a 4,000-year overview'', In: Journal of Economic Studies, MCB UP 2000, Band 27, Nr. 4/5, S. 344 - 363.
    • Schlömilch, Oskar Xaver  (1879, Hrsg.). Handbuch der Mathematik. E. Trewendt. [S. 183]
    • Pfeffer, Karl-Heinz  (2003). Analysis für Fachoberschulen. Ein Lehr- und Arbeitsbuch zur modernen Mathematik. Wiesbaden: Vieweg, 6. Auflage (2003), [S. 167, Aufgabe 3.82]
    • Hudson, Michael (2000). The mathematical economics of compound interest: a 4,000-year overview'', In: Journal of Economic Studies, MCB UP 2000, Band 27, Nr. 4/5, S. 344 - 363.
    Links zum Josephspfennig:
    • https://www.neuesgeld.com/page.php?id=25.
    ___
    Mail an Dirk Müller (2.11.11):
      "Sehr geehrter Herr Müller,
      Sie haben ein außerordentlich eindrucksvolles Beispiel zum Zinseszins gebracht (Gratulire!). 1 Eurocent zu Christi Geburt - und 2000 Jahre später. Sie kamen auf 295 Milliarden Erdkugeln in Gold. Ich habe das Beispiel nachgerechnet und komme "nur" auf rund 118 Milliarden Erdkugeln: Meine Parameter waren:
      1.05^2000 = 2.3911^40 Euro (Sextilliarden).
      Volumen der Erde: 1.083.319.780.000  km^3
      Spezifisches Gewicht Gold: 19,302 g/cm^3.
      Goldpreis 2000: 9.7301 Euro pro Gramm (nach DBB).
      Goldpreis einer Erde: 2.0346 * 10^29.
      Ergebniss: 117,52  Milliarden Erden.
      Wo liegt die Abweichung? Wie haben Sie grechnet? Wo ist das einsehbar?
      Danke, auch für Ihre sonstige aufklärerische Arbeit..
      Mit freundlichen Grüßen: Rudolf Sponsel"
        Antwort vom 3.11.11:
      "Sehr geehrter Herr Sponsel,
      zunächst einmal vielen lieben Dank für Ihr Interesse an Herrn Müllers Expertise. Im Moment erreichen uns nahezu 100 Anfragen täglich, weshalb Herr Müller all diese Fragen nicht direkt und persönlich beantworten kann. Wir versuchen in der Regel die Informationen über die Homepage www.cashkurs.com bereitzustellen.
      Wir werden jedoch Ihren Beitrag dahingehend verwenden und es in unseren Fragenkatalog aufzunehmen, um solche Fragen wie diese in einem geplanten Webinar zu beantworten. Wir bitten diesbezüglich um Ihr Verständnis und bedanken uns für Ihren Beitrag. Mit freundlichen Grüßen,
      Sascha Vrzogic, Ethos GmbH, Alter Wall 34-36, 20457 Hamburg, www.ethosgroup.eu"
    ___
    Namen für große Zahlen: Nach: https://www.arndt-bruenner.de/mathe/scripts/zahlwoerter.htm.
    Im Zeichen der Finanzkrise und Derivateschlamassels reine Pflicht ;-)
    " ^ "  lies "hoch".  1 000 000 = 10^6 :=  Million; 1 000 000 000 = 10^9 :=  Milliarde (amerikanisch Billion); 1 000 000 000 000 = 10^12 := Billion (amerikanisch Trillion).
     
    10^15   Eine Billiarde 10^25  zehn Quadrillionen 10^35   hundert Quintilliarden  10^45  eine Septilliarde
    10^16   10 Billiarden  10^26  hundert Quadrillionen 10^36   eine Sextillion  10^46  zehn Septilliarden
    10^17   100 Billiarden 10^27  eine Quadrilliarde 10^37   zehn Sextillionen  10^47  hundert Septilliarden
    10^18   1000 Billiarden := 1 Trillion 10^28  zehn Quadrilliarden 10^38   hundert Sextillionen  10^48  eine Oktillion
    10^19   10 Trillionen 10^29  hundert Quadrilliarden 10^39   eine Sextilliarde  10^49  zehn Oktillionen
    10^20   100 Trillionen  10^30  eine Quintillion 10^40   zehn Sextilliarden 10^50  hundert Oktillionen
    10^21   1000 Trillionen := Trilliarde 10^31  zehn Quintillionen 10^41   hundert Sextilliarden 10^51  eine Oktilliarde
    10^22   10 Trilliarden 10^32  hundert Quintillionen 10^42   eine Septillion 10^52  zehn Oktilliarden
    10^23   100 Trilliarden 10^33  eine Quintilliarde 10^43   zehn Septillionen 10^53  hundert Oktilliarden
    10^24   1000 Trilliarden := 1Quadrillion 10^34  zehn Quintilliarden 10^44   hundert Septillionen 10^54  eine Nonillion

    10^100 = zehn Sexdezilliarden - oder 'ein Googol';  10^1000 =  zehn Centsexsexagintilliarden; 10^10000 = zehn Milliasescentsexsexagintilliarden;
    10^100000 = zehn Sexdezmilliasescentsexsexagintilliarden.
     
    10^0=1
    10^1=10
    10^2=100
    10^3=1 000 
    10^4=10 000
    10^5=100 000
    10^6=1 000 000 (Million)
    10^7=10 000 000
    10^8=100 000 000
    10^9=1 000 000 000 (Milliarde)
    10^10=10 000 000 000
    10^11=100 000 000 000
    10^12=1 000 000 000 000 (Billion)
    10^13=10 000 000 000 000
    10^14=100 000 000 000 000
    10^15=1 000 000 000 000 000 (Billiiarde)
    10^16=10 000 000 000 000 000
    10^17=100 000 000 000 000 000
    10^18=1 000 000 000 000 000 000 (Trillion)
    10^19=10 000 000 000 000 000 000
    10^20=100 000 000 000 000 000 000    		 10^21=1 000 000 000 000 000 000 000 (Trilliarde)
    10^22=10 000 000 000 000 000 000 000
    10^23=100 000 000 000 000 000 000 000
    10^24=1 000 000 000 000 000 000 000 000 (Quadrillion)
    10^25=10 000 000 000 000 000 000 000 000
    10^26=100 000 000 000 000 000 000 000 000
    10^27=1 000 000 000 000 000 000 000 000 000 (Quadrilliarde)
    10^28=10 000 000 000 000 000 000 000 000 000
    10^29=100  000 000 000 000 000 000 000 000 000
    10^30=1 000 000 000 000 000 000 000 000 000 000 (Quintillion)
    10^31=10 000 000 000 000 000 000 000 000 000 000
    10^32=100 000 000 000 000 000 000 000 000 000 000
    10^33=1 000 000 000 000 000 000 000 000 000 000 000 (Quintilliarde)
    10^34=10 000 000 000 000 000 000 000 000 000 000 000
    10^35=100 000 000 000 000 000 000 000 000 000 000 000
    10^36=1 000 000 000 000 000 000 000 000 000 000 000 000 (Sextillion)
    10^37=10 000 000 000 000 000 000 000 000 000 000 000 000
    10^38=100 000 000 000 000 000 000 000 000 000 000 000 000
    10^39=1 000 000 000 000 000 000 000 000 000 000 000 000 000 (Sextilliarde)
    10^40=10 000 000 000 000 000 000 000 000 000 000 000 000 000
    10^41=100 000 000 000 000 000 000 000 000 000 000 000 000 000 
    ___
    Spezifisches Gewicht Gold im Internet und in der Literatur (> Zum Chaos medizinischer Laborwertnormen)

    • Brockhaus Konversationslexikon (1894): "Das specifische Gewicht des geschmolzenen Goldes beträgt 19,27, durch Hämmern kann es auf 19,3 bis 19,65 erhöht werden; das gefällte Gold hat ein specifisches Gewicht von 19,55 bis 20,7. "
    • Brockhaus Kleines Konversationslexikon (5.A. 1911): "spez. Gewicht 19,3 bis 20,7;"
    • Der Grosse Brockhaus (1954): 19,3.
    • Dubach Uhren: Spezifisches Gewicht: 19,32 (2.11.11)
    • Edelmetallhandel Christian Brünisholz Au = Gold 19,32 g/cm³ = Gramm je Kubikzentimeter (2.11.11)
    • Farbiges Grosses Volkslexikon (1981): Dichte 19,32.
    • Frontier.net: "Gold's density is 18.88 g/cm^3" (3.11.11)
    • Fundamental aspects of electrochemical deposition and dissolution (2000): "Sine the densitiy of gold ist 18.88,..."  (GB 3.11.11)
    • Goldhandeln: (2.11.11)"

      •     999er Gold (24 Karat) hat ein spezifisches Gewicht von 19,3 g/cm^3;.
          900 = 17,5 g/cm^3;
          750 = 15,8 g/cm^3;
          585 = 13,6 g/cm^3;
          375 = 11,2 g/cm^3;
          333 = 10,9 g/cm^3;
    • Goldlexikon: "Das spezifische Gewicht von Gold liegt bei 19,32." (2.11.11)
    • Goldschmuck Shop: Spezifisches Gewicht:  19,5 (2.11.11)
    • Juwelier Stoekl: Spezifisches Gewicht: 19.3 Gramm pro Kubikzentimeter (2.11.11)
    • Lenntech: 19,32 (3.11.11)
    • Lueger's Lexikon der gesamten Technik (1904-20): 19,3.
    • Maiers Goldankauf; "Gold: chemisches Zeichen Au > lateinischer Name Aurum, spezifisches Gewicht 19,3 (Dichte g/cm3 bei 20Grad Celsius)," (2.11.11)
    • Nanoscale materials in chemistry (2009): "The density of gold ist 18.88 g cm -3" (GB 3.11.11)
    • Pierer's Universal-Lexikon (1857-65): Das specifische Gewicht des geschmiedeten Goldes ist = 19,5, das des gegossenen = 19,2;
    • Physik Lexikon Spektrum der Wissenschaften.Spezifisches Gewicht von Gold: 19,93 g/cm^3
    • Wikipedia: 19,302 g/cm^3  (1.11.11)
    ___
    Parameter der Rechnung oder wo und wie man sich verrechnen kann:
      Währung (Euro oder Dollar), Währungseinheit (Cent oder Euro), Maßeinheiten (g, kg, cm, m, km, ...) und Dimensionen, Konstanten, Anfangswert, Endwert, Goldpreis, Rechnen und Umrechnen, Formel.
    ___
    Querverweise
    Standort: Wachstums-Tabellen und Schaubilder.
    *
    Wachstum - Kritische Reflexionen zu einem äußerst fragwürdigen Konzept.
    Staatsverschuldung der Länder im Vergleich 1950-2002.
    Überblick Schuldenporträts. * Was zum Teufel heißt eigentlich "Sparkurs"?
     * Überblick Staatsverschuldung 0_* 1 * Neuverschuldung * Privat *  Geldtabu * Psychopathologie Geld1, Geld2 *   Adam Smith zur Staatsverschuldung *
    Juliusturm. Antizyklische Haushaltspolitik der Vernunft. Fritz Schäffer und John Meynard Keynes.
    Überblick Statistik in der IP-GIPT: Methoden, Daten, Geschichte, Verwandtes.
    Beweis und beweisen in Politik, gesellschaftlichem Leben, Medien und Öffentlichkeit.
    Überblick Programm Politische Psychologie in der IP-GIPT
    *
    Suchen in der IP-GIPT, z.B. mit Hilfe von "google": <suchbegriff> site:www.sgipt.org
    z.B. Wachstum site:www.sgipt.org. 
    *
    Dienstleistungs-Info.
    *
    Zitierung
    Sponsel, Rudolf  (DAS). Wachstums-Tabellen und Schaubilder. Zur Veranschaulichung des Schuldenproblems. Aus unserer Abteilung Wirtschaft und Soziales. IP-GIPT. Erlangen: https://www.sgipt.org/wirtsch/wachst/schau_01.htm
    Copyright & Nutzungsrechte
    Diese Seite darf von jeder/m in nicht-kommerziellen Verwertungen frei aber nur original bearbeitet und nicht  inhaltlich verändert und nur bei vollständiger Angabe der Zitierungs-Quelle benutzt werden. Das Einbinden in fremde Seiten oder Rahmen, die die Urheberschaft der IP-GIPT nicht jederzeit klar erkennen lassen, ist nicht gestattet. Sofern die Rechte anderer berührt sind, sind diese dort zu erkunden. Sollten wir die Rechte anderer unberechtigt genutzt haben, bitten wir um Mitteilung. Soweit es um  (längere) Zitate aus  ...  geht, sind die Rechte bei/m ... zu erkunden oder eine Erlaubnis einzuholen.

      Ende__Wachstums-Schaubilder__Überblick__Rel. Aktuelles __Rel. Beständiges __ Titelblatt__ Konzept__ Archiv__ Region__Service-iec-verlag__Mail: sekretariat@sgipt.org__
    ___Anmeldung _Wichtiger Hinweis zu Links und zu Empfehlungen

    kontrolliert: 02.06.04 irs


    Änderungen wird gelegentlich überarbeitet, ergänzt und vertieft * Anregungen und Kritik willkommen
    28.08.08    Fehler bei 100 Jahren 2-10% korrigiert. Danke an Christian Grundmann.
    08.04.06    Layout, Links.