Internet Publikation für Allgemeine und Integrative Psychotherapie
(ISSN 1430-6972)
IP-GIPT DAS=03.05.2001 Internet-Erstausgabe, letzte Änderung 24.9.12
Impressum: Diplom-PsychologInnen Irmgard Rathsmann-Sponsel und Dr. phil. Rudolf Sponsel
Kommunikation:  Stubenlohstr. 20    D-91052 Erlangen * Mail:_sekretariat@sgipt.org__Zitierung & Copyright
Anfang _ Ähnlichkeit _  Überblick _ Relativ Aktuelles  _ Rel. Beständiges  _ Titelblatt  _  Konzept  _  Archiv _ Region _ Service iec-verlag   _Wichtige Hinweise zu Links und Empfehlungen_
Willkommen in der Abteilung Wissenschaftstheorie, Methodologie und Statistisch-Mathematische Methoden in der Allgemeinen und Integrativen Psychologie, Psychodiagnostik und Psychotherapie, hier zu Matrizen in der Psychologie und Psychotherapie:
Ähnlichkeit und Repräsentation von Matrizen

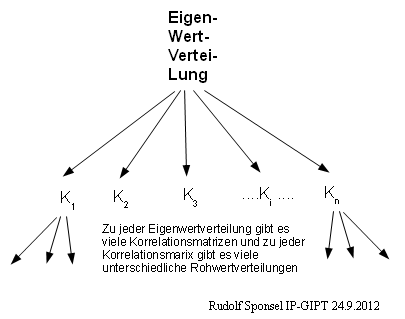
Permutation und Determinanten Graphik 4 k_

     
    Die Mathematik der Ähnlichkeit bei Matrizen 
    Es bedeuten INV(T)  =: Inverse und  T' =: Transponierte von T.
     
  1. Zwei Matrizen A und B heißen ähnlich, wenn es eine reguläre Matrix T gibt mit der Eigenschaft B = INV(T) A T 
  2. Ähnliche Matrizen haben gleiche Eigenwerte.
  3. Ist T orthogonal gilt: B = T' A T.
  4. Ist A symmetrisch, so kann stets eine passende orthogonale Matrix T gefunden werden, so dass B = T' A T Diagonalgestalt hat.

    5. _
    Intuitiver Begriff der Ähnlichkeit für Matrizen
    Zwei Matrizen O und R heißen ähnlich in dem Maße, wie die Größen und Relationen der Originalmatrix O in der Repräsentationsmatrix R übereinstimmen. 

    Satz zur Ähnlichkeit bei Korrelationsmatrizen und Faktorenanalysen
    Wird eine Korrelationsmatrix K vom Rang r auf eine durch Faktoren gewonnene Matrix  R = F F' vom Rang f<r reduziert, so kann eine solche durch rangreduzierte Faktorenmatrix der ursprünglichen Korrelationsmatrix nur dann mathematisch und intuitiv in dem Maße ähnlich sein, wenn die ursprüngliche Korrelationsmatrix r-f  Eigenwerte gleich oder nahe Null aufweist.

    Satz zur Prüfung legitimer Datenreduktion durch Faktorenanalysen
    Ob eine rangreduzierte durch Faktorenanalyse gewonnene Matrix geeignet ist, eine ursprüngliche Korrelationsmatrix zu repräsentieren, hängt genau davon ab, wie gut die Reproduktion der ursprünglichen Korrelationsmatrix aus den Faktoren gelingt. Da dies für FaktorenanalytikerInnen nicht selbstverständlich ist  (Sponsel 1994) merken wir an: Zu einer Korrelationsmatrix gehören natürlich - und wesentlich - die Werte in der Hauptdiagonalen (> Kommunalität). 

 

Beispiele ähnlicher Korrelationsmatrizen mit verschiedenen Rohwertdatensätzen
 
Aus den im folgenden aufgezeigten Möglichkeiten lässt sich der Satz zur Ähnlichkeit von Matrizen auch für Rohdatensätze spezifizieren, was sich z.B. darin ausdrücken sollte, dass alle Rohwertmatrizen, die zu den gleichen Korrelationsmatrizen führen, gleiche Singulärwerte haben sollten. Tatsächlich produzieren alle 9 Rohwertmatrizen die gleichen Singulärwerte: 1.5076, 1.2309, 0.8705, 0.6155 und 0.2752.
 
 

 

Unterschiedliche Korrelationsmatrizen mit gleichen Eigenwerten.

Korrelationsmatrix 01 > drei unterschiedliche Beispiele für erfüllende Rohdaten.
Eigenwerte:   2.2727     1.5152     0.7576     0.3788     0.0758

    1.0000     -0.7095     0.5949    0.4778     0.2352
 -0.7095      1.0000    -0.1302   -0.3072    -0.2353
  0.5949     -0.1302   1.0000   -0.0582     0.4023
  0.4778     -0.3072    -0.0582    1.0000    -0.3452
  0.2352     -0.2353     0.4023   -0.3452     1.0000

Korrelationsmatrix 02  >drei unterschiedliche Beispiele für erfüllende Rohdaten.
Eigenwerte:   2.2727     1.5152     0.7576     0.3788    0.0758

 1.0000     0.3175    -0.5923     0.3581     0.3385
 0.3175     1.0000    -0.5007     0.2470    -0.2517
-0.5923    -0.5007     1.0000    -0.3703     0.0610
 0.3581     0.2470    -0.3703   1.0000    -0.6178
 0.3385    -0.2517     0.0610    -0.6178     1.0000

Korrelationsmatrix 03  >drei unterschiedliche Beispiele für erfüllende Rohdaten.
Eigenwerte:   2.2727     1.5152     0.7576     0.3788     0.0758

 1.0000    -0.1068     0.6714     0.1837     0.3677
-0.1068     1.0000    -0.1882     0.3917    -0.5693
 0.6714    -0.1882   1.0000     0.4952     0.3737
 0.1837     0.3917     0.4952     1.0000     0.2513
 0.3677    -0.5693     0.3737     0.2513     1.0000
 

Unterschiedliche Rohwertdatensätze zu gleichen Korrelationsmatrizen
Zugehörige Korrelationsmatrizen mit gleichen Eigenwerten: > 01, 02, 03.

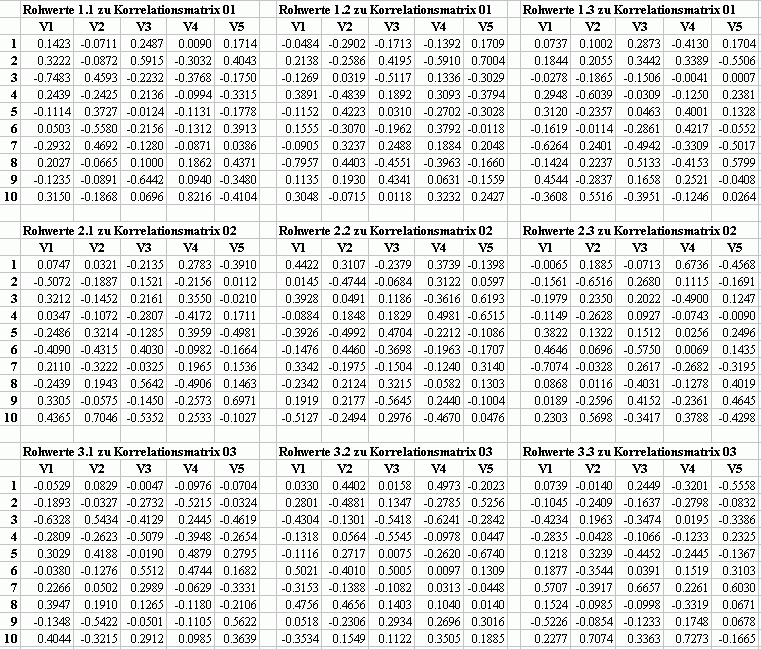
[Intern: ... /rs_dat/excel/ähnlich.xls]


Glossar, Anmerkungen und Endnoten
1) GIPT= General and Integrative Psychotherapy, internationale Bezeichnung für Allgemeine und Integrative Psychotherapie.
___
SVD - Singulärwertzerlegung.
Zur Beziehung Eigenwerte/ Singulärwerte führt Cleve Moler - der auch eine allgemeine Einführung in (Mathworks) gibt - aus: "Wenn A quadratisch, symmetrisch und positiv definit ist, sind ihre Singulärwerte sogar mit den Eigenwerten identisch und die linken und rechten Singulärvektoren sind mit einander und mit den Eigenvektoren der Matrix identisch. Allgemeiner ausgedrückt sind die Singulärwerte von A die Quadratwurzeln der Eigenwerte von ATA oder AAT. Singulärwerte sind dann wichtig, wenn man eine Matrix als Transformation eines Raums in einen anderen Raum mit möglicherweise anderen Dimensionen betrachtet. Eigenwerte dagegen sind wichtig, wenn man eine Matrix als Transformation eines Raum in sich selbst ansieht, beispielsweise bei gewöhnlichen linearen Gleichungen."

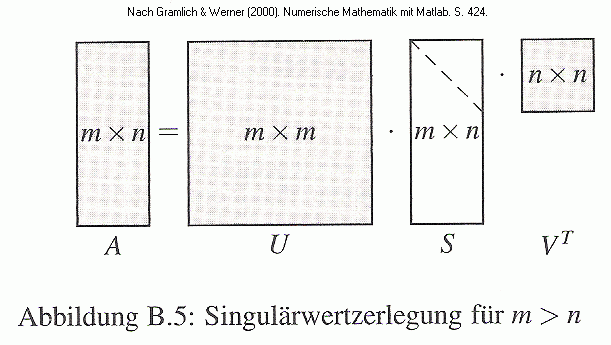
Anmerkung: Der neuere Ausdruck der Singulärwertzerlegung liegt dem mathematischen Sachverhalt der Faktoren- Analyse zugrunde, 1936 auch im Rahmen der Arbeit des Eckart-Young-Theorems dargelegt, das z.B. in der Bildkompression eine moderne Anwendung gefunden hat: Gramlich, Günter (2004). Anwendung der Singulärwertzerlegung: Bildkompression. In: Anwendungen der Linearen Algebra mit Matlab. Leipzig: Fachbuchverlag, S. 106-108. Zur Geschichte der Singulärwertzerlegung [PDF].
___
FN01  Sponsel, Rudolf & Hain, Bernhard (1994). Numerisch instabile Matrizen und Kollinearität in der Psychologie. Diagnose, Relevanz & Utilität, Frequenz, Ätiologie, Therapie.  Ill-Conditioned Matrices and Collinearity in Psychology. Deutsch-Englisch. Übersetzt von Agnes Mehl. Kapitel 6 von Dr. Bernhard Hain: Bemerkungen über Korrelationsmatrizen. Erlangen: IEC-Verlag [ISSN-0944-5072  ISBN 3-923389-03-5]. Aktueller Preis: www.iec-verlag.de.
Bd. 2.: Sponsel, R. (2005). Fast- Kollinearität in Korrelationsmatrizen mit Eigenwert-Analysen erkennen Ergänzungsband - Band II zu Numerisch instabile Matrizen und Kollinearität in der Psychologie. Erlangen: IEC-Verlag.
___

Querverweise:

Zitierung
Sponsel, Rudolf  (DAS). Ähnlichkeit und Repräsentation von Matrizen. Hilfsseite zu: Numerisch instabile Matrizen und Kollinearität in der Psychologie - Ill-Conditioned Matrices and Collinearity in Psychology -   Diagnose, Relevanz & Utilität, Frequenz, Ätiologie, Therapie.  IP-GIPT. Erlangen: https://www.sgipt.org/wisms/nis/aehnlich.htm
Copyright & Nutzungsrechte
Diese Seite darf von jeder/m in nicht-kommerziellen Verwertungen frei aber nur original bearbeitet und nicht  inhaltlich verändert und nur bei vollständiger Angabe der Zitierungs-Quelle benutzt werden. Das Einbinden in fremde Seiten oder Rahmen, die die Urheberschaft der IP-GIPT nicht jederzeit klar erkennen lassen, ist nicht gestattet. Sofern die Rechte anderer berührt sind, sind diese dort zu erkunden. Sollten wir die Rechte anderer unberechtigt genutzt haben, bitten wir um Mitteilung. Soweit es um (längere) Zitate aus  ...  geht, sind die Rechte bei/m ... zu erkunden oder eine Erlaubnis einzuholen.

  Ende_ Ähnlichkeit_ Überblick _ Relativ Aktuelles  _ Rel. Beständiges  _ Titelblatt  _  Konzept  _  Archiv _ Region _ Service iec-verlag  _ Mail: _ Sekretariat@sgipt.org  _ _Wichtige Hinweise zu Links und Empfehlungen_

korrigiert irs 24.5.8


Änderungen wird gelegentlich überarbeitet, ergänzt und vertieft * Anregungen und Kritik willkommen
24.09.12    Graph zur Situation Eigenwerte, Korrelationsmatrizen und Rohdatensätze.
31.05.08    Hinweis auf einen Artikel bei Mathworks zur SVD.
24.05.08    Beispiele ähnlicher Korrelationsmatrizen mit verschiedenen Rohwertdatensätzen und gleichen Eigenwerten.
14.10.07    Layout, Links.