Internet Publikation für Allgemeine und Integrative Psychotherapie
    (ISSN 1430-6972)
    IP-GIPT DAS=25.05.2021  Internet-Erstausgabe, letzte Änderung: 20.11.22
    Impressum: Diplom-Psychologe Dr. phil. Rudolf Sponsel Stubenlohstr. 20 D-91052 Erlangen
    Mail: sekretariat@sgipt.org_ Zitierung  &  Copyright_
    Anfang_ Wachstum_Datenschutz_Überblick_ Rel. Aktuelles _ Rel. Beständiges_ Titelblatt_ Konzept_ Archiv_ Region_ Service iec-verlag_  _ Wichtige Hinweise zu externen Links und Empfehlungen_
    Willkommen in unserer Internet-Publikation IP-GIPT 1)  für Allgemeine und Integrative Psychotherapie, Abteilung Wissenschaft, Bereich Logik,  Methodologie und  Analogie, hier speziell zum Thema:

    Wachstum
    Analyse eines grundlegenden Begriffs in Wissenschaft und Leben
    mit Schwerpunkt Wachstum in der Mathematik

    Originalarbeit von von Rudolf Sponsel, Erlangen
    _

    Inhaltsverzeichnis
    Einführung.
       Ausgangsbeispiel mit 30 Werten.
       Vergleich Ausgangsbeispiel mit drei Glättungsvarianten; 3, 5, 7-Tage-Mittelwert-Glättung.
       Grundbedingung jeder Wachstumsmessung.
       Bezeichnungen.
       Wachstumskriterien oder Wachstumsvarianten.
       Wachstums-Grundmodelle. 
            Lineares Wachstum.
            Quadratisches Wachstum.
            Kubisches Wachstum.
            Exponentielles Wachstum.
            Praktisches Feststellen, ob eine exponentielle Entwicklung vorliegt.
            Zinses-Zins-Modell.
            Organisches Wachstum.
        Wachstumsfragen der Corona-Pandemie.
            Wachstum in der Corona-Pandemie.
               Tagesschau-Vergleiche.
               Prüfung auf exponentielle Entwicklung der 7-Tage-Mittelwerte der Neuinfektionen der
               Exponentielle Wachstumsanalyen Corona 10. Welle (RKI Sprech 4. Welle) 1.7.21-aktuell.
           Exponentielle Wachstumsanalyse Intensivbehandlungen.
           Exponentielle Wachstumsanalyse der Z-Tage-Mittelwerte der Neuinfektionen.
               Die Tücken des Kurvenfittens am Beispiel Bayern-Fit-Vergleich cubic und 4th degree
            der 7-Tage-Mittelwerte der 9. Welle 07.04.-24.05.2021.
               Explorative Kurvenfitstudie Grad 2-9 der 3. großen Welle in Schweden.
               Analyse der 4. Welle in Großbritannien (UK) 24.05.-08.07.2021.
    Materialien - Konzept (grau noch nicht ausgeführt):
        Wachstum im Alltag:
            Wachstum Anzahl der Sachen.
            Wachstums zweckloser Sachen.
            Wachstum der Geburtstage (Lebensjahre)
        Wachstum in der Biologie. > Medizin, Epidemiologie.
        Wachstum in der Demographie:
            Bevölkerungswachstum.
            Wachstum Nahrungsbedarf.
            Wachstum der Lebensspanne.
       Wachstum in der Epidemiologie. > Medizin, Biologie.
       Wachstum in der Finanzwissenschaft.
           Wachstum der Schulden.
               Überblick Staatsverschuldungsanalysen.
           Zinseszinseffekte. > Zinseszinstabellen.
        Wachstum in der Mathematik.
           Analyse und Auswertung der Inhaltsverzeichnisse, Sachregister und teilweise der
           Texte von 45 mathematischen Werken in 5 Abteilungen: 
             20 Allgemeine mathematische Werke.
             9  biomathematische Werke.
             4  mathematische Werke Daten-, Zeitreihenanalyse und Statistik.
             2  finanzmathematische Werke.
             10 mathematische Werke Schulmathematik.
           Literaturbelege und Zitatreferenzen der 45 Werke.
        Wachstum in der Kultur
            Wachstum der Literatur.
            Wachstum der Kunstwerke.
        Wachstum in der Medizin. > Epidemiologie, Biologie.
            Wachstum der Anzahl der ÄrztInnen.
            Wachstum der Gesundheitskosten.
            Wachstum der multiresistenten Keime.
            Wachstum der Krankheiten. (> Blech "Die Krankheitserfinder")
               Wie krank sind wir wirklich?
       Wachstum in der Natur.
            Periodisches Wachstum
            Die Expansion des Universums.
       Wachstum in der Psychologie: Lernen und Vergessen.
       Wachstum in der Ökologie
        Wachstum der Umweltbelastung.
            Wachstum der Erd-Erwärmung.
            Wachstum der Umweltverschmutzung.
       Wachstum in der Ökonomie (Wirtschaft).
            Geschichte der Wirtschaftswachstumsideen.
            Wachstum der Ressourcenausbeutung.
               Postwachstum.
            Wirtschaftswachstumsanalysen.
            Wachstum der Konzentration (Großkonzerne, Monopole und Kartelle)
            Wachstum des Angebots.
            Wachstum der Sättigung der Märkte.
       Wachstum in der Soziologie:
            Wachstum der Bürokratie.
            Wachstum von Organisationen und Institutionen.
            Wachstum von Armut und Reichtum.
               Armut- und Reichtumsberichte der Bundesregierung.
                Wachstum der Vermögen.
                Wachstum der Schere zwischen arm und reich.
        Wachstum der Wissenschaft.
            Wachstum der Anzahl der Publikationen.
    Literatur * Links * Querverweise
    Glossar
    Zitierung und Copyright
    Änderungen

    Einführung
    Wachstumsfragen sind in der Covid-19 Pandemie besonders interessant geworden. Wachsen und Wachstum werden im Alltag meist ohne Probleme verstanden und kommuniziert mit der Kernbedeutung: etwas wird mehr. Komplizierter wird es erst, wenn es um bestimmte Wachstumsweisen geht, diskret oder stetig, schwer zu bestimmende Funktionen und wie man sie erfassen, schätzen ("fitten") oder messen kann, besonders wenn unregelmäßige Zeitreihen mit steigenden und fallenden Werten vorliegen wie z.B. diese hier 1, 4, 2, 6, 3, 8, 7, 13, 10, 9, 14, 17, 15, 16, 18, 14, 19, 21, 17, 17, 24, 31, 46, 58, 55, 51, 68, 62, 69, 70, im Graph Ausgangsbeispiel:

    Obwohl hier keine Monotonie steigender Werte vorliegt, würden doch die meisten Beurteiler sagen, dass hier ein Wachstum in mehreren Wellen vorliegt. Das lässt sich aber auch genau analysieren, wie man oben im Graph sieht. Lässt man auch "Glättungen" zu, z.B. durch 3, 5 oder 7-Tage-Mittelwerte, klärt sich der Wachstumsverlauf noch deutlicher:

    Vergleich Ausgangsbeispiel mit drei Glättungsvarianten; 3, 5, 7-Tage-Mittelwert-Glättung


     


    Grundbedingung jeder Wachstumsmessung
    Für jede Wachstumsmessung werden mindestens zwei Werte benötigt: einen Basis- (Anfangs-, Bezugswert) und ein aktueller Wert von dem Wachstum bezüglich der Basis (Anfangs- oder Bezugswert) bestimmt werden soll. Liegen n Werte vor, so gibt es n über 2 Wachstumsvergleiche. Bei 2 Werten gibt es nur einen einzigen Vergleich, bei 3 gibt es drei, bei 4 sind es 6 und bei 5 sind es 10 Vergleiche. Im Beispiel oben wurden 30 Werte gewählt, damit gibt es (30 über 2) = 435 Möglichkeiten (Binomialkoeffizientrechner), Wachstumsaussagen zu treffen. Verlangt man fortgesetztes Wachstum, so müssten die 30 Werte eine strenge Monotonie aufweisen, d.h. jeder Nachfolger muss größer als Vorgänger sein. Das ist im Beispiel nicht der Fall. Es werden zwar immer weniger Nachfolgerwerte, die fallen. Aber selbst bei der 7-Tage-Glättung wird die Monotonie zwischen dem dem 12. und 13. Wert nicht erfüllt, weil diese mit 17.143 bei Rundung auf drei Stellen gleich sind. Bei strenger Monotonie darf es zwischen keinem Nachfolger und seinem Vorgänger einen  negative Abstand geben. Nachdem es bei n Werten n über 2 Möglichkeiten für Wachstumsvergleiche gibt, muss man genau sagen, welchen Vergleich und welche Wachstumsvariante man betrachten will.

    Bezeichnungen
    W := allgemein für einen Wert ohne nähere Spezifikation.
    A := Anfangswert (Bezugs- oder Basiswert), wobei jeder beliebige Wert vor dem Wert als Anfangswert definiert werden kann..
    E :=  betrachteter aktueller- oder Endwert, dessen Wachstum im Vergleich zu einem Anfangswert A festgestellt werden soll.
    n :=  Anzahl der Werte, die in die Wachstumsbetrachtung eingehen.
    h :=  Abstand der Intervalle der Werte voneinander, in Zeitreihen gewöhnlich 1.
    t :=   Anzahl der Zeitintervalle für die ein Wachstumsverlauf aufgestellt werden soll.
    f :=   Funktion der Wachstumsbestimmung (allgemein), wird auch als Formel bezeichnet:
        Allgemeine Differenzmodelle

    • Unmittelbarer Vorgänger als Anfangs- oder Bezugswert
      • (N-V) :=  absolute Differenz zwischen unmittelbarem, direkten Nachfolger und Vorgänger (ohne Index).
      • (N-V)/N :=  relative Differenz zwischen unmittelbarem, direkten Nachfolger und Vorgänger (ohne Index).
      • [(N-V)/N]*100 :=  relative Differenz in Prozent zwischen unmittelbarem, direkten Nachfolger und Vorgänger (ohne Index).
      • (Nj-Vi) :=  absolute Differenz zwischen dem Nachfolger mit der Ordnungszahl j und Vorgänger mit der Ordnungszahl i.
      • (Nj-Vi)/Nj]*100 :=  relative Differenz in Prozent zwischen dem Nachfolger mit der Ordnungszahl j und Vorgänger mit der Ordnungszahl i.
    • Irgendein ein Vorgänger als Anfangswert, z.B. der Wert an dem Tag in der Vorwoche (>Tagesschau).
      • (E-A) :=  absolute Differenz zwischen Endwert und Anfangswert (ohne Index).
      • (Ej-Ai) :=  absolute Differenz zwischen dem Endwert mit der Ordnungszahl j und dem Anfangswert mit der Ordnungszahl i.
      • (E-A)/n :=  absolute durchschnittliche Differenz zwischen Endwert und Anfangswert (ohne Index).
      • (Ej-Ai)/n :=  absolute durchschnittliche Differenz zwischen dem Endwert mit der Ordnungszahl j und dem Anfangswert mit der Ordnungszahl i.
      • (E-A)/Ai) :=  relative Differenz zwischen Endwert und Anfangswert (ohne Index).
      • (Ej-Ai)/Ai)*100 :=  relative Differenz in Prozent zwischen dem Endwert mit der Ordnungszahl j und dem Anfangswert mit der Ordnungszahl i.
        Allgemeine Quotientenmodelle
    • (N/V) :=  Quotient zwischen unmittelbarem, direkten Nachfolger und Vorgänger (ohne Index), oft als Wachstumsrate bezeichnet.
    • (Nj/Vi) := Quotient zwischen dem Nachfolger mit der Ordnungszahl j und Vorgänger mit der Ordnungszahl in, oft als Wachstumsrate bezeichnet.
    • (E/A) :=  Quotient zwischen Endwert und Anfangswert (ohne Index), oft als Wachstumsrate bezeichnet.
    • (Ej/Ai) := Quotient zwischen Endwert mit der Ordnungszahl j und Anfangswert mit der Ordnungszahl in, oft als Wachstumsrate bezeichnet.
    • (E/A)/n :=  Normierung auf n: Quotient zwischen Endwert und Anfangswert (ohne Index) geteilt durch einen Normwert,
    • (Ej/Ai)/n := Normierung auf n: Quotient zwischen Endwert mit der Ordnungszahl j und Anfangswert mit der Ordnungszahl i, oft als Wachstumsrate bezeichnet.
    • Allgemein exponentielles Wachstum liegt vor, wenn der Zuwachs Z wächst, das gilt schon für die quadratische Gleichung.
        Mathematische Wachstumsmodelle
    • y=fit(x,y, 'typ') Klasse der Kurvenfit-Algorithmen > Beispiel Fitten der 7. Tage-Mittelwerte der Neu-Infektionen der 9. Welle vom 07.04.-23.05.2021.
    • y=ax+b   Lineares Wachstum
    • y=ax^2+b  Quadratisches Wachstum
    • y=ax^n   Polynomiales Wachstum
    • y=a^x   Exponentielles Wachstum, verkürzt das Wachstum, das durch eine Exponentialgleichung beschreibbar ist, meist ist aber y=e^xt gemeint.
    • LN(E/A)/n :=  Exponentielles Wachstumsmodell: Quotient zwischen Endwert und Anfangswert (ohne Index) geteilt durch die Anzahl der Zähleinheiten, oft als Wachstumsrate bezeichnet.
    • LN(Ej/Ai)/n := Exponentielles Wachstumsmodell: Quotient zwischen Endwert mit der Ordnungszahl j und Anfangswert mit der Ordnungszahl i geteilt durch die Anzahl der Zähleinheiten, oft als Wachstumsrate bezeichnet.
    • Logistisches Wachstum. S oder ogivenförmig, exponentielles Wachstum mit Sättigungsgrenze.
    V := Vorgänger eines Wertepaares
    N := Nachfolger eines Wertepaares
    i := Index für die Ordnungsposition in der Anordnung der Wachstumswerte, W6 ist z.B. der Wert an siebter Stelle in der Anordnung. Im Beispiel der 30 Werte oben ist das der Wert 8.
    Z := Zuwachs 1. Ordnung
    ZZ :=  Zuwachs2 Zuwachs des Zuwachses 1. Ordnung
    ZZZ:=  Zuwachs3 Zuwachs des Zuwachses 2. Ordnung
    Zz :=  Zuwachsz Zuwachs des Zuwachses z. Ordnung
    3M := Gleitender Mittelwert über die letzten 3 Werte (inklusive)
    5M := Gleitender Mittelwert über die letzten 5 Werte (inklusive)
    7M := Gleitender Mittelwert über die letzten 7 Werte (inklusive)
    GM := Gleitender Mittelwert über die letzten G Werte (inklusive), G = 1,2,3, ....


    Wachstumskriterien oder Wachstumsvarianten
    Monotonie:
        strenge Monotonie: jeder Nachfolger ist größer als der Vorgänger.
        schwache Monotonie: kein Nachfolger ist kleiner als der Vorgänge, also mindestens gleich.
    Differenzkriterien zwischen Nachfolger und Vorgänger
    Schwellenwertkriterien
    Wachstumsraten


    Wachstums-Grundmodelle

    Allgemeines Grundmodell.

    Lineares Wachstum
    Wachsen z.B. Neuinfektionen täglich konstant um 1000, dann liegt zwar lineares Wachstum vor, aber nach 10 Tagen ist man bei A+10.000. Je nach Anfangswert A kann dies sehr viel oder auch weniger sein. Bei A=1000, hat sich der Wert 1 Tag später verdoppelt und 10 Tage später verzehnfacht. Auch wenn dies kein exponentielles Wachstumsmodell erfüllt, so ist es gewöhnlich doch ein extremes Wachstum. Je nachdem welche Wachstumsmessung f  man vornimmt, ergeben sich ganz unterschiedliche Wachstumsraten.

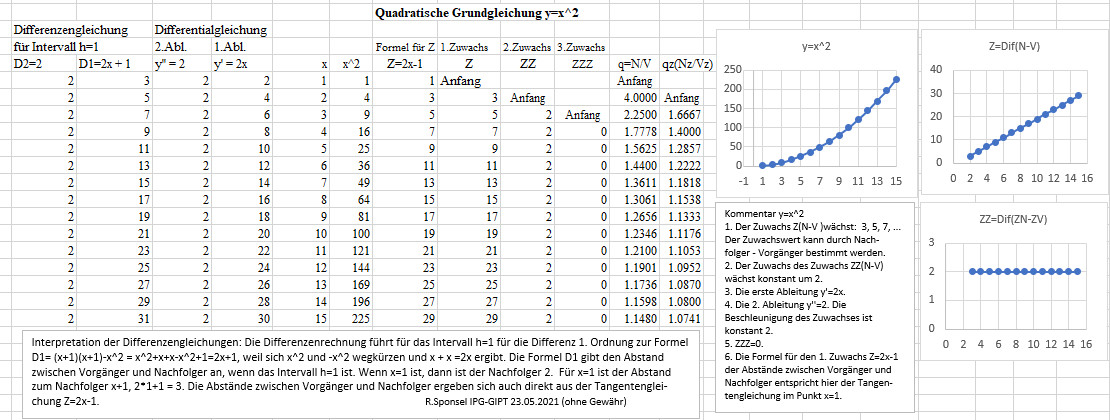
    Quadratisches Wachstum
    Auch diese einfache Quadratfunktion beschreibt eine exponentielle Entwicklung, weil der Zuwachs wächst. Exponentielle Entwicklungen, definiert als der Zuwachs wächst, sind also keineswegs an Exponentialgleichungen gebunden.


     

    Kubisches Wachstum
    Wie diese kubische Wachstumsformel x^3 zeigt, gibt es Nichtexponentialgleichungen, die hochgradig exponentielle Entwicklungen (das Wachstum wächst) anzeigen.


     

    Exponentielles Wachstum
    Die klassische Formel für exponentielles Wachstum ist die des sog. "organischen" Wachstums y= Aeqt mit a als Anfangswert, e als Eulersche Zahl 2.71828..., q als Wachstumsrate und t als Anzahl der Zeiteinheiten (Stunden, Tage, ...Jahre ...).

    Praktisches Feststellen, ob eine exponentielle Entwicklung vorliegt
    In jeder Zeitreihe, die durch eine Exponentialgleichung beschreibbar ist, wachsen die Zuwächse (>Zinses-Zins-Modell, Organisches Wachstum). "Wachsen die Zuwächse nicht, handelt es sich nicht um Daten, die einer Exponentialgleichung folgen. Daher ist es ganz leicht und ohne jede Kenntnis mehr oder minder komplizierter mathematischer Formeln herauszufinden, ob eine Zeitreihe eine exponentielle Entwicklung zeigt. Man muss nur die Zuwächse Z = Nachfolgerwert - Vorgängerwert bilden und sehen, ob diese fortlaufend größer werden. Ist das nicht der Fall, kann es sicht nicht um eine exponentielle Entwicklung handeln. Einfaches allgemeines

    Beispiel und Gegenbeispiel:
     
    Beispiel exponent. Entw.
    Einheit  Wert    Zuwachs
    Tag-7     28       7
    Tag-6     21       6
    Tag-5     15       5
    Tag-4     10       4
    Tag-3     6        3
    Tag-2     3        2
    Tag-1     1      Anfang 
    Tag-0  Anfang     		 Man sieht im linken Abschnitt, dass die Werte und die Zuwächse zwischen den Werten steigen, d.h. es handelt sich um eine exponentielle Entwicklung.
    Und man sieht im rechten Abschnitt, betrachtet man nur die unmittelbaren  Vorgänger und Nachfolger, dass die Zuwachsbedingungen zwei Mal verletzt sind: von Tag-3 auf Tag-4 und von Tag-6 auf Tag-7.    		 Gegenbeispiel exponent. Entw.
    Einheit  Wert    Zuwachs
    Tag-7     16      -2
    Tag-6     18       8
    Tag-5     10       4
    Tag-4     6        1
    Tag-3     7        4
    Tag-2     3        2
    Tag-1     1      Anfang 
    Tag-0  Anfang 

    Anmerkung: es ist natürlich möglich, dass Zwischenbereiche exponentielle Entwicklungen enthalten. Es ist daher natürlich immer wichtig, den Zeitraum mit Anfangs- und Endwert genau anzugeben.
     

    Logistisches Wachstum

    Zinses-Zins-Modell
    kn = aqn  mit a:= Anfangswert ("Anfangskapital"), Wachstumsfaktor q= 1 + p/100 (Zinsfaktor)
     
    Kommentar:
    Man sieht, dass nicht nur der Zuwachs (Z), sondern auch der Zuwachs des Zuwachs (ZZ) usw. wächst, was für alle steigenden Exponentialgleichungen gilt. Umgekehrt gibt es daher für die Prüfung, ob eine exponentielle Entwicklung vorliegt ein einfaches Kriterium: der Zuwachs muss wachsen. Man braucht gar keine Formeln, man bildet einfach die Zuwächse durch Nachfolgerwert - Vorgängerwert, wobei man kleinere Abweichungen mit Toleranz- bereichen tolerieren kann.

    Organisches-Wachstum (der mathematisch-naturwissenschaftliche Klassiker unter den Wachstumsfunktionen)
    Auch hier sieht man sehr schön, dass beim organischen Wachstum die Zuwächse Z, ZZ, ZZZ, ... wachsen. Wachsen die Zuwächse nicht, liegt keine exponentielle Wachstumsfunktion vor.
        Kommentar zu den Graphiken: Zunächst verläuft das Wachstum mit dem Anfangswert 1 sehr langsam und dem Anschein nach linear. Dass es sich hier um ein gefährliches exponentielles Wachstum handelt, sieht man an den Steigerungen ab etwa 100. Wäre die Zeiteinheit 1 Tag, so hätte sich nach 100 Tagen (beige Markierung, linke Tabelle) der Anfangswert ver7.4facht. In einem Jahr hätte sich der Anfangswert bei einer Wachstumsrate von 2%, also 0.02, um das 1480fache (blaue Markierung, linke Tabelle) vervielfacht. Beträgt die Wachstumsrate 5%, also 0.05, so betrüge die Vervielfachung bei 100 Tagen (beige Markierung, rechte Tabelle) schon das 148fache und für ein Jahr schon das 84 Millionenfache (blaue Markierung, rechte Tabelle).
    Das Wachstum für den jeweils betrachteten Endwert y hängt von vier Größen (Parametern) ab: (1) Vom  Anfangswert A. (2) Von der Wachstumsrate q, im Beispiel 0.02. (3) von der Anzahl der Zeiteinheiten t, im Beispiel von 1 bis 1000. (4) Von der Formel des Wachstumsmodells, hier y=Ae^qt.
    Anmerkung: Zum mathematischen Wesen der Exponentialgleichungen gehört, dass sie beliebig oft abgeleitet werden können und jeder Zuwachs Z, ZZ, ZZZ, ... weiter wächst.


    Wachstumsfragen in der Corona-Pandemie  > Aktuell

    Zur  Wachstumsmessung  der Covid-19 Entwicklung braucht man eine klares Wellen- und Wachstumskonzept und zuverlässige Zahlen. Beides stellt das RKI für Deutschland und seine Gebietskörperschaften nicht zur Verfügung, so dass wir uns mit sehr groben und fehlerbehafteten Schätzzahlen abfinden müssen. Entsprechend schlecht ist auch die Berichterstattung der Qualitäts- und Wahrheitsmedien, die im wesentlichen ungeprüft und unkritisch wiedergeben, was das RKI so von sich gibt oder eigene Methoden entwickeln müssen. So behilft sich z.B. die Tagesschau z.B. Vergleichswerten der Neuinfektionszahlen zur Vorwoche. Besser wäre natürlich 7-Tage-Mittelwerte, aber diese gehen in die Inzidenzentwicklung ein über die auch berichtet wird. Wer  Wellen  nur bis 3 wahrnehmen und zählen kann, der verfügt auch höchstens über drei Anfangswerte zum Bezug und Vergleich.

    Tagesschau-Vergleiche


     


    Exponentielle-Wachstumsanalysen-Corona

    Verhältnis 7TM-Intensivbehandlungen / 7TM-Neu-Infektionen[Neue Rechnung; alte Rechnung 2]
     
    Kommentar 29.01.2022

    Obwohl die Omikronzahlen explodieren, sinken die Intensivbettenbelegeungen bis 28.01.2022. Die stark sinkende Kurve wird also durch zwei Faktoren bestimmt:  einerseits durch die hohen Neu-Infektionszahlen (Nenner) und andererseits durch die sinkenden Intensivbetten-
    belegungen (Zähler). 
     
     
     
     
     
     
     
     
     
     
     
     
     
     
     

     
    _
    Kurvenanalyse Intensivbettenbelegungen 4. Welle 22.07.21 -aktuell.  Zum Verhältnis.
    Korrekturen 6.10.21, 5.10..21, 16.9-19.9.21
     
    Die Intensivbehandlungen werden hier nicht länger dokumentiert, weil dies schon in mehreren öffentlichen Seiten geschieht: Intensivbehandlungen, Hospitalisierungen, RKI-Radar.

    31.10.2022  Der 7TM der Intensivbettenbelegungen fallen zum 8. Mal nach 31x steigen: 7TM=1640.4 nach 1666.1,  TW=1571 nach 1573
    30.10.2022  Der 7TM der Intensivbettenbelegungen fallen zum 7. Mal nach 31x steigen: 7TM=1666.1 nach 1686.6,  TW=1573 nach 1580
    29.10.2022  Der 7TM der Intensivbettenbelegungen fallen zum 6. Mal nach 31x steigen: 7TM=1686.6 nach 1707.3,  TW=1580 nach 1631
    28.10.2022  Der 7TM der Intensivbettenbelegungen fallen zum 5. Mal nach 31x steigen: 7TM=1707.3 nach 1723.0,  TW=1631 nach 1670
    27.10.2022  Der 7TM der Intensivbettenbelegungen fallen zum 4. Mal nach 31x steigen: 7TM=1723.0 nach 1740.0,  TW=1670 nach 1707
    26.10.2022  Der 7TM der Intensivbettenbelegungen fallen zum 3. Mal nach 31x steigen: 7TM=1740.0 nach 1753.1,  TW=1707 nach 1751
    25.10.2022  Der 7TM der Intensivbettenbelegungen fallen zum 2. Mal nach 31x steigen: 7TM=1753.1 nach 1762.6,  TW=1751 erneut nach 1751
    24.10.2022  Der 7TM der Intensivbettenbelegungen fallen zum 1. Mal nach 31x steigen: 7TM=1762.6 nach 1764.6,  TW=1751 nach 1716
    23.10.2022  Der 7TM der Intensivbettenbelegungen steigen zum 31x  nach 8.x fallen: 7TM=1764.6 nach 1760.0,  TW=1716 nach 1725
    22.10.2022  Der 7TM der Intensivbettenbelegungen steigen zum 30x  nach 8.x fallen: 7TM=1760.0 nach 1747.1,  TW=1725 nach 1741
    21.10.2022  Der 7TM der Intensivbettenbelegungen steigen zum 29x  nach 8.x fallen: 7TM=1747.1 nach 1735.6,  TW=1741 nach 1789
    20.10.2022  Der 7TM der Intensivbettenbelegungen steigen zum 28x  nach 8.x fallen: 7TM=1735.6 nach 1721.1,  TW=1789 nach 1799
    19.10.2022  Der 7TM der Intensivbettenbelegungen steigen zum 27x  nach 8.x fallen: 7TM=1721.1 nach 1700.0,  TW=1799 nach 1817
    18.10.2022  Der 7TM der Intensivbettenbelegungen steigen zum 26x  nach 8.x fallen: 7TM=1700.0 nach 1675.7,  TW=1817 nach 1765
    17.10.2022  Der 7TM der Intensivbettenbelegungen steigen zum 25x  nach 8.x fallen: 7TM=1675.7 nach 1650.9,  TW=1765 nach 1684
    16.10.2022  Der 7TM der Intensivbettenbelegungen steigen zum 24x  nach 8.x fallen: 7TM=1650.9 nach 1617.9,  TW=1684 nach 1635
    15.10.2022  Der 7TM der Intensivbettenbelegungen steigen zum 23x  nach 8.x fallen: 7TM=1617.9 nach 1585.1,  TW=1635 nach 1660
    14.10.2022  Der 7TM der Intensivbettenbelegungen steigen zum 22x  nach 8.x fallen: 7TM=1585.1 nach 1543.1,  TW=1660 nach 1688
    13.10.2022  Der 7TM der Intensivbettenbelegungen steigen zum 21x  nach 8.x fallen: 7TM=1543.1 nach 1493.9,  TW=1688 nach 1651
    12.10.2022  Der 7TM der Intensivbettenbelegungen steigen zum 20x  nach 8.x fallen: 7TM=1493.9 nach 1442.9,  TW=1651 nach 1647
    11.10.2022  Der 7TM der Intensivbettenbelegungen steigen zum 19x  nach 8.x fallen: 7TM=1442.9 nach 1378.3,  TW=1647 nach 1591
    10.10.2022  Der 7TM der Intensivbettenbelegungen steigen zum 18x  nach 8.x fallen: 7TM=1378.3 nach 1298.4,  TW=1591 nach 1453
    09.10.2022  Der 7TM der Intensivbettenbelegungen steigen zum 17x  nach 8.x fallen: 7TM=1298.4 nach 1230.4,   TW=1453 nach 1406
    08.10.2022  Der 7TM der Intensivbettenbelegungen steigen zum 16x  nach 8.x fallen: 7TM=1230.4 nach 1161.9,   TW=1406 nach 1366
    07.10.2022  Der 7TM der Intensivbettenbelegungen steigen zum 15x  nach 8.x fallen: 7TM=1161.9 nach 1095.3,  TW=1366 nach 1343
    06.10.2022  Der 7TM der Intensivbettenbelegungen steigen zum 14x  nach 8.x fallen: 7TM=1095.3 nach 1026.9,  TW=1343 nach 1294
    05.10.2022  Der 7TM der Intensivbettenbelegungen steigen zum 13x  nach 8.x fallen: 7TM=1026.9 nach 962.0,  TW=1294 nach 1195
    04.10.2022  Der 7TM der Intensivbettenbelegungen steigen zum 12x  nach 8.x fallen: 7TM=962.0 nach 909.7,  TW=1195 nach 1032
    03.10.2022  Der 7TM der Intensivbettenbelegungen steigen zum 11x  nach 8.x fallen: 7TM=909.7 nach 871.9 ,  TW=1032 nach 977 02.10.2022  Der 7TM der Intensivbettenbelegungen steigen zum 10x  nach 8.x fallen: 7TM=871.9 nach 833.9 ,  TW=977 nach 926.
    01.10.2022  Der 7TM der Intensivbettenbelegungen steigen zum 9x  nach 8.x fallen: 7TM=833.9 nach 800.9,  TW=926 nach 900.
    30.09.2022  Der 7TM der Intensivbettenbelegungen steigen zum 8x  nach 8.x fallen: 7TM=800.9 nach 774.6 ,  TW=900 nach 864.
    29.09.2022  Der 7TM der Intensivbettenbelegungen steigen zum 7x  nach 8.x fallen: 7TM=774.6 nach 750.7,  TW=864 nach 840.
    28.09.2022  Der 7TM der Intensivbettenbelegungen steigen zum 6x  nach 8.x fallen: 7TM=750.7 nach 728.7,  TW=840 nach 829.
    27.09.2022  Der 7TM der Intensivbettenbelegungen steigen zum 5x  nach 8.x fallen: 7TM=728.7 nach 707.0,  TW=829 nach 767.
    26.09.2022  Der 7TM der Intensivbettenbelegungen steigen zum 4x  nach 8.x fallen: 7TM=707.0 nach 690.9,  TW=767 nach 711.
    25.09.2022  Der 7TM der Intensivbettenbelegungen steigen zum 3x  nach 8.x fallen: 7TM=690.9 nach 679.4,  TW=711 nach 695.
    24.09.2022  Der 7TM der Intensivbettenbelegungen steigen zum 2x  nach 8.x fallen: 7TM=679.4 nach 672.1,  TW=695 nach 716.
    23.09.2022  Der 7TM der Intensivbettenbelegungen steigen zum 1x  nach 8.x fallen: 7TM=672.1 nach 666.1,  TW=716 nach 697.
    22.09.2022  Der 7TM der Intensivbettenbelegungen fallen zum 8.x nach 1x steigen nach zuvor 45x fallen und davor 50 Anstiegen: 7TM=666.1 nach 667.0,  TW=697 nach 686.
    21.09.2022  Der 7TM der Intensivbettenbelegungen fallen zum 7.x nach 1x steigen nach zuvor 45x fallen und davor 50 Anstiegen: 7TM=667.0 nach 672.3,  TW=686 nach 677.
    20.09.2022  Der 7TM der Intensivbettenbelegungen fallen zum 6.x nach 1x steigen nach zuvor 45x fallen und davor 50 Anstiegen: 7TM=672.3 nach 677.0,  TW=677 nach 654.
    19.09.2022  Der 7TM der Intensivbettenbelegungen fallen zum 5.x nach 1x steigen nach zuvor 45x fallen und davor 50 Anstiegen: 7TM=677.0 nach 680.3,  TW=654 nach 631.
    18.09.2022  Der 7TM der Intensivbettenbelegungen fallen zum 4.x nach 1x steigen nach zuvor 45x fallen und davor 50 Anstiegen: 7TM=680.3 nach 684.3 ,  TW=631 nach 644.
    17.09.2022  Der 7TM der Intensivbettenbelegungen fallen zum 3.x nach 1x steigen nach zuvor 45x fallen und davor 50 Anstiegen: 7TM=684.3 nach 687.3 ,  TW=644 nach 674.
    16.09.2022  Der 7TM der Intensivbettenbelegungen fallen zum 2.x nach 1x steigen nach zuvor 45x fallen und davor 50 Anstiegen: 7TM=687.3 nach 691.1,  TW=674 nach 703
    15.09.2022  Der 7TM der Intensivbettenbelegungen fallen nach 1x steigen nach zuvor 44x fallen und davor 50 Anstiegen: 7TM=691.1 nach 692.4,  TW=703 nach 7230
    14.09.2022  Der 7TM der Intensivbettenbelegungen steigen zum 1. Mal nach 44x fallen und davor 50 Anstiegen: 7TM=692.4 nach 690.4,  TW=723 nach 710
    13.09.2022  Der 7TM der Intensivbettenbelegungen fallen 44. Mal nach 50 Anstiegen: 7TM=690.4 nach 692.6,  TW=710 nach 677
    12.09.2022  Der 7TM der Intensivbettenbelegungen fallen 43. Mal nach 50 Anstiegen: 7TM=692.6 nach 703.0,  TW=677 nach 659
    11.09.2022  Der 7TM der Intensivbettenbelegungen fallen 42. Mal nach 50 Anstiegen: 7TM=703.0 nach 713.6,  TW=659 nach 665
    10.09.2022  Der 7TM der Intensivbettenbelegungen fallen 41. Mal nach 50 Anstiegen: 7TM=713.6 nach 723.6,  TW=665 nach 701
    09.09.2022  Der 7TM der Intensivbettenbelegungen fallen 40. Mal nach 50 Anstiegen: 7TM=723.6 nach 730.7,  TW=701 nach 712
    08.09.2022  Der 7TM der Intensivbettenbelegungen fallen 39. Mal nach 50 Anstiegen: 7TM=730.7 nach 736.7,  TW=712 nach 709
    07.09.2022  Der 7TM der Intensivbettenbelegungen fallen 38. Mal nach 50 Anstiegen: 7TM=736.7 nach 746.9,  TW=709 nach 725
    06.09.2022  Der 7TM der Intensivbettenbelegungen fallen 37. Mal nach 50 Anstiegen: 7TM=746.9 nach 758.9,  TW=725 nach 750
    05.09.2022  Der 7TM der Intensivbettenbelegungen fallen 36. Mal nach 50 Anstiegen: 7TM=758.9 nach 770.7,  TW=750 nach 733
    04.09.2022  Der 7TM der Intensivbettenbelegungen fallen 35. Mal nach 50 Anstiegen: 7TM=770.7 nach 771.0,  TW=733 nach 735
    03.09.2022  Der 7TM der Intensivbettenbelegungen fallen 34. Mal nach 50 Anstiegen: 7TM=784.7 nach 800.0,  TW=735 nach 751
    02.09.2022  Der 7TM der Intensivbettenbelegungen fallen 33. Mal nach 50 Anstiegen: 7TM=800.0 nach 816.1,  TW=751 nach 754
    01.09.2022  Der 7TM der Intensivbettenbelegungen fallen 32. Mal nach 50 Anstiegen: 7TM=816.1 nach 833.7,  TW=754 nach 780
    31.08.2022  Der 7TM der Intensivbettenbelegungen fallen 31. Mal nach 50 Anstiegen: 7TM=833.7 nach 849.1,  TW=780 nach 809
    30.08.2022  Der 7TM der Intensivbettenbelegungen fallen 30. Mal nach 50 Anstiegen: 7TM=849.1 nach 868.7,  TW=809 nach 833
    29.08.2022  Der 7TM der Intensivbettenbelegungen fallen 29. Mal nach 50 Anstiegen: 7TM=868.7 nach 889.0,  TW=833 nach 831
    28.08.2022  Der 7TM der Intensivbettenbelegungen fallen 28. Mal nach 50 Anstiegen: 7TM=889.0 nach 910.0,  TW=831 nach 842
    27.08.2022  Der 7TM der Intensivbettenbelegungen fallen 27. Mal nach 50 Anstiegen: 7TM=910.0 nach 928.9,  TW=842 nach 864
    26.08.2022  Der 7TM der Intensivbettenbelegungen fallen 26. Mal nach 50 Anstiegen: 7TM=928.9 nach 951.9,  TW=864 nach 877
    25.08.2022  Der 7TM der Intensivbettenbelegungen fallen 25. Mal nach 50 Anstiegen: 7TM=951.9 nach 981.6,  TW=877 nach 888
    24.08.2022  Der 7TM der Intensivbettenbelegungen fallen 24. Mal nach 50 Anstiegen: 7TM=981.6 nach 1005.1,  TW=888 nach 946
    23.08.2022  Der 7TM der Intensivbettenbelegungen fallen 23. Mal nach 50 Anstiegen: 7TM=1005.1 nach 1028.9,  TW=946 nach 975
    22.08.2022  Der 7TM der Intensivbettenbelegungen fallen 22. Mal nach 50 Anstiegen: 7TM=1028.9 nach 1051.0,  TW=975 nach 978
    21.08.2022  Der 7TM der Intensivbettenbelegungen fallen 21. Mal nach 50 Anstiegen: 7TM=1051.0 nach 1074.0,  TW=978 nach 974
    20.08.2022  Der 7TM der Intensivbettenbelegungen fallen 20. Mal nach 50 Anstiegen: 7TM=1074.0 nach 1095.01,  TW=974 nach 1025
    19.08.2022  Der 7TM der Intensivbettenbelegungen fallen 19. Mal nach 50 Anstiegen: 7TM=1095.01 nach 111.7,  TW=1025 nach 1085
    18.08.2022  Der 7TM der Intensivbettenbelegungen fallen 18. Mal nach 50 Anstiegen: 7TM=1111.7 nach 1123.6 ,  TW=1085 nach 1053
    17.08.2022  Der 7TM der Intensivbettenbelegungen fallen 17. Mal nach 50 Anstiegen: 7TM=1123.6 nach 1148.4,  TW=1053 nach 1112
    16.08.2022  Der 7TM der Intensivbettenbelegungen fallen 16. Mal nach 50 Anstiegen: 7TM=1148.4 nach 1169.9,  TW=1112 nach 1130
    15.08.2022  Der 7TM der Intensivbettenbelegungen fallen 15. Mal nach 50 Anstiegen: 7TM=1169.9 nach 1196.3,  TW=1130 nach 1139
    14.08.2022  Der 7TM der Intensivbettenbelegungen fallen 14. Mal nach 50 Anstiegen: 7TM=1196.3 nach 1214.6,  TW=1139 nach 1124
    13.08.2022  Der 7TM der Intensivbettenbelegungen fallen 13. Mal nach 50 Anstiegen: 7TM=1214.6 nach 1244.0,  TW=1124 nach 1142
    12.08.2022  Der 7TM der Intensivbettenbelegungen fallen 12. Mal nach 50 Anstiegen: 7TM=1244.0 nach 1274.1,  TW=1142 nach 1168
    11.08.2022  Der 7TM der Intensivbettenbelegungen fallen 11. Mal nach 50 Anstiegen: 7TM=1274.1 nach 1304.7,  TW=1168 nach 1227
    10.08.2022  Der 7TM der Intensivbettenbelegungen fallen 10. Mal nach 50 Anstiegen: 7TM=1304.7 nach 1325.1,  TW=1227 nach 1262
    09.08.2022  Der 7TM der Intensivbettenbelegungen fallen 9. Mal nach 50 Anstiegen: 7TM=1325.1 nach 1347.6,  TW=1262 nach 1315
    08.08.2022  Der 7TM der Intensivbettenbelegungen fallen 8. Mal nach 50 Anstiegen: 7TM=1347.6 nach 1365.9,  TW=1315 nach 1267
    07.08.2022  Der 7TM der Intensivbettenbelegungen fallen 7. Mal nach 50 Anstiegen: 7TM=1365.9 nach 1387.6, TW=1267 nach 1327
    06.08.2022  Der 7TM der Intensivbettenbelegungen fallen 6. Mal nach 50 Anstiegen: 7TM=1387.6 nach 1402.9, TW=1327 nach 1353
    05.08.2022  Der 7TM der Intensivbettenbelegungen fallen 5. Mal nach 50 Anstiegen: 7TM=1402.9 nach 1419.7, TW=1353 nach 1382
    04.08.2022  Der 7TM der Intensivbettenbelegungen fallen 4. Mal nach 50 Anstiegen: 7TM=1419.7 nach 1439.6, TW=1382 nach 1370
    03.08.2022  Der 7TM der Intensivbettenbelegungen fallen 3. Mal nach 50 Anstiegen: 7TM=1439.6 nach 1466.7, TW=1370 nach 1419
    02.08.2022  Der 7TM der Intensivbettenbelegungen fallen 2. Mal nach 50 Anstiegen: 7TM=1466.7 nach 1491.9, TW=1419 nach 1443
    01.08.2022  Der 7TM der Intensivbettenbelegungen fallen 1. Mal nach 50 Anstiegen: 7TM=1491.9 nach 1504.6, TW=1443 nach 1419
    31.07.2022  Der 7TM der Intensivbettenbelegungen steigen zum 50. Mal nach 75 Mal fallen: 7TM=1504.6 nach 1503.9, TW=1419 nach 1434
    30.07.2022  Der 7TM der Intensivbettenbelegungen steigen zum 49. Mal nach 75 Mal fallen: 7TM=1503.9 nach 1493.7, TW=1434 nach 1471
    29.07.2022  Der 7TM der Intensivbettenbelegungen steigen zum 48. Mal nach 75 Mal fallen: 7TM=1493.7 nach 1478.3, TW=1471 nach 1521
    28.07.2022  Der 7TM der Intensivbettenbelegungen steigen zum 47. Mal nach 75 Mal fallen: 7TM=1478.3 nach 1455.7, TW=1521 nach 1560
    27.07.2022  Der 7TM der Intensivbettenbelegungen steigen zum 46. Mal nach 75 Mal fallen: 7TM=1455.7 nach 1419.0,  TW=1560 nach 1595
    26.07.2022  Der 7TM der Intensivbettenbelegungen steigen zum 45. Mal nach 75 Mal fallen: 7TM=1419.0 nach 1377.4,  TW=1595 nach 1532
    25.07.2022  Der 7TM der Intensivbettenbelegungen steigen zum 44. Mal nach 75 Mal fallen: 7TM=1377.4 nach 1344.0,  TW=1532 nach 1414
    24.07.2022  Der 7TM der Intensivbettenbelegungen steigen zum 43. Mal nach 75 Mal fallen: 7TM=1344.0 nach 1322.1,  TW=1414 nach 1381
    23.07.2022  Der 7TM der Intensivbettenbelegungen steigen zum 42. Mal nach 75 Mal fallen: 7TM=1322.1 nach 1296.3 ,  TW=1381 nach 1363
    22.07.2022  Der 7TM der Intensivbettenbelegungen steigen zum 41. Mal nach 75 Mal fallen: 7TM=1296.3 nach 1272.1 ,  TW=1363 erneut nach 1363
    21.07.2022  Der 7TM der Intensivbettenbelegungen steigen zum 40. Mal nach 75 Mal fallen: 7TM=1272.1 nach 1251.4 ,  TW=1363 nach 1303
    20.07.2022  Der 7TM der Intensivbettenbelegungen steigen zum 39. Mal nach 75 Mal fallen: 7TM=1251.4 nach 1238.3,  TW=1303 nach 1304
    19.07.2022  Der 7TM der Intensivbettenbelegungen steigen zum 38. Mal nach 75 Mal fallen: 7TM=1238.3 nach 1221.3, TW=1304 nach 1298
    18.07.2022  Der 7TM der Intensivbettenbelegungen steigen zum 37. Mal nach 75 Mal fallen: 7TM=1221.3 nach 1199.3, TW=1298 nach 1243
    17.07.2022  Der 7TM der Intensivbettenbelegungen steigen zum 36. Mal nach 75 Mal fallen: 7TM=1199.3 nach 1175.3, TW=1243 nach 1200
    16.07.2022  Der 7TM der Intensivbettenbelegungen steigen zum 35. Mal nach 75 Mal fallen: 7TM=1175.3 nach 1150.7, TW=1200 nach 1194
    15.07.2022  Der 7TM der Intensivbettenbelegungen steigen zum 34. Mal nach 75 Mal fallen: 7TM=1150.7 nach 1129.7, TW=1194 nach 1218
    14.07.2022  Der 7TM der Intensivbettenbelegungen steigen zum 33. Mal nach 75 Mal fallen: 7TM=1129.7 nach 1102.3, TW=1218 nach 1211
    13.07.2022  Der 7TM der Intensivbettenbelegungen steigen zum 32. Mal nach 75 Mal fallen: 7TM=1102.3 nach 1076.1, TW=1211 nach 1185
    12.07.2022  Der 7TM der Intensivbettenbelegungen steigen zum 31. Mal nach 75 Mal fallen: 7TM=1076.1 nach 1056.7, TW=1185 nach 1144
    11.07.2022  Der 7TM der Intensivbettenbelegungen steigen zum 30. Mal nach 75 Mal fallen: 7TM=1056.7 nach 1042.7, TW=1144 nach 1075
    10.07.2022  Der 7TM der Intensivbettenbelegungen steigen zum 29. Mal nach 75 Mal fallen: 7TM=1042.7 nach 1030.0, TW=1075 nach 1028
    09.07.2022  Der 7TM der Intensivbettenbelegungen steigen zum 28. Mal nach 75 Mal fallen: 7TM=1030.0 nach 1021.6, TW=1028 nach 1047
    08.07.2022  Der 7TM der Intensivbettenbelegungen steigen zum 27. Mal nach 75 Mal fallen: 7TM=1021.6 nach 1009.6, TW=1047 nach 1026
    07.07.2022  Der 7TM der Intensivbettenbelegungen steigen zum 26. Mal nach 75 Mal fallen: 7TM=1009.6 nach 994.0, TW=1026 nach 1028
    06.07.2022  Der 7TM der Intensivbettenbelegungen steigen zum 25. Mal nach 75 Mal fallen: 7TM=994.0 nach 977.7, TW=1028 nach 1049
    05.07.2022  Der 7TM der Intensivbettenbelegungen steigen zum 24. Mal nach 75 Mal fallen: 7TM=977.7 nach 964.9, TW=1049 nach 1046
    04.07.2022  Der 7TM der Intensivbettenbelegungen steigen zum 23. Mal nach 75 Mal fallen: 7TM=964.9 nach 945.0, TW=1046 nach 986
    03.07.2022  Der 7TM der Intensivbettenbelegungen steigen zum 22. Mal nach 75 Mal fallen: 7TM=945.0 nach 920.4, TW=986 nach 969
    02.07.2022  Der 7TM der Intensivbettenbelegungen steigen zum 21. Mal nach 75 Mal fallen: 7TM=920.4 nach 892.0, TW=969 nach 963
    01.07.2022  Der 7TM der Intensivbettenbelegungen steigen zum 20. Mal nach 75 Mal fallen: 7TM=892.0 nach 865.7, TW=963 nach 917
    30.06.2022  Der 7TM der Intensivbettenbelegungen steigen zum 19. Mal nach 75 Mal fallen: 7TM=865.7 nach 847.3, TW=917 nach 914
    29.06.2022  Der 7TM der Intensivbettenbelegungen steigen zum 18. Mal nach 75 Mal fallen: 7TM=847.3 nach 825.4 , TW=914 nach 959
    28.06.2022  Der 7TM der Intensivbettenbelegungen steigen zum 17. Mal nach 75 Mal fallen: 7TM=825.4 nach 800.0,  TW=959 nach 907
    27.06.2022  Der 7TM der Intensivbettenbelegungen steigen zum 16. Mal nach 75 Mal fallen: 7TM=800.0 nach 774.4,  TW=907 nach 814
    26.06.2022  Der 7TM der Intensivbettenbelegungen steigen zum 15. Mal nach 75 Mal fallen: 7TM=774.4 nach 758.1,  TW=814 nach 770
    25.06.2022  Der 7TM der Intensivbettenbelegungen steigen zum 14. Mal nach 75 Mal fallen: 7TM=758.1 nach 743.4,  TW=770 nach 779
    24.06.2022  Der 7TM der Intensivbettenbelegungen steigen zum 13. Mal nach 75 Mal fallen: 7TM=743.4 nach 728.3,  TW=779 nach 788
    23.06.2022  Der 7TM der Intensivbettenbelegungen steigen zum 12. Mal nach 75 Mal fallen: 7TM=728.3 nach 695.3,  TW=788 nach 761
    22.06.2022  Der 7TM der Intensivbettenbelegungen steigen zum 11. Mal nach 75 Mal fallen: 7TM=710.6 nach 695.3,  TW=761 nach 781
    21.06.2022  Der 7TM der Intensivbettenbelegungen steigen zum 10. Mal nach 75 Mal fallen: 7TM=695.3 nach 678.1,  TW=781 nach 728
    20.06.2022  Der 7TM der Intensivbettenbelegungen steigen zum 9. Mal nach 75 Mal fallen: 7TM=678.1 nach 665.6,  TW=728 nach 700
    19.06.2022  Der 7TM der Intensivbettenbelegungen steigen zum 8. Mal nach 75 Mal fallen: 7TM=665.6 nach 652.9,  TW=700 nach 667
    18.06.2022  Der 7TM der Intensivbettenbelegungen steigen zum 7. Mal nach 75 Mal fallen: 7TM=652.9 nach 643.4,  TW=667 nach 673
    17.06.2022  Der 7TM der Intensivbettenbelegungen steigen zum 6. Mal nach 75 Mal fallen: 7TM=643.4 nach 635.7,  TW=673 nach 664
    16.06.2022  Der 7TM der Intensivbettenbelegungen steigen zum 5. Mal nach 75 Mal fallen: 7TM=635.7 nach 628.4,  TW=664 nach 654
    15.06.2022  Der 7TM der Intensivbettenbelegungen steigen zum 4. Mal nach 75 Mal fallen: 7TM=628.4 nach 622.7,  TW=654 nach 661
    14.06.2022  Der 7TM der Intensivbettenbelegungen steigen zum 3. Mal nach 75 Mal fallen: 7TM=622.7 nach 615.7,  TW=661 nach 640
    13.06.2022  Der 7TM der Intensivbettenbelegungen steigen zum 2. Mal nach 75 Mal fallen: 7TM=615.7 nach 613.3,  TW=640 nach 611
    12.06.2022  Der 7TM der Intensivbettenbelegungen steigen zum 1. Mal nach 75 Mal fallen: 7TM=613.3 nach 612.6,  TW=611 nach 601
    11.06.2022  Der 7TM der Intensivbettenbelegungen fallen zum 75 Mal nach 17x steigen: 7TM=612.6 nach 613.4,  TW=601 nach 619
    10.06.2022  Der 7TM der Intensivbettenbelegungen fallen zum 74 Mal nach 17x steigen: 7TM=613.4 nach 614.7,  TW=619 nach 613
    09.06.2022  Der 7TM der Intensivbettenbelegungen fallen zum 73 Mal nach 17x steigen: 7TM=614.7 nach 618.1,  TW=613 nach 614
    08.06.2022  Der 7TM der Intensivbettenbelegungen fallen zum 72 Mal nach 17x steigen: 7TM=618.1 nach 624.7, TW=614 nach 612
    07.06.2022  Der 7TM der Intensivbettenbelegungen fallen zum 71 Mal nach 17x steigen: 7TM=624.7 nach 633.1, TW=612 nach 623
    06.06.2022  Der 7TM der Intensivbettenbelegungen fallen zum 70 Mal nach 17x steigen: 7TM=633.1 nach 638.3, TW=623 nach 606
    05.06.2022  Der 7TM der Intensivbettenbelegungen fallen zum 69 Mal nach 17x steigen: 7TM=638.3 nach 643.6, TW=606 nach 607
    04.06.2022  Der 7TM der Intensivbettenbelegungen fallen zum 68 Mal nach 17x steigen: 7TM=643.6 nach 649.7, TW=607 nach 628
    03.06.2022  Der 7TM der Intensivbettenbelegungen fallen zum 67 Mal nach 17x steigen: 7TM=649.7 nach 657.4, TW=628 nach 637
    02.06.2022  Der 7TM der Intensivbettenbelegungen fallen zum 66 Mal nach 17x steigen: 7TM=657.4 nach 664.1, TW=637 nach 660
    01.06.2022  Der 7TM der Intensivbettenbelegungen fallen zum 65 Mal nach 17x steigen: 7TM=661.1 nach 669.3, TW=660 nach 671
    31.05.2022  Der 7TM der Intensivbettenbelegungen fallen zum 64 Mal nach 17x steigen: 7TM=669.3 nach 673.3, TW=671 nach 659
    30.05.2022  Der 7TM der Intensivbettenbelegungen fallen zum 63 Mal nach 17x steigen: 7TM=673.3 nach 692.7, TW=659 nach 643
    29.05.2022  Der 7TM der Intensivbettenbelegungen fallen zum 62 Mal nach 17x steigen: 7TM=692.7 nach 715, TW=643 nach 650
    28.05.2022  Der 7TM der Intensivbettenbelegungen fallen zum 61 Mal nach 17x steigen: 7TM=715 nach 733.6, TW=650 nach 682
    27.05.2022  Der 7TM der Intensivbettenbelegungen fallen zum 60 Mal nach 17x steigen: 7TM=733.6 nach 749.9, TW=682 nach 684
    26.05.2022  Der 7TM der Intensivbettenbelegungen fallen zum 59 Mal nach 17x steigen: 7TM=749.9 nach 773.9, TW=684 nach 696
    25.05.2022  Der 7TM der Intensivbettenbelegungen fallen zum 58 Mal nach 17x steigen: 7TM=773.9 nach 801.0, TW=696 nach 720
    24.05.2022  Der 7TM der Intensivbettenbelegungen fallen zum 57 Mal nach 17x steigen: 7TM=801.0 nach 830.6, TW=720 nach 774
    23.05.2022  Der 7TM der Intensivbettenbelegungen fallen zum 56 Mal nach 17x steigen: 7TM=830.6 nach 852.3, TW=774 nach 799
    22.05.2022  Der 7TM der Intensivbettenbelegungen fallen zum 55 Mal nach 17x steigen: 7TM=852.3 nach 867.3, TW=799 nach 780
    21.05.2022  Der 7TM der Intensivbettenbelegungen fallen zum 54 Mal nach 17x steigen: 7TM=867.3 nach 883.3, TW=780 nach 796
    20.05.2022  Der 7TM der Intensivbettenbelegungen fallen zum 53 Mal nach 17x steigen: 7TM=883.3 nach 912.3, TW=796 nach 852
    19.05.2022  Der 7TM der Intensivbettenbelegungen fallen zum 52 Mal nach 17x steigen: 7TM=912.3 nach 932.0, TW=852 nach 886
    18.05.2022  Der 7TM der Intensivbettenbelegungen fallen zum 51 Mal nach 17x steigen: 7TM=932.0 nach 951.4, TW=886 nach 927
    17.05.2022  Der 7TM der Intensivbettenbelegungen fallen zum 50 Mal nach 17x steigen: 7TM=951.4 nach 969.1, TW=927 nach 926
    16.05.2022  Der 7TM der Intensivbettenbelegungen fallen zum 49 Mal nach 17x steigen: 7TM=969.1 nach 991.6, TW=926 nach 904
    15.05.2022  Der 7TM der Intensivbettenbelegungen fallen zum 48 Mal nach 17x steigen: 7TM=991.6 nach 1016.1, TW=904 nach 927
    14.05.2022  Der 7TM der Intensivbettenbelegungen fallen zum 47 Mal nach 17x steigen: 7TM=1016.1 nach 1035.3, TW=927 nach 964
    13.05.2022  Der 7TM der Intensivbettenbelegungen fallen zum 46 Mal nach 17x steigen: 7TM=1035.3 nach 1054.9, TW=964 nach 990
    12.05.2022  Der 7TM der Intensivbettenbelegungen fallen zum 45 Mal nach 17x steigen: 7TM=1054.9 nach 1079.64, TW=990 nach 1022
    11.05.2022  Der 7TM der Intensivbettenbelegungen fallen zum 44 Mal nach 17x steigen: 7TM=1079.6 nach 1104.4, TW=1022 nach 1051
    10.05.2022  Der 7TM der Intensivbettenbelegungen fallen zum 43 Mal nach 17x steigen: 7TM=1104.4 nach 1134.4, TW=1051 nach 1083
    09.05.2022  Der 7TM der Intensivbettenbelegungen fallen zum 42 Mal nach 17x steigen: 7TM=1134.4 nach 1166.1, TW=1083 nach 1076
    08.05.2022  Der 7TM der Intensivbettenbelegungen fallen zum 41 Mal nach 17x steigen: 7TM=1166.1 nach 1200.6, TW=1076 nach 1061
    07.05.2022  Der 7TM der Intensivbettenbelegungen fallen zum 40 Mal nach 17x steigen: 7TM=1200.6 nach 1275.0, TW=1061 nach 1101
    06.05.2022  Der 7TM der Intensivbettenbelegungen fallen zum 39 Mal nach 17x steigen: 7TM=1275.0 nach 1238.6, TW=1101 nach 1163
    05.05.2022  Der 7TM der Intensivbettenbelegungen fallen zum 38 Mal nach 17x steigen: 7TM=1275.0 nach 1275.0, TW=1163 nach 1196
    04.05.2022  Der 7TM der Intensivbettenbelegungen fallen zum 37 Mal nach 17x steigen: 7TM=1306.4 nach 1338.9, TW=1196 nach 1261
    03.05.2022  Der 7TM der Intensivbettenbelegungen fallen zum 36 Mal nach 17x steigen: 7TM=1338.9 nach 1373.3, TW=1261 nach 1305
    02.05.2022  Der 7TM der Intensivbettenbelegungen fallen zum 35 Mal nach 17x steigen: 7TM=1373.3 nach 1409.1, TW=1305 nach 1317
    01.05.2022  Der 7TM der Intensivbettenbelegungen fallen zum 34 Mal nach 17x steigen: 7TM=1409.1 nach 1442.3, TW=1317 nach 1327
    30.04.2022  Der 7TM der Intensivbettenbelegungen fallen zum 33 Mal nach 17x steigen: 7TM=1442.3 nach 1480.3, TW=1327 nach 1356
    29.04.2022  Der 7TM der Intensivbettenbelegungen fallen zum 32 Mal nach 17x steigen: 7TM=1480.3 nach 1514.0, TW=1356 nach 1383
    28.04.2022  Der 7TM der Intensivbettenbelegungen fallen zum 31 Mal nach 17x steigen: 7TM=1514.0 nach 1548.4, TW=1383 nach 1423
    27.04.2022  Der 7TM der Intensivbettenbelegungen fallen zum 30 Mal nach 17x steigen: 7TM=1548.4 nach 1588.7, TW=1423 nach 1502
    26.04.2022  Der 7TM der Intensivbettenbelegungen fallen zum 29 Mal nach 17x steigen: 7TM=1588.7 nach 1627.6, TW=1502 nach 1556
    25.04.2022  Der 7TM der Intensivbettenbelegungen fallen zum 28 Mal nach 17x steigen: 7TM=1627.6 nach 1654.4, TW=1556 nach 1549
    24.04.2022  Der 7TM der Intensivbettenbelegungen fallen zum 27 Mal nach 17x steigen: 7TM=1654.4 nach 1682.0, TW=1549 nach 1593
    23.04.2022  Der 7TM der Intensivbettenbelegungen fallen zum 26 Mal nach 17x steigen: 7TM=1682.0 nach 1700.0, TW=1593 nach 1592
    22.04.2022  Der 7TM der Intensivbettenbelegungen fallen zum 25 Mal nach 17x steigen: 7TM=1700.0 nach 1725.3, TW=1592 nach 1624
    21.04.2022  Der 7TM der Intensivbettenbelegungen fallen zum 24 Mal nach 17x steigen: 7TM=1725.3 nach 1749.3, TW=1624 nach 1705
    20.04.2022  Der 7TM der Intensivbettenbelegungen fallen zum 23 Mal nach 17x steigen: 7TM=1749.3 nach 1766.1, TW=1705 nach 1774
    19.04.2022  Der 7TM der Intensivbettenbelegungen fallen zum 22 Mal nach 17x steigen: 7TM=1766.1 nach 1781.1, TW=1774 nach 1741
    18.04.2022  Der 7TM der Intensivbettenbelegungen fallen zum 21 Mal nach 17x steigen: 7TM=1781.1 nach 1810.4, TW=1741 nach 1745
    17.04.2022  Der 7TM der Intensivbettenbelegungen fallen zum 20 Mal nach 17x steigen: 7TM=1810.4 nach 1840.7, TW=1745 nach 1719
    16.04.2022  Der 7TM der Intensivbettenbelegungen fallen zum 19 Mal nach 17x steigen: 7TM=1840.7 nach 1873.6, TW=1719 nach 1769
    15.04.2022  Der 7TM der Intensivbettenbelegungen fallen zum 18 Mal nach 17x steigen: 7TM=1873.6 nach 1905.3, TW=1769 nach 1792
    14.04.2022  Der 7TM der Intensivbettenbelegungen fallen zum 17 Mal nach 17x steigen: 7TM=1905.3 nach 1938.0, TW=1792 nach 1823
    13.04.2022  Der 7TM der Intensivbettenbelegungen fallen zum 16 Mal nach 17x steigen: 7TM=1938.0 nach 1974.6, TW=1823 nach 1879
    12.04.2022  Der 7TM der Intensivbettenbelegungen fallen zum 15 Mal nach 17x steigen: 7TM=1974.6 nach 2010.7, TW=1879 nach 1946
    11.04.2022  Der 7TM der Intensivbettenbelegungen fallen zum 14 Mal nach 17x steigen: 7TM=2010.7 nach 2047.6, TW=1946 nach 1957
    10.04.2022  Der 7TM der Intensivbettenbelegungen fallen zum 13 Mal nach 17x steigen: 7TM=2047.6 nach 2079.4, TW=1957 nach 1949
    09.04.2022  Der 7TM der Intensivbettenbelegungen fallen zum 12 Mal nach 17x steigen: 7TM=2079.4 nach 2119.9, TW=1949 nach 1991
    08.04.2022  Der 7TM der Intensivbettenbelegungen fallen zum 11 Mal nach 17x steigen: 7TM=2119.9 nach 2154.4, TW=1991 nach 2021
    07.04.2022  Der 7TM der Intensivbettenbelegungen fallen zum 10 Mal nach 17x steigen: 7TM=2154.4 nach 2189.4, TW=2021 nach 2079
    06.04.2022  Der 7TM der Intensivbettenbelegungen fallen zum 9 Mal nach 17x steigen: 7TM=2189.4 nach 2246.7, TW=2079 nach 2132
    05.04.2022  Der 7TM der Intensivbettenbelegungen fallen zum 8 Mal nach 17x steigen: 7TM=2246.7 nach 2262.6, TW=2132 nach 2204
    04.04.2022  Der 7TM der Intensivbettenbelegungen fallen zum 7 Mal nach 17x steigen: 7TM=2246.7 nach 2262.6, TW=2204 nach 2180
    03.04.2022  Der 7TM der Intensivbettenbelegungen fallen zum 6 Mal nach 17x steigen: 7TM=2262.6 nach 2276.3, TW=2180 nach 2232
    02.04.2022  Der 7TM der Intensivbettenbelegungen fallen zum 5 Mal nach 17x steigen: 7TM=2276.3 nach 2286.2, TW=2232 nach 2233
    01.04.2022  Der 7TM der Intensivbettenbelegungen fallen zum 4. Mal nach 17x steigen: 7TM=2286.2 nach 2292.7, TW=2233 nach 2266
    31.03.2022  Der 7TM der Intensivbettenbelegungen fallen zum 3. Mal nach 17x steigen: 7TM=2292.7 nach 2296.0, TW=2266 nach 2283
    30.03.2022  Der 7TM der Intensivbettenbelegungen fallen zum 2. Mal nach 17x steigen: 7TM=2296.0 nach 2298.2, TW=2283 nach 2329
    29.03.2022  Der 7TM der Intensivbettenbelegungen fallen erstmals nach 17x steigen: 7TM=2298.2 nach 2301.0, TW=2329 nach 2315
    28.03.2022  Der 7TM der Intensivbettenbelegungen steigt das 17. Mal nach 19x fallen: 7TM=2301.0  nach ????,  TW=2315 nach ????
    27.03.2022  Sonntagswerte heute (Mo) nicht ausgewiesen.
    26.03.2022  Der 7TM der Intensivbettenbelegungen steigt das 16. Mal nach 19x fallen: 7TM=2290.4 nach 2278.6,  TW=2291 nach 2272
    25.03.2022  Der 7TM der Intensivbettenbelegungen steigt das 15. Mal nach 19x fallen: 7TM=2278.6 nach 2275.0, TW=2272 nach 2286
    24.03.2022  Der 7TM der Intensivbettenbelegungen steigt das 14. Mal nach 19x fallen: 7TM=2275.0 nach 2268.6, TW=2286 nach 2296
    23.03.2022  Der 7TM der Intensivbettenbelegungen steigt das 13. Mal nach 19x fallen: 7TM=2268.6 nach 2262.9, TW=2296 nach 2346
    22.03.2022  Der 7TM der Intensivbettenbelegungen steigt das 12. Mal nach 19x fallen: 7TM=2262.9 nach 2250.4, TW=2346 nach 2311
    21.03.2022  Der 7TM der Intensivbettenbelegungen steigt das 11. Mal nach 19x fallen: 7TM=2250.4 nach 2238.3, TW=2311 nach 2231
    20.03.2022  Der 7TM der Intensivbettenbelegungen steigt das 10. Mal nach 19x fallen: 7TM=2238.3 nach 2228.1, TW=2231 nach 2208
    19.03.2022  Der 7TM der Intensivbettenbelegungen steigt das 9. Mal nach 19x fallen: 7TM=2228.1 nach 2210.1, TW=2208 nach 2247
    18.03.2022  Der 7TM der Intensivbettenbelegungen steigt das 8. Mal nach 19x fallen: 7TM=2210.1 nach 2187.6, TW=2247 nach 2241
    17.03.2022  Der 7TM der Intensivbettenbelegungen steigt das 7. Mal nach 19x fallen: 7TM=2187.6 nach 2165.4, TW=2241 nach 2256
    16.03.2022  Der 7TM der Intensivbettenbelegungen steigt das 6. Mal nach 19x fallen: 7TM=2165.4 nach 2142.1, TW=2256 nach 2259
    15.03.2022  Der 7TM der Intensivbettenbelegungen steigt das 5. Mal nach 19x fallen: 7TM=2142.1 nach 2123.4, TW=2259 nach 2226
    14.03.2022  Der 7TM der Intensivbettenbelegungen steigt das 4. Mal nach 19x fallen: 7TM=2123.4 nach 2109.1, TW=2226 nach 2160
    13.03.2022  Der 7TM der Intensivbettenbelegungen steigt das 3. Mal nach 19x fallen: 7TM=2109.1 nach 2096.6, TW=2160 nach 2082
    12.03.2022  Der 7TM der Intensivbettenbelegungen steigt das 2. Mal nach 19x fallen: 7TM=2096.6 nach 2094.7, TW=2082 nach 2089
    11.03.2022  Der 7TM der Intensivbettenbelegungen steigt das 1. Mal nach 19x fallen: 7TM=2094.7 nach 2092.6, TW=2089 nach 2086
    10.03.2022  Der 7TM der Intensivbettenbelegungen fällt  das 19. Mal nach 16x steigen: 7TM=2092.6 nach  2108., TW=2086 nach 2093
    09.03.2022  Der 7TM der Intensivbettenbelegungen fällt  das 18. Mal nach 16x steigen: 7TM=2097.3 nach  2108., TW=2093 nach 2128
    08.03.2022  Der 7TM der Intensivbettenbelegungen fällt  das 17. Mal nach 16x steigen: 7TM=2108.1 nach 2126.7, TW=2128 nach 2126
    07.03.2022  Der 7TM der Intensivbettenbelegungen fällt  das 16. Mal nach 16x steigen: 7TM=2126.7 nach 2145.0, TW=2126 nach 2072
    06.03.2022  Der 7TM der Intensivbettenbelegungen fällt  das 15. Mal nach 16x steigen: 7TM=2145.0 nach 2164.9, TW=2072 nach 2069
    05.03.2022  Der 7TM der Intensivbettenbelegungen fällt  das 14. Mal nach 16x steigen: 7TM=2164.9 nach 2187.7, TW=2069 nach 2074
    04.03.2022  Der 7TM der Intensivbettenbelegungen fällt  das 13. Mal nach 16x steigen: 7TM=2187.7 nach 2213.4, TW=2074 nach 2119.
    03.03.2022  Der 7TM der Intensivbettenbelegungen fällt  das 12. Mal nach 16x steigen: 7TM=2213.4 nach 2231.1, TW=2119 nach 2169
    02.03.2022  Der 7TM der Intensivbettenbelegungen fällt  das 11. Mal nach 16x steigen: 7TM=2231.1 nach 2257.3, TW=2169 nach 2258
    01.03.2022  Der 7TM der Intensivbettenbelegungen fällt  das 10. Mal nach 16x steigen: 7TM=2257.3 nach 2270.0, TW=2258 nach 2254
    28.02.2022  Der 7TM der Intensivbettenbelegungen fällt  das 9. Mal nach 16x steigen: 7TM=2270.0 nach 2286.0, TW=2254 nach 2211
    27.02.2022  Der 7TM der Intensivbettenbelegungen fällt  das 8. Mal nach 16x steigen: 7TM=2286.0 nach 2306.7, TW=2211 nach 2229
    26.02.2022  Der 7TM der Intensivbettenbelegungen fällt  das 7. Mal nach 16x steigen: 7TM=2306.7 nach 2326.7, TW=2229 nach 2254
    25.02.2022  Der 7TM der Intensivbettenbelegungen fällt  das 6. Mal nach 16x steigen: 7TM=2326.7 nach 2346.1, TW=2254 nach 2243
    24.02.2022  Der 7TM der Intensivbettenbelegungen fällt  das 5. Mal nach 16x steigen: 7TM=2346.1 nach 2371.6, TW=2243 nach 2352
    23.02.2022  Der 7TM der Intensivbettenbelegungen fällt  das 4. Mal nach 16x steigen: 7TM=2371.6 nach 2382.7, TW=2352 nach 2347
    22.02.2022  Der 7TM der Intensivbettenbelegungen fällt  das 3. Mal nach 16x steigen: 7TM=2382.7 nach 2396.7, TW=2347 nach 2366
    21.02.2022  Der 7TM der Intensivbettenbelegungen fällt  das 2. Mal nach 16x steigen: 7TM=2396.7 nach 2406.0, TW=2366 nach 2356
    20.02.2022  Der 7TM der Intensivbettenbelegungen fällt  erstmals nach 16x steigen: 7TM=2406.0 nach 2410.3, TW=2356 nach 2369
    19.02.2022  Der 7TM der Intensivbettenbelegungen steigt 16. Mal nach 52 Mal Fallen: 7TM=2410.3 nach 2409.1, TW=2369 nach 2390.
    18.02.2022  Der 7TM der Intensivbettenbelegungen steigt 15. Mal nach 52 Mal Fallen;7TM=2409.1 nach 2404.9, TW=2390 nach 2421.
    17.02.2022  Der 7TM der Intensivbettenbelegungen steigt 14. Mal nach 52 Mal Fallen;7TM=2404.9 nach 2395.3, TW=2421 nach 2425.
    16.02.2022  Der 7TM der Intensivbettenbelegungen steigt 13. Mal nach 52 Mal Fallen;7TM=2395.3 nach 2385.00, TW=2425 nach 2450
    15.02.2022  Der 7TM der Intensivbettenbelegungen steigt 12. Mal nach 52 Mal Fallen;7TM=2385.00 nach 2357.1, TW=2450 nach 2431.
    14.02.2022  Der 7TM der Intensivbettenbelegungen steigt 11. Mal nach 52 Mal Fallen;7TM=2371.0 nach 2357.1, TW=2431 nach 2386.
    13.02.2022  Der 7TM der Intensivbettenbelegungen steigt 10. Mal nach 52 Mal Fallen;7TM=2357.1 nach 2345.0, TW=2386 nach 2361,  2360, 2354, 2353, 2352.
    12.02.2022  Der 7TM der Intensivbettenbelegungen steigt 9. Mal nach 52 Mal Fallen;7TM=2345.0 nach 2332.7, TW=2361 nach 2360, 2354, 2353, 2352.
    11.02.2022  Der 7TM der Intensivbettenbelegungen steigt 8. Mal nach 52 Mal Fallen;7TM=2332.7 nach 2320.1 , TW=2360 nach 2354, 2353, 2352.
    10.02.2022  Der 7TM der Intensivbettenbelegungen steigt 7. Mal nach 52 Mal Fallen;7TM=2320.1 nach 2301.9, TW=2354 nach 2353, 2352.
    09.02.2022  Der 7TM der Intensivbettenbelegungen steigt 6. Mal nach 52 Mal Fallen;7TM=2301.9 nach 2290.9, TW=2353 nach 2352.
    08.02.2022  Der 7TM der Intensivbettenbelegungen steigt 5. Mal nach 52 Mal Fallen;7TM=2290.9 nach 2272.6, TW=2352 nach 2334.
    07.02.2022  Der 7TM der Intensivbettenbelegungen steigt 4. Mal nach 52 Mal Fallen;7TM=2272.6 nach .2262.3, TW=2334 nach 2301.
    06.02.2022  Der 7TM der Intensivbettenbelegungen steigt 3. Mal nach 52 Mal Fallen;7TM=2262.3 nach 2252.4, TW=2301 nach 2275.
    05.02.2022  Der 7TM der Intensivbettenbelegungen steigt 2. Mal nach 52 Mal Fallen;7TM=2252.4 nach 2240.6, TW=2275 nach 2272.
    04.02.2022  Der 7TM der Intensivbettenbelegungen steigt 1. Mal nach 52 Mal Fallen;7TM=2240.6 nach 2236.6, TW=2272 nach 2276.
    03.02.2022  Der 7TM der Intensivbettenbelegungen fällt 52. Mal in Folge;7TM=2236.6 nach 2239.3, TW=2226 nach 2276.
    02.02.2022  Der 7TM der Intensivbettenbelegungen fällt 51. Mal in Folge;7TM=2239.3 nach 2247.4, TW=2276 nach 2224.
    01.02.2022  Der 7TM der Intensivbettenbelegungen fällt 50. Mal in Folge;7TM=2247.4 nach 2267.4, TW=2224 nach 2262.
    31.01.2022  Der 7TM der Intensivbettenbelegungen fällt 49. Mal in Folge;7TM=2267.4 nach 2288.9, TW=2262 nach 2232.
    30.01.2022  Der 7TM der Intensivbettenbelegungen fällt 48. Mal in Folge;7TM=2288.9 nach 2312.6, TW=2232 nach 2192.
    29.01.2022  Der 7TM der Intensivbettenbelegungen fällt 47. Mal in Folge;7TM=2312.6 nach 2338.1, TW=2192 nach 2244.
    28.01.2022  Der 7TM der Intensivbettenbelegungen fällt 46. Mal in Folge;7TM=2338.1 nach 2359.0, TW=2244 nach 2245.
    27.01.2022  Fällt 45. Mal in Folge;7TM=2359.0 nach 2382.6, TW=2245 nach 2333.
    26.01.2022  Fällt 44. Mal in Folge;7TM=2382.6 nach 2413.1, TW=2333 nach 2364.
    25.01.2022Fällt das 43. Mal in Folge;7TM=2413.1 nach 2452.0, TW=2364 nach 2412.
    24.01.2022  Die 7TM der Intensivbettenbelegungen sind am 24.01.2022 zum 42. Mal gefallen: 7TM=2452.0 (TW=2412) nach 7TM=2540.1 (TW=2371). Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen weiter deutlich gestiegen, auf 46.5 nach 40.2%. Todesfälle wieder leicht gestiegen.
    23.01.2022
    22.01.2022  Die 7TM der Intensivbettenbelegungen sind am 22.01.2022 zum 40. Mal gefallen: 7TM=2540.1 (TW=2371) nach 7TM=2597.1 (TW=2390). Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen weiter deutlich gestiegen, auf 40.2% nach 37.5%. Todesfälle wieder leicht gestiegen.
    21.01.2022  Die 7TM der Intensivbettenbelegungen sind am 21.01.2022 zum 39. Mal gefallen: 7TM=2597.1 (TW=2390) nach 7TM=2661.6 (TW=2410). Auch die Corona Todesfälle sind zum 8. Mal in Folge gefallen. Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen weiter deutlich gestiegen, auf 37.5% nach 33.6%.
    20.01.2022  Die 7TM der Intensivbettenbelegungen sind am 20.01.2022 zum 38. Mal gefallen:  nach 7TM=2661.6 (TW=2410) nach 7TM=2735.9 (TW=2547). Auch die Corona Todesfälle sind zum 7. Mal in Folge gefallen.  Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen weiter deutlich gestiegen, auf 33.6 nach 30.1%.
    19.01.2022  Die 7TM der Intensivbettenbelegungen sind am 19.01.2022 zum 37. Mal gefallen: 7TM=2735.9 (TW=2547) nach 7TM=2803.6 (TW=2636). Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist weiter deutlich gestiegen, auf 30.1% nach 26.8%. Naht die Trendwende bei den Intensivbelegungen?
    18.01.2022 Die 7TM der Intensivbettenbelegungen sind am 18.01.2022 zum 36. Mal gefallen:  7TM=2803.6 (TW=2636) nach 7TM=2873.1 (TW=2712). Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist weiter deutlich gestiegen, auf 26.8% nach 24.5%. Naht die Trendwende bei den Intensivbelegungen.
    17.01.2022 Die 7TM der Intensivbettenbelegungen sind am 17.01.2022 zum 35. Mal gefallen:  7TM=2873.1 (TW=2712) nach 7TM=2946.3 (TW=2715). Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist weiter deutlich gestiegen, auf 24.5 nach 22.5%. Naht die Trendwende bei den Intensivbelegungen.
    16.01.2022 Die 7TM der Intensivbettenbelegungen sind am 16.01.2022 zum 34. Mal gefallen:  7TM=2946.3 (TW=2715) nach 7TM=3021.6 (TW=2770) . Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist weiter deutlich gestiegen, auf 22.5% nach 21.5%.
    15.01.2022 Die 7TM der Intensivbettenbelegungen sind am 15.01.2022 zum 33. Mal gefallen:  7TM=3021.6 (TW=2770) nach 7TM=3095.4 (TW=2841). Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist weiter deutlich gestiegen, auf 21.5% nach 20.3%.
    14.01.2022 Die 7TM der Intensivbettenbelegungen sind am 14.01.2022 zum 32. Mal gefallen:  7TM=3095.4 (TW=2841) nach 7TM=3167.4 (TW=2930). Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist weiter deutlich gestiegen, auf 20.3% nach 18.8%.
    13.01.2022 Die 7TM der Intensivbettenbelegungen sind am 13.01.2022 zum 31. Mal gefallen: 7TM=3167.4 (TW=2930) nach 7TM=3235.7 (TW=3021). Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist weiter deutlich gestiegen, auf 18.8 nach 16.8%.
    12.01.2022 Die 7TM der Intensivbettenbelegungen sind am 12.01.2022 zum 30. Mal gefallen: 7TM=3235.7 (TW=3021) nach 7TM=3308.6 (TW=3123). Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist weiter deutlich gestiegen, auf 16.8% nach 15.7%.
    11.01.2022 Die 7TM der Intensivbettenbelegungen sind am 11.01.2022 zum 29. Mal gefallen: 7TM=3308.6 (TW=3123) nach 7TM=3382.4 (TW=3224). Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist weiter deutlich gestiegen, auf 15.7378 nach 14.4856.
    10.01.2022 Die 7TM der Intensivbettenbelegungen sind am 10.01.2022 zum 28. Mal gefallen: 7TM=3382.4 (TW=3224) nach 7TM=3460.6 (TW=3242). Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist weiter deutlich gestiegen, auf 14.4856 nach 13.5338.
    09.01.2022 Die 7TM der Intensivbettenbelegungen sind am 09.01.2022 zum 27. Mal gefallen: 7TM=3460.6 (TW=3242) nach 7TM=3536.6 (TW=3287). Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist weiter deutlich gestiegen, auf 13.5338 nach 12.9704.
    08.01.2022 Die 7TM der Intensivbettenbelegungen sind am 08.01.2022 zum 26. Mal gefallen:  7TM=3536.6 (TW=3287) nach 7TM=3609.3 (TW=3345). Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist wieder deutlich gestiegen,  auf 12.9704 nach 11.7582.
    07.01.2022 Die 7TM der Intensivbettenbelegungen sind am 08.01.2022 zum 25. Mal gefallen: 7TM=3609.3 (TW=3345) nach 7TM=3674.6 (TW=3408). Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist wieder drastisch gestiegen,  auf 11.7582 nach 8.1772. [korrigiert]
    06.01.2022 Die 7TM der Intensivbettenbelegungen sind am 06.01.2022 zum 24. Mal gefallen: 7TM=3674.6 (TW=3408) nach 7TM=3743.3 (TW=3531). Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist erstmals wieder gefallen (k= 1 nach -6) auf 8.1772 nach 9.6353.
    05.01.2022 Die 7TM der Intensivbettenbelegungen sind am 05.01.2022 zum 23. Mal gefallen: 7TM=3743.3 (TW=3531)  nach 7TM=3807.6 (TW=3640). Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist weiter gestiegen (k= -6) auf 9.6353 nach 8.6635.
    04.01.2022 Die 7TM der Intensivbettenbelegungen sind am 04.01.2022 zum 22. Mal gefallen: 7TM=3807.6 (TW=3640) nach 7TM=3872.9 (TW=3771) . Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist weiter gestiegen (k= -5) auf 8.6635 nach 7.8213.
    03.01.2022 Die 7TM der Intensivbettenbelegungen sind am 03.01.2022 zum 21. Mal gefallen: 7TM=3872.9 (TW=3771) nach 7TM=3930.0 (TW=3774). Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist weiter gestiegen (k= -4) auf 7.8213 nach 7.3631 .
    02.01.2022 Die 7TM der Intensivbettenbelegungen sind am 02.01.2022 zum 20. Mal gefallen: 7TM=3930.0 (TW=3774) nach 7TM=3991.0 (TW=3796). Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist weiter gestiegen (k= -3) auf 7.3631 nach 7.0854.
    01.01.2022 Die 7TM der Intensivbettenbelegungen sind am 01.01.2022 zum 19. Mal gefallen: 7TM=3991.0 (TW=3796) nach 7TM=4054.3 (TW=3802) . Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist weiter gestiegen (k= -2) auf 7.0854 nach 6.8897.
    31.12.2021 Die 7TM der Intensivbettenbelegungen sind am 31.12.2021 zum 18. Mal gefallen: 7TM=4054.3 (TW=3802) nach 7TM=4118.3 (TW=3889). Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist wieder deutlich gestiegen (k= -1) auf 6.8897 nach 5.5202.
    30.12.2021 Die 7TM der Intensivbettenbelegungen sind am 30.12.2021 zum 17. Mal gefallen: 7TM=4118.3 (TW=3889) nach 7TM=4184.3 (TW=3981). Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist wieder deutlich gefallen (k= 1) auf 5.5202 nach 6.3349%.
    29.12.2021 Die 7TM der Intensivbettenbelegungen sind am 29.12.2021 zum 16. Mal gefallen: 7TM=4184.3 (TW=3981) nach 7TM=4250.1 (TW=4097). Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist wieder leicht gestiegen (k= -1) auf 6.3349 nach 6.3094%.
    28.12.2021 Die 7TM der Intensivbettenbelegungen sind am 28.12.2021 zum 15. Mal gefallen: 7TM=4250.1 (TW=4097) nach 7TM=4312.0 (TW=4171) Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist wieder gefallen (k= 1) auf 6.3094 nach 6.4047%.
    27.12.2021 Die 7TM der Intensivbettenbelegungen sind am 27.12.2021 zum 14. Mal gefallen: 7TM=4312.0 (TW=4171) nach 7TM=4370.9 (TW=4201). Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist zum 2. Mal minimal gestiegen (k=-2) auf 6.4047 nach 6.3950%.
    26.12.2021 Die 7TM der Intensivbettenbelegungen sind am 26.12.2021 zum 13. Mal gefallen: 7TM=4370.9 (TW=4201) nach 7TM=4426.1 (TW=4239). Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist zum zweiten Mal minimal gestiegen (k=-1) auf 6.40% nach 6.39%.
    25.12.2021 Die 7TM der Intensivbettenbelegungen sind am 25.12.2021 zum 12. Mal gefallen: 7TM=4426.1 (TW=4239) nach 7TM=4480.6 (TW=4250). Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist weiter gefallen (k=30) auf 6.39% nach 6.92%.
    24.12.2021 Die 7TM der Intensivbettenbelegungen sind am 24.12.2021 zum 11. Mal gefallen: 7TM=4480.6 (TW=4250)  nach 7TM=4537.0 (TW=4351). Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist weiter gefallen (k=29) auf 6.92% nach 7.48% .
    23.12.2021 Die 7TM der Intensivbettenbelegungen sind am 23.12.2021 zum 10. Mal gefallen: 7TM=4537.0 (TW=4351) nach 7TM=4592.0 (TW=4442) . Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist weiter gefallen (k=28) auf 7.48% nach 7.88%.
    22.12.2021 Die 7TM der Intensivbettenbelegungen sind am 22.12.2021 zum 9. Mal gefallen: 7TM=4592.0 (TW=4442) nach 7TM=4639.1 (TW=4530). Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist weiter gefallen (k=27) auf 7.88% nach 8.16%.
    21.12.2021 Die 7TM der Intensivbettenbelegungen sind am 21.12.2021 zum 8. Mal gefallen: 7TM=4639.1 (TW=4530)  nach 7TM=4686.3 (TW=4583) . Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist weiter gefallen (k= 26) auf 8.16% nach 8.25%.
    20.12.2021 Die 7TM der Intensivbettenbelegungen sind am 20.12.2021 zum 7. Mal gefallen:  7TM=4686.3 (TW=4583) nach 7TM=4730.9 (TW=4588). Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist weiter gefallen (k= 25) auf 8.25% nach 8.40%.
    19.12.2021 Die 7TM der Intensivbettenbelegungen sind am 19.12.2021 zum 6. Mal gefallen: 7TM=4730.9 (TW=4588) nach  7TM=4771.7 (TW=4620) . Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist weiter gefallen (k= 24) auf 8.40% nach 8.49.
    18.12.2021 Die 7TM der Intensivbettenbelegungen sind am 18.12.2021 zum 5. Mal gefallen: 7TM=4771.7 (TW=4620) nach 7TM=4807.9 (TW=4645). Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist weiter gefallen (k= 23) auf 8.49 nach 8.53% .
    17.12.2021 Die 7TM der Intensivbettenbelegungen sind am 17.12.2021 zum 4. Mal gefallen: 7TM=4807.9 (TW=4645) nach 7TM=4847.0 (TW=4736). Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist weiter gefallen (k= 22) auf 8.53% nach 8.78%.
    16.12.2021 Die 7TM der Intensivbettenbelegungen sind am 16.12.2021 zum 3. Mal gefallen: 7TM=4847.0 (TW=4736) nach 7TM=4873.0 (TW=4772). Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist weiter gefallen (k= 21) auf 8.78% nach 9.03%.
    15.12.2021 Die 7TM der Intensivbettenbelegungen sind am 15.12.2021 zum zweiten Mal gefallen: 7TM=4873.0 (TW=4772) nach 7TM=4887.1 (TW=4860). Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist weiter gefallen (k= 20) auf 9.03% nach 9.49%.
    14.12.2021 Die 7TM der Intensivbettenbelegungen sind am 15.12.2021 erstmals gefallen:  7TM=4887.1 (TW=4860)  nach 7TM=4896.4 (TW=4895). Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist weiter gefallen (k= 19) auf 9.49% nach 9.93%
    13.12.2021 Die 7TM der Intensivbettenbelegungen sind am 13.12.2021 weiter gestiegen: 7TM=4896.4 (TW=4895) nach 7TM=4894.3 (TW=4874) . Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist weiter gefallen (k= 18) auf 9.93% nach 10.1%.
    12.12.2021 Die 7TM der Intensivbettenbelegungen sind am 12.12.2021 weiter gestiegen: 7TM=4894.3 (TW=4874) nach 7TM=4884.1 (TW=4873). Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist weiter gefallen (k= 17) auf 10.1% nach 10.29%.
    11.12.2021 Die 7TM der Intensivbettenbelegungen sind am 11.12.2021 weiter gestiegen: 7TM=4884.1 (TW=4873) nach 7TM=4871.0 (TW=4919). Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist weiter gefallen (k= 16) auf 10.29% nach 10.59%.
    10.12.2021 Die 7TM der Intensivbettenbelegungen sind am 10.12.2021 weiter gestiegen: 7TM=4871.0 (TW=4919) nach 7TM=4850.1 (TW=4918). Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist weiter gefallen (k= 15) auf 10.59% nach  10.96%.
    09.12.2021 Die 7TM der Intensivbettenbelegungen sind am 09.12.2021 weiter gestiegen: 7TM=4850.1 (TW=4918) nach 7TM=4829.6 (TW=4871). Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist weiter gefallen (k= 14) auf 10.96% nach 11.39%.
    08.12.2021 Die 7TM der Intensivbettenbelegungen sind am 08.12.2021 weiter gestiegen: 7TM=4829.6 (TW=4871)  nach 7TM=4800.6 (TW=4925). Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist weiter gefallen (k= 13) auf 11.39% nach 11.54%.

    07.12.2021 Die 7TM der Intensivbettenbelegungen sind am 07.12.2021 weiter gestiegen: 7TM=4800.6 (TW=4925) nach 7TM=4756.4 (TW=4880) . Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist weiter gefallen (k= 12) auf 11.54% nach 11.57%.
    06.12.2021 Die 7TM der Intensivbettenbelegungen sind am 06.12.2021 weiter gestiegen: 7TM=4756.4 (TW=4880) nach 7TM=4712.9 (TW=4803) . Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist weiter gefallen (k= 11) auf 11.57% nach 11.97%.
    05.12.2021 Die 7TM der Intensivbettenbelegungen sind am 05.12.2021 weiter gestiegen: 7TM=4712.9 (TW=4803) nach 7TM=4659.9 (TW=4781) . Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist weiter gefallen (k= 10) auf 11.97% nach 12.15%.
    04.12.2021 Die 7TM der Intensivbettenbelegungen sind am 04.12.2021 weiter gestiegen: 7TM=4659.9 (TW=4781) nach 7TM=4596.6 (TW=4773). Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist weiter gefallen (k= 9) auf 12.15% nach 12.39%.
    03.12.2021 Die 7TM der Intensivbettenbelegungen sind am 03.12.2021 weiter gestiegen: 7TM=4696.6 (TW=4773) nach 7TM=4529.0 (TW=4774) . Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist weiter gefallen (k= 8) auf 12.39% nach 12.66%.
    02.12.2021 Die 7TM der Intensivbettenbelegungen sind am 02.12.2021 weiter gestiegen: 7TM=4529.0 (TW=4774) nach 7TM=4444.0 (TW=4668). Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist weiter gefallen (k= 7) auf 12.66% nach 12.97% [korrigiert]
    01.12.2021 Die 7TM der Intensivbettenbelegungen sind am 01.12.2021 weiter gestiegen: 7TM=4444.0 (TW=4668) nach 7TM=4355.0 (TW=4616) . Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist gefallen (k= 6) auf 12.97% [korrigiert 13.02%] nach 13.32%.
    30.11.2021 Die 7TM der Intensivbettenbelegungen sind am 30.11.2021 weiter gestiegen: 7TM=4355.0 (TW=4616) nach 7TM=4261.9 (TW=4575). Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist gefallen (k= 5) auf 13.32% nach 13.61% .
    29.11.2021 Die 7TM der Intensivbettenbelegungen sind am 29.11.2021 weiter gestiegen: 7TM=4261.9 (TW=4575) nach 7TM=4155.0 (TW=4432). Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist gefallen (k= 4) auf 13.61 nach 13.94% .
    28.11.2021 Die 7TM der Intensivbettenbelegungen sind am 28.11.2021 weiter gestiegen: 7TM=4155.0 (TW=4432) nach 7TM=4044.3 (TW=4338). Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist gefallen (k= 3) auf 13.94% nach 14.37%%.
    27.11.2021 Die 7TM der Intensivbettenbelegungen sind am 27.11.2021 weiter gestiegen: 7TM=4044.3 (TW=4338) nach 7TM=3931.1 (TW=4300) . Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist gefallen (k= 2 nach 1, -4, -3, -2, -1, 1, -2, -1, 1, -11, ...) auf 14.37% nach 14.75%.
    26.11.2021 Die 7TM der Intensivbettenbelegungen sind am 26.11.2021 weiter gestiegen: 7TM=3931.1 (TW=4300) nach 7TM=3815.6 (TW=4179). Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist gefallen (k= 1 nach -4, -3, -2, -1, 1, -2, -1, 1, -11, ...) auf 14.75% nach 15.05%.
    25.11.2021 Die 7TM der Intensivbettenbelegungen sind am 25.11.2021 weiter gestiegen: 7TM=3815.6 (TW=4179) nach 7TM=3706.0 (TW=4045). Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist wenn auch nur leicht aber erneut auf einen neuen Höchstwert gestiegen (k= -4 nach -3, -2, -1, 1, -2, -1, 1, -11, ...) auf 15.05% nach 14.58%.
    24.11.2021 Die 7TM der Intensivbettenbelegungen sind am 24.11.2021 weiter gestiegen: 7TM=3706.0 (TW=4045) nach 7TM=3608.3 (TW=3964) . Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist wenn auch nur leicht aber erneut auf einen neuen Höchstwert gestiegen (k= -3 nach -2, -1, 1, -2, -1, 1, -11, ...) auf 14.58% 14.56%.
    23.11.2021 Die 7TM der Intensivbettenbelegungen sind am 23.11.2021 weiter gestiegen: 7TM=3608.3 (TW=3964) nach 7TM=3508.6 (TW=3827). Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist erneut auf neuen Höchstwert gestiegen (k= -2 nach -1, 1, -2, -1, 1, -11, ...) auf 14.6 nach 14.4%
    22.11.2021 Die 7TM der Intensivbettenbelegungen sind am 22.11.2021 weiter gestiegen: 7TM=3508.6 (TW=3827) nach 7TM=3414.9 (TW=3657). Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist leicht gestiegen (k= -1 nach 1, -2, -1, 1, -11, ...) auf 14.4% nach 14.25% Spitzenwert bislang 25.08.2021 mit 11.49%.
    21.11.2021 Die 7TM der Intensivbettenbelegungen sind am 21.11.2021 weiter gestiegen: 7TM=3414.9 (TW=3657) nach 7TM=3324.0 (TW=3546) . Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist leicht gefallen (k= 1 nach -2) auf 14.25% nach 14.33%. Spitzenwert bislang 25.08.2021 mit 11.49%.
    20.11.2021 Die 7TM der Intensivbettenbelegungen sind am 20.11.2021 weiter gestiegen: 7TM=3324.0 (TW=3546) nach 7TM=3235.3 (TW=3491). Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist wieder gestiegen (k= -2) auf 14.33% nach 14.32%. Spitzenwert bislang 25.08.2021 mit 11.49%.
    19.11.2021 Die 7TM der Intensivbettenbelegungen sind am 19.11.2021 weiter gestiegen: 7TM=3235.3 (TW=3491) nach  7TM=3143.9 (TW=3412) . Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist wieder gestiegen (k= -1) auf 14.32% nach 13.36. Spitzenwert bislang 25.08.2021 mit 11.49%.
    18.11.2021 Die 7TM der Intensivbettenbelegungen sind am 18.11.2021 weiter gestiegen: 7TM=3143.9 (TW=3412) nach 7TM=3066.0 (TW=3361). Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist erstmals seit 11 Tagen gefallen (k= 1) auf 13.36 nach 13.76%. Spitzenwert bislang 25.08.2021 mit 11.49%.
    17.11.2021 Die 7TM der Intensivbettenbelegungen sind am 17.11.2021 weiter gestiegen: 7TM=3066.0 (TW=3361) nach 7TM=2968.9 (TW=3266). Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist gestiegen (k= -11) auf neuen Höchstwert 14.03% nach 13.76%. Spitzenwert bislang 25.08.2021 mit 11.49%.
    16.11.2021  Die 7TM der Intensivbettenbelegungen sind am 16.11.2021 weiter gestiegen: 7TM=2968.9 (TW=3266) nach 7TM=2884.9 (TW=3171).  Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist gestiegen (k= -10) auf  neuen Höchstwert 13.76% nach 13.51%. Spitzenwert bislang 25.08.2021 mit 11.49%.
    15.11.2021  Die 7TM der Intensivbettenbelegungen sind am 15.11.2021 weiter gestiegen: 7TM=2884.9 (TW=3171) nach 7TM=2804.2 (TW=3021).  Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist gestiegen (k= -9) auf  neuen Höchstwert 13.51% nach 13.37%. Spitzenwert bislang 25.08.2021 mit 11.49%.
    14.11.2021  Die 7TM der Intensivbettenbelegungen sind am 14.11.2021 weiter gestiegen: 7TM=2804.2 (TW=3021) nach 7TM=2733 (TW=2925).  Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist gestiegen (k= -8) auf  neuen Höchstwert 13.37% nach 13.3%. Spitzenwert bislang 25.08.2021 mit 11.49%.
    13.11.2021  Die 7TM der Intensivbettenbelegungen sind am 13.11.2021 weiter gestiegen: 7TM=2733 (TW=2925) nach 7TM=2663.9 (TW=2732) Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist gestiegen (k= -7) auf  neuen Höchstwert 13.3% nach 13.11% Spitzenwert bislang 25.08.2021 mit 11.49%.
    12.11.2021  Die 7TM der Intensivbettenbelegungen sind am 12.11.2021 weiter gestiegen: 7TM=2663.9 (TW=2732) nach 7TM=2601 (TW=2816). Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist gestiegen (k= -6) auf  neuen Höchstwert 13.11% nach 12.93% Spitzenwert bislang 25.08.2021 mit 11.49%).
    11.11.2021  Die 7TM der Intensivbettenbelegungen sind am 11.11.2021 weiter gestiegen: 7TM=2601 (TW=2816) nach 7TM=2530.7 (TW=2732) nach 7TM=2457.7 (TW=2678). Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist gestiegen (k= -5) auf  neuen Höchstwert 12.93% nach 12.53% (Spitzenwert bislang 25.08.2021 mit 11.49%).
    10.11.2021  Die 7TM der Intensivbettenbelegungen sind am 10.11.2021 weiter gestiegen: 7TM=2530.7 (TW=2732) nach 7TM=2457.7 (TW=2678)  . Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist gestiegen (k= -4) auf  neuen Höchstwert 12.53% nach 11.95% (Spitzenwert bislang 25.08.2021 mit 11.49%).
    09.11.2021  Die 7TM der Intensivbettenbelegungen sind am 09.11.2021 weiter gestiegen: 7TM=2457.7 (TW=2678) nach 7TM=2379.6 (TW=2607) . Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist gestiegen (k= -3) auf  neuen Höchstwert 11.95% nach 11.19% (Spitzenwert bislang 25.08.2021 mit 11.49%).
    08.11.2021  Die 7TM der Intensivbettenbelegungen sind am 08.11.2021 weiter gestiegen: 7TM=2379.6 (TW=2607) nach 7TM=2300.3 (TW=2522) . Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist gestiegen (k= -2) auf  11.19% nach 10.87% (Spitzenwert 25.08.2021 mit 11.49%).
    07.11.2021  Die 7TM der Intensivbettenbelegungen sind am 07.11.2021 weiter gestiegen: 7TM=2300.3 (TW=2522) nach 7TM=2222.4 (TW=2441) . Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist gestiegen (k= -1) auf  10.87% nach 9.06% (Spitzenwert 25.08.2021 mit 11.49%).
    06.11.2021  Die 7TM der Intensivbettenbelegungen sind am 06.11.2021 weiter gestiegen: 7TM=2222.4 (TW=2441) nach 7TM=2148.6 (TW=2411). Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist gefallen (k= 1) auf  9.06% nach 10.83%  (Spitzenwert 25.08.2021 mit 11.49%).
    05.11.2021  Die 7TM der Intensivbettenbelegungen sind am 05.11.2021 weiter gestiegen:  7TM=2148.6 (TW=2411) nach 7TM=2069.9 (TW=2325)  . Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist erneut gestiegen (k= -3) auf  10.83% nach 10.38% (Spitzenwert 25.08.2021 mit 11.49%).
    04.11.2021  Die 7TM der Intensivbettenbelegungen sind am 04.11.2021 weiter gestiegen: 7TM=2069.9 (TW=2325) nach 7TM=1994.9 (TW=2200) . Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist erneut gestiegen (k= -2) auf  10.38% nach 9.87% (Spitzenwert 25.08.2021 mit 11.49%).
    03.11.2021  Die 7TM der Intensivbettenbelegungen sind am 03.11.2021 weiter gestiegen: 7TM=1994.9 (TW=2200) nach 7TM=1929.3 (TW=2131). Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist erneut gestiegen (k= -1) auf  9.87% nach 9.77% (Spitzenwert 25.08.2021 mit 11.49%).
    02.11.2021  Die 7TM der Intensivbettenbelegungen sind am 02.11.2021 weiter gestiegen: 7TM=1929.3 (TW=2131) nach 7TM=1867.4 (TW=2052). Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist zum 4. Mal gefallen (k= 4) auf  9.77% nach 10.32% (Spitzenwert 25.08.2021 mit 11.49%).
    01.11.2021  Die 7TM der Intensivbettenbelegungen sind am 01.11.2021 weiter gestiegen: 7TM=1867.4 (TW=2052) nach 7TM=1813.6 (TW=1977). Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist zum 3. Mal gefallen (k= 3) auf  10.32% nach 10.59% (Spitzenwert 25.08.2021 mit 11.49%).
    31.10.2021  Die 7TM der Intensivbettenbelegungen sind am 31.10.2021 weiter gestiegen: 7TM=1813.6 (TW=1977) nach 7TM=1761 (TW=1924). Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist zum 2. Mal gefallen (k= 2) auf  10.59% nach 10.65% (Spitzenwert 25.08.2021 mit 11.49%).
    30.10.2021  Die 7TM der Intensivbettenbelegungen sind am 30.10.2021 weiter gestiegen:  7TM=1761 (TW=1924) nach 7TM=1713.6 (TW=1860) nach 7TM=1666.4 (TW=1800). Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist gefallen (k= 1) auf  10.65% nach 10.69% (Spitzenwert 25.08.2021 mit 11.49%).
    29.10.2021  Die 7TM der Intensivbettenbelegungen sind am 29.10.2021 weiter gestiegen:  7TM=1713.6 (TW=1860) nach 7TM=1666.4 (TW=1800)  . Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist gestiegen (k= -19) auf  10.69% nach 10.45%  (Spitzenwert 25.08.2021 mit 11.49%).
    28.10.2021  Die 7TM der Intensivbettenbelegungen sind am 28.10.2021 weiter gestiegen:  7TM=1666.4 (TW=1800) nach 7TM=1627.3 (TW=1761) . Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist gestiegen (k= -18) auf  10.45%  nach 10.25%  (Spitzenwert 25.08.2021 mit 11.49%).
    27.10.2021  Die 7TM der Intensivbettenbelegungen sind am 27.10.2021 weiter gestiegen: 7TM=1627.3 (TW=1761) nach 7TM=1586 (TW=1698). Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist gestiegen (k= -17) auf  10.25% nach 9.44% (Spitzenwert 25.08.2021 mit 11.49%).
    26.10.2021  Die 7TM der Intensivbettenbelegungen sind am 26.10.2021 weiter gestiegen: 7TM=1586 (TW=1698) nach 7TM=1552.9 (TW=1675). Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist gestiegen (k= -16) auf 9.44% nach 9.07% (Spitzenwert 25.08.2021 mit 11.49%).
    25.10.2021  Die 7TM der Intensivbettenbelegungen sind am 25.10.2021 weiter gestiegen: 7TM=1552.9 (TW=1675) nach 7TM=1520.6 (TW=1609) . Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist gestiegen (k= -15) auf 9.07% nach 8.91%  (Spitzenwert 25.08.2021 mit 11.49%).
    24.10.2024  Die 7TM der Intensivbettenbelegungen sind am 24.10.2021 weiter gestiegen: 7TM=1520.6 (TW=1609) 7TM=1492.6 (TW=1592). Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist gestiegen (k= -14) auf 8.91% nach 8.84% (Spitzenwert 25.08.2021 mit 11.49%).
    23.10.2023  Die 7TM der Intensivbettenbelegungen sind am 23.10.2021 weiter gestiegen: 7TM=1492.6 (TW=1592) nach 7TM=1465.6 (TW=1530)  . Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist gestiegen (k= -13) auf 8.84% [korrigiert] nach 8.46% (Spitzenwert 25.08.2021 mit 11.49%).
    22.10.2022  Die 7TM der Intensivbettenbelegungen sind am 22.10.2021 weiter gestiegen: 7TM=1465.6 (TW=1530) [korrigiert] nach 7TM=1446.6 (TW=1526) . Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist gestiegen (k= -12) auf 8.46% nach 8.21% (Spitzenwert 25.08.2021 mit 11.49%).
    21.10.2022  Die 7TM der Intensivbettenbelegungen sind am 21.10.2021 weiter gestiegen: 7TM=1446.6 (TW=1526) nach 7TM=1427.3 (TW=1472). Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist gestiegen (k= -11) auf 8.21% nach 7.51% (Spitzenwert 25.08.2021 mit 11.49%).
    20.10.2021  Die 7TM der Intensivbettenbelegungen sind am 20.10.2021 weiter gestiegen: 7TM=1427.3 (TW=1472) nach 7TM=1416.0 (TW=1466) . Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist gestiegen (k= -10) auf 7.51% nach 7.2% (Spitzenwert 25.08.2021 mit 11.49%).
    19.10.2021  Die 7TM der Intensivbettenbelegungen sind am 19.10.2021 weiter gestiegen: 7TM=1416.0 (TW=1466) nach 7TM=1402.9 (TW=1449). Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist gestiegen (k= -9) auf 7.2% nach 6.75%  (Spitzenwert 25.08.2021 mit 11.49%).
    _18.10.2021 Die 7TM der Intensivbettenbelegungen sind am 18.10.2021 weiter gestiegen: 7TM=1402.9 (TW=1449) nach 7TM=1388.1 (TW=1413). Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist gestiegen (k= -8) auf 6.75% nach 6.63% (Spitzenwert 25.08.2021 mit 11.49%).
    17.10.2021  Die 7TM der Intensivbettenbelegungen sind am 17.10.2021 weiter gestiegen: 7TM=1388.1 (TW=1413) nach  7TM=1377.1 (TW=1403) . Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist gestiegen (k= -7) auf 6.63% nach 6.55% (Spitzenwert 25.08.2021 mit 11.49%).
    16.10.2021  Die 7TM der Intensivbettenbelegungen sind am 16.10.2021 weiter gestiegen: 7TM=1377.1 (TW=1403) nach 7TM=1367.4 (TW=1397). Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist gestiegen (k= -6) auf 6.55% nach 6.52% (Spitzenwert 25.08.2021 mit 11.49%).
    15.10.2021  Die 7TM der Intensivbettenbelegungen sind am 15.10.2021 weiter gestiegen: 7TM=1367.4 (TW=1397) nach 7TM=1359.6 (TW=1391). Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist deutlich gestiegen (k= -5) auf 6.52 nach 6.34% (Spitzenwert 25.08.2021 mit 11.49%).
    14.10.2021  Die 7TM der Intensivbettenbelegungen sind am 14.10.2021 weiter gestiegen: 7TM=1359.6 (TW=1391) nach 7TM=1355.7 (TW=1393). Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist deutlich gestiegen (k= -4) auf 6.34% nach 6.24%   (Spitzenwert 25.08.2021 mit 11.49%).
    13.10.2021  Die 7TM der Intensivbettenbelegungen sind am 13.10.2021 wieder gestiegen: 7TM=1355.7 (TW=1393) nach 7TM=1349.0 (TW=1374). Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist gestiegen (k= -3) auf 6.24% (korrigiert) nach 6.20%   (Spitzenwert 25.08.2021 mit 11.49%).
    12.10.2021  Die 7TM der Intensivbettenbelegungen sind am 12.10.2021 wieder gestiegen: 7TM=1349.0 (TW=1374) nach 7TM=1345.3 (TW=1346). Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist leicht gestiegen (k= -2) auf 6.20% nach 6.18%   (Spitzenwert 25.08.2021 mit 11.49%).
    11.10.2021  Die 7TM der Intensivbettenbelegungen sind am 11.10.2021 wieder leicht gestiegen: 7TM=1345.3 (TW=1346) nach 7TM=1343.9 (TW=1336). Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist leicht gestiegen (k= -1) auf 6.18% nach 6.16%   (Spitzenwert 25.08.2021 mit 11.49%).
    10.10.2021  Die 7TM der Intensivbettenbelegungen sind am 10.10.2021 wieder leicht gestiegen: 7TM=1343.9 (TW=1336) nach 7TM=1341.9 (TW=1335). Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist leicht gefallen (k= 1) auf 6.16% nach 6.17%    (Spitzenwert 25.08.2021 mit 11.49%).
    09.10.2021  Die 7TM der Intensivbettenbelegungen sind am 09.10.2021 wieder leicht gestiegen: TW=1335 (7TM=1341.9) nach 1342 (7TM=1339.9).Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist leicht gestiegen (k= -3) auf 6.17% nach 6.03%   (Spitzenwert 25.08.2021 mit 11.49%).
    08.10.2021  Die 7TM der Intensivbettenbelegungen sind am 08.10.2021 wieder minimal gefallen:  TW=TW=1342 (7TM=1339.9) nach TW=1364 (7MW=1340.1). Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist gestiegen (k= -2) auf 6.03% nach 5.99  (Spitzenwert 25.08.2021 mit 11.49%).
    07.10.2021  Die 7TM der Intensivbettenbelegungen sind am 07.10.2021 zum ersten Mal seit 16 Senkungen wieder gestiegen: TW=1364 (7MW=1340.1) nach TW=1346 (7TM=1737.0). Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist wieder minimal gestiegen (k= -1) auf 5.99 nach  5.97% (Spitzenwert 25.08.2021 mit 11.49%).
    06.10.2021  Die 7TM der Intensivbettenbelegungen sind am 06.10.2021 zum 16. mal weiter gefallen: TW=1346 (7TM=1737.0) nach TW=1348 (7TM=1337.7). Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist nach 3 Anstiegen wieder gefallen auf 5.97% nach 6.02%  (Spitzenwert 25.08.2021 mit 11.49%).
    05.10.2021  Die 7TM der Intensivbettenbelegungen sind am 05.10.2021 zum 15. mal weiter gefallen: TW=1348 (7TM=1337.7) nach  TW=1336 [korrigiert] (7TM=1345.6). Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist zum 3. mal gestiegen auf 6.02% nach 6.01%   (Spitzenwert 25.08.2021 mit 11.49%).
    04.10.2021  Die 7TM der Intensivbettenbelegungen sind am 04.10.2021 zum 14. mal weiter gefallen: TW=1336 [korrigiert] (7TM=1345.6) nach TW=1322  (7TM=1357.7). Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist zum 2. mal gestiegen auf 6.01% nach 5.89%  (Spitzenwert 25.08.2021 mit 11.49%).
    03.10.2021  Die 7TM der Intensivbettenbelegungen sind am 03.10.2021 weiter gefallen gefallen: TW=1322 (7TM=1357.7) nach TW=1321 (7TM=1372.6). Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist gestiegen auf 5.89% nach 5.82% (Spitzenwert 25.08.2021 mit 11.49%).
    02.10.2021  Die 7TM der Intensivbettenbelegungen sind am 02.10.2021 wieder gefallen: TW=1321 [korrigiert am 4.10.21]  (7TM=1372.6) nach TW=1344 (7TM=1387.4). Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen ist wieder gefallen auf 5.82% nach 5.92% (Spitzenwert 25.08.2021 mit 11.49%).
    01.10.2021  Die 7TM der Intensivbettenbelegungen sind am 01.10.2021 weiter gefallen: TW=1344 (7TM=1387.4) nach TW=1342 (7TM=1394.7). Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen, der seit 25.08.2021 fortlaufend sank, ist zum 5. Mal in Folge wieder gestiegen auf 5.92% nach 5.76%  (Spitzenwert 25.08.2021 mit 11.49%).
    30.09.2021  Die 7TM der Intensivbettenbelegungen sind am 30.09.2021 weiter gefallen: TW=1342 (7TM=1394.7) nach TW=1351 (7TM=1412.8). Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen, der seit 25.08.2021 fortlaufend sank, ist zum 4. Mal in Folge wieder gestiegen auf 5.76% nach 5.64% (Spitzenwert 25.08.2021 mit 11.49%).
    29.09.2021  Die 7TM der Intensivbettenbelegungen sind am 29.09.2021 weiter gefallen: TW=1351 (7TM=1412.8) nach TW=1403 (7TM=1436.3). Der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen, der seit 25.08.2021 fortlaufend sank, ist zum 3. Mal in Folge wieder gestiegen  auf 5.64% nach 5.41% (Spitzenwert 25.08.2021 mit 11.49%).
    28.09.2021  Die 7TM der Intensivbettenbelegungen sind am 28.09.2021 weiter gefallen, wobei der Höhepunkt seit 16.09.21 vorerst überschritten wurde, so dass der kubische Kurvenfit für die Exponentialdiagnose nicht mehr angemessen ist, weil er die Seitwärts- oder Abwärtsbewegung nachvollzieht und ein hohes rsquare anzeigt, obwohl die Werte nicht mehr ansteigen. TW=1403 (7TM=1436.3) nach TW=1421(7TM=1451.7). Allerdings ist der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen, der seit 25.08.2021 fortlaufend sank, zuletzt am 28.09.2021 auf 5.41% gestiegen nach 4.20% (Spitzenwert 25.08.2021 mit 11.49%).
    27.09.2021  Die 7TM der Intensivbettenbelegungen sind am 27.09.2021 weiter gefallen, wobei der Höhepunkt seit 16.09.21 vorerst überschritten wurde, so dass der kubische Kurvenfit für die Exponentialdiagnose nicht mehr angemessen ist, weil er die Seitwärts- oder Abwärtsbewegung nachvollzieht und ein hohes rsquare anzeigt, obwohl die Werte nicht mehr ansteigen. TW=1421(7TM=1451.7) nach TW=1425 (1470.2). Man sollte zudem berücksichtigen, dass der Anteil  der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen seit 25.08.2021 fortlaufend sinkt, zuletzt, am 26.09.2021 auf 5.1993% nach 5.2034% (Spitzenwert 25.08.2021 mit 11.49%).
    26.09.2021  Die 7TM der Intensivbettenbelegungen sind am 26.09.2021 weiter gefallen, wobei der Höhepunkt seit 16.09.21 vorerst überschritten wurde, so dass der kubische Kurvenfit für die Exponentialdiagnose nicht mehr angemessen ist, weil er die Seitwärts- oder Abwärtsbewegung nachvollzieht und ein hohes rsquare anzeigt, obwohl die Werte nicht mehr ansteigen. TW=1425 (1470.2) nach 1426 (7TM=1487.7). Man sollte zudem berücksichtigen, dass der Anteil  der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen seit 25.08.2021 fortlaufend sinkt, zuletzt, am 26.09.2021 auf 5.20% nach 5.21% (Spitzenwert 25.08.2021 mit 11.49%).
    25.09.2021  Die 7TM der Intensivbettenbelegungen sind am 25.09.2021 weiter gefallen, wobei der Höhepunkt seit 16.09.21 vorerst  überschritten wurde, so dass der kubische Kurvenfit für die Exponentialdiagnose nicht mehr angemessen ist, weil er die Seitwärts- oder      Abwärtsbewegung nachvollzieht und ein hohes rsquare anzeigt, obwohl die Werte nicht mehr ansteigen.  TW=1426 (7TM=1487.7) nach TW=? (7TM=?). Man sollte zudem berücksichtigen, dass der Anteil  der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen seit 25.08.2021 fortlaufend sinkt, zuletzt, am 25.09.2021 auf 5.21% nach ? (Spitzenwert 25.08.2021 mit 11.49%).
    24.09.2021  Die 7TM der Intensivbettenbelegungen sind auch am 26.09.2021 dem Graphen des Intensiregister nicht zu entnehmen.
    23.09.2021  Die 7TM der Intensivbettenbelegungen sind am 23.09.2021 weiter gefallen, wobei der Höhepunkt seit 16.09.21 vorerst überschritten wurde, so dass der kubische Kurvenfit für die Exponentialdiagnose nicht mehr angemessen ist, weil er die Seitwärts- oder  Abwärtsbewegung nachvollzieht und ein hohes rsquare anzeigt, obwohl die Werte nicht mehr ansteigen.  TW=1451 (7TM=1507.0) nach TW=1492 (7TM=1519.7). Man sollte zudem berücksichtigen, dass der Anteil  der 7TM der Intensivbehandlungen an den 7TM der  Neu-Infektionen seit 25.08.2021 fortlaufend sinkt, zuletzt, am 23.09.2021 auf 5.26% nach 5.33%  (Spitzenwert 25.08.2021 mit 11.49%).
    22.09.2021  Die 7TM der Intensivbettenbelegungen sind am 22.09.2021 weiter gefallen, wobei der Höhepunkt seit 16.09.21 vorerst  überschritten wurde, so dass der kubische Kurvenfit für die Exponentialdiagnose nicht mehr angemessen ist, weil er die Seitwärts- oder      Abwärtsbewegung nachvollzieht und ein hohes rsquare anzeigt, obwohl die Werte nicht mehr ansteigen.  TW=1492 (7TM=1519.7) nach      TW=1495 (7TM=1523.6).  Man sollte zudem berücksichtigen, dass der Anteil  der 7TM der Intensivbehandlungen an den 7TM der  Neu-Infektionen seit 25.08.2021 fortlaufend sinkt, zuletzt, am 22.09.2021 auf 5.33% nach  5.53% (Spitzenwert 25.08.2021 mit 11.49%).

    21.09.2021  Die 7TM der Intensivbettenbelegungen sind am 20.09.2021 gefallen, wobei der Höhepunkt seit 16.09.21 vorerst überschritten wurde, so dass der kubische Kurvenfit für die Exponentialdiagnose nicht mehr angemessen ist, weil er die Seitwärts- oder Abwärtsbewegung nachvollzieht und ein hohes rsquare anzeigt, obwohl die Werte nicht mehr ansteigen.  TW=1495 (7TM=1523.6) nach 1532 (1528.1).  Man sollte zudem berücksichtigen, dass der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen seit 25.08.2021 fortlaufend sinkt, zuletzt, am 21.09.2021 auf  5.53% nach 5.70% (Spitzenwert 25.08.2021 mit 11.49%).
    _

    20.09.2021  Die 7TM der Intensivbettenbelegungen sind am 22.09.2021 wieder gestiegen, aber der Höhepunkt ist seit 16.09.21 vorerst überschritten, so dass der kubische Kurvenfit für die Exponentialdiagnose nicht mehr angemessen ist, weil er die Seitwärts- oder Abwärtsbewegung nachvollzieht und ein hohes rsquare anzeigt, obwohl die Werte nicht mehr ansteigen.  TW=1532 (1528.1) nach 1530 (7TM=1522.3).  Man sollte zudem berücksichtigen, dass der Anteil  der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen seit 25.08.2021 fortlaufend sinkt, zuletzt, am 20.09.2021 auf  5.70% nach 5.88%  (Spitzenwert 25.08.2021 mit 11.49%).
    _
    19.09.2021  Die 7TM der Intensivbettenbelegungen sind am 20.09.2021 wieder gestiegen, aber der Höhepunkt ist seit 16.09.21 vorerst überschritten, so dass der kubische Kurvenfit für die Exponentialdiagnose nicht mehr angemessen ist, weil er die Seitwärts- oder Abwärtsbewegung nachvollzieht und ein hohes rsquare anzeigt, obwohl die Werte nicht mehr ansteigen. TW=1530 (7TM=1522.3) nach 1515 (7TM=1509.4). Man sollte zudem berücksichtigen, dass der  Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen seit 25.08.2021 fortlaufend sinkt, zuletzt, am 19.09.2021 auf  5.88% nach 6.10%  (Spitzenwert 25.08.2021 mit 11.49%).
    _
    18.09.2021  Die 7TM der Intensivbettenbelegungen sind am 20.09.2021 wieder gestiegen, aber der Höhepunkt ist seit 16.09.21 vorerst überschritten, so dass der kubische Kurvenfit für die Exponentialdiagnose nicht mehr angemessen ist, weil er die Seitwärts- oder Abwärtsbewegung nachvollzieht und ein hohes rsquare anzeigt, obwohl die Werte nicht mehr ansteigen. TW=1515 (1509.4) nach 1534 (7TM=1496.7).  Man sollte zudem berücksichtigen, dass der  Anteil  der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen seit 25.08.2021 fortlaufend sinkt, zuletzt, am 18.09.2021 auf  6.10% nach 6.15% (Spitzenwert 25.08.2021 mit 11.49%).

    17.09.2021  Die 7TM der Intensivbettenbelegungen sind am 20.09.2021 wieder gestiegen, aber der Höhepunkt ist seit 16.09.21 vorerst überschritten, so dass der kubische Kurvenfit für die Exponentialdiagnose nicht mehr angemessen ist, weil er die Seitwärts- oder Abwärtsbewegung nachvollzieht und ein hohes rsquare anzeigt, obwohl die Werte nicht mehr ansteigen. TW=1534 (7TM=1496.7) nach 1540 (7TM=1477.7). Man sollte aber auch berücksichtigen, dass der  Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen seit 25.08.2021 fortlaufend sinkt, zuletzt, am 17.09.2021 auf  6.15% nach 6.456  (Spitzenwert 25.08.2021 mit 11.49%).
    _
    16.09.2021  Die 7TM der Intensivbettenbelegungen sind am 20.09.2021 wieder gestiegen, aber der Höhepunkt ist seit 16.09.21 vorerst überschritten, so dass der kubische Kurvenfit für die Exponentialdiagnose nicht mehr angemessen ist, weil er die Seitwärts- oder Abwärtsbewegung nachvollzieht und ein hohes rsquare anzeigt, obwohl die Werte nicht mehr ansteigen. TW=1540 (7TM=1477.7) nach 1518 (7TM=1455.9). Man muss aber auch berücksichtigen, dass der  Anteil  der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen seit 25.08.2021 fortlaufend sinkt, zuletzt, am 16.09.2021 auf  6.456 nach 6.75%. (Spitzenwert 25.08.2021 mit 11.49%).
    _
    15.09.2021  Die 7TM der Intensivbettenbelegungen sind am 15.09.2021 erstmals gefallen steigen aber noch weiter exponentiell und zeigen aktuell TW=1518 (7TM=1455.9) nach 1527 )  (7TM=1436.1). Zudem muss man berücksichtigen, dass der Anteil der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen seit 25.08.2021 fortlaufend sinkt, zuletzt, am 15.09.2021 noch 6.75% nach 7.09% betrug. (Spitzenwert 25.08.2021 mit 11.49%).
    _
    14.09.2021  Die Intensivbettenbelegungen steigen weiter exponentiell und zeigen aktuell TW=1527 (14.9.) nach 1491 (7TM=1409.4) nach TW=1440 (7TM=1384.9). Der kleine Hoffnungsknick auf Sättigung von vorgestern war gestern schon wieder verschwunden und war wohl ein Wochenendartefakt. Anderseits muss man auch berücksichtigen, dass der  Anteil  der 7TM der Intensivbehandlungen an den 7TM der Neu-Infektionen seit 25.08.2021 fortlaufend sinkt, zuletzt, am 14.09.2021 noch 7.09% betrug. (Spitzenwert 25.08.2021 mit 11.49%).
    _
    13.09.2021  Die Intensivbettenbelegungen steigen weiter exponentiell und zeigen aktuell TW=1491 (7TM=1409.4) nach TW=1440 (7TM=1384.9).  Der kleine Hoffnungsknick auf Sättigung von gestern ist heute schon wieder verschwunden und war wohl ein Wochenendartefakt.

    12.09.2021  Die Intensivbettenbelegungen steigen weiter exponentiell und zeigen aktuell 1440 Fälle mit rquare(cubic)=0.9940 an. Das sind 14 mehr als am Vortag gemeldet. Bei den 7-Tage-Mittelwerten sind es 1384.9 mit rsquare(cubic)=0.9958 nach 1361.9. Die 7TM zeigen eine ogivenhafte Entwicklungsform, was bei den Wachstumskurven auf eine Sättigung hindeutet.
    _

    _
    11.09.2021  Die Intensivbettenbelegungen zeigen aktuell eine leicht abflauende, aber fortgesetzte exponentielle Entwicklung (wenn Kriterium rsquare > 0.98 dann ist die Anpassungsgüte hoch): Tageswert 1426 nach 1401 mit einem  rsquare=0.9945. Schätzwert (Basis 22.7.-11.9.21)=1490 (statt real 1426) mit einer Überschätzung von 4.49%.
    _


    Prüfung aufexponentielle Entwicklung der 7-Tage-Mittelwerte der Neuinfektionen der 12. Omikron-Welle Beginn 29.12.2021. 12. "Omikronwelle" Beginn am 29.12.21; 11. Welle (RKI Sprech 4. Welle), Beginn 28.09.201 mit Anfangswert 7769  bis 29.12.2021. Basisdatenquelle Dashboard RKI (NeuInf), 7 Tage Mittelwert eigene Berechnung.

    47.KW22, Fr 25.11.22:

    KF221118  7TM=24573 nach 25007, 25881, 26647, 27963, Missing Data, Missing Data; k= 8 (Pos. Trendumkehr De seit 21.10.22); rsquare wird erst wieder erfasst, wenn es Anzeichen für eine neue exponentielle Entwicklung gibt
    KF221117  7TM=25007 nach 25881, 26647, 27963, Missing Data, Missing Data, Nicht erfasst; k= 7 (Pos. Trendumkehr De seit 21.10.22); rsquare wird erst wieder erfasst, wenn es Anzeichen für eine neue exponentielle Entwicklung gibt
    KF221116  7TM=25881 nach 26647, 27963, Missing Data, Missing Data, Nicht erfasst, 30209; k= 6 (Pos. Trendumkehr De seit 21.10.22); rsquare wird erst wieder erfasst, wenn es Anzeichen für eine neue exponentielle Entwicklung gibt
    KF221115  7TM=26647 nach 27963, Missing Data, Missing Data, Nicht erfasst, 30209, 31068; k= 5 (Pos. Trendumkehr De seit 21.10.22); rsquare wird erst wieder erfasst, wenn es Anzeichen für eine neue exponentielle Entwicklung gibt
    KF221114  7TM=27963 nach Missing Data, Missing Data, Nicht erfasst, 30209, 31068, 34063; k= 4 (Pos. Trendumkehr De seit 21.10.22); rsquare wird erst wieder erfasst, wenn es Anzeichen für eine neue exponentielle Entwicklung gibt
    KF221113  7TM=Missing Data nach Missing Data, Nicht erfasst, 30209, 31068, 34063, 39191; k= 3 (Pos. Trendumkehr De seit 21.10.22); rsquare wird erst wieder erfasst, wenn es Anzeichen für eine neue exponentielle Entwicklung gibt
    KF221112  7TM=Missing Data nach Nicht erfasst, 30209, 31068, 34063, 39191, Missing Data (So-0-Runde); k= 3 (Pos. Trendumkehr De seit 21.10.22); rsquare wird erst wieder erfasst, wenn es Anzeichen für eine neue exponentielle Entwicklung gibt
    KF221111  nicht erfasst.
    KF221110  7TM=30209 nach 31068, 34063, 39191, Missing Data (So-0-Runde) nach Missing Data (Sa-0-Runde), 36092; k= 3 (Pos. Trendumkehr De seit 21.10.22); rsquare wird erst wieder erfasst, wenn es Anzeichen für eine neue exponentielle Entwicklung gibt
    KF221109  7TM=31068 nach 34063, 39191, Missing Data (So-0-Runde) nach Missing Data (Sa-0-Runde), 36092, 37357, 38051; k= 2 (Pos. Trendumkehr De seit 21.10.22); rsquare wird erst wieder erfasst, wenn es Anzeichen für eine neue exponentielle Entwicklung gibt
    KF221108  7TM=34063 nach 39191, Missing Data (So-0-Runde) nach Missing Data (Sa-0-Runde), 36092, 37357, 38051, ; k= 1 (Pos. Trendumkehr De seit 21.10.22); rsquare wird erst wieder erfasst, wenn es Anzeichen für eine neue exponentielle Entwicklung gibt
    KF221107  7TM=39191 nach Missing Data (So-0-Runde) nach Missing Data (Sa-0-Runde), 36092, 37357, 38051, 38090 (5 BL Missing Data), 47351 (8 BL Missing Data); k= -1 (Pos. Trendumkehr De seit 21.10.22); rsquare wird erst wieder erfasst, wenn es Anzeichen für eine exponentielle Entwicklung gibt
    KF221106  7TM=Missing Data (So-0-Runde) nach Missing Data (Sa-0-Runde), 36092, 37357, 38051, 38090 (5 BL Missing Data), 47351 (8 BL Missing Data); k= 5 (Pos. Trendumkehr De seit 21.10.22); rsquare wird erst wieder erfasst, wenn es Anzeichen für eine exponentielle Entwicklung gibt
    KF221105  7TM=Missing Data (Sa-0-Runde) nach 36092, 37357, 38051, 38090 (5 BL Missing Data), 47351 (8 BL Missing Data), 56920 (bis auf 1 NeuInf Missing Data), 56919 (Missing Data); k= 5 (Pos. Trendumkehr De seit 21.10.22); rsquare wird erst wieder erfasst, wenn es Anzeichen für eine exponentielle Entwicklung gibt
    KF221104  7TM=36092 nach 37357, 38051, 38090 (5 BL Missing Data), 47351 (8 BL Missing Data), 56920 (bis auf 1 NeuInf Missing Data), 56919 (Missing Data); k= 5 (Pos. Trendumkehr De seit 21.10.22); rsquare wird erst wieder erfasst, wenn es Anzeichen für eine exponentielle Entwicklung gibt
    KF221103  7TM=37357 nach 38051, 38090 (5 BL Missing Data), 47351 (8 BL Missing Data), 56920 (bis auf 1 NeuInf Missing Data), 56919 (Missing Data), 56920; k= 4 (Pos. Trendumkehr De seit 21.10.22); rsquare wird erst wieder erfasst, wenn es Anzeichen für eine exponentielle Entwicklung gibt
    KF221102  7TM=38051 nach 38090 (5 BL Missing Data), 47351 (8 BL Missing Data), 56920 (bis auf 1 NeuInf Missing Data), 56919 (Missing Data), 56920, 60764; k= 3 (Pos. Trendumkehr De seit 21.10.22); rsquare wird erst wieder erfasst, wenn es Anzeichen für eine exponentielle Entwicklung gibt
    KF221101  7TM=38090 (5 BL Missing Data) nach 47351 (8 BL Missing Data), 56920 (bis auf 1 NeuInf Missing Data), 56919 (Missing Data), 56920, 60764, 65164; k= 2 (Pos. Trendumkehr De seit 21.10.22); rsquare wird erst wieder erfasst, wenn es Anzeichen für eine exponentielle Entwicklung gibt
    KF221031  7TM=47351 (8 BL Missing Data) nach 56920 (bis auf 1 NeuInf Missing Data), 56919 (Missing Data), 56920, 60764, 65164, 70579, 75620, Missing Data; k= 1 (Pos. Trendumkehr De seit 21.10.22); rsquare wird erst wieder erfasst, wenn es Anzeichen für eine exponentielle Entwicklung gibt
    KF221030  7TM=56920 (bis auf 1 Missing Data) nach 56919 (Missing Data), 56920, 60764, 65164, 70579, 75620, Missing Data; k= -1 (Pos. Trendumkehr De seit 21.10.22); rsquare wird erst wieder erfasst, wenn es Anzeichen für eine exponentielle Entwicklung gibt
    KF221029  7TM=56919 (Missing Data) nach 56920, 60764, 65164, 70579, 75620, Missing Data; k= +13 (Pos. Trendumkehr De); rsquare wird erst wieder erfasst, wenn es Anzeichen für eine exponentielle Entwicklung gibt
    KF221028  7TM=56920 nach 60764, 65164, 70579, 75620, Missing Data, Missing Data; k= +12 (Pos. Trendumkehr De); rsquare wird erst wieder erfasst, wenn es Anzeichen für eine exponentielle Entwicklung gibt
    KF221027  7TM=60764 nach 65164, 70579, 75620, Missing Data, Missing Data, 80551; k= +11 (Pos. Trendumkehr De); rsquare wird erst wieder erfasst, wenn es Anzeichen für eine exponentielle Entwicklung gibt
    KF221026  7TM=65164 nach 70579, 75620, Missing Data, Missing Data, 80551, 82962; k= +10 (Pos. Trendumkehr De); rsquare wird erst wieder erfasst, wenn es Anzeichen für eine exponentielle Entwicklung gibt
    KF221025  7TM=70579 nach 75620, Missing Data, Missing Data, 80551, 82962, 86091; k= +9 (Pos. Trendumkehr De); rsquare wird erst wieder erfasst, wenn es Anzeichen für eine exponentielle Entwicklung gibt
    KF221024  7TM=75620 nach Missing Data, Missing Data, 80551, 82962, 86091, 90150; k= +8 (Pos. Trendumkehr De); rsquare wird erst wieder erfasst, wenn es Anzeichen für eine exponentielle Entwicklung gibt
    KF221023  7TM=Missing Data nach Missing Data, 80551, 82962, 86091, 90150, 91103; k= +7 (Pos. Trendumkehr De); rsquare wird erst wieder erfasst, wenn es Anzeichen für eine exponentielle Entwicklung gibt.
    KF221022  7TM=Missing Data nach 80551, 82962, 86091, 90150, 91103, Missing Data; k= +7 (Pos. Trendumkehr De); rsquare wird erst wieder erfasst, wenn es Anzeichen für eine exponentielle Entwicklung gibt, was aktuell nicht der Fall ist.
    KF221021  7TM=80551 nach 82962, 86091, 90150, 91103, Missing Data, Missing Data; k= +7 (Pos. Trendumkehr De); rsquare wird erst wieder erfasst, wenn es Anzeichen für eine exponentielle Entwicklung gibt, was aktuell nicht der Fall ist.
    KF221020  7TM=82962 nach 86091, 90150, 91103, Missing Data, Missing Data, 94315; k= +6; rsquare wird erst wieder erfasst, wenn es Anzeichen für eine exponentielle Entwicklung gibt, was aktuell nicht der Fall ist.
    KF221019  7TM=86091 nach 90150, 91103, Missing Data, Missing Data, 94315, 98709; k= +5; rsquare wird erst wieder erfasst, wenn es Anzeichen für eine exponentielle Entwicklung gibt, was aktuell nicht der Fall ist.
    KF221018  7TM=90150 nach 91103, Missing Data, Missing Data, 94315, 98709, 107268; k= +4; rsquare wird erst wieder erfasst, wenn es Anzeichen für eine exponentielle Entwicklung gibt, was aktuell nicht der Fall ist.
    KF221017  7TM=91103 nach Missing Data, Missing Data, 94315, 98709, 107268, 105421; k= +3; rsquare wird erst wieder erfasst, wenn es Anzeichen für eine exponentielle Entwicklung gibt, was aktuell nicht der Fall ist.

    KF221016  7TM=Missing Data nach Missing Data, 94315, 98709, 107268, 105421, 104962; k= +2; rsquare wird erst wieder erfasst, wenn es Anzeichen für eine exponentielle Entwicklung gibt, was aktuell nicht der Fall ist.
    KF221015  7TM=Missing Data nach 94315, 98709, 107268, 105421, 104962, Missing Data; k= +2; rsquare wird erst wieder erfasst, wenn es Anzeichen für eine exponentielle Entwicklung gibt, was aktuell nicht der Fall ist.
    KF221014  7TM=94315 nach 98709, 107268, 105421, 104962, Missing Data, Missing Data; k= +2; rsquare wird erst wieder erfasst, wenn es Anzeichen für eine exponentielle Entwicklung gibt, was aktuell nicht der Fall ist.
    KF221013  7TM=98709 nach 107268, 105421, 104962, Missing Data, Missing Data, 80314; k= +1; rsquare wird erst wieder erfasst, wenn es Anzeichen für eine exponentielle Entwicklung gibt, was aktuell nicht der Fall ist.
    KF221012  7TM=107268 nach 105421, 104962, Missing Data, Missing Data, 80314, 73398; k= -7; rsquare wird erst wieder erfasst, wenn es Anzeichen für eine exponentielle Entwicklung gibt, was aktuell nicht der Fall ist.
    KF221011  7TM=105421 nach 104962, Missing Data, Missing Data, 80314, 73398, 62292; k= -6; rsquare wird erst wieder erfasst, wenn es Anzeichen für eine exponentielle Entwicklung gibt, was aktuell nicht der Fall ist.
    KF221010  7TM=104962 nach Missing Data, Missing Data, 80314, 73398, 62292, 54660; k= -5; rsquare wird erst wieder erfasst, wenn es Anzeichen für eine exponentielle Entwicklung gibt, was aktuell nicht der Fall ist.
    KF221009  7TM=Missing Data nach Missing Data, 80314, 73398, 62292, 54660, 49271; k= -4; rsquare wird erst wieder erfasst, wenn es Anzeichen für eine exponentielle Entwicklung gibt, was aktuell nicht der Fall ist.
    KF221008  7TM=Missing Data nach 80314, 73398, 62292, 54660, 49271, Missing Data; k= -4; rsquare wird erst wieder erfasst, wenn es Anzeichen für eine exponentielle Entwicklung gibt, was aktuell nicht der Fall ist.
    KF221007  7TM=80314 nach 73398, 62292, 54660, 49271, Missing Data, Missing Data; k= -4; rsquare wird erst wieder erfasst, wenn es Anzeichen für eine exponentielle Entwicklung gibt, was aktuell nicht der Fall ist.
    KF221006  7TM=73398 nach 62292, 54660, 49271, Missing Data, Missing Data, 62026; k= -3; rsquare wird erst wieder erfasst, wenn es Anzeichen für eine exponentielle Entwicklung gibt, was aktuell nicht der Fall ist.
    KF221005  7TM=62292 nach 54660, 49271, Missing Data, Missing Data, 62026, 58184; k= -2; rsquare wird erst wieder erfasst, wenn es Anzeichen für eine exponentielle Entwicklung gibt, was aktuell nicht der Fall ist.
    KF221004  7TM=54660 nach 49271, Missing Data, Missing Data, 62026, 58184, 51674; k= -1; rsquare wird erst wieder erfasst, wenn es Anzeichen für eine exponentielle Entwicklung gibt, was aktuell nicht der Fall ist.
    KF221003  7TM=49271 nach Missing Data, Missing Data, 62026, 58184, 51674, 48548; k= 1; rsquare wird erst wieder erfasst, wenn es Anzeichen für eine exponentielle Entwicklung gibt, was aktuell nicht der Fall ist.
    KF221002  7TM=Missing Data nach Missing Data, 62026, 58184, 51674, 48548, 42963; k= -19 (Nullrunde); rsquare wird erst wieder erfasst, wenn es Anzeichen für eine exponentielle Entwicklung gibt, was aktuell nicht der Fall ist.
    KF221001  7TM=Missing Data nach 62026, 58184, 51674, 48548, 42963, Missing Data; k= -19; (Nullrunde) rsquare wird erst wieder erfasst, wenn es Anzeichen für eine exponentielle Entwicklung gibt, was aktuell nicht der Fall ist.
    KF220930  7TM=62026 nach 58184, 51674, 48548, 42963, Missing Data, Missing Data; k= -19; rsquare wird erst wieder erfasst, wenn es Anzeichen für eine exponentielle Entwicklung gibt, was aktuell nicht der Fall ist.
    KF220929  7TM=58184 nach 51674, 48548, 42963, Missing Data, Missing Data, 38814; k= -18; rsquare wird erst wieder erfasst, wenn es Anzeichen für eine exponentielle Entwicklung gibt, was aktuell nicht der Fall ist.
    KF220928  7TM=51674 nach 48548, 42963, Missing Data, Missing Data, 38814, 37335; k= -17; rsquare wird erst wieder erfasst, wenn es Anzeichen für eine exponentielle Entwicklung gibt, was aktuell nicht der Fall ist.
    KF220927  7TM=48548 nach 42963, Missing Data, Missing Data, 38814, 37335, 35613; k= -16; rsquare wird erst wieder erfasst, wenn es Anzeichen für eine exponentielle Entwicklung gibt, was aktuell nicht der Fall ist.
    KF220926  7TM=42963 nach Missing Data, Missing Data 38814, 37335, 35613, 34118; k= -15; rsquare wird erst wieder erfasst, wenn es Anzeichen für eine exponentielle Entwicklung gibt, was aktuell nicht der Fall ist.
    KF220925  7TM=Missing Data nach Missing Data 38814, 37335, 35613, 34118, 33345; k= -14 (Missing Data); rsquare wird erst wieder erfasst, wenn es Anzeichen für eine exponentielle Entwicklung gibt, was aktuell nicht der Fall ist.
    KF220924  7TM=Missing Data nach 38814, 37335, 35613, 34118, 33345, Missing Data; k= -14 8Missing Data); rsquare wird erst wieder erfasst, wenn es Anzeichen für eine exponentielle Entwicklung gibt, was aktuell nicht der Fall ist.
    KF220923  7TM=38814 nach 37335, 35613, 34118, 33345, Missing Data, Missing Data, k= -14; rsquare wird erst wieder erfasst, wenn es Anzeichen für eine exponentielle Entwicklung gibt, was aktuell nicht der Fall ist.
    KF220922  7TM=37335 nach 35613, 34118, 33345, Missing Data, Missing Data, 325865, k= -13; rsquare wird erst wieder erfasst, wenn es Anzeichen für eine exponentielle Entwicklung gibt, was aktuell nicht der Fall ist.
    KF220921  7TM=35613 nach 34118, 33345, Missing Data, Missing Data, 32586, 31665; k= -12; rsquare wird erst wieder erfasst, wenn es Anzeichen für eine exponentielle Entwicklung gibt, was aktuell nicht der Fall ist.
    KF220920  7TM=34118 nach 33345, Missing Data, Missing Data, 32586, 31665, 31272; k= -11; rsquare wird erst wieder erfasst, wenn es Anzeichen für eine exponentielle Entwicklung gibt, was aktuell nicht der Fall ist.
    KF220919  7TM=33345 nach Missing Data, Missing Data, 32586, 31665, 31272, 30635; k= -10; rsquare wird erst wieder erfasst, wenn es Anzeichen für eine exponentielle Entwicklung gibt, was aktuell nicht der Fall ist.
    KF220918  7TM=Missing Data nach Missing Data, 32586, 31665, 31272, 30635, 29949; k= -9; rsquare wird erst wieder erfasst, wenn es Anzeichen für eine exponentielle Entwicklung gibt, was aktuell nicht der Fall ist.
    KF220917  7TM=Missing Data nach 32586, 31665, 31272, 30635, 29949, Missing Data; k= -8; rsquare wird erst wieder erfasst, wenn es Anzeichen für eine exponentielle Entwicklung gibt, was aktuell nicht der Fall ist.
    KF220916  7TM=32586 nach 31665, 31272, 30635, 29949, Missing Data, Missing Data; k= -8; rsquare wird erst wieder erfasst, wenn es Anzeichen für eine exponentielle Entwicklung gibt, was aktuell nicht der Fall ist..
    KF220915  7TM=31665 nach 31272, 30635, 29949, Missing Data, Missing Data, 29203; k= -7; rsquare wird erst wieder erfasst, wenn es Anzeichen für eine exponentielle Entwicklung gibt.
    KF220914  7TM=31272 nach 30635, 29949, Missing Data, Missing Data, 29203, 29086; k= -6; rsquare  jenseits < 0.98, wird so lange der Trend weiter nach unten geht nicht mehr erfasst. Ungeachtet dessen sind die hohen Zahlen, besonders bei den Toten, immer noch beunruhigend.
    KF220913  7TM=30635 nach 29949, Missing Data, Missing Data, 29203, 29086; k= -5; rsquare, jenseits < 0.98, wird so lange der Trend weiter nach unten geht nicht mehr erfasst. Ungeachtet dessen sind die hohen Zahlen, besonders bei den Toten, immer noch beunruhigend.
    KF220912  7TM=29949 nach Missing Data, Missing Data, 29203, 29086, 28791, 28411; k= -4; rsquare, jenseits < 0.98, wird so lange der Trend weiter nach unten geht nicht mehr erfasst. Ungeachtet dessen sind die hohen Zahlen, besonders bei den Toten, immer noch beunruhigend.
    KF220911  7TM=Missing Data nach Missing Data, 29203, 29086, 28791, 28411, 28812; k= -3; rsquare, jenseits < 0.98, wird so lange der Trend weiter nach unten geht nicht mehr erfasst. Ungeachtet dessen sind die hohen Zahlen, besonders bei den Toten, immer noch beunruhigend.
    KF220910  7TM=Missing Data nach 29203, 29086, 28791, 28411, 28812, Missing Data; k= -3; rsquare, jenseits < 0.98, wird so lange der Trend weiter nach unten geht nicht mehr erfasst. Ungeachtet dessen sind die hohen Zahlen, besonders bei den Toten, immer noch beunruhigend.
    KF220909  7TM=29203 nach 29086, 28791, 28411, 28812, Missing Data, Missing Data; k= -3; rsquare, jenseits < 0.98, wird so lange der Trend weiter nach unten geht nicht mehr erfasst. Ungeachtet dessen sind die hohen Zahlen, besonders bei den Toten, immer noch beunruhigend.
    KF220908  7TM=29086 nach 28791, 28411, 28812, Missing Data, Missing Data, 29497; k= -2; rsquare, jenseits < 0.98, wird so lange der Trend weiter nach unten geht nicht mehr erfasst. Ungeachtet dessen sind die hohen Zahlen, besonders bei den Toten, immer noch beunruhigend.
    KF220907  7TM=28791 nach 28411, 28812, Missing Data, Missing Data, 29497, 30051; k= -1; rsquare, jenseits < 0.98, wird so lange der Trend weiter nach unten geht nicht mehr erfasst. Ungeachtet dessen sind die hohen Zahlen, besonders bei den Toten, immer noch beunruhigend.
    KF220906  7TM=28411 nach 28812, Missing Data, Missing Data, 29497, 30051, 30539; k= 29; rsquare, jenseits < 0.98, wird so lange der Trend weiter nach unten geht nicht mehr erfasst. Ungeachtet dessen sind die hohen Zahlen, besonders bei den Toten, immer noch beunruhigend.
    KF220905  7TM=28812 nach Missing Data, Missing Data, 29497, 30051, 30539, 31939; k= 28; rsquare, jenseits < 0.98, wird so lange der Trend weiter nach unten geht nicht mehr erfasst. Ungeachtet dessen sind die hohen Zahlen, besonders bei den Toten, immer noch beunruhigend.
    KF220904  7TM=Missing Data nach Missing Data, 29497, 30051, 30539, 31939, 34459; k= 27; rsquare, jenseits < 0.98, wird so lange der Trend weiter nach unten geht nicht mehr erfasst. Ungeachtet dessen sind die hohen Zahlen, besonders bei den Toten, immer noch beunruhigend.
    KF220903  7TM=Missing Data nach 29497, 30051, 30539, 31939, 34459, Missing Data, k= 27; rsquare, jenseits < 0.98, wird so lange der Trend weiter nach unten geht nicht mehr erfasst. Ungeachtet dessen sind die hohen Zahlen, besonders bei den Toten, immer noch beunruhigend.
    KF220902  7TM=29497 nach 30051, 30539, 31939, 34459, Missing Data, Missing Data, k= 27; rsquare, jenseits < 0.98, wird so lange der Trend weiter nach unten geht nicht mehr erfasst. Ungeachtet dessen sind die hohen Zahlen, besonders bei den Toten, immer noch beunruhigend.
    KF220901  7TM=30051 nach 30539, 31939, 34459, Missing Data, Missing Data, 33309, k= 26; rsquare, jenseits < 0.98, wird so lange der Trend weiter nach unten geht nicht mehr erfasst. Ungeachtet dessen sind die hohen Zahlen, besonders bei den Toten, immer noch beunruhigend.
    KF220831  7TM=30539 nach 31939, 34459, Missing Data, Missing Data, 33309, 33748, k= 25; rsquare, jenseits < 0.98, wird so lange der Trend weiter nach unten geht nicht mehr erfasst. Ungeachtet dessen sind die hohen Zahlen, besonders bei den Toten, immer noch beunruhigend.
    KF220830  7TM=31939 nach 34459, Missing Data, Missing Data, 33309, 33748, 35088, k= 24; rsquare, jenseits < 0.98, wird so lange der Trend weiter nach unten geht nicht mehr erfasst. Ungeachtet dessen sind die hohen Zahlen, besonders bei den Toten, immer noch beunruhigend.
    KF220829  7TM=34459 nach Missing Data, 33309, 33748, 35088, 36443, 38508, k= 23; rsquare, jenseits < 0.98, wird so lange der Trend weiter nach unten geht nicht mehr erfasst. Ungeachtet dessen sind die hohen Zahlen, besonders bei den Toten, immer noch beunruhigend.
    KF220828  7TM=Missing Data nach Missing Data, 33309, 33748, 35088, 36443, 38508, k= 22; rsquare, jenseits < 0.98, wird so lange der Trend weiter nach unten geht nicht mehr erfasst. Ungeachtet dessen sind die hohen Zahlen, besonders bei den Toten, immer noch beunruhigend.
    KF220827  7TM=Missing Data nach 33309, 33748, 35088, 36443, 38508, Missing Data (So-Nullrunde), k= 22; rsquare, jenseits < 0.98, wird so lange der Trend weiter nach unten geht nicht mehr erfasst. Ungeachtet dessen sind die hohen Zahlen, besonders bei den Toten, immer noch beunruhigend.
    KF220826  7TM=33309 nach 33748, 35088, 36443, 38508, Missing Data (So-Nullrunde), Missing Data (Sa-Nullrunde), k= 22; rsquare, jenseits < 0.98, wird so lange der Trend weiter nach unten geht nicht mehr erfasst. Ungeachtet dessen sind die hohen Zahlen, besonders bei den Toten, immer noch beunruhigend.
    KF220825  7TM=33748 nach 35088, 36443, 38508, Missing Data (So-Nullrunde), Missing Data (Sa-Nullrunde), 38977, k= 21; rsquare, jenseits < 0.98, wird so lange der Trend weiter nach unten geht nicht mehr erfasst. Ungeachtet dessen sind die hohen Zahlen, besonders bei den Toten, immer noch beunruhigend.
    KF220824  7TM=35088 nach 36443, 38508, Missing Data (So-Nullrunde), Missing Data (Sa-Nullrunde), 38977, 40343, k= 20; rsquare, jenseits < 0.98, wird so lange der Trend weiter nach unten geht nicht mehr erfasst. Ungeachtet dessen sind die hohen Zahlen, besonders bei den Toten, immer noch beunruhigend.
    KF220823  7TM=36443 nach 38508 nach Missing Data (So-Nullrunde), Missing Data (Sa-Nullrunde), 38977, 40343, 40788, 40960, k= 19; rsquare, jenseits < 0.98, wird so lange der Trend weiter nach unten geht nicht mehr erfasst. Ungeachtet dessen sind die hohen Zahlen, besonders bei den Toten, immer noch beunruhigend.
    KF220822  7TM=38508 nach 3894 nach Missing Data (So-Nullrunde), Missing Data (Sa-Nullrunde), 38977, 40343, 40788, 40960, k= 18; rsquare, jenseits < 0.98, wird so lange der Trend weiter nach unten geht nicht mehr erfasst. Ungeachtet dessen sind die hohen Zahlen, besonders bei den Toten, immer noch beunruhigend. [korrigiert]
    KF220821  7TM=Missing Data (So-Nullrunde) nach Missing Data (Sa-Nullrunde), 38977, 40343, 40788, 40960, 41723, k= 17; rsquare, jenseits < 0.98, wird so lange der Trend weiter nach unten geht nicht mehr erfasst. Ungeachtet dessen sind die hohen Zahlen, besonders bei den Toten, immer noch beunruhigend.
    KF220820  7TM=Missing Data (Sa-Nullrunde) nach 38977, 40343, 40788, 40960, 41723, Missing Data (So-Nullrunde), k= 16; rsquare, jenseits < 0.98, wird so lange der Trend weiter nach unten geht nicht mehr erfasst. Ungeachtet dessen sind die hohen Zahlen, besonders bei den Toten, immer noch beunruhigend.
    KF220819  7TM=38977 nach 40343, 40788, 40960, 41723,  Missing Data (So-Nullrunde), Missing Data (Sa-Nullrunde), k= 16; rsquare, jenseits < 0.98, wird so lange der Trend weiter nach unten geht nicht mehr erfasst. Ungeachtet dessen sind die hohen Zahlen, besonders bei den Toten, immer noch beunruhigend.
    KF220818  7TM=40343 nach 40788, 40960, 41723,  Missing Data (So-Nullrunde), Missing Data (Sa-Nullrunde), 43575, k= 15; rsquare, jenseits < 0.98, wird so lange der Trend weiter nach unten geht nicht mehr erfasst. Ungeachtet dessen sind die hohen Zahlen, besonders bei den Toten, immer noch beunruhigend.
    KF220817  7TM=40788 nach 40960, 41723,  Missing Data (So-Nullrunde), Missing Data (Sa-Nullrunde), 43575, 44111, k= 14; rsquare, jenseits < 0.98, wird so lange der Trend weiter nach unten geht nicht mehr erfasst. Ungeachtet dessen sind die hohen Zahlen, besonders bei den Toten, immer noch beunruhigend.
    KF220816  7TM=40960 nach 41723,  Missing Data (So-Nullrunde), Missing Data (Sa-Nullrunde), 43575, 44111, 45492, k= 13; rsquare, jenseits < 0.98, wird so lange der Trend weiter nach unten geht nicht mehr erfasst. Ungeachtet dessen sind die hohen Zahlen, besonders bei den Toten, immer noch beunruhigend.
    KF220815  7TM=41723 nach Missing Data (So-Nullrunde) nach Missing Data (Sa-Nullrunde), 43575, 44111, 45492, 47600, k= 12; rsquare, jenseits < 0.98, wird so lange der Trend weiter nach unten geht nicht mehr erfasst. Ungeachtet dessen sind die hohen Zahlen, besonders bei den Toten, immer noch beunruhigend.
    KF220814  7TM=Missing Data (So-Nullrunde) nach Missing Data (Sa-Nullrunde), 43575, 44111, 45492, 47600, 49735, k= 11; rsquare, jenseits < 0.98, wird so lange der Trend weiter nach unten geht nicht mehr erfasst. Ungeachtet dessen sind die hohen Zahlen, besonders bei den Toten, immer noch beunruhigend.
    KF220813  7TM=Missing Data (Sa-Nullrunde) nach 43575, 44111, 45492, 47600, 49735, Missing Data, k= 11; rsquare, jenseits < 0.98, wird so lange der Trend weiter nach unten geht nicht mehr erfasst. Ungeachtet dessen sind die hohen Zahlen, besonders bei den Toten, immer noch beunruhigend.
    KF220812  7TM=43575 nach 44111, 45492, 47600, 49735, Missing Data, Missing Data, k= 11; rsquare, jenseits < 0.98, wird so lange der Trend weiter nach unten geht nicht mehr erfasst. Ungeachtet dessen sind die hohen Zahlen, besonders bei den Toten, immer noch beunruhigend.
    KF220811  7TM=44111 nach 45492, 47600, 49735, Missing Data, Missing Data, 53572, k= 10; rsquare, jenseits < 0.98, wird so lange der Trend weiter nach unten geht nicht mehr erfasst. Ungeachtet dessen sind die hohen Zahlen, besonders bei den Toten, immer noch beunruhigend.
    KF220810  7TM=45492 nach 47600, 49735, Missing Data, Missing Data, 53572, 55914, k= 9; rsquare, jenseits < 0.98, wird so lange der Trend weiter nach unten geht nicht mehr erfasst. Ungeachtet dessen sind die hohen Zahlen, besonders bei den Toten, immer noch beunruhigend.
    KF220809  7TM=47600 nach 49735, Missing Data, Missing Data, 53572, 55914, 59527, k= 8; rsquare, jenseits < 0.98, wird so lange der Trend weiter nach unten geht nicht mehr erfasst. Ungeachtet dessen sind die hohen Zahlen, besonders bei den Toten, immer noch beunruhigend.
    KF220808  7TM=49735 nach Missing Data, Missing Data, 53572, 55914, 59527, 63310, k= 7; rsquare, jenseits < 0.98, wird so lange der Trend weiter nach unten geht nicht mehr erfasst. Ungeachtet dessen sind die hohen Zahlen, besonders bei den Toten, immer noch beunruhigend.
    KF220807  7TM=Missing Data nach Missing Data, 53572, 55914, 59527, 63310, 68181, k= 6; rsquare, jenseits < 0.98, wird so lange der Trend weiter nach unten geht nicht mehr erfasst. Ungeachtet dessen sind die hohen Zahlen, besonders bei den Toten, immer noch beunruhigend.
    KF220806  7TM=Missing Data nach 53572, 55914, 59527, 63310, 68181, Missing Data (So Nullrunde), k= 5; rsquare, jenseits < 0.98, wird so lange der Trend weiter nach unten geht nicht mehr erfasst. Ungeachtet dessen sind die hohen Zahlen, besonders bei den Toten, immer noch beunruhigend.
    KF220805  7TM=53572 nach 55914, 59527, 63310, 68181, Missing Data (So Nullrunde), Missing Data (Sa-Nullrunde), k= 5; rsquare, jenseits < 0.98, wird so lange der Trend weiter nach unten geht nicht mehr erfasst. Ungeachtet dessen sind die hohen Zahlen, besonders bei den Toten, immer noch beunruhigend.
    KF220804  7TM=55914 nach 59527, 63310, 68181, Missing Data (So Nullrunde), Missing Data (Sa-Nullrunde), 74168, k= 4; rsquare, jenseits < 0.98, wird so lange der Trend weiter nach unten geht nicht mehr erfasst. Ungeachtet dessen sind die hohen Zahlen immer noch beunruhigend.
    KF220803  7TM=59527 nach 63310, 68181, Missing Data (So Nullrunde), Missing Data (Sa-Nullrunde), 74168, 77884, k= 3; rsquare, jenseits < 0.98, wird so lange der Trend weiter nach unten geht nicht mehr erfasst. Ungeachtet dessen sind die hohen Zahlen immer noch beunruhigend.
    KF220802  7TM=63310 nach 68181, Missing Data (So Nullrunde), Missing Data (Sa-Nullrunde), 74168, 77884, 81172, k= 2; rsquare, jenseits < 0.98, wird so lange der Trend weiter nach unten geht nicht mehr erfasst. Ungeachtet dessen sind die hohen Zahlen immer noch beunruhigend.
    KF220801  7TM=68181 nach Missing Data (So Nullrunde), Missing Data (Sa-Nullrunde), 74168, 77884, 81172, 86243, k= 1; rsquare, jenseits < 0.98 wird so lange der Trend weiter nach unten geht nicht mehr erfasst. Ungeachtet dessen sind die hohen Zahlen immer noch beunruhigend.
    KF220731  7TM=Missing Data (So Nullrunde) nach Missing Data (Sa-Nullrunde), 74168, 77884, 81172, 86243, 89989, k= -2 (Trendwende); rsquare, jenseits < 0.98 wird so lange der Trend weiter nach unten geht nicht mehr erfasst. Ungeachtet dessen sind die hohen Zahlen immer noch beunruhigend.
    KF220730  7TM=Missing Data (Sa-Nullrunde) nach 74168, 77884, 81172, 86243, 89989, Missing Data, k= -1 (Trendwende); rsquare, jenseits < 0.98 wird so lange der Trend weiter nach unten geht nicht mehr erfasst. Ungeachtet dessen sind die hohen Zahlen immer noch beunruhigend.
    KF220729  7TM=74168 nach 77884, 81172, 86243, 89989, Missing Data, Missing Data, k= 8 (Trendwende); rsquare =0.6710 nach geschätzt, geschätzt, geschätzt, nicht sinnvoll, nicht sinnvoll, 0.8239 <  0.98, also rein rechnerisch keine exp. Entw. Ungeachtet dessen sind die hohen Zahlen immer noch beunruhigend. .


    KF220728  7TM=77884 nach 81172, 86243, 89989, Missing Data, Missing Data 91163, k= 7 (Trendwende); rsquare =geschätzt nach geschätzt, geschätzt, geschätzt, nicht sinnvoll, nicht sinnvoll, 0.8239 <  0.98, also rein rechnerisch keine exp. Entw. Ungeachtet dessen sind die hohen Zahlen immer noch beunruhigend. Der Trende weist nach unten, morgen neuer Graph.
    KF220727  7TM=81172 nach 86243, 89989, Missing Data, Missing Data 91163, 95597, k= 6; rsquare =geschätzt nach geschätzt, geschätzt, nicht sinnvoll, nicht sinnvoll, 0.8239, geschätzt <  0.98, also rein rechnerisch keine exp. Entw. Ungeachtet dessen sind die hohen Zahlen immer noch beunruhigend. Wegen Missing Data aktuell schwer beurteilbar, erst wieder, Do, Fr besser, Sa neuer Graph.
    KF220726  7TM=86243 nach 89989, Missing Data, Missing Data 91163, 95597, 95865, k= 5; rsquare =geschätzt nach geschätzt,  nicht sinnvoll, nicht sinnvoll, 0.8239, geschätzt <  0.98, also rein rechnerisch keine exp. Entw. Ungeachtet dessen sind die hohen Zahlen immer noch beunruhigend. Wegen Missing Data aktuell schwer beurteilbar, erst wieder, Do, Fr besser, Sa neuer Graph.
    KF220725  7TM=89989 nach Missing Data, Missing Data 91163, 95597, 95865, 98083, k= 4; rsquare =geschätzt nach nicht sinnvoll, nicht sinnvoll, 0.8239, geschätzt, geschätzt,  0.8478 <  0.98, also rein rechnerisch keine exp. Entw. Ungeachtet dessen sind die hohen Zahlen immer noch beunruhigend. Wegen Missing Data aktuell nicht beurteilbar, erst wieder ca. Mitte dieser Woche.
    KF220724  7TM=Missing Data nach Missing Data 91163, 95597, 95865, 98083, 96170, k= 3; rsquare =nicht sinnvoll nach nicht sinnvoll, 0.8239, geschätzt, geschätzt,  0.8478,  0.8493 <  0.98, also rein rechnerisch keine exp. Entw. Ungeachtet dessen sind die hohen Zahlen immer noch beunruhigend. Wegen Missing Data aktuell nicht beurteilbar, erst wieder ca. Mitte dieser Woche.
    KF220723  7TM=Missing Data nach 91163, 95597, 95865, 98083, 96170, Missing Data, k= 3; rsquare =nicht sinnvoll nach 0.8239, geschätzt, geschätzt,  0.8478,  0.8493, Missing Data <  0.98, also rein rechnerisch keine exp. Entw. Ungeachtet dessen sind die hohen Zahlen immer noch beunruhigend. Wegen Missing Data aktuell nicht beurteilbar, erst wieder ca. Mitte nächster Woche.
    KF220722  7TM=91163 nach 95597, 95865, 98083, 96170, Missing Data, Missing Data, k= 3; rsquare =0.8239 nach geschätzt, geschätzt,   0.8478,  0.8493, Missing Data, Missing Data <  0.98, also rein rechnerisch keine exp. Entw. Ungeachtet dessen sind die hohen Zahlen immer noch beunruhigend. Nach dem Anstieg aus dem Plateau deutet sich aktuell eine Rückbildung an.

    KF220721  7TM=95597 nach 95865, 98083, 96170, Missing Data, Missing Data, 95818, k= 2; rsquare =geschätzt nach geschätzt <  0.8478,  0.8493, Missing Data, Missing Data, 0.8594 <  0.98, also rein rechnerisch keine exp. Entw. Ungeachtet dessen sind die hohen Zahlen immer noch beunruhigend. Dynamik könnte in neues Plateau münden, aber erst wieder zuverlässiger morgen/übermorgen beurteilbar, dann auch neuer Graph.
    KF220720  7TM=95865 nach 98083, 96170, Missing Data, Missing Data, 95818, 91942, k= 1; rsquare =geschätzt <  0.8478,  0.8493, Missing Data, Missing Data, 0.8594,  0.8611 <  0.98, also rein rechnerisch keine exp. Entw. Ungeachtet dessen sind die hohen Zahlen immer noch beunruhigend. Dynamik könnte in neues Plateau münden, aber erst wieder zuverlässiger morgen/übermorgen beurteilbar.
    KF220719  7TM=98083 nach 96170, Missing Data, Missing Data, 95818, 91942, 93091, k= -3; rsquare =0.8478 nach 0.8493, Missing Data, Missing Data, 0.8594,  0.8611, 0.8682  <  0.98, also rein rechnerisch keine exp. Entw. Ungeachtet dessen sind die hohen Zahlen immer noch beunruhigend. Dynamik nimmt wieder Fahrt auf, aber erst wieder zuverlässiger Mi-Do beurteilbar.
    KF220718  7TM=96170 nach Missing Data, Missing Data, 95818, 91942, 93091, 90698, k= -2; rsquare =0.8493 nach Missing Data, Missing Data, 0.8594,  0.8611, 0.8682, 0.8728  <  0.98, also rein rechnerisch keine exp. Entw. Ungeachtet dessen sind die hohen Zahlen immer noch beunruhigend. Dynamik erst wieder zuverlässiger Mi-Do beurteilbar.
    KF220717  7TM=Missing Data nach Missing Data, 95818, 91942, 93091, 90698, 91144, k= -1; rsquare =Missing Data nach Missing Data, 0.8594,  0.8611, 0.8682, 0.8728, 0.8810  <  0.98, also rein rechnerisch keine exp. Entw. Ungeachtet dessen sind die hohen Zahlen immer noch beunruhigend. Dynamik erst wieder Mi-Do beurteilbar.
    KF220716  7TM=Missing Data nach 95818, 91942, 93091, 90698, 91144, 90109 (nicht valide), k= -1; rsquare =Missing Data nach 0.8594,  0.8611, 0.8682, 0.8728, 0.8810, MD  <  0.98, also rein rechnerisch keine exp. Entw. Ungeachtet dessen sind die hohen Zahlen immer noch beunruhigend. Dynamik seit 10.7. deutlich zugenommen, was die nächsten 2 Tage durch die Wochenend-Nullrunden falsch ausgewiesen wird.
    KF220715  7TM=95818 nach 91942, 93091, 90698, 91144, 90109 (nicht valide), 89948 (nicht valide) k= -1; rsquare =0.8594 nach 0.8611,  0.8682,  0.8728, 0.8810, MD, MD  <  0.98, also rein rechnerisch keine exp. Entw. Ungeachtet dessen sind die hohen Zahlen immer noch beunruhigend. Dynamik seit 10.7. deutlich zugenommen, was die nächsten 2 Tage durch die Wochenend-Nullrunden falsch ausgewiesen wird.
    KF220714  7TM=91942 nach 93091, 90698, 91144, 90109 (nicht valide), 89948 (nicht valide), 89948 k= 1; rsquare =0.8611 nach 0.8682,  0.8728, 0.8810, MD, MD, 0.9048  <  0.98, also rein rechnerisch keine exp. Entw. Ungeachtet dessen sind die hohen Zahlen immer noch beunruhigend. Dynamik 7TM wieder zugenommen. Man kann sicher von einer 14. Omikron Welle seit 31.05.22 ausgehen.
    KF220713  7TM=93091 nach 90698, 91144, 90109 (nicht valide), 89948 (nicht valide), 89948, 90341, k= -1; rsquare =0.8682 nach 0.8728,  0.8810, MD, MD, 0.9048, 0.9126  <  0.98, also rein rechnerisch keine exp. Entw. Ungeachtet dessen sind die hohen Zahlen immer noch beunruhigend. Dynamik wieder zugenommen, zuverlässige Beurteilung erst wieder Do möglich nach den WE-Nullrunden und den Nachmeldeexzessen. Man kann sicher von einer 14. Omikron Welle seit 31.05.22 ausgehen.
    KF220712  7TM=90698 nach 91144, 90109 (nicht valide), 89948 (nicht valide), 89948, 90341, 89679, k= 1; rsquare =0.8728 nach 0.8810, MD, MD, 0.9048, 0.9126, 0.9189  <  0.98, also rein rechnerisch keine exp. Entw. Ungeachtet dessen sind die hohen Zahlen immer noch beunruhigend. Dynamik lässt nach, zuverlässige Beurteilung erst wieder Mi-Do möglich nach den WE-Nullrunden und den Nachmeldeexzessen. Man kann sicher von einer 14. Omikron Welle seit 31.05.22 ausgehen.
    KF220711  7TM=91144 nach Missing Data, 89948, 90341, 89679, 89289, 89749, k= -2; rsquare =0.8810 nach Missing Data, 0.9048, 0.9126, 0.9189, 0.9254, 0.9315  <  0.98, also streng  rechnerisch keine exp. Entw. Ungeachtet dessen sind die hohen Zahlen immer noch beunruhigend. Dynamik lässt nach, zuverlässige Beurteilung erst wieder Mi-Do möglich nach den WE-Nullrunden und den Nachmeldeexzessen. Man kann sicher von einer 14. Omikron Welle seit 31.05.22 ausgehen.
    KF220710  7TM=Missing Data nach Missing Data, 89948, 90341, 89679, 89289, 89749, Missing Data, k= -1; rsquare =Missing Data nach Missing Data, 0.9048, 0.9126, 0.9189, 0.9254, 0.9315  <  0.98, also streng  rechnerisch noch keine exp. Entw. Ungeachtet dessen sind die hohen Zahlen immer noch beunruhigend. Dynamik lässt nach, zuverlässige Beurteilung erst wieder Mi-Do möglich nach den WE-Nullrunden und den Nachmeldexzessen. Man kann sicher von einer 14. Omikron Welle seit 31.05.22 ausgehen.
    KF220709  7TM=Missing Data nach 89948, 90341, 89679, 89289, 89749, Missing Data, k= 1; rsquare =Missing Data nach 0.9048, 0.9126, 0.9189, 0.9254, 0.9315, Missing Data   <  0.98, also streng  rechnerisch noch keine exp. Entw. Ungeachtet dessen sind die hohen Zahlen immer noch beunruhigend. Dynamik lässt nach. Man kann aber sicher von einer 14. Omikron Welle seit 31.05.22 ausgehen.
    KF220708  7TM=89948 nach 90341, 89679, 89289, 89749, Missing Data, Missing Data, k= 1; rsquare =0.9048 nach 0.9126, 0.9189, 0.9254, 0.9315, Missing Data, 0.9401, ,   <  0.98, also streng  rechnerisch noch keine exp. Entw. Ungeachtet dessen sind die hohen Zahlen immer noch beunruhigend. Dynamik lässt nach. Man kann aber sicher von einer 14. Omikron Welle seit 31.05.22 ausgehen.
    KF220707  7TM=90341 nach 89679, 89289, 89749, Missing Data, Missing Data, 88788, k= -2; rsquare =0.9126 nach 0.9189, 0.9254, 0.9315, Missing Data, 0.9401, 0.9389, 0.9367,  ...,   <  0.98, also streng  rechnerisch noch keine exp. Entw. Ungeachtet dessen sind die hohen Zahlen immer noch beunruhigend. Dynamik lässt nach.  Man kann aber sicher von einer 14. Omikron Welle seit 31.05.22 ausgehen.
    KF220706  7TM=89679 nach 89289, 89749,  Missing Data, Missing Data, 88788, 87455, k= -1; rsquare =0.9189 nach 0.9254, 0.9315, Missing Data, 0.9401, 0.9389, 0.9367,  ...,   <  0.98, also streng  rechnerisch noch keine exp. Entw. Ungeachtet dessen sind die hohen Zahlen immer noch beunruhigend. Dynamik lässt nach.  Man kann aber sicher von einer 14. Omikron Welle seit 31.05.22 ausgehen.
    KF220705  7TM=89289 nach 89749,  Missing Data, 88788, 87455, k= 1; rsquare =0.9254 nach 0.9315, Missing Data, 0.9401, 0.9389, 0.9367, 0.9397,  ...,   <  0.98, also streng  rechnerisch noch keine exp. Entw. Ungeachtet dessen sind die Anstiege immer noch beunruhigend. Dynamik lässt nach.  Man kann aber sicher von einer 14. Omikron Welle seit 31.05.22 ausgehen.
    KF220704  7TM=89749 nach nach Missing Data, 88788, 87455, k= -7; rsquare =0.9315 nach Missing Data, 0.9401, 0.9389, 0.9367, 0.9397,  ...,   <  0.98, also streng  rechnerisch noch keine exp. Entw. Ungeachtet dessen sind die Anstiege beunruhigend. Dynamik erst wieder ab MI-Do besser beurteilbar.  Man kann aber sicher von einer 14. Omikron Welle seit 31.05.22 ausgehen.
    KF220703  7TM=Missing Data nach Missing Data, 88788, 87455, k= -6; rsquare = = Missing Data nach Missing Data nach 0.9401, 0.9389, 0.9367, 0.9397,  ..., ..., 0.8951  <  0.98, also streng  rechnerisch noch keine exp. Entw. Ungeachtet dessen sind die Anstiege beunruhigend. Dynamik erst wieder am Dienstag beurteilbar.  Man kann aber sicher von einer 14. Omikron Welle seit 31.05.22 ausgehen.
    KF220702  7TM=Missing Data nach 88788, 87455, k= -5; rsquare = Missing Data nach 0.9401, 0.9389, 0.9367, 0.9397,  ..., ..., 0.8951  <  0.98, also streng  rechnerisch noch keine exp. Entw. Ungeachtet dessen sind die Anstiege beunruhigend. Dynamik erst wieder am Dienstag beurteilbar.  Man kann aber sicher von einer 14. Omikron Welle seit 31.05.22 ausgehen.
    KF220701  7TM=88788 nach 87455, k= -5; rsquare = 0.9401 nach 0.9389, 0.9367, 0.9397,  ..., ..., 0.8951  <  0.98, also streng  rechnerisch noch keine exp. Entw. Ungeachtet dessen sind die Anstiege beunruhigend. Die Dynamik lässt leicht nach. Man kann von einer 14. Omikron Welle seit 31.05.22 ausgehen.
    KF220630  7TM=87455 nach 86754, k= -4; rsquare = 0.9389 nach 0.9367, 0.9397,  ..., ..., 0.8951, 0.876 <  0.98, also streng  rechnerisch noch keine exp. Entw. Ungeachtet dessen sind die Anstiege beunruhigend. Die Dynamik stagniert auf hohem Niveau. Man kann von einer 14. Omikron Welle seit 31.05.22 ausgehen.
    KF220629  7TM=86754 nach 84852, k= -3; rsquare =0.9367 nach 0.9397,  ..., ..., 0.8951, 0.876, 0.855 <  0.98, also streng  rechnerisch noch keine exp. Entw. Ungeachtet dessen sind die Anstiege beunruhigend. Die Dynamik stagniert auf hohem Niveaut. Man kann von einer 14. Omikron Welle seit 31.05.22 ausgehen.
    KF220628  7TM=84852 nach 82750, k= -2; rsquare =0.9397 nach 0.9257, ..., ..., 0.8951, 0.876, 0.855  <  0.98, also streng  rechnerisch noch keine exp. Entw. Ungeachtet dessen sind die Anstiege beunruhigend. Die Dynamik setzt sich fort. Man kann von einer 14. Omikron Welle seit 31.05.22 ausgehen.
    KF220627  7TM=82750 nach 80002, k= -1; rsquare =0.9257, ..., ..., 0.8951, 0.876, 0.855  <  0.98, also streng  rechnerisch noch keine exp. Entw. Ungeachtet dessen sind die Anstiege beunruhigend. Die Dynamik hat am 24.06.22 nachgelassen. Man kann von einer 14. Omikron Welle seit 31.05.22 ausgehen. Eine realistische Beurteilung dürfte erst wieder gegen Mitte derWoche möglich sein.
    KF220626  7TM=80002 nach 80880, k= 1; rsquare Missing Data nach Missing Data, 0.8951, 0.876, 0.855  <  0.98, also streng  rechnerisch noch keine exp. Entw. Ungeachtet dessen sind die Anstiege beunruhigend. Die Dynamik hat am 24.06.22 nachgelassen. Man kann von einer 14. Omikron Welle seit 31.05.22 ausgehen. Eine realistische Beurteilung dürfte erst wieder gegen Mitte derWoche möglich sein.
    KF220625  7TM=Missing Data nach 80880, k= -7; rsquare Missing Data nach 0.8951, 0.876, 0.855  <  0.98, also streng  rechnerisch noch keine exp. Entw. Ungeachtet dessen sind die Anstiege beunruhigend. Die Dynamik hat am 24.06.22 nachgelassen. Man kann von einer 14. Omikron Welle seit 31.05.22 ausgehen.
    KF220624  7TM=80880 nach 79584, k= -7; rsquare 0.8951 nach 0.876, 0.855  <  0.98, also streng  rechnerisch noch keine exp. Entw. Ungeachtet dessen sind die Anstiege beunruhigend. Die Dynamik hat am 24.06.22 nachgelassen. Man kann von einer 14. Omikron Welle seit 31.05.22 ausgehen.
    KF220623  7TM=79584 nach 68145, k= -6; rsquare 0.876 nach 0.855  <  0.98, also streng  rechnerisch noch keine exp. Entw. Ungeachtet dessen sind die Anstiege beunruhigend. Man kann von einer 14. Omikron Welle seit 31.05.22 ausgehen.
    KF220622  7TM=68145 nach 63828 (Nachmeldungseffekte) k= -5; rsquare 0.85  <  0.98, also streng  rechnerisch noch keine exp. Entw., berücksichtigt man das Pfingstmeldechaos, würde rsquare höher sein. Ungeachtet dessen sind die Anstiege beunruhigend. Man kann von einer 14. Omikron Welle seit 31.05.22 ausgehen.
    KF220621  7TM=63828 (Nachmeldungseffekte) nach 59987 (Nachmeldungseffekte),  k= -5; rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle:exponentielle Entwicklung nach Exp1 gebrochen.  *  Graph der 13. Welle 02.03.-02.06.2022.
    KF220620  7TM=59987 (Nachmeldungseffekte) nach 57470 nicht interpretierbar (So),  k= -3; rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen.  *  Graph der 13. Welle 02.03.-02.06.2022.
    KF220619  7TM=57470 nicht interpretierbar nach 57247 nicht interpretierbar, 59481,  k= -2; rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen.  *  Graph der 13. Welle 02.03.-02.06.2022.
    KF220618   7TM=Nicht interpretierbar nach 57247, 59481,  k= -1; rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen.  *  Graph der 13. Welle 02.03.-02.06.2022.
    KF220617  7TM=57247 nach 55114, 59481,  k= -1; rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen.  *  Graph der 13. Welle 02.03.-02.06.2022.
    KF220616  7TM=55114 nach 62223, 59481,  k= 1; rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen.  *  Graph der 13. Welle 02.03.-02.06.2022.
    KF220615  7TM=62223 nach 60579, 59481,  k= -8; rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen.  *  Graph der 13. Welle 02.03.-02.06.2022.
    KF220614  7TM=60579 nach 59481,  k= -7, damit negative Trendwende; rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen.  *  Graph der 13. Welle 02.03.-02.06.2022.
    KF220613  7TM=59481 (falsch wegen der vielen Nachmeldungen nach 2 WE-Nullrunden) nach 44662,  k= -6; rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen.  *  Graph der 13. Welle 02.03.-02.06.2022.
    KF220612 Das RKI konterkariert seine eigene Entscheidung von gestern und teilt wieder lauter falsche und damit nicht interpretierbare Zahlen mit: 7TM=44662 nach 44376 (falsch wegen der vielen Nichtmeldungen) nach 40912 (falsch wegen der vielen Nichtmeldungen), k= -5; rsquare geschätzt Exp1 < 0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen.  *  Graph der 13. Welle 02.03.-02.06.2022.


    KF220611

    KF220610: 7TM=44376 (falsch wegen der vielen Nachmeldungen) nach 40912 (falsch wegen der vielen Nachmeldungen) nach 35885 , k= -4; rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen.  *  Graph der 13. Welle 02.03.-02.06.2022.
    KF220609: 7TM=40912 (falsch wegen der vielen Nachmeldungen) nach 35885 (falsch wegen der vielen Nachmeldungen), k= -3; rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen.  *  Graph der 13. Welle 02.03.-02.06.2022.
    KF220608: 7TM=35885 (falsch wegen der extrem vielen Nachmeldungen) nach 31723 (falschwegen der extrem vielen Nachmeldungen), k= -2; rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen.  *  Graph der 13. Welle 02.03.-02.06.2022.
    KF220607: 7TM=31723 (falsch wegen der extrem vielen Nachmeldungen) nach 27481 (falsch weger der extrem vielen Nachmeldungen) , k= -1; rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen.  *  Graph der 13. Welle 02.03.-02.06.2022.
    KF220606: 7TM=27481 (falsch, weil 15 von 16 Bundesländern  Regionen mit 0 und NTW mit drastisch unterdurchschnittlichen  neuen Fällen gemeldet wurden) nach 36072, k= 1; rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen.  *  Graph der 13. Welle 02.03.-02.06.2022.
    KF220605: 7TM=36072 (falsch, weil alle 17 Regionen mit 0 (13) oder unterdurchschnittlichen (4) neuen Fällen gemeldet wurden)  nach 35698, k= -1; rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen.  *  Graph der 13. Welle 02.03.-02.06.2022.
    KF220604: 7TM=35698 (falsch, weil alle 17 Regionen mit 0 neuen Fällen gemeldet wurden) nach 36085, k= 1; rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen.  *  Graph der 13. Welle 02.03.-02.06.2022.
    KF220603: 7TM=36085 nach 35926, k= -4 (!); rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen.
    KF220602: 7TM=35926 nach 30092, k= -3 (!); rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen.
    KF220601: 7TM=30092 nach 28835, k= -2 (!); rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen.
    KF220531: 7TM=28835 nach 28004, k= -1 (!); rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen.
    KF220530: 7TM=28004 nach 28368, k= 35; rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen.
    KF220529: 7TM=28368 nach 28438, k= 34; rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen.
    KF220528: 7TM=28438 nach 28597, k= 33; rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen.
    KF220527: 7TM=28597 nach 28940, k= 32; rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen.
    KF220526: 7TM=28940 nach 35662, k= 31; rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen.
    KF220525: 7TM=35662 nach 38379, k= 30; rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen.
    KF220524: 7TM=38379 nach 41651, k= 29; rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen.
    KF220523: 7TM=41651 nach 44768, k= 28; rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen.
    KF220522: 7TM=44768 nach 44919, k= 27; rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen.
    KF220521: 7TM=44919 nach 45252, k= 26; rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen.
    KF220520: 7TM=45252 nach 48035, k= 25; rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen.
    KF220519: 7TM=48035 nach 50905, k= 24; rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen.
    KF220518: 7TM=50905 nach 55225, k= 23; rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen.
    KF220517: 7TM=55225 nach 58791, k= 22; rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen.
    KF220516: 7TM=58791 nach 61836, k= 21; rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen.
    KF220515: 7TM=61836 nach 61985, k= 20; rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen.
    KF220514: 7TM=61985 nach 62319, k= 19; rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen.
    KF220513: 7TM=62319 nach 63804, k= 18; rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen.
    KF220512: 7TM=63804 nach 66100, k= 17; rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen.
    KF220511: 7TM=66100 nach 67130, k= 16; rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen.
    KF220510: 7TM=67130 nach 68504, k= 15; rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen.
    KF220509: 7TM=68504 nach 69355, k= 14; rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen.
    KF220508: 7TM=69355 nach 69452, k= 13; rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen.
    KF220507: 7TM=69452 nach 69914, k= 12; rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen.
    KF220506: 7TM=69914 nach 72063, k= 11; rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen.
    KF220505: 7TM=72063 nach 74425, k= 10; rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen.
    KF220504: 7TM=74425 nach 79274, k= 9; rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen.
    KF220503: 7TM=79274 nach 84278, k= 8; rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen.
    KF220502: 7TM=84278 nach 87603, k= 7; rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen.
    KF220501: 7TM=87603 nach 89896, k= 6; rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen.
    KF220430: 7TM=89896 nach 93819, k= 5; rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen.
    KF220429: 7TM=93819 nach 100645, k= 4; rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen.
    KF220428: 7TM=100645 nach 109232, k= 3; rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen.
    KF220427: 7TM=109232 nach 117263, k= 2; rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen.
    KF220426: 7TM=117263 nach 125395, k= 1; rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen.
    KF220425: 7TM=125395 nach 109064, k=-1; rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen.
    KF220424: 7TM=109064 nach 109121, k=2; rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen.
    KF220423: 7TM=109121 nach 109208, k=1; rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen.
    KF220422: 7TM=109208 nach 95278, k=-4; rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen.
    KF220421: 7TM=95278 nach 94584, k=-3; rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen.
    KF220420: 7TM=94584 nach 91590, k=-2  ; rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen.
    KF220419: 7TM=91590 nach 88407, k=-1  ; rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen.
    KF220418: 7TM=88407 nach 108451, k=21  ; rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen.
    KF220417: 7TM=108451 nach 109924, k=20  ; rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen.
    KF220416: 7TM=109924 nach 112165, k=19  ; rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen.
    KF220415: 7TM=112165 nach 128323, k=18  ; rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen.
    KF220414: 7TM=128323 nach 130951, k=17  ; rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen.
    KF220413: 7TM=130951 nach 136146, k=16  ; rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen.
    KF220412: 7TM=136146 nach 141672, k=15  ; rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen.
    KF220411: 7TM=141672 nach 144187, k=14  ; rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen.
    KF220410: 7TM=144187 nach 145664, k=13  ; rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen.
    KF220409: 7TM=145664 nach 148319, k=12  ; rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen.
    KF220408: 7TM=148319 nach 154859, k=11  ; rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen.
    KF220407: 7TM=154859 nach 165897, k=10  ; rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen.
    KF220406: 7TM=165897 nach 176350, k= 9  ; rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen.
    KF220405: 7TM=176350 nach 183992, k= 8  ; rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen.
    KF220404: 7TM=183992 nach 192128, k= 7  ; rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen.
    KF220403: 7TM=192128 nach 195896, k= 6  ; rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen.
    KF220402: 7TM=195896 nach 201206, k= 5  ; rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen.
    KF220401: 7TM=201206 nach 209144, k= 4  ; rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen.
    KF220331: 7TM=209144 nach 215427, k= 3  ; rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen.
    KF220330: 7TM=215427 nach 221638, k= 2  ; rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen?

    KF220329: 7TM=221638 nach 223817, k= 1  ; rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen?

    KF220328: 7TM=223817 nach 221635, k= -1  ; rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen oder droht noch eine Bärenfalle? Nachdem BGM, RKI und vor allem die Länderbehörden seit 2J völlig unfähig sind, verlässliche Tageswerte zu liefern, bleibt die Beurteilung einer Trendwende insbesondere nach Wochenenden schwierig. Der neue Anstieg ist wesentlich auch eine Kompensation der Lücken vom Wochenende.


    13.Welle220327 -  Immer noch "Bärenfalle" zu befürchten?

    KF220327: 7TM=221635 nach 228118, k= 3 ; rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1 gebrochen oder droht noch eine Bärenfalle?
    13.Welle220325 - Neue "Bärenfalle"?


    KF220325: 7TM=228118 nach 229292, k= 2 ; rsquare geschätzt Exp1 <  0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp1: neue Bärenfalle?
    KF220324: 7TM=229292 nach 229484, k= 1 ; rsquare geschätzt Exp2 > 0.98. 13. (Omikron) Welle: exponentielle nach Exp2 Entwicklung noch intakt
    KF220323: 7TM=229484 nach 226133, k= -3 ; rsquare geschätzt > 0.98. 13. (Omikron) Welle: exponentielle Entwicklung wieder intakt
    KF220322: 7TM=226133 nach 223113, k= -2  (-Trendwende De); rsquare geschätzt > 0.98. 13. (Omikron) Welle: exponentielle Entwicklung wieder intakt?
    13.Welle220322

    KF220321: 7TM=223113 nach 219800, k= -1  (-Trendwende De); rsquare geschätzt > 0.98. 13. (Omikron) Welle: exponentielle Entwicklung nach Exp2 wieder intakt?
    13.Welle220320

    KF220320: 7TM=219800 nach 219809, k= 2  (-Trendwende De); rsquare geschätzt > 0.98. 13. (Omikron) Welle: exponentielle Entwicklung gebrochen?
    KF220319: 7TM=219809 nach 221926, k= 1  (-Trendwende De); rsquare geschätzt > 0.98. 13. (Omikron) Welle: exponentielle Entwicklung setzt sich fort.
    KF220318: 7TM=221926 nach 218618, k= -16 (-Trendwende De); rsquare geschätzt > 0.98. 13. (Omikron) Welle: exponentielle Entwicklung setzt sich fort.
    KF220317: 7TM=218618 nach 212188, k= -15 (-Trendwende De); rsquare geschätzt > 0.98. 13. (Omikron) Welle: exponentielle Entwicklung setzt sich fort.
    KF220316: 7TM=212188 nach 207591, k= -14 (-Trendwende De); rsquare geschätzt > 0.98. 13. (Omikron) Welle: exponentielle Entwicklung setzt sich fort.
    KF220315: 7TM=207591 nach 200914, k= -13 (-Trendwende De); rsquare geschätzt > 0.98. 13. (Omikron) Welle: exponentielle Entwicklung setzt sich fort.
    KF220314: 7TM=200914 nach 194902, k= -12 (-Trendwende De); rsquare geschätzt > 0.98. 13. (Omikron) Welle: exponentielle Entwicklung setzt sich fort.
    KF220313: 7TM=194902 nach 192909, k= -11 (-Trendwende De); rsquare geschätzt > 0.98. 13. (Omikron) Welle: exponentielle Entwicklung setzt sich fort.
    KF220312: 7TM=192909 nach 188663, k= -10 (-Trendwende De); rsquare geschätzt > 0.98. 13. (Omikron) Welle: exponentielle Entwicklung setzt sich fort.
    KF220311: 7TM=188663 nach 182252, k= -9 (-Trendwende De); rsquare =0.9968 > 0.98. 13. (Omikron) Welle: exponentielle Entwicklung setzt sich fort.
    KF220310: 7TM=182252 nach 177218, k= -8 (-Trendwende De); rsquare > 0.98. 13. (Omikron) Welle: exponentielle Entwicklung setzt sich fort.
    KF220309: 7TM=177218 nach 169778, k= -7 (-Trendwende De); rsquare =0.9973 > 0.98. 13. (Omikron) Welle: exponentielle Entwicklung setzt sich fort.

      13.Welle220309
    KF220308: 7TM=169778 nach 165571, k= -6 (+Trendwende De); rsquare nicht bestimmt. 13. Welle entwickelt sich exponentiell
    KF220307: 7TM=165571 nach 160616, k= -5 (+Trendwende De); rsquare nicht bestimmt. 13. Welle entwickelt sich exponentiell
    KF220306: 7TM=160616 nach 158319, k= -4 (+Trendwende De); rsquare nicht bestimmt. 13. Welle entwickelt sich exponentiell
    KF220305: 7TM=158319 nach 157036, k= -3 (+Trendwende De); rsquare nicht bestimmt. 13. Welle entwickelt sich exponentiell
    KF220304: 7TM=157036 nach 154697, k= -2 (+Trendwende De); rsquare nicht bestimmt. 13. Welle entwickelt sich
    KF220303: 7TM=154697 nach 153718, k= -1 (+Trendwende De); rsquare nicht bestimmt. 13. Welle entwickelt sich
    KF220302: 7TM=153718 nach 154525, k=21 (+Trendwende De); rsquare nicht bestimmt. 13. Welle beginnt.
    KF220301: 7TM=154525 nach 157760, k=20 (+Trendwende De); rsquare < 0.98. Omikron-Welle am 10.02.22 gebrochen
    KF220228: 7TM=157760 nach 158302, k=19 (+Trendwende De); rsquare < 0.98. Omikron-Welle am 10.02.22 gebrochen
    KF220227: 7TM=158302 nach 159947, k=18 (+Trendwende De); rsquare < 0.98. Omikron-Welle am 10.02.22 gebrochen
    KF220226: 7TM=159947 nach 161393, k=17 (+Trendwende De); rsquare < 0.98. Omikron-Welle am 10.02.22 gebrochen
    KF220225: 7TM=161393 nach 163289, k=16 (+Trendwende De); rsquare < 0.98. Omikron-Welle am 10.02.22 gebrochen
    KF220224: 7TM=163289 nach 164618, k=15 (+Trendwende De); rsquare < 0.98. Omikron-Welle am 10.02.22 gebrochen
    KF220223: 7TM=164618 nach 167377, k=14 (+Trendwende De); rsquare < 0.98. Omikron-Welle am 10.02.22 gebrochen
    KF220222: 7TM=167377 nach 168937, k=13 (+Trendwende De); rsquare < 0.98. Omikron-Welle am 10.02.22 gebrochen
    KF220221: 7TM=168937 nach 173697, k=12 (+Trendwende De); rsquare < 0.98. Omikron-Welle am 10.02.22 gebrochen
    KF220220: 7TM=173697 nach 174068, k=11 (+Trendwende De); rsquare < 0.98. Omikron-Welle am 10.02.22 gebrochen
    KF220219: 7TM=174068 nach 175086, k=10 (+Trendwende De); rsquare < 0.98. Omikron-Welle am 10.02.22 gebrochen
    KF220218: 7TM=175086 nach 178041, k=9 (+Trendwende De); rsquare < 0.98. Omikron-Welle am 10.02.22 gebrochen
    KF220217: 7TM=178041 nach 180916, k=8 (+Trendwende De); rsquare < 0.98. Omikron-Welle am 10.02.22 gebrochen
    KF220216: 7TM=180916 nach 182662, k=7 (+Trendwende De); rsquare < 0.98. Omikron-Welle am 10.02.22 gebrochen

    KF220215: 7TM=182662 nach 184702, k=6; rsquare < 0.98. Omikron-Welle gebrochen
    KF220214: 7TM=184702 nach 188867, k=5; rsquare < 0.98. Omikron-Welle gebrochen
    KF220213: 7TM=186181 nach 188867, k=4; rsquare < 0.98. Omikron-Welle gebrochen
    KF220212: 7TM=188867 nach 190012, k=3; rsquare < 0.98. Omikron-Welle gebrochen
    KF220211: 7TM=190012 nach 191159, k=2; rsquare = 0.9526. Omikron-Welle gebrochen

    KF220210: 7TM=191159 nach 192297, k=1; 12. Omikronwelle gebrochen, ob nachhaltig muss abgewartet werden, hierfür ein k=7 erforderlich.
    KF220209: 7TM=192297 nach 190719, k= -42; rsquare= > 0.98 (geschätzt); 12. Omikron-Welle in vollem Gang (am 6.1.22 rekonstruiert und dargestellt)
    KF220208: 7TM=190719 nach 187040, k= -41; rsquare= > 0.98 (geschätzt); 12. Omikron-Welle in vollem Gang (am 6.1.22 rekonstruiert und dargestellt)
    KF220207: 7TM=187040 nach 186046, k= -40; rsquare= > 0.98 (geschätzt); 12. Omikron-Welle in vollem Gang (am 6.1.22 rekonstruiert und dargestellt)
    KF220206: 7TM=186046 nach 183625, k= -39; rsquare= > 0.98 (geschätzt); 12. Omikron-Welle in vollem Gang (am 6.1.22 rekonstruiert und dargestellt)
    KF220205: 7TM=183625 nach 181596, k= -38; rsquare= > 0.98 (geschätzt); 12. Omikron-Welle in vollem Gang (am 6.1.22 rekonstruiert und dargestellt)
    KF220204: 7TM=181596 nach 177503, k= -37; rsquare= > 0.98 (geschätzt); 12. Omikron-Welle in vollem Gang (am 6.1.22 rekonstruiert und dargestellt)
    KF220203: 7TM=177503 nach 169119, k= -36; rsquare= > 0.98 (geschätzt); 12. Omikron-Welle in vollem Gang (am 6.1.22 rekonstruiert und dargestellt)
    KF220202: 7TM=169119 nach 164407, k= -35; rsquare= > 0.98 (geschätzt); 12. Omikron-Welle in vollem Gang (am 6.1.22 rekonstruiert und dargestellt)
    KF220201: 7TM=164407 nach 158050, k= -34; rsquare= > 0.98 (geschätzt); 12. Omikron-Welle in vollem Gang (am 6.1.22 rekonstruiert und dargestellt)
    KF220131: 7TM=158050 nach 152956, k= -33; rsquare= > 0.98 (geschätzt); 12. Omikron-Welle in vollem Gang (am 6.1.22 rekonstruiert und dargestellt)
    KF220130: 7TM=152956 nach 150824, k= -32; rsquare= > 0.98 (geschätzt); 12. Omikron-Welle in vollem Gang (am 6.1.22 rekonstruiert und dargestellt)
    KF220129: 7TM=150824 nach 146034, k= -31; rsquare= > 0.98 (geschätzt); 12. Omikron-Welle in vollem Gang (am 6.1.22 rekonstruiert und dargestellt)
    KF220128: 7TM=146034 nach 138362, k= -30; rsquare= > 0.98 (geschätzt); 12. Omikron-Welle in vollem Gang (am 6.1.22 rekonstruiert und dargestellt)
    KF220127: 7TM=138362 nach 131221, k= -29; rsquare= > 0.98 (geschätzt); 12. Omikron-Welle in vollem Gang (am 6.1.22 rekonstruiert und dargestellt)
    KF220126: 7TM=131221 nach 121278, k= -28; rsquare= > 0.98 (geschätzt); 12. Omikron-Welle in vollem Gang (am 6.1.22 rekonstruiert und dargestellt)
    KF220125: 7TM=121278 nach 113895, k= -27; rsquare= > 0.98 (geschätzt); 12. Omikron-Welle in vollem Gang (am 6.1.22 rekonstruiert und dargestellt)
    KF220124: 7TM=113895 nach 102210, k= -26; rsquare= > 0.98 (geschätzt); 12. Omikron-Welle in vollem Gang (am 6.1.22 rekonstruiert und dargestellt)
    KF220123:
    KF220122: 7TM=102210, k= -24; rsquare= > 0.98 (geschätzt); 12. Omikron-Welle in vollem Gang (am 6.1.22 rekonstruiert und dargestellt)
    KF220121: 7TM=97505, k= -23; rsquare= > 0.98 (geschätzt); 12. Omikron-Welle in vollem Gang (am 6.1.22 rekonstruiert und dargestellt)
    KF220120: 7TM=89299, k= -22; rsquare= > 0.98 (geschätzt); 12. Omikron-Welle in vollem Gang (am 6.1.22 rekonstruiert und dargestellt)
    KF220119: 7TM=82451, k= -21; rsquare= > 0.98 (geschätzt); 12. Omikron-Welle in vollem Gang (am 6.1.22 rekonstruiert und dargestellt)
    KF220118: 7TM=75006, k= -20; rsquare= > 0.98 (geschätzt); 12. Omikron-Welle  in vollem Gang (am 6.1.22 rekonstruiert und dargestellt)
    KF220117: 7TM=70392, k= -19; rsquare= > 0.98 (geschätzt); 12. Omikron-Welle  in vollem Gang (am 6.1.22 rekonstruiert und dargestellt)
    KF220116: 7TM=66347, k= -18; rsquare= > 0.98 (geschätzt); 12. Omikron-Welle  in vollem Gang (am 6.1.22 rekonstruiert und dargestellt)
    KF220115: 7TM=65077, k= -17; rsquare= > 0.98 (geschätzt); 12. Omikron-Welle  in vollem Gang (am 6.1.22 rekonstruiert und dargestellt)
    KF220114: 7TM=62798, k= -16; rsquare= > 0.98 (geschätzt); 12. Omikron-Welle  in vollem Gang (am 6.1.22 rekonstruiert und dargestellt)
    KF220113: 7TM=59637, k= -15; rsquare= > 0.98 (geschätzt); 12. Omikron-Welle in vollem Gang (am 6.1.22 rekonstruiert und dargestellt)
    KF220112: 7TM=54510, k= -14; rsquare= > 0.98 (geschätzt); 12. Omikron-Wellein vollem Gang (am 6.1.22 rekonstruiert und dargestellt)
    KF220111: 7TM=52070, k= -13; rsquare= > 0.98 (geschätzt); 12. Omikron-Wellein vollem Gang (am 6.1.22 rekonstruiert und dargestellt)
    KF220110: 7TM=48996, k= -12; rsquare= > 0.98 (geschätzt); 12. Omikron-Welle in vollem Gang (am 6.1.22 rekonstruiert und dargestellt)
    KF220109: 7TM=46835, k= -11; rsquare= > 0.98 (geschätzt); 12. Omikron-Welle in vollem Gang (am 6.1.22 rekonstruiert und dargestellt)
    KF220108: 7TM=45872, k= -10; rsquare= > 0.98 (geschätzt); 12. Omikron-Welle in vollem Gang (am 6.1.22 rekonstruiert und dargestellt)
    KF220107: 7TM=42439, k= -9; rsquare= > 0.98 (geschätzt); 12. Omikron-Welle in vollem Gang (am 6.1.22 rekonstruiert und dargestellt)
    KF220106: 7TM=38225, k= -8; rsquare= > 0.98 (geschätzt); 12. Omikron-Welle in vollem Gang (am 6.1.22 rekonstruiert und dargestellt)


    _
    KF220105: 7TM=36068, k= -7; rsquare=0.9945; 12. Omikron-Welle im Aufbau (am 6.1.22 rekonstruiert und dargestellt)
    KF220104: 7TM=32987, k= -6; 12. Omikron-Welle im Aufbau (am 6.1.22 rekonstruiert)
    KF220103: 7TM=30291, k= -5; 12. Omikron-Welle im Aufbau  Gang (am 6.1.22 rekonstruiert)
    KF220102: 7TM=28937, k= -4; 12. Omikron-Welle im Aufbau (am 6.1.22 rekonstruiert)
    KF220101: 7TM=28278, k= -3; 12. Omikron-Welle im Aufbau (am 6.1.22 rekonstruiert)
    KF211231: 7TM=27933, k= -2; 12. Omikron-Welle im Aufbau (am 6.1.22 rekonstruiert)
    KF211230: 7TM=27336, k= -1; 12. Omikron-Welle im Aufbau (am 6.1.22 rekonstruiert)
    KF211229: 7TM=26507, k= 22; Anfangswert 12. Omikron-Welle (am 6.1.22 rekonstruiert)
    KF211228: 7TM=26815, k= 21; rsquare < 0.98, Trendwende setzt sich fort. > Trendwendestand De&Bl.
    KF211227  7TM=27617, k= 20; rsquare  < 0.98, Trendwende setzt sich fort. > Trendwendestand De&Bl.
    KF211226  7TM=27952, k= 19; rsquare  < 0.98, Trendwende setzt sich fort. > Trendwendestand De&Bl.
    KF211225  7TM=28264, k= 18; rsquare  < 0.98, Trendwende setzt sich fort. > Trendwendestand De&Bl.
    KF211224  7TM=31013, k= 17; rsquare  < 0.98, Trendwende setzt sich fort. > Trendwendestand De&Bl.
    KF211223  7TM=33956, k= 16; rsquare < 0.98, Trendwende setzt sich fort. > Trendwendestand De&Bl.
    KF211222  7TM=36176, k= 15; rsquare  < 0.98, Trendwende setzt sich fort. > Trendwendestand De&Bl.
    KF211221  7TM=37854, k= 14; rsquare  < 0.98, Trendwende setzt sich fort. > Trendwendestand De&Bl.
    KF211220  7TM=38660, k= 13; rsquare  < 0.98, Trendwende setzt sich fort. > Trendwendestand De&Bl.
    KF211219  7TM=39717, k= 12; rsquare < 0.98, Trendwende setzt sich fort. > Trendwendestand De&Bl.
    KF211218  7TM=40525, k= 11; rsquare  < 0.98, Trendwende setzt sich fort. > Trendwendestand De&Bl.
    KF211217  7TM=40996, k= 10; rsquare < 0.98, Trendwende setzt sich fort. > Trendwendestand De&Bl.
    KF211216  7TM=42551, k=  9; rsquare  < 0.98, Trendwende setzt sich fort. > Trendwendestand De&Bl.
    KF211215  7TM=44025, k=  8; rsquare  < 0.98, Wendeneigung setzt sich fort. > Trendwendestand De&Bl.
    KF211214  7TM=46016, k=  7; rsquare  < 0.98, Wendeneigung setzt sich fort. > Trendwendestand De&Bl.
    KF211213  7TM=48630, k=  6; rsquare  < 0.98, Wendeneigung setzt sich fort. > Trendwendestand De&Bl.
    KF211212  7TM=49378, k=  5; rsquare  < 0.98, Wendeneigung setzt sich fort. > Trendwendestand De&Bl.
    KF211211  7TM=50248, k=  4; rsquare  < 0.98, Wendeneigung setzt sich fort. > Trendwendestand De&Bl.
    KF211210  7TM=51592, k=  3; rsquare  < 0.98, Wendeneigung setzt sich fort. > Trendwendestand De&Bl.
    KF211209  7TM=53137, k=  2; rsquare  < 0.98, Wendeneigung setzt sich fort. > Trendwendestand De&Bl.
    KF211208  7TM=55003, k=  1; rsquare  < 0.98, Wendeneigung setzt sich fort. > Trendwendestand De&Bl.
    KF211207  7TM=55375, k= -1; rsquare < 0.98, Wendeneigung setzt sich fort. > Trendwendestand De&Bl.
    KF211206  7TM=55030, k=  6; rsquare  < 0.98, Wendeneigung setzt sich fort. > Trendwendestand De&Bl.
    KF211205  7TM=56414, k=  5; rsquare  < 0.98, Wendeneigung setzt sich fort. > Trendwendestand De&Bl.
    KF211204  7TM=56636, k=  4; rsquare  < 0.98, Wendeneigung setzt sich fort. > Trendwendestand De&Bl.
    KF211203  7TM=56968, k=  3; rsquare = 0.9723, also < 0.98, Wendeneigung graphisch erkennbar. > Trendwendestand De&Bl.

    KF211202  7TM=57341, k=  2; rsquare = geschätzt , Plateaubildung bei unterbrochener exponentiellen Entwicklung
    KF211201  7TM=57636, k=  1; rsquare = geschätzt > 0.98, Plateaubildung bei abgeschwächter exponentieller Entwicklung
    KF211130  7TM=58039, k= -2; rsquare = geschätzt > 0.98, Plateaubildung bei abgeschwächter exponentieller Entwicklung
    KF211129  7TM=57986, k= -1; rsquare = 0.9878, also > 0.98, exponentielle Entwicklung noch in Gang, aber abgeschwächt.

    KF211128  7TM=57925, k= 1; rsquare = geschätzt > 0.98, exponentielle Entwicklung noch in Gang.
    KF211127  7TM=58108, k= -25; rsquare = geschätzt > 0.98, exponentielle Entwicklung weiter in Gang - mehr denn je.
    KF211126  7TM=57869, k= -24; rsquare = geschätzt > 0.98, exponentielle Entwicklung weiter in Gang - mehr denn je.
    KF211125  7TM=57411, k= -23; rsquare = geschätzt > 0.98, exponentielle Entwicklung weiter in Gang - mehr denn je.
    KF211124  7TM=54062, k= -22; rsquare = geschätzt > 0.98, exponentielle Entwicklung weiter in Gang - mehr denn je.
    KF211123  7TM=52549, k= -21; rsquare = geschätzt > 0.98, exponentielle Entwicklung weiter in Gang - mehr denn je.
    KF211122  7TM=50541, k= -20; rsquare = geschätzt > 0.98, exponentielle Entwicklung weiter in Gang - mehr denn je.
    KF211121  7TM=48644, k= -19; rsquare = geschätzt > 0.98, exponentielle Entwicklung weiter in Gang - mehr denn je.
    KF211120  7TM=47639, k= -18; rsquare = geschätzt > 0.98, exponentielle Entwicklung weiter in Gang - mehr denn je.
    KF211119  7TM=46321 (mit doppelt Sachsen), k= -17; rsquare = geschätzt > 0.98, exponentielle Entwicklung weiter in Gang - mehr denn je.
    KF211118  7TM=43629 (ohne Sachsen), k= -16; rsquare = geschätzt > 0.98, exponentielle Entwicklung weiter in Gang - mehr denn je.
    KF211117  7TM=43010, k= -15; rsquare = geschätzt > 0.98, exponentielle Entwicklung weiter in Gang - mehr denn je.
    KF211116  7TM=40842, k= -14; rsquare = geschätzt > 0.98, exponentielle Entwicklung weiter in Gang - mehr denn je.
    KF211115  7TM=38964, k= -13; rsquare = geschätzt > 0.98, exponentielle Entwicklung weiter in Gang - mehr denn je.
    KF211114  7TM=37504, k= -12; rsquare = geschätzt > 0.98, exponentielle Entwicklung weiter in Gang - mehr denn je.
    KF211113  7TM=36348, k= -11; rsquare = geschätzt > 0.98, exponentielle Entwicklung weiter in Gang - mehr denn je.
    KF211112  7TM=34926, k= -10; rsquare = geschätzt > 0.98, exponentielle Entwicklung weiter in Gang - mehr denn je.
    KF211111  7TM=33343, k= -9; rsquare = geschätzt > 0.98, exponentielle Entwicklung weiter in Gang - mehr denn je.
    KF211110  7TM=31697, k= -8; rsquare = geschätzt > 0.98, exponentielle Entwicklung weiter in Gang - mehr denn je.
    KF211109  7TM=29376, k= -7; rsquare = geschätzt > 0.98, exponentielle Entwicklung weiter in Gang.
    KF211108  7TM=26622, k= -6; rsquare = geschätzt > 0.98, exponentielle Entwicklung weiter in Gang.
    KF211107  7TM=25048, k= -5; rsquare = geschätzt > 0.98, exponentielle Entwicklung weiter in Gang.
    KF211106  7TM=24212, k= -4; rsquare = 0.9825, also > 0.98, exponentielle Entwicklung wieder in Gang.

    KF211105  7TM=23261, k= -3; rsquare = 0.9796, also < 0.98, exponentielle Entwicklung eben noch gebrochen.
    KF211104  7TM=21481, k= -2; rsquare = 0.9760, also < 0.98, exponentielle Entwicklung gebrochen.
    KF211103  7TM=19702, k= -1; rsquare = 0.9732, also < 0.98, exponentielle Entwicklung gebrochen.
    KF211102  7TM=18858, k= 1; rsquare < 0.98, exponentielle Entwicklung gebrochen.


     

    KF211101  7TM=19260, k= -26; rsquare > 0.98, zeigt eine exponentielle Entwicklung an.
    KF211031  7TM=19211, k= -25; rsquare > 0.98, zeigt eine exponentielle Entwicklung an.
    KF211030  7TM=18770, k= -24; rsquare > 0.98, zeigt eine exponentielle Entwicklung an.
    KF211029  7TM=18320, k= -23; rsquare > 0.98, zeigt eine exponentielle Entwicklung an.
    KF211028  7TM=17406, k= -22; rsquare > 0.98, zeigt eine exponentielle Entwicklung an.
    KF211027  7TM=16678, k= -21; rsquare > 0.98, zeigt eine exponentielle Entwicklung an.
    KF211026  7TM=14969, k= -20; rsquare > 0.98, zeigt eine exponentielle Entwicklung an.
    KF211025  7TM=14084, k= -19; rsquare > 0.98, zeigt eine exponentielle Entwicklung an.
    KF211024  7TM=13555, k= -18; rsquare > 0.98, zeigt eine exponentielle Entwicklung an.
    KF211023  7TM=13195, k= -17; rsquare > 0.98, zeigt eine exponentielle Entwicklung an.
    KF211022  7TM=12474, k= -16; rsquare > 0.98, zeigt eine exponentielle Entwicklung an.
    KF211021  7TM=11875, k= -15; rsquare > 0.98, zeigt eine exponentielle Entwicklung an.
    KF211020  7TM=10724, k= -14; rsquare =0.9847, zeigt eine exponentielle Entwicklung an.
    KF211019  7TM=10196, k= -13; rsquare 0.9744.
    Neu-Interpretation der Wellenentwicklung in De. 10. Welle  1.7.-28.9.21 mit Scheitel am 8.9.21. Beginn 11. Welle am 28.9.21, die ab 10.10.21 eine angenäherte exponentielle Entwicklung anzeigt.

    KF211018  7TM=9466, k= -12; rsquare geschätzt  k=43
    KF211017  7TM=9209, k= -11; rsquare geschätzt  k=42
    KF211016  7TM=9027, k= -10; rsquare geschätzt  k=41
    KF211015  7TM=8921, k= -9; rsquare geschätzt  k=40  Graph zum aktuellen Verlauf siehe bitte oben: Anteil.
    KF211014  7TM=8622, k= -8; rsquare geschätzt  k=39
    KF211013  7TM=8466, k= -7; rsquare geschätzt  k=38
    KF211012  7TM=8361, k= -6; rsquare geschätzt  k=37
    KF211011  7TM=8310, k= -5; rsquare geschätzt  k=36
    KF211010  7TM=8285, k= -4; rsquare geschätzt  k=35
    KF211009  7TM=8282, k= -3; rsquare geschätzt  k=34
    KF211008  7TM=8075, k= -2; rsquare geschätzt  k=33
    KF211007  7TM=8027, k= -1; rsquare geschätzt  k=32
    KF211006  7TM=7982, k=  2; rsquare geschätzt  k=31
    KF211005  7TM=8055, k=  1; rsquare geschätzt  k=30
    KF211004  7TM=8088, k= -2; rsquare geschätzt  k=29
    KF211003  7TM=7998, k= -1; rsquare 0.6806 also weit unter 0.98 wie man auch sieht  k=28

    KF211002  7TM=7989, k= 1;  rsquare geschätzt  k=27
    KF211001  7TM=8219, k= -5; rsquare geschätzt  k=26
    KF210930  7TM=8032, k= -4; rsquare geschätzt  k=25
    KF210929  7TM=7976, k= -3; rsquare geschätzt  k=24
    KF210928  7TM=7769, k= -2; rsquare geschätzt  k=23
    KF210927  7TM=7579, k= -1; rsquare geschätzt  k=22
    KF210926  7TM=7650, k=  1; rsquare geschätzt  k=21
    KF210925  7TM=7752, k= -1;  rsquare  0.7711  k=20

    KF210924  7TM=  7689, k= 12; rsquare geschätzt k=19
    KF210923  7TM=  7931, k= 11; rsquare geschätzt k=18
    KF210922  7TM=  8113, k= 10; rsquare geschätzt k=17
    KF210921  7TM=  8431, k= 9;   rsquare geschätzt k=16
    KF210920  7TM=  8717, k= 8;  rsquare geschätzt k=15
    KF210919  7TM=  8954, k= 7;  rsquare geschätzt k=14
    KF210918  7TM=  9208, k= 6;   rsquare geschätzt k=13
    KF210917  7TM=  9209, k= 5;  rsquare geschätzt k=12
    KF210916  7TM=  9540, k= 4;  rsquare geschätzt k=11
    KF210915  7TM=  9821, k= 3;   rsquare geschätzt k=10
    KF210914  7TM=10179, k= 2;  rsquare geschätzt k=9
    KF210913  7TM=10337, k= 1;   rsquare geschätzt k=8
    KF210912  7TM=10394, k= -1; rsquare geschätzt k=7

    KF210911 De 10. Welle (RKI Sprech 4. Welle) 01.07.-11.09.2021: exponentielle Entwicklung zum 6. Mal gebrochen mit rsquare 0.9533 und b=0.03835 nach 0.9639 und b=0.03999 (Kriterium rsquare > 0.98). 7TM=10286 (11.9.) nach 10730 (10.9.). Die aktuelle Tendenz mit k(rsquare)=6 spricht für nachhaltig. Erstmal scheint der exponentielle Trend nachhaltig gebrochen und die täglich aufwändige Berechnung und Präsentation wird einstweilen eingestellt bis neue bedrohliche Entwicklungen eine Wiederaufnahme nahelegen, die man gut an den 7-Tage-Mittelwerten der Neu-Infektionen erkennen kann.
    _
    KF210910 De 10. Welle (RKI Sprech 4. Welle) 01.07.-10.09.2021: exponentielle Entwicklung zum 5. Mal gebrochen mit rsquare 0.9639 und b=0.03999 nach 0.9664 und b=0.04082 (Kriterium rsquare > 0.98). 7TM=10730 (10.9.) nach 10675 (9.9.). Die aktuelle Tendenz spricht für nachhaltig. Ob die Tendenz anhält, müssen die Zahlen der nächsten Tage zeigen. k(rsquare)=5. Immerhin: eine klare 5. Schwalbe im Spätsommer.
    _

    _
    _KF210909 De 10. Welle (RKI Sprech 4. Welle) 01.07.-09.09.2021: exponentielle Entwicklung zum 4. Mal gebrochen mit rsquare 0.9664 und b=0.04082 nach 0.9711 und b=0.04201  (Kriterium rsquare > 0.98). 7TM=10675 (9.9.) nach 10859 (8.9.). Die aktuelle Tendenz spricht für nachhaltig. Ob die Tendenz anhält, müssen die Zahlen der nächsten Tage zeigen. k(rsquare)=4. Immerhin: eine starke 4. Schwalbe im Spätsommer.
    _
    _KF210908De 10. Welle (RKI Sprech 4. Welle) 01.07.-08.09.2021: exponentielle Entwicklung zum 3. Mal gebrochen mit rsquare 0.9711 und b=0.04201 nach 0.9741 und b=0.04309  (Kriterium rsquare > 0.98). 7TM=10859 (8.9.) nach 10613 (7.9.) Ob der Bruch anhaltend ist, müssen die Zahlen der nächsten Tage zeigen. k(rsquare)=3. Immherin: die 3. Schwalbe im Spätsommer.
    _
    KF210907 De 10. Welle (RKI Sprech 4. Welle) 01.07.-07.09.2021: exponentielle Entwicklung zum 2. Mal gebrochen mit rsquare 0.9741 und b=0.04309 nach 0.9777 und b=0.04427 (Kriterium rsquare > 0.98). 7TM=10613 (7.9.) nach 10609(6.9.). Ob der Bruch anhaltend ist, müssen die Zahlen der nächsten Tage zeigen. k(rsquare)=2.
    _
    KF210906 De 10. Welle (RKI Sprech 4. Welle) 01.07.-06.09.2021: exponentielle Entwicklung erstmals gebrochen mit rsquare 0.9777 und b=0.04427 nach  0.9803 und b=0.0454 (Kriterium rsquare > 0.98). k(rsquare)=1.  7TM=10609(6.9.) nach 10469(5.9.). Ob der Bruch anhaltend ist, müssen die Zahlen der nächsten Tage zeigen, denn eine Schwalbe macht bekanntlich noch keinen Sommer.
    _

    _
    KF210905 De 10. Welle (RKI Sprech 4. Welle) 01.07.-05.09.2021: exponentielle Entwicklung anhaltend mit rsquare 0.9803 und b=0.0454 nach 0.9833 und b=0.04654 (Kriterium rsquare > 0.98). 7TM=10469(5.9.) nach 10442(4.9.).
    _
    KF210904 De 10. Welle (RKI Sprech 4. Welle) 01.07.-04.09.2021: exponentielle Entwicklung anhaltendmit rsquare 0.9833 und b=0.04654 nach  0.9852 und b=0.0476 (Kriterium rsquare > 0.98). 7TM=10442(4.9.) nach 10151 (3.9.):
    _

    _
    KF210903 De 10. Welle (RKI Sprech 4. Welle) 01.07.-03.09.2021: exponentielle Entwicklung anhaltend mit rsquare 0.9852 und b=0.0476 nach 0.9874 und b=0.04874 (Kriterium rsquare > 0.98). 7TM=10151 (3.9.) nach 10075(2.9.).
    _
    KF210902 De 10. Welle (RKI Sprech 4. Welle) 01.07.-02.09.2021: exponentielle Entwicklung anhaltend mit rsquare 0.9874 und b=0.04874 nach 0.9889 und b=0.04977 (Kriterium rsquare > 0.98). 7TM=10075(2.9.) nach 9758(1.9.).
    _
    KF210901 De 10. Welle (RKI Sprech 4. Welle) 01.07.-01.09.2021: exponentielle Entwicklung anhaltend mit rsquare 0.9889 und b=0.04977 nach 0.9909 und b=0.0509 (Kriterium rsquare > 0.98). 7TM=9758(1.9.) nach 9602(31.8.).
    _
    KF210831 De 10. Welle (RKI Sprech 4. Welle) 01.07.-31.08.2021: exponentielle Entwicklung anhaltend mit rsquare 0.9909 und b=0.0509 nach 0.9920 und b=0.05195 (Kriterium rsquare > 0.98). 7TM=9602(31.8.) nach 9321(30.8.).
    _
    KF210830 De 10. Welle (RKI Sprech 4. Welle) 01.07.-30.08.2021: exponentielle Entwicklung anhaltendmit rsquare 0.9920 und b=0.05195 nach 0.9934 und b= 0.05303 (Kriterium rsquare > 0.98). 7TM=9321(30.8.) nach 9320(29.8.).
    _
    KF210829 De 10. Welle (RKI Sprech 4. Welle) 01.07.-29.08.2021: exponentielle Entwicklung anhaltendmit rsquare 0.9934 und b= 0.05303 nach 0.9935 und b=0.05375 (Kriterium rsquare > 0.98). 7TM=9320(29-8-) nach 9193(28.8.).
    _
    KF210828 De 10. Welle (RKI Sprech 4. Welle) 01.07.-28.08.2021: exponentielle Entwicklung anhaltend mit rsquare 0.9935 und b=0.05375 nach 0.9929 und b=0.05411 (Kriterium rsquare > 0.98). 7TM=9193(28.8.) nach 8998(27.8.).
    _
    KF210827 De 10. Welle (RKI Sprech 4. Welle) 01.07.-27.08.2021: exponentielle Entwicklung anhaltendmit rsquare 0.9929 und b=0.05411 nach 0.9919 und b=0.05409 (Kriterium rsquare > 0.98). 7TM=8998(27.8.) nach 8662(26.8.):
    _

    _
    KF210826 De 10. Welle (RKI Sprech 4. Welle) 01.07.-26.08.2021: exponentielle Entwicklung anhaltend mit rsquare 0.09919 und b=0.05409 nach 0.9909 und b=0.05381 (Kriterium rsquare > 0.98). 7TM=8662(26.8.) nach 8289(25.8).
    _
    KF210825 De 10. Welle (RKI Sprech 4. Welle) 01.07.-25.08.2021: exponentielle Entwicklung anhaltendmit rsquare 0.9909, b=0.05381 nach 0.9899,  b=0.05331 (Kriterium rsquare > 0.98). 7TM=8289(25.8) nach 7685(24.8.).
    _
    KF210824 De 10. Welle (RKI Sprech 4. Welle) 01.07.-24.08.2021: exponentielle Entwicklung anhaltend mit rsquare 0.9899,  b=0.05331 nach 0.9885, b=0.05030 (Kriterium rsquare > 0.98). 7TM=7685(24.8) nach 7223(23.8.).
    _
    KF210823 De 10. Welle (RKI Sprech 4. Welle) 01.07.-23.08.2022: exponentielle Entwicklung anhaltend mit rsquare 0.9885 nach 0.9869 (Kriterium rsquare > 0.98). 7TM=7223(238.) nach 6961(22.8.).
    _
    KF210822 De 10. Welle (RKI Sprech 4. Welle) 01.07.-22.08.2022: exponentielle Entwicklung anhaltend mit rsquare 0.9869 nach 0.9854 (Kriterium rsquare > 0.98). 7TM=6961(22.8.) nach 6741(21.8.).
    _
    KF210821 De 10. Welle (RKI Sprech 4. Welle) 01.07.-21.08.2021: exponentielle Entwicklung anhaltend mit rsquare 0.9854 nach 0.9847 (Kriterium rsquare > 0.98). 7TM=6741(21.8.) nach 6409(20.8.).

    KF210820 De 10. Welle (RKI Sprech 4. Welle) 01.07.-20.08.2021: exponentielle Entwicklung anhaltend mit rsquare 0.9847 nach 0.9850 (Kriterium rsquare > 0.98). 7TM=6409(20.8.) nach 6059(19.8.)

    KF210819 De 10. Welle (RKI Sprech 4. Welle) 01.07.-19.08.2021: exponentielle Entwicklung anhaltend mit rsquare 0.9850 nach 0.9868 (Kriterium rsquare > 0.98). 7TM=6059(19.8.) nach 5530(18.8.)

    KF210818 De 10. Welle (RKI Sprech 4. Welle) 01.07.-18.08.2021: exponentielle Entwicklung anhaltend mit rsquare 0.09868 nach 0.9876 (Kriterium rsquare > 0.98). 7TM=5530(18.8.) nach 5136(17.8.).

    KF210817 De 10. Welle (RKI Sprech 4. Welle) 01.07.-17.08.2021: exponentielle Entwicklung anhaltend mit rsquare 0.9876 nach 0.9881 (Kriterium rsquare > 0.98). 7TM=5136(17.8.) nach 4660(16.8.).

    KF210816 De 10. Welle (RKI Sprech 4. Welle) 01.07.-16.08.2021: exponentielle Entwicklung anhaltend mit rsquare 0.9881 nach 0.9871, 0.9864 (Kriterium rsquare > 0.98). 7TM=4660(16.8.) nach 4456(15.8.), 4321(14.8.).

    KF210815 De 10. Welle (RKI Sprech 4. Welle) 01.07.-15.08.2021: exponentielle Entwicklung anhaltend mit rsquare 0.9871 nach 0.9864 (Kriterium rsquare > 0.98). 7TM=4456(15.8.) nach 4321(14.8.).

    KF210814 De 10. Welle (RKI Sprech 4. Welle) 01.07.-14.08.2021: exponentielle Entwicklung anhaltend mit rsquare 0.9864 nach 0.9873, 0.9893, 0.9897, 0.9885, 0.9875, 0.9868,   0.9860,  0.9845,  0.9834,  0.9825,  0.9834 (Kriterium rsquare> 0.98). 7TM= 4321(14.8.) nach 4092(13.8.).

    KF210813 De 10. Welle (RKI Sprech 4. Welle) 01.07.-13.08.2021: exponentielle Entwicklung anhaltend mit rsquare 0.9873 nach 0.9893, 0.9897, 0.9885, 0.9875, 0.9868,   0.9860,  0.9845,  0.9834,  0.9825,  0.9834 (Kriterium rsquare > 0.98). 7TM=4092(13.8.) nach 3744(12.8.).

    KF210812 De 10. Welle (RKI Sprech 4. Welle) 01.07.-12.08.2021: exponentielle Entwicklung anhaltend mit rsquare 0.9893 nach 0.9897, 0.9885, 0.9875, 0.9868,   0.9860, 0.9845,  0.9834,  0.9825,  0.9834 (Kriterium rsquare > 0.98). 7TM=3744(12.8.) nach  3440 (11.8.).

    KF210811 De 10. Welle (RKI Sprech 4. Welle) 01.07.-11.08.2021: exponentielle Entwicklung anhaltend mit rsquare 0.9897 nach 0.9885, 0.9875, 0.9868,   0.9860,  0.9845,  0.9834,  0.9825,  0.9834 (Kriterium rsquare > 0.98). 7TM=3440 (11.8.) nach 3140 (10.8.).

    KF210810 De 10. Welle (RKI Sprech 4. Welle) 01.07.-10.08.2021: exponentielle Entwicklung anhaltend mit rsquare 0.9885 nach 0.9875, 0.9868,   0.9860,  0.9845,  0.9834,  0.9825,  0.9834 (Kriterium rsquare  > 0.98). 7TM=3140 (10.8.) nach 2936 (9.8.).

    KF210809 De 10. Welle (RKI Sprech 4. Welle) 01.07.-09.08.2021: exponentielle Entwicklung anhaltend mit rsquare 0.9875 nach 0.9868,   0.9860,  0.9845,  0.9834, 0.9825,  0.9834 (Kriteriumrsquare  > 0.98). 7TM(9.8.)=2936 nach 2834 (8.8).

    KF210808 De 10. Welle (RKI Sprech 4. Welle) 01.07.-08.08.2021: exponentielle Entwicklung mit rsquare 0.9868 nach  0.9860,  0.9845,  0.9834,  0.9825,  0.9834 anhaltend (Kriterium rsquare  > 0.98). 7TM(8.8.)=2834 nach 2786 (7.8).
    KF210807 De 10. Welle (RKI Sprech 4. Welle) 01.07.-07.08.2021: exponentielle Entwicklung mit rsquare 0.9860 nach 0.9845,  0.9834,  0.9825,  0.9834 anhaltend (Kriterium rsquare > 0.98). 7TM(7.8.)=2786 nach 2639 (6.8).

    KF210806 De 10. Welle (RKI Sprech 4. Welle) 01.07.-06.08.2021: exponentielle Entwicklung mit rsquare 0.9845 nach 0.9834,  0.9825,  0.9834 anhaltend (Kriterium  rsquare  > 0.98). 7TM(6.8.)=2639 nach 2524 (5.8.).
    KF210805  De 10. Welle (RKI Sprech 4. Welle) 01.07.-05.08.2021: exponentielle Entwicklung mit rsquare 0.9834 nach 0.9825,  0.9834 anhaltend (Kriterium  rsquare  > 0.98). 7TM(5.8.)=2524 nach 2382 (4.8).
    KF210804  De 10. Welle (RKI Sprech 4. Welle) 01.07.-04.08.2021: exponentielle Entwicklung mit rsquare 0.9825 nach 0.9834 anhaltend (Kriterium  rsquare  > 0.98). 7TM(4.8.)=2382 nach 2325.
    KF210803  Kurvenfitvergleich 10. Welle (RKI Sprech 4. Welle) Deutschland 0.1.07.-03.08.2021:
    Exponentielle Entwicklung anhaltend. [Aktualisierung und Korrektur der gestrigen Falschmeldung]
    7TM(3.8.)=2325 nach 2211.


     

    KF210802  Kurvenfitvergleich 10. Welle (RKI Sprech 4. Welle) Deutschland 0.1.07.-02.08.2021:
    Exponentielle Entwicklung gebrochen
     
    FALSCH! Die exponentielle Entwicklung hält an. Statt des 7TM= 2211 wurde irrtümlich der Tageswert=1766 verarbeitet.

    Neu hinzugekommene 7TM:
    02.08.2021  1766 FAlSCH. Richtig 2211. [Korrektur 4.8.21]
    01.08.2021  2179
    31.07.2021  2195

    Kurvenfitvergleiche 10. Welle (RKI Sprech 4. Welle) Deutschland (De) 01.07.-30.07.2021
    Beim Kurvenfitten schätzt man die Anpassungsgüte an den tatsächlichen Daten durch verschiedene Modelle, meist mit der Methode der kleinsten Quadrate. D.h. man sucht die Formel für ein Modell, das die geringsten Abweichungen zu den tatsächlichen Daten liefert. Im allgemeinen schätzt man die Anpassung mit dem Korrelationskoeffizientenund dessen Quadrat, dem sog. Determinationskoeffizienten ("rsquare"), der ein Maß für die gemeinsame Varianz zwischen Modell und den tatsächlichen Daten liefert. Z.B. ist der Determinationskoeffizient beim exponentiellen Fit rsquare=0.9865, was einen  Korrelationskoeffizienten der Quadratwurzel (0.9865)=0.9932 ergibt. Im vorliegenden Vergleich liefern alle drei Fits (quadratic, cubic und exponentiell) zufriedenstellende Ergebnisse, am besten von allen drei untersuchten schneidet die kubische ab mit rsquare=0.9943. Sie hat auch den Vorteil, dass die Schere am kleinsten ist. Aktuell kann man aber von einer fitgestützten exponentiellen Entwicklung sprechen. Prognosen über einen Zeitraum, der über mehrere Tage hinausgeht, sind schwierig und problematisch. Allerdings kann man natürlich die Kurvenfits täglich neu berechnen. Doch die 7-Tage-Mittelwerte und ihr Verlauf signalisieren ebenfalls schon ganz gut die Entwicklung. Ein interessanter mathematischer Nebenbefund ist, dass exponentielle Entwicklungen auch durch quadratische oder kubische Modelle ausgedrückt werden können.
     

    Mit Matlab R2021a Home Lizenz gerechnet.

    Mit den 7-Tage-Mittelwerten der Neu-Infektionen der 10. Welle (RKI Sprech 4. Welle) vom 01.07.-30.07.2021 wurden mehrere Kurvenfits durchgeführt. Sowohl der quadratische als auch der exponentielle Fit zeigen sehr gute Anpassungswerte, sämtliche Determinationskoeffi- zienten sind > 0.98. Aber die beste Näherung zeigt der cubische Fit, der auch fast parallel zum 7TM verläuft.


     


    Schätzen der Wachstumsfunktion der 7-Tage-Mittelwerte der Neu-Infektionen der 9. Welle 07.04.-23.05.2021 für Deutschland


     

    Die Tücken des Kurvenfittens am BeispielBayern-Fit-Vergleich cubic und 4th degree der 7-Tage-Mittelwerte der 9. Welle 07.04.-24.05.2021
    Der Fit-Vergleich zeigt einige Tücken und dass es für die Prognose sehr sehr wichtig sein kann, welcher Fit gewählt wird.


     

    Explorative Kurvenfitstudie Grad 2-9 der 3. großen Welle in Schweden 01.02.-26.5.2021


    UK210708  Analyse der 4. Welle in Großbritannien (UK) 24.05.-08.07.2021
    Hier wird gezeigt, dass das Kriterium für eine exponentielle Entwicklung - der Zuwachs wächst - nicht erfüllt ist.

    Materialien

    Wachstum spielt in vielen Lebens- und Wissenschaftsbereichen eine Rolle, z.B.:
        Wachstum im Alltag:
            Wachstum Anzahl der Sachen.
            Wachstums zweckloser Sachen.
            Wachstum der Geburtstage (Lebensjahre)
        Wachstum in der Biologie. > Medizin, Epidemiologie.
        Wachstum in der Demographie:
            Bevölkerungswachstum.
            Wachstum Nahrungsbedarf.
            Wachstum der Lebensspanne.
       Wachstum in der Epidemiologie. > Medizin, Biologie.
       Wachstum in der Finanzwissenschaft.
           Wachstum der Schulden.
               Überblick Staatsverschuldungsanalysen.
           Zinseszinseffekte. > Zinseszinstabellen.
        Wachstum in der Mathematik.
        Wachstum in der Kultur
            Wachstum der Literatur.
            Wachstum der Kunstwerke.
        Wachstum in der Medizin. > Epidemiologie, Biologie.
            Wachstum der Anzahl der ÄrztInnen.
            Wachstum der Gesundheitskosten.
            Wachstum der multiresistenten Keime.
            Wachstum der Krankheiten. (> Blech "Die Krankheitserfinder")
               Wie krank sind wir wirklich?
       Wachstum in der Natur.
            Periodisches Wachstum
            Die Expansion des Universums.
       Wachstum in der Psychologie: Lernen und Vergessen.
       Wachstum in der Ökologie
        Wachstum der Umweltbelastung.
            Wachstum der Erd-Erwärmung.
            Wachstum der Umweltverschmutzung.
       Wachstum in der Ökonomie (Wirtschaft).
            Geschichte der Wirtschaftswachstumsideen.
            Wachstum der Ressourcenausbeutung.
               Postwachstum.
            Wirtschaftswachstumsanalysen.
            Wachstum der Konzentration (Großkonzerne, Monopole und Kartelle)
            Wachstum des Angebots.
            Wachstum der Sättigung der Märkte.
       Wachstum in der Soziologie:
            Wachstum der Bürokratie.
            Wachstum von Organisationen und Institutionen.
            Wachstum von Armut und Reichtum.
               Armut- und Reichtumsberichte der Bundesregierung.
                Wachstum der Vermögen.
                Wachstum der Schere zwischen arm und reich.
        Wachstum der Wissenschaft.
            Wachstum der Anzahl der Publikationen.
     


    Wachstum in der Mathematik

    Analyse und Auswertung der Inhaltsverzeichnisse, Sachregister und teilweise der Texte von 45 mathematischen Werken in 5 Abteilungen:
    Zusammenfassung der Analyse. Ein allgemeiner Wachstumsbegriff wird nur in zwei der hier 45 erfassten Werke (A20 allgemeine; B9 Biomathe; D4 Datenanalyse, Zeitreihenanalyse & Statistik); F2 Finanzmathematik; S10 Schulmathe, allgemein erklärt und erörtert: einmal in der Finanzmathematik und in Wikipedia. Der Sachverhalt scheint für die Mathematik zu selbstverständlich, "trivial" oder uninteressant. Damit werden aber die allermeisten tatsächlichen und auch allgemeinen Wachstumsphänomene mathematisch nicht analysiert und aufbereitet. Jedenfalls nicht ausdrücklich in Worte gefasst. Tatsächlich kann die Mathematik fast jede Wachstumsfunktion mit Hilfe der Kurven-Fit-Algorithmen bestimmen.
     
            Suchbegriffe Wachstum,
             Exponent...
    Mathematische Abteilung    		 Wachstum, wachsen im Inhalts- verzeichnis IV, bei Lexika, Wörterbüchern o.ä. Eintrag
    + := Ja,  - := Nein.    		 Exponentiell, Exponential... im Inhaltsverzeichnis IV, bei Lexika, Wörterbüchern o.ä. Eintrag
    + := Ja,  - := Nein.    		 Wachstum, wachsen im Sachregister SR, bei Lexika, Wörterbüchern o.ä. Eintrag
    + := Ja,  - := Nein.    		 Allgemeine Erörterung des Wachstumsbegriffs_begB im Text nicht nur bloße Erwähnun- gen_begE. + := Ja,  - := Nein.
    [A] Allgemeine mathematische Werke, Handbücher und Lexika.

    Bislang 20 (A1-A20) erfasst. 

    _

    		 A1-, A2-, A3-, A4-, A5-, A6-, A7-, A8-, A9-,A10-, A11+, A12-, A13-,A14+, A15+, A16-, A17-, A18-, A19+, A20+.
    Ergebnis: 5+, 15-.    		 A1+, A2+, A3+, A4+, A5-, A6+, A7+, A8+, A9+, A10+, A11+, A12+, A13+,A14+, A15+, A16-, A17+,A18+, A19+,A20-. 
    Ergebnis IV: 17+, 3-.    		 A1+, A2+, A3+,A4-, A5+,A6-, A7-, A8-, A9-, A10-, A11+, A12-, A13-, A14+, A15+, A16-, A17-,A18+, A19+, A20- [kein SR]
    Ergebnis SR: 9+, 11-.    		 A1-, A2-, A3-, A4-, A5-, A6-, A7-, A8-, A9-, A10-, A11-,A12-, A13-, A14-, A15+, A16-, A17-, A18+, A19-, A20-,
    Ergebnis: 2+, 18-.
    [B] Biomathematik. Werke, die im Titel oder Untertitel Bio-
    mathematik, Mathematik für Bio- logen oder Mediziner enthalten.
    Bisher 9 (B1-B9) erfasst.    		 B1-, B2+, B3-, B4-, B5-, B6-, B7+, B8-, B9+, 
    Ergebnis: 3+, 6-.

    _

    		 B1-, B2+, B3-, B4-, B5-, B6+, B7+,B8-, B9-,
    Ergebnis: 3+, 6-.

    _

    		 B1-, B2+, B3-, B4+, B5+, B6+, B7+, B8+, B9+,
    Ergebnis: 7+, 2-

    _

    		 B1-, B2+, B3-, B4-, B5-, B6-, B7-, B8-, B9-, 
    Ergebnis: 1+, 8-.

    _
    [D] Datenanalyse, Datenmo- dellierung, Zeitreihenanalyse & Statistik.  Bisher 4 erfasst (D1-D4).  D1-, D2-, D3-, D4+,
    Ergebnis: 1+, 3-.
    _    		 D1-, D2-, D3+, D4-, 
    Ergebnis: 1+, 3-.
    _    		 D1-, D2- [kein SR], D3+, D4+,
    Ergebnis: 2+, 2-.
    _    		 D1-, D2-, D3-, D4+
    Ergebnis: 1+, 3-.
    _
    [F] Finanzmathematik. Bisher 2 erfasst (F1-F2) F1+, F2-,
    Ergebnis: 1+, 1-.    		 F1+, F2-,
    Ergebnis:  1+, 1-.    		 F1+, F2- [kein SR],
    Ergebnis: 1+, 1-.    		 F1+, F2-
    Ergebnis: 1+, 1-.
    [S] Schule: Schulbücher und Lexika. In der Regel bis Abitur. Bisher 10 erfasst (S1-S10). S1+, S2-, S3-, S4-, S5-,S6-,S7-, S8+, S9+, S10+,
    Ergebnis:  4+, 6-.    		 S1+, S2-, S3-, S4-, S5-, S6-, S7+, S8+, S9+, S10+,
    Ergebnis: 5+, 5-.    		 S1+, S2-, S3-, S4-, S5-, S6-, S7-, S8+, S9+, S10+,
    Ergebnis: 4+, 6-.    		 S1-, S2-, S3-, S4-, S5-,S6-, S7-, S8-, S9-, S10-,
    Ergebnis: 0+, 10-

    Literaturbelege und Zitatreferenzen der 45 Werke
    Bibliographische Ordnung nach Lexikanamen (Schüler-Duden unter Duden, innerhalb absteigend chronologisch) bzw. nach Autoren

    1. [A1] Im  abc fachlexikon mathematik  (1978) hat "Wachstum", "wachsen" keinen Eintrag. "Exponentialfunktion" hat einen umfangreichen Eintrag und wird wie üblich als Exponentialgleichung mit der Variable im Exponenten definiert.
    2. [A2] In Athen & Bruhn  Rechnen und Mathematik  (1976) gibt es im Sachregister einen Eintrag "Wachstum, ökonomisches" 384. Dort, im Abschnitt Operations Research, wird lediglich erwähnt: "Prognosen des ökonomischen Wachstums". Wachstum und wachsen werden also weder allgemein noch spezifisch behandelt. Die Exponentialfunktion wird im SR S. 229 zugeordnet. Dort wird die übliche Bestimmung gegeben: Die Variable steht im Exponenten. Einen eigenen Abschnitt hat die Zinseszinsrechnung und Rentenrechnung S. 135-139 erhalten, wobei Wachstum und wachsen keine besondere Besprechung erfahren.
    3. [A3] In  Bartsch Taschenbuch mathematischer Formeln  (1982, 3. - 6. A.) gibt es die Sachregister-Einträge "Wachstum 443" und "Wachstumsgesetz 37".  S. 443 erwähnt nur im Zusammenhang Geometrisches Mittel das "durchschnittliche Wachstumstempo". Das Thema Wachstum wird nicht erörtert wie auch das Wort selbst nicht auf S. 443 vorkommt. S. 37 erwähnt im Rahmen der Rentenrechnung (1.8.5.) "organisches wachsen" mit w=b0eat   was anscheinend mit "Wachstumsgesetz" gemeint ist wenn ausgeführt wird: "Für a < 0 beschreibt das Wachstumsgesetz Abklingprozesse (Radioaktiver Zerfall mit a = -Lamda; Abkühlung; Kondensatorentladung) ". Zum Thema exponential gibt es die Einträge: "Exponential-form der komplexen Zahlen 13, — -funktion 101, 164, — — Periode 15,  — -gleichungen 70,  — -integral 337, — -reihen 402." Im Inhaltsverzeichnis wird "Wachstum" nicht angeführt. Selbst im Abschnitt 1.8.4 Zinseszinsrechnung, S, 34f, wird "Wachstum" und "wachsen" nicht genannt, wenn auch natürlich implizit verarbeitet (Endbetrag, Grundbetrag, Anzahl Zinsschritte, Zinsfuß, Zinsfaktor, Rate).
    4. [B1] Biebler, Karl-Ernst; Jäger, Bernd & Wodny, Michael (2001) Biomathematik. Vorlesungen und Übungen für Mediziner. Aachen: Shaker. Weder im Inhaltsverzeichnis kommt Wachstum vor noch gibt es einen entsprechenden Sachregistereintrag, auch nicht "exponentiell".  [Inhaltsverzeichnis/ Sachregister]
    5. [B2] Bohl, Erich (2006) Mathematik in der Biologie. 4. vollständig überarbeitete und erweiterte A. Berlin: Springer. Das ist ein sehr informatives Buch, aber der Wachstumsbegriff wird, wie üblich in der Mathematik, nicht allgemein erklärt und erörtert. [Inhaltsverzeichnis und SR] Im Text gibt es zu "Wachstum" 62 Fundstellen [Beispiele]
    6. [A4] Im  Bronstein  (1981, 20. A.) enthält das Sachregister keinen Eintrag "Wachstum" oder "wachsen", auch nicht im Ergänzungsband (1984). Das Thema exponential hat mehrere Einträge: "Exponentialfunktion 133, 237; natürliche 566; Exponentialfunktionen, Tabelle 40, 44; Exponentialgleichung; 190 Exponentialverteilung 703 exponentielle Form komplexer Zahlen 560".
    7. [A18] In  Der kleine Duden Mathematik  (1986) gibt es die Einträge "Exponent, Exponentialfunktion, Exponentialgleichung, Exponentialverteilung." Exponentielles wachsen oder exponentielles Wachstum kommt nicht vor. Auch "Wachstum" hat keinen Eintrag, nur "Wachstumsspirale" mit Verweis auf  "logarithmische Spirale".
    8. [S1] Im  dtv - Atlas Schulmathematik  (2003) gibt es die Sachregistereinträge "Wachstum" mit den Untereinträgen "exponentielles 84" und "lineares 84". Auf den Seiten 84-86 finden sich inhaltliche Ausführungen, Definitionen und Beispiele zum exponentiellen und linearen Wachstum, zu "Wachstumsvorgänge", "Verdoppelungszeit", "exponentielle Abnahme", "Halbwertszeit". "Wachsen" oder "Wachstum" der Wachstumsbegriff wird allgemein nicht erklärt.
    9. [A5] Im  dtv-Atlas zur Mathematik  Bd. I (5. A. 1982) gibt es keinen Sachregistereintrag "exponentiell" (nur "Exponentenbewertung") und keinen Eintrag zu "Wachstum". Exponentiell wird nicht allgemein erklärt und erörtert.
    10. [A6] Im  dtv-Atlas zur Mathematik  Bd. II (4. A. 1982) gibt es keinen Sachregistereintrag "exponentiell" (nur "Exponentenbewertung") und keinen Eintrag zu "Wachstum", wohl aber zu "Exponentialfunktion" 309 (Besprechung Darstellung der Exponential- und Logarithmusfunktion), 437 ("Sie zeigen, daß im Komplexen auch die Exponentialfunktion und die Hyperbelfunktionen periodisch sind, wenn auch mit einer komplexen Periode, nämlich 2pi."). Wachstum wird nicht allgemein erklärt und erörtert.
    11. [A7] Im  Duden Rechnen und Mathematik  (1994) gibt es die Einträge "Exponentialfunktion, Exponentialgleichung, Exponentialverteilung." Exponentielles wachsen oder exponentielles Wachstum kommt nicht vor. Auch "Wachstum" selbst kommt nicht vor.
    12. [D5] In Dürr, Rolf & Ziegenbalg (1984)  Dynamische Prozesse und ihre Mathematisierung durch Differenzengleichungen. Paderborn: Schöningh. handelt das VI. Kapitel vom Wachstum und im Sachregister finden sich viele Einträge. Noch nicht in die Auswertung eingearbeitet.
    13. [S2] Im  Schüler-Duden Die Mathematik  II (1991, 3. bearb. und erw. A.) gibt es keinen Sachregistereintrag "Wachstum" oder "wachsen".
    14. [S3] Im  Schüler-Duden Die Mathematik  I (1990, 5. neu bearbeitete A.) gibt es keinen Sachregistereintrag "Wachstum" oder "wachsen".
    15. [S4] Im  Schüler-Duden Die Mathematik  II (1982, 2. völlig neu bearb. und erw. A.) gibt es keinen Sachregistereintrag "Wachstum" oder "wachsen".
    16. [S5] Im  Schüler-Duden Die Mathematik  I (1972) gibt es keinen Sachregistereintrag "Wachstum" oder "wachsen".
    17. [S6] Im  Schüler-Duden Die Mathematik  II (1972) gibt es keinen Sachregistereintrag "Wachstum" oder "wachsen".
    18. [A8] Im umfangreichen  Meyers Großen Rechenduden  (BI, 1964) hat "Wachstum" keinen Sachregistereintrag (S. 902). Das Thema exponential wird in den Einträgen "Exponentialfunktion", "Exponentialgleichung" und "Exponentialreihen" wie üblich dargestellt.
    19. [S7] Im  Schüler-Rechenduden  (1966) gibt es die Einträge "Exponentialfunktion, Exponentialgleichung." Exponentielles wachsen oder exponentielles Wachstum hat keinen Sachregistereintrag.
    20. [D4] Engel, Joachim (2010) Anwendungsorientierte Mathematik: Von Daten zur Funktion. Eine Einführung in die mathematische Modellbildung für Lehramtsstudierende. Berlin, Heidelberg: Springer. [UB-Volltext] Das ganze Kapitel 4 behandelt das Thema Wachstum und enthält auch eine diskrete und stetige Modellierung von Epidemien. Ein umfassendes Werk besonders auch zu Wachstumsvorgängen. Im IV und im Sachregister gibt es viele Einträge zu "Wachstum", aber keinen zu "Exponent...".  Im Text selbst gibt es zu "Wachstum" 336 Fundstellen mit vielen informativ-interessanten Standardmodellen und Beispielen (Abschnitt 2.2., S. 39-42), wenn auch keine allgemeine Erörterung und  Erklärung des Wachstumsbegriffs.
    21. [A9] In  DasFischer Lexikon Mathematik I.  (1964) gibt es keinen Sachregistereintrag zu "wachsen" oder "Wachstum", aber zu "Exponentialfunktion" (44f Thema Funktionentheorie, 139 "5. Exponentialfunktion"). Wachstum wird nicht allgemein erklärt und erörtert.
    22. [A10] In  Das Fischer Lexikon Mathematik II. (1966) gibt es keinen Sachregistereintrag zu "wachsen" oder "Wachstum". Der Eintrag "Exponentialfunktion" verweist auf die Einträge in Bd. I. Darüberhinaus gibt es einen Eintrag zu "Exponentialverteilung" (364, Thema Wahrscheinlichkeitsrechnung). Wachstum wird nicht allgemein erklärt und erörtert.
    23. [B5] Horstmann, Dirk (2020) Mathematik für Biologen. Ausgabe: 3rd ed.  Berlin, Heidelberg: Springer. [UB Volltext] Das Thema Wachstum und wachsen wird in dem umfangreichen Werk (394 Seiten) in 18 Kapiteln (Inhaltsverzeichnis-PDF) nicht allgemein erörtert und als solches behandelt. Im Sachregister findet man: "wachsend, monoton 172, streng monoton 172": "Wie wir von der Motivation her gesehen haben, beschreibt die Ableitung einer Funktion ihr Steigungsverhalten."; Exponentialfunktion, 146, allgemeine, 153" [Anmerkung: S. 120 enthält: "6.1.1 Wie erhält man eine Funktionsgleichung aus experimentellen Daten?]
    24. [F1] Ihrig, Holger & Pflaumer, Holger (2001). Finanzmathematik. Intensivkurs. 8. verbesserte und erweiterte Auflage. München: Oldenbourg. im IV: 5.1 Wachstumsraten 21; 5.2 Verdoppelungs-, Verdreifachungs- und Halbierungszeiten Wachstum hat keinen eigenen allgemeinen Sachregistereintrag, hingegen schon Wachstumsrate, - durchschnittliche 21f, 24, -stetige 23f;  Wachstumsfaktor 21 ff.  S. 21 liefert eine allgemeine Wachstumsbestimmung: "Absolutes Wachstum pro Periode ist die Differenz zwischen Anfangs- und Endbestand, d.h. K1 - K0. Bezieht man den absoluten Zuwachs (K1 - K0) auf den Anfangsbestand, so erhält man das relative Wachstum (bzw. Wachstum im engeren Sinne) . (K1 - K0) / K0 = K1 / K0 - 1 = p/100 = q - 1. Merke: Im Zusammenhang mit Wachstumsprozessen wird p Wachstumsrate und q Wachstumsfaktor genannt."
    25. [B4] Jost, Jürgen (2019) Biologie und Mathematik. Berlin: Springer Spektrum [UB Volltext] SR: "Wachstumsgesetz13". "Exponent..." kommt im SR nicht vor, aber 10 mal im Text. Wachstum wird nicht allgemein erörtert und erklärt. Im Text gibt es 24 Fundstellen zu "Wachstum", z.B. S. 173: "Die Entwicklungsbiologie befasst sich im Unterschied zur Physiologie nicht mit dem Stoffwechsel und dessen Aufrechterhaltung und den entsprechenden Funktionen von Zellen, Geweben und Organen, sondern untersucht die Wachstumsvorgänge von Organismen. Sie untersucht also die Entwicklung von einer einzelnen Zelle zu einem vielzelligen, differenzierten Organismus."  Obwohl hier allgemein von Wachstumsvorgängen gesprochen wird, findet eine allgemeine Erörterung und Erklärung von Wachstum oder wachsen nicht statt.
    26. [A17] Kleine Enzyklopädie Mathematik (1980). Nachdruck der 2. völlig überarbeiteten Auflage. Leipzig, Frankfurt aM: Harri Deutsch Verlag. Im IV gibt es keinen Eintrag mit "Wachstum", aber mit "Zinsrechnung", darin "6.3 Zinseszinsrechnung". Das Sachregister enthält keinen Eintrag zu "Wachstum", aber zu "Wachstumsfunktion 141" ["Die Exponentialfunktion wird oft als Wachstumsfunktion bezeichnet, weil jeder Naturvorgang auf diese Funktion führt, in dem die Zu- bzw. Abnahme ± dN/dt einer Anzahl N betrachteter Objekte in der Zeit t von ihrer jeweiligen Anzahl abhängt; ... "]. "Wachstum" wird nicht allgemein erörtert und geklärt. Weitere Einträge:  "Exponent 49, Exponentialfunktion 60, 140 —, Ableitung 447 -, Stetigkeit 442 -, Tafel 792 —, Taylor-Reihe 537 Exponentialkurve, Quadratur 504."
    27. [B3] Klemm, Peter G. (1993) Keine Angst vor Biomathematik : medizinische Statistik ohne Formeln. 1. Aufl. Berlin: Ullstein Mosby. "Wachstum" und "wachsen" kommen weder im Inhaltsverzeichnis noch im Sachregister vor.  [Inhaltsverzeichnis/ Sachregister]
    28. [F2] Kosiol, Erich (1973) Finanzmathematik. Lehrbuch der Zinseszins-, Renten-, Tilgungs-, Kurs- und Rentabilitätsrechnung für Praktiker und Studierende. Wiesbaden: Gabler. Kosiol enthält kein Sachregister. Aus den rechnerischen Grundlagen ergibt sich, dass Kosiol sich auf arithmetische und geometrische Folgen und Reihen fokussiert. Wachstum wird nicht allgemein erörtert und erklärt.
    29. [A11] Knerr (1991) in  Mathematik Lexikon für jedermann  verweist im Sachregister beim Stichwort Wachstumsfunktion auf Exponentialfunktion 82, zu der ein umfangreicher Eintrag S. 80-86 vorliegt.  Exponentiell wird nicht allgemein erklärt und erörtert, sondern streng mathematisch formal gefasst, d.h. die Variable steht im Exponenten. Zwar gilt für jede Exponentialgleichung mit positiver Basis und positiven Exponenten, dass der Zuwachs wächst, aber die Umkehrung gilt nicht allgemein: wenn der Zuwachs wächst, kann der Verlauf in einer Exponentialgleichung beschrieben werden. Denn auch bei der quadratischen Gleichung y=x^2 wächst der Zuwachs, obwohl es sich nicht um eine Exponentialgleichung handelt.
    30. [D1] Kreiß, Jens-Peter & Neuhaus, Georg (2006) Einführung in die  Zeitreihenanalyse.  Mit 86 Abbildungen und 8 Tabellen. Berlin, Heidelberg: Springer. An Zeitreihen interessieren Verlauf und Veränderungen, weniger die Wachstumsfrage. Eine allgemeine Erörterung und Erklärung von Wachstum ist im Zeitreihenanalysekontext eher nicht zu erwarten und wird hier auch nicht geleistet. Im Sachregister gibt es keinen Eintrag "Wachstum" oder "wachsen". Im IV findet sich der Eintrag "11.3 Parameterschätzung in autoregressiven Modellen mit wachsender Ordnung 201".
    31. [B6] Köhler, Wolfgang; Schachtel, Gabriel; Voleske, Peter (2012) Biostatistik. Eine Einführung für Biologen und Agrarwissenschaftler. Fünfte, aktualisierte und erweiterte Auflage. Berlin, Heidelberg: Springer Spektrum. [UB Volltext] Inhaltsverzeichnis-PDF.RegisterPDF. "Wachstum" oder "wachsen" kein Eintrag im Sachregister. Wohl: "Exponentialfunktion  70; exponentielle Beziehung  68".
    32. [D2] Leiner, Bernd (1986) Einführung in die Zeitreihenanalyse.  2. Auflage. München: Oldenbourg. An Zeitreihen interessieren Verlauf und Veränderungen, weniger die Wachstumsfrage, wohl aber Modellierungen für Prognosen. Eine allgemeine Erörterung und Erklärung von Wachstum ist im Zeitreihenanalysekontext eher nicht zu erwarten. Grundlegend S.2: "Eine Zeitreihe ist formal gesehen eine nach dem Zeitindex (für den man zumeist das Symbol t verwendet) geordnete Menge von Beobachtungen xt einer genau definierten Variablen xt, wobei wir davon ausgehen, daß bereits eine endliche Anzahl T von Beobachtungen zur Verfügung steht." Im ökonomischen Standardmodell geht man von vier Komponenten aus, S. 5 f: I. glatte Komponente (Trend, 50-100 Jahre, Kondratieff Zyklen, 1935); II. Konjunkturkomponente (2-10 Jahre); III. Saisonkomponente (2-12 Monate) und IV. irreguläre Komponente (Störfaktoren, Fehler, Rauschen, Status einer Zufallsvariablen). Im Inhaltsverzeichnis gibt es keinen Eintrag mit "Wachstum"; das "8. Kapitel: exponential smoothing" [S. 127: "Der Name exponential smoothing wurde gewählt, weil die Koeffizienten gleichsam exponentiell mit zunehmender Zeitverschiebung abnehmen. Wegen der Ähnlichkeit mit der geometrischen Verteilung wäre auch der Name geometrical smoothing berechtigt."].  Das Buch enthält kein Sach-Register.
    33. [A12] Im  Lexikon der Mathematik von Spektrum  (6 Bde.) gibt es im Band 2 "Eig bis Inn" folgende Einträge (Abruf 31.03.2021) : "Exponent, Exponent einer Gruppe, Exponentenbewertung, Exponentenüberlauf, Exponentenunterlauf, Exponentialabbildung, Exponentialansatz, Exponentialbewertung, Exponentialfamilie, Exponentialfunktion, Exponentialfunktion einer Matrix, Exponentialfunktion zu allgemeiner Basis, Exponentialprinzip, Exponentialreihe, Exponentialsumme, Exponentialverteilung, exponentiell diophantische Gleichung." Wachstum als mathematisches Phänomen hat keinen eigenen Eintrag, genannt wird "Wachstumsordnung" und dort gibt es einen Verweis auf "ganze Funktion".
    34. [S8] Im 4-bändigen  Lexikon der Schulmathematik  (1984) finden sich die Einträge "wachsende Folge" mit Querverweis "monotone Folge" und "wachsende Funktion" mit Querverweise "monotone Funktion".  "monotone Folge (griech. monoton-einförmig; engl. monotone-increasing, decrea sequence; franz, suite monotone). Die Folge <a1, a2; ...> wächst monoton (steigt) wenn a1 <= a2 <= ... ); ist; ist das Gleichheitszeichen ausgeschlossen, wächst (fällt) die Folge streng monoton (strictement monotone)."
    35. [A19]  Mathebibel [Abruf 01.05.2021] "In diesem Kapitel schauen wir uns an, was Wachstum in der Mathematik bedeutet. Viele Wachstumsvorgänge lassen sich mathematisch erfassen und beschreiben. Je nach Art des Wachstums kann man verschiedene Typen unterscheiden. Die beiden wichtigsten sind:" lineares und exponentielles Wachstum. "Für exponentielles Wachstum ist eine konstante prozentuale Zunahme in gleichen Zeitspannen charakteristisch." Der Wachstumsbegriff wird nicht allgemein erörtert und erklärt.
    36. [A13] Im  Mathematischen Wörterbuch  von Naas & Schmid (Hrsg) Bd. I (1972) gibt es eine Reihe von Einträgen zum Thema exponential. Zu Exponentialfunktion heißt es: "1. Im weiteren Sinne: Jede Funktion, in der die unabhängige Veränderliche z als Exponent einer >Potenz (III) auftritt, z.B. ... Im Bd. II. (1974) gibt es keinen Eintrag zu "Wachstum" oder "wachsen." Das Thema Wachstum / wachsen wird weder allgemein noch speziell erörtert.
    37. [A14] In Meersmann, Willy (Hrsg.)  Mathematik Lexikon  (2004) gibt es S. 284 einen Eintrag: "Wachstum bedeutet wie in der Biologie, dass bestimmte Objekte im Laufe der Zeit größere Werte bekommen. Diese Vorgänge werden in der Mathematik durch Funktionen beschrieben und je nach Art des Wachstums eingeteilt.

      38. Lineares Wachstum: Wenn Conny jeden Monat 10, — € in ihre Sparbüchse steckt, dann wird sie in t Monaten 10 € * t € besitzen. Die Funktion, welche das Wachstum beschreibt, ist f(t) = 10 * t, also eine lineare Funktion. Die Wachstumsrate ist mit 10, — € konstant. Exponentielles Wachstum: Bringt Conny aber z. B. 200, — € zur Bank, die ihr Zinsen zahlt, dann hat sie bei einem Zinssatz von 5% nach t Jahren 200 * 1,05t €. Der Funktionsterm ist jetzt der einer Exponentialfunktion. Allgemein gilt für eine Zeitspanne h: f(h) = qh * f(t0). Der Funktionswert am Ende der Zeitspanne, das ist f(h), ergibt sich aus dem Funktionswert f(t0) am Anfang der Zeitspanne, multipliziert mit dem gleichen positiven Faktor qh, dem Wachstumsfaktor. Werden die Werte immer kleiner statt größer, dann heißt die Veränderung >Zerfall. Der Wachstumsfaktor q ist größer als 1, falls Wachstum vorliegt, beim Zerfall gilt q < 1."
    38. [B7] Peil, Jürgen (1985) Grundlagen der Biomathematik. Frankfurt aM: Harri Deutsch. [Ausführlich] Im IV im Abschnitt Differentialgleichungen. SR-Einträge: Wachstum. 162 [e-Funktion], 219 [allgemeine Erwähnung], 222 [Erwähnung Wachstum von Populationen], 224 [biokybernetische Modellierung von Wachstumsprozessen in Fußnote 1], 240 ["2. Wachstum multizellulärer Lebewesen ..."], 245 [Aufgaben zu verschiedenen Wachstumsparametern], 268f [Ausdruck "Wachstum" S. 268 nicht gefunden, S. 269 " Körperlängenwachstum"], 281 [Wachstumskinetik von Weizenkeimlingen; Einfluss Wirkstoffkonzentration auf das Wachstum; Erwähnung Wachstumsvorgänge; ], 304 [Ausdruck "Wachstum" S. 304 nicht gefunden], 343 ["... auch in den Beispielen für Wachstum (vgl. 3,3,1.3) ..."], 347 ["3.3.13. Differentialgleichungen des Wachstums von Populationen und Organismen"]; [im SR nicht ausgewiesen: 348-350 mehrere Ausführungen]; 351 ["Anmerkung 1: Wachstumsdifferentialgleichungen", auch Anmerkung 2], 353 [Ausführungen zu wechselwirkenden Populationen; Fußnote 1 "Neuere Ansätze der Modellierung von Wachstumsvorgängen ..."], 362 [Gompertzsche Wachstumsdifferentialgleichung], [369 im SR nicht eingeführt: "Richtungsfeld der (Wachstums)Differentialgleichung ..."]; 376 [Ausdruck "Wachstum" S. 376 nicht gefunden], 378 [Literaturhinweis: Knorre 1971 Wachstum von Mikroorganismen ...], 381 ["Wachstumsuntersuchungen"], 427 ["... deterministische Komponente des (Wachstums-)Verlaufs ..."] Eine allgemeine Erörterung von Wachstum und seinen vielfältigen Formen und Weisen findet bei den allgemeinen SR-Einträgen nicht statt.
    39. [S9] In Preckur, Helmuth mentor Abiturhilfe Mathematik Oberstufe Analysis 2 (1998) gibt es folgende Einträge im Sachregister: "Wachstum, stetiges 156ff" und "Wachstumssatz, lokaler 46". S. 156 führt aus: "Stetiges Wachstum und e-Funktion. In den Naturwissenschaften (Physik, Chemie, Biologie) und vielen anderen Bereichen (Bankgewerbe, Medizin) wird das Verhalten von Größen untersucht, die sich mit der Zeit t ändern. Beispiele hierzu sind: Verzinsung eines Kapitals; Abnahme der unzerfallenen Atome beim natürlichen radioaktiven Zerfall; Wachstum eines Holzbestandes (einer Bakterienkultur, einer Population); Verhalten der Stromstärke beim Ein- und Ausschalten eines Gleichstroms in einem Stromkreis mit Widerstand und Induktivität." Wachstum und wachsen werden also nicht allgemein nur spezifisch (e-Funktion) behandelt. Lokaler Wachstumssatz: "Ist f'(x0)>0 (bzw. f'(x0)<0), dann ist die Funktion f bei Durchgang durch die Stelle x0 streng monoton zunehmend (bzw. abnehmend)." Im IV findet sich Kapitel 16 S. 156 "Stetiges Wachstum und e-Funktion".
    40. [D3] In Rinnes  Taschenbuch der Statistik (1995) gibt es folgende Einträge im Sachregister: Wachstumsfaktor 142 [xt/(xt-1), also Nachfolger / Vorgänger], 192; Wachstumsfunktion 176 ff [176-178 nicht gefunden], 192 [9, mit Sättigungsgrenze 179 f [auch Logistische Funktion und S. 180 Gompertz-Funktion]; Wachstumsrate 142 [wt := xt/(xt-1) - 1, also Nachfolger / Vorgänger. Als durchschnittlicher Wachstumsfaktor wird n-1 Wurzel von  xn/x1]. Wachstum wird nicht allgemein erklärt und erörtert. Zu exponentiell gibt es mehrere Sachregister-Einträge: Exponentialfunktion 178f; - einfach modifizierte 179; Exponentialindex 151; Exponentialverteilung 272ff, - doppelte 307ff; Exponentielles Glätten 192ff, - Initialisierung 195, - konstantes Modell 193, - lineares Trendmodell 194, - saisonal nach WINTERS 194f.  Teil A, Kapitel 8 behandelt "Einführung in die Analyse und Prognose von Zeitreihen.".
    41. [S10] In Schweizer, Wilhelm Analysis kurz (1967) wird im Inhaltsverzeichnis ein "§ 6 Wachstumsfunktionen 24-27 [27 Aufgaben]" ausgewiesen. Darin werden die Abschnitte "Sprunghaftes Wachstum" (S.24), "Stetiges Wachstum" (S.25) und der Begriff "Organisches Wachstum" (S. 26) benannt. Im Sachregister wird angeführt: "Wachstum, sprunghaft 24, stetig 25, ''-sfaktor 24, ~sfunktion 24ff, 126, -ssatz 24, 26". Wachstum und wachsen wird nicht allgemein entwickelt und erörtert. Speziell wird Wachstum am Zinseszinsbeispiel ausgeführt. Quelle: Schweizer, Wilhelm (1967) Analysis kurz. Mathematisches Unterrichtswerk für höhere Schulen. 6. A. Nachdruck. Stuttgart: Klett.
    42. [B8] Spielmann, Raj (2020) Biomathematik : deterministische Modelle aus Evolutionsbiologie, Populationsgenetik und Epidemiologie. Berlin; Boston: De Gruyter [UB Volltext] Im Sachregister findet sich: "Wachstumsgrenze - bei Insekten 6". "Exponentiell" hat keinen Eintrag, wird im Text aber 5x gefunden, z.B. S. 169: die Wahrscheinlichkeitsfunktion einer geometrischen Verteilung nehme exponentiell ab.  Im Text wird "Wachstum" 9x gefunden, z.B.: ""  Wachstum und wachsen wird nicht allgemein erörtert und erklärt. [Inhaltsverzeichnis/ Sachregister]
    43. [B9] Timischl, Werner (2016) Mathematische Methoden in den Biowissenschaften : Eine Einführung mit R. 3., überarbeitete und erweiterte Auflage.  Berlin, Heidelberg: Springer Spektrum. [UB Volltext] Im Inhaltsverzeichnis wird "2.3.3  Logistisches Wachstum 79" angeführt. SR: Wachstum -allometrisches, 268; -dichtereguliertes, 208, 278, 282; -geometrisches, 208; Wachstumsrate, 64; -exponentielle, 224. -Pro Kopf-, 208. [Inhaltsverzeichnis.PDF] [Sachregister.PDF]. In dem umfangreichen Buch gibt es 113 Fundstellen zu "Wachstum". Eine Ausführung S. 64 kann man zwar in Richtung eines allgemeinen Wachstumsbegriffs interpretieren, weil hier die Änderung fokussiert wird: "Den Quotienten aus der Änderung pro Zeiteinheit und dem jeweiligen Wert der betrachteten Größe nennt man Wachstumsrate", aber eine allgemeine Erörterung und Erklärung des Wachstumsbegriffs erfolgt nicht. Manche im Text genannten Spezifika werden im Sachregister nicht aufgeführt, z.B. S. 433 "hyperbolisches Wachstum". "Exponentiell" hat keinen eigenen Eintrag im Sachregister, aber "Wachstumsrate, exponentielle".
    44. [A15]  Wikipedia  (Abruf 01.05.2021 Wachstum, Mathematik): "Wachstum bezeichnet die Zunahme einer bestimmten Messgröße im Zeitverlauf." Diese Bestimmung ist allgemein, wenn auch nicht an Beispieldaten ausführlich dargelegt. Ausführlicher sind dargelegt lineares, exponentielles, beschränktes, logistisches, quadratisches Wachstum.
    45. [A16] In Wygodskis Höhere Mathematik griffbereit  (1977) enthält das Sachregister keinen Eintrag zu "Wachstum" oder "wachsen".  Es gibt einen Sachregister-Eintrag zur Exponentialfunktion S. 278 zugewiesen, tatsächlich S. 279, die als eine von fünf Elementarfunktionen im Thema Klassifikation der Funktionen aufgeführt wird.
    46. [A20] Winter, Heinrich (1994) Über Wachstum und Wachstumsfunktionen. "Das Phänomen des Wachstums ist in Natur, Gesellschaft und Wirtschaft von einer derart eminenten Bedeutung und Tragweite, daß es für den Analysisunterricht geradezu ein Pflichtprogramm ist, die qualitativen Aspekte von Wachstumserscheinungen so klar wie möglich der Erfahrung und dem Verständnis zugänglich zu machen.“ Heinrich Winter (1994)" [Zitiert von Engel S. 145] Der mathematische und naturwissenschaftliche Unterricht 47(6), 330–339. S. 330 ganz am Anfang "1 Grundeigenschaften von Wachstumsfunktionen" wird der allgemeine Wachstumsbegriff nicht erörtert und erklärt, sondern schon vorausgesetzt: "Es sei f eine Funktion, die geeignet ist, das Wachstum einer Größe befriedigend zu modellieren. Es sei also bekannt, wie jedem definierten (i. a. positiven) Wert x (überwiegend der Zeit) ein (i. a. positiver) Wert y = f(x) zugeordnet ist. Der Definitionsbereich sei ein reelles nicht leeres Intervall, die Zielmenge IR. Ist  f(x) ein expliziter Rechenausdruck und f außerdem noch überall in seinem DefinitionsintervallD (mehrfach) differenzierbar, so können wir nach solchen Eigenschaften von f: D -> IR fragen, die fundamentale Aussagen über die Art des modellierten Wachstums ermöglichen, nämlich:  ... [S. 330: "1.1 Wachstumsgeschwindigkeit und - beschleunigung f' und f''"; S.331: "1.2 Wachstumssatz f'/f"; S 332: "1.3 Elastizität E(y.x)"; S. 333: "1.4 Verdoppelungszeit xV. ..."Es ist also die Gleichung  f(x + xV) = 2f(x) nach xV aufzulösen (Abb. 6). Üblicherweise wird nur bei exponentiellem Wachstum nach der Verdoppelungs (bzw. Halbierungs-, Halbewerts-)Zeit gefragt. Eine Überwindung dieser Einengung wäre förderlich."].



    Inhaltsverzeichnisse und Sachregister
    Bohl, Dürr & Ziegenbalg, Engel, Klemm, Peil, Spielmann, Winter.

    Bohl, Erich (2006) Mathematik in der Biologie. 4. vollständig überarbeitete und erweiterte A. Berlin: Springer.
    Das ist ein sehr informatives Buch, aber der Wachstumsbegriff wird, wie üblich in der Mathematik, nicht allgemein erklärt und erörtert.
     

      Inhaltsverzeichniseinträge mit expliziter Nennung:
        2.5.6 Exponentielles Wachstum   64
        3.3.6 Quantitative Analyse: exponentielles und logistisches Wachstum  89
        4.2.2 Wachstum einer Population auf einem Substrat   109
      Sachregistereinträge:
        Wachstum
            einer Population auf einem Substrat   108
            exponentielles   91
            logistisches   71, 91
        Wachstumsgeschwindigkeit   17 [nur Erwähnung, keine Rechnung oder Formel]
      Textvorkommnisse "Wachstum" 62, hier die ersten Beispiele.
      1. Vorwort 2. Auflage, S. XV: "So überzeugt der Ansatz: das Wachstum einer Population X geschieht proportional zu ihrem Umfang - es gewinnt durch steigende Anzahl der Individuen an Geschwindigkeit."
      2. XVI-1: "Entwicklung setzt Abhängigkeit von der Zeit voraus. Die in (0.3) auftretende Größe x(t) beschreibt die Veränderung des Umfangs x(t) von X in der Zeit. Eine nähere Analyse des Ansatzes (0.3) überzeugt davon, dass damit ein ungebremstes Wachstum der Population X im Laufe der Zeit t beschrieben wird, eine Situation, welche man in der Natur im Allgemeinen nicht beobachtet.
      3. XVI-2: "Das Wachstum einer Population ist begrenzt, muss sie doch im Verein mit anderen existieren und diesen Partnern Lebensraum im allgemeinen Sinne gewähren. Dazu gehören tatsächlicher Platz in der Natur, Nahrung, Licht usw. ..."
      4. XVI-3: "Allein das präzise Niederschreiben der Vorstellung Wachstum ist proportional zum Populationsumfang als Gleichung (0.3) und ihre Analyse führt dazu, dass unsere Vorstellungen ergänzt werden müssen.
      5. ... "

    Dürr, Rolf & Ziegenbalg (1984)  Dynamische Prozesse und ihre Mathematisierung durch Differenzengleichungen. Paderborn: Schöningh.

        Wachstum im Sachregister:

      Wachstum bei Selbstvergiftung 206
      Wachstum einer Bakterienkultur 225
      Wachstum, prozentuales 20
      Wachstumsfaktor 20
      Wachstumsprozesse 193
      Wachstumsrate, 195 def
      Wachstum, explosives 205
      Wachstum, exponentielles 199
      Wachstum, freies 199
      Wachstum, geometrisches 19, 199
      Wachstum, hyperexponentielles
      Wachstum, logistisches 201, 203 def
      Wachstum, logistisches mit Schwellenwert 212


        Kapitel VI im Inhaltverzeichnis:

      VI Wachstumsprozesse in rekursiver Darstellung 193
      § 25 Vorbemerkungen zu Fragen der Begriffsbildung: Abgrenzung der behandelten Problemkreise 193
      § 26 Einige Typen vorwiegend endogen erklärter Wachstumsprozesse von isolierten Populationen 197
        26.1 Freies Wachstum und Tilgungswachstum 198
        26.2 Logistisches Wachstum 201
        26.3 Ertrag, Phasenkurve, Gleichgewicht 203
        26.4 Wachstum bei Selbstvergiftung 206
      § 27 Einige Typen vorwiegend exogen erklärter Wachstumsprozesse von isolierten Populationen 210
        27.1 Sättigungswachstum 210
        27.2 Sättigungswachstum mit Schwellenwert 211
        27.3 Abhängigkeit der Zuwachsrate von der Populationsgröße; Linearisierung 213
      § 28 Zwei interagierende Populationen 216
        28.1 Räuber-Beute-Systeme (Modellbeschreibung) 217
        28.2 Gleichgewichtszustände in Räuber-Beute-Systemen 219
        28.3 Konkurrenz 223
      § 29 Modelle mit drei Populationen 225
        29.1 Wachstum und Absterben einer Bakterienkultur 225
        29.2 Stoffmengenänderungen bei chemischen Reaktionen 226

    [A17]Engel, Joachim (2010) Anwendungsorientierte Mathematik: Von Daten zur Funktion. Eine Einführung in die mathematische Modellbildung für Lehramtsstudierende. Berlin, Heidelberg: Springer. [UB-Volltext] Ein umfassendes Werk besonders auch zu Wachstumsvorgängen. Im IV und im Sachregister gibt es viele Einträge zu "Wachstum". Im Text selbst gibt es zu "Wachstum" 336 Fundstellen mit vielen informativ-interessanten Standardmodellen und Beispielen (Abschnitt 2.2., S. 39-42). Ganz allgemein S. 145: "Der einfachste Modellansatz lautet: Neue Populationsgröße = alte Populationsgröße + Änderung. Damit ist klar, dass die Änderung auch negativ sein kann und der Begriff  'Wachstum' auch ein Schrumpfen oder Zerfallen mit einschließt."

        Inhaltsverzeichnis

      Vorwort     VII

      1 Was heißt: "Mathematik anwenden“?   1
      1.1 Was ist Modellbilden?   4
      1.2 Modellieren funktionaler Abhängigkeiten   17
      1.3 Überblick über die folgenden Kapitel   18
      1.4 Rolle von realen Daten   20
      1.5 Rolle von Software und Multimedia   23

      2 Standardmodelle und Naturgesetz   29
      2.1 Einleitung   31
      2.2 Einige Standardmodelle im Überblick   39
      2.3 Spezielle Eigenschaften einiger Standardmodelle   44
      2.3.1 Proportionalität und lineare Funktionen   44
      2.3.2 Antiproportionalität   49
      2.3.3 Polynome und Potenzfunktionen   58
      2.3.4 Exponential- und Logarithmusfunktionen   69
      2.3.5 Winkelfunktionen   77
      2.4 Techniken zum Modellieren mit Funktionen   88
      2.4.1 Operationen mit Funktionen   89
      2.4.2 Logistische Funktionen   91
      2.4.3 Sinus Hyperbolicus und Cosinus Hyperbolicus   95
      2.4.4 Verketten von Funktionen   97
      2.4.5 Transformation der Achsen   99
      2.4.6 Ockhams Rasiermesser, Platons Bart und die Warnung vor zu viel Komplexität   104

      3 Lass die Daten sprechen   109
      3.1 Einleitung   111
      3.2 Lineare Interpolation   112
      3.3 Interpolation durch Polynome   113
      3.3.1 Lagrange-Polynome   118
      3.3.2 Newton-Polynome   121
      3.3.3 Maximale Geschwindigkeit und Beschleunigung des Sprinters   125
      3.3.4 Interpolationsfehler   127
      3.4 Splines   132
      3.4.1 Minimaleigenschaft   136
      3.4.2 Konvergenzverhalten von Splines   138

      4 Die Grenzen des Wachstums   143
      4.1 Einleitung   145
      4.2 Diskrete Modellierung von Wachstumsprozessen   146
      4.2.1 Lineares Wachstum   147
      4.2.2 Quadratisches Wachstum   148
      4.2.3 Freies oder exponentielles Wachstum   150
      4.2.4 Graphische Iterationen und Spinnwebdiagramme   151
      4.2.5 Begrenztes Wachstum   152
      4.2.6 Logistisches Wachstum   154
      4.2.7 Zeitverzögertes Wachstum: Ein Beispiel   157
      4.2.8 Ein Mordfall   161
      4.3 Logistische Differenzengleichung und Chaos   167
      4.3.1 Exkurs: Mathematische Analyse der logistischen Differenzengleichung   170
      4.3.2 Zusammenfassung   173
      4.4 Diskrete Modellierungen gekoppelter Populationen   175
      4.4.1 Masernepidemien   175
      4.4.2 Populationen in Wechselwirkung   179
      4.5 Stetige Modellierungen von Wachstumsprozessen   187
      4.5.1 Exkurs Lösen von Differenzialgleichungen   191
      4.5.2 Logistisches Wachstum   196
      4.5.3 Weitere Wachstumsformen   201
      4.6 Stetige Modellierung gekoppelter Systeme   207
      4.6.1 Epidemien   207
      4.6.2 Population in Wechselwirkung: Stetige Version   209
      4.6.3 Der Kampf ums Dasein: Räuber-Beute-Modelle   211

      5 Verrauschte Signale und funktionale Modelle   219
      5.1 Einleitung   221
      5.2 Prinzip der kleinsten Quadrate: Regressionsgerade   227
      5.3 Eigenschaften der Regressionsgeraden   234
      5.4 Korrelation   244
      5.5 Varianzanalyse   249
      5.6 Regression und Lineare Algebra   256
      5.7 Nichtlineare Zusammenhänge: Der Transformationsansatz  262
      5.8 Funktionsanpassung logistischer Modelle   273
      5.9 Grundzüge der nichtlinearen Regression   277
      5.9.1 Spezialfall: Lineare Regression   279
      5.9.2 Der allgemeine Fall   280
      5.9.3 Der Gauß-Newton-Algorithmus   282
      5.9.4 Zur Konvergenz des Gauß-Newton-Algorithmus   285
      5.9.5 Der Gauß-Newton-Algorithmus für einparametrige Funktionen  286
      5.10 Zusammenfassung: Parametrische Kurvenanpassung   297

      6 Durch Glätten der Daten zur Funktion   305
      6.1 Einleitung   307
      6.2 Bivariate Verteilungen, gleitende Boxplots und Regressogramm   308
      6.3 Gleitende Mittelwerte   314
      6.4 Zeitreihen   317
      6.5 Von der gleitenden Mittelwertkurve zum Kernschätzer   322

      7 Nichtparametrische Methoden zum Kurvenschätzen  333
      7.1 Einleitung   335
      7.2 Kernschätzer unter festem Design   337
      7.2.1 Faltungsschätzer: Definition und Beispiele   337
      7.2.2 Mathematische Eigenschaften: Bias, Varianz   342
      7.2.3 Wahl der Kernfunktion K   347
      7.2.4 Wahl der Bandbreite   351
      7.2.5 Randverhalten   355
      7.3 Kernschätzer unter zufälligem Design   360
      7.4 Lokal-lineare Approximation   363
      7.5 Lokal-polynomiale Anpassung   368
      7.6 Ergänzungen und Vertiefungen   371
      7.6.1 Zur Asymptotik des lokal-polynomialen Schätzers  371
      7.6.2 Schätzen von Ableitungen   375
      7.6.3 Glätten ohne parametrischen Bezug   377
      7.6.4 Glätten mit Splines   379
      7.6.5 Komplexere Modelle   381
      7.7 Zusammenfassung  385

      A Beschreibung der Datensätze   389
      B Anmerkungen zur Software   419
      B.1 Fathom   421
      B.2 Excel   436
      B.3 R   437
      C Lösungen zu ausgewählten Aufgaben   441
      Literatur   459
      Sachverzeichnis   465


    Im Sachregister finden sich folgende Einträge
        Wachstum

      Begrenzt   91
      begrenzt   152, 191
      exponentiell   150, 190
      linear   147, 189
      Logistisch   273
      logistisch   154, 196
      quadratisch   148
      selbstvergiftet   203
      vergiftet   202, 203
      zeitverzögert   157
    Wachstumsfaktor   147
    Wachstumsintensität   200
    Wachstumsrate   147


    Klemm, Peter G. (1993) Keine Angst vor Biomathematik: medizinische Statistik ohne Formeln. 1. Aufl. Berlin: Ullstein Mosby. "Wachstum" und "wachsen" kommen im Inhaltsverzeichnis und im Sachregister nicht vor.
       
      Inhaltsverzeichnis
      Vorwort   9

      1 Der schlechte Ruf der Statistik   11

      2 Ein paar Worte über Mengen   15

      3 Medizinalstatistik   19
      3.1 Ziffern, Zahlen und Kennziffern   21
      3.1.1 Schwierigkeiten mit Anteilziffern - Strukturen   24
      3.1.2 Die drehbaren Verhältnisziffern   31
      3.1.3 Indexziffern gehen mit der Zeit   32
      3.2 Von der Wiege bis zum Grabe   36
      3.2.1 Ein Mensch erblickt das Licht der Welt   38
      3.2.2 Säuglingssterblichkeit und Lebenserwartung   42
      3.2.3 Wie krank sind wir eigentlich? — Der Mensch und der Fall   47
      3.2.4 Bloß so stirbt keiner — Todesursachenstatistik   52

      4 Epidemiologie   57
      4.1 Alles bewegt sich, auch die Krankheit   59
      4.1.1 Bewegungsmengen und Bewegungsgrößen   61
      4.1.2 Rein in die Krankheit — raus aus der Krankheit   64
      4.2 Lebt der Mensch gefährlich? - Gesundheitsrisiken  70
      4.2.1 Wer sich in Gefahr begibt   72
      4.2.2 Der große Popanz: die Risikofaktoren   75

      5 Biometrie   81
      5.1 Gesetze des Zufalls   82
      5.2 Der Einzelfall ist nichts, die Verteilung ist alles   84
      5.2.1 Was fängt man mit Parametern an?   88
      5.2.1.1 Mittelwerte   89
      5.2.1.2 Streuungsmaße   91
      5.2.1.3 Zusammenhangsmaße   93
      5.2.1.4 Regression   96
      5.3 Ohne Vergleich keine Wissenschaft   100
      5.3.1 Alles oder nichts? — Vom Nutzen der Stichproben   102
      5.3.2 Stichprobengröße und Stichprobengüte   106
      5.3.3 Die Logik statistischer Tests   111
      5.3.4 Vom Nutzen des Zweifels —  Die Irrtums Wahrscheinlichkeit  114
      5.3.5 Wie man sich doch irren kann   116
      5.3 6 Das magische Wort „signifikant“   118
      5.3.6.1 Das Triviale und das Unerwartete   120
      5.4 Was prüft man eigentlich?   121
      5.4.1 Differenzen   123
      5.4.2 Korrelationen und Kontingenzen   126
      5.5 In höheren Sphären   129
      5.5.1 Varianzanalyse   129
      Faktorenanalyse   131
      Clusteranalyse   139
      Diskriminanzanalyse   141
      6 Der Wortbruch - doch noch ein paar Formeln   145
      Sachwortverzeichnis


    Peil, Jürgen (1985) Grundlagen der Biomathematik. Frankfurt aM: Harri Deutsch.
        SR Einträge:
      Wachstum. 162 [e-Funktion], 219 [allgemeine Erwähnung], 222 [Erwähnung Wachstum von Populationen], 224 [biokybernetische Modellierung von Wachstumsprozessen in Fußnote 1], 240 ["2. Wachstum multizellulärer Lebewesen ..."], 245 [Aufgaben zu verschiedenen Wachstumsparametern], 268f [Ausdruck "Wachstum" S. 268 nicht gefunden, S. 269 "< /g Körperlängenwachstum"], 281 [Wachstumskinetik von Weizenkeimlingen; Einfluss Wirkstoffkonzentration auf das Wachstum; Erwähnung Wachstumsvorgänge; ], 304 [Ausdruck "Wachstum" S. 304 nicht gefunden], 343 ["... auch in den Beispielen für Wachstum (vgl. 3,3,1.3) ..."], 347 ["3.3.13. Differentialgleichungen des Wachstums von Populationen und Organismen"]; [im SR nicht ausgewiesen: 348-350 mehrere Ausführungen]; 351 ["Anmerkung 1: Wachstumsdifferentialgleichungen", auch Anmerkung 2], 353 [Ausführungen zu wechselwirkenden Populationen; Fußnote 1 "Neuere Ansätze der Modellierung von Wachstumsvorgängen ..."], 362 [Gompertzsche Wachstumsdifferentialgleichung], [369 im SR nicht eingeführt: "Richtungsfeld der (Wachstums)Differentialgleichung ..."]; 376 [Ausdruck "Wachstum" S. 376 nicht gefunden], 378 [Literaturhinweis: Knorre 1971 Wachstum von Mikroorganismen ...], 381 ["Wachstumsuntersuchungen"], 427 ["... deterministische Komponente des (Wachstums-)Verlaufs ..."]
      -, allometrisches   381
      -, exponentielles   348f.
      -, logistisches   349, 356, 362
      Wachstumsdifferentialgleichung   348f., 351, 372, s. auch Wachstumsgesetz
      -, Bertalanffysche   240, 349
      -, Gompertzsche   352f., 362, 365, 380, 382
      -, logistische   368
      Wachstumsfunktion   170, 352
      -, Gompertzsche   349f., 352f.
      -, logistische   170, 245
      Wachstumsgeschwindigkeit   240, 269, 348, 351, 381
      Wachstumsgesetz   245, s. auch Wachstumsdifferentialgleichung
      -, Gompertzsches   382
      -, logistisches   245, 349, 351ff., 355f.
      -, Verhulstsches   345, 349 .
      Wachstumsgröße   240, 245, 348, 350f., 365, 373, 881f., 423
      Wachstumskurve   350
      Wachstumsmodell   350f.
      Wachstumsprozeß   143, 150, 162, 167, 170, 224, 240, 281, 349ff., 362, 367, 369
      Wachstumsrate   240, 348, 352, s. auch Wachstumsgeschwindigkeit
      Wachstumsrate, spezifische   348 bis 353, 362, 381
      Wachstumsschub   224, 245
      Wachstumsterm   349ff.
       
    Spielmann, Raj (2020) Biomathematik : deterministische Modelle aus Evolutionsbiologie, Populationsgenetik und Epidemiologie
    Berlin, Boston: De Gruyter [UB Volltext] Im Sachregister findet sich: "Wachstumsgrenze - bei Insekten 6". "Exponentiell" hat keinen Eintrag. Im Text wird "Wachstum" 9x gefunden.
     
      Inhalt
      Vorwort — V

      1 Die Mathematik des Stoffwechsels — 1
      1.1 Stoffwechselraten-Gesetze   1
      1.2 Triebfedern der Evolution   7
      1.3 Ein hierarchisches Versorgungssystem   10
      1.4 Anpassung und ökogeografische Regeln   15
      1.5 Biologische Uhren   18
      1.6 Medikamente und ihre Wirkdauer   23

      2 Risiken, Mutationen und Immunitäten — 33
      2.1 Das Hardy-Weinberg-Gesetz   33
      2.2 Neubewertung von Mutationen   34
      2.3 Zeitverlauf bei positiver Selektion   37
      2.4 Erbkrankheiten   43
      2.5 Heterozygote Vorteile   46
      2.6 Zeitverlauf bei negativer Selektion   60
      2.7 Heterozygote Nachteile   63

      3 Gene, Umwelt und Gesellschaft — 69
      3.1 Das Wright-Fisher-Modell   69
      3.2 Verlustrisiken bei Isolation   75
      3.3 Koaleszenz   77
      3.4 Evolutionäre Chancen der Frühgeschichte   82
      3.5 Individuum und Inzucht   85
      3.6 Mutationen vs. Gendrift   101
      3.7 Der Flaschenhals-Effekt   104

      4 Endemien, Epidemien und Virulenz —113
      4.1 Das SIR-Modell und die Herdenimmunität   113
      4.2 Eine Episode aus der Kolonialmedizin   117
      4.3 Optimale Virulenz   124
      4.4 Konkurrenz unter Parasiten   133
      4.5 Von der Neolithischen Transition zur Globalisierung  138

      A Grundlegende Definitionen und Formeln —151
      A.l Skalengesetze   151
      A.2 Ausgleichsrechnung   152
      A.3 Mengenlehre und Kombinatorik   153
      A.4 Zahlenfolgen und Summenformeln   155
      A.5 Grenzwerte   156
      A.6 Reihenentwicklungen und Näherungsformeln   156
      A.7 Fixpunktsatz von Banach   157
      A.8 Stabilität von Fixpunkten   157

      B Überblick zu Wahrscheinlichkeiten —159
      B.1 Ereignisse und Wahrscheinlichkeiten   159
      B.2 Bedingte Wahrscheinlichkeit und Unabhängigkeit   162
      B.3 Formel von Bayes   163
      B.4 Totale Wahrscheinlichkeit   164
      B.5 Zufallsgrößen   165
      B.6.Geometrische Verteilung   168
      B.7 Binomialverteilung   170
      B.8 Poisson-Verteilung   172

      Bildrechte —175
      Literatur   177
      Stichwortverzeichnis —185


    Winter, Heinrich (1993) Mathematisches Grundwissen für Biologen. Mannheim: BI. Das ist ein sehr informatives Buch, aber der Wachstumsbegriff wird nicht, wie üblich in der Mathematik, allgemein erklärt und erörtert.

        Inhaltsverzeichnis:
     

      1 Form und Grösse   7
          1.1 Ähnlichkeit   8
          1.2 Die Massigkeit   12
          1.3 Die Massigkeit in der Biologie   14
              1.3.1 Wärmehaushalt   14
              1.3.2 Sprung vermögen   16
              1.3.3 Knochenfestigkeit   17
              1.3.4 Schlankheitsgrad   19
          1.4 Zerteilen und Zergliedern   21
          1.5 Fraktale und Selbstähnlichkeit   26

      2 Diskretes Wachstum, Folgen und Reihen   31
      2.1 Exponentielles Wachstum, geometrische Folgen   32
      2.2 Lineares Wachstum   44
      2.3 Logistisches Wachstum   48
      2.4 Fibonacci-Folgen   51
      2.5 Folgen und Folgenkonvergenz   55
      2.6 Ein Blick ins Chaos   57

      3 Vollständige Induktion   63
      3.1 Unvollständige und vollständige Induktion   64
      3.2 Beispiele zur vollständigen Induktion   68
      3.3 Der binomische Lehrsatz   73
      3.4 Die Siebformel   80

      4 Kombinatorik und Wahrscheinlichkeit   83
      4.1 Kombinatorische Grundformeln   84
      4.2 Klassische Wahrscheinlichkeitsrechnung   94
      4.3 Elementare Wahrscheinlichkeitsaufgaben   99
      4.4 Die Binominalverteilung   102
      4.5 Das Hardy-Weinberg-Gesetz   108

      5 Lineare und quadrat. Funktionen   115
      5.1 Lineare Funktionen und Verwandte   116
      5.2 Quadratische Funktionen und Gleichungen   123
      5.3 Varianz   128
      5.4 Flächeninhalt unter der Parabel   130
      5.5 Lineare Regression   133

      6 Polynomfunktionen   139
      6.1 Kasten maximalen Volumens   140
      6.2 Funktionen vom Typ f(x) = xn   143
      6.3 Differentiationsregeln   145
      6.4 Kurvendiskussion   149
      6.5 Beispiele für Extremwertaufgaben   156

      7 Rationale Funktionen   161
      7.1 Die Funktion y = /(#) = 4   162
      7.2 Weitere Ableitungsregeln   165
      7.3 Kurvendiskussion   171
      7.4 Angewandte Extremwertaufgaben   174

      8 Wurzelfunktionen, Potenzfunktionen   179
      8.1 Wurzelfunktion und Umkehrregel   180
      8.2 Die verallgemeinerte Potenzregel   183
      8.3 Die Bienenwabenaufgabe   185
      8.4 Allometrisches Wachstum   187
      8.5 Weitere Extremwertaufgaben   190

      9 Exponential- und Logarithmusfunktionen   193
      9.1 Einführung   194
      9.2 Spezielle Exponentialfunktionen   197
      9.3 Eulersche Zahl   199
      9.4 Die Funktion f(x) = es   202
      9.5 Die allgemeine Exponentialfunktion   204
      9.6 Beispiele exponentiellen Wachstums   206
      9.7 Die logistische Funktion   208
      9.8 Logarithmusfunktionen   210
      9.9 Anwendungen   212

      10 Kreisfunktionen   219
      10.1 Periodische Vorgänge   220
      10.2 Die sinus - Funktion   221
      10.3 Periodische Funktionen   227
      10.4 Die Arcusfunktionen als Umkehrfunktionen   231
      10.5 Anwendungen der trigon. Funktionen   233
      10.6 Oszillierende Funktionen   239

      11 Einblick in die Integralrechnung   243
      11.1 Das unbestimmte Integral   244
      11.2 Das bestimmte Integral   246
      11.3 Eigenschaften des bestimmten Integrals   251
      11.4 Hauptsatz (HDI)   255
      11.5 Integrationsmethoden   260

      12 Anwendungen der Integralrechnung   271
      12.1 Geometrische Grössen   272
      12.2 Schwerpunkt ebener Flächen   287
      12.3 Integration und Wahrscheinlichkeit   290
      12.4 Beispiele aus der Physik   302

      13 DGL. der Populationsdynamik   311
      13.1 Richtungsfelder   312
      13.2 Formen des ungebremsten Wachstums   315
      13.3 Formen des gebremsten Wachstums   322
      13.4 Das Räuber-Beute-Modell   332

      Symbol Verzeichnis   340
      Literaturverzeichnis   341
      Liste von Beispielen   343
      Stichwortverzeichnis   345
       

        Sachregister:
      Exponentialfunktion,
          allgemeine,   204
      exponential verteilt,   299
      exponentielles Wachstum, [32 "Die [Verdoppelungs] Folge wächst nicht gleichmäßig in dem Sinne, dass nach jedem Schritt immer wieder derselbe Betrag dazu kommt, vielmehr wächst das, was dazu kommt, ebenfalls von Schritt zu Schritt, sogar nach demselben Gesetz. ... Die Folge wächst beschleunigt."],   33, 316
      Wachstum
          allometrisches,   187, 314
          exponentielles,   33, 36, 316
          gebremstes,   322
          geometrisches,   34
          lineares,   44, 316
          logistisches,   48, 208, 326, 328
          polynomisches,   317
          quadratisches,   317
          überexponentielles,   319
          ungebremstes,   315
          vergiftetes,   323
        Wachstumsfaktor,   34, 198
        Wachstumssatz,   36, 50
      mittlerer,   198
      momentaner,   199



    Weitere Informationen

    Literatur

    Links

    Medien


    Glossar, Anmerkungen und Fußnoten > Eigener wissenschaftlicher Standort > Weltanschaulicher Standort
    1) GIPT= General andIntegrative Psychotherapy, internationale Bezeichnung für Allgemeine und Integrative Psychotherapie.
    __
    __

    Querverweise
    Standort: Wachstum.
    *
    Beweis und beweisen in Wissenschaft und Leben.
    Überblick: Abstrakte Grundbegriffe aus den Wissenschaften.
    Wissenschaft in der IP-GIPT.
    *
    Suchen in der IP-GIPT, z.B. mit Hilfe von "google": <suchbegriff> site: www.sgipt.org
     * Logik site: www.sgipt.org * Analogie site: www.sgipt.org *
    *
    Dienstleistungs-Info.
    *
    Zitierung
    Sponsel, Rudolf  (DAS). Wachstum. Analyse eines grundlegenden Begriffs in Wissenschaft und Leben mit Schwerpunkt Wachstum in der Mathematik. Aus unserer Abteilung Arbeiten zur Definitionslehre, Methodologie, Meßproblematik, Statistik und Wissenschaftstheorie besonders in Psychologie, Psychotherapie und Psychotherapieforschung. Internet Publikation  für Allgemeine und Integrative Psychotherapie IP-GIPT. Erlangen: https://www.sgipt.org/wisms/gb/Wachstum/wachstum0.htm
    Copyright & Nutzungsrechte
    Diese Seite darf von jeder/m in nicht-kommerziellen Verwertungen frei aber nur original bearbeitet und nicht  inhaltlich verändert und nur bei vollständiger Angabe der Zitierungs-Quelle benutzt werden. Das direkte, zugriffsaneignende Einbinden in fremde Seiten oder Rahmen ist nicht gestattet, Links und Zitate sind natürlich willkommen. Sofern die Rechte anderer berührt sind, sind diese dort zu erkunden. Sollten wir die Rechte anderer unberechtigt genutzt haben, bitten wir um Mitteilung. Soweit es um (längere) Zitate aus  ...  geht, sind die Rechte bei/m ... zu erkunden oder eine Erlaubnis einzuholen.
    Ende    _ Wachstum_Datenschutz_ Überblick_Rel. Aktuelles _Rel. Beständiges_ Titelblatt_ Konzept_ Archiv_Region_ Service iec-verlag_ Mail: sekretariat@sgipt.org_ _ Wichtige Hinweise zu externen Links und Empfehlungen.
    _
    korrigiert: irs 20.08.2021 Rechtschreibprüfung ; irs 23.05.2021 Rechtschreibprüfung; 15. / 16.05.2021


    Änderungen wird gelegentlich überarbeitet, ergänzt und vertieft * Anregungen und Kritik willkommen
    20.09.21 Korrekturen bei den Intensivbettbelegungen 16.9.-19.9.21
    ... 08.21   Aktualisierungen Kurvenfits: Der 10. Welle, 1.7.21-....
    06.08.21    Aktualisierung 5.8.21  Corona De: exponentielle Entwicklung hält an.
    05.08.21    Aktualisierung 4.8.21  Corona De: exponentielle Entwicklung hält an.
    04.08.21    Aktualisierung und Korrektur der gestrigen Falschmeldung.
    03.08.21    Kurvenfitvergleich 10. Welle (RKI Sprech 4. Welle) Deutschland 0.1.07.-02.08.2021: Exponentielle Entwicklung gebrochen. [FALSCH]
    01.08.21    Kurvenfitvergleiche.
    23.07.21    Organisches Wachstum.
    22.07.21    Zinses-Zins-Modell.
    15.07.21    Hinweis auf die exponentielle Entwicklungsstudie der 4. Welle in Großbritannien.
    29.05.21    Kurvenfitstudie Schweden 3. große Welle.
    26.05.21    Bayern-Fit-Vergleiche
    25.05.21    Nach rund 2 Monaten Arbeit die Grundversion erstmals ins Netz gestellt. Die Seite wird weiter entwickelt.
    28.03.21    angelegt.

    Alte-Rechnung-2
    Anteil 7TM-Intensivbehandlungen an den 7TM-Neu-Infektionen [alte Rechnung]
     
    Kommentar 05.01.2022

    Die Verhältnisberechnung 7TM der Intensivbehandlungen zu den 7TM Mittelwerten der Neuinfektionen war bei der 10.  Welle als Vorlaufs- indikator informativ, weil der fallende Gipfel ca. 14 Tage vorher auf den nahenden Gipfel der 7TM der Neu-Infektionen hinwies.

    Das hat sich bei der 11. Welle geändert, wo der Vorlauf graphisch kaum erkennbar auf einen Tag zusammengeschmol- zen ist. Allerdings fällt der Anteil viel steiler als der 7TM.
     
     
     
     
     
     
     
     
     
     

     
    _
    Alte Rechnung Verlauf Intensivbehandlungen.
     
    Kommentar

    Die Verhältnisberechnung 7TM der Intensivbehandlungen zu den 7TM Mittelwerten der Neuinfektionen ist informativ, weil sie einen Hinweis liefert, ob der Gipfel der 7TM der Intensivbehandlungen der betrachteten Phase erreicht sein könnte. 
    _
    _
    _
    _
    _
    _
    Man sieht, dass die Prozentverhältniszahl seit dem 26.8.21 fällt, obwohl die 7TM der Intensivbehandlungen noch bis zum 09.09.2021 ansteigt. Das sind gut 14 Tage.

    Angewandt auf die aktuelle Situation bedeutet das, dass das Prozentverhältnis noch keinen Hinweis darauf liefert, dass der aktuelle Gipfel erreicht sein könnte. 
    _