Internet Publikation für Allgemeine und Integrative Psychotherapie
(ISSN 1430-6972)
IP-GIPT DAS=09.06.2006 Internet-Erstausgabe, letzte Änderung: 18.01.20
Impressum: Diplom-Psychologe Dr. phil. Rudolf Sponsel  Stubenlohstr. 20    D-91052 Erlangen
Mail: sekretariat@sgipt.org_ Zitierung & Copyright

---

Anfang_Kommunalität_ Überblick  _ Relativ Aktuelles  _ Rel. Beständiges  _ Titelblatt  _ Konzept  _  Archiv  _ Region _ Service iec-verlag __Wichtige Hinweise zu Links und Empfehlungen

---

Willkommen in der Abteilung Wissenschaftstheorie, Methodologie und Statistisch-Mathematische Methoden
in der Allgemeinen und Integrativen Psychologie, Psychodiagnostik und Psychotherapie, hier:

Kommunalität
- Communality -

Zur Geschichte und Kritik einer Idee und ihrer fragwürdigen Operationalisierung
Von der multiplen Paradoxie wie willkürliche Definitionen unlösbare Scheinprobleme schaffen und lösen.

von Rudolf Sponsel, Erlangen
_

Überblick Abstract - Zusammenfassung - Summary.     Graph: Vergleich der Kommunalitätsmodelle.     Grundwiderspruch.     Fazit. Einführung.    Zur Geschichte des Begriffs.    Thurstones Figure 2.    Kritik an Thurstones Figure 2.    Kommunalitätszerlegung einer Korrelationsmatrix.    Thurstones Beispiel zu einer Kommunalitätsmatrix  (Figure 7 und 8).    Rangreduktion auf 1 im Generalfaktorbeispiel einer 10x10 Extraversionsmatrix.    Diskussion.    Exkurs 1.10.12: Proberechnungen zur Prüfung der positiven    Semidefinitheit Kommunalitätsmatrizen mit Determinations-    statt Korrelationskoeffizienten. Literatur (Auswahl).    Literatur zur Geschichte der Faktorenanalyse.  Anmerkungen:    Absurdität, Antinomie, Aporie, Konfusion, Paradoxie, ....     Fehlerfaktoren.     Variablenreduktion.    Kommunalitäts-Definitionen in der Faktorenanalyse Literatur:         Encyclopedia of Statistical Sciences.        Fernuni Hagen.        Überla zum Begriff.        Zum Begriff gemeinsamer und spezifischer Faktor.          Kritische Anmerkung.        Kritisches von Überla.    Abstracts von kritischen Beiträgen zur Faktorenanalyse:        Fischer * Guttman * Kallina, 1000 Billionen Zellen * Kalveram 1,         Haagen & Oberhofer zu Kalveram 1,         Sponsel zu Haagen & Oberhofer * Heywood * Kalveram 2 *         Kalveram 3   * Kalveram 4 *  Kempf * Lukesch & Kleiter * Orlik *         Rinne * Sixtl     unendlich viele Möglichkeiten der Reproduktion.      operationale Definition.     homo ludens psychomathematicus.     Hauptkomponentenmethode.     Rang.      Thurstones Bedeutung aus der Perspektive Harmans.      Geschichte, Pioniere und Gestalter der Faktorenanalyse:        Albert * Bargmann * Burt * Cattell, R.B. * Eckart * Guttman * Harman *       Holzinger * Horst * Hotelling * Householder * Jöreskog * Kaiser * Kelly *       Kalveram * Lawley, D.N.  * Lederman * Maxwell, A.E.  * Pawlik * Pearson *       Rao, C.R. *   Spearman * Thomson  * Tucker * Thurstone  * Young, G.  *     Literatur zur Geschichte der Faktorenanalyse.   Querverweise.

Abstract - Zusammenfassung - Summary
 

Die Kommunalitätsmatrix ist ein Bastard (Hybrid), weil sie in ihren Größen in der Faktorenanalyse nicht homogen ist. Während in der Hauptdiagonale mit den Kommunalitätenschätzern h2 - meist die quadrierten multiplen Korrelationskoeffizienten - 2er-Potenzgrößen, nämlich Varianzen eingetragen werden, stehen in den Zellen außerhalb 1er-Potenzgrößen, nämlich die linearen Korrelationskoeffizienten. Homogenität ließe sich auf zwei Arten herstellen: (1) alle Größen als 1er-Potenzgrößen, also die Korrelationsmatrix mit 1en in der Hauptdiagonale - so wie wir sie kennen. (2) Oder alle Größen als 2er-Potenzgrößen, dann müssen in den Zellen außerhalb der Hauptdiagonale ebenfalls 2er-Potenzgrößen stehen, also z.B. die Determinationskoeffizienten, das sind die Quadrate der Korrelationskoeffizienten.       Bei (2) entginge man in der Bastard-Variante aber trotzdem nicht dem unüberwindlichen Problem aller Kommunalitätsmatrizen mit Hauptdiagonalelementen < 1, dass die Kommunalitätsmatrix im allgemeinen weder der Korrelationsmatrix mathematisch ähnlich ist noch die Minimalforderung einer positiv semidefiniten Matrix erfüllt (Lauwerth 1980, Kap.6).       Einige Proberechnungen aus reiner Neugier haben tatsächlich ergeben, dass Kommunalitätsmatrizen mit den Determinations- statt Korrelationskoeffizienten außerhalb der Hauptdiagonale positiv semidefinit waren (falls die Ausgangsmatrix positiv semidefinit und nicht indefinit ist; bei der indefiniten Spearman & Hart Matrix ist es misslungen), was mathematisch nichts bedeuten muss. Aber auch hier gilt: die Kommunalitätsmatrix ist in keinem Fall wegen der eingebüßten mathematischen Ähnlichkeit eine Repräsentation der ursprünglichen Korrelationsmatrix. Und in diesem Falle schon gar nicht, weil quadratische Größen etwas qualitativ anderes sind als lineare. Vielleicht liegt das Scheitern der Lösung des sog. "Kommunalitätenproblems" seit nunmehr 86 Jahren in dieser grundlegenden  Fehlkonstruktion begründet.

Idee und Begriff der Kommunalität als Anteil der Varianz gemeinsamer Faktoren ist grundsätzlich verständlich und wissenschaftlich interessant, wenn auch der Nutzen, das Modell und vor allem die Modell-Interpretation gar nicht klar sind. Das Grundmodell der Faktorenanalyse von Thurstone geht von drei Faktortypen aus: gemeinsamen (g), spezifischen (s) und Fehlerfaktoren (e). Spezifische und Fehlerfaktoren werden von Thurstone ohne Angabe von näheren Gründen zu den Uniqueness-Faktoren zusammengefasst, so als ob die gemeinsamen Faktoren keine Fehler hätten. Theoretisch ist es möglich, dass jeder dieser drei Faktoren (g, s, e) unterschiedlich ausgeprägt in einer Variable und unterschiedlich verteilt zwischen den Variablen sein kann, wobei mögliche Stichprobeneffekte an dieser Stelle nicht zusätzlich komplizierend berücksichtigt werden sollen. In jede Korrelation gehen per Voraussetzung und Modellansatz gemeinsame Faktoren (g), spezifische Faktoren (s) und Fehler (e) ein. Mathematische Grundlage der Faktorenanalyse ist die Faktorisierung einer - gewöhnlich nicht-singulären - Matrix, sie ist immer möglich, und durch die Multiplikation von orthogonalen Matrizen gibt es zusätzlich immer unendlich viele Möglichkeiten der Reproduktion. Außerdem fand Thurstone, dass eine Rangreduktion durch Manipulation der Hauptdiagonalelemente in einer Korrelationsmatrix möglich ist, zum Teil bis auf Rang 1 reduzierbar. Thurstone zeigt selbst, dass die Koeffizienten außerhalb der Hauptdiagonalen bei einer 8x8 Matrix durch 2 Faktoren bei geeigneter Hauptdiagonalmanipulation perfekt reproduziert werden können (ich habe das Beispiel nachgerechnet und dokumentiert). Und ich zeige selbst am Beispiel einer Extraversionsmatrix, wie die Koeffizienten außerhalb der Hauptdiagnonalen bei einer 10x10 Matrix durch einen einzigen Generalfaktor, also sogar Reduktion auf Rang 1, bis auf die dritte Nachkommastelle genau reproduziert werden können. Kommunalität ist klar und eindeutig definiert bei Thurstone als Quadratsumme der Faktorenladungen, aber ist diese nominalistische Operationalisierung oder operationale Definition auch angemessen? Erreicht sie ihre Ziele und Zwecke? Das Kommunalitätsmodell von Thurstone liefert eine Kommunalitätsmatrix mit Rang k <= m, die die Koeffizienten außerhalb der Hauptdiagonalen der Korrelationsmatrix praktisch hinreichend genau zu reproduzieren gestattet. Die mathematisch-technische Realisation ist zwar möglich, aber nur um den Preis eines Modelles, das sein Grundanliegen durch einen definitorischen Willkürakt "löst" und nicht vernünftig interpretierbar ist:

Vergleich der Kommunalitätsmodelle



Grundwiderspruch: Wieso sollte die Wirkung eines spezifischen Faktors nur auf die Interkorrelation der Variablen mit sich selbst und nicht auch in der Interkorrelation mit anderen wirksam werden? Entweder modelliert und manipuliert man also alle Koeffizienten oder keinen und bleibt bei der mathematisch fundierten Hauptkomponentenmethode. Unglücklicherweise wurde von Thurstone und den FaktorenanalytikerInnen von Anfang an nicht sehr klar getrennt zwischen den Faktorenladungen der Kommunalitätsmatrix und den Faktorenladungen der Korrelationsmatrix und zusätzlich komplizierend das Kommunalitätsproblem mit dem Problem der Variablenreduktion u.a. vermischt, obwohl es damit, grundsätzlich betrachtet, gar nichts zu tun hat. Denn das Problem, welches sind die Anteile gemeinsamer und spezifiischer Faktoren stellt sich bei jeder Ordnung <= m und Reduktion k < m. Die grundlegende logische Inkonsistenz des Thurstone'schen Ansatzes besteht also darin, die spezifischen Faktoren ausschließlich in der Hauptdiagonale und die gemeinsamen Faktoren außerhalb der Hauptdiagonale zu suchen. Gemeinsame, spezifische und Fehlerfaktoren müssen ihrer Natur nach auf jede Zelle der Korrelationsmatrix wirken und nicht nur die spezifischen in oder die gemeinsamen außerhalb der Hauptdiagonale. In den Zellen der Hauptdiagonale wirken sie jeweils einfach, da es dort nur um eine Variable geht. In den Zellen außerhalb der Hauptdiagonale wirken sie jeweils zweifach, weil es dort jeweils um zwei Variablen geht, wobei Interaktionseffekte kompensatorisch, stärkend oder schwächend wirken können und  zudem noch technische Artefakte durch unterschiedliche Polungen von Items kontrolliert werden müssen. Eine wiederum andere Frage ist, um welchen Preis eine Approximation durch eine Matrix niedrigeren Ranges möglich ist. Rein mathematisch kann jede Korrelationsmatrix vom Rang m durch eine mit k < m bis hin zu Rang=1 rechentechnisch "approximiert" werden, indem man nur den ersten und größten Eigenwert behält. Aber eine wirklich korrekte Reproduktion einer Korrelationsmatrix der Ordnung m durch weniger Faktoren k < m ist nur dann korrekt möglich, wenn die Korrelationsmatrix m-k (Fast-) Kollinearitäten, d.h. Eigenwerte_gleich oder nahe 0 enthält [s.a. Kalveram]. Ansonsten führt die Datenreduktion zu Matrizen, die zwar aus weniger Faktoren reproduziert werden können, die dafür aber wenig bis nichts mehr mit der ursprünglichen Korrelationsmatrix zu tun haben oder aber ein falsches Thurstone'sches Kommunalitätsmodell erfordern.

Fazit: Die Metaphysik der Hauptdiagonalen der FaktorenanalytikerInnen erinnert an die Spitzfindigkeiten des scholastisch-sophistischen Mittelalters (Wie viele Engel haben auf einer Nadelspitze Platz?). Geht man von der Realität aus, so müssten in den kleinen Beträgen 1-h² die Fehler der gemeinsamen und spezifischen Faktoren sowie die Fehler überhaupt verdichtet versteckt sein. Das ist weder mathematisch und theoretisch begründet oder plausibel und schon gar nicht empirisch fundiert. Die einzige systematische größere und kontrollierte Fehlerstudie (Quaderversuch), die ich kenne, habe ich selbst durchgeführt, um den Unsinn des Screetests ("Knickerbocker-Kriterium") nachzuweisen. Es spricht daher einiges dafür, das von Thurstone vorgeschlagene Kommunalitätsmodell zu streichen, wie es überhaupt nach 102 Jahren Faktorenanalyse an der Zeit scheint, Inventur zu machen und kritisch Bilanz zu ziehen - bald 40 Jahre nach dem kritischen Münchner Symposion über Faktorenanalyse (Fischer, Kallina, Orlik, Sixtl) und den kritischen Arbeiten von Kalveram und Kempf.

Einführung:
Zum Verständnis der Geschichte der Idee der Kommunalität ist es hilfreich, wenn man sich vergegenwärtigt, dass im Modell der Faktorenanalyse davon ausgegangen wird, dass sich die Varianz der betrachteten Variablen zusammensetzt aus den Quadraten der gemeinsamen Faktorenladungen (inklusive Generalfaktor), spezifischen Faktorenladungen und Fehlerladungen. Das ist im Prinzip eine nachvollziehbare und vernünftige Idee - wenn sie angemessen, richtig und nicht in sich widerspruchsvoll wie bei Thurstone fehlkonstruiert wird.

Zur Geschichte des Begriffs
In Spearmans Abilities of Man von 1932 - Nachdruck 1970 - wird der Begriff nicht im Sachregister aufgeführt. Thurstones Multiple- Factor Analysis von 1947 enthält das heute noch verbreitete Konzept bereits vollständig. Der Begriff wird von Thurstones schon in The Vectors of Mind (1934, eingereicht im September 1933) benutzt, und zwar erstmals in folgendem Abschnitt (fett-kursive Hervorhebung durch RS):

"... We need in factor theory another term to indicate that part of the total variance which is attributable only to the common factors and which eliminates not only the variance of chance errors but also the specific variance. We have used the term communality to indicate that part of the total variance of each test which is attributable to the common factors. It is always less than the reliability unless a specific factor is absent, in which case the communality becomes identical with the reliability. It is these communalities that should be recorded in the diagonal cells, but they are the unknowns to be discovered by the factorial analysis. ..."

Thurstones Figure 2: Ausführlich dargestellt wird das Konzept von Thurstone, seinem Erfinder (im Kontext hier):



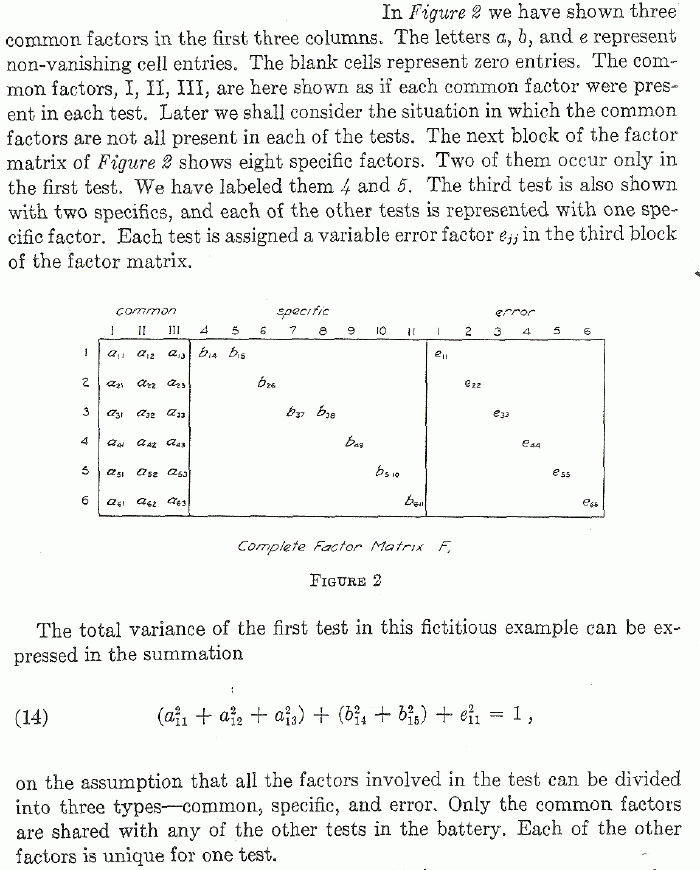
Die widerspruchsvolle Definition  Thurstones und sein Grundmodell hat sich bis heute unverändert und weitgehend unkritisiert erhalten.  (siehe: Definitionen in der Faktorenanalyse Literatur).

Kritik an Thurstones Figure 2.
Nachdem Thurstone mehr spezifische Faktoren als Variable zulässt - in seinem Beispiel in Figure 2 sind es 6 Testvariable und 8 spezifische Faktoren, fragt man sich natürlich, wie 8 spezifische Faktoren in 6 Hauptdiagonalzellen Platz haben und wie die dorthin gelangen? Genauso fragt sich, wieso er auf genau 6 Fehlerfelder kommt, wo doch 36 Felder vorliegen, in die alle Fehler eingehen. Figure 2 wird nicht entwickelt und begründet, sie ist plötzlich da. Die Faktorisierung führt bei einer m*m Korrelationsmatrix zu m*m Faktorladungen. Für jede der m*m Zellen gilt nun, daß in sie gemeinsame Faktoren, spezifische Faktoren und Fehlerfaktoren unter der Randbedingung g+s+e=1 eingehen. Es ist ja überhaupt nicht einzusehen, durch welches deus ex machina Verfahren die Faktorladungsmatrix plötzlich nur noch g repräsentieren soll? Kleine Eigenwerte sind auch nicht zum Wegwerfen da. Sie zeigen auch keine Fehler oder Rauschen, sondern (fast-) kollineareGesetz- oder Regelhaftigkeiten an, die, wenn man schon Wissenschaft betreiben möchte, untersuchen und nicht wegwerfen sollte. Das Modell ist falsch, weil seine Anwendung dazu führt, dass bei Reproduktion der Korrelationsmatrix aus den Faktorenladungen - F*F' im orthogonalen, F*C*F' im obliquen Modellfall - die Korrelationskoeffizienten außerhalb der Hauptdiagonale die Koeffizienten beibehalten werden sollen, so dass sich die Frage stellt: Wieso sollten sich die spezifischen Faktoren und die Fehler nur in der Hauptdiagonale zeigen? Rein psychologisch kann man nachvollziehen, was in den Köpfen der FaktorenanalytikerInnen vor sich ging. Thurstone und seine NachfolgerInnen nutzten die mathematische Tatsache aus, dass Korrelationsmatrizen der Ordnung m durch k < m Faktoren außerhalb der Hauptdiagonalen perfekt reproduzierbar sein können, wenn man die Hauptdiagonalelemente manipuliert, d.h. von 1 nach unten skaliert´- Beispiel:

Kommunalitätszerlegung einer Korrelationsmatrix



Wie man sieht, lässt sich der Rang einer Korrelationsmatrix durch Manipulation der Hauptdiagonalelemente reduzieren, aber das ist dann natürlich keine Korrelationsmatrix mehr, sondern eine Kommunalitätsmatrix. Mathematisch-rechentechnisch war eine Möglichkeit gefunden worden, Rangreduktion durch Manipulation der Hauptdiagonalelemente zu erzielen, ohne dass man sich psychologisch plagen musste, indem man entsprechend durchdachte Skalen, Tests oder Experimentalvariablen empirisch erforschte und begründete. Es war nicht mehr nötig. Mit Hilfe von Cattells dubiosem Screetest-Kriterium und Hauptdiagonalelement-Manipulationen kann man mit etwas Geschick die meisten - dann Pseudo - Korrelationsmatrizen mathematisch so "hinbiegen", bis sie das hergeben, was man sich wünscht. Im folgenden sei zunächst das Beispiel Thurstones vor- bzw. nachgerechnet:

Thurstones Beispiel zu einer Kommunalitätsmatrix  (Figure 7 und 8, Zahlenwerte p. 88):


 

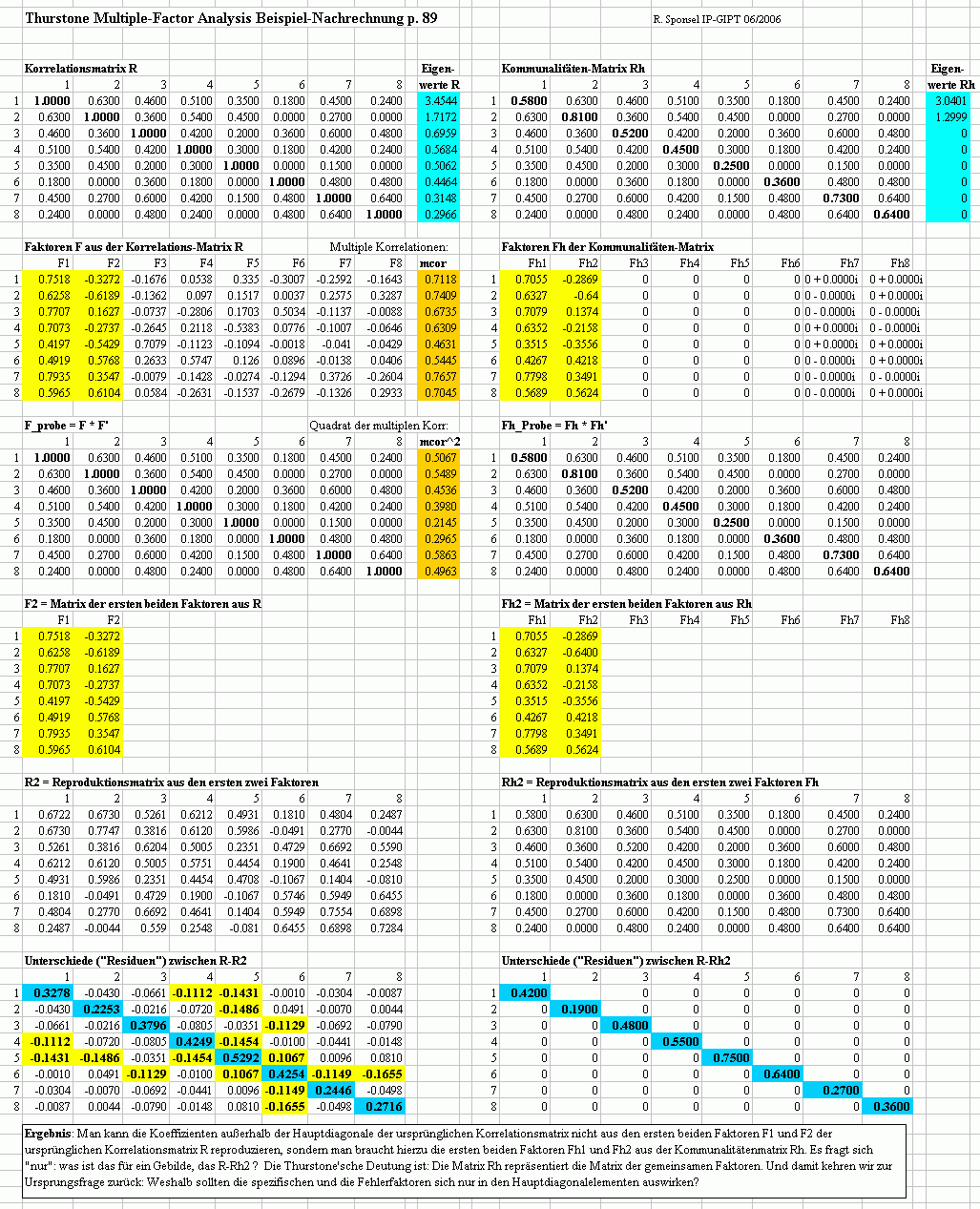
Rangreduktion auf 1 im Generalfaktorbeispiel einer 10x10 Extraversionsmatrix



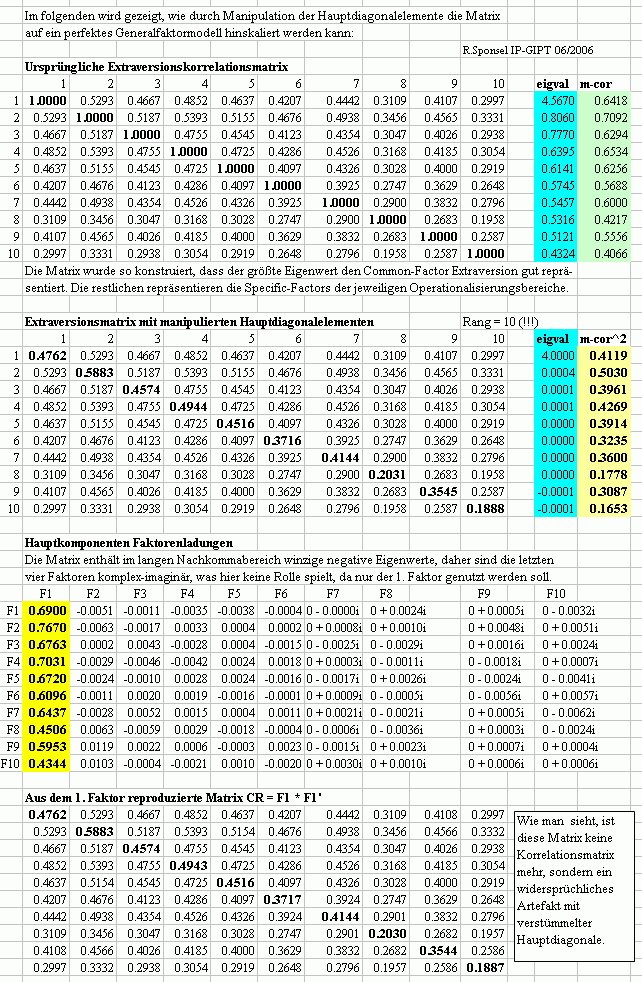
Diskussion: Wie man sieht, gelingt es, Elemente außerhalb der Hauptdiagonale bis auf die dritte Nachkommastelle genau aus dem einzigen Generalfaktor zu reproduzieren. Es kostet den Preis, dass die Korrelationsmatrix verloren geht. Und das passiert regelmäßig, wenn die Hauptdiagonalen aus den faktorenanalytischen Schlachthäusern verstümmelt zurückkehren. Rein mathematisch-rechnerisch  lässt sich dieses Beispiel einer konstruierten eindimensionalen Extraversions-Korrelationsmatrix im Sinne von Thurstones Idee interpretieren, auch die These der unteren Schwelle für die Kommunalitäten durch die Quadrate der multiplen Korrelationskoeffizienten wird hier erfüllt. Die Extraversionsmatrix wurde ursprünglich so konstruiert, dass die spezifischen Faktoren ungefähr 0.5 Eigenwertanteile pro Variable ausmachen sollten. Wie man sieht, ist das nicht ganz, aber mit 0.6 im Mittel fast gelungen. Der größte Eigenwert  mit  4.567 zeigt einen großen Common Factor, ja sogar einen Generalfaktor an, wenn man die Größenordnungen im Verhältnis sieht. Da es 10 Variablen sind, muss im größten Eigenwert auch noch ein spezifischer Faktor stecken, so dass man sagen kann, der Generalfaktor wird ungefähr von einem Eigenwert um 4 ausgeschöpft. Und genau dieser Wert lässt sich durch die Hauptdiagonalmanipulationen reproduzieren. Nicht vernünftig erklären lässt sich, weshalb die spezifischen Faktoren und Fehler nur bei den Hauptdiagonalelementen wirksam werden sollen, während alle Koeffizienten außerhalb gleich bleiben. Das kann man also mathematisch herbeiführen, aber vernünftig interpretierbar ist es bislang nicht. Thurstones Kommunalitätsmodell liefert eine rechnerische Teil-Lösung -  nur für die Koeffizienten außerhalb der Hauptdiagonalen - aber eine unverständliche.

---


Exkurs 1.10.12: Proberechnungen zur Prüfung der positiven Semidefinitheit Kommunalitätsmatrizen mit Determinations- statt Korrelationskoeffizienten

Wie man sieht und nachrechnen kann, sind die Eigenwerte der Kommunalitätsmatrizen mit den Determinations- statt den Korrelationskoeffizienten sämtlich positiv, die Matrizen also positiv definit.



---

Einige wichtigere praktische Sätze zur Kommunalität  (3.10.12)

Die aus n-m (m<n) Faktoren reproduzierte Kommunalitätsmatrix ist immer - bis auf geringfügige Rundungsfehler - positiv semidefinit. Dies folgt aus der Mathematik symmetrischer Matrizen.
In der Hauptduagonalen der aus den Faktoren reprodzierten Kommunalitätsmatrix lassen sich unmittelbar Kommunalitäten ablesen, die die wichtige positive Semidefinitheitsbedingung erfüllen.
Allerdings muss dabei in Kauf nehmen, dass die Korrelationskoeffizienten außerhalb der Hauptdiagonale mit der Ausgangskorrelationsmatrix nicht nur meist nicht mehr übereinstimmen, sondern auch schwerwiegende Widersprüche enthalten. Z.B. wenn aus als gemeinsam angenommenen Faktoren reproduzierte "Korrelationskoeffizienten" ij  > eines ursprünglichen Korrelationskoeffizienten ij ist. Nachdem die Korrelationskoeffizienten sich aus gemeinsamen und spezifischen Faktoren konstituieren sollen, könnten größere rfij gegenüber rij nur dadurch erklärt werden, dass man negative spezifische Faktoren animmt, was der Intention aber zu widersprechen scheint und auch sonst allerlei Zusatzprobleme mit sich brächte.
Für die Kommunalität wurde der quadrierte multiple Korrelationskoeffizient als unter Schranke bewiesen. Daraus ergeben sich unmittelbar Vergleichsmöglichkeiten, ob diese Bedingung erfüllt ist - oft ist sie es nicht.

---


Literatur (Auswahl) [Literatur zur Geschichte der Faktorenanalyse hier]
Hier werden hauptsächlich Grundlagentexte und kritische Arbeiten aufgenommen, teilweise werden auch GIF-Faksimiles der Zusammenfassung an Ort und Stelle geboten.
• Albert, A.A. (1944). The Matrices of Factor Analysis. Proceedings of the National Academiy of Sciences of the USA, Vol 30, 90-95.

Quintessenz in meiner Interpretation: wenn es eine Kommunalitätsmatrix mit kleinerem Rang als die zugehörige Korrelationsmatrix gibt, dann kann man sie auch finden, wobei man bei den Startwerten probieren muß. Anmerkung zu zwei Notationsfehlern._
• Albert, A. A. (1944). The minimum rank of a correlation matrix. Proceedings of the National Academiy of Sciences of the USA, Vol 30, 144—146.
• Bock, H.H. (1974). Automatische Klassifikation. Göttingen: Vandenhoeck & Ruprecht. [nach Lauwerth 1980 wichtig zur Ermittlung der maximal vollständigen Untergraphen oder Clique S. 318ff  für die Lösung des Kommunalitätsproblems] [GB]
• Dwyer, P. S.  (1939). The contribution of an orthogonal multiple factor solution to multiple correlation. Psychometrika 4, 163-171.

[Enthält einen Beweis für die Ungleichung: R²_i.j...m <= h_i² , i=1,...m.]
• Eckart, Carl & Young, Gale (1936). The approximation of one matrix by an other of  lower rank. Psychometrika, 1, 211-218.
• Eckart, Carl & Young, Gale (1939). A principal axis transformation for non-hermitian matrices. Bull. Americ. Math. Soc. 45, 118-21.
• Fischer, Gerhard H. (1967). Zum Problem der Interpretation faktorenanalytischer Ergebnisse. Münchner Symposion über Faktorenanalyse. Psychologische Beiträge, 122-135. [Abstract]
• Guttman, L. (1944). General theory and methods for matrix factoring. Psychometrika 9, 1-16.
• Guttman, L. (1952). Multiple group methods for common factor analysis: their basis, computation, and interpretation. Psychometrika 17, 209-223
• Guttman, L. (1953). A new approach to factor analysis: the radex. In: Lazarsfeld, P. F. (1953, Ed.): Mathematical thinking in the Social Sciences, p. 258-348. New York: .
• Guttman, L. (1954). Some necessary conditions for common-factor analysis. Psychometnka 19, 149- 161. [Abstract]
• Guttman, L. (1956). "Best possible" systematic estimates of communalities. Psychometrika 21, 273-285.
• Guttman, L. (1957). A necessary and sufficient formula for matrix factoring. Psychometrika 22, 79-81.
• Guttman, L. (1957). Simple proofs of relations between the communality problem and multiple correlation. Psychometrika 22. 147-157.
• Guttman, L. (1958). What lies ahead for factor analysis? Educ. psychol. Meas. 18, 497-515.
• Guttman, L. (1957). Successive approximation for communalities. Res. Rep. 12, Univ. Calif., Berkeley. Pp. 13.

Anmerkung: Der Artikel ist leider nicht wissenschaftsöffentlich zugänglich. Wie mir die Fernleihe der UB Erlangen mitteilte, wird die Arbeit nicht in der US-Nationalbibliographie aufgeführt und ist daher nicht beschaffbar. Es erscheint mir eine ziemliche wissenschaftliche Unart, Artikel zu zitieren, die allgemein wissenschaftlich nicht zugänglich sind. Besonders dann, wenn u.B. ein Werk wie das von Harman (1970, p. 83) darauf Bezug nimmt:  "The specific iterative process which Kaiser [289] employed is (5.32)  with e = 1 and H_1 = I. As noted above, this process generally does  not converge for empirical data. Guttman [182] makes several  recommendations, the principal one being to take e =1/2 and H_1 as the  diagonal matrix of squared multiple correlations of each variable with  the n — 1 remaining variables (further use of this concept is made in  5.7). While this work seems promising, the real proof of the usefulness  of these procedures must await the test of time." Ich habe die Methode überprüft, sie liefert in vielen überprüften Fällen semi positiv definite Ergebnisse, wo Kaisers Methode indefinit entgleist, aber in manchen leider auch nicht. Man kann sich zwar denken, wenn die Guttman Methode wirklich zu zuverlässigen und semi positiv definiten Kommunalitätenschätzungen führen würde, dann wäre sie sicher in der Psychometrika entsprechend gefeiert worden. Nachdem das meines Wissens nicht der Fall war, nehme ich mal an, Guttman, ein gewöhnlich zuverlässiger, kritischer und guter Mann, war von dieser Methode selbst nicht überzeugt. Falls jemand weiss, wie man an die Arbeit gelangen kann, bin ich für Hinweise dankbar.
• Guttman, L. (1958). To what extent can communalities reduce rank ? Psychometrika 23, 297-308.
• Haagen, Klaus (1976). Kritik zur Anwendung der Faktorenanalyse. Dissertation Wirtschaftswissenschaftliche Fakultät Universität Regensburg. [FA02]
• Haagen, Klaus & Oberhofer, Walter (1977). Kritische Bemerkungen zu einem Aufsatz von K. T. Kalveram "Über Faktorenanalyse. Kritik eines theoretischen Konzepts und seine mathematische Neuformulierung". Archiv für Psychologie. 1977; 129(3): 187-194. [Abstract]
• Harman, Harry H. (1970). The problem of communality. In: Modern Factor Analysis, 68-92. Chicago: The University of Chicago Press. [Quintessenz letzte Auflage]
• Harman, Harry H. (1970). Modern Factor Analysis. Chicago: The University of Chicago Press.
• Heywood, H,B. (1931). On finite sequences of real numbers. Proc. Roy. Soc. Lond., 134, 486-501. [Ergebnis]
• Holzinger, Karl J. & Harman, Harry H. (1941). Determination of the Common-Factor Space. In (Chapter IV, p. 64-88): Factor Analysis. A Synthesis of Factorial Methods. Chicago: The University of Chicago Press.
• Kaiser, Henry, F. (1957). Solution for the communalities: A preiliminary report. Research Report, No. 5. Berkeley: University of California. Pp. 11.
• Kaiser, H. F.(1959). A note on the TRYON-KAISER solution for the communalities. Psychometrika 24, 269-271.
• Kaiser, H.F. & Dickman, K. (1959). Analytic determination of common factors. Amer. Psychol. 14, 425.
• Kaiser, H. F.(1961). A note on GUTTMAN'S lower bound for the number of common factors. Brit. J. Statist. Psychol. 14, 1-2.
• Kallina, Herbert (1967), Das Unbehagen in der Faktorenanalyse. Münchner Symposion über Faktorenanalyse. Psychologische Beiträge, 81-86. [Abstract]
• Kalveram, K. T. (1970a). Über Faktorenanalyse. Kritik eines theoretischen Konzepts und seine mathematische Neuformulierung. Archiv für Psychologie, Bd. 122, S. 92-118 [Abstract]
• Kalveram, K. T. (1970b). Probleme der Selektion in der Faktorenanalyse. I. Die theoretische Behandlung der Selektion. Archiv für Psychologie, Bd. 122, S. 199-214. [Abstract]
• Kalveram, K. T. (1970c). Probleme der Selektion in der Faktorenanalyse. II. Kritik an einschlägigen Arbeiten. Archiv für Psychologie, Bd. 122, S. 215-222. [Abstract]
• Kalveram, K. T. (1970d). Probleme der Selektion in der Faktorenanalyse. III. Die "Invarianz" von Faktorenlösungen unter Selektion. Archiv für Psychologie, Bd. 122, S. 223-230. [Abstract]
• Kempf, Wilhelm (1972). Zur Bewertung der Faktorenanalyse als psychologische Methode. Psychologische Beiträge, 610-625.[PDF] [Abstract]
• Lukesch, Helmut und Kleiter, G. (1974) Die Anwendung der Faktorenanalyse: Darstellung und Kritik der Praxis einer Methode. Archiv für Psychologie 126 , pp. 265-308.
• Lauwerth, Werner (1975). Faktorenanalyse und Multikollinearitaet. Volume 3 of  Diskussionspapier. Karlsruhe: Institut für Entscheidungstheorie und Unternehmensforschung.
• Lauwerth, Werner (1980). Zum Kommunalitätenproblem in der Faktorenanalyse. Königstein/Ts.: Hain. [FA02]
• Ledermann, W. (1937). On the rank of the reduces correlation matrix in multiple-factor analysis.Psychometrika, 2, 85-93.
• Lukesch, H. & Kleiter, G. T. (1974). Die Darstellung der Faktorenanalyse. Darstellung und Kritik der Praxis einer Methode. Archiv für die gesamte Psychologie, 126, 1974, 265-307.  [Abstract]
• Mackie, John (1928/29). Mathematical Consequenness of Certain Theories of Mental Ability. Proc. Roy. Soc. Edinburgh, 49, 16-37.
• Madansky, A. (1965). On admissible communalities in factor analysis. Psychometrika 30, 455-458.
• McDonald, Roderick, P. (1974). The Measurement of Factor Indeterminacy. Psychometrika, 39, 2, 203-222. [Summary and Conclusions]
• Orlik, Peter (1967). Das Dilemma der Faktorenanalyse - Zeichen einer Aufbaukrise in der modernen Psychologie. Münchner Symposion über Faktorenanalyse. Psychologische Beiträge, 87-98. [Abstract]
• Rinne, Horst (2000). Statistische Analyse multivariater Daten. München: Oldenbourg.
• Rinne, Horst (2003). Taschenbuch der Statistik. Frankfurt: Deutsch.
• Röhr, Michael (1993). Statistische Strukturanalysen. Stuttgart: G. Fischer.
• Roff, M. (1936). Some properties of the communality in multiple factor theory. Psychometrika, 1, 1-6.
• Sixtl, Friedrich (1967). Faktoreninvarianz und Faktoreninterpretation. Münchner Symposion über Faktorenanalyse. Psychologische Beiträge, 99-111. [Abstract]
• ten Berge, J.M.E (1998). Some recent developments in factor analysis and the search for proper communalities. In: A. Rizzi, M. Vichi, & H.H. Bock (Eds), Advances in data science and classification (pp. 325-334). Heidelberg, Germany: Springer.
• Thurstone , L. L. (1934). The Vectors of Mind.[kompletter Artikel im Netz]
• Thurstone , L. L. (1947, ⁵1957). Multiple-Factor Analysis. A Development and Expansion of The Vectors of Mind. Chicago: The University of Chicago Press. [Kapitel 2 der Grundgleichungen]

Tryon, R. C. (1957). Communality of a variable: Formulation by cluster analysis. Psych. 22: 241-60.
Tryon, R. C. (1958a). Cumulative communality cluster analysis. Ed. Psych. Meas. 18:3-35.
• Überla, K. (1971). Faktorenanalyse. Berlin: Springer. [teilweise kritisch, Auszug zur Kommunalität]
• Wittmann, Werner W. (1977). Faktorenanalytische Modelle, Methodenstudien und Probleme der Reproduzierbarkeit. Dissertation Freiburg.

[U. Wolff im ZPID hierzu: "Die Faktorenanalyse, welche lange Zeit als bestgeeignetes methodisches Instrument in der psychologischen Forschung angesehen wurde, ist seit laengerem starker Kritik ausgesetzt. Diese Kritik wird in der Arbeit naeher dargestellt, und es wird versucht, mittels einer umfassenden Analyse die Brauchbarkeit und die Grenzen der Faktorenanalyse herauszuarbeiten. Zunaechst wird auf die geaeusserte Kritik naeher eingegangen, und Gruende fuer die auffallende Diskrepanz in der theoretischen Behandlung der Faktorenanalyse im deutschen und  im anglo-amerikanischen Sprachraum werden aufgezeigt ... "]
• Wrigley, C. F.:  (1957).  The distinction between common and specific variance in factor theory. Brit. J. Statist. Psychol. 10, 81-91.
• Wrigley, C. F. (1959). The effect upon the communalities of changing the estimate of the number of factors. Brit. J. Statist. Psychol. 12, 35-54.

_


---


Links (Auswahl: beachte)
• Factor Analysis by Richard B. Darlington [Link]
• Factor Analysis Bibliography [Link]
• Kritik an der Faktoreninflation in Das Rotationsproblem in der FA von Suitbert Ertel [Link]
• Behavior-genetic analysis of mouse emotionality. I. Factor analysis. [Link]
• Glossary statistical terms. [Link]  [Link]




---


Anmerkungen und Endnoten:
1) GIPT= General and Integrative Psychotherapy, internationale Bezeichnung für Allgemeine und Integrative Psychotherapie.
___
Absurdität, Antinomie, Aporie, Konfusion, Paradoxie, Pseudo-Paradoxie, Sophisma, Widerspruch, X-Strittiges / Sonstiges. [Quelle]
Der Begriff der Paradoxie wird unterschiedlich gebraucht. Es seien daher die verschiedenen Begriffsumfelder und wie sie in der IP-GIPT verwendet werden, etwas genauer bestimmt:
• Absurdität. > Paradoxie.
• Antinomie. Ein echter logischer > Widerspruch. Die Existenz von Mengen, die sich selbst als Element enthalten (z.B. die Menge aller abstrakten Begriffe) oder nicht (die Nullmenge). Russellsche Antinomie 1903 der Mengen aller Mengen, die sich nicht selbst als Element enthalten. Empirischer Widerspruch Datenreduktion Faktorenanalyse und Reproduzierbarkeit der Ursprungsmatrix, wenn nicht wenigstens ein Eigenwert nahe 0 ist. Ist das nicht der Fall, kann man mit einer Faktorenanalyse zwar die Daten reduzieren, aber nur um den Preis, dass sie dann nicht mehr die ursprünglichen Daten repräsentieren, man hat durch einen methodologischen Beschluß virtuell neu skaliert, ohne es konsequent und logisch an den Rohdaten zu vollziehen. Weitere Antinomien: Burali-Forti 1897 [1,2,3];  Richards 1905 u. 1909;  [1,2,3].
• Aporie. Etwas erwiesenermaßen Unlösbares (Quadratur des Kreises, Gödel'sche Sätze; Heilmittelaporie in der Psychotherapie).
• Fehlschluß, Trugschluß, Problemschluß.
• Konfusion. Verwirrung, unklare, verworrene, undurchsichtige Lage.
• Paradoxie. Eine absurd oder widersinnig erscheinende Aussage, gegen die sich der Verstand sträubt, ohne zwingend falsch zu sein. > Sophisma. Rüstow (1910, S. 135) definiert: "Ein Paradoxon ist eine Argumentation, die von anscheinend richtigen Prämissen ausgehend durch anscheinend richtige Schlüsse zu einem offenbar widersprechenden Resultat gelangt."
• Pseudo-Paradoxie > Sophisma.
• Rabulistik. Die Kunst, recht zu behalten, egal wie.
• Sophisma. Zenons Achilles und die Schildkröte  [1,2,3],  Lügner-Problem  [1,2,3],  Statistische Paradoxien [Stegmüller, 2,3], Hat der gegenwärtige König von Frankreich eine Glatze? [1,2,3],
• Widerspruch. Hier können auch noch logische und empirische Widersprüche unterschieden werden. > Antinomie.
• X-Strittiges. Natürlich gibt es nach Überzeugung und Standpunkt auch strittige Beurteilungen, z. B.: Nach Cantor sind die Mengen der natürlichen und die Mengen der rationalen Zahlen gleichmächtig, obwohl es offensichtlich mehr rationale als natürliche Zahlen gibt, aber nach den Cantoristen offenbar nur im Endlichen. Die einen werten dies als verständlich und keineswegs merkwürdig (Mathematiker, die Cantor schätzen), andere bezeichnen es als Paradox (Basieux Top Ten), wieder andere als Antinomie und Widerspruch. Die Definition der unendlichen Menge (Cantor 1878, Dedekind 1887) verletzt nach Hausdorff 1914, S. 48 das "geheiligte Axiom 'totum parte majus'", nämlich Euklids Axiom 8: Das Ganze ist größer als sein Teil. Hempels Paradoxon: [1,2,3,] . Hilberts Hotel [1,2,3],  .
Querverweis: Beweis und beweisen in Rhetorik, Sophistik und Rabulistik, Lit, auch [1, ]
Literaturhinweis: Meschkowski.
___
Fehlerfaktoren. Man kann als Fundamental-Satz der Empirie ansehen, dass jede Messung fehlerbehaftet ist. Dass sich die Fehler wie durch märchenhafte Gotteshand gelenkt wundersam multinormalverteilt herausmitteln und sämtlich unkorreliert sein sollen, ist ein anderes Kapitel der sog. "klassischen" Testtheorie und der Faktorenanalyse, die daher besser deus ex machina Testtheorie aus dem Hause per fiat hiesse als "klassisch".
___
Metaphysik der Hauptdiagonalen. Es gehört zu den großen Geheimnissen oder gar Mysterien der Wissenschaft, wie ein solch grandioser Unsinn, wie er von den FaktorenanalytikerInnen mit der Hauptdiagonale einer Korrelationsmatrix nun bald ein Jahrhundert praktiziert wird, sich bis auf den heutigen Tag erhalten kann. Da dematerialisieren sich die Fehlerfaktoren (e) und spezifischen Varianzanteile (s) in den Koeffizienten außerhalb der Hauptdiagnonale und reinkarnieren auf ebenso geheimnisvolle Weise durch mathematisch- okkultue Wanderungsbewegungen zu den Hauptdiagonalelementen in den Größen 1-h², wobei die Korrelation einer Variablen mit sich selbst nahezu verschwinden kann. Dieser  blühende Unsinn wird getragen von einem mächtigen wissenschaftspsychologischen Motiv: ernsthaftes, empirisch-experimentelles Bemühen, also richtige Arbeit und Kreativität durch numerologische Spielereien des homo ludens psychomathematicus zu ersetzen
___
Variablenreduktion. Die FaktorenanalytikerInnen waren von Anfang völlig verblendet und fixiert, ja geradezu besessen von der Idee der Variablenreduktion. Statt erst einmal psychologische Gesetzmäßigkeiten zu suchen, die sich z.B. in Eigenwerten 0 (Kollinearität) oder nahe 0 (Fast-Kollinearität) ausdrücken, warf man jeden Eigenwert < 1 ("Screetest") ohne auch nur eine Sekunde nachzudenken, was man da eigentlich macht, weg. Ein neuer Persönlichkeitstyp eroberte die Psychologie: der homo ludens psychomathematicus. Ein neues Paradies der Unendlichkeit (Hilbert über Cantors Werk) wurde mit der Faktorenanalyse geschaffen; fast alles war möglich, und heute, mit Hilfe der für jeden verfügbaren Computer und Programme, mehr denn je, denn es kommt immer etwas raus. Nur vernünftige Begründungen und Interpretationen sucht man fast immer vergeblich. Zum Mekka dieser homo ludens psychmathematicus Bewegung wurde die "Psychometrika". Einer ihrer Präsidenten, Dunlap, sprach zum 25-jährigen Jubiläum mehr ironisierend als selbstkritisch, aber sehr trefflich von "PSYCHOMETRICS - A SPECIAL CASE OF THE BRAHMAN THEORY" (Psychometrika 26,1,1961, p.65). Er ahnte wohl nicht, wie Recht er damit hatte und bis heute behielt. So hat die Psychmetrika hat mit Psychologie so gut wie nichts zu tun, sie ist reduziert - offenbar konsistent mit dem dort gepflegten faktorenanalytischen Reduktionsfuror - auf eine bloße "metrika" ohne hinreichend theoretische, empirische oder anwendungspraktische Fundierung oder gar kritische Reflexion.
    Zusatz: Der Reduktionsfuror ist auch aus grundsätzlicher Sicht sehr fragwürdig, weil in jede Testung mindestens mehrere allgemeine Faktoren für jede Testperson eingehen: 1) Motivation zur Bearbeitung, 2) richtige Erfassung der Aufgabe, 3) die Fähigkeit zur Bearbeitung, 4) Filterung einzelner Aspekte der Aufgaben im Lichte der eigenen Interessen, Stärken und Schwächen (Abwehr) z.B. der Einfluss sozialer Erwünschtheit. Jede Testbearbeitung erfordert bereits diese 4 "Generalfaktoren", selbst ein Test, der nur eine einzige Dimension (Variable) erhöbe, erforderte diese vier "Generalfaktoren". Aber der Variablen-Reduktionsfuror hat die FaktorenanalytikerInnen für solche elementaren Gegebenheiten blind gemacht.
Statt die Datenvielfalt zu reduzieren, wurde eine chaotische Inflation von Faktoren erzeugt, wie Ertel (2002) schön ausführt:


___
BRAHMAN. Indische Religion; Gott; Religionsgelehrter, oberste Kastenangehöriger. Hier offenbar eine Metapher für metaphysische Betätigung [Wikipedia].
___
Kommunalitäts-Definitionen in der Faktorenanalyse Literatur (Beispiele, Auswahl)
1) "COMMUNALITY For a variable in a factor analysis* model, the communality is defined as the sum of squares of its factor loadings* over all the factors. These values give an indication of the extent to which the variables overlap [>60] with the factors or, equivalently, they give the proportion of the variance in the variables that can be accounted by the scores in  the factors. In many methods of factor extraction the estimates of communality values are inserted in the diagonal cells of the original correlation matrix* before the factor analysis is carried out. [Quelle Bd.2 Encyclopedia of Statistical Sciences, Vol. 2, 1982, p. 59f]
2) [FernUni Hagen] Kommunalität: Die Kommunalität gibt an, in welchem Ausmaß eine Variable i durch die Faktoren aufgeklärt bzw. erfaßt wird. Sie berechnet sich als Summe der quadrierten Ladungen einer Variablen.
3) Kommunalität aus Überla, K. (1971). Faktorenanalyse. Berlin: Springer. S. 57:



Anmerkung: Das ist keine klare Definition zur Identifikation einen gemeinsamen Faktors. Zuvor erklärt Überla:

Zum Begriff gemeinsamer und spezifischer Faktor



Kritische Anmerkung (Überla S. 55): Entscheidend ist natürlich, was es heißt, daß sich mindestens zwei Faktoren, damit sie "gemeinsam" (common) heißen, "beträchtlich von Null unterscheiden". Also was heißt "beträchtlich"? 0,05, 0,10, 0,15, ...? Unverständlich bleibt auch, wozu gemeinsame Faktoren überhaupt nützlich sein sollen und weshalb nicht n (n Ordnung der Korrelationsmatrix) spezifische genau ein Modell liefert, das eine gute Operationalisierung eigentlich anstreben sollte?
___
weitgehend unkritisiert. Überla (1971, S. 156) schreibt immerhin:


___
Quintessenz letzte Auflage, Third Edition Revised,  Harman (1976, p. 84):



Abstracts von kritischen Beiträgen zur Faktorenanalyse

Abstract Fischer, Gerhard H. (1967). Zum Problem der Interpretation faktorenanalytischer Ergebnisse. Münchner Symposion über Faktorenanalyse. Psychologische Beiträge, 122-135.

_
Abstract Guttman, L. (1954). Some necessary conditions for common-factor analysis. Psychometnka 19, 149- 161.


Abstract Kallina, Herbert (1967), Das Unbehagen in der Faktorenanalyse. Münchner Symposion über Faktorenanalyse. Psychologische Beiträge, 81-86.

 

50-dimensionaler Raum mit 1000-Billionen-Zellen (a.a.O., S.82):


___
Abstract Kalveram, K. T. (1970a). Über Faktorenanalyse. Kritik eines theoretischen Konzepts und seine mathematische Neuformulierung. Archiv für Psychologie, Bd. 122, S. 92-118 _


Abstract Haagen, Klaus & Oberhofer, Walter (1977). Kritische Bemerkungen zu einem Aufsatz von K. T. Kalveram "Ueber Faktorenanalyse. Kritik eines theoretischen Konzepts und seine mathematische Neuformulierung". Archiv-fuer-Psychologie. 1970; 129(3): 187-194.


Anmerkung: Kalveram hat natürlich vollkommen Recht, wenn er sagt: "Eine vorgegebene symmetrische Matrix Q besitzt genau dann (mindestens) eine reproduzierende Matrix, wenn die Ausgangsmatrix positiv semidefinit ist. Diese Tatsache wird so häufig in der Faktorenanalyse benutzt, daß hier auf einen Beweis verzichtet wird. Wenn also Q nicht positiv semidefinit ist, so existiert auch keine reproduzierende Matrix zu Q." Auf diesen fundamentalen Kritikpunkt Kalverams gehen Haagen & Oberhofer überhaupt nicht ein. Alle vier Kritikpunkte am Ende der Arbeit sind sehr dürftig, fraglich und in keiner Weise überzeugend - umsomehr wenn man sich vergegenwärtigt, dass diese Kritik 6 Jahre gebraucht hat. Zum ersten Argument, dass q > n keine sinnvolle Annahme sei, geht kurioserweise der Schöpfer der multiplen Faktorenanalyse, Thurstone, in Figure 2 gerade von einem solchen Beispiel aus (n=6, q=8; n Anzahl der Variablen, q Anzahl der spezifischen Faktoren).
_
Ergebnis: Heywood, H,B. (1931). On finite sequences of real numbers. Proc. Roy. Soc. Lond., 134, 486-501.
Nanny Wermuth fasst - teils missverständlich - zusammen [Quelle]:

missverständlich: Im zweiten Teil zitiert Wermuth "Heywood says: He excluded ...", wobei man
das "He" dem Zusammenhang nach auf Spearman bezieht. Tatsächlich schreibt Heywood eine
Zeile vorher: "This case has been dealt by Garnett [RS: 1919]; he eassumed that the consequences
had normal distributions, and this paper hat two further restrictions. He excluded ...".

Anmerkung: Heywood war ein seriöser Mathematiker und kein homo ludens psychomathematicus. Seinen guten Namen mit den dubiosen Praktiken faktorenanalytischer Freistilmathematik in der Floskel "The Heywood Case" zu missbrauchen zeugt weder von historischem Wissen noch von wissenschaftlicher Redlichkeit. Der würde sich noch im Grabe rumdrehen, bekäme er mit, was mit seinem Namen für ein Schindluder betrieben wird. Viel angemessener wäre es, von einem "Fall Spearman" oder vom "Fall Faktorenanalyse" zu sprechen.
___
Abstract Kalveram, K. T. (1970b). Probleme der Selektion in der Faktorenanalyse. I. Die theoretische Behandlung der Selektion. Archiv für Psychologie, Bd. 122, S. 199-214.
_

_
Abstract Kalveram, K. T. (1970c). Probleme der Selektion in der Faktorenanalyse. II. Kritik an einschlägigen Arbeiten. Archiv für Psychologie, Bd. 122, S. 215-222


_
Abstract Kalveram, K. T. (1970d). Probleme der Selektion in der Faktorenanalyse. III. Die "Invarianz" von Faktorenlösungen unter Selektion. Archiv für Psychologie, Bd. 122, S. 223-230.

___
_
Abstract Kempf, Wilhelm (1972). Zur Bewertung der Faktorenanalyse als psychologische Methode. Psychologische Beiträge, 610-625.


___
Abstract Lukesch, H. & Kleiter, G. T. (1974). Die Darstellung der Faktorenanalyse. Darstellung und Kritik der Praxis einer Methode. Archiv für die gesamte Psychologie, 126, 1974, 265-307:

_
Summary and Conclusions McDonald, Roderick, P. (1974). The Measurement of Factor Indeterminacy. Psychometrika, 39, 2, 203-222.


Abstract Orlik, Peter (1967). Das Dilemma der Faktorenanalyse - Zeichen einer Aufbaukrise in der modernen Psychologie. Münchner Symposion über Faktorenanalyse. Psychologische Beiträge, 87-98.
_

___
Zusammenfassung Rinne, Horst (2000). 5.4 Kritische Bemerkungen. In: Statistische Analyse multivariater Daten. München: Oldenbourg, S. 142f:
"5.4    Kritische Bemerkungen
Die Faktorenanalyse ist hier vergleichsweise knapp dargestellt worden, da diese Methode — außer vielleicht in der Soziologie und Psychologie — umstritten ist. Die Gründe dafür sind im wesentlichen die folgenden:

1. Bei der FA sind sehr viele Annahmen zu treffen, die in der Praxis nicht immer realistisch sind.
2. Eine wichtige Prämisse ist, daß überhaupt Faktoren existieren. Nicht in allen empirisch ausgerichteten Wissenschaften darf man von dieser Annahme ausgehen.
3. Die FA unterstellt die Kenntnis von p, der Faktorenanzahl. In der Praxis ist p i.d.R. unbekannt, so daß man beginnend bei p = l sequentiell verschiedene Werte „ausprobiert". Es gibt zwar einen Test für p (vgl. LAWLEY/MAXWELL,  [> 143] 1971, Abs. 4.4), der jedoch recht kompliziert ist und von den Modellprämissen abhängt. Was verwirren kann, ist die Tatsache, daß mit p sich häufig die Form der Faktoren in dem Sinne ändert, daß sich die Ladungen wesentlich verschieben. In dieser Beziehung ist die HKA [RS: Hauptkomponentenanalyse] robust, es sei denn, es gibt gleiche Eigenwerte.
4. Selbst bei festem p sind die Faktoren nicht eindeutig, da verschiedene Rotationsverfahren recht unterschiedlich konfigurierte, an ihren Ladungen gemessene Sätze von Faktoren erzeugen können. Damit sind der Willkür und Subjektivität eine Tür geöffnet. Ein Forscher kann i.a. so lange an den Daten „drehen", bis er die gewünschten Faktoren gefunden hat. Aus ein und demselben Datensatz können so leicht ganz unterschiedliche Faktoren extrahiert werden.
5. Ahnlich wie die Faktorenlösung von p abhängt, wird sie auch stark von der gezogenen Stichprobe geprägt, besonders wenn diese einen geringen Umfang hat. Eine wiederholte Stichprobe aus derselben Gesamtheit kann leicht zu einer total anderen Faktorenlösung führen.
6. Ebenso wie die Interpretation der HK schwierig ist, so auch die der Faktoren. Eine komplizierte Technik wie die FA kann so lange nicht als nützlich und sinnvoll angesehen werden, wie sie nicht zu einem tieferen Verständnis der Daten führt.


Monographien zur Faktorenanalyse

• HARMAN, H.H. (1976) Modern Factor Analysis, 3  ed.; Univ. of Chicago Press, Chicago
• KIM, J.-O. / MUELLER, C.W. (1986) Factor Analysis: Statistical Methods and Practical Issues; Sage, Beverly Hills
• KIM, J.-O. / MUELLER, C.W. (1986) Introduction to Factor Analysis: What it is and how to do it; Sage, Beverly Hills
• LAWLEY, D.N. / MAXWELL, A.E. (1971) Factor Analysis as a Statistical Method, 2n ed.; Butterworth, London
• LONG, J.S. (1986) Confirmatory Factor Analysis; Sage, Beverly Hills
• ÜBERLA, K. (1971) Faktorenanalyse; Springer, Berlin
"
____
Abstract Sixtl, Friedrich (1967). Faktoreninvarianz und Faktoreninterpretation. Münchner Symposion über Faktorenanalyse. Psychologische Beiträge, 99-111.


___

unendlich viele Möglichkeiten der Reproduktion. Am Beispiel der Faktorisierung der Korrelationsmatrix: R = F*F' = F*Q*Q'*F' für Q orthogonal, da die Transponierte im  Falle der Orthogonalität gleich der Inversen ist: Q'=Q^-1 = E, also die Einheitsmatrix gibt, die als neutrales Element auch weggelassen werden kann. Also kann man unendlich viele Faktorisierungen durchführen, die alle ein und dieselbe Korrelationsmatrix zu reproduzieren gestatten. Damit ergibt sich ein kaum überwindbares Konstruktions- und Interpretationsproblem, was die extreme Vielfalt bis zur Beliebigkeit von Faktorenanalysen deutlich macht.
Nachtrag Rotation (11.6.6): Durch systematische Versuche mit vorgegebenen Faktorenmodellen Typ Thurstone Figure 2, halte ich es inzwischen für möglich, für bestimmte Modelle die richtige und einzige Rotationsmatrix, die die Originaldaten reproduzieren kann, herauszufinden. Da aber immer verschiedene Modelle gelten können und man ja nicht weiß, welches gilt, hilft das auch noch nicht so recht weiter. Man braucht also zusätzliche empirisch-experimentelle Untersuchungsverfahren, die den Modell-Typ zu schätzen gestatten, dann könnte man mit einem gezielten Rotationsverfahren eine faktorenanalytische Rekonstruktion durchführen. Auch diese Überlegungen unterstreichen: Faktorenanalysen ohne theoretisch-empirsche Einbettung und fundierte Modellannahmen sind im Grunde genommen psychomathematische Spielereien ohne wissenschaftlichen Sinn und Nutzen. An dieser Stelle zeigen sich die meisten FaktorenanalytikerInnen völlig unfähig oder uninteressiert, was in praxi auf dasselbe hinausläuft. Betrachtet man sich etwa die Bücher Reventorfs zur Faktorenanalyse (1976, 1980), so kann man die StudentInnen nur bedauern, die solch einen ziemlich unpsychologischen, wissenschaftstheoretisch und experimentell-empirischen extrem verdünnten, dafür mathematisch umso mehr überfrachteten Stoff lernen sollen.
___
Kommunalitätsmatrix. In der Faktorenanalyse bezeichnet man die Kommunalitätsmatrix gerne euphemistisch als "reduzierte Korrelationsmatrix" und suggeriert damit, als ob die Kommunalitätmatrix etwas mit einer Korrelationsmatrix zu tun hätte. In Wahrheit ist sie nicht einmal ähnlich. und oft genug nicht einmal positiv semi definit, also eine komplex-imaginäre Schimäre. Es ist daher wichtig, sich klar zu machen, was eine Korrelationsmatrix ist: 1) sie ist symmetrisch; 2) sie hat in der Hauptdiagnoalen 1en; 3) die Werte in sämtlichen Zellen erfüllen -1 <= r <= 1; 4) sämtliche Werte stammen aus der gleichen Stichprobe oder Population mit ein und demselben Stichprobenumfang; 5) die Korrelationsmatrix ist positiv semidefinit, d.h. sämtliche Eigenwerte >= 0. Ich finde die Bezeichnung Kommunalitätsmatrix daher treffender und korrekter.
___
operationale Definition. Definitionen sind weitgehend nicht einfach wahr oder falsch, sondern zweckan- oder unangemessen. Zur Akzeptanz einer Definition ist es daher wichtig, ihre Nützlichkeit für diesen oder jenen Zweck zu zeigen. Im Falle der Kommunalitätsdefinition müsste gezeigt werden, dass diese willkürliche operationale Definiton h_i.² = a_i1² +  a_i2² + ... +  a_ij² +... + ...  a_im² die Erfassung der gemeinsamen Faktoren vernünftig nachvollziehbar erlaubt, was so wie sie erfolgte nicht möglich ist. Die Thurstone'sche Definition ist nicht nur zweckunangemessen, sie ist in ihrem Realteil sogar falsch. Obwohl es sich um hypothetische Konstrukte handelt, muss unabhängig von der völligen Willkür der Thurstone'schen formalen Definition auf jeden Fall gefordert werden, den Unterscheidungen gemeinsamer Faktor (Common Factor), spezifischer Faktor (Specific Factor) und Fehler-Faktor (Error Factor) einen empirisch prüfbaren Sinn zu geben, ansonsten bleibt es eine unverbindliche Spielwiese des homo ludens psychomathematicus. Die willkürliche Definition und ihre Benennung suggerieren nur, daß hier die "gemeinsamen" Faktoren im Sinne der Grundidee erfasst werden. Überblick zur Definitionsproblematik in der IP-GIPT.
___
homo ludens psychomathematicus. Spielen ist zweckfreie Betätigung, die lustvoll erlebt wird ("Flow"), darin liegt sozusagen der "höhere" Zweck. Man spielt, weil es vergnüglich ist, Spaß macht und die Zeit vertreibt. So gesehen ist Spielen eine feine Sache und es bereichert das Leben. Das Spiel mit Formeln und  Zahlen in n-dimensionalen Räumen, das Jonglieren mit imposanten Zeichen und Begriffen und vor allem die Tatsache, dass immer etwas herauskommt und eine Niederlage oder selbst ein Patt so gut wie nie eintritt, macht das Spielen mit Faktorenanalysen offenbar für viele recht attraktiv. Wer mag sich da schon an Voraussetzungen, z.B. Intervallskalierung, Multinormalverteilung und Zufallsauswahl (falls getestet wird), semi positive Definitheit (alle Eigenwerte >= 0) oder gar mit dem Schreckgespenst Begründung oder Interpretation plagen? Die Mathematik ist eine tolle Wissenschaft und ein unverzichtbares Hilfsmittel auch in der Psychologie. Man vergesse hierbei aber nicht, dass der bloße Gebrauch und die Anwendung von Mathematik noch kein Garant für Wissenschaft ist. Spätestens seit der Astrologie und Numerologie sollte man hier vorsichtig sein. Eine besonders raffinierte Variante moderner Esoterik ist die szientistische Verkleidung mit Mathematik. Was also ist gewonnen, wenn 16 Variable durch den Filter von 4 orthogonalen, varimaxrotierten Faktoren betrachtet werden können?
___
Freistilmathematik. Die mathematischen Gesetze und Regeln der Linearen Algebra werden in der Faktorenanalyse seit ihren ersten Anfängen bis auf den heutigen Tag grob mißachtet, im wesentlichen die notwendige positive semi Definitheits Bedingung ("Gramian") <==> alle Eigenwerte >= 0. Daraus resultieren unsinnige Kennwerte - z.B. multiple Korrelationskoeffizienten [1] oder "Kommunalitäten" >> 1, Verlust der Ähnlichkeit und damit der Repräsentativität einer rangreduzierten Kommunalitätsmatrix,  imaginär-komplexe Faktoren oder imaginär-komplexe Rohdatensätze, widersprüchliche partielle Korrelationskoeffizienten u.a.m.
___
Hauptkomponentenmethode. Die Hauptkomponentenmethode - in der Mathematik auch unter dem Namen "Eigenwertproblem" bekannt - gestattet, eine Korrelationsmatrix einfach zu faktorisieren: C = F*F'. So ist eine Hauptkomponentenanalyse z.B.  in Matlab mit Hilfe zweier einfacher Befehle durchzuführen: Sei C die Korrelationsmatrix, dann gilt [V,D]=eig(C), wobei V die Eigenvektoren und D die Eigenwerte der Korrelationsmatrix sind. Die Faktoren ergeben sich dann durch F = V*SQRT(D). Genau genommen unterscheidet sich die Faktorenanalyse von der Hauptkomponentenanalyse durch einen anderen Modellansatz unter Einbeziehung des fragwürdigen Konzepts der Kommunalität: C = F_c*F_c' + D_k mit F_c als "gemeinsame" Faktoren und als komplementäre Diagonalmatrix (zu den Kommunalitäten in der Hauptdiagonalen der Kommunalitätsmatrix F_c*F_c') mit D_k = 1-h² in der Hauptdiagonalen.
___
Rang. Der Rang einer Matrix gibt die Zahl der linear unabhängigen Zeilen oder Spalten an (Zeilenrang = Spaltenrang). Bei der Beurteilung des Ranges muss man streng zwischen "reiner" Mathematik und numerisch-praktischer auf einem Computer unterscheiden. Auch numerisch extrem instabile Matrizen haben oft vollen Rang, wenn in der vom Rechner erfassten Genauigkeit im Nachkommabereich ein winziges "Rauschen" vorliegt, z.B. eine "1" an der 15. Nachkommastelle vor lauter Nullen (0,000000000000001) steht. Der Rang sagt praktisch-numerisch nichts. Wenn man wissen will, wie in/stabil eine Korrelationsmatrixkonditioniert ist, muss man die Eigenwerte betrachten, deren Bedeutung man kaum überschätzen kann. Hierzu auch (Quelle):


___
Grundmodell. Nicht ganz klar ist mir die Priorität der Grundgleichungen. Harman (1970, p. 19, (2.20)) verwendet mit Ausnahme eines anderen Zeichens (d) für Uniqueness die gleiche Formenln wie Thurstone. Nachdem Harman mit Holzinger schon 1941 ein Buch zur Faktorenanalyse herausgab, ist es natürlich auch möglich, daß Thurstone die Grundgleichungen von Holzinger & Harman übernommen hat:


Tatsächlich präsentiert das Buch von Holzinger & Harman (1941) p. 14 folgende Grundgleichungen:


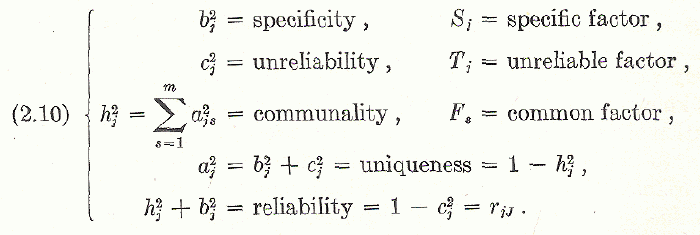
Zur vollständigen Beurteilung muss nun noch die Buchausgabe - nicht des Artikels von 1934 - von The vectors of mind, der Vorläufer der multiplen Faktorenanalyse eingesehen werden. Dort finden sich in der Ausgabe von 1935 (mir lag eine Fernleihe der Staatsbibliothek Berlin vor) auf p. 68 die bekannten Formeln, so dass die Prioritätenfrage (Notation und System der Grundbegriffe) vorerst zu Gunsten Thurstones ausgeht:


Ansonsten fällt auf, dass Thurstones Verdienste um die Grundlagen der Faktorenanalyse ein wenig von Harman relativiert werden (p. 4):
Thurstones Bedeutung aus der Perspektive Harmans


___
Nadelspitze ... in der Faktorenanalyse der kleine Bereich zwischen 1-h², wobei als untere Schranke für h das Quadrat der multiplen Korrelationskoeffizienten und als obere Schranke das Quadrat der Reliabilität gilt. Im Mittel dürfte hier die 0.5 ein praktischer brauchbarer Schätzer sein. Da nach dem Spursatz die Summe der Eigenwerte die Summe der Diagonalwerte der Korrelationsmatrix ist und damit ihrer Ordnungszahl entspricht, ergäbe sich bei einer Variablenzahl von 10 die Faustregel, dass ungefähr 50% der in den Eigenwerten ausgedrückten Varianz den "gemeinsamen" Faktoren, 50% den spezifischen und den Fehlern zugeordnet werden kann. Gibt es hohe Interkorrelationen, die auch durch die spezifischen Faktoren bewirkt sein können, steigt der Anteil der Varianz nach dem Faktorenanalysemodell zwangsläufig. Mit anderen Worten: erhöht man den Varianzanteil der spezifischen Faktoren, sinkt dieser im Faktorenanalysemodell - weil die multiplen Korrelationen höher werden und damit auch h zunimmt, also sinkt der Varianzanteil formal, wenn er real steigt, also eine weitere absurde Antinomie des traditionellen Faktorenanalysemodells.
___
untere Schranke. Ob der Satz, daß die Quadrate des multiplen Korrelationskoeffizienten, eine untere Schranke für die Kommunalität bilden, erfüllt werden kann, hängt nach meinen Untersuchungen davon ab, (1) ob die ursprüngliche Ausgangsmatrix eine korrekt gebildete Korrelationsmatrix, also positiv semi definit ist und (2) welche Kommunalitäteniteration verwendet wird. Die Kommunalitäteniterationen von Kaiser (1956) und Guttman (1957) erfüllen diesen Satz nach meinen Untersuchungen mehrfach nicht, wohl die Kommunalitäteniteration, die der Mathematiker Karl Wiesent, Erlangen, programmiert hat und das Bisektionsverfahren nutzt. Beide Methoden wurden programmiert von dem Mathematiker Karl Wiesent, Erlangen, nach den Angaben aus Harman (1970, p. 82-83; die Originalarbeit Guttmans ist leider universitätsöffentlich nicht zugänglich).
___
Geschichte, Pioniere und Gestalter der Faktorenanalyse (Auswahl): [In Arbeit]  [Querverweis: Pioniere der Korrelationsrechnung].
Siehe auch: [PDF] Index Psychometrika 1936-1970 VOLUMES 1-35; Annual indices 1971-2002



Kurzgeschichte (gestützt auf Harman, Pawlik, Überla u.a.: Lit. ). 1901 Hauptachsenmethode durch Pearson bekannt gegeben; die Biometrika wird in Londin gegründet. Spearman veröffentlicht 1904 General intelligence, objectively determined and measured. Seine Idee eines Generalfaktors und die Auseinandersetzung darüber bestimmte die "Gründerjahre" der Pioniere. Thurstone 1931: Multiple factor analysis (Psychological Review), 1934 erscheint The Vectors of Mind.1936 erscheint in der Psychometrika, 1935 an der Universität von Chicago gegründet, dem Mekka des homo ludens psychomathematicus, die berühmte Grundlagenarbeit von Eckart & Young (numerischen Mathematikern auch als SVD-Zerlegung (Singular Value Decomposition) bekannt, die auch bei numerisch instabilen Matrizen eingesetzt wird), beide, nach Muliak (1986, p.25), Mathematiker an der Universitity of Chicago. Mit der Psychometrika setzt eine ungeheure Forschungsaktivität zur Faktorenanalyse ein, die unzählige Varianten, Kriterien und Methoden hervorbringt, was letztlich zu einer ebenso ungeheuren Anzahl von Faktoren führt, die relativ beziehunglos die Zeitschriften und Bücher bevölkern. Dies führte zunehmend mehr auch zur Kritik der Faktorenanalyse und ihrer Methoden, was z.B. auch im Münchner Symposion zur Faktorenanalyse 1967 zum Ausdruck kam, etwa im Einführungsthmea des Organisators Herbert Kallinas mit dem sinnigen Titel "Das Unbehagen in der Faktorenanalyse" (Abstract). U.a. führt er aus:

:

Zwei Jahre vorher, 1965, June 14-19, begannen die internationalen Symposien zu Multivariate Analysis in Dayton, Ohio, dessen 5. 1978 an der University von Pittsburg stattfand. Zu allen Symposien erschien ein Sammelband. Im IV. Bd. befindet sich auch ein Artikel von Bose zum sehr nahen Thema "Early History of Multivariate Statistical Analysis", die heute in allen Programmpaketen nahezu jedermann zur Verfügung steht. Auch das hat die - nicht immer kundige und verantwortungsvolle - Anwendung der Faktorenanalyse sehr stark gefördert.
___
Albert, A.A. (1905-1972): Mathematiker am Department of Mathematics in Chicago, den Thurstone offenbar für eine Analyse gewinnen konnte. The Matrices of Factor Analysis und The Minimum Rank of a Correlation Matrix, beide Arbeiten 1944. [Biographie: 1,2,3,]:


Anmerkung: ein befreundeter Mathematiker, der meine Matrizenprogramme programmiert, hat sich die Arbeit durchgesehen und meint zwei Fehler auf p. 91 gefunden zu haben: In (1) muß die rechte obere Matrix nicht C'sondern  G' lauten und in (2) muß die mittlere Gleichung B = B₀ + Y durch C = C₀ + Y ersetzt werden. Im selben Band wie im Folgeband fand sich kein entsprechender Errata-Eintrag von Albert. Eine Prüfung, ob Alberts Ergebnisse beeinträchtigt werden, wenn die numerischen "Fast-Ränge" in der realen Rechenpraxis berücksichtigt werden, steht noch aus (12.6.6).

Bargmann, R. (1955). Signifikanzuntersuchungen der einfachen Struktur in der Faktoren-Analyse. Mittbl. math. Statist., 7, 1-24. Bargmann, R.E. (1957). A study of independence and dependence in multivariate normal analysis. Chapel Hill: University of North Carolina, Institute of Statistics. Mimeo Series, 186.[Biographie: 1,2,3,]: Unsicher: Bargmann scheint nach den USA gegangen zu sein und in Georgia sowie an der University of North Carolina, Department of Statistics, gelehrt zu haben. Aus einer Quelle: "Professor Rolf Bargmann came from the old school- originally Berlin and then the University of North Carolina-and graduate students were expected to solve linear models on a Wang calculator even as computers were coming of age. "It was good for you," he said." [Q]

Burt, Cyril Lodowic (1883-1973). Burt-Kriterium für die reduzierte Faktorenzahl (Pawlik 1968, S. 169); Kritik des Generalfaktormodells und Vorschlag des Gruppenfaktormodells.  [Biographie: 1,2,3,].

Anmerkung: Burt fiel unangenehm durch äußerst unwahrscheinliche Daten (Korrelationskoeffizitenten bei unterschiedlichen Studien bis auf die dritte Nachkommastelle genau) auf, was ihm posthum den Vorwurf der Datenfälschung einbrachte und natürlich auch ein grundsätzliches Misstrauen in seine sonstigen Arbeiten förderte.


Cattell, Raymond B. (1905-1998):  Versuchte Ordnung in die Flut der Variablen zu bringen und fand ca.50-60 Faktoren in ca. 2000 Testverfahren (Überla S. 6), aber ähnlich wie bei Pawlik letztlich viel allgemein und nichtssagend, wenn mitgeteilt wird, daß dieser oder jener Faktor in diesem oder jenen Zusammenhang gefunden wurde. Wissenschaft, noch dazu, wenn sie mit so viel mathematischen Aufwand betrieben wird, sollte weit mehr herausfinden.  [Biographie: 1,2,3, Bibliohgraphy,]: Screetest. (widerlegt durch Sponsels Fehler-Simulationsstudie und grundlegende Betrachtungen zur Bedeutung der Eigenwerte). Cattell, R. B., Autobiography.  In G. Lindsey (Ed.), A history of psychology in autobiography. New York: Appleton-Century-Crofts, 1973.  pp. 61-100.

Eckart, Carl (1902-1973): Verfasste zusammen mit Young im Band I., Nr. 3, der Psychometrika (1936) die grundlegende Arbeit The approximation of one matrix by an other of  lower rank. [Biographie: 1,2,3,]:

Abstract  The mathematical problem of approximating one matrix by another of lower rank is closely related to the fundamental postulate of factor-theory. When formulated as a least-squares problem, the normal equations cannot be immediately written down, since the elements of the approximate matrix are not independent of one another. The solution of the problem is simplified by first expressing the matrices in a canonic form. It is found that the problem always has a solution which is usually unique. Several conclusions can be drawn from the form of this solution. A hypothetical interpretation of the canonic components of a score matrix is discussed.
Eckart, Carl & Young, Gale (1939). A principal axis transformation for non-hermitian matrices. Bull. Americ. Math. Soc. 45, 118-21.

Garnett, J.C. M  ():  [Biographie: 1,2,3,]: Britischer Faktorenanalytiker. Er soll die Idee der multiplen Faktorenanalyse 1919 entwickelt haben [Q]

• Garnett, J.C. M.  (1919). On Certain Independant Factors in Mental Measurement. Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character, Vol. 96, No. 675 (Sep. 4, 1919),  91-111.
• Garnett, J.C. M.  (1919). General ability, cleverness , and purpose. British Journal of Psychology, IX, 345-366.
• Garnett, J.C. M.  (1932). Further Notes on the Single General Factor  in Mental Measurement. British Journal of Psychology, XXII, 364-72.
[Bislang konnte ich noch nicht einmal die Lebensdaten recherchieren; Hinweise: In seiner Arbeit von 1919 wird er gekennzeichnet als "late Fellow of Trinity College, Cambridge"]

Guttman, Louis (1916-1987): Zahlreiche wichtige und kritische Arbeiten zur Faktorenanalyse, statistisch-orientierten Methodologie und Skalentheorie (u.a. Guttman-Skala). In New York, Brooklyn, als drittes von fünf Kindern geboren und in jüdischen Gemeinschaft von Minneapolis, Minnesota aufgewachsen, wo er während eines Sabbathjahres 1987 auch starb. Magister artium, 1939 an der Universität Minnesota, seine Doktorarbeit 1942 über soziale und psychologische Meßtheorie 1942. Von 1941 bis 1947 war Guttman Professor der Soziologie an der Universität von Cornell, während des Zweiten Weltkriegs Berater der US-Armee. Danach ging er mit seiner Frau, Verhaltensgenetikerin, nach Israel. Er gründete das Israel Institute for Applied Social Research, später in Guttman-Institue umbenannt. In der internationalen Liste der wichtigsten sozialwissenschaftlichen ForscherInnen belegte er Rangplatz 62; viele Preise und Ehrungen. Image-Analyse 1953 (Faktorenanalyse, die nur die durch die multiplen Korrelationen bestimmte Korrelationsmatrix zugrunde legt, was die semi positive Definitheit - die bei den meisten Kommunalitätsmatrizen zerstört ist - erhalten soll); Radextheorie 1953; stabilerer - wenn auch kein sicherer - Algorithmus (im Gegensatz zur Kaiser-Iteration) für eine positiv semi definite Kommunalitätsmatrix (siehe).  Findet 1958, daß die Faktoren-Reduktionsungleichung m <= 1/2(2n+1-SQRT(8n+1) falsch ist. [Biographie: 1,2,3,4,5,]: Dancer, S. (1990) Louis Guttman (1916-1987). American Psychologist, 45, 773- 774.

• Guttman, L. (1938). A note on the derivation of formulae for multiple and partial correlation. Annals of  mathem. Statistics, 9,305-308.
• Guttman, L. (1940). Multiple rectlinear prediction and the resolution into components I. Psychometrika 5, 75-99.
• Guttman, Louis (1941). The quantification of a class attributes: A theory and method of scale construction. In Paul Horst (Ed.), The Prediction of Personal Adjustment (S. 321-348). New York: Social Science Research Council.
• Guttman, L. & Cohen, J. (1943). Multiple rectilinear prediction and the resolution into components II. Psychometrika 8, 169-183.
• Guttman, L. (1944). General theory and methods for matrix factoring. Psychometrika 9, 1-16.
• Guttman, L. (1944). A basis for scaling qualitative data. American Sociological Review, 9, 139-150.
• Guttman, L. (1945). A basis for analysing test-retest reliability. Psychometrika 10, 255-282.
• Guttman, L. (1946). The test-retest reliability of qualitative data. Psychometrika 11, 81-95.
• Guttman, L. (1947). The Cornell Technique for Scale and Intensity Analysis. Educational and Psychological Measurement, (Summer 1947), pp. 247-280.
• Guttman, L. (1950). "The Intensity Component in Attitude and Opinion Research," Studies in Social Psychology in World War II, Vol. 4. In: Samuel A. Stouffer, Louis Guttman, Edward A. Suchman, Paul F. Lazarsfeld, Shirley A. Star, and John A. Clausen. Measurement and Prediction. Princeton, N. J.: Princeton University Press, 1950, pp. 213-277.
• Guttman, L. (1952). Multiple group methods for common factor analysis: their basis, computation, and interpretation. Psychometrika 17, 209-222.
• Guttman, L. (1953). Reliability formulas that do not assume experimental independence. 18, 225-239.
• Guttman, L. (1953). Image theory for the structure of quantitative variates. Psychometrika 18, 277-296.
• Guttman, L. (1953). A new approach to factor analysis: the radex. In: Lazarsfeld, P. F. (1953, Ed.): Mathematical thinking in the Social Sciences, pp. 258-348. New York: Free Press.
• Guttman, Louis (1954). The principal components of scalable attitudes. In Paul F. Lazarsfeld (Ed.), Mathematical thinking in the social sciences (S. 216-257). Glencoe, Ill.: Free Press 1954.
• Guttman, L. (1954). Some necessary conditions for common-factor analysis. Psychometrika 19, 149- 161.
• Guttman, L. (1955). A generalized simplex for factor analysis. Psychometrika 20, 173-191.
• Guttman, L. (1955). The determinancy of factor score matrices with implication for five other basic problems of common-factor theory. Brit. J. Statist. Psychol. 8, 65-81.
• Guttman, L. (1955). Reliability formulas for noncompleted or speeded tests. Psychometrika 20, 113-124.
• Guttman, L. (1956). "Best possible" systematic estimates of communalities. Psychometrika 21, 273-285.
• Guttman, L. (1957). A necessary and sufficient formula for matrix factoring. Psychometrika 22, 79-81.
• Guttman, L. (1957). Simple proofs of relations between the communality problem and multiple correlation. Psychometrika 22. 147-157.
• Guttman, L. (1957). Successive approximation for communalities. Res. Rep. 12, Univ. Calif., Berkeley.
• Guttman, L. (1958). What lies ahead for factor analysis? Educ. psychol. Meas. 18, 497-515.
• Guttman, L. (1958). To what extent can communalities reduce rank ? Psychometrika 23, 297-308.
• Guttman, L. (1968). A general nonmetric technique for finding the smallest coordinate space for a configuration of points. Psychometrika 33, 469-506.
• Guttman, L. (1971). Measurement as structural theory. Psychometrika 36, 329-347.
• Guttman, L. (1977). What Is Not What In Theory Construction. Wissenschaftszentrum Berlin. Internationales Institut für Management und Verwaltung. discussion papers. dp/ 77 - 28.
• Guttman, L. (1977).  Factor Analysis Is But Is Not Image Analysis.  Wissenschaftszentrum Berlin. Internationales Institut für Management und Verwaltung. discussion papers. dp/ 77 - 33.
• Guttman, L. (1977). The Green-McDonald Proof Of The Non-Existence Of Factor Analysis. Wissenschaftszentrum Berlin. Internationales Institut für Management und Verwaltung. discussion papers. dp/ 77 - 36.

Shye, Samuel; Guttman, Louis, Theory Construction and Data Analysis in the Behavioral Sciences. San Francisco, CA: Jossey-Bass, 1978.
_
Harman, Harry H. (1913-1976). Zusammen mit Holzinger 1941 Factor Analysis. A Synthesis of Factorial Methods. [Biographie: 1,2,3,]:  Samuel Messick, Harry Horace Harman (1913–1976), Psychometrika, Volume 42, Issue 1, Mar 1977, Pages 4 - 6. Douglas N. Jackson (1976). Harry H. Harman (1913-1976). Multivariate Behavioral Research. Vol. 11, No. 4, Pages 378-379

Holzinger, Karl J. (1892-1954): Promovierte 1922 an der University of Chicago mit The Indexing of a Mental Characteristic, nach Harman (1954) in Mathematik und Pädagogik mit summa cum laude. Nach der Promotion ging er für kurze Zeit nach London, wo er bei Karl Pearson statistische Theorie und bei Charles Spearman statistische Anwendungen studierte. Danach arbeitete er 32 Jahre nahezu ausschließlich in der Ausbildung an der Universität von Chicago. Bi-Factor Theory (1937). Zusammen mit Harman 1941 Factor Analysis. A Synthesis of Factorial Methods. Er war Präsident der Psychometrischen Gesellschaft 1940 und Vizepräsident der American Statistical Association.

[Biographie: 1,2,3,]:  Harry H. Harman: Karl John Holzinger, Psychometrika Volume 19, Number 2 Date:  June 1954 Pages: 95 - 96. Anmerkung: Das Geburtsjahr wird von der Psychometrika mit 1893? angegeben. Frau Kötter von der UB Erlangen-Nürnberg fand im NUC (National Union Catalogue der Libr. of Congress) das Geburtsjahr 1892 (Danke).
Holzinger, K. J. (1930).  Statistical resume of the Spearman two-factor theory. Chicago: University of Chicago Press.
Holzinger, K. J. (1936). Preliminary reports on Spearman-Holzinger unitary trait study, nos. 1-9. Chicago: University of Chicago. Statistical Laboratory, Dept. of Education.
Holzinger, K. J., Swineford, F., (1937). The bi-factor method. Psychometrika, 2, 41-54.
Holzinger, K. J., assisted by Swineford, F., and Harman, H. H. (1937). Student manual of factor analysis. Chicago: University of Chicago, Dept. of Education.
Holzinger, K. J., Harman, H. H. (1937). Relationships between factors obtained from certain analyses. JEP 28: 321-345.
Holzinger, K. J., Harman, H. H. (1938). Comparison of two factorial analyses. Psych. 3:45-60. 1941. Factor analysis. Chicago: University of Chicago Press.
Holzinger, K. J., Swineford, F., (1939). A study in factor analysis: The stability of a bi-factor solution. Supplementary Educational Monographs, no. 48. Chicago: University of Chicago, Dept. of Education.
Holzinger, K. J. (1942). Why do people factor? Psych. 7:147-156.
Holzinger, K. J. (1944a). Factoring test scores and implications for the method of averages. Psych. 9:155-167.
Holzinger, K. J. (1944b). A simple method of factor analysis. Psych. 9:257-262.
Holzinger, K. J. (1945). Interpretation of second-order factors. Psych. 10:21-25.
Links: [Google Karl J. Holzinger Bibliograpy]


Horst, Paul  (1904?-1999): Vorwegnahme 1937 Idee der Gruppenmethode.  [Biographie: 1,2,3,]: Psychometrika, Vol. 64, No. 2, June 1999 [Not included on CD]

Horst, P. (1937).  A method of factor analysis by means of which all coordinates of the factor matrix are given simultaneously. Psych. 2:225-36.
Horst, P. (1941). A non-graphical method for transforming an arbitrary factor matrix into a simple structure factor matrix. Psych. 6:79-99. 1956.
Horst, P. &  Schaie, K. W. (1956). The multiple group method of factor analysis and rotation to a simple structure hypothesis. J. Exp. Ed. 24:231-37.
Horst, P. (1956). Simplified computations for the multiple group method of factor analysis. Ed. Psych. Meas. 16:101-9.
Horst, P. (1961a. Relations among m sets of measures. Psych. 26:129-49.
Horst, P. (1961b). Generalized canonical correlations and their applications to experimental data. J. Clinical Psych. 14:331-47.
Horst, P. (1962.  Matrix reduction and approximation to principal axes. Psych. 27:169-78.
Horst, P. (1965). Factor analysis of data matrices. New York: Holt, Rinehart, & Winston.
Horst, P. (1972).  Factor matching transformations. Tech. Report 12, no. 3. Eugene: Oregon Research Institute.


Hotelling, Harold (1895-1973): 1933 exakte Ableitung der Hauptachsenmethode. [Biographie: 1,2,3,]: "Hotelling, Harold. Economist, born in Fulda, Minnesota, USA. He was a pioneering economic and statistical theorist who taught at Stanford (1924-31) and Columbia University (1931-46) before establishing a department of mathematical statistics at the University of North Carolina in 1946. His reputation was based on relatively few published articles, but they launched many ideas regarding the economics of location and the ‘new’ welfare economics. His paper, ‘The Economics of Exhaustible Resources’ (Journal of Political Economy, Apr 1931), was ‘rediscovered’ after the oil crisis of 1973." [2]

Hotelling, Harold (1933). Analysis of a complex of statistical variables into principal components. JEP 24:417-41, 498-520.
Hotelling, Harold (1936). Relations betwenn two sets of variates. Biometrika, 1936, 28, 321-377. [Erfindung der kanonischen Korrelationsanalyse]


Householder, A.S. (1904-1993): Zusammen mit Gale Young 1938 Matrix approximation and latent roots. AMM, 45, 165-71.[Biographie: 1,2,3,]. Anmerkung: Householder ist ein bekannter Name in der Mathematik (Householder Transformation).

Jöreskog, (). [LISREL] [Jöreskog University Uppsala]

Joreskog, K. G. (1966). Testing a simple structure hypothesis in factor analysis. Psychometrika, 31, 165-178.
Joreskog, K.G. (1969). A general approach to confirmatory maximum liklihood factor analysis. Psychometrika, 34, 183-202.
Joreskog, K. G. (1970). A general method for analysis of covariance structures. Biometrika, 57, 239-251. [Abstract]
Joreskog, K. G. (1971). Statistical analysis of sets of congeneric tests. Psychometrika, 36, 109-132.
Joreskog, K.G. (1973), "A General Method for Estimating a Linear Structural Equation System," in Goldberger, A.S. and Duncan, O.D., eds., Structural Equation Models in the Social Sciences, New York: Academic Press.
Joreskog, K. G. (1974). Analyzing psychological data by structural analysis of covariance matrices. In R.C. Atkinson, D.H. Krantz, R.D. Luce and P. Suppes (Eds.), Contemporary developments in mathematical psychology - Vol. II (pp. 1-56). San Francisco: W.H. Freeman.
Joreskog, K.G. (1978) Structural analysis of covariance and correlation matrices. Psychometrika, 43, 443-478.
Joreskog, K.G. and Sorbom, D. (1979), Advances in Factor Analysis and Structural Equation Models, Cambridge, MA: Abt Books.
Joreskog, K. G. (1980). Structural analysis of covariance and correlation matrices. Psychometrika, 43, 443-477.
Joreskog, K.G. & Sorbom, D. (1982). Recent developments in structural equation modeling. Journal of Marketing Research, 19, 404-416.
Joreskog, K.G. and Sorbom, D. (1988), LISREL 7: A Guide to the Program and Applications, Chicago: SPSS.
Joreskog, K. G., & Sorbom, D. G. (1989), LISREL 7 user’s reference guide. Mooresville, IN: Scientific Software.
Reyment, Richard & Jöreskog, K. G. (1993). Applied Factor Analysis in the Natural Science. Appendix Computer Programs by Leslie F. Marcus. Cambridge: Cambridge University Press.
Joreskog, K. G. (1994) On the Estimation of Polychoric Correlations and their Asymptotic Covariance Matrix. Psychometrika, 59:3, 381-389.
Joreskog, K. G. and Sorbom, D. (1996) PRELIS 2: User’s Reference Guide. Chicago: Scientific Software International.


Kaiser, Henry F. (1927-1992):  Erfinder des berühmten und beliebten Varimax Kriteriums (1958), das erstaunliche Interpretationsleistungen von varimax rotierten Faktorladungen erbringt (aber). Er entwickelte auch die Alpha-Faktorenanalyse, eine Überprüfungvon mir ergab keinen Vorteil. [Biographie: 1,2,3,]: Stanley A. Mulaik (1992). Henry Felix Kaiser 1927-1992. Multivariate Behavioral Research, Vol. 27, No. 1, Pages 159-171.

Kaiser, Henry F. (1956). Solution for the communalities: A preliminary report. Research report, No. 5 (1956). Berkeley, Calif.: U. of California. Pp. 19.
Kaiser, Henry F. (1956). Note on Carroll's analytic simple structure. Psych., 21 (1956), 89-92.
Kaiser, Henry F. (1956). The varimax method of factor analysis. Unpublished Ph.D. Thesis, U. of California, 1956.
Kaiser, Henry F. (1957).  Further numerical investigation of the Tryon-Kaiser solution for the communalities. Research report, No. 14 (1957). Berkeley, Calif.: U. of California. Pp. 11.
Kaiser, Henry F. (1958). The varimax criterion for analytic rotation in factor analysis. Psych., 23 (1958), 187-200.
Kaiser, Henry F. (1959). Computer program for varimax rotation in factor analysis. Ed. Psych. Measurement, 19 (1959), 413-420.
Kaiser, Henry F. ().  A note on the Tryon-Kaiser solution for the communalities. Psych., 24(1959), 269-71.
Kaiser, Henry F. ().  The application of electronic computers to factor analysis. Ed. Psych. Measurement, 20 (1960), 141-51.
Kaiser, Henry F. (). A note on Guttman's lower bound for the number of common factors. BJ Stat. Psych., 14 (1961), 1-2.
Kaiser, Henry F. ().  Formulas for component scores. Psych., 27 (1962), 83-87.
Kaiser, Henry F. ().  Scaling a simplex. Psych., 27 (1962), 155-62.
Kaiser, Henry F. ().  Image analysis. Chapter in C. W. Harris (ed.), Problems in measuring change. U. of Wisconsin Press, 1963.
Kaiser, Henry F. ().  A method for determining eigenvalues. J. SI AM, 12 (1964), 238-48.
Kaiser, Henry F. & Caffrey, John (). Alpha factor analysis. Psych., 30 (1965), 1-14.
Kaiser, Henry F. & Dickman, Kern W. (1959). Analytic determination of common factors. Unpublished manuscript, U. of Illinois, 1959. Pp. 7 + 12.


Kelly, Truman Lee (1884-1961?).

Kelley, Truman Lee (1935). Essential traits of mental life. Harvard Studies in Education, 26 (1935). Cambridge, Mass.: Harvard U. Press. Pp. 146.
Kelley, Truman Lee (1940). Comment on Wilson and Worcester's "Note on factor analysis." Psych., 5 (1940), 117-20.
Kelley, Truman Lee (1940). Talents and tasks: Their conjunction in a democracy for wholesome living andnational defense. Harvard Education Papers, No. 1 (1940). Cambridge, Mass.: Grad. School of Ed., Harvard U. Pp. 48.


Kalveram, K.T. (? -):  Einer der wenigen, der 1970 klipp und klar den Standpunkt vertreten hat, daß eine Korrelationsmatrix der Ordnung m nur in dem Umfang m-k auf Faktoren k < m zurückgeführt werden kann wie sie positiv semi definit ist - also Eigenwerte von 0 oder nahe 0 aufweist. [Biographie: 1,2,3,]:

Lawley, D.N.(? - ?):  1940 Schätzung der Faktorenladungen nach der Maximum Likelihood Methode [Implementierung in Matlab]. Zusammen mit Maxwell, A.E. (1963) Factor analysis as a statistical method. Werke Im Prinzip wird hier das übliche statistische Ritual gespielt: es wird unter unrealistischen (multinormnalverteilte Variable) und unprüfbaren Annahmen (orthogonale gemeinsame Faktoren liegen vor) getestet, ob und wie ein Ergebnis mit einer solchen Anahmen verträglich ist oder nicht. Aber immerhin: es wird getestet und eine strukturelle Hypothese vorgegeben [aber]. [Biographie: 1,2,3,]: In der Arbeit der Biometrika, TESTS OF SIGNIFICANCE IN CANONICAL ANALYSIS, wird Lawley zugeordnet dem Mathematical Institute, University of Edinburgh.

Lawley, D. N. (1938).  A generalization of Fisher's z test. Biometrika, 30, 180-187.
Lawley, D. N. (1939).  A Correction to "A Generalization of Fisher's z test" Biometrika, January 1939; 30: 467 - 469.
Lawley, D. N. (1940) The estimation of factor loadings by the method of maximum likelihood, Proceedings of the Royal Society of Edinburgh, 60, 64-82.
Lawley, D. N. (1941) Further investigations in factor estimation, Proceedings of the Royal Society of Edinburgh, 61, 176-185
Lawley, D. N. (1943). A note on Karl Pearson's selection formulae. Proceedings of the Royal Society Edinburgh, Section A, 62, 28±30
Lawley, D. N. (1953). A modified method of estimation in factor analysis and some large sample results. In: Uppsala Symposium on Psychological Factor Analysis, Number 3 in Nordisk  Psykologi Monograph Series, pp. 35–42. Uppsala: Almqvist and Wiksell.
Lawley D. N.  (1956). Tests of significance for the latent roots of covariance and correlation matrices. Biometrika.1956; 43: 128-136
Lawley, D. N. (1956).  A general method for approximating to the distribution of likelihood ratio criteria Biometrika, December 1956; 43: 295 - 303.
Lawley D. N. Tests of significance in canonical analysis. J. Biometrika 1959; 46:59-66.
Joreskog, K. G., & Lawley, D. N. (1968). New methods in maximum likelihood factor analysis. British Journal of Mathematical and Statistical Psychology, 21, 85-96.
Lawley, D. N., Maxwell, A. E. (1971) Factor Analysis as a Statistical Method, 2nd edn, Butterworth, London
Lawley, D. N., Maxwell, A. E.  (1973). "Regression and Factor Analysis." Biometrika 60(2): 331-338.


Maxwell, A.E. (). [Biographie: 1,2,3,]:

Maxwell, A. E.: (1959). Statistical methods in factor analysis. Psychol. Bull. 56, 22S-235
Maxwell, A. E.: (1961). Recent trends in factor analysis. J. roy. Statist. Soc. A  124,  49-59


Pawlik, Kurt (1934*): 1968 Umfangreiche Sammlung und Zusammenschau empirischer Ergebnisse, aber letztlich viel zu allgemein und nichtssagend, wenn mitgeteilt wird, daß dieser oder jener Faktor in diesem oder jenen Zusammenhang gefunden wurde. Wissenschaft, noch dazu, wenn sie mit so viel mathematischen Aufwand betrieben wird, sollte weit mehr herausfinden. [Biographie: 1,2,3,]


Pearson, Karl (1857-1936) : 1901 Hauptachsenmethode. [Biographie: 1,2,3,]:

Rao, C.R. (1920-): 1955 Signifikanztests, kanonische Faktorenanalyse. [Biographie: 1,2,3,]:

Spearman, Charles (1863-1945): 1904 General intelligence, objectively determined and measured. Idee des Generalfaktors. [Biographie: 1,2,3,]:

Spearman, Charles (1904). General intelligence, objectively determined and measured. Am. J. of Psychology 15:201-93.
Spearman, Charles (1913). Correlations of sums and differences. BrJP 5:417-26.
Spearman, Charles & Holzinger, K. J. (1924).  The sampling error in the theory of two factors. BrJP 15:17-19.
Spearman, Charles & Holzinger, K. J. (1925).  Note on the sampling error of tetrad differences. BrJP 16:86-88.
Spearman, Charles & Holzinger, K. J. (1929). Average value for the probable error of tetrad-difference. BrJP 20:368-70.
Spearman, Charles (1927). The abilities of man. New York: Macmillan.
Spearman, Charles (1937). Abilities as sums of factors, or as their products. JEP 28:629-31.
Korrelationsmatrizenanalysen in der IP-GIPT:  Numerisch instabile Korrelations-Matrizen bei Spearman. * Kollinearitätsanalyse und Therapie der indefiniten Spearman- & Hart- Matrix (1913).

Thomson, Godfrey H. (1881-1955): [Biographie: 1,2,3,]: Frei nach Thurstones Nachruf (Psychometrika, 20,3,171f) : Godfrey Thomson wurde in Carlisle, England am 27. März 1881 geboren. Er studierte an der Universität von Rutherford, Armstrong Universität (jetzt King's College), der Universität von Durham und der Universität von Straßburg. In der Armstrong Universität war er "Open Exhibitioner",  "Junior Pemberton Scholar", und "Charles Mather Scholar". Später wurde er zum Pemberton Fellow der Universität von Durham ernannt, wo er den M.Sc. Grad in der Mathematik und Physik erhielt. Im Anschluss daran war er an der Universität Strassbourg in Deutschland auf und 1906 wurde ihm der Ph.D. [Dr. phil], summa cum laude, zuerkannt. An diesem Punkt wandelte sich sein Interesse von den Naturwissenschaften hin zur Psychologie. Nach dem Empfang des D.Sc. Grads in der Psychologie 1913 akzeptierte er die Position eines Lecturer in Education  der Ausbildung in der Armstrong Universität. 1920 wurde er Professor und Chef der Ausbildungsabteilung bis 1925. Während dieser Periode besuchte er die Vereinigten Staaten als Gastprofessor der Ausbildung an der Universität von Columbia, 1923-24. Sein zweiter Besuch in USA 1933 verbrachte er als als  Lehrender der Yale Summer School.. Von 1925 bis zu seinem Ruhestand 1951 hielt er den gemeinsamen Posten des Professors der Ausbildung an der Universität Edinburghs und Studiendirektors, Edinburghs Provinzielles Komitee für die Ausbildung von Lehrern. Er nahm zahlreiche wichtige Funktionen und erhielt zahlreiche Ehrungen; 1949 wurde er geadelt ("Sir").

Thomson, Godfrey H. (1916). A hierarchy without a general factor. BrJP 8:271-81.
Thomson, Godfrey H. (1934). Retelling's method modified to give Spearman's g. JEP 25:366-74.
Thomson, Godfrey H. (1935).  On complete families of correlation coefficients and their tendency to zero tetrad-differences: Including a statement of the sampling theory of abilities. BrJP 26: 63-92.
Thomson, Godfrey H. (1936).  Boundary conditions in the common-factor-space, in the factorial analysis of ability. Psych. 1: 155-63.
Thomson, Godfrey H. (1938a). Methods of estimating mental factors. Nature 141: 246.
Thomson, Godfrey H. (1938b). The estimation of specific and bi-factors. JEP 29: 355-62.
Thomson, Godfrey H. (1939). The Factorial Analysis Of Human Ability. London: The University of London Press.
Thomson, Godfrey H. (1949).  On estimating oblique factors. BrJP Slat. Sec. 2: 1-2.
Thomson, Godfrey H. (1951).  The factorial analysis of human ability. 5th ed. New York: Houghton Mifflin.


Tucker (1910-2004) [Biographie: 1,2,3,]:

Thurstone, L.L. (1887-1955):  Multiple Faktorenanalyse. [Biographie: 1,2,3,]: Psychometrika: Thurstone, Vol. 20, No. 4, December 1955 und  A Tribute To L. L. Thurstone, Vol. 21, No. 4, December, 1956.

Thurstone, L. L. (1931). Multiple factor analysis. Psych. Rev. 38:406-27.
Thurstone, L. L. (1934). The vectors of mind.  Psychological Review, 41, 1-32.
Thurstone, L. L. (1935).  The vectors of mind. Chicago: University of Chicago Press.
Thurstone, L. L. (1938a). A new rotational method in factor analysis. Psych. 3:199-218.
Thurstone, L. L. (1938b). Primary mental abilities.  Psychometric Monographs.  No.   1.  Chicago: University of Chicago Press.
Thurstone, L. L. (1940). Current issues in factor analysis. Psych. Bull. 37:189-236.
Thurstone, L. L. (1944).  Second-order factoring. Psych. 9:71-100.
Thurstone, L. L. (1945a). A multiple group method of factoring the correlation matrix. Psych. 10: 73-78.
Thurstone, L. L. (1945b). The effects of selection in factor analysis. Psych. 10:165-98.
Thurstone, L. L. (1947). Multiple factor analysis. Chicago: University of Chicago Press. [Chapter 2: Fundamental Equations]
Thurstone, L. L. (1954). An analytical method for simple structure. Psych. 19:173-82.
Thurstone, L. L. (1955). A method of factoring without communalities. Proceedings of the 1954 Invitational Conference on Testing Problems. Princeton, N.J.: Educational Testing Service. Pp. 59-62, 64-66.


Young, Gale (? - ?): Hat zusammen mit Eckart in der Psychometrika 1936 das sog. Eckart-Young Theorem veröffentlicht (heute SVD-Zerlegung): Internet-Quelle. [Biographie: 1,2,3,]:
___
Literatur zur Geschichte der Faktorenanalyse [In Arbeit] * Links zur Geschichte der Psychologie *
Hinweis: Die 25jährigen Jubiläumshefte der Psychometrika enthalten auch historische Rückblicke zum Gesamtfeld Psychometrie, wobei die Faktorenanalyse erfahrungsgemäßig einen größeren Anteil hat (25 Jahre: 1961; 50 Jahre: 1986; der  75 Jahre-Rückblick wird also 2011 zu erwarten sein.). Eine weitere Quelle sind die Nachrufe in der Psychometrika (Überblick).

• Bose, R. C. (1975). Early History of Multivariate Statistical Analysis. In (3-22): Krishnaiah, Paruchuri R. (1975, Ed.), Multivariate Analysis. Proceedings oft the fourth International Symposion on Multivariate Analisis. Amsterdam: North Holland.
• Burt, Cyril (1966). The early history of of multivariate techniques in psychological research. Multivar. Behv. Res.,1, 24-42.
• Cattell, R. B. (1990). The birth of the Society of Multivariate Experimental Psychology.  Journal of the History of the Behavioral Sciences, 26, January, 1pp. 48-57.
• Dodd, S, C. (1928). The theory of factors. I., II. Psychological Review 35, 211-234; 261-279.
• Dunlap, Jack W. (1961). Psychometrics - A special Case Of The Brahman Theory. Psychometrika, 26,1, 65-71.
• Guilford, J.P. (1936). History of Factor Theory and Factor Methods. In (458-471): Psychometric Methods.New York: McGraw-Hill. [Das Buch beginnt mit einer Galerie der "Pioneers in Psychometric Methods": Weber, Fechner, Müller, Galton, Binet, J.McKeen Cattell * Spearman, Terman, Urban, Thorndike, Thurstone, Kelly.]
• Harman, Harry H. (1970). Brief History of Factor Analysis. In: Modern Factor Analysis, 3-6.Chicago: The University of Chicago Press.
• Maxwell, A. E.: (1961). Recent trends in factor analysis. J. roy. Statist. Soc. A  124,  49-59
• Millsap, Roger E. & Meredith, William  (2004). Factorial Invariance: Historical Trends and New Developments.
• Mulaik, Stanley A. (1972). Brief History Of Factor Analaysis As A Linear Model. In (p.5-10): The Foundations Of Factor Analysis. New York: McGraw-Hill.
• Moody, Caesar B. (1953). Historical Outline of Concepts of Mental Ability As a Background for Current Factor Theories. Peabody Journal of Education, Vol. 30, No. 4 (Jan., 1953) , pp. 194-204
• Muliak, Stanley A. (1986). Factor Analysis and Psychometrika: Major Developments. Psychometrika 51, 23-33.
• Pawlik, Kurt (1968). Die Entwicklung der faktorenanalytischen Forschung in der Psychologie. In: Dimensionen des Verhaltens, 21-27. Bern: Huber.
• Royce, J.R. (1958). The development of factor analysis. Journal of General Psychology, 92, 139-164. [Auszug]
• Schönemann, P. H., & Wang, M. M. (1972). Some new results on factor indeterminacy. Psychometrika, 37, 61-91.
• Steiger, J. H., & Schönemann, P. H. (1978). A history of the factor indeterminacy. In S. Shye (Ed.), Theory construction and data analysis in the behavioral sciences.. San Francisco: Jossey-Bass.
• Stephenson, W. (1936). The foundations of psychometry: Four factor systems. Psychometrika, I, 195-209.
• Überla, K. (1971). Die historische Entwicklung. In (7-10): Faktorenanalyse. Berlin: Springer.
• Vincent, P.F. (1953). The origin and development of factor analysis. Applied Statistics,2, 107-117.
• Wolfle Dael (1940). Factor Analysis to 1940. Chicago: University of Chicago Press. [Quelle Dodd, p.204]
__
Sonstiges Faktorenanalyse
• Revenstorf, D. (1978) Vom unsinnigen Aufwand in der Faktorenanalyse. Archiv für Psychologie, 1978, 13, 1 - 36.
__
Links zur Geschichte der Faktorenanalyse:
• Factorial Invariance: Historical Trends and New Developments.
• History of LISREL.
• [PDF] Factor Analysis in the 1980’s and the 1990’s: Some Old Debates and ...

 
___
statistische Rituale. Teilweise besteht die die Test- und Signifikanzstatistik aus völlig absurden oder nichtssagenden szientistischen Ritualen, wenn etwa eine Annahme gegen eine andere Annahme gestestet wird, statt zu prüfen, ob eine Annahme stimmt. Wenn die Daten multinormalverteilt wären und wenn eine Zufallsstichprobe gezogen worden wäre, und wenn die Daten Intervallniveau hätten und wenn die hypothetischen Faktoren orthogonal wären, dann ...  Man spielt in einer Welt der Möglichkeiten, statt die Realität vernünftig zu untersuchen. Hinzu kommt, daß es kaum etwas Nichtssagenderes gibt als die Aussage, irgend etwas sei signifikant - of relativ zu abenteuerlichen Anahmen, die meistens gar nicht mitgeteilt, geschweige denn begründet werden. Im formalen szientistischen Theater gehen dann sämtliche Inhalte und eigentlichen Fragen ganz schnell unter. Die Schnittstelle zwischen angewandter Mathematik, Wirklichkeit und Empirie, Theorie und Begründung und praktischer Nützlichkeit ist empfindlich gestört.
___

---

Querverweise
Standort: Kommunalität.

Überblick der Dokumentationen zur Handhabung der Faktorenanalyse.
Kritik der Handhabung der Faktorenanalyse.
Was für ein Typ Matrix entsteht durch Faktorenanalysen?.
Zur Widerlegung des dubiosen Screetest-Kriteriums:
Fortlaufende und vorläufige Hauptergebnisse des Eigenwertverhaltens bei den F%*30 Fehlersimulationsversuchen vom Typ Quader.
* Korrelation * Partielle Korrelation *
Überblick Numerisch Instabile Matrizen und Kollinearität in der Psychologie.
Zahlenmystik und numerologische Esoterik in Statistik und Testtheorie.
Überblick Arbeiten zur Definitionslehre, Methodologie, Meßproblematik, Statistik und Wissenschaftstheorie.
*

Suchen in der IP-GIPT, z.B. mit Hilfe von "google": <suchbegriff> site:www.sgipt.org z.B. Faktorenanalyse site:www.sgipt.org.

*
Dienstleistungs-Info.
*

---


Zitierung
Sponsel, Rudolf  (DAS). Kommunalität. Zur Geschichte und Kritik einer Idee und ihrer fragwürdigen Operationalisierung. Von der multiplen Paradoxie wie willkürliche Definitionen unlösbare Scheinprobleme schaffen und lösen.
https://www.sgipt.org/wisms/fa/com/Kommun0.htm
Copyright & Nutzungsrechte
Diese Seite darf von jeder/m in nicht-kommerziellen Verwertungen frei aber nur original bearbeitet und nicht  inhaltlich verändert und nur bei vollständiger Angabe der Zitierungs-Quelle benutzt werden. Das Einbinden in fremde Seiten oder Rahmen, die die Urheberschaft der IP-GIPT nicht jederzeit klar erkennen lassen, ist nicht gestattet. Sofern die Rechte anderer berührt sind, sind diese dort zu erkunden. Sollten wir die Rechte anderer unberechtigt genutzt haben, bitten wir um Mitteilung. Soweit es um (längere) Zitate aus  ...  geht, sind die Rechte bei/m ... zu erkunden oder eine Erlaubnis einzuholen.

---


  Ende_Kommunalität_ Überblick  _ Relativ Aktuelles  _ Rel. Beständiges  _ Titelblatt  _ Konzept  _  Archiv  _ Region _ Service iec-verlag _ Mail: sekretariat@sgipt.org  _Wichtige Hinweise zu Links und Empfehlungen


---

---

Änderungen wird gelegentlich überarbeitet, ergänzt und vertieft * Anregungen und Kritik willkommen
03.10.12    Einige wichtigere praktischen Sätze zur Kommunalität  (begonnen)
01.10.12    Kommunalitätsmatrix ein Bastard (Hybrid).  Zwei Arbeiten von Lauwerth nachgetragen (u.a. die Dissertation zur Kommunalität)
07.01.11    Guttman-Literaturliste überarbeitet.
07.01.10    Nachtrag Kritik Rinnes (2000) an der Faktorenanalyse.
29.11.07    Nachtrag Eckart & Young (1939).
22.07.07    Nachtrag Garnett, J.C.M.
06.09.06    Korrektur: richtig: Wolfle, falsch: Wolfe.
13.08.06    Nachtrag Kallina: 50-dimensionaler Raum mit 1000-Billionen-Zellen.
26.07.06    Mulaik "A brief history ..."
16.07.06    Anmerkung zur teils missverständlichen Darstellung Wermuths zu Heywood.
06.07.06    GIF-Faksimile: Grundbegriffe und Notation von Thurstone 1935.
05.07.06    Ergebnis zu Heywoods Kritik an der FA * Giftige Anmerkung zum Missbrauch von Heywoods Namen * Kreation Freistilmathematik *
30.06.06    Kritische Fußnote untere Schranke der multiplen Bestimmtheitsmaße - biographische Angaben zu Guttman.
28.06.06    Abstract Guttman (1954):  Some necessary conditions for common-factor analysis.
25.06.06    Biographische und bibliographische Ergänzungen.
22.06.06    Quintessenz Kommunalitätenlösung nach Harmans letzter Auflage 76 * Anmerkung zur Metaphysik der Hauptdiagnonalen * Quelle Nachrufe in der Psychometrika aufgenommen * Holzinger Lebensdaten. *
21.06.06    Wichtige historische Daten nach Royce * Einschränkende Bemerkung zu Guttmans Kommunalitäten-Iterations-Algorithmus (nicht immer erfolgreiche positiv semi definite Lösung). Kritische Anmerkung zu Harman, Literatur zu zitieren, die wissenschaftsöffentlich nicht zugänglich ist.
20.06.06    Notation von Holzinger & Harman (1941).
14.06.06    statistische Rituale * Geschichte, Pioniere und Gestalter der Faktorenanalyse, Lit-Nachträge *
13.06.06    Abstract Lukesch & Kleiter. * Relativierung zur Priorität der Grundgleichungen im Grundmodell (Holzinger & Harman versus Thurstone).
12.06.06    Anmerkung zu zwei Notationsfehlern in Albert (1944) * GIF-Faksimile aus Alberts Einleitung mit Bezug auf Thurstone * GIF-Faksimile Beleg Grundgleichungen nach Thurstone (1947) und Harman (1970).
11.06.06    Anmerkung zum Begriff Kommunalitätsmatrix * Nachtrag Zusammenschau Pawlik * Lit. Gesch. d. FA * Nachtrag Rotation *Auszug aus Kallina Münchner Symposion 1967 *  Ergänzung Ktitik an Thurstones Figure 2. * Zum Begriff gemeinsamer und spezifischer Faktor, * kritische Anmerkung.
09.06.06    Kritische Bemerkung Suibert Ertels zur angeblichen Variablenreduktion aufgenommen. * Ergänzende Krititik (Fazit) * Pioniere und Gestalter der Faktorenanalyse angelegt [in Arbeit].