(ISSN 1430-6972)
IP-GIPT DAS=07.03.2004 Internet-Erstausgabe, letzte Änderung: 08.08.20
Impressum: Diplom-Psychologe Dr. phil. Rudolf Sponsel Stubenlohstr. 20 D-91052 Erlangen
Mail: sekretariat@sgipt.org_ Zitierung & Copyright
Anfang_ ProzentRANG_ Datenschutz_Überblick_ Rel. Aktuelles _ Rel. Beständiges_ Titelblatt_ Konzept_ Archiv_ Region_ Service iec-verlag_ _Wichtige Hinweise zu externen Links und Empfehlungen_
Willkommen in der Abteilung Wissenschaft unserer Internet-Publikation GIPT 1) , Bereich Meß- und Testtheorie, hier speziell zum Thema:
ProzentRANG
Bedeutung, Berechnung, Problemlösungen,
Literatur, Links.
von Rudolf Sponsel, Erlangen [Quelle]
- Inhaltsübersicht
- Was ist ein ProzentRANG (PR) ?.
- Testpsychologische Interpretation.
- Testtheoretischer und statistischer Sinn und Nutzen des ProzentRANGmaßes.
- ProzentRANG-Kuriositäten.
- Abhängigkeit statistischer Normen von den Stichproben und Grundgesamtheiten.
- Dichte und Differenziertheit von ProzentRÄNGen.
- Unterschiedliche ProzentRANG-Bestimmungsmethoden.
- Beispielberechnung unmittelbare direkte und häufigkeitsinterpretierbare Methode.
- Umgang mit fehlenden Prozentrangnormen in der Bezugs-(Eich)-Stichprobe.
- 1) Intervallgrenzen-Regel.
- 2) Näherungsregel.
- 3) Auf- und Abrundregel zugunsten der ProbandIn.
- 4) Interpolations-Regel.
- Beispiel ProzentRANGberechnung der Anzahl der Corona-Neuinfektionen Deutschland.
- Beispiel ProzentRANGberechnung der Anzahl der Corona-Neuinfektionen Berlin.
- Prozentrang-Interpretationen bei Vergleichen.
- Exkurs: Messen in der Psychologie.
- Exkurs: Berücksichtigung der ProzentRANGidee im Alltag und Leben.
- Literatur (Auswahl).
- Links (Auswahl).
- Querverweise.
Was ist
ein ProzentRANG (PR) ?
Stellen Sie sich 100 unterschiedlich große Menschen der Größe
nach von links nach rechts aufsteigend geordnet vor. Der kleinste in dieser
Reihe hat nun den ProzentRANG PR=1, der größte
den PR=100. Derjenige mit dem ProzentRANG von 50 ist größer
als die 49 vor ihm und kleiner als die 50 nach ihm in der Reihe. Der ProzentRANG
sagt uns also etwas über den RANG oder die STELLUNG,
die jemand in einer bestimmten Stichprobe einnimmt - und nicht, wie groß
jemand ist..
Wie man sieht, kann man den ProzentRANG
sehr schön und klar verstehen. Das Wort RANG hat hier
auch seine wichtige Bedeutung. Aus dem RANG oder der Stellung
in der Stichprobe erfahren wir nämlich nicht, wie stark oder wie sehr
die Unterschiede sind, wir erhalten nur eine RANG-Information
vom Typ, mehr, weniger oder größer, kleiner. Es ist also möglich,
daß zwei nahe beieinander liegende Testwerte weit auseinanderliegende
ProzentRÄNGE aufweisen ebenso wie, daß zwei weiter
auseinanderliegende Testwerte nahe beieinander liegende ProzentRÄNGE
zeigen.
| DerProzentRANG ist ein
außerordentlich nützliches und unmittelbar verständliches
statistisches Rang-Maß. Er gibt die relative Stellung
an, die man bezüglich eines bestimmten Merkmals in einer Vergleichs-
oder Bezugsgruppe einnimmt. Daher ist eine ProzentRANG-Angabe
ohne Nennung der Vergleichs- oder Bezugsgruppe wenig sinnvoll, wie
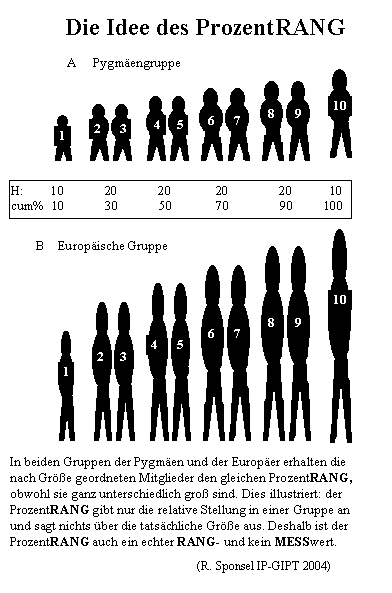
man der Illustration entnehmen kann: Der "Kleine" (Große) unter den
"Kleinen" (Großen) erhält einen ebenso geringen (großen)
ProzentRANG wie unter den Großen. Man muß aufpassen, ihn nicht
mit dem Prozentwert (Anteil von einem Ganzen) zu verwechseln,
obwohl natürlich die Berechnung auch auf einer Prozentrechnung beruht.
In der Illustration bezeichnen die Ziffern 1-10 die Namen der Mitglieder. In beiden Bezugs- oder Vergleichsgruppen könnte man 2 und 3, 4 und 5, 6 und 7, 8 und 9, vertauschen, da diese gleich groß sind. An den ProzentRÄNGEN würde sich nichts ändern. Die Häufigkeiten H, der Prozentanteil von der Größe der Stichprobe, hier N(Pygmäen) = 10, N( Europäer) = 10 ändern sich nicht. |
 |
Begriffsumfeld ProzentRANG
>
Normwerte.
Häufigkeit, relative Häufigkeit, Häufigkeitsverteilung,
Quantil, Quantile, Quartil,
1. Quartil, 3. Quartil, Median,
Mittelwerte,
Modalwert,
Percentil, Normen, Flächennorm, T-Werte
(McGall),
Transformation,
Ausprägung, Rohwerte, Rang, nonparametrisch, Verteilung.
Testpsychologische Interpretation:
Der Prozentrang PR gibt an, welche Rangposition eine BearbeiterIn in einer Bezugs-Stichprobe einnimmt. Ein PR=50 bedeutet im allgemeinen (hochgerechnet), sofern die Stichprobe und die Feindifferenzierung der Werte groß genug sind, daß jemand mit seinem Testwert 49% der Stichprobe übertrifft und selbst von 50% übertroffen wird. Als statistischen Durchschnittsbereich zählt man gewöhnlich die mittleren 50 Prozent, also den Bereich 25<=PR<=75. Der PR=25 hat den Namen "1. Quartil", der PR=50 heißt Median und PR=75 heißt 3. Quartil.
Die Psycho-Fachschaft der Uni-Osnabrück definiert kurz und bündig: "Prozentrangnormen = Wahrscheinlichkeit, einen solchen oder kleineren Rohwert in der Normverteilung zu finden."
Prozentrangnormen sind vernünftige und unmittelbar nachvollziehbare
Ausprägungs-Normen. Vereinfacht kann man sagen: wer viele Aufgaben
im Sinne des Merkmals löst, verfügt über viel Ausprägung
des Merkmals. Voraussetzungen
für eine wissenschaftlich einwandfreie Interpretation sind:
- die Anzahl der im Sinne der Bewertung erfolgten Bearbeitungen ist eine repräsentative Abbildung der Ausprägung des erfaßten Merkmals;
- die Bearbeitung erfolgte wahrheitsorientiert und motiviert. Bei introspektiven Verfahren (wo die BearbeiterIn etwas über ihr Innenleben und sich selbst mitteilt) muß man
- zusätzlich voraussetzen, daß sie über diese Fähigkeit verfügt und sie auch richtig anwendet.
Bei Leistungstests ist Voraussetzung (1) und (2) eher als erfüllbar
anzusehen als im Persönlichkeitsbereich. Außerdem muß
man streng zwischen den verschiedenen Erhebungssituationen unterscheiden:
Menschen bearbeiten Tests ganz unterschiedlich, je nachdem um was es für
sie geht und was davon abhängt. Tests - wie auch jede andere Art der
Informationsgewinnung - unkritisch in interessegeleiteten psychologischen
Untersuchungen anzuwenden ist daher ein Kunstfehler. Nirgendwo dürfte
Wahrheit und Wirklichkeit von den Parteien so individuell interessegeleitet
wahrgenommen und ausgedrückt werden, wie dort, wo es für die
Betroffenen um etwas geht (Wirtschaft, Gericht, Prüfung, Erwerb eines
Privilegs usw.).
Testtheoretischer
und statistischer Sinn und Nutzen des ProzentRANGmaßes
Gutjahr (1971,
S. 94) schreibt: "Die Prozentrang-Transformation führt zu psychologisch
relevanten Werten. ... Mit der Prozentrangskala sind die Willkürlichkeit
und Zufälligkeiten der Rohskalen überwunden."
Anmerkung: Das logistische Testmodell
von Rasch will mit seinem Konzept der spezifisichen Objektivität
die Stichprobenabhängigkeit der Testwerte ganz überwinden, was
m.E. sehr fraglich und unrealistisch ist.
ProzentRANG-Kuriositäten
Auch sehr geringe Ausprägungen können hohe ProzentRÄNGE
bekommen, wenn sehr viele in der Stichprobe geringe Ausprägungen ankreuzen
(z.B. die Frage nach einem Phäochromozytom).
Zur richtigen Interpretation eines ProzentRANGs muß
man neben der Polung
des erhobenen Sachverhalts auch den Testwert selbst berücksichtigen.
Manche Merkmale haben nur hohe ProzentRÄNGE, wenn etwa in einem Fragebogen
als letzte Frage "Ich habe alle Fragen verstanden und sorgfältig bearbeitet"
erfaßt wird.
Abhängigkeit
statistischer Normen von den Stichproben und Grundgesamtheiten
Statistische Werte wie der ProzentRANG sind grundsätzlich
abhängig von der Stichprobe bzw. der Grundgesamtheit (Population)
aus der die ProbandInnen ausgewählt werden. Eine statistische Norm
erfordert daher stets eine Bezugsangabe zu einer Stichprobe und Grundgesamtheit.
Dichte
und Differenziertheit von ProzentRÄNGen
Theoretisch können die ProzentRÄNGE beliebig
dicht und genau gefaßt werden, wenn 1) die Test- oder Meß-Werte
fein genug und 2) genügend ProbandInnen zur Verfügung stehen
und 3) die Testwerte dieser ProbandInnen sich entsprechend differenziert
verteilen. Wenn in einem Test (Untertest), nur wenige numerische Differenzierungen
zur Verfügung stehen, können auch nur wenige ProzentRANGnormen
erfaßt werden (die ProzentRÄNGE sind in der Praxis
also meist diskret und quantisch).
Unterschiedliche
ProzentRANG-Bestimmungsmethoden
Es gibt unterschiedliche ProzentRANG-Definitionen und
damit auch Bestimmungsmethoden. Welche man wählt, hängt von den
Zielen und Zwecken ab, die man verfolgt. Die hauptsächlichsten Methoden
sind:
- Unmittelbar direkte und häufigkeitsinterpretierbare Methode
- Intervalle und Klassenbildung mit Mittengrenzen [Formel z.B. bei Lienert 1969, S. 333]
- Spezielle Bestimmungen, um PR=0 oder PR=100 zu vermeiden
- Spezielle Schätzmethoden zur Bestimmung in der Eichstichprobe nicht vorkommender Werte
Beispielberechnung
unmittelbare direkte und häufigkeitsinterpretierbare Methode
Prozentrangbestimmung bei einem Test mit 14 Ausprägungsmöglichkeiten
Testwerte W1 W2 W3 W4 W5
W6 W7 W8 W9 W10 W11 W12 W13 W14
Häufigkeit 0 0 0
3 0 5 6 3 0
9 4 7 0 0
Summiert 0 0 0
3 3 8 14 17 17 26
30 37 37 37
ProzentRANG 0 0 0 8
8 22 38 46 46 70 81 100
100 100
Hier besteht die ProzentRANGbestimmung darin: Man bestimmt nun die relative Häufigkeit H, mit der jeder Wert in der Stichprobe vorkommt und trägt bei jedem Wert ein (Zeile Häufigkeit), wie oft er in der Stichprobe vorkommt. Anschließend summieren wir die relative Häufigkeit von jedem Wert zum nächsten Wert auf (Zeile Summiert).
Umgang mit fehlenden Prozentrangnormen in der Bezugs-(Eich)-Stichprobe
Die in die verschiedenen Normstichproben eingegangenen Werte erschöpfen oft nicht sämtliche theoretisch möglichen Werte. Es kann daher sein, daß man auf einen Testwert stößt, für den es noch keine direkt zugeordnete Prozentrangnorm in den Tabellen gibt. Im wesentlichen sind drei Fälle zu unterscheiden: (1) es gibt ein neues Minimum; (2) es gibt ein neues Maximum; (3) es gibt einen neuen Zwischenwert. Auch hier gibt es eine Reihe unterschiedlicher Methoden, für fehlende Testwerte in der Normstichprobe die ProzentRÄNGE zu schätzen.
1) Intervallgrenzen-Regel
Nach dieser Regel muß man gar nicht rechnen, sondern man gibt
einfach die obere und untere Intervallgrenze der Prozentränge an zwischen
denen sich der gesuchte befinden muß. Liegt ein erhaltener Testwert,
z.B. 56, zwischen den schon statistisch verarbeiteten von TW< = 48 mit
PR(48) = 65 und TW> = 61 mit PR(61) = 76, so gibt man einfach nur an PR
= 65(48) < PR(56) < PR = 76(61). Ist der kleinste Testwert bei einer
Dimension in der Normstichprobe z.B. 11 für den sich ein ProzentRANG
von z.B. 4 ergab und erzielt eine ProbandIn ein neues Minimum mit Testwert
0, dann ist die beste Angabe PR < 4.
2) Näherungsregel
Man wähle den Prozentrang, der dem Testwert am nächsten kommt.
Beispiel: Gegeben seien folgende Testwerte mit zugeordneten ProzentRANGwerten:
TW< = 17 mit PR< = 57 und TW> = 33 mit PR> = 62, erhaltener Testwert
sei TWerhalten = 22. Der TWerhalten ist näher an 17 als an 33. Also
wähle man nach der Näherungsregel den PRgeschätzt = 57.
Diese Regel ist anwendbar für Fälle bei denen die erhaltenen
Testwerte nahe bei einem schon statistisch erfaßten liegen. Hat eine
ProbandIn ein neues Minimum oder Maximum, das bei der statistischen ProzentRANGbestimmung
noch nicht vorlag, so kann man als Schätzung dem neuen Minimum oder
Maximum den ProzentRANG des alten Minimums oder Maximums zuordnen. Die
bessere Regel ist aber die oben beschriebene Intervallgrenzen-Methode.
3)
Auf- und Abrundregel zugunsten der ProbandIn
Auf- und Abrundregel, wie es für die ProbandIn günstiger
ist. Bei schwerwiegenden Folgen wird man eher konservativ, d.h. ungünstig
schätzen, um entsprechende Sicherungsmaßnahmen zu fördern.
4) Interpolations-Regel
Eine genauere Möglichkeit ist die Interpolation, die man wie folgt
rechnen kann: Wenn wir das Zeichen „>" für den jeweils größeren
Wert - Testwert TW und ProzentRANGwert PR - und das Zeichen
„<" und für den jeweils kleineren Wert - Testwert TW und ProzentRANGwert
PR - mit TWi erhaltener und zu interpolierender Testwert verwenden,
ergibt sich allgemein:
PRi = PR< + [( TWi - TW< ) / ( TW> - TW< )] * ( PR> - PR< )
Beispiel: Enthalte der Wertevorrat nur die Testwerte 7 mit PR=11 und 0 mit PR=5, aber nicht den Testwert 4, so ergibt sich interpolativ für den Testwert 4 ein ProzentRANG von gerundet 8, nämlich wie folgt:
PRi = PR< + [( TWi - TW<
)
/ ( TW> - TW< )] * ( PR> - PR<
)
PRi = 5 + [ (4 -0) / (7-0)] * (11-5)
PRi = 5 + [ (4 / 7)] * 6
PRi = 5 + .57142 * 6
PRi = 5 + 3,42857
PRi = 8,42857
PRi = 8 [abgerundet]
Der gesuchte (interpolierte) Prozentrang für den erhaltenen
Testwert 4 beträgt 8 (gerundet).
Anwendungsprobe für die Werte im Beispiel 1) Intervallgrenzenregel:
TW = 56; TW< = 48, TW> = 61, PR<
= 65 , PR>= 76.
PRi = PR< + [( TWi - TW<
)
/ ( TW> - TW< )] * ( PR> - PR<
)
PRi = 65 + [( 56 - 48 ) / (61 - 48 )]
* ( 76 - 65)
PRi = 65 + [ 8 / 13)] * (11)
PRi = 65 + .61538 * 11
PRi = 65 + 6,769
PRi = 71,769
PRi = 72 [gerundet]
Der gesuchte (interpolierte) Prozentrang für den erhaltenen
Testwert 56 beträgt 72 (gerundet).
Beispiel ProzentRANGberechnung der Anzahl der Corona-Neuinfektionen Deutschland.
> ProzentRAENGE für Neuinfektionen. > Aktualisierung mit Vergleich 02.08.2020.

[noch nicht 2. kontrolliert, gültig unter Vorbehalt]
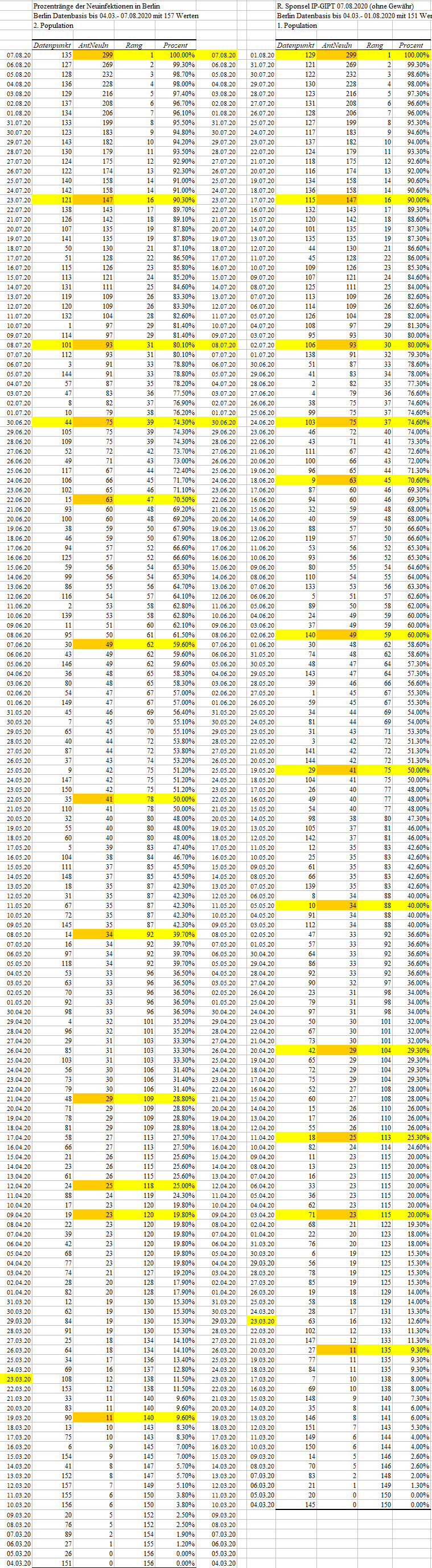
Beispiel ProzentRANGberechnung der Anzahl der Corona-Neuinfektionen Berlin.
Bei der Neuberechnung der Prozentränge Berlin am 07.08.2020 ist mir aufgefallen, dass die Häufigkeiten für Neuinfektionen bei den aktuellen 157 Werten gegenüber den etwas älteren 151 die gleichen Quartils- und Quantilsgrenzen markieren (>PR-Ampel-Berlin). Ich dachte erst an einen Rechenfehler und habe insgesamt drei Mal gerechnet, weil ich es nicht glauben wollte, aber jedes Mal ergaben sich die gleichen Ergebnisse. Das finde ich so ungewöhnlich - immerhin sind es reale Werte - dass ich diesen empirischen Befund hier dokumentieren möchte. Fazit: Kommen bei einer Prozentrangberechnung neue Werte hinzu, so können die Quartils- und Quantilsgrenzen die gleichen bleiben.
Prozentrang-Interpretationen bei Vergleichen
ProzentRANG-Interpretationen im Vergleich sind nicht immer einfach, insbesondere wenn unterschiedliche Polungen vorliegen. Sinnvoll ist es daher, die Polungen einheitlich auszurichten (hohe Rohwerte bedeuten dann hohe Merkmalsausprägungen) wie in den beiden folgenden Beispielen Depressiv und Radikales Erleben.
Beispiel Depressiv bei 6 Vergleichsgruppen
| Beispiel Merkmal
Depressivität |
Zufriedene /
Gesunde |
Normgruppe
_ |
Fallgruppe Anfang | Fallgruppe Ende
_ |
Nachunter-
suchung |
Spezialgruppe
Depressive |
| Rohwert |
|
|
|
|
|
|
| ProzentRANG |
|
|
|
|
|
|
Depressiv-Interpretationssätze zu den einzelnen ProzentRÄNGEN
Nur 1 von 100 in der Gruppe Zufriedene / Gesunde
erreicht mehr als 5 Rohwertpunkte, 99 haben höchstens einen Rohwert
von 5. Das heißt, bei den Zufriedenen / Gesunden kommt Depressivität
in mittlerer Rohwertausprägung (5 von 10) nur zu 1/100 vor. Ein solches
Ergebnis kann man als Bestätigung dafür ansehen, dass die Skala
das schätzt, was sie schätzen soll (man sagt auch: die Skala
ist für Depressivität valide).
Nur 5 von 100 in der Normgruppe erreichen
mehr als 5 Rohwertpunkte, 95 haben höchstens einen Rohwert von 5.
Nur 35 von 100 in der Fallgruppe Anfangsphase erreichen
mehr als 5 Rohwertpunkte, 65 haben höchstens einen Rohwert von 5.
Nur 15 von 100 in der Fallgruppe Endphase erreichen
mehr als 5 Rohwertpunkte, 85 haben höchstens einen Rohwert von 5.
Nur 10 von 100 in der Fallgruppe Nachuntersuchung
erreichen mehr als 5 Rohwertpunkte, 90 haben höchstens einen Rohwert
von 5.
65 von 100 in der Spezialgruppe Depressive erreichen
mehr als 5 Rohwertpunkte, 35 haben höchstens einen Rohwert von 5.
Depressiv-Interpretationssätze zu den Vergleichen der ProzentRÄNGE
Die Depressivität wird offensichtlich gut geschätzt, weil
Depressive beim Merkmal Depressivität deutlich höhere Rohwerte
haben. Das heißt, niedrigere ProzentRÄNGE zeigen beim Vergleich
höhere Rohwertausprägungen an.
Beispiel Radikales Erleben (Borderline-Merkmal)
| Beispiel Merkmal
Radikales Erleben |
Normgruppe
_ |
Fallgruppe
Psychotherapie |
Waffenrechts-
Probanden |
| Rohwert |
|
|
|
| ProzentRANG |
|
|
|
Radikalerleben-Interpretationssätze zu den einzelnen ProzentRÄNGEN
76 von 100 der Normgruppe erzielen einen höheren Rohwert als 10;
24 von 100 der Normgruppe haben höchstens einen Rohwert von 10.
86 von 100 der Fallgruppe Psychotherapie erzielen einen höheren
Rohwert als 10; 14 von 100 haben höchstens einen Rohwert von 10.
58 von 100 der Waffenrechts-Probanden erzielen einen höheren Rohwert
als 10; 42 von 100 haben höchstens einen Rohwert von 10.
Radikalerleben-Interpretationssätze zu den Vergleichen der ProzentRÄNGE
In der Fallgruppe Psychotherapie gibt es bei diesem Vergleich mehr
Probanden, die einen höheren Rohwert als 10 haben als bei der Normgruppe
und den Waffenrechts-Probanden, bei denen die Ausprägung deutlich
am niedrigsten beschrieben wird.
Allgemeine InterpretationsREGEL bei ProzentRANG-Vergleichen mit positiver
Merkmalspolung
Betrachtung in einer Gruppe: Bei gegebenem Rohwert X in einer Vergleichsgruppe
(VG) bedeutet ein ProzentRANG PR, dass dieser Rohwert X in der Vergleichsgruppe
(VG) von 100-PR überschritten wird und höchstens PR Probanden
den Rohwert X in dieser Vergleichsgruppe (VG) erreichen.
Hohe ProzentRÄNGE bedeuteten, dass viele (genau
PR) höchstens einen solchen Rohwert X erreichen.
Ist der Rohwert X niedrig und der ProzentRANG niedrig,
dann haben viele in der Vergleichsgruppe höhere Merkmalsausprägungen.
Ist der Rohwert X niedrig und der ProzentRANG hoch,
dann haben viele in der Vergleichsgruppe kleinere Merkmalsausprägungen.
Ist der Rohwert X hoch und der ProzentRANG niedrig,
dann haben viele in der Vergleichsgruppe höhere Merkmalsausprägungen.
Ist der Rohwert X hoch und der ProzentRANG hoch,
dann haben viele in der Vergleichsgruppe kleinere Merkmalsausprägungen.
Exkurs:
Messen in der Psychologie
In der (Test-) Psychologie
sind Messungen, wie aus Naturwissenschaft und Technik bekannt, in
aller Regel nicht möglich. Daher ist die gesamte traditionelle
psychologische Testtheorie, die gewöhnlich wenigstens intervallskalierte
Daten voraussetzt zutiefst wissenschaftlich fragwürdig und im Grunde
genommen, wie es Orth 1974 nach wie vor trefflich ausdrückte, nur
ein Messen "per fiat", also eine Art "wissenschaftstheologische" Entscheidung
und damit ein Widerspruch in sich, eine contradictio in adjecto: eine Art
"schwarzer Schimmel" oder "viereckiger Kreis".
ProzentRANGnormen setzen nur ein RANGdaten-Niveau
voraus und sind daher für psychologische Zwecke besonders - wie nonparametrische
und Rang-Methoden - geeignet. Das gilt natürlich nur dann, wenn nicht
auch sonst verdeckte Rechenprozeduren verwendet werden, die stillschweigend
ein höheres Datenniveau voraussetzen.
Exkurs:
Berücksichtigung der ProzentRANGidee im Alltag und Leben
Sport am Beispiel der Ligen: Man kann den Rang 1,2, ... in der Bundesliga,
2. Bundesliga, ..., Regionalliga, ... bis hin zur Kreisklasse C einnehmen.
Die verschiedenen Gewichtsklassen, Trennung von Frauen und Männern
geht ebenfalls von verschiedenen Bezugsgruppen aus. In Nationalgarden
werden oft nur Männer ab einer bestimmten Mindestgröße
aufgenommen; selbst kleine Prozentränge bedeuten dort schon hohe Körpergrößen
wie z.B. auch in Basketballmannschaften. Das Sprichwort "Unter den Blinden
ist der Einäugige König" enthält ebenfalls die Idee der
relativen Tüchtigkeit je nach Voraussetzungen innerhalb der Bezugsgruppe.
Gegenbeispiele: Eine vielfach vertretene Rechtsidee besagt: vor dem Gesetz
sind alle gleich. Auch die Wählerstimmen werden selbst in den modernen
Hollywooddemokratien gleichwertig behandelt. Gute Noten in der Grundschule
setzen sich nicht unbedingt an den höheren Schulen fort. Die verschiedenen
Schultypen repräsentieren daher verschiedene Bezugs- und Vergleichsbasen.
Einser-AbiturientInnen sind nicht unbedingt an Universitäten gleichermaßen
erfolgreich. Ungeachtet der Bildung kann sich auch der Geschäfts-
oder der Lebenserfolg entwickeln.
- Gutjahr, W. (1971). Die Messung psychischer Eigenschaften. Berlin: VEB Deutscher Verlag der Wissenschaften.
- Kotz, S. & Johnson, N. (1982-1989, Ed.). Encyclopedia of Statistical Science. Vol. 1-10. New York: Wiley. [hier das Begriffsumfeld nachschlagen]
- Lienert, G. A. (1962). Über die Anwendung von Variablen-Transformationen in der Psychologie. Biometrische Zeitschrift 4, 3, 145-181.
- Lienert, G. A. (1969 ff). Testaufbau und Testanalyse. Weinheim: Beltz. [Formeln S. 333]
- McGall, W. A. (1922). How to measure in Education. New York: McMillan.
- Orth, B. (1974). Einführung in die Theorie des Messens. Stuttgart: Kohlhammer.
Links (Auswahl: Beachte)
- Fern-Uni-Hagen Glossar Prozentrang: [Fehler 404]
- Fern-Uni-Hagen Glossar Häufigkeitsverteilung: [Fehler 404]
- Psycho-Fachschaft-Uni-Osnabrück: "Prozentrangnormen = Wahrscheinlichkeit, einen solchen oder kleineren Rohwert in der Normverteilung zu finden." [Fehler 404]
IP-GIPT-Links
- Testtheorie der Allgemeinen und Integrativen Psychotherapie.
- "Zahlen". Die Grundlagen praktischer ArithMETRIK für die Messung im Unscharfen, Unklaren und Flüchtigen in der Allgemeinen und Integrativen Psychologie und Psychotherapie.
- Normen und Normieren * Vergleichen * Beweisen * Statistik in der IP-GIPT *
- Überblick Wissenschaft in der IP-GIPT.
Glossar, Anmerkungen und Endnoten
___
1) GIPT= General and Integrative Psychotherapy, internationale Bezeichnung für Allgemeine und Integrative Psychotherapie.
___
Quelle: Die Darstellung nutzt wesentliche Teile aus: Sponsel, Rudolf (2002). Prozentrangnormen und Kennwerte zur Handanweisung des AD-H-D-Tests für Erwachsene. [auch mit Prozenträngen zum DSM-IV-Rückblick] Erlangen: IEC-Verlag.
___
Phäochromozytom. Seltene medizinische Erkrankung: Ein Nebennierenmarkstumor, der das Bild einer Angstneurose erzeugen kann, hat seinen Gipfel zwischen dem 20. und 50. Lebensjahr, also in dem Zeitraum, aus dem auch die meisten PsychotherapienachfragerInnen kommen dürften. Check: 1. Grundsymptom: Hochdruck. Leitsymptome: Kopfschmerzen, Herzklopfen, übermäßiges Schwitzen, Blässe, vorwiegend im Gesicht, Nervosität oder Angstgefühl; hierzu: CLASSEN / DIEHL / KOCHSIEK (19943). Innere Medizin, S. 817. München: Urban & Schwarzenberg]: "Phäochromozytome sind selten." "Auch die Angaben bezüglich der Häufigkeit unter Hypertonuspatienten schwanken zwischen einem und fünf auf 1000 Patienten" (!). Die Wahrscheinlichkeit, daß also eine GIPTin einen Nebennierenmarkstumor übersehen könnte ist weit geringer als daß er medizinisch zu spät bemerkt wird. Sicherung der Differentialdiagnose: Extrem hoher Plasma- Noradrenalinspiegel, während Adrenalin und Dopamin im Normbereich liegen (nach Sponsel, 1995, S. 447).
Eine Frage nach Phäochromozytomzeichen, wie sie Sponsel (2002) z.B: im AD-H-D-Test erhebt, wird also bei der Ausprägung 0 bereits einen sehr hohen direkten und unmittelbar berechneten ProzentRANG aufweisen, weil eben sehr, sehr viele diese Zeichen - real verteilungsbedingt - verneinen werden.
___
Formel z.B. bei Lienert 1969, S. 333:

Querverweise
Standort: ProzentRANG.
*
Testtheorie der Allgemeinen und Integrativen Psychotherapie.
"Zahlen". Die Grundlagen praktischer ArithMETRIK für die Messung im Unscharfen, Unklaren und Flüchtigen in der Allgemeinen und Integrativen Psychologie und Psychotherapie.
Normen und Normieren * Vergleichen * Beweisen * Statistik in der IP-GIPT *
Überblick Wissenschaft in der IP-GIPT.
*
| Suchen in der IP-GIPT,
z.B. mit Hilfe von "google": <suchbegriff>
site: www.sgipt.org
z.B. Prozentrang Normen site: www.sgipt.org. |
Dienstleistungs-Info.
*
Zitierung
Sponsel, R. (DAS). ProzentRANG. Bedeutung, Berechnung, Problemlösungen, Literatur, Links. Überblick Arbeiten zur Definitionslehre, Methodologie, Meßproblematik, Statistik und Wissenschaftstheorie besonders in Psychologie, Psychotherapie und Psychotherapieforschung. Internet Publikation für Allgemeine und Integrative Psychotherapie IP-GIPT. Erlangen: https://www.sgipt.org/wisms/mtt/pr.htm
Copyright & Nutzungsrechte
Diese Seite darf von jeder/m in nicht-kommerziellen Verwertungen frei aber nur original bearbeitet und nicht inhaltlich verändert und nur bei vollständiger Angabe der Zitierungs-Quelle benutzt werden. Das direkte, zugriffsaneignende Einbinden in fremde Seiten oder Rahmen ist nicht gestattet. Zitate und Links sind natürlich erwünscht. Sofern die Rechte anderer berührt sind, sind diese dort zu erkunden. Sollten wir die Rechte anderer unberechtigt genutzt haben, bitten wir um Mitteilung. Soweit es um (längere) Zitate aus ... geht, sind die Rechte bei/m ... zu erkunden oder eine Erlaubnis einzuholen.
Ende_ ProzentRANG _ Datenschutz_ Überblick_ Rel. Aktuelles _ Rel. Beständiges_ Titelblatt_ Konzept_ Archiv_ Region_ Service iec-verlag_ Mail: sekretariat@sgipt.org_ Wichtige Hinweise zu externen Links und Empfehlungen.
Änderungen wird gelegentlich überarbeitet, ergänzt und vertieft * Anregungen und Kritik willkommen
08.08.20 Korrekturen.
07.08.20 Ungewöhnlicher Befund bei zwei Prozentrangbestimmungen (157, 151 Werte) Corona Neuinfektionen Berlin.
30.07.20 Beispiel ProzentRANGberechnung der Anzahl der Corona-Neuinfektionen Berlin.
25.07.20 ProzentRANGtabelle für die Anzahl der Corona Neuinfektionen.
17.10.17 Fern Uni Hagen entlinkt, da Fehler 404.
29.01.17 Neuer Abschnitt: Prozentrang-Interpretationen bei Vergleichen.
03.03.15 Linkfehler geprüft und korrigiert.
20.12.11 Fehler in einem Sprichwort korrigiert (Danke an AS).
23.04.07 Korrektur der fehlerhaften Interpolationsformel. Den Hinweis (Danke) verdanke ich Patrick Müller, Psychologe FSP, Neuropsychologischer Dienst, Rehabilitationszentrum, Bürgerspital Solothurn, 4500 Solothurn.
08.09.06 Intervalle und Klassenbildung mit Mittengrenzen [Formel z.B. bei Lienert 1969, S. 333]