Der Bayes'sche Ansatz

Der Bayes'sche Ansatz gibt die Wahrscheinlichkeit dafür an, ob ein Kandidat zur Gruppe der gesuchten Merkmalsträger gehört unter der Bedingung, daß der Kandidat ein Kriterium erfüllt und er willkürlich aus der Population herausgegriffen wird. Voraussetzung ist lediglich, daß folgende Informationen gegeben sind oder angenommen werden können:
 

Kürzel	Bedeutung
p(m+)	Merkmalsträger-Rate in der Population
p(m-)	Kein Merkmalsträger-Rate in der Population p(m-)= 1 - p(m+)
p(v+|m+)	Verfahrenspositiv-Rate unter den Merkmalsträgern (Treffer-Rate I): richtig positiv.
p(v+|m-)	Verfahrenspositiv-Rate unter den Nichtmerkmalsträgern (Fehler-Rate I): falsch positiv.
p(v-|m+)	Verfahrensnegativ-Rate unter den Merkmalsträgern (Fehler-Rate II): falsch negativ.
p(v-|m-)	Verfahrensnegativ-Rate unter den Nichtmerkmalsträgern (Treffer-Rate II): richtig negativ.

wobei bedeute:
 

m    =: Merkmal	v   =: Verfahren
m+  =: Merkmalsträger	v+ =: Verfahrens-Positiv
m-  = Kein Merkmalsträger	v-  =: Verfahrens-Negativ

Damit kann nun ein Schema wie folgt gebildet werden:
 

Merkmalsträger \    Verfahren	Verfahrens-Positiv v+	Verfahrens-Negativ v-
Merkmalsträger m+	p(m+v+)	p(m+v-)	p(m+)
Nicht-Merkmalsträger m-	p(m-v+)	p(m-v-)	p(m-)
	p(v+)	p(v-)	1

Dies führt zur Bayes-Formel:
 

p(m+)* p(v+|m+) p(m+|v+) =  _______________________________             p(m+)*p(v+|m+) + p(m-)*p(v+|m-) In Worten: Die Bayes'sche Formel gibt die Wahrscheinlichkeit für richtig erkannte (diagnostizierte) Merkmalsträger an. Im Zähler steht die Wahrscheinlichkeit für positiv Erkannte (Diagnostizierte), im Nenner steht die Wahrscheinlichkeit für alle, nämlich die richtig und falsch Erkannten (Diagnostizierten). Damit werden im Bayes'schen Theorem beide Fehlerarten berücksichtigt: richtig positiv und falsch positiv Erkannte.

1. Anwendungs-Beispiel tbc-Test nach GOLDBERG 1973 S.97

Von tbc Kranken werden     p(v+|m+)= .90  durch Röntgen entdeckt,
                           p(v-|m+)= .10  bleiben unentdeckt
Von den tbc-Freien werden  p(v-|m-)= .99  als solche erkannt,
                           p(v+|m-)= .01  falsch verdächtigt.
tbc Rate der Population    p(m+) = .001

p(m+v+) = .001 *.90 =.00090 (tbc-Träger und röntgen-positiv)
p(m+v-) = .001 *.10 =.00010 (tbc-Träger und Nicht-röntgen-positiv)
p(m-v+) = .999 *.01 =.00999 (Kein tbc-Träger und röntgen-positiv)
p(m-v-) = .999 *.99 =.98901 (Kein tbc-Träger und nicht-röntgen-positiv)
 
 

Merkmalsträger \    Verfahren	röntgen-positiv	röntgen-negativ
tbc	.00090	.00010	.001
Nicht-tbc	.00999	.98901	.999
	.01089	.98911	1.000

Einsetzen in
 

                         p(m+)* p(v+|m+)
    p(m+|v+) =  -------------------------------
                p(m+)* p(v+|m+)+ p(m-)* p(v+|m-)

ergibt

                         .001 * .90
    p(m+|v+) =  -------------------------------
                .001 * .90    +    .999 * .01
 

p(m+|v+) = .0009/(.0009 + .00999)
p(m+|v+) = .0009/.01089
p(m+|v+) = .083
 

Traditionelle Bayes'sche Ergebnis-Interpretation:
 

Die Wahrscheinlichkeit, daß jemand, der willkürlich aus Population herausgegriffen wird, tatsächlich an tbc erkrankt, wenn er röntgenpositiv ist, ist p=0,083 oder  8,3%.

Man kann nun darüber streiten, ob diese traditionelle Ergebnisinterpretation so sinnvoll ist. Die meist unerwartet kleine Zahl suggeriert, als sei es sehr schwierig, einen Merkmals- Befund zu diagnostizieren:

Warnung
 

Das Bayes'sche Theorem wird manchmal auch benutzt, um zu überraschen und den gesunden Menschenverstand, der trotz (oder gerade auch ;-)) Wissenschaft, Statistik und Bayes natürlich seine Berechtigung hat - neben seinen Fehlern, Mängeln und Schwächen - zu erschüttern, weil viele Ergebnisse schwer zu glauben sind bzw. sich teilweise sogar paradox anhören. Das ist meist dann der Fall, wenn ein Merkmal in einer Population eine extreme Verteilung vom Typ 1 : 100 oder noch ausgeprägter hat. Nicht selten kommt das ungläubige Moment, gegen das sich unser Verstand und unsere Erfahrung sträubt, daher, daß zwei Sachverhalte vermischt werden, die in unserer Anschauung wenig oder keinen Erfahrungsfokus haben. Auch mit fast 100% treffsicheren  Tests erzielt man bei einer solchen verschränkten Betrachtung tendenziell eher unwahrscheinliche und dem gesunden Mesnchenverstand und der Ewartung daher widersprechend anmutende Ergebnisse.

Würfelte man in unserem Beispiel, ob jemand rönten-positiv ist, so wäre die Chance 1:1000.
Setzt man die diagnostische Wahrscheinlichkeit unter der Bedingung, daß jemand röntgen- positiv ist p(v+|m+) = 0,083 zur Würfelwahrscheinlichkeit p=(m+) = 0,001 in Beziehung, so ergibt sich, daß die Wahrscheinlichkeit durch das Diagnoseverfahren Röntgen um das 0,083/ 0,001 = 83-fache verbessert wird. Und diese Betrachtung stimmt nun wieder sehr gut mit unserer Intuition und dem gesunden Menschenverstand überein. Die Validitäts-Trefferquote war im Beispiel 90%, d.h. die Fehler- oder Irrtumsrate 10%. Anders gesagt: Von 10 tbc Kranken werden nach den obigen Voraussetzungen 9 entdeckt, einer wird falschlicherweise nicht erkannt. Hinzu kommt der 2. Fehlertyp der Falsch Positiv Diagnostizierten.

Und die Konsequenzen für Validitätsangaben: Müßte man nicht für jeden Test fünf Gütemaße (Validitäten) angeben?, nämlich:
 

Richtige Diagnosen bei denen, die das Merkmal haben: p (D=wahr: X hat M). [Sensititvität = p(positives Testergebnis | Merkmalsträger)] Falsche Diagnosen derer, die das Merkmal haben: p (D=falsch: X hat M) Richtige Diagnosen bei denen, die das Merkmal nicht haben: p (D=wahr: X hat M nicht). [Spezifität = p(negatives Testergebnis | kein Merkmalsträger)] Falsche Diagnosen derer, die das Merkmal nicht haben  p(D=falsch: X hat M nicht) Gesamtmaß, das 1-4 zueinander in beziehung setzt und einer Zahl trefflich ausgedrückt wird.

Hierfür spricht sich auch Massimo Piatelli-Palmarini (dt. 1997, S. 102) aus.
 

2. Anwendungsbeispiel: Vorüberlegungen zur Konstruktion einer "Risikoliste Amokläufer"
Zur Frage des Für und Wider, was z.B. die Entwicklung einer "Risikoliste Amokläufer" statistisch-diagnostisch, ordnungs- und rechtspolitisch und ökonomisch (Kosten-Nutzen) brächte, können Bayes'sche Betrachtungen hilfreich sein, selbst wenn man die drei Bayes'schen Parameter nicht tatsächlich kennt. Nach dieser Methode werden verschiedene Annahmen in Modellrechnungen "durchgespielt", so dass man den statistisch-diagnostischen, den ordnungs- und rechtspolitischen sowie den ökonomischen Kosten-Nutzen-Aspekt besser beurteilen und bewerten kann. Letztlich steht vielleicht die Frage: Lohnte sich die Entwicklung einer Risikoliste Amokläufer überhaupt?

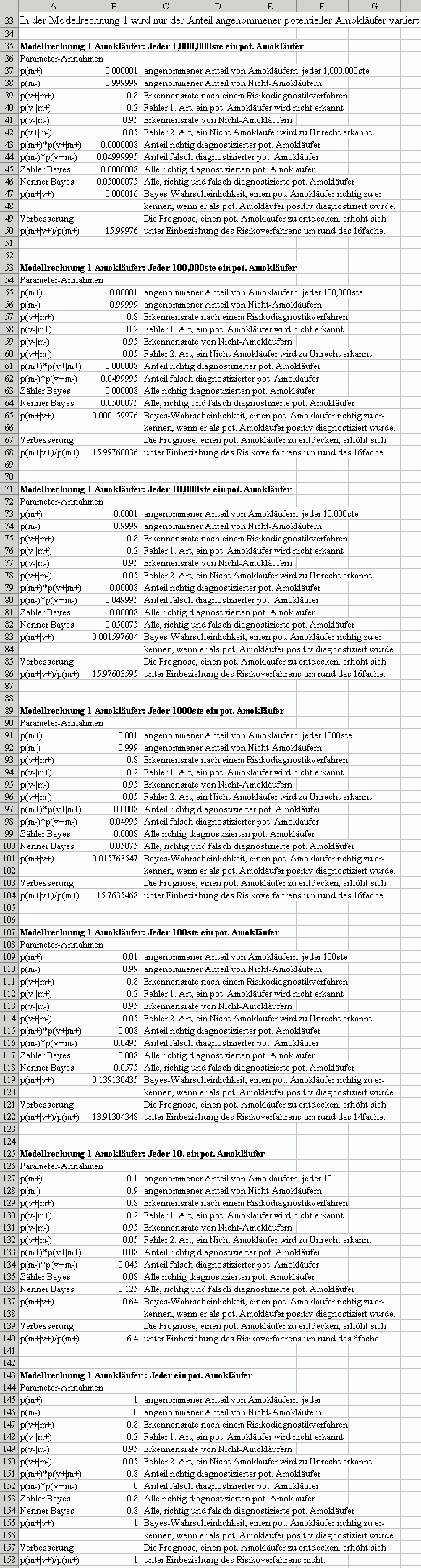
Die folgende Modellrechnung 1 geht von einer "Risikoliste Amokläufer" mit einer Erkennensrate von 0.80 (80%) für Merkmalstäger und von einer Erkennensrate von 0.95 für Nichtmerkmalsträger aus. Es wurden nun die Verbesserungen für die Trefferqueote unter Einbeziehung des Bayes-Wahrscheinlichkeit für folgende angenommene  Merkmalsträgerraten in der Population durchgerechnet:

• Jeder Ein-Millionste ist ein potentieller Amokläufer: 15.99976
• Jeder Hundertausendste ist ein potentieller Amokläufer: 15.9976
• Jeder Zehntausendste ist ein potentieller Amokläufer: 15.976
• Jeder Tausendste ist ein potentieller Amokläufer: 15.763
• Jeder Hunderste ist ein potentieller Amokläufer: 13.913
• Jeder 10. ist ein potentieller Amokläufer: 6.4
• Jeder ist ein potentieller Amokläufer: 1

Ergebnis Modellrechnung 1: (1) Bei einer Risikoliste, die potentielle Amokläufer mit 80%iger Sicherheit und Nichtmerkmalsträger mit 95%iger Sicherheit erkennt, beträgt die mutmaßliche maximale Verbesserung der Trefferquote, also positiv Diagnostizierte richtig zu erkennen, das 16fache gegenüber eine willkürlichen oder zufälligen Auswahl. (2) Paradoxerweise nimmt die Verbesserung der Trefferquote zu, wenn die Merkmalsträgerrate abnimmt. (3) Es bietet sich die zu untersuchende Hypothese an, für den mutmaßlichen maximalen Grenzwert der Verbesserungsrate die Schätzung 20 * p(v+|m+) anzunehmen.

Die Modellrechnungen 1:

[Interne Quelle: ... Eigene Bilder/Woisms/Stat/AmokMR1.gif  - gerechnet 13.4.9]

Der Einfluss der Parameter im Bayes'schen Ansatz auf die Verbesserung der Trefferrate
Wie verändert sich die Verbesserung der Trefferquote, wenn sich jeweils m+, v+(m+), v-(m-) verändern?

Bei den Modellrechnungen zur "Risikoliste Amokläufer" haben sich nebenbei, sozusagen unbeabsichtigt, einige interessante Befunde über den mutmaßlichen Grenzwert der Verbesserungsrate für P(m+|v+) ergeben, wenn p(m+) variiert wird. Es hatte hier den Anschein, als ob die Verbesserungsrate dem Grenzwert 100 * 2 * v+ zustrebt.
 

Links
https://www.kardiolab.ch/BayesKompakt_d.html