|
r12 - r13 r23 r12.3 = ______________________ SQR[(1-r213 ) (1-r223 )] |
Die partielle Korrelation r12.3 gibt die Korrelation zwischen Variable 1 und 2 an, wenn Variable 3 konstant gehalten wird. Hierzu sagt man auch, daß der Einfluß der Variablen 3 "ausgeschaltet" wird. Damit läßt sich mit der partiellen Korrelation die wichtige experimentelle Technik des Konstanthaltens simulieren. |
Rekursionsformel für die vollständige Partialisierung zweier Variablen aus m
|
r12.34...(m-1) - r1m.34...(m-1) r2m.34...(m-1)
r12.34....m = ______________________________________________ SQR[(1-r21m.34...(m-1) ) (1-r22m.34...(m-1))] |
Tücken
und Fallen partieller Korrelationsrechnungen
| Hinweis 1: Der Mathematiker Dr. B. Hain hat gezeigt (1994, Kap. VI, S. 38 ff), daß die Korrelationsmatrix bei vollständiger Partialisierung - rij.n-2 - nicht notwendig positiv definit sein muß. Hier ist also größte Vorsicht geboten, wenn Verdacht auf lineare Abhängigkeit besteht, was Eigenwerte 'nahe' 0 anzeigen (Storch-Beispiel). |
| Hinweis 2: Der Statistiker O. Anderson (S. 299f) hat darauf hingewiesen, daß bei linearen Abhängigkeiten - besonders tückisch bei verborgenen - partielle Korrelationen zu unsinnigen Ergebnissen und Interpretationen führen können: |
|
| Bestehen also zwischen den Variablen näherungsweise funktionale Abhängigkeiten, so können unsinnige Korrelationskoeffizienten erzielt werden. |
Rechen-Beispiel zur Anderson Warnung
Wir nehmen Spalte 1=x und 2=y aus dem Basisversuch Quader
q00 und bilden z = x - y, N=100.
| x y
z
1 94 -93 2 65 -63 3 19 -16 4 70 -66 5 85 -80 6 97 -91 7 46 -39 8 19 -11 9 13 -4 10 58 -48 11 13 -2 12 1 11 13 41 -28 14 32 -18 15 82 -67 16 19 -3 17 97 -80 18 72 -54 19 87 -68 20 79 -59 |
x y z
21 54 -33 22 82 -60 23 40 -17 24 74 -50 25 79 -54 26 80 -54 27 46 -19 28 53 -25 29 32 -3 30 36 -6 31 78 -47 32 64 -32 33 44 -11 34 60 -26 35 6 29 36 58 -22 37 92 -55 38 16 22 39 72 -33 40 67 -27 |
x y z
41 52 -11 42 34 8 43 15 28 44 76 -32 45 95 -50 46 98 -52 47 75 -28 48 25 23 49 47 2 50 91 -41 51 84 -33 52 49 3 53 92 -39 54 43 11 55 96 -41 56 87 -31 57 64 -7 58 98 -40 59 90 -31 60 9 51 |
x y z
61 36 25 62 55 7 63 83 -20 64 60 4 65 54 11 66 36 30 67 13 54 68 78 -10 69 80 -11 70 46 24 71 38 33 72 4 68 73 52 21 74 61 13 75 82 -7 76 7 69 77 79 -2 78 12 66 79 40 39 80 51 29 |
x y z
81 4 77 82 56 26 83 79 4 84 75 9 85 3 82 86 72 14 87 96 -9 88 31 57 89 65 24 90 42 48 91 54 37 92 9 83 93 53 40 94 24 70 95 47 48 96 1 95 97 97 0 98 92 6 99 27 72 100 47 53 |
Dies führt zu der Korrelationsmatrix:
x y z
und in der Tat: Die Korrelation zwischen x und y wird nach Auspar-
tialisierung von z rxy.z = .999, also 1, wenn man sich die Rundungs-
fehler weg denkt, wie Anderson ausgeführt hat.
|
Korrelationskoeffizienten von File C:\OMI\NUMERIK\MATRIX\KK\ODOD\QXYZ.K03
in File C:\OMI\NUMERIK\MATRIX\KK\ODOD\QXYZ.PKA
11/23/02 23:51:54. Korrelationen der 3 Items in Promille:
2 3
-97 744
1
-737
2
Mit * gekennzeichnete Zeilen in folgenden Tabellen =
Differenz zwischen Korrelation und partieller Korrelation
Partielle Korrelationen unter Ausschluß des Einflusses der
Items 1 in Promille:
3
263 *
-1000 2
Partielle Korrelationen unter Ausschluß des Einflusses der
Items 2 in Promille:
3
-256 *
1000 1
Partielle Korrelationen unter Ausschluß des Einflusses der
Items 3 in Promille:
2
-1096 *
999 1
Ergebnis
Rechenbeispiel zu Anderson:
| Man muß der Argumentation Andersons zwingend entnehmen, daß der Eigenwertanalyse auf lineare Abhängigkeiten, also dem Suchen nach Eigenwerten 'nahe' 0, größte Bedeutung zukommt, weil bei multivariater Weiterverarbeitung sonst möglicherweise formal nicht zu beanstandende aber inhaltlich unsinnige Ergebnisse entstehen können, wie obiges Beispiel eindringlich deutlich macht. |
Weiteres Beispiel: Vollständige Partielle Korrelation der Partition 7,11,14 und 16 beim beim Extraversionsfragebogen, die zu einer indefiniten Matrizen führt.
Wichtige Anwendungen partieller Korrelation in der Psychologie
Entwicklungspsychologie:
Hier spielt oft das Alter eine wichtige Rolle, das die Korrelation
zwischen zwei Variablen verfälschen kann. Möchte man also den
echten Zusammenhang unabhängig vom Alter zwischen zwei entwicklungspsychologischen
Variablen i und j wissen, partialisiert man den korrelativen Einfluß
des Alters aus. Beispiel nach Guilford
(1950, p. 346):

Beispiel Alter, Blutdruck und Cholesterin
nach Sachs,
L. (1984, 6.A., S. 353)

Paradoxien:
Storchennester und Geburtenrate:
Paradoxien wie der ("schein") korrelative
Zusammenhang zwischen der Anzahl der Storchennester und der Geburtenrate
lassen sich mit partieller Korrelationsanalyse ebenfalls aufklären.
Tatsächlich stellt sich heraus, daß die vermittelnde Variable
die Industrialisierung ist. Partialisiert man also die Variable
Industrialisierung
aus, verschwindet der Zusammenhang. Nachdem die Links
immer sehr schnell aus dem Netz verschwanden, habe ich ein eigenes Beispiel
konstruiert:
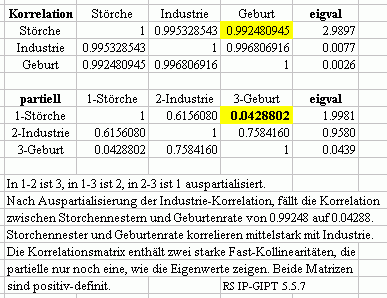 |
Die positive Definitheit der vollständigen Partia- lisierungsmatrix ist nicht notwendig, wie Hain ((1994, Kap. VI, S. 38 ff) gezeigt hat. Hier ist sie aber gegeben, wie ein Blick auf die Eigenwerte zeigt, wenn auch die Korrelationsmatrix aus nur einem Generalfaktor "Industriealisierung" besteht. Das ist hier demonstrativ gewollt und geglückt. Dieser einzige und damit Generalfaktor ver- schwindet und macht einem Bifactormodell Platz, wenn man vollständig auspartialisiert, dann gibt es nur noch eine Fast-Kollinearität. Welches Faktor- modell stimmt nun? Beide, wenn man die Be- deutungen der Korrelationen berücksichtigt. Denn beide Korrelationsmatrizen repräsentieren eben Unterschiedliches: Korrelationen und partielle Korrelationen. |
Anmerkung: Sachs (1984, S. 307) bemerkt
zu Recht: "Der Ausdruck 'Scheinkorrelation' ist für diese Zusammenhänge
üblich, er ist jedoch besser zu verrmeiden, da ja auch eine Scheinkorrelation
zwischen zwei Prozentzahlen nicht Schein, sondern für die betrachteten
Variablen Tatsache ist."
Partielle Korrelationsanalyse Omikron% und Inzidenz.
Kombinatorik: Anzahl aller m Auspartialisierungsmöglichkeiten bei N Variablen bzw. Korrelationskoeffizienten
Zählt man kombinatorisch aus ergeben sich beispielsweise für:
|
|
|
Entwicklung | Formeln für m, n Î N und n >= 3 |
| 3 | 3 | 3 | |
| 4 | 10 | 4+6 | Rekursion: m = Kn = 2 * Kn-1 + n |
| 5 | 25 | 5+10+10 | Regel: Wert des Vorgängers verdoppeln + n |
| 6 | 56 | 6+15+20+15 | |
| 7 | 119 | 7+21+35+35+21 | Direkte Formel: m = Kn = 2n - (n+2) |
| 8 | 246 | 8+28+56+70+56+28 | Regel: Zwei hoch n abzüglich n+2 |
| 9 | 501 | 9+36+84+126+126+84 | +36 |
| 10 | 1012 | 10+45+120+210+252+ | 210+120+45 |
| 11 | 2035 | 1+55+165+330+462+ | 462+330+165+55 |
| 12 | 4082 | 12+66+220+495+792+ | 924+792+495+220+66 |
| 13 | 8177 | 3+78+286+715+1287 | +1716+1716+1287+715+286+78 |
| 14 | 16368 | 14+91+364+1001+ | 2002+3003+3432+3003+2002+1001+364+91 |
| 15 | 32751 | ... | |
| 16 | 65518 | ... | |
| 17 | 131053 | ... | |
| 18 | 262124 | ... | |
| 19 | 524267 | ... | |
| 20 | 1048554 | ... |
Ergebnis zu Anzahl
und Wachstum der Auspartialisierungsmöglichkeiten und damit der relevanten
Korrelationskoeffizienten im Untersuchungsraum:
| Die Anzahl der Partialisierungen wächst sogar etwas schneller und stärker als das berühmte Reiskornbeispiel auf dem Schachbrett. Bereits bei einer relativ kleinen Korrelationsmatrix der Ordnung 20 gibt es 1 Million, 48 Tausend und 554 verschiedene Partialisierungen. Bei einer Ordnung N=100 sind es dann 1,26765 * 10^30 Möglichkeiten. Dies alles spricht für das Ökonomieprinzip der Wissenschaft: mit so wenig wie möglich relevanten Variablen versuchen auszukommen. Je weniger Grundgrößen, Parameter oder Variablen es gibt, desto leichter und überschaubarer können die Beziehungen untersucht werden. |
| Aus der Kombinatorik der Partialiserungs- Möglichkeiten folgt: Aus Korrelationen ohne systematischen und inhaltlichen Systembezug des relevanten Variablenraumes kann überhaupt nichts Zuverlässiges gefolgert werden [1]. Formale Korrelationsrechnungen und auf sie aufgebaute multivariate Analysen sind im Grunde nicht selten nur numerologische Rituale vom Typ Astrologie oder Tarot - allerdings meist gut szientistisch verkleidet und getarnt. |
Literatur


Glossar, Anmerkungen und Fußnoten
1) GIPT= General and Integrative Psychotherapy, internationale Bezeichnung für Allgemeine und Integrative Psychotherapie.
___
Links zum Storchen-Geburtenrate-Phänomen, die aus dem Netz verschwanden:
- https://www.uni-karlsruhe.de/~humangeographie/ergaenzung/storch.pdf
https://www.soziologie.uni-freiburg.de/multimedia/kurse/methoden%204%20ss%202002/ms4teil3.pdf
https://mspcdip.mathematik.uni-karlsruhe.de/german/personen/klar/biopraktikum_unterl_ps.ps
Standort: Partielle Korrelation
*
Partielle Korrelationsanalyse Omikron% und Inzidenz.
Partielle Korrelationsmatrix nicht notwendig positiv [semi] definit. * Vollständige Partialisierung von 5 Börsenindices *
Vollständige 501 partielle Korrelationsanalysen am Beispiel IST 70 * Korrelation * Fast- Kollinearität in Korrelationsmatrizen mit Eigenwertanalysen erkennen. * Wissenschaft in der IP-GIPT * Kritik Handhabung Faktorenanalyse * Numerisch instabile Matrizen und Kollinearität in der Psychologie * Fehlersimulation und Faktorenanalyse * Zahlen * Der Kardinal-Skalenbeweis zur Summen-Score-Funktion * Grundzüge einer ideographischen Wissenschaftstheorie * Welten *
*
| Suchen in der IP-GIPT,
z.B. mit Hilfe von "google": <suchbegriff>
site:www.sgipt.org
z.B. z.B. Korrelation site:www.sgipt.org. |
Dienstleistungs-Info.
*
Zitierung
Sponsel, R. (DAS). Partielle Korrelationen. Definition und Methode * Tücken und Fallen * Wichtige Anwendungen in der Psychologie * Kombinatorik der Anzahlen. Abteilung Arbeiten zur Definitionslehre, Methodologie, Meßproblematik, Statistik und Wissenschaftstheorie besonders in Psychologie, Psychotherapie und Psychotherapieforschung. Internet Publikation für Allgemeine und Integrative Psychotherapie IP-GIPT. Erlangen: https://www.sgipt.org/wisms/statm/kor/partkor.htm
Copyright & Nutzungsrechte
Diese Seite darf von jeder/m in nicht-kommerziellen Verwertungen frei aber nur original bearbeitet und nicht inhaltlich verändert und nur bei vollständiger Angabe der Zitierungs-Quelle benutzt werden. Das Einbinden in fremde Seiten oder Rahmen, die die Urheberschaft der IP-GIPT nicht jederzeit klar erkennen lassen, ist nicht gestattet. Sofern die Rechte anderer berührt sind, sind diese dort zu erkunden. Sollten wir die Rechte anderer unberechtigt genutzt haben, bitten wir um Mitteilung. Soweit es um (längere) Zitate aus ... geht, sind die Rechte bei/m ... zu erkunden oder eine Erlaubnis einzuholen.
Ende Partielle Korrelation_Datenschutz_Überblick_ Rel. Aktuelles _Rel. Beständiges_ Titelblatt_ Konzept_ Archiv_Region_Service iec-verlag _Mail: sekretariat@sgipt.org__Wichtiger Hinweis zu Links und Empfehlungen
Änderungen
16.01.22 Partielle Korrelationsanalyse Omikron% und Inzidenz.
05.05.07 Eigenes Beispiel für die Storchennest-Geburtenrate Paradoxie.
02.05.07 Hinweis: Vollständige Partialisierung von 5 Börsenindices.
28.06.06 Beweis Dr. Hain: Partielle Korrelationsmatrix nicht notwendig positiv [semi] definit.
30.05.06 Beispiel einer vollständig partiellen Korrelation (Partition 7,11,14 und 16 ) beim Extraversionsfragebogen, die zu einer indefiniten Matrix führt.
19.01.04 Link auf Korrelation.