(ISSN 1430-6972)
IP-GIPT DAS=04.06.2006 Internet-Erstausgabe, letzte Änderung: 04.09.18
Impressum: Diplom-Psychologe Dr. phil. Rudolf Sponsel Stubenlohstr. 20 D-91052 Erlangen
Mail: sekretariat@sgipt.org_ Zitierung & Copyright
Anfang_ Dimension_ Überblick_ Rel. Aktuelles _ Rel. Beständiges_ Titelblatt_ Konzept_ Archiv_ Region_ Service iec-verlag_ _ Wichtige Hinweise zu externen Links und Empfehlungen_
Willkommen in unserer Internet-Publikation für Allgemeine und Integrative Psychotherapie GIPT 1) , Abteilung Wissenschaft, Bereich Mess- und Testtheorie, hier speziell zum Thema:
Dimension, Dimensionalität,
Dimensionsanalyse
Begriff und Probleme in der Psychologie
und psychologischen Testtheorie
mit allgemein-integrativen Blicken über
den Zaun: Dokumente und Materialien aus Alltag, Wissenschaftstheorie, Mathematik,
Informatik, Physik, Chemie, Biologie, Kunst, Test- und Messtheorie, Psychologie
u.a.m.
von Rudolf Sponsel, Erlangen
_
Abstract - Zusammenfassung - Summary.
Der Dimensionsbegriff ist ein vielfältiges Homonym, wodurch wie so oft zahlreiche Unklarheiten und Missverständnisse entstehen. Die Arbeit versucht einen Überblick über die Bedeutungs- und Anwendungsvielfalt des Dimensionsbegriffes und entwickelt hieraus terminologische Vorschläge zur "Dimensionierung" der Dimensionssachverhalte. Hierzu wurde der Begriff homogene und heterogene Dimension eingeführt und mit einfacher bzw. mehrfacher Reihung (Kettung) oder Potenzierung kombiniert. Als Grundproblem erscheint die Frage der jeweiligen Basiseinheit, die im Sprach-, Anwendungs- und Wissenschaftsgebrauch auf unterschiedlichen Verallgemeinerungsebenen vorgenommen wird. Während der Dimensionsbegriff in der lineraren Algebra einigermaßen klar ist, gilt das in der Psychologie und in der dort so geschätzten multivariaten Analyse nicht. Der Rang r eines Vektorraumes oder Matrix wird dort mit der Anzahl der Dimensionen gleich gesetzt, also Rang = Dimension (woran sich in der Forschungspraxis fast niemand hält). Die Frage der Dimensionierung stellt sich bei der Klassifizierung und Gruppierung von Merkmalen und Daten.
Qualitaet, Merkmal, Dimension
Sachverhalte oder Objekte können unterschiedliche Merkmale oder
Qualitäten haben, was man als Dimensionen interpretatieren kann. Letztlich
könnte man demnach alles qualitativ Unterscheidbare als Dimension
interpretieren. Das sinnliche Erleben hat so viele Haupt-Dimensionen, wie
es Sinnesunterscheidungen gibt, also mindestens fünf, wahrscheinlich
mehr. Aber es gibt Millionen von Gerüchen. Nur einen Bruchteil davon
riecht der Mensch, sein Hund erheblich mehr.Soll man die unterschiedlichen
Gerüche auch als Dimensionen unterschieden und bezeichnen?
Das Dimensionsproblem in der Wissenschaftstheorie
Das Dimensionsthema in der Enzyklopaedie für Wissenschaftstheorie (Mittelstraß 2005)
"Dimension (lat. dimensio, Ausmessung,
Berechnung), in der Bedeutung Ausmessung bzw. Ausdehnung des Raumes Terminus
der Philosophie, Mathematik, Physik und Physiologie.
(1) Euklid bestimmte die Dreidimensionalität in der Körperdefinition
seiner »Elemente<<, wonach ein Körper ist, >was Länge,
Breite und Tiefe hat<. Aristoteles suchte in >>de coelo<< zu beweisen,
daß es außer Linie, Fläche und Körper keine weiteren
Ausmessungen gibt, da alles vollkommen und daher nach pythagoreischer Auffassung
(iPythagoreismus) durch die Dreizahl geordnet sei. Weiterhin seien nur
die dreidimensionalen Körper nach allen Seiten hin stetig und teilbar.
Dieser an der Ausmessung von Körpern orientierte D.sbegriff wird erst
in der Neuzeit (seit R. Descartes) durch die Vorstellung verdrängt,
daß unter D. die Anzahl der Koordinaten eines Punktes zu verstehen
sei. ....
Um 1900 führten Untersuchungen der Cantarsehen tMengenlehre zu
der Erkenntnis, daß die seit Descartes übliche D.sdefinition
durch Koordinaten nicht mehr ausreicht. So kann die Punktmenge M aller
Punkte der x-Achse mit rationalen Koordinaten zum einen die D. 1 haben,
da sie wie die Gerade selbst überall dicht ist, zum anderen aber auch
die D. 0, da zwischen zwei rationalen Punkten aus M immer noch ein nicht
zu M gehöriger irrationaler Punkt liegt wie bei einer endlichen Punktmenge.
H. Poincare regte 1913 eine induktive Definition des D.sbegriffs an, die
nur von topalogischen Grundbegriffen (>Topologie) Gebrauch macht."
"Dimensionsanalyse, Analyse zur Bestimmung der >Dimension einer physikalischen Größe. Eine physikalische Größe setzt sich aus dem Produkt eines (reellen) Zahlenwerts und einer physikalischen Einheit zusammen (z. B. 3,5 kg). Eine physikalische Einheit ist entweder eine Grundeinheit oder eine abgeleitete Einheit. Die Wahl der Grundeinheiten ist im Grundsatz willkürlich; eingeführt ist das >MKJA<-System, das Meter, Kilogramm, Sekunde und Ampere als Grundeinheiten umfaßt. Grundeinheiten müssen eindeutig und einfach (iEinfachheitskriterium) reproduzierbar sein. ... "
Dimensionsanalyse Ereignis
Zu jedem Ereignis gehört ein Raumzeitpunkt an dem es stattfindet,
wobei seit Einstein das mit der Zeit so eine Sache ist. Wir können
fragen: was ereignet sich? Wie ereignet es sich? Hat es Anfang und Ende?
Soeben, 22.02.2018, 14.34 Uhr fährt ein Fahrradfahrer vor unserem
Haus vorbei. Das ist eigentlich kein Ereignis, sondern ein Geschehen, sozusagen
fortgesetzte Ereignisse. Dem üblichen Ereignisbegriff haftet im Sprachgebrauch
etwas Diskretes, Punktuelles an.
Weitere Beispiele
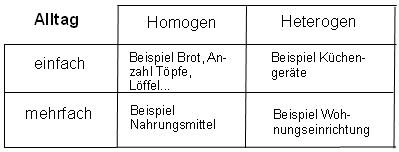
Alltag, Chemie, Texte, Wirtschaft
 |
 |
 |
 |
Die Anzahl der verschiedenen Elemente in der Chemie könnte man als stoffliche Dimensionen interpretieren.
Einführung: Der Dimensionsbegriff in der Psychologie ist wenig klar bis vielfältig verworren. Das ist mit "der" Faktorenanalyse - die angeblich eine Dimensionsanalyse leisten will - keineswegs besser, sondern eher viel schlechter geworden. Und auch die fünf Bände Forschungsmethoden der Psychologie in der Enzyklopädie wie auch viele andere Werke zeigen sich nicht in der Lage, dem Dimensionsbegriff entsprechende Aufmerksamkeit und Klärungsenergie zu widmen (Ausnahme: Wottawa 1979). Im folgenden wird daher versucht, den Dimensionsbegriff in der Psychologie ansatzweise zu klären und einige Kriterien und Vorschläge für seine Anwendung zu entwickeln. Hierbei erscheint es sinnvoll, ein wenig über den Zaun der Psychologie hinauszublicken (Alltagsraum, Mathematik, Informatik, Physik, Chemie, Ästhetik und Kunst) und auch ein paar ungewöhnliche Betrachtungen (Dimensionsanalyse eines Backsteins, Löffels) oder einer Küche) anzustellen - ohne Anspruch auf Vollständigkeit.
Zunächst seien einige, auch ungewöhnliche Beispiele für erste Näherungen betrachtet:
Dimensionen in der
Alltagssprache
In anderen, höheren Dimensionen sein "er bewegte sich in anderen
Dimensionen"; in anderen Dimensionen denken; auf eine andere Ebene gehen.
Dimension im Bedeutungswörterbuch des Duden (1970, S. 168):


Quelle S. 291: Schneider, Hermann
& Leo (1989). Lexikon Naturwissenschaft in der Alltagssprache. Krüger.
Dimensionsanalyse
des Alltagsraumes
Dieser ist uns vertraut, da fast jeder die drei Dimensionen des Raumes:
Länge, Breite, Höhe (Tiefe), also Volumen, eindimensionale Begriffe
(z.B. Gerade), zweidimensionale Begriffe (z.B. Fläche), als geistige
Kategorien zur Verfügung hat und sich den dreidimensionalen Raum der
alltäglichen Anschauung leicht vorstellen kann [Nichteuklidische
Geometrie]. Auch wenn wir meistens intuitiv die Koordinatenachsen des
Raumes paarweise senkrecht denken und vorstellen, so muss das natürlich
nicht so sein. Auch die gerade Form ist nicht zwingend, sie kann ebenso
mehr oder weniger gekrümmt, stetig oder unstetig usw. gedacht werden.
Die Vielfalt kann man sich leicht vorstellen, wenn man sich z.B. einmal
überlegt, wie viele Varianten von Dreiecken
es gibt.
Dimensionsanalyse
einer Küche und ihrer Funktionen.
Kerndimension einer jeden Küche ist das Kochen. Damit sind die
primären Dimensionen vorbestimmt, nämlich: was braucht man zum
Kochen? Doch wird in Küchen nicht nur gekocht. Es wird gebraten, gegart,
gedünstet, gedämpft, frittiert. Eine Küche ist gewöhnlich
ein Raum, der offen oder geschlossen sein kann. Die Küchengrundfläche
hat eine Form, meist viereckig, was nicht zwingend ist, und eine Höhe,
sie könnte aber auch keine Decke oder Dach haben und damit nach oben
offen sein: so etwa eine „Küche“ in der freien Natur: als Lagerfeuerstätte
hätte sie gar keine klaren Begrenzungen. Davon ausgehend kann man
sagen: typisch für Küchen sind Kochstätten oder Herde. Damit
gibt es die verschiedenen Dimensionen der Energiezufuhr: Elektro, Gas,
Holz, Kohle, Öl, Mikrowelle. Es gibt Großküchen und Kleinküchen.
Die meisten westlichen Küchen haben auch einen Kühlschrank, mit
oder ohne Gefrierfach oder zusätzlich eine Gefriertruhe. Sehr wichtig
für die meisten Küchen sind auch Spülen oder Waschbecken,
um die Küchengeräte oder das Geschirr zu reinigen. Damit braucht
man Wasserzufuhr und Abflussmöglichkeiten. In „Naturküchen“ muss
es zuweilen auch ein Eimer oder Bottich Wasser tun. Das Dimensionsprinzip
heißt hier Reinigung. Die Multidimensionalität einer Küche
und ihrer Funktionen kann man z.B. sehr schön dem Duden Bildwörterbuch
(1992) entnehmen:

Dimensionsanalyse
eines Backsteins
Der Backstein selbst hat drei Dimensionen: Länge, Breite, Höhe.
Zudem befindet er sich an einem raumzeitlichen Ort, der durch ein entsprechendes
Bezugssystem und Ortskoordinaten angegeben wird. Außerdem befindet
er sich bezüglich eines Betrachters in einer bestimmten Lage. Der
Backstein hat eine gewisse Geschichte und ein Alter, eine bestimmte stoffliche
Zusammensetzung, Dichte, Masse und Gewicht, Oberfläche und Farbe.
Hinzu kommt, dass er für verschiedene Ziele und Zwecke Anwendung finden
kann und je nachdem auch einen bestimmten Wert oder Preis hat. Wie man
an dieser Ausführung sehen kann, hat ein Backstein eine vielfältige
Dimensionalität. [Bilder:
Google:
1,
2,
3,
4,]
Dimensionsanalyse
eines Löffels.
Ein Löffel dient zum Löffeln und gehört neben Messer
und Gabel zu den drei Grundbestecken, die gewöhnlich beim Essen benutzt
werden. Ein Löffel kann unterschiedliche Größe haben, besteht
aus unterschiedlichen Stoffen, Plastik etwa für gekochte Eier und
aus Metall für Kaffee oder Suppen. Um seine Grundform herum variieren
kleine Veränderungen, mehr rundlich, mehr länglich, tiefer oder
flacher, mehr oder minder gebogen, mit diesen oder jenen Verzierungen und
am Haltestengel mit diesem oder jenem Stoff verschalt, z.B. um die Wärmeübertragung
zu dämpfen. Wie der Backstein, ja überhaupt alle ausgedehnten
Objekte dieser Welt, nimmt er einen dreidimensionalen Raum und einen bestimmten
raumzeitlichen Ort ein, er hat ein Alter, eine Geschichte. Mit ihm sind
womöglich spezifische Erinnerungen verbunden u.a.m. [Bilder:
Google:
1,
2,
3,
4,]

Dimension im Brockhaus Naturwissenschaft und Technik 1989

Dimensionen in der Mathematik. > Spezielle ...
Allgemeine, traditionelle
Mathematik
Aus Anwendersicht sind hier in der Hauptsache drei Dimensionsbegriffe
zu unterscheiden: (1) der allgemein vertraute der Geometrie, (2)
der Dimensionsbegriff in der linearen Algebra, gewöhnlich durch den
Rang eines Vektoreraumes oder einer Matrix gegeben und (3) der für
Außenstehende ungewöhnliche Hausdorffsche Dimensionsbegriff
der Topologie, der auch gebrochene Dimensionen wie die fractale Geometrie
zulässt.
Aus: Der kleine Duden Mathematik (1986, S. 98 - 99):

Siehe auch: Wikipedia: Dimension in der Mathematik. [URL verändert 404]
Spezielle
Dimensionsbegriffe in der Mathematik
Die moderne Mathematik ist für außenstehende AnwenderInnen
weitgehend unverständlich und kaum zu nutzen. Im ersten Band des 6bändigen
Lexikons der Mathematik (2001) gibt es folgende Einträge:
- Dimensionen des Anschauungsraumes
- Dimension einer Algebra
- Dimension einer analytischen Menge
- Dimension einer Codierung
- Dimension eines Moduls
- Dimension eines Rings
- Dimension eines Vektorraumes
- Dimensionsformel
- Dimensionssatz für lineare Abbildungen
Literatur Dimensionen in der Mathematik
- Carathéodory, C. (1914). Über das nichtleere Maß von Punktmengen - eine Verallgemeinerung des Längenbegriffs. Nach. Ges. Wiss. Göttingen 406-424.
- Pasch, M. (1925). Dimension und Raum in der Mathematik. Zeitschrift Annalen der Philosophie und philosophischen Kritik. Heft Volume 5, Number 1 / Dezember 1925, 109-120
Dimensionen in der Informatik.
Tabellen und Datenbanken können als Felder mit n Zeilen (Datensatzeinträgen) und m Spalten (Rubriken, Bereiche) aufgefasst werden. Im Schüler Duden Informatik (1991) gibt es zwar keinen Eintrag mit "Dimension". Implizit steckt der Dimensionsbegriff aber im Begriff des Feldes, das bei den meisten Programmiersprachen bevor es genutzt werden kann, "dimensioniert" werden muss, d.h. gewöhnlich, die Anzahlen der zu reservierenden Zeilen und Spalten müssen festgelegt werden (Auszug aus S. 192):

Der Dimensionsbegriff
in der Physik
Wesentlich für eine Dimension in der Physik ist der Begriff der
Größe. Eine Größe besteht aus Maßzahl und Maßeinheit,
wobei in der Maßeinheit die Dimensionen stecken.
Dimension aus Brockhaus abc Physik I., 1972, S. 258:

Siehe auch: Wikipedia:
Dimension in der Physik.
Rudolf
Carnaps Konzept physikalischer Größen
Sehr interessant sind auch Rudolf Carnaps Ausführungen in seinem
Büchlein "Physikalische Begriffsbildung". Wissenschaftliche Begriffsbildung
hängt bei ihm sehr stark von einer Theorie und Messbarkeit ab. Der
Begriff "eindimensional" wird im Sachregister fünf mal erwähnt
(S. 19, 22, 26, 32 und 38). Der Begriff der Eindimensionalität taucht
im folgenden Text (S. 22 ff) auf:

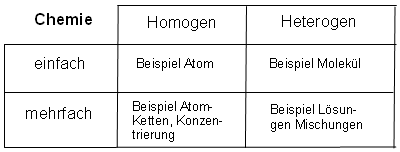
Dimensionen in der Chemie.
In meinen Chemiebüchern habe ich keine Sachregistereinträge zum Begriff Dimension gefunden. Aber es ist klar, dass die Elemente die grundlegenden Dimensionen dieser bedeutenden Naturwissenschaft bilden, in die man einige strukturelle Ähnlichkeit mit der differentiellen Psychologie der Persönlichkeit hineinsehen kann, was z.B. Revenstorf veranlasste sein Faktorenanalysebuch (1980, S. 9) mit einem Vergleich zur Chemie einzuleiten:

Dimensionen in der Biologie
Die Vielfalt der Arten und Klassen der biologischen Erscheinungen und Lebensformen kann man als "Dimensionen" der Biologie auffassen.
Querverweise: [, Wikipedia: Nomenklatur_(Biologie, ).
Dimensionsanalyse in Ästhetik und Kunsttheorie.
Eine Unterscheidung ("Dimensionsunterraum") betrifft die verschiedenen Kunstrichtungen und Objekte: Bildende Kunst (z.B. Architektur, Graphik, Malerei, Bildhauerei; Träger, Material, Form, Farbe), Darstellende Kunst und Musik (z.B. Ballett, Tanz, Theater, Oper, Operette, Musical, Konzert, Gesang, Film, Fernsehen, Unterhaltung), Literatur (z.B. Roman, Novelle, Kurzgeschichte, Anekdote, Fabel, Märchen, Lyrik). Die Lebenskunst (Lebensformen, z.B.: bürgerlich, großbürgerlich, kleinbürgerlich, bohemien, elitär, revolutionär, anarchistisch-autonom, proletarisch, eigen-sonderlich) wird im allgemeinen nicht zu den Künsten gezählt, obschon man sie mit guten Gründen - auch als Alltagskunst - dazu rechnen könnte. Ein Film ist in seiner Vielfalt kaum dimensionsanalytisch zu erfassen. Betrachten wir uns aber z.B. die Präsentation eines Films, so werden meist folgende Dimensionen genannt (siehe z.B. Das Buch Eva): Hersteller, Regisseur, Schauspieler, Drehbuch, Musik, Kamera, Bauten, Effekte, Schnitt, Kostüme u.a.m. Rein formal lässt sich ein Film wie folgt "dimensionieren":
Struktogramm oder formale Dimensionierung eines Films

Filme kommen dem Leben ziemlich nahe, es fehlen ihm noch die Sinnesqualitäten Geschmack und Geruch, wobei durch Identifizieren, Einfühlen und Mitgehen ziemlich viel Erleben bewirkt werden kann.
Dimensionen der Welt und des Wissens.
Aus alltäglicher Sicht gibt einen sehr guten Überblick das Bildwörterbuch des Duden, eine Informationsquelle, die die Psychologie des Wissens sehr gut nutzen kann.

Dimensionsanalyse Technik-Lexikon (Online)

Dimensionsbeispiele aus der Psychologie
Viele psychologische Werke enthalten keinen Eintrag zum Dimensionsbegriff. Eine rühmliche Ausnahme ist:
Dimension im Psychologischen Wörterbuch von Dorsch 1994

Dimensionsanalyse psychischer Grund-Funktionen.
Psychologie wird gewöhnlich definiert als die Wissenschaft vom
Erleben und Verhalten. Hiervon ausgehend kann man fragen: was sind nun
die grundlegenden "Dimensionen" des Erleben und Verhaltens?
 |
Zu den psychischen Grundfunktionen des Erlebens zählen
wir:
|
Siehe bitte auch.
Dimensionsanalyse
des Selbstbildes.
Dimension Identität * Dimension Körper und
äußere Erscheinung * Dimension Herkunft, Familie und Sozialisation
* Dimension Anlage und Begabungen * Dimension Fähigkeiten und Fertigkeiten
* Dimension Bildung, Ausbildung, Arbeit und Beruf * Dimension Vitalität
und Vitalbedürfnisse * Dimension Wünsche, Interessen, Ziele,
Träume * Dimension Charakter und Werte * Dimension Lebens- und Wohnformen
* Dimension Erfahrungen * Dimension Haben, Geld und Besitz * Dimension
Sozialbeziehungen * Dimension Entspannung, Erholung, Freizeit, Spiel, Sport,
Muse, Muße, Vergnügen * Meta-Dimensionen: Wertigkeit * Stabilität
* Kongruenz.
Dimensionen der Entwicklungspsychologie.
Schnittpunkte des Lebens (Lernen, Rollen, Bewältigungsaufgaben): Schwangerschaft * Geburt * Säuglingsalter * Kleinkindalter * Kindergartenalter * Vorschulalter * Grundschulalter * Hauptschulalter * Schulübertrittsalter * Vorpubertät * Pubertät * Heranwachsenden Alter, Berufswahl / Berufseintrittsalter * Frühes Erwachsenenalter * Heiratsalter * Eigener Haushalt * Eigene Kinder * Karrierealter * Kindererziehung * Lebensmitte * Nachelterliche Gefährtenschaft * Vorruhestand * Rentenalter * Altersphase * Greisenalter * Sterben & Tod * Danach.
Dimensionen der Psychopathologie: Kritik der Achsen im DSM.
Dimension Identität * Dimension Körper und äußere Erscheinung * Dimension Herkunft, Familie und Sozialisation * Dimension Anlage und Begabungen * Dimension Fähigkeiten und Fertigkeiten * Dimension Bildung, Ausbildung, Arbeit und Beruf * Dimension Vitalität und Vitalbedürfnisse * Dimension Wünsche, Interessen, Ziele, Träume * Dimension Charakter und Werte * Dimension Lebens- und Wohnformen * Dimension Erfahrungen * Dimension Haben, Geld und Besitz * Dimension Sozialbeziehungen * Dimension Entspannung, Erholung, Freizeit, Spiel, Sport, Muse, Muße, Vergnügen.
Dimensionsbeispiele aus der methodologischen und Test-Psychologie.
Dimensionen
von Quantoren oder verschiedener Ausprägungsqualitäten:
Auswahl_Quantoren (Qualität) * Begrenzungs_Quantoren
* Beschleunigungs_Quantoren * Dauer_Quantoren * Geschwindigkeits_Quantoren
* Häufigkeits_Quantoren* Intensitäts_Quantoren * Komplexitäts_Quantoren
* Kontinuitäts_Quantoren * Mengen_Quantoren * Meta_Quantoren * Ordnungs_Quantoren
* Periodizitäts_Quantoren * Beeinträchtigungs-Quantoren.
Das Dimensions- (Untertest, Skalenformations-) Problem.
Siehe dort auch: Items in ihrer nominalen und realen Bedeutung.
Dimensionen von Vektoren und Matrizen in der Testpsychologie
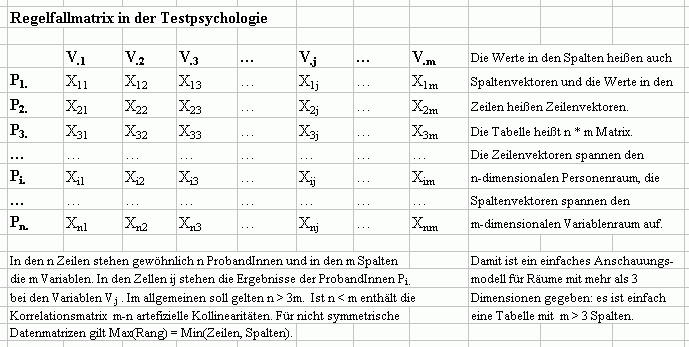
Grundlagen
und Probleme von Dimensionen in der Psychologie - Aus Wottawas (1979)
"Einleitung
Die Worte "Dimension" und "dimensional" werden in
der Psychologie gerne gebraucht. So spricht man von Dimensionen der Persönlichkeit,
Dimensionen des Verhaltens, Dimensionalität der Wahrnehmung, eindimensionaler
bzw. mehrdimensionaler Messung, ein- oder mehrdimensionalen Modellen, Dimensionalität
von Tests, mehrdimensionaler Skalierung u. v. a. m. Was bedeutet "Dimension"
eigentlich?
Das Wort "Dimension" kommt aus dem Lateinischen und bedeutet Ausmessung,
Ausdehnung.
Demzufolge wäre ein Objekt soviel "dimensional", als es "Ausdehnungen"
hat. Geht man davon aus, daß man zur Kennzeichnung jeder dieser "Ausdehnungen"
eine und nur eine Maßzahl benötigt, wäre ein Objekt soviel
dimensional, als Maßzahlen zur Kennzeichnung der "Größe"
dieses Objektes erforderlich sind. Wieviel Maßzahlen man benötigt,
hängt außer von den Objekten auch vom jeweiligen Kontext ab.
Die Auffassung, daß die Anzahl der Dimensionen festgelegt ist durch
die Anzahl der Kennzahlen, die jedem Objekt zugeordnet werden müssen,
ist der Konsens, der allen im folgenden besprochenen Dimensionsbegriffen
zugrunde liegt.
Die einzelnen Ansätze unterscheiden sich wesentlich
in der Art der Konstruktion von Dimensionen, der Bedeutung und Interpretierbarkeit
dieser Maßzahlen und insbesondere auch hinsichtlich der Rolle, die
der jeweils zu definierende Kontext spielt. Da der Zusammenhang, in dem
die Kennzeichnung eines Objektes durch eine oder mehrere Dimensionen erfolgen
soll, die Art und Anzahl der Dimensionen wesentlich mitbestimmt, muß
dies bei der Interpretation bedacht werden. Daraus ergeben sich gewisse
Schwierigkeiten dimensionalen Denkens im Rahmen psychologischer Hypothesen.
...
Versucht man die formalen Ansätze, die im Rahmen
der Psychologie besonders häufig zur Konstruktion von Dimensionen
verwendet wurden, zu ordnen, so erhält man im wesentlichen drei
Gruppen. ..."
Dimensionalität
aus
Krauths Testkonstruktion und Testtheorie (1995, S. 33; fett-kursive Hervorhebung
von mir).
"Da psychologische Konstrukte bzw. latente Variablen nach Definition
nie direkt beobachtbar sind, macht es naturgemäß kaum Sinn,
für solche Variablen von einem Skalenniveau zu sprechen. Jedoch kann
man sich überlegen, wenn man die latenten und die manifesten Variablen
durch ein Modell verknüpft, inwieweit Modellparameter zu den latenten
Variablen eindeutig aufgrund der Realisierungen der manifesten Variablen
schätzbar sind. Wenn sich dabei z. B. herausstellt, daß der
Nullpunkt und die Einheit der latenten Variablen unabhängig von den
Werten der manifesten Variablen noch willkürlich festlegbar sind,
wobei gleichen Differenzen für Werte der latenten Variablen die gleiche
Bedeutung zukommt, so könnte man in übertragenem Sinn von einem
"Intervallskalenniveau" der latenten Variablen sprechen.
Durch manifeste Variablen, bei denen die zugehörigen Reaktionen
mindestens auf Ordinalskalenniveau gemessen werden, können Testpersonen
angeordnet werden. Man hofft dabei, daß diese Anordnung der durch
die zu messende latente Variable möglichen Anordnung der Testpersonen
möglichst ähnlich ist. Damit wird implizit angenommen, daß
die zu messende latente Variable überhaupt eine Anordnung der Testpersonen
nach wachsendem Grad ihrer Ausprägung ermöglicht, z. B. eine
Anordnung von Personen nach steigender "Intelligenz". Eine solche Ordnung
der Personen ist aber nur möglich, wenn die latente Variable eindimensional
ist. Bei einer mehrdimensionalen latenten Variablen können
nicht mehr alle Personen angeordnet werden, auch wenn dieses für alle
eindimensionalen
Komponenten gilt.
Es bestehe etwa das Konstrukt "Intelligenz" aus den Teilkonstrukten
"Theoretische Intelligenz"' und "Praktische Intelligenz". Ferner sei es
möglich, daß Personen mit hoher theoretischer und geringer praktischer
Intelligenz sowie andere Personen mit geringer theoretischer und hoher
praktischer Intelligenz existieren. Dann können nicht alle Personen
der Population mit Hilfe der zweidimensionalen latenten Variablen
"Intelligenz" in sinnvoller Weise nach wachsender "Intelligenz" angeordnet
werden. Dieses Problem der Dimensionalität hat natürlich
auch Auswirkungen auf die Testkonstruktion, da es mit eindimensionalen
manifesten Variablen (Items) nicht möglich ist, in sinnvoller Weise
mehrdimensionale
latente Variablen (Konstrukte) zu beschreiben. Die übliche Vorgehensweise
ist, daß man ein mehrdimensionales Konstrukt in seine
eindimensionalen
Komponenten aufzuspalten versucht, um jede Komponente gesondert zu messen."
Fischer zum circulus
vitiosus in der psychologischen Testtheorie (1974, S. 18f; fett-kursive
Hervorhebung von mir).
"Die klassische Testtheorie blieb allerdings schuldig, was ihr Name
versprach. Als eine Theorie der psychologischen Messung kann die
Anwendung der Korrelationsrechnung auf psychologische Testergebnisse nicht
verstanden werden: Sie setzt nämlich, lediglich an der ,,Messgenauigkeit"
interessiert, die Definition und Existenz der zu messenden Dimensionen
einfach voraus, so wie man bei der Beurteilung der Genauigkeit eines Thermometers
natürlich voraussetzt, dass die Temperatur ein bereits wohldefinierter
physikalischer Begriff ist; letzteres ist auch tatsächlich der Fall,
denn die Temperatur wird in der Thermodynamik, d. h. in einer physikalischen
Theorie, eindeutig definiert. Intelligenz etwa ist aber kein Begriff, welcher
schon vor und unabhängig von ihrer Messung definiert wäre; vielmehr
wird Intelligenz ja eben als der ,,Leistungsgrad der psychischen Funktionen
bei der Lösung neuer Probleme" (ROHRACHER, 197l10) verstanden,
wobei der Leistungsgrad fraglos wiederum durch eine Messung, durch ein
oder mehrere Testergebnisse, erfasst werden muss. Es fehlt gerade jene
Theorie, welche ,,Intelligenz" (oder spezifische Intelligenzdimensionen)
definiert. Sieht man sich in der Psychologie nach derartigen Theorien um,
so ist wohl die faktorenanalytische Intelligenzforschung jener Bereich,
in welchem Intelligenzdimensionen relativ am klarsten definiert
und beschrieben werden - doch beruhen diese Forschungen ihrerseits auf
Intelligenztestergebnissen, womit der circulus vitiosus geschlossen ist.
Vom heutigen wissenschaftstheoretischen Verständnis
und von einer kritischen Selbstdurchleuchtung der Psychologie aus kann
also die klassische Testtheorie nicht mehr befriedigen, und es wird notwendig,
eine hinreichend allgemeine Theorie der psychologischen Messung zu entwickeln.
Eine solche muss spezifisch für den Gegenstandsbereich der Humanwissenschaften
sein, jedoch ohne notwendige Beschränkung auf die Psychologie allein.
Auch die Messprobleme der Soziologie und verwandter Sozialwissenschaften
sind durchaus vergleichbar, wobei wir übrigens heute rückblickend
sagen müssen, dass das Bedürfnis nach einer theoretisch befriedigenden
Fundierung des Messens verbunden mit einer exakten Definition der zu messenden
Dimensionen,
der „latenten Eigenschaften" oder „Konstrukte" — wie auch
immer sie genannt werden — anscheinend in der Soziologie und Ökonomie
schon früher als in der Psychologie zu grundlegenden Lösungsansätzen
geführt hat; siehe zum Beispiel die „latent structure theory" von
LAZARSFELD, 1950, oder NEUMANN & MORGENSTERN, 1944, welche den im Grunde
psychologischen Begriff des Nutzens auf eine wissenschaftliche Basis gestellt
haben." [Anmerkung Fischer]
Dimensionsanalyse in der Meßtheorie.
Aus: Krantz et. al. (1971):

Anmerkung: Im wesentlichen scheinen Krantz et al. ihre Dimensionsanalyse
auf den Bereich der Physik zu beschränken, was auf den ersten Blick
wenig verständlich erscheint.
Grundproblem
bei Anwendung formaler Prozeduren und Modelle:
Was man in die Welt an Modell hineinsteckt, das kommt auch heraus.
Man findet allzu leicht empirisch wieder, was man an formalen Voraussetzungen, Modellen oder Filtern in seine empirische Untersuchungsmethode hineingesteckt hat, wie z.B. mit "der" Faktorenanalyse: Gibt man unabhängige "orthogonale" oder abhängige ("oblique") Faktoren vor, so kann man natürlich nur solche finden, was den meisten FaktorenanalytikerInnen nicht aufzufallen scheint, wenn sie sich ihre Spielergebnisse zusammen "kommunalitieren", "rotieren" und "reduzieren" (durch den generösen Wegwurf aller Eigenwerte < 1 [Screetest]). Gibt man Ja/ Nein Antwortkategorien vor, so erhält man natürlich eine Datenwelt, die durch den vorgegebenen Antwortfilter Ja/Nein bereits vorstrukturiert ist. So haftet fast allen Verfahren eine gewisse Willkür an. Andererseits geht es natürlich gar nicht anders. Wer die Welt untersucht, wird dies immer nur mit bestimmten Methoden tun können, ja müssen. Man kann also dem Problem, dass die angewandten Methoden die Ergebnisse im Lichte und in der Struktur dieser Untersuchungsmethoden filtern gar nicht entgehen. Wenn wir diesem Dilemma aber schon nicht entgehen können, so wäre es auf jeden Fall zu wünschen, darüber ein klares Bewusstsein, Wissen und Kontrollmöglichkeiten zu entwickeln, damit die methodischen Artefakte nicht fälschlich für die Wirklichkeit gehalten werden. Und ebenso stellt sich verschärft die Frage: welche Methoden sind für welche Untersuchungs- und Forschungsziele angemessen? Wer ein orthogonales Modell vorgibt, wird orthogonale Resultate erhalten, solche oder solche, auf jeden Fall orthogonale, weil es vom Untersuchungsmodell vorgegeben, ja erzwungen wird. Wie will man gemeinsame Faktoren (common factors) finden, wenn man sie unabhängig voneinander konstruiert und so im Modell vorgibt? Dieser Grundwiderspruch scheint den FaktorenanlytikerInnen so wenig aufzufallen wie die Bedeutung kleiner Eigenwerte.
Es gibt
potentiell unendlich viele "Dimensionen"
Bei vielen Merkmalen können sehr viele, mitunter potentiell unendlich
viele Unterscheidungen getroffen werden. Daher ist die Frage, wie viele
Dimensionen ein Merkmal "hat" oder wie viele es gibt,
falsch, weil so getan wird, als würden sich soundso viele Merkmale
objektiv vorfinden. Wer nur nach sechs Dimensionen sucht, wird wohl auch
höchstens sechs finden. Doch wie, wenn die Wirklichkeit 17, 28 oder
mehr bereit hält? Wer besessen ist von Datenreduktion, kann leicht
auf Reduktionsmethoden verfallen, die gar nicht angemessen sind und blind
sein für alles andere.
So manches existiert nur unter bestimmten Bedingungen.
So gibt es in der Natur "eigentlich" keine Farben, aber wenn Licht, Brechung,
das Sinnesorgan Auge, das verarbeitende Gehirn und bewusstes wahrnehmendes
Erleben hinzukommen, dann "gibt"
es potentiell unendlich viele Farben.
Pragmatisch könnte man sagen: zu einer Dimension
wird ein Sachverhalt, wenn er gründlich untersucht ist und von mehren
Fachleuten anerkannte Methoden vorliegen, ihn festzustellen. Sofern möglich
und angemessen, sind Messungen bzw. Ausprägungsschätzungen anzustreben.
Querverweise: Was-ist-Fragen? * Definitionslehre in der GIPT * Terminologie * Welten * Konstruktuvismus * Vulgärkonstruktuvismus * Beweisen *
Methoden, die Dimensionalität eines Merkmals festzustellen.
| Je nach Verallgemeinerung oder Unterscheidung kann jedes Merkmal ein- oder mehrdimensional interpretiert werden. |
Die praktischen Grundfragen an die Dimensionalität eines Merkmals
lauten: Aus was ist das Merkmal zusammengesetzt? In welche Umgebung ist
das Merkmal eingebettet? Unter welchen Perspektiven, Zielen und Zwecken
kann man es betrachten? Wie lässt sich das Merkmal operational erfassen?
Entspricht der Operationalisierung
tatsächlich eine Wirklichkeit oder handelt es sich nur um eine konstruktive
Projektion? Welche Kriterien stehen zur Verfügung, um die (Un-) Angemessenheit
der Konstruktion zu erweisen? Poppers Falsifikationskriterium
wäre hier durch ein konstruktives Angemessenheitskriterium
zu
ersetzen.
Je nach Verallgemeinerung (Abstraktion) oder
Unterscheidung kann jedes Merkmal ein- oder mehrdimensional interpretiert
werden. Es kommt daher entscheidend auf die Ziele und Zwecke an,
die man verfolgt. Was soll erreicht werden ist daher eine der ersten Fragen?
Zu den wichtigsten Meta-Methoden könnte daher eine genaue Ziel-Mittel-Analyse
gehören: was möchte man wozu tun? Und hierbei können dann
die traditionellen Methoden wie Analysieren, Begriffsanalyse, Experimente,
formale Prozeduren und Modelle helfen.
Für was zum Beispiel ist es wichtig oder nützlich,
ob ein Variablensatz von 12 auf 9, 5 oder auf 3 Faktoren reduziert werden
kann? Wäre es nicht wichtiger oder nützlicher zu wissen, was
aus diesem oder jenem Ergebnis an Erklärungen oder Prognosen mit dieser
oder jener Sicherheit unter diesen oder jenen Bedingungen gefolgert werden
kann?
Item-Dimensions-Theorie
beim CST - Charakter-Struktur-Test.
Aus: Sponsel, R. (1982): CST-System Handbuch.
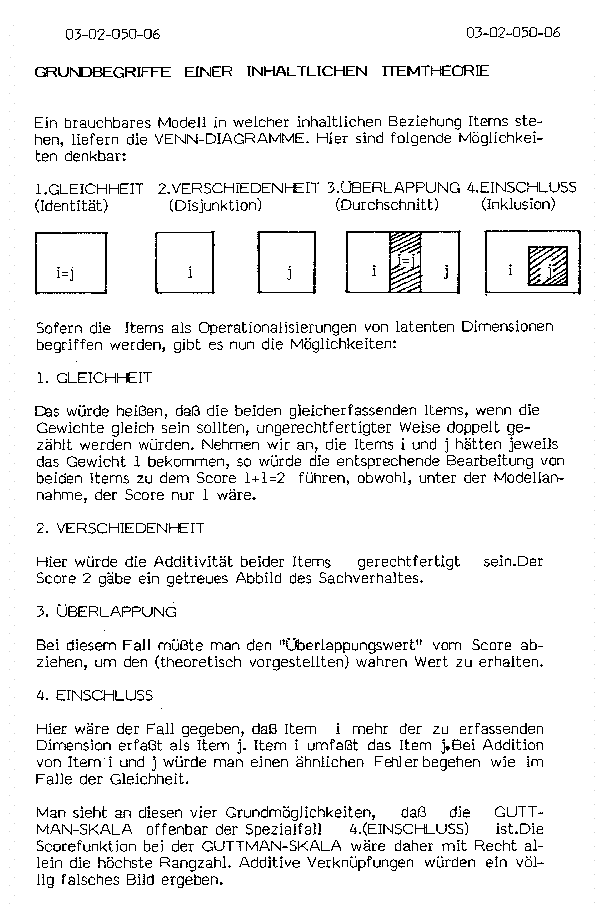

Dimensionsmodelle beim Konstrukt Extraversion.
Es wird ein eindimensionales Modell mit 10 Operationalisierungsvariablen konstruiert und faktorenanalytisch untersucht.
Eindimensionalitaet
Im Korrelationsmodell bedeutet Eindimensionalität, dass es nur einen großen Eigenwert gibt. Damit wäre z.B. ganz leicht zu prüfen, ob man Cronbach's alpha rechnen darf, was in der psychologischen Testtheorie und Statistik allerdings niemanden interessiert. In n-dimensionalen Modellen sollte es daher n große Eigenwerte geben. Siehe bitte auch Screetest.
Empirisches Beispiel für Eindimensionalitaet
In der empirischen Sprachstudie-01
wurden drei Skalierungsvarianten untersucht und korreliert. Die Eigenwert-
und Kollinaritätsanalyse der Matrix der Skalierungen ergab, dass hier
echte Eindimensionaltät vorliegt mit einem großen Eigenwert
und zwei fast-kollinearen). D.h. in allen drei Skalierungsvarianten steckt
die gleiche Dimension (Skalenwerte für die Realisierungsgrade). Damit
ist bewiesen, dass Eindimensionaltät
empirisch existiert.
Können bipolare Merkmalsausprägungen eindimensional sein ?
Aus der Logik wissen wir, dass es das Konträre (nicht weiß) und Kontradiktorische (schwarz) gibt. Es gibt bipolare ("kontradiktorische") Merkmale, z.B. Stimmung (gut-schlecht), Geduld (Ungeduld), Zufriedenheit (Unzufriedenheit), Beherrst (unbeherrscht), ...
Von der Bipolarität der Merkmale ist das Polungsproblem
streng zu unterscheiden: man kann Merkmale positiv oder negativ erheben:
dies heißt Polung. Und man kann Merkmale bipolar denken: das nennt
man Bipolarität.
Monopolare Dimensionalität liegt z.B. vor bei Länge, Breite,
Höhe, Angst, Intelligenz, Wille, Antrieb, Motivation vor, Extraversion
und Introversion werden indessen bipolar gedacht, ähnlich zufrieden
und unzufrieden, sicher und unsicher, gehemmt und gelöst. Auch Lernen
und Vergessen sind Gegenpole und können bipolar gedacht werden.
Beispiele:
Negative Polung: Ich habe selten Angst. Positive Polung: Ich habe oft
Angst.
Negative bipolare Polung: ich werde fast nie ungeduldig. Positive bipolare
Polung: Ich bin ziemlich geduldig.
Ich sehe derzeit keinen überzeugenden Grund, bipolaren Ausprägungen
die Eindimensionalität abzusprechen.
Analogie: positive und negative Zahlen.
Dimensionsanalyse des psychischen Merkmals Geduld
Nach dem ersten Eindruck ist Geduld ein eindimensionales psychisches (elementares) Merkmal, das man global (die gesamte Persönlichkeit betreffend) oder spezifiziert (verschiedneen Lebensbezügen oder Situationen) zuordnen kann.
Nach der Alltagserfahrung können wir mehr oder minder geduldig oder ungeduldig sein. Das muss auch nicht immer gleich, sondern kann auch je nach Lebenssituation unterschiedlich sein. Und unsere Geduld oder Ungeduld kann sich in verschiedenen Lebensbezügen mehr oder minder ausgeprägt zeigen. Während man sich z.B. einem Menschen eher ungeduldig sein, kann sies bei einem anderen Menschen anders sein.
Will man die Ausprägung von Geduld skalieren, so kann man folgenden (Grund-) Skalentyp (MinMax) annehmen. Das heißt wir spannen die Ausprägung von einem (natürlichen) Minimum bis zu einem Maximum auf. Maximum, z.B. 0 .... 100.
Der Wert 0 könnte hier keine Geduld und 100 maximale Geduld bedeuten. Genauso kann man es mit der Ungeduld machen. Hier würde dann 0 keine Ungeduld (=Geduld, nicht näher spezifiziert) und -100 maximale Ungeduld bedeuten.
Bei der Zusammenfassung zu einer biploaren Skala ergäbe sich hier ein Problem, weil:
maximale Ungeduld (-100) .............................. keine Ungeduld (0) keine Geduld (0) ........ maximale Geduld (100) bei 0 unverträglich sind, denn keine Ungeduld (0) = Geduld und keine Geduld (0) = Ungeduld, woraus sich ergäbe Geduld = Ungeduld. Sinvollerweiße wird in einer gemeinsamen bipolaren Skala den Nullpunkt (0) als Indifferenz- und Übergangspunkt zwischen Ungeduld und Geduld interpretieren:
Homogenität und Dimensionalität in der psychologischen Testtheorie und -praxis.
Wottawa (1980, S. 30) führt aus: "Im Gegensatz dazu muß bei einem Vorgehen auf der Basis der Annahme einer latenten Dimension geklärt werden, ob die zunächst ausgewählten Items tatsächlich alle dieselbe Dimension ansprechen („homogen" sind). Trifft dies nicht zu, muß die Itemauswahl entsprechend geändert werden, so daß der Test zunächst nicht als eine feststehende Einheit aufgefaßt werden kann. Da die Items nur Indikatoren für die latente Dimension sind, und man aufgrund der Itembeantwortungen auf den Ausprägungsgrad der latenten Dimension schließen möchte, interessiert man sich im wesentlichen für die Möglichkeit, zwischen den Personen Vergleiche auf der Basis der Ausprägungsgrade dieser latenten Dimension durchzuführen. Analog dazu ist weniger die Wiederholbarkeit der Testergebnisse als solche von Interesse, sondern die Genauigkeit des Rückschlusses von den Testwerten auf die Ausprägungsgrade der latenten Dimension.
Für die Bearbeitung dieser Probleme stehen verschiedene methodische Ansätze (Testtheorien) zur Verfügung, die sich hinsichtlich ihrer Grundkonzeption, ihrer Leistungsfähigkeit be- [<30] züglich der einzelnen Fragestellungen und hinsichtlich der erforderlichen Ressourcen bei der Testkonstruktion unterscheiden."
Literatur (Auswahl)
Textbeispiele außerhalb der Psychologie werden hier nicht noch einmal gesondert aufgeführt.
- Ahrens, Hans Joachim (1974). Multidimensionale Skalierung. Weinheim: Beltz.
- Bridgman, Percy Williams (1922), Dimensional analysis, New Haven (Yale University Press) (dt. u. d. T.: Theorie der physikalischen Dimensionen. Ähnlichkeitsbetrachtungen in der Physik, hg. von H. Holl, Leipzig: Teubner.
- Carnap, Rudolf (1926). Physikalische Begriffsbildung. Karlsruhe: Braun. Nachdruck WBG Darmstadt 1968.
- Cronbach, Lee J. & Meehl, Paul E. (1955). Construct validity in psychological tests. Psychological Bulletin, 52, 281-302. [The origin of the term "construct validity"]
- Duden Redaktion. Das Bildwörterbuch. Die Gegenstände und ihre Benennung. Umfassende Darstellung der Dinge unserer Umwelt in Wort und Bild. 384 zum Teil mehrfarbige Bildtafeln. Register mit 27000 Stichworten. Mannheim: Dudenverlag.
- Fischer, Gerhard (1975). Einführung in die Theorie psychologischer Tests. Grundlagen und Anwendung. Bern: Huber. [Schwerpunkt: Raschmodell]
- Herrmann, T. & Stapf, K. H. (1971). Über theoretische Konstruktionen in der Psychologie. Psychologische Beiträge, 336-354.
- Jüttemann, G. (1972). Was nützen uns Eigenschaftskonstrukte ? Psychologische Rundschau, 91-114.
- Krantz, David H.; Luce, Duncan, R.; Suppes, Patrick & Tversky, Amos (1971). Dimensional Analysis and Numerical Law. In (p. 454-544): Foundations of Measurement. Vol. I. Additive and Polynomial Representations. New York: Academic Press.
- Krauth, Joachim (1995). Dimensionalität. In (S.33): Testkonstruktion und Testtheorie. Weinheim: Beltz / PsychologieVerlagsUnion.
- Langhaar, H. L. (1951). Dimensional Analysis and Theory of Models. New York: Wiley & Sons.
- MacCorquodale, Kenneth & Meehl, Paul E. (1948). On a distinction between hypothetical constructs and intervening variables. Psychological Review, 55, 95-107.
- Menger, Karl (1928) Dimensionstheorie. Springer Nature.
- Mittelstraß, Jürgen (1980-1996, Hrsg.). Enzyklopädie Philosophie und Wissenschaftstheorie. 4 Bde. Die ersten beiden Bände erschienen bei BI, Mannheim. Die letzten beiden Bände bei Metzler, Stuttgart. 2. Auflage 2005.
- Pawlik, Kurt (1968). Dimensionen des Verhaltens. Eine Einführung in Methodik und Ergebnisse faktorenanalytischer psychologischer Forschung. Bern: Huber.
- Rauch, Wolfgang & Moosbrugger, Helfried (2011). Klasische Testtheorie. Grundlagen und Erweiterungen für Mehrfacettenmodelle. In (1-86): Hornke, Lutz; Amelang, Manfred & Kerstin, Martin (2011, Hsrg.) Methoden der Psychologischen Diagnostik. Enzyklopädie der Psychologie Thema B, Serie II, Band 2. Göttingen: Hogrefe.
- Schiepek, Günter & Strunk, Guido (1994). Dimensionskonzepte. In (Glossar, S. 111-120): Dynamische Systeme. Grundlagen und Analysemethoden für Psychologen und Psychiater. Heidelberg: Asanger. [Effektive Dimension, Topologische Dimension, Die Hausdorff-Besicovitch-Dimension, Selbstähnlichkeitsdimension, Box-Dimension, Dimensionalität und Attraktoren, Fraktale Dimension]
- Überla, Karl (1971). Faktorenanalyse. Eine systematische Einführung für Psychologen, Mediziner, Wirtschafts- und Sozialwissenschaftler. Berlin: Springer.
- Völz, Horst & Ackermann, Peter (1996). Die Welt in Zahlen und Skalen. Heidelberg: Spektrum.
- Wottawa, Heinrich (1977). Psychologische Methodenlehre. München: Juventa.
- Wottawa, Heinrich (1979). Grundlagen und Probleme von Dimensionen in der Psychologie. Meisenheim am Glan: Anton Hain.
- Wottawa, Heinrich (1980). Dimensionsproblematik. In (S. 70-82): Grundriß der Testtheorie. München: Juventa.
- Yaremko, R.M.; Harari, H. ; Harrison, R.C.& Lynn, E. (1982/83). Handbook of Methods in Psychology. New York: Harper.
- Wikipedia: Dimensionsanalyse (einseitig und verkürzt bei Abruf 13.10.12)
Links (Auswahl: beachte)
- Dimensionsbegriffe in Wikipedia. * Taxonomie *
- Big Five.
- Wikipedia: Dimension in der Mathematik.
- Wikipedia: Dimension in der Physik.
- Wikipedia: Nomenklartut_(Biologie).
- Wikipedia: Dimension in der Semantik.
Glossar, Anmerkungen und Endnoten:
1) GIPT= General and Integrative Psychotherapy, internationale Bezeichnung für Allgemeine und Integrative Psychotherapie.
___
Anmerkung Fischer: Obwohl Fischer des öfteren den Begriff Dimension benutzt, bleibt er doch eine klare Analyse schuldig, was wir nun unter einer psychologischen Dimension zu verstehen haben, wenn man seinem Text auch entnehmen kann, dass er eine Theorie, Messung und den Nachweis der Existenz einer solchen Dimension fordert.
___
Andere Werke: Feger, H. & Bredenkamp, J. (1983, Hrsg.). Messen und Testen, Bd. 3 der Forschungsmethoden der Psychologie, Enzyklopädie der Psychologie enthält keinen Sachregistereintrag "Dimension" oder "Dimensionsanalyse". Das gleiche gilt merkwürdigerweise auch für den Bd. 4, Strukturierung und Reduzierung von Daten (auch 1983) und auch für den Bd. 1, Methodologische Grundlagen der Psychologie, 1994 herausgegeben von Theo Herrmann & Werner H. Tack. Auch bei Theo Herrmann (1976). Lehrbuch der empirischen Persönlichkeitsforschung. Göttingen: Hogrefe findet man im Sachregister keinen Eintrag "Dimension" oder "Dimensionsanalyse". Bei Amelang & Bartussek (1990). S. 485 wird unter "4.2.1 Dimensionierung der Umwelt" der Begriff erwähnt. Die Mutmaßung, dass die Faktorenanalyse allerdings zur Dimensionsanalyse der Umwelt geeignet sein könnte (a.a.O.) klingt reichlich abenteuerlich. Auch im Handbuch der Psychologie in 12 Bdn., Bd. 4 Persönlichkeitsforschung und Persönlichkeitstheorie, 1960 herausgegeben von Lersch & Thomae enthält keinen Sachregistereintrag zu "Dimension". Noch kurioser ist, dass selbst Friedrich Sixtl in seinem grundlegenden Werk "Meßmethoden der Psychologie" in der zweiten, überarbeiteten Auflage 1982 den Sachregistereintrag "Dimensionsanalyse" herausgenommen hat, der in der ersten Auflage 1967 noch enthalten war. In Gordon W. Allport (dt. 1959). Persönlichkeit. Struktur, Entwicklung und Erfassung der menschlichen Eigenart. Meisenheim am Glan: Anton Hain gibt es nur einen Sachregistereintrag zu den Dimensionen der Fühlens (S. 570). Und in J. P. Guilfords Persönlichkeit, dt. 4.A. 1970 findet sich ebenfalls kein Sachregistereintrag zum Thema Dimension, obwohl Guilford mehrere Bücher zu Meß-, Testtheorie und Statistik geschrieben hat und er explizit von somatischen, Eignungs-, Temperaments-, Motivations- und psychopathologischen Dimensionen im Inhaltsverzeichnis spricht. Auch das lexikalisch aufgebaute Handbook of Methods in Psychology von Yaremko et al. (1982/83) enthält ebenso wenig einen Eintrag zu "dimension" oder "dimensionality" wie die Mathematische Psychologie von Coombs, Dawes & Tversky (dt. 1975 ) oder das Methoden-Lexikon für Mediziner, Psychologen, Soziologen von Kriz & Lisch (1988).
Fazit: trotz hochentwickelter Testtheorie und mathematischer Modelle und Methoden herrscht weitgehend ein desolates Chaos zum Dimensionsbegriff in der Psychologie, so dass man sich fragt, wann die methodisch-wissenschaftstheoretischen und testtheoretischen Lehrstühle ihre Arbeit richtig beginnen wollen, was ja nach über 100 Jahren Faktorenanalyse - ihren Beginn setzt z.B. Überla (1971, S. 8) mit dem Jahre 1904 an:

___
Ausnahme: Wottawa 1979.
Das interessante Werk ist aber fast ausschließlich testtheoretisch
orientiert, methodenlastig aber auch methodenkritisch; grundlegende inhaltliche
Überlegungen kommen zu kurz.
___
"der" Faktorenanalyse.
"Die" Faktorenanalyse gibt es nicht, sondern eine Heerschar von
zig-unterschiedlichsten Deutungen und Realisationsmethoden des Ansatzes:
Xij = ai1*Fi1 + ai2*Fi2
+ ... + aij*Fij + ... + aim*Fim
, i = 1...n, j = 1 ... m. Je nachdem, ob die Faktoren F unabhängig
("orthogonal") oder abhängig (korrelierend und "oblique") angenommen
- d.h. den Daten aufgezwungen - und wie die F aus den unterschiedlichen
Faktorentypen ("general", "common", "specific", "error", "communality",
Kommunalität)
zusammengesetzt und gedacht werden, ergeben sich unzählige Varianten
von Faktorenanalysen. Allein im orthogonalen Fall sind rein aus mathematischen
Gründen unendlich viele Lösungen ein und desselben Datensatzes
möglich, weil unendlich viele orthogonale Rotationen möglich
sind, die alle ein und dieselbe Ausgangsmatrix zu reproduzieren gestatten.
Die unendlich vielen Ergebnismöglichkeiten vervielfachen sich noch,
wenn der Lieblingstick der FaktorenanalytikerInnen ausgelebt wird: Datenreduktion
durch Faktoren wegwerfen, auch wenn damit ganz andere Rohdatensätze
impliziert werden, d.h. man reduziert seine Variablen um den Preis, dass
sie gar nicht mehr die ursprünglichen Rohdaten repräsentieren,
sondern ganz andere reproduziert werden, was die meisten gar nicht merken,
weil sie ihre Korrelations- und Faktorwertematrizen gar nicht, wie es sich
gehört, richtig zurückrechnen und somit vertuschen, was sie anrichten.
Zur Kritik des faktorenanalytischen Ansatzes am Beispiel
Extraversion.
___
drei Gruppen nach Wottawa:
(1) Typ Faktorenanalyse oder Multidimensionale Skalierung, (2) Vergleiche
von Objekten (formal z.B. die Versuche von Guttman oder Lazarsfeld zur
Konstruktion eindimensionaler Skalen oder auch das Raschmodell), (3) Formalisierung
psychologischer Hypothesen durch die Konstruktion mathematischer Modelle:
"Sehen diese Modelle für jedes Objekt einen oder mehrere Parameterwerte
vor, so sind in der Regel diese Parameter als Schätzwerte für
die Ausprägungsgrade latenter Dimensionen anzusehen." (S. 3)
___
Faktoren reduziert. Die Faktorenanalyse
hat nicht zur Reduktion von irgendwas beigetragen, sondern alles vervielfacht.
Der Reduktionsfuror hat sich im Ergebnis also umgekehrt.
___
Heterogenität in der
KTT
"4.1 Definition von Heterogenität. Die in Abschnitt
6 besprochenen „klassischen" Ansätze zur Reliabilitätsschätzung
basierten auf einer mehr oder weniger starken Anahmen für die Äquivalenz
der Testteilvariablen sowie auf der Annahme der linearen Unabhängigkeit
der Testteilvariablen. Es wurde gezeigt, dass sich die Kongeneritätsannahme
für eine Reihe von m Test(-teil-)variablen auch als Ein-Faktoren-Modell
darstellen lässt, was prinzipiell auch für die stärkeren
Äquivalenzannahmen gilt. Insbesondere in den letzten Jahren wurden
aber Ansätze zur Reliabilitätsschätzung entwickelt, die
auf noch schwächeren oder auch qualitativ anderen Äquivalenzannahmen
beruhen, da ein einfaktoriell kongenerisches Testmodell mit linearer Unabhängigkeit
in der Praxis häufig unhaltbar ist (vgl. Lücke, 2005a, b; Raykov,
1998, 2001; ten Berge & Socàn, 2004). Das Aufgeben jeweils einer
der beiden Annahmen, also linearer Unabhängigkeit oder einfaktorieller
Kongenerität, führt zu sogenannten heterogenen Testmodellen (vgl.
z.B. Raykov, 1998), die in der Praxis oft angemessener sind. Der Begriff
heterogen ist dabei im faktorenanalytischen Sinn zu verstehen: Bei heterogenen
Tests korrelieren die True-Score-Variablen nicht zu l, und die Dimensionalität
(der Rang) der Korrelationsmatrix der Testteilvariablen ist nicht . mehr
gleich l, sondern es liegt Mehrdimensionalität der Korrelationsmatrix
vor."
Ich kann hier keine Definition von Heteroegenig
umd damit implzit von Homogenität erkennen; und schon gar keine vernünftige
Begründung.
___
Stichworte: Alltag, Alltagsraum, Chemie
(Elemente und Verbindungen), Mathematik (Geometrie, Lineare Algebra, Topologie),
Physik (vierdimensionale Raum-Zeit), Psychologie (Funktionen, Erleben,
Verhalten, Psychologische Testtheorie und Tests). Andere Aspekte: Differenzieren
i.S. von unterscheiden, Dimensionsanalyse, Diskriminieren, eindimensional,
Einteilen, Klassifizieren, mehrdimensional, Ordnen, Sortieren, unterscheiden,
trennen, vergleichen.
___
Standort: Dimension.
Was-ist-Fragen? * Definitionslehre in der GIPT * Terminologie * Welten * Konstruktuvismus * Vulgärkonstruktuvismus * Normen und Normieren * Vergleichen * Beweisen * Statistik in der IP-GIPT *
Testtheorie der Allgemeinen und Integrativen Psychotherapie * Überblick Faktorenanalyse *
"Zahlen". Die Grundlagen praktischer ArithMETRIK für die Messung im Unscharfen, Unklaren und Flüchtigen in der Allgemeinen und Integrativen Psychologie und Psychotherapie.
| Suchen in der IP-GIPT,
z.B. mit Hilfe von "google": <suchbegriff>
site:www.sgipt.org
z.B. Testtheorie site:www.sgipt.org. |
Dienstleistungs-Info.
*
Zitierung
Sponsel, R. (DAS). Dimension, Dimensionalität, Dimensionsanalyse. Begriff und Probleme in der Psychologie und psychologischen Testtheorie mit allgemein-integrativen Blicken über den Zaun: Dokumente und Materialien aus Alltag, Mathematik, Informatik, Physik, Chemie, Biologie, Kunst, Test- und Messtheorie, Psychologie u.a.m. Internet Publikation für Allgemeine und Integrative Psychotherapie IP-GIPT. Erlangen: https://www.sgipt.org/wisms/mtt/DIM/dim0.htm
Copyright & Nutzungsrechte
Diese Seite darf von jeder/m in nicht-kommerziellen Verwertungen frei aber nur original bearbeitet und nicht inhaltlich verändert und nur bei vollständiger Angabe der Zitierungs-Quelle benutzt werden. Das Einbinden in fremde Seiten oder Rahmen, die die Urheberschaft der IP-GIPT nicht jederzeit klar erkennen lassen, ist nicht gestattet. Sofern die Rechte anderer berührt sind, sind diese dort zu erkunden. Sollten wir die Rechte anderer unberechtigt genutzt haben, bitten wir um Mitteilung. Soweit es um (längere) Zitate aus ... geht, sind die Rechte bei/m ... zu erkunden oder eine Erlaubnis einzuholen.
Ende_Dimension_ Überblick_ Rel. Aktuelles _ Rel. Beständiges_ Titelblatt_ Konzept_ Archiv_ Region_ Service iec-verlag_ Mail: sekretariat@sgipt.org_ _ Wichtige Hinweise zu externen Links und Empfehlungen.
g_KKorrektur gelesen am: irs 04.06.2006
Änderungen wird gelegentlich überarbeitet, ergänzt und vertieft * Anregungen und Kritik willkommen
05.08.18 Linkfehler korrigiert. * Dimensionsanalyse des psychischen Merkmals Geduld. * Eindimensionalität.
22.02.18 Wissenschaftstheorie: Qualität, Merkmal, Dimension; Dimension und Dimensionanalyse; Qualität, Merkmal, Dimension; Ereignisanalyse.
13.10.12 Zusammenfassung: Begriffsklärungen und terminologische Vorschläge * Dimensionsanalyse aus dem Online Wörterbuch der Technik
30.09.09 Hinweis spezielle Dimensionsbegriffe der Mathematik * Dimensionsbegriffe bei Schiepek & Strunk.
13.11.07 Zwei Verlinkungen zur "Kommunalität".
05.06.06 Extraversionmodell: Wie müßte ein Faktorenmodell, das diese Ideen erfüllt, aussehen?
04.06.06 Neuaufnahmen: Dimension im Psychologischen Wörterbuch von Dorsch 1994. * Dimensionen in der Informatik * Dimensionsanalyse einer Küche und ihrer Funktionen.



