Positiv semi definit heißt, daß alle Eigenwerte der Korrelationsmatrix >= 0 sind. Nur wenn das der Fall ist, darf überhaupt von einer Korrelationsmatrix gesprochen werden. Positive Semi Definitheit ist also eine notwendige mathematische Bedingung, damit eine Matrix eine Korrelationsmatrix genannt werden darf. Dies wird in der Geschichte und Anwendung der Korrelationsrechnung häufig nicht berücksichtigt - und in der Handhabung der Faktorenanalyse ist diese souveräne Ignoration (Beweis) geradezu der "Normalfall".

Dr. Bernhard Hain bewies 1994, daß bei einer "vollständigen" Partialisierung einer Korrelationsmatrix, also bei Auspartialisieren aller  n-2  Koeffizienten gegen beliebige zwei, die resultierende Korrelationsmatrix nicht notwendig positiv definit ist, ein beachtliches Ergebnis, vor allem, wenn man bedenkt, dass unsinnige Ergebnisse bereits bei rein äußerlich ("phänotypisch intakten") vollständig partiellen Korrelationsmatrizen auftreten können. Das ist ein Befund, der unbedingt weiterer Aufklärung bedarf.
 
 

• Liebestrio nach vollständiger Partialisierung indefinit (10.02.2024).
• Liebesquintett  nach vollständiger Partialisierung indefinit (10.02.2024).
• 1 SZS Äußere Erscheinung und 20 SZS sexuelle Lust nach vollständiger Partialisierung pc=1.388.

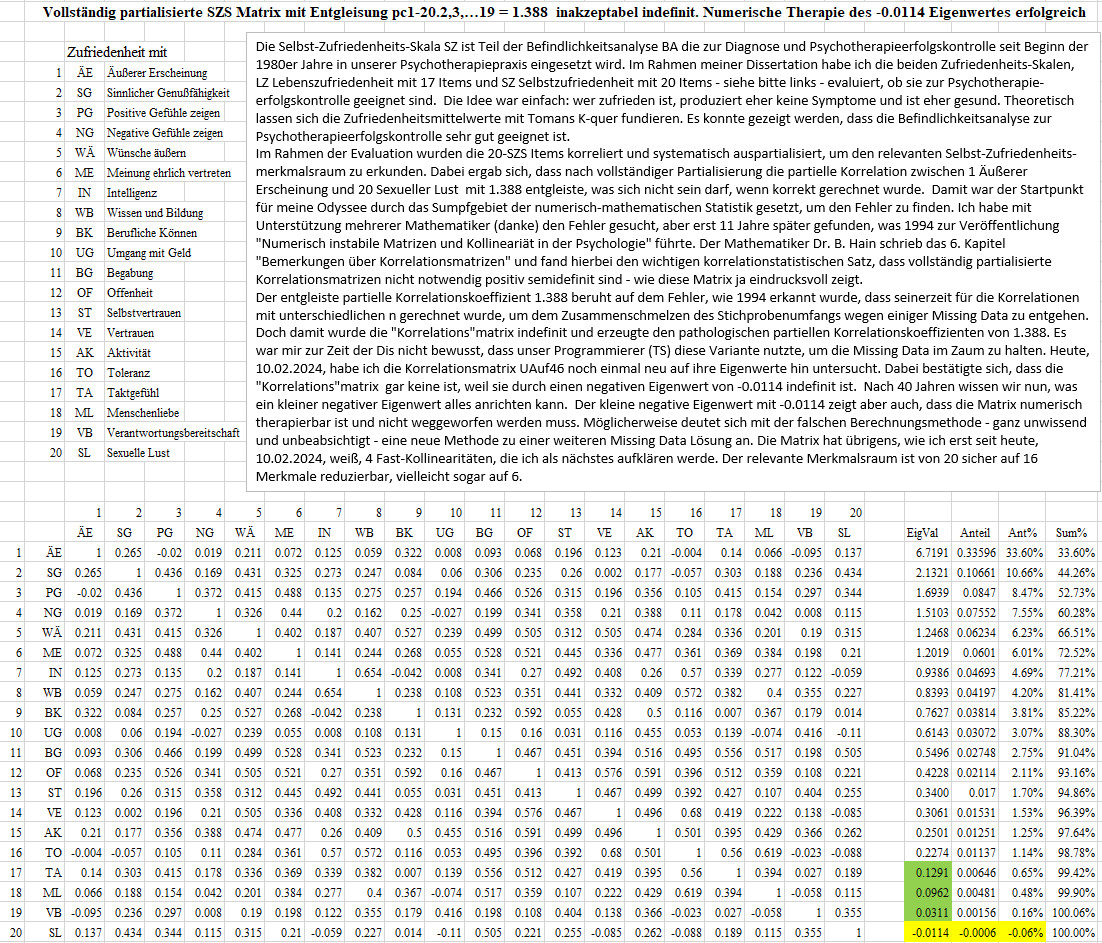
1 SZS Äußere Erscheinung und 20 SZS sexuelle Lust nach vollständiger Partialisierung pc=1.388.
Die Selbst-Zufriedenheits-Skala SZS ist Teil der Befindlichkeitsanalyse BA die zur Diagnose und Psychotherapieerfolgskontrolle seit Beginn der 1980iger Jahre in unserer Psychotherapiepraxis eingesetzt wird. Im Rahmen meiner Dissertation habe ich die beiden Zufriedenheits-Skalen, LZ Lebenszufriedenheit mit 17 Items und SZ Selbstzufriedenheit mit 20 Items - siehe bitte unten im Graph - evaluiert, ob sie zur Psychotherapieerfolgskontrolle geeignet sind.  Die Idee war einfach: wer zufrieden ist, produziert eher keine Symptome und ist eher gesund. Theoretisch lassen sich die Zufriedenheitsmittelwerte mit  Tomans K-quer  fundieren. Es konnte gezeigt werden, dass die Befindlichkeitsanalyse zur Psychotherapieerfolgskontrolle sehr gut geeignet ist.
    Im Rahmen der Evaluation wurden die 20-SZS Items korreliert und systematisch auspartialisiert, um den relevanten Zufriedenheitsmerkmalsraum zu erkunden. Dabei ergab sich, dass nach vollständiger Partialisierung die partielle Korrelation zwischen 1 Äußerer Erscheinung und 20 Sexueller Lust  mit 1.388 entgleiste, was sich nicht sein darf, wenn korrekt gerechnet wurde. Damit war der Startpunkt für meine Odyssee durch das Sumpfgebiet der numerisch-mathematischen Statistik gesetzt, um den Fehler zu finden. Ich habe mit Unterstützung mehrerer Mathematiker (danke) den Fehler gesucht, aber erst 11 Jahre später gefunden, was 1994 zur Veröffentlichung  "Numerisch instabile Matrizen und Kollinearität in der Psychologie" führte. Der Mathematiker Dr. B. Hain schrieb das 6. Kapitel "Bemerkungen über Korrelationsmatrizen" und fand hierbei den wichtigen korrelationstatistischen Satz, dass vollständig partialisierte Korrelationsmatrizen nicht notwendig positiv semi definit sind (oben dokumentiert) - wie diese Matrix auch eindrucksvoll zeigt.
    Der entgleiste partielle Korrelationskoeffizient 1.388 beruht auf dem Fehler, wie 1994 erkannt wurde, dass seinerzeit für die Korrelationen mit unterschiedlichen n gerechnet wurde, um dem Zusammenschmelzen des Stichprobenumfangs wegen einiger Missing Data zu entgehen. Doch damit wurde die "Korrelations"matrix indefinit und erzeugte den pathologischen partiellen Korrelationskoeffizienten von 1.388. Es war mir zur Zeit der Dis nicht bewusst, dass unser Programmierer (TS) diese Variante nutzte, um die Missing Data im Zaum zu halten. Heute, 10.02.2024, habe ich die Korrelationsmatrix UAuf46 noch einmal neu auf ihre Eigenwerte hin untersucht. Dabei bestätigte sich, dass die "Korrelations"matrix" gar keine ist, weil sie durch einen negativen Eigenwert von -0.0114 indefinit ist. Nach 40 Jahren wissen wir nun, was ein kleiner negativer Eigenwert alles anrichten kann. Der kleine negative Eigenwert mit -0.0114 zeigt aber auch, dass die Matrix numerisch therapiebar ist und nicht weggeworfen werden muss. Möglicherweise deutet sich mit der falschen Berechnungsmethode - ganz unwissend und unbeabsichtigt - eine neue Methode zu einer weiteren Missing Data Lösung ab. Die Matrix hat übrigens, wie ich erst seit heute, 10.02.2024, weiß, 4 Fast-Kollinearitäten, die ich als nächstes aufklären werde. Der  relevante Merkmalsraum  ist von 20 sicher auf 16 Merkmale reduzierbar, vielleicht sogar auf 6.

• Literatur zur Korrelation * Speziell im Zusammenhang (Multi-) Kollinearität.

• Partielle Korrelation *
• Korrelation. Was bedeutet der lineare Korrelationskoeffizient? Probleme, Kurioses, Paradoxes, Ungereimtheiten und Widersprüchliches in der Korrelationsrechnung und wie man dem begegnen kann. *