Zusammenfassung - Abstract - Summary
Die  Korrelationsanalysen zeigen sehr hohe Korrelationen mit Ausnahme des Sterblichkeitsrisikos, das negativ korreliert, weil die Sterblichkeitsrisikowerte grob betrachtet relativ konstant bleiben, während alle anderen Größen wachsen.
Eigenwerte < 0.20 zeigen an, ob es in einer Korrelationsmatrix lineare Fast-Abhängigkeiten gibt. Hier ist zu erwarten, dass es zwischen den absoluten Häufigkeiten (6 Größen) und ihren logarithmierten Werten (6 Größen) starke Abhängigkeiten gibt, dass man also deshalb von 6 Fast-Kollinearitäten ausgehen kann. Tatsächlich enthält die Gesamtmatrix 9 Fast-Kollinearitäten, also drei mehr als technisch gesehen zu erwarten waren. Das zeigt, dass die Größen sehr stark zusammenhängen. Die Korrelationsmatrix zeigt einen großen Eigenwert oder Generalfaktor, wir nennen ihn den Corona-Virus-Wachstumsfaktor, der 86% der Varianz ausschöpft. Betrachtet man nur die fünf  Größen Zeiteinheit, Infizierte, neue Infizierte, Todesfälle, neue Todesfälle, nimmt also die Sterblichkeitsrate, die ja nicht wächst, heraus, so steigt der größte Eigenwert und Corona-Virus-Wachstumsfaktor auf 97%. Das kann man so interpretieren, dass die fünf Größen sehr eng zusammenhängen. Etwas überraschend (für mich) ist auch der Befund, dass es kaum nennenswerte Unterschiede zwischen den Korrelationen und Eigenwerten gibt, ob man nun die absoluten Häufigkeiten oder die logarithmierten Werte betrachtet.

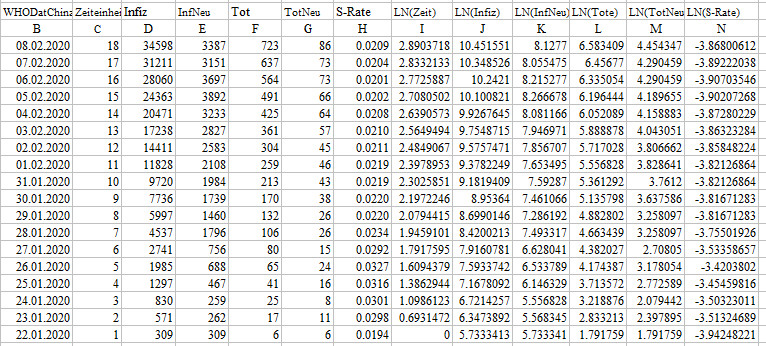
Daten Erlaeuterungen und Lesebeispiele:
Die Datenmatrix enhält neben den Zeiteinheiten (C) nur 5 verschiedene Variablen. Nämlich die absoluten Zahlen für Infizierte (D), neu Infizierte (E), Todesfälle (F), neue Todesfälle (G) und die Sterblichkeitsrate (H), also den Anteil der Todesfälle an den Infizierten. In den Spalten I, J, K. L, M wurden die logarithmierten Werte der 5 Häufigkeiten erfasst.
Infizierte: Am 31.01.2020 werden 9720 Infizierte ausgewiesen.
Neu Infizierte: Am 27.01.2020 werden 756 neu Infizierte angegeben.
Todesfälle: Am 04.02.2020 werden 425 Todesfälle genannt.
Neue Todesfälle: Am 08.02.2020 werden 86 neue Todesfälle angegeben.
Sterblichkeitsrate  [(Tote/Infizierte)*100]: Die Sterblichkeitsrate ist am 22.01.2020 mit 0.0194, also mit 1,94% angegeben.

Korrelationen der Daten der WHO vom 22.01.2020 - 08.02.2020

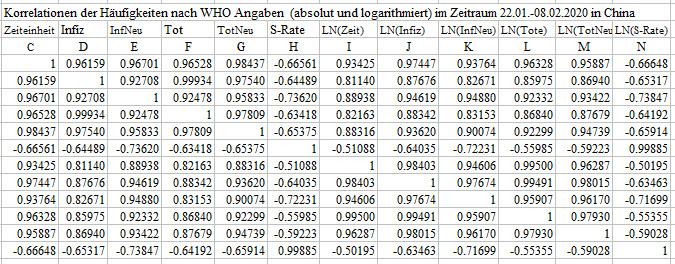
Korrelationen Erlaeuterungen und Lesebeispiele:
Zeiteinheit-Infizierte Absolutzahl: r = 0.96159,
Zeiteinheit-Infizierte logarithmiert: r = 0.97447.
Zeiteinheit-Todesfälle Absolutzahl:  r = 0.96528.
Zeiteinheit-Todesfälle logarithmiert:  r = 0.96328.
Die Korrelationen zu oder zwischen den logarithmierten Werte bewegen sich in der gleichen Größenordnung.

Eigenwerte der Korrelationen der Daten der WHO vom 22.01.2020 - 08.02.2020

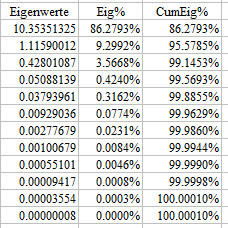
Eigenwerte Erlaeuterungen und Lesebeispiele:
Die Eigenwerte gehören zu keinen Variablen, sondern zur Korrelationsmatrix insgesamt. Ordnete man die Variablen um, ergäben sich trotzdem die gleichen Eigenwerte. Die Eigenwerte zeigen an, wie viele Fast-Abhängigkeiten oder Fast-Kollinearitäten in der Korrelations-Matrix enthalten sind. Man sieht, dass die Matrix von einem einzigen großen Eigenwert, der 86% der Varianz ausschöpft, einem sogenannten Generalfaktor beherrscht wird. Das ist nicht überraschend, zeigen doch alle Werte außer der Sterblichkeitsrate ein starkes Wachstum. Daher kann man diesen Generalfaktor auch General-Wachstumsfaktor des Corona-Virus in China nennen.

Korrelationen und Eigenwerte nur der logarithmierten Häufigkeiten

 

Unterschiede der Korrelationen und Eigenwerte absoluter und logarithmierter Häufigkeiten

Ich finde das Ergebnis der Vergleiche überraschend. Die Unterschiede zwischen den Korrelationen- und Eigenwerten ob auf absoluten Häugikeiten oder auf logarithmierten Häufigkeiten beruhend sind sehr gering und fallen praktisch nicht ins Gewicht.

• Sponsel, Rudolf & Hain, Bernhard (1994). Numerisch instabile Matrizen und Kollinearität in der Psychologie. Diagnose, Relevanz & Utilität, Frequenz, Ätiologie, Therapie.  Ill-Conditioned Matrices and Collinearity in Psychology. Deutsch-Englisch. Ins Englische übersetzt von Agnes Mehl. Kapitel 6 von Dr. Bernhard Hain: Bemerkungen über Korrelationsmatrizen. Erlangen: IEC-Verlag [ISSN-0944-5072  ISBN 3-923389-03-5]. Aktueller Preis: www.iec-verlag.de.
• Sponsel, R. (2005). Fast- Kollinearität in Korrelationsmatrizen mit Eigenwert-Analysen erkennen. Ergänzungsband - Band II zu Numerisch instabile Matrizen und Kollinearität in der Psychologie. Erlangen: IEC-Verlag.

Fast-Kollinearitäts- über Eigenwertanalysen

• Fast-Kollinearitätsanalyse einer Emotions- & Persönlichkeitsmatrix nach Becker.
• Kollinearitäts- und Faktorenanalysestudie einer Korrelationsmatrix von Wegge et al. 2012, Report Psychologie, 37,9, S. 352.
• Eigenwertanalyse Geldumlauf, Produktion und Preise Deutschland 1950-1970.
• Fast- Kollinearität in Korrelationsmatrizen mit Eigenwert-Analysen erkennen
• Überblicks- und Verteilerseite: Numerisch instabile Matrizen und Kollinearität in der Psychologie - Ill-Conditioned Matrices and Collinearity in Psychology -   Diagnose, Relevanz & Utilität, Frequenz, Ätiologie, Therapie.
• Zum Konzept der Relationentreue.

Multivariate Links

• Einführung und Überblick. Kritik der Handhabung der Faktorenanalyse, Kommunalität.
• Korrelation. Was bedeutet der lineare Korrelationskoeffizient? Probleme, Kurioses, Paradoxes, Ungereimtheiten und Widersprüchliches in der Korrelationsrechnung und wie man dem begegnen kann,  Partielle Korrelation.
• Bedeutung der Eigenwerte einer Korrelationsmatrix.
• Pseudo-Korrelationsmatrizen.
• Vollständig Partielle Korrelationsmatrix nicht notwendig positiv definit. Der Beweis von Dr. Bernhard Hain (1994).
• Systematische Veränderungs-Paradoxie beim linearen Produkt- Moment- Korrelationskoeffizienten und Effekten von Lernen, Üben, Vergessen, Entwicklung, Fortschritt, Rückschritt und ganz allgemein bei systematischen Veränderungen relativ konstanter Zunahmen oder Abnahmen.
• Übersicht Eigenwertstrukturen für Generalfaktormodelle für n = 3, 4, ... , 50.
• Generalfaktormodelle in Intelligenz-Tests an der Eigenwertstruktur erkennen. (hier untersucht: AID, BIS, HAWIE, IST70 und LPS)
• Beweis und beweisen in Wissenschaft und Leben.
• Überblick Arbeiten zur Theorie, Definitionslehre, Methodologie, Meßproblematik, Statistik und Wissenschaftstheorie besonders in Psychologie, Psychotherapie und Psychotherapieforschung.