| Korrelationskoeffizienten können
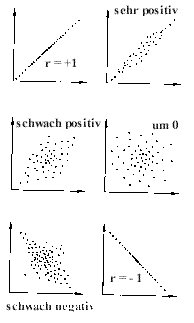
Werte zwischen -1 und +1 annehmen: -1 <= r <= +1. Eine negative
Korrelation bedeutet einen gegenläufigen Zusammenhang
zwischen z.B. a und b: steigt a, fällt b und umgekehrt. Eine positive
Korrelation bedeutet einen gleichsinnigen Zusammenhang zwischen
a und b. Steigt a, steigt b, fällt a, fällt auch b und umgekehrt.
Eine Korrelation um 0 zeigt keinen Zusammenhang zwischen a und b und
den mit ihnen verbundenen Variablen. Das kann sich schnell ändern,
wenn auspartialisiert wird. Partialisieren ist der korrelationsrechnerische
Ausdruck für "Einfluß ausschalten durch konstant halten". Man
untersucht also die Zusammenhänge zwischen a und b und hält die
bekannten Einflüsse von c,d,e, ... konstant. Partielle Korrelationen
werden wie folgt gekennzeichnet und gelesen: rXY.ABC... , d.h. es wird
die Korrelation zwischen X und Y betrachtet wobei die Einflüsse von
ABC ... ausgeschaltet = konstant gehalten werden.
Info Korrelation * Info partielle Korrelation * Info Beweis in der Statistik * Info Statistik IP-GIPT * |
 |
Der IST 70 ist ein Intelligenz-Struktur-Test, daher das
Kürzel IST, der von Rudolf Amthauer zuerst 1953 und in einer Überarbeitung
1970 mit vielen Auflagen und Übersetzungen veröffentlicht wurde.
Die Normierung beruht auf über 30.000 Fällen. Der IST umfaßt
8 reguläre und eine Zusatzskala mit folgenden Bedeutungen:
| 1 =: SE =: Satzergänzung
2 =: WA =: Wortauswahl 3 =: AN =: Analogien 4 =: GE =: Gemeinsamkeiten 5 =: RA =: Rechenaufgaben 6 =: ZR =: Zahlenreihen 7 =: FA =: Figurenauswahl 8 =: WÜ =: Würfelaufgaben 9 =: ME =: Merkaufgaben |
Die folgende partielle Korrelationsanalyse mit allen, also 501 Partialisierungen geht von der Korrelationsmatrix aus von: Amthauer, Rudolf (1973, 4.u.A.). Intelligenz-Struktur-Test IST 70. Handanweisung für die Durchführung und Auswertung. Göttingen: Hogrefe.
Original-Korrelationsmatrix IST 70 S. 32, N=799.
Die Korrelation "Ges.", Gesamtwert, wurde hier weggelassen, weil sie per definitionem kollinear zu den anderen Werten ist. Hierdurch würden von vornherein numerische Instabilitäten angelegt, die zu korrelativen Absurditäten und numerischen Entgleisungen führen könnten, die die Korrelationsmatrix mit negativen Eigenwerten "psychotisch" werden lassen könnte.
Korrelationskoeffizienten von File C:\OMI\NUMERIK\MATRIX\KK\ODOD\IST709.K09
in File C:\OMI\NUMERIK\MATRIX\KK\ODOD\IST709.PKA
11/23/02 19:38:08
Korrelationskoeffizienten in Promill, d.h. z.B. 337 = 0,337
Original-Korrelationen
der 9 Items in Promille
| 1=:SE=:Satzergänzung | 4=:GE=:Gemeinsamkeiten | 7=:FA=:Figurenauswahl |
| 2=:WA=:Wortauswahl | 5=:RA=:Rechenaufgaben | 8=:WÜ=:Würfelaufgaben |
| 3=:AN=:Analogien | 6=:ZR=:Zahlenreihen | 9=:ME=:Merkaufgaben |
| 2
3 4 5
6 7 8
9
337 425 388 330 363 316 227 165 1 406 427 218 413 304 256 300 2 391 251 395 380 299 322 3 206 254 253 226 156 4 169 309 27 89 5 576 353 315 6 322 278 7 436 8 |
Ablesebeispiel Zeile 1, Spalte
7
Die Korrelation zwischen Satzergänzung und Figurenauswahl beträgt r17 = 0.316 Ablesebeispiel Zeile 5, Spalte 8: Die Korrelation zwischen Rechen- und Würfelaufgaben beträgt r58 =0,027 |
| Anmerkung: Zwischen Rechen- und Würfelaufgaben und den mit ihnen verbundenen Variablen gibt es also so gut wie keine Korrelation. Würde diese Korrelation auch über die Partialisierungen durchgehalten, bedeutete dies, daß hier zwei echt verschiedene Intelligenzkomponenten vorliegen. Mit anderen Worten: die arithmetischen und geometrischen Fähigkeiten haben "nichts" miteinander zu tun. Dies wird möglicherweise etwas eingeschränkt, wenn man sich die vollständig partialisierte Korrleation zwischen den Variabe 6 (Zahlrenreihen) und 7 (Figurenauswahl) ansieht. Die gemeinsame "Brücke" zwischen beiden könnte Gesetzmäßigkeiten erkennen sein, einmal mehr arithmetisch (6 - Zahlenreihen), zum andern mehr geometrisch (7 - Figurenauswahl). |
Insgesamt sind die Korrelationen zwischen den Untertestest und der mit ihnen verbundenen Variablen (Dimensionen) wünschenswert mäßig, allerdings weiß man an dieser Stelle noch nicht, was geschieht, wenn partialisiert wird.
Abstract / Zusammenfassung Ergebnisse
Die 126 partiellen Korrelationskoeffizienten zur Korrelation zwischen 1 und 2
Betrachtet man die Korrelation zwischen den ersten beiden Variablen,
also zwischen Satzergänzung und Wortauswahl,
so gibt es folgende Möglichkeiten:
| 0 auspartialisiert:
000 r12 = .337 _ 1 auspartialisiert 7: r12 = .337 Min: r12.3 = .199 Max: r12.9 = .306 SW: .107 001 r12.3 = .199 002 r12.4 = .206 003 r12.5 = .288 004 r12.6 = .220 005 r12.7 = .267 006 r12.8 = .296 007 r12.9 = .306 _ 2 auspartialisiert: 21 r12 = .337 Min: r12.46 = .114 Max: r12.89 = .288 SW= .174 008 r12.34 = .125 009 r12.35 = .172 010 r12.36 = .138 011 r12.37 = .172 012 r12.38 = .184 013 r12.39 = .196 014 r12.45 = .173 015 r12.46 = .114 016 r12.47 = .160 017 r12.48 = .183 018 r12.49 = .183 019 r12.56 = .183 020 r12.57 = .242 021 r12.58 = .243 022 r12.59 = .260 023 r12.67 = .211 024 r12.68 = .209 025 r12.69 = .214 026 r12.78 = .248 027 r12.79 = .255 028 r12.89 = .288 _ |
3 auspartialisiert: 35
r12 = .337 Min: r12.346 = .070 Max: r12.789 = .246 SW: .239 _ 029 r12.345 = .105 030 r12.346 = .070 031 r12.347 = .104 032 r12.348 = .115 033 r12.349 = .122 034 r12.356 = .115 035 r12.357 = .156 036 r12.358 = .154 037 r12.359 = .170 038 r12.367 = .136 039 r12.368 = .134 040 r12.369 = .142 041 r12.378 = .164 042 r12.379 = .174 043 r12.389 = .188 044 r12.456 = .089 045 r12.457 = .143 046 r12.458 = .147 047 r12.459 = .153 048 r12.467 = .111 049 r12.468 = .109 050 r12.469 = .110 051 r12.478 = .150 052 r12.479 = .151 053 r12.489 = .175 054 r12.567 = .180 055 r12.568 = .168 056 r12.569 = .177 057 r12.578 = .217 058 r12.579 = .228 059 r12.589 = .238 060 r12.678 = .202 061 r12.679 = .207 062 r12.689 = .209 063 r12.789 = .246 _ _ |
4 auspartialisiert: 35
r12 = .337 Min: r12.3456 = .052 Max: r12.5789 = .216 SW: .164 _ 064 r12.3456 = .052 065 r12.3457 = .092 066 r12.3458 = .093 067 r12.3459 = .102 068 r12.3467 = .069 069 r12.3468 = .068 070 r12.3469 = .073 071 r12.3478 = .099 072 r12.3479 = .106 073 r12.3489 = .118 074 r12.3567 = .115 075 r12.3568 = .109 076 r12.3569 = .119 077 r12.3578 = .144 078 r12.3579 = .157 079 r12.3589 = .159 080 r12.3678 = .133 081 r12.3679 = .141 082 r12.3689 = .140 083 r12.3789 = .170 084 r12.4567 = .089 085 r12.4568 = .082 086 r12.4569 = .086 087 r12.4578 = .129 088 r12.4579 = .133 089 r12.4589 = .143 090 r12.4678 = .107 091 r12.4679 = .109 092 r12.4689 = .109 093 r12.4789 = .148 094 r12.5678 = .167 095 r12.5679 = .176 096 r12.5689 = .170 097 r12.5789 = .216 098 r12.6789 = .203 _ _ |
5 auspartialisiert: 21
r12 = .337 Min: r12.34568 = .049 Max: r12.35789 = .150 SW: .101 099 r12.34567 = .052 100 r12.34568 = .049 101 r12.34569 = .056 102 r12.34578 = .085 103 r12.34579 = .093 104 r12.34589 = .097 105 r12.34678 = .068 106 r12.34679 = .074 106 r12.34689 = .073 107 r12.34789 = .104 108 r12.35678 = .109 109 r12.35679 = .119 110 r12.35689 = .115 111 r12.35789 = .150 112 r12.36789 = .140 113 r12.45678 = .082 114 r12.45679 = .086 115 r12.45689 = .084 116 r12.45789 = .128 117 r12.46789 = .108 118 r12.56789 = .169 _ 6 auspartialisiert: 7 r12 = .337 Min: r12.345678 = .049 Max: r12.356789 = .115 SW: .066 119 r12.345678 = .049 120 r12.345679 = .056 121 r12.345689 = .055 122 r12.345789 = .090 123 r12.346789 = .074 124 r12.356789 = .115 125 r12.456789 = .084 _ 7 auspartialisiert: r12 = .337 126 r12.3456789 = .055 |
7 auspartialisiert - Achtung: Hier werden alle restlichen gegenüber dem Paar 12 auspartialisiert. Diese Matrix ist nach den Hain'schen Untersuchungen nicht notwendig positiv definit, es könnten also unsinnige Korrelationskoeffzienten resultieren. Bei der Interpretation ist allgemein die größte Vorsicht geboten. In diesem speziellen Fall kann jedoch gezeigt werden, daß die vollständige Partialisierung die Qualität und Robustheit der Matrix nicht beeinträchtigt.
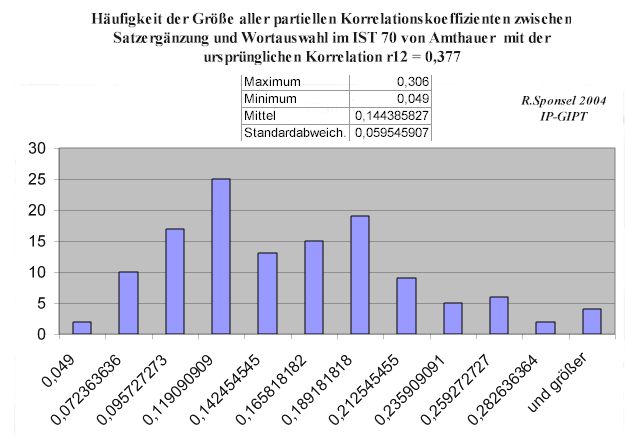
4572 Korrelationskoeffizienten.
Es sind 9 Variablen (Unterteste). Wird jeweils eine auspartialisiert, verbleiben 8. Aus 8 Variablen können nach der Formel (n/2(n-1) 28 Paare gebildet werden. Also gibt es für den ersten Fall, eine aus 9 Variablen auspartialisieren, 28 * 9 = 252 partielle Korrelationskoeffizienten.
Werden aus 9 zwei auspartialisiert, verbleiben 7 Variable. Aus 7 Variablen können 21 Paare gebildet werden. Und aus 9 Variablen können nach der Formen (n über i) insgesamt 36 Partialisierungskombinationen gebildet werden (1: 12, 2: 13, 3: 14, 4: 15, 5: 16, 6: 17, 7: 18, 8: 19, 9: 23, 10: 24, 11: 25, 12: 26, 13: 27, 14: 28, 15: 29, 16: 34, 17: 35, 18: 36, 19: 37, 20: 38, 21: 39, 22: 45, 23: 46, 24: 47, 25: 48, 26: 49, 27: 56, 28: 57, 29: 58, 30: 59, 31: 67, 32: 68, 33: 69, 34: 78, 35: 79, 36: 89).
Werden aus 9 drei auspartialisiert, verbleiben 6 Variable. Aus 6 Variablen können 15 Paare gebildet werden. Und aus 9 Variablen können nach (n über i) 84 verschiedenen 3-er-Partialisierungskombinationen gebildet werden, so daß sich insgesamt 15 * 84 = 1260 verschiedene partielle Korrelationskoeffizienten ergeben.
Fährt man so fort, ergibt sich als Gesamtrechnung: 252 + 756 + 1260 + 1260 + 756 + 252 + 36 = 4572 partielle Korrelationskoeffzienten für den Typ IST 70 mit 9 Variablen (das ist dann für alle Korrelationsmatrizen mit 9 Variablen so).
___
welche Variable. Neben den test-internen Variablen (Untertests, "Dimensionen") gibt es natürlich noch viele andere, die auf das Testergebnis - auch erheblichen - Einfluß nehmen können: Alter, Bildung, Kulturkreis, (Leistungs-) Motivation, Erfahrung, Begabung, Übung und Routine, Befindlichkeit und Verfassung (müde, wach, ausgeruht, gesund, krank), Anspannung u.a.m.
___
Sponsel, Rudolf & Hain, Bernhard (1994). Numerisch instabile Matrizen und Kollinearität in der Psychologie. Diagnose, Relevanz & Utilität, Frequenz, Ätiologie, Therapie. Ill-Conditioned Matrices and Collinearity in Psychology. Deutsch-Englisch. Übersetzt von Agnes Mehl. Kapitel 6 von Dr. Bernhard Hain: Bemerkungen über Korrelationsmatrizen. Erlangen: IEC-Verlag [ISSN-0944-5072 ISBN 3-923389-03-5] Aktueller Preis: http://ww.iec-verlag.de.
- Dokumentation der 501 vollständigen partiellen Korrelationsanalysen zum IST 70:
- Sie sind jetzt hier: Einführung und Ergebnisse der Untersuchung
- Die ersten 129 partiellen Korrelationsanalysen mit auspartialisieren 1,2 und 3 Variablen
- Die zweiten 126 partiellen Korrelationsanalysen mit auspartialisieren 4 Variabler.
- Die dritten 126 partiellen Korrelationsanalysen mit auspartialisieren 5 Variabler.
- Die letzten 120 partiellen Korrelationsanalysen mit auspartialisieren 6 und 7 Variabler.
- Analyse der Korrelationsmatrix des Intelligenz-Struktur-Test IST 70 von Amthauer.
- Standard Matrix Analyse der Korrelationsmatrix des Intelligenz-Struktur-Test IST 70 von Amthauer mit Gesamtwert nur zum Zwecke der Kollinaritäts-Demonstration und ihrer extremen Auswirkungen.
- Analyse der vollständig partialisierten Korrelationsmatrix des Intelligenz-Struktur-Test IST 70 von Amthauer.
- Vollständige Faktorenanalysen zum IST 70 mit Rückrechnung und Residualanalysen aus 1,2,3,4,5,6,7,8 und allen 9 Faktoren.
Multivariate und numerische Studien zum IST 70 (Intelligenz-Struktur-Test):
- Extern: Kollinearität bei Wikipedia
- Für NichtmethodikerInnen: worauf kommt es an bei Korrelationsmatrizen.
- Für professionell Interessierte: Abkürzungen, Definition, Erklärung und Bedeutung zur Standard- (Korrelations)- Matrix- Analyse (SMA)
- Gesamtzusammenfassung: "Numerisch instabile Matrizen und Kollinearität in der Psychologie".
- Hintergrund und Entstehungsgeschichte der Arbeit "Numerisch instabile Matrizen und Kollinearität in der Psychologie".
- Einführung und Überblick. Kritik der Handhabung der Faktorenanalyse.
- Was bedeutet der lineare Korrelationskoeffizient? Kurioses, Paradoxes, Ungereimtheiten und Widersprüchliches in der Korrelationsrechnung und wie man dem begegnen kann.
- Partielle Korrelationen: Definition und Methode - Tücken und Fallen - Wichtige Anwendungen in der Psychologie - Kombinatorik der Anzahlen - Schlußfolgerungen - Literatur.
- Überblick Arbeiten zur Theorie, Definitionslehre, Methodologie, Meßproblematik, Statistik und Wissenschaftstheorie besonders in Psychologie, Psychotherapie und Psychotherapieforschung.
- Überblick Statistik in der IP-GIPT: Methoden, Daten, Geschichte, Verwandtes.
- Der Kardinal-Skalen-Beweis zur Summen-Score-Funktion und seine praktische Bedeutung.
- Welten und die Konstruktion unterschiedlicher Wirklichkeiten in der GIPT.
- Über den Aufbau einer präzisen Wissenschaftssprache in Psychologie, Psychopathologie, Psychodiagnostik und Psychotherapie.
- Testtheorie der Allgemeinen und Integrativen Psychotherapie.
Zitierung
Sponsel, R. (DAS). Multivariate und numerische Studien zum IST 70. Vollständige 501 partielle Korrelationsanalysen am Beispiel IST 70. Einführung und Ergebnisse der Untersuchung. Abteilung Arbeiten zur Definitionslehre, Methodologie, Meßproblematik, Statistik und Wissenschaftstheorie besonders in Psychologie, Psychotherapie und Psychotherapieforschung. Internet Publikation für Allgemeine und Integrative Psychotherapie IP-GIPT. Erlangen: https://www.sgipt.org/wisms/statm/kor/ist70pk0.htm
Copyright & Nutzungsrechte
Diese Seite darf von jeder/m in nicht-kommerziellen Verwertungen frei aber nur original bearbeitet und nicht inhaltlich verändert und nur bei vollständiger Angabe der Zitierungs-Quelle benutzt werden. Das direkte, zugriffsaneignende Einbinden in fremde Seiten oder Rahmen ist nicht gestattet, Links sind natürlich willkommen. Zitiert kann mit Quellenangabe beliebig werden. Sofern die Rechte anderer berührt sind, sind diese dort zu erkunden. Sollten wir die Rechte anderer unberechtigt genutzt haben, bitten wir um Mitteilung. Soweit es um (längere) Zitate aus ... geht, sind die Rechte bei/m ... zu erkunden oder eine Erlaubnis einzuholen.
Ende IST 70 ParKor 0_Datenschutz_Überblick_Rel. Aktuelles _ Rel. Beständiges_ Titelblatt_ Konzept_ Archiv_ Region_Service iec-verlag _Mail: sekretariat@sgipt.org___
Änderungen
20.07.2025 Einführung: "weil die vollständig partialisierte Matrix positiv ist." ersetzt durch "weil die vollständig partialisierte Matrix positiv definit (alle Eigenwerte > 0) ist."
30.04.2001 Linkfehler beseitigt: Danke an Gottfried Helms: Vollständige Faktorenanalysen zum IST 70 mit Rückrechnung und Residualanalysen aus 1,2,3,4,5,6,7,8 und allen 9 Faktoren.
23.01.2004 Kleine Fehlerkorrekturen, letzte ca. 21.40: Falsch: "der IST 90". Richtig: des IST 70. 21.50: Ergänzung welche Variable.