Kollinearitäts-, Eigenwert- und Faktorenanalysen
einer Korrelationsmatrix von Revenstorf der 16 Extraversionsfragen nach
Brengelmann & Brengelmann
Ist Extraversion multifaktoriell bedingt oder die Faktorenanalyse
ein falsches Modell?
von Rudolf Sponsel, Erlangen
_
Zusammenfassung,
Summary, Abstract:
Es wird gezeigt, wie die Untersuchung der Fast-Kollinearität
mit Eigenwertanalysen beim Extraversionsfragebogen von Brengelmann
& Brengelmann (1960), von dem Revenstorf
(1980, S. 74) eine numerisch instabile
Korrelationsmatrix veröffentlichte, erfolgreich durchgeführt
werden kann. Die neuen Methoden für die in der 1994 durchgeführten
Studie 7.4 in Sponsel
(1994) standen damals noch nicht zur Verfügung. Obwohl die Matrix
keine hohen Korrelationen, meist sogar nur gering ausgeprägte, aufweist,
enthält sie demgegenüber überraschend eine Fast-Kollinearität,
wie der kleinste Eigenwert der Korrelationsmatrix mit 0.0125 klar
anzeigt (womit die 16x16 Matrix höchstens
auf eine 15x15 Matrix reduzierbar wäre). Daraus folgt ein wichtiger
Satz: Fast-Kollinearität ist von der Höhe der Beträge der
Korrelationskoeffizienten unabhängig. Mit Hilfe einer vollständigen
Eigenwertanalyse aller 65519 Partialisierungen der 16*16 Matrix konnte
das fast-kollineare Subsystem gefunden werden: die Variablen 7, 11, 14
und 16. Ein weiteres wichtiges methodisches Ergebnis dieser neuen Studie
ist, dass die Hauptkomponentenanalyse im Gegensatz zur Quartimax- oder
Varimax Rotation sehr deutlich ergibt, dass die Variablen 11 und 14 mit
dem Common-Faktor
Verlegenheit diese Fast-Kollinearität
hervorrufen. Während die Hauptkomponentenmethode den Common-Factor
sehr klar zum Ausdruck bringt, verschwindet diese Deutlichkeit bei der
Quartimax- und Varimax Rotation. Betrachtet man sich die Itemliste (Fragebogen)
so hätten es inhaltlich betrachtet ebenso gut die Fragen 5 und 7 (Lebhaftigkeit)
sein können. Bei einer 16*16-Matrix gibt es maximal 458753
Fast-Kollinearitäten, wovon hier bezüglich des Eigenwertkriteriums
< 0.20 insgesamt 7631 (mit der Gesamtmatrix) gefunden werden konnten.
Das sind 1,6635% aller möglichen, womit die Fast-Kollinearität
dieser Matrix bestimmt ist. Rechner und Programm gerieten allerdings durch
die kombinatorische Explosion in die Nähe ihrer praktischen Grenzen.
Eine alte Studentenversion von Matlab rechnete und schrieb - einschließlich
aller partiellen und multiplen Korrelationen
- ca. 4,5 Stunden und erzeugte eine 113 Megabyte große Auswertedatei.
Bemerkt sei noch, dass die vollständig partielle
Korrelationsmatrix (2 jeweils gegen den Rest) nicht positiv semi definit,
sondern indefinit ist und unsinnige, wenn auch - und das ist besonders
tückisch - phänotypisch formal korrekte
Ergebnisse liefert, ein Resultat, das bereits Dr. B. Hain
1994 allgemein untersuchte, bewies und davor warnte (das betrifft auch
die Partition 7, 11,14,16). Inhaltlich
bleibt als Nebenergebnis bemerkenswert, dass das Faktorenanalysemodell
nicht hergibt, was es hergeben soll. Man sollte erwarten, dass bei einem
Extraversionsfragebogen - der hier trotz der Polungsprobleme zweifellos
vorliegt - ein einziger Generalfaktor
Extraversion erscheint. Tatsächlich zeigt der größte
Eigenwert mit 4.2050 aber, dass damit nur (4.2050/16)*100 = 26,28%
Varianz aufklärt werden: viel zu wenig und im Grunde ein absonderliches
Resultat, was Revenstorf
nicht kritisch reflektiert. Wenn man akzeptiert, dass Extraversion
hier hinreichend gut operationalisiert wurde, bedeutet das also entweder,
dass Extraversion multifaktoriell erklärt werden muß oder das
orthogonale Modell der Faktorenanalyse nicht angemessen ist (ein theoretisch
begründetes Modell wird vorgeschlagen).
Datenquellen
Quellen der hier analysierten Daten: (1) Korrelationen in Revenstorf,
D. (1980). Faktorenanalyse. Stuttgart: Kohlhammer. S. 74, Tab. 4.1, Extraversionsfragebogen,
S. 74, N=997. Die 16 Fragen und ihre Polung aus (2): Brengelmann, J. C.
& Brengelmann, L. (1960). Deutsche Validierung Von Fragebogen Der Extraversion,
Neurotischen Tendenz Und Rigidität. In: Zeitschrift für experimentelle
und angewandte Psychologie, VII, 291-331. Bemerkung zu den Fragen (Variablen)
15 und 16: Es ist schwer nachzuvollziehen, wieso die Autoren der Originalarbeit
(S. 308) Item 15 und 16 positiv polen, da doch offensichtlich
scheint, dass nur die Verneinung im Sinne von Extraversion gewertet
werden kann, also negative Polung vorliegen sollte, worauf ja auch die
Interkorrelationen hindeuten (8, 9, 11, 14 mit 15 und 16); die Analyse
der Korrelationsmatrix ist davon jedoch nicht beeinträchtigt:
Die Extraversionsfragen
+1. Haben Sie fast immer eine passende Antwort auf
Bemerkungen, die an Sie gerichtet sind?
+2. Pflegen Sie schnell und sicher zu handeln?
+3. Können Sie sich in einer vergnügten Gesellschaft
meistens ungezwungen und unbeschwert auslassen?
+4. Bezeichnen Sie sich selbst als gesprächig?
+5. Halten andere Leute Sie für lebhaft?
+6. Übernehmen Sie bei gemeinsamen Aktionen gerne die Führung?
+7. Halten Sie sich für einen lebhaften Menschen?
-8. Fällt es Ihnen schwer, selbst in einer ungezwungenen
Gesellschaft richtig aus sich herauszugehen?
-9. Halten Sie sich bei gesellschaftlichen Verpflichtungen
lieber im Hintergrund auf?
+10. Machen Sie gewöhnlich den Anfang, wenn Sie neue Bekannte
gewinnen?
-11. Sind Sie leicht verlegen?
+12. Waren Sie aktiv an der Organisation eines Vereins oder irgendeiner
Gruppe beteiligt?
+13. Spielen Sie gerne eine aktive Rolle bei gesellschaftlichen Ereignissen?
-14. Macht es Sie verlegen, wenn Leute auf der Straße oder in
den Läden Sie beobachten?
+15. Sind Sie im Umgang mit anderen ziemlich behindert, so daß
Sie nicht so erfolgreich sind, wie Sie es sein könnten?
+16. Fällt es Ihnen schwer, vor einer großen Gruppe von
Menschen zu sprechen oder vorzutragen? |
Die Korrelationsmatrix
und ihre Eigenwerte
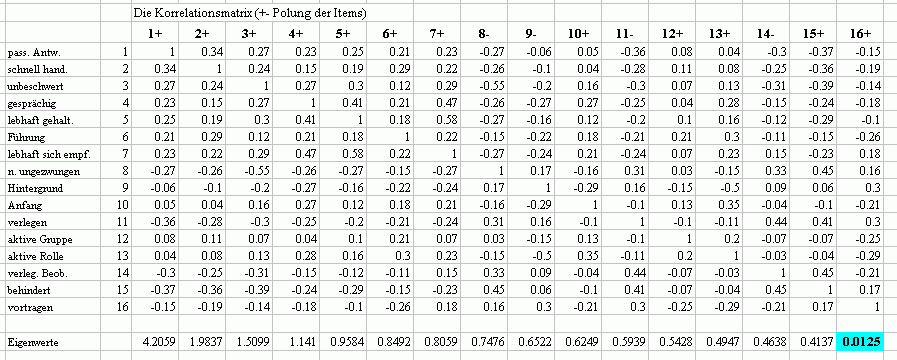
Multiple Korrelationen der
Matrix:
 |
Betrachtet man die multiplen Korrelationen, so wird die
Hypothese nahegelegt, dass die Fast-Kollinearitätspartition die Variablen
7, [11], 14 und 16 bilden. Die Hypothese wird sich hier dergestalt bestätigen,
daß 7, [11], 14 und 16 tatsächlich beteiligt sind. Aber diese
Hypothese stimmt leider nicht immer (Sponsel 2005), sonst gäbe es
ein einfaches, der kombinatorischen Explosion entgehendes Verfahren, die
Fast-Kollinearitätspartitionen leicht aufzuspüren.
Wie unten gezeigt wird, bestehen die kleinsten Partitionen, die Fastkollinearitäten
in sich bergen, aus 5 Variablen, wobei eine Viererpartition nur knapp den
Kriteriumsgrenzwert Eigenwert < 0,20 überschreitet.
|
Die Faktorenladungen
nach der Hauptkomponentenmethode
Zur Interpretation
der Faktorenladungen. * Dimensionsanalyse
* Eindimensionale Extraversions
Konstruktion *

Die
Faktorenladungen nach der Quartimax Rotation
Zur Interpretation
der Faktorenladungen. * Dimensionsanalyse
* Eindimensionale Extraversions
Konstruktion *

Die
Faktorenladungen nach der Varimax-Rotation
Zur Interpretation
der Faktorenladungen. * Dimensionsanalyse
* Eindimensionale Extraversions
Konstruktion *
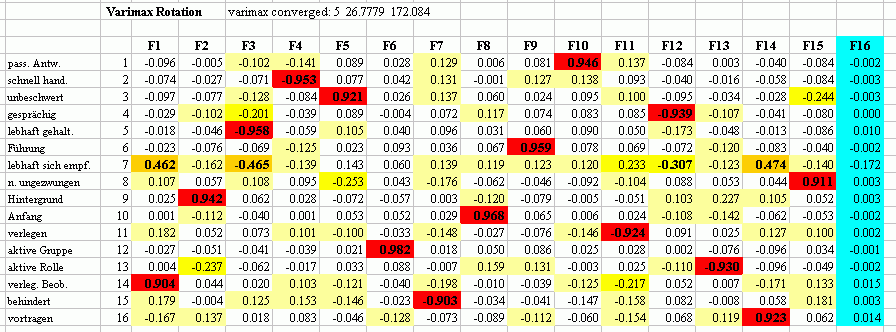
Anmerkung: Die Varimaxrotationergebnisse
von Revenstorf (1980, S. 115) weichen von den hier dargestellten deshalb
ab, weil er nur vier Faktoren varimaxrotiert - hier werden alle 16 varimaxrotiert.
Dies zeigt eine weitere extreme Schwäche und Willkür dieser Methode:
jenachdem, wie viele Faktoren man nimmt, erhält man ganz unterschiedliche
Interpretationsvorgaben (ich habe die Matrix zur Kontrolle mit ALMO 6.4
von Kurt Holm nachgerechnet, der zu ziemlich übereinstimmenden Ergebnissen
wie unser Programm kommt). Unsere Varimaxrotation mit nur vier Faktoren
[varimax converged: 5 28.3659 114.533)] kann Revenstorfs
Ergebnisse ungefähr replizieren, wenn man Faktor 2 und 3 umbenennt.
ABC-Eigenwertanalyse
der Fast-Kollinearität (nach Sponsel
2005).

Varianten suchen
nur in Quintetten (5er Partitionen):
Die systematische Suche in Partitionen führte aufsteigend zu ersten
Ergebnissen bei den 5er Partitionen. Hier wurde das Suchkriterium, ist
ein Eigenwert < 0,20, von folgenden Partitionen erfüllt. Zur Notation:
Die Ziffern links des Punktes geben die Variablen an, die in der Partition
sind, die Ziffern rechts des Punktes geben die Variablen an, die herausgenommen
wurden:
part: 1_7_11_14_16 . 2_3_4_5_6_8_9_10_12_13_15
A=1
part: 2_7_11_14_16 . 1_3_4_5_6_8_9_10_12_13_15
A=1
part: 3_7_11_14_16 . 1_2_4_5_6_8_9_10_12_13_15
A=1
part: 4_7_11_14_16 . 1_2_3_5_6_8_9_10_12_13_15
A=1
part: 5_7_11_14_16 . 1_2_3_4_6_8_9_10_12_13_15
A=1
part: 6_7_11_14_16 . 1_2_3_4_5_8_9_10_12_13_15
A=1
part: 7_8_11_14_16 . 1_2_3_4_5_6_9_10_12_13_15
A=1
part: 7_9_11_14_16 . 1_2_3_4_5_6_8_10_12_13_15
A=1
part: 7_10_11_14_16 . 1_2_3_4_5_6_8_9_12_13_15
A=1
part: 7_11_12_14_16 . 1_2_3_4_5_6_8_9_10_13_15
A=1
part: 7_11_14_15_16 . 1_2_3_4_5_6_8_9_10_12_13
A=1
Die Ergebnisse kann jeder im Prinzip nachprüfen, wenn
aus der Korrelationsmatrix die entsprechenden Partitionen gebildet und
die Eigenwerte jeweils berechnet werden.
In Quartetten werden keine A=1 gefunden. Betrachtet man sich die Quintette
genauer, fällt auf, dass 7, 11, 14 und 16 immer dabei sind. Dies legte
nahe, die Konfiguration 7, 11, 14 und 16 noch einmal gesondert zu untersuchen,
was folgende Eigenwerte ergab: 1.4597, 1.2029, 1.1206 und 0.2168,
d.h. der vierte liegt nur knapp über dem Suchgrenzwert 0,20.
Vergleichende
Faktorenanalysen der Partition der Variablen 7, 11, 14 und 16
Zur Interpretation
der Faktorenladungen. * Dimensionsanalyse
* Eindimensionale Extraversions
Konstruktion *

Wie man sieht, erklärt die Faktorenladungsmatrix nach der Hauptkomponentenmethode
die Fastkollinearität durch den Common-Faktor F-I in Variable 11 und
14 am deutlichsten. Das mag überraschen, weil im allgemeinen die Varimax-Methode
am besten zur Interpretation geeignet erscheint. Als bedeutungsvoll wurden
Beträge über .10 gefärbt. Es fällt auf, dass die kleine
4x4-Matrix der Fast-Kollinearitätspartition 7, 11,14 und 16 fast durchgängig
Einfärbungen aufweist. Dies führt zu einer neuen Forschungshypothese:
Zeigen fast durchgängige Common-Cluster Fast-Kollinearität an?
Exkurs:
Ist eine 4-Faktorenlösung angemessen ?
Zur Interpretation
der Faktorenladungen. * Dimensionsanalyse
* Eindimensionale Extraversions
Konstruktion *
Nach Revenstorfs Interpretation, die nicht überzeugt (Anmerkung),
ist Extraversion ein 4-faktorielles Konzept, bestehend aus Unbeschwertheit
(I mit den Items 3, 8, 11, 14 15), Lebhaftigkeit (II mit
den Items 4, 5, 7), Kontaktfreude (III mit den Items 9, 10,
13), Initiative (IV mit den Items 2, 6, 16).
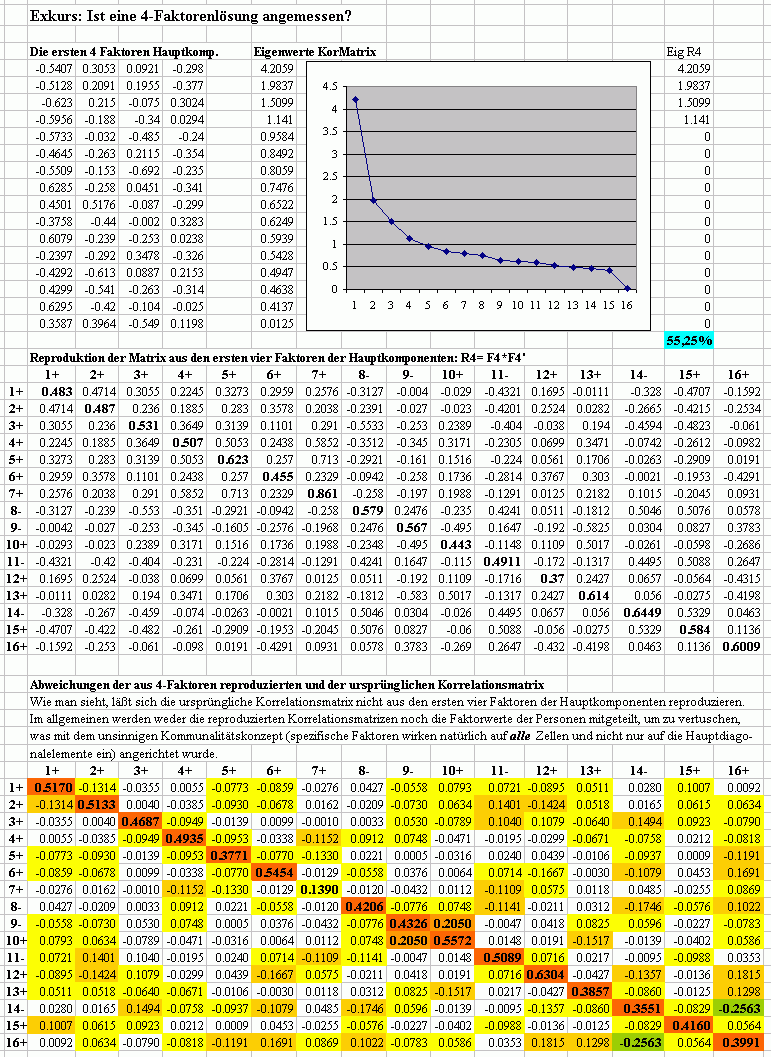
Fazit: Die Datenreduktion auf vier Faktoren kostet den Preis, daß
Daten reproduziert werden, die mit den ursprünglichen Korrelationsdaten
nicht mehr viel zu tun haben: Wissenschaft?
Siehe auch: höchstens
auf 15 Faktoren-Matrix reduzierbar.
Was müßte
und sollte eine Faktorenanalyse des Konstruktes Extraversion leisten
?
Alle Variablen, die Extraversion operational erfassen, sollten einen
gemeinsamen Faktor haben: das Extravertierte. Und alle Operationalierungsbereiche
(Projektionen auf Äußerungsformen) sollten einen spezifischen
Faktor aufweisen. Damit ergibt sich aus diesen theoretischen, hypothesengeleiteten
Gründen eine schiefwinkliges Grundmodell, weil nur dieses mit R =
F * C * F' - wobei R die Korrelationmatrix der Variablen, F die Faktoren
und C die Korrelationsmatrix zwischen den Faktoren ist - von vorneherein
das gemeinsame, nämlich das Extravertierte, entsprechend berücksichtigt.
Die Frage ist, wie kommt man zu einem gut begründbaren C? Die einfachste
Lösung ist, C nach theoretischen Überlegungen so zu wählen,
wie man möchte, z.B. indem man verlangt, daß ein Item wenigstens
in jeder Variable mit dem Betrag b laden muß. Die von Revenstorf
(1980, S. 119f) mitgeteilten schiefwinkligen Ergebnisse mit einer Faktorenkorrelation
von 0.26 erfüllen dieses Kriterium meist nicht, am besten noch die
Variablen 1, 2 und 16. eispiel: Eindimensionale
Extraversions Konstruktion *
Literatur (Auswahl)
Brengelmann J.
C. & Brengelmann, L. (1960). Deutsche Validierung Von Fragebogen der
Extraversion, Neurotischen Tendenz Und Rigidität. Zeitschrift für
experimentelle und angewandte Psychologie, VII, 291-331.
Hain, Bernhard
(1994). Die Matrix (rx,y.rest) ist nicht notwendig positiv definit.
In: Hain, B. (1994). Bemerkungen über Korrelationsmatrizen. In: Sponsel
(1994), Kapitel 6, S. 38.
Revenstorf, D. (1980).
Faktorenanalyse. Stuttgart: Kohlhammer. S. 74 Tab. 4.1, Korrelationen des
Extraversionsfragebogens (N=997).
Sponsel, Rudolf (1994).
STUDY 7.4. Empirischer Beleg für die Kollinearität durch S_CTau
und S_COve am Beispiel des deutschen Extraversionsfragebogens von BRENGELMANN
& BRENGELMANN. In: Sponsel (1984), Kap. 7.4, 1-7.
Sponsel, Rudolf
(1994). Numerisch instabile Matrizen und Kollinearität in der Psychologie.
Diagnose, Relevanz & Utilität, Frequenz, Ätiologie, Therapie.
Ill-Conditioned Matrices and Collinearity in Psychology. Deutsch-Englisch.
Übersetzt von Agnes Mehl. Kapitel 6 von Dr. Bernhard Hain: Bemerkungen
über Korrelationsmatrizen. Erlangen: IEC-Verlag [ISSN-0944-5072
ISBN 3-923389-03-5]. Aktueller Preis:
www.iec-verlag.de.
Sponsel, R. (2005).
Fast-
Kollinearität in Korrelationsmatrizen mit Eigenwert-Analysen erkennen.
Ergänzungsband - Bd. II. zu den Numerisch instabilen Matrizen und
Kollinearität in der Psychologie. Erlangen: IEC-Verlag.
_
Links (Auswahl: beachte)
Anmerkungen
und Endnoten:
1) GIPT= General and Integrative
Psychotherapy,
internationale Bezeichnung für Allgemeine und Integrative Psychotherapie.
___
numerisch instabil: (1) Kleinster
Eigenwert = .01247. (2) Konditionszahl
= 337 (= größter Eigenwert / kleinster Eigenwert). (3) HADAMARD
HIR 8.84 D-14, (4) Kleinste Norm
.0178 und damit fast eine Relation, (5) Input/
Output Ratio 7469, d.h. ändert man den Input um 1 Einheit, so
verändert sich der Output um das 7469-fache. Instabil heißen
Systeme, wenn eine kleine Veränderung auf der Eingangsseite eine große
Veränderung auf der Ausgansgseite nach sich zieht.
___
höchstens
auf eine 15x15 Matrix reduzierbar:

___
Revenstorf nicht
kritisch reflektiert (Faktorenanalyse 1980, S.107): "... Es gibt fast
immer einen »Generalfaktor« und im übrigen weniger gut
interpretierbare, varianzschwache Restfaktoren, die zusammengenommen kein
sinnvolles Modell der Daten ergeben. ..."
Ein großer Eigenwert bedeutet noch längst
keinen "Generalfaktor". Ein solcher wäre vielleicht bei >80% Varianzaufklärung
diskutierbar. Außerdem ist kritisch anzumerken, dass die FaktorenanalytikerInnen
- vermutlich wegen ihrer Fixierung auf Datenreduktion - von Anfang an bis
in die jüngste Gegenwart nicht verstanden haben, was ein kleiner Eigenwert
bedeutet. Wie diese Analyse zeigt, wird es hier erst richtig spannend.
Darüberhinaus muss man natürlich
fragen, ob für ein offensichtlich eindimensionales Konstrukt wie Extraversion
ein Faktormodell mit unabhängig ("orthogonal") - und damit unkorreliert
- konstruierten Faktoren überhaupt vom Ansatz her sinnvoll ist. Auch
die kritische Erörterung dieser Frage gehörte in ein Lehrbuch.
Ein psychologisch vernünftiges Faktorenmodell müsste einen allgemeinen
Common-Faktor und einen operationalisierungsabhängigen spezifischen
Faktor zugrunde legen. Quantitativ etwa in der Art, dass z.B. 75% der jeweiligen
Variablenvarianz durch den Common-Faktor "Extraversion" und 25% durch die
spezifische Operationalisierung "erklärt" werden.
___
458753. Nach Formel kmax = (n-2)*2^(n-1))+1,
tabelliert in Sponsel (2005), S. 77 Anhang 2: Tabelle Partitionen, Maximale
Kollinearitäten und beteiligte Variable. Hier: n-2= 14. 2^15=32768.
___
positiv polen. Vielleicht ist es auch
nur ein Darstellungs- oder Druckfehler. Falls nicht, wären die Summen-Scores
fraglich und damit natürlich auch die Korrelationskoeffizienten.
___
Partition 7, 11,14,16 der
Korrelationsmatrix:

___
phänotypisch. Eine phänotypische
Korrelationsmatrix sieht äußerlich so aus, wie man es erwartet:
symmetrisch, in der Hauptdiagonalen 1en und in den Zellen -1 <= Werte
<= 1. Zu einer mathematisch korrekten Korrelationsmatrix gehört
aber auch, dass sämtliche Eigenwerte
positiv semi definit, d.h. >= 0 sind. Diese positive Semi Definitheit kann
gestört sein durch Fälschung, falsche Formeln
(z.B. "correction
for attenuation", tetrachorische Koeffizienten, Assoziationsmaße
oder vollständige Partialisierungen [zwei gegen alle = den ganzen
Rest], falsche Missing Data Lösungen und andere unsachgemäße
Manipulationen (z.B. der Hauptdiagonalelemente bei der sog. "Kommunalität"
oder unangemessenen Faktorenreduktion in der Faktorenanalyse), aber auch
durch Rundungsfehler bei fast-kollinearen
Korrelationsmatrizen können Eigenwerte negativ werden und die
Matrix dadurch entgleisen.
___
ungefähr replizieren.
"Ungefähr" ist wenig befriedigend, zumal doch einige recht unterschiedliche
Ergebnisse zu verzeichnen sind. Als ich das erste Mal Kaisers Varimaxmethode
auf meinem Atari unter Omikronbasic implementieren ließ, war der
Mathematiker erstaunt, daß hier eine maschinenabhängige Größe
einzustellen war, womit sich wieder einmal zeigt, wie instabil diese Matrizenoperationen
von Haus aus sind. Die folgenden Varimaxrotation wurde mit einer Studenversion
in Matlab gerechnet, zur Kontrolle eine zweite Rechnung mit ALMO
6.4 (gegenüber Revenstorf Faktor 2 und 3 vertauschen):
| Mit Matlab 5.3 (StudVersion): Rechtwinklig Varimax-rotierte
Faktorladungen
Faktor 1 Faktor 2 Faktor 3
Faktor 4
V1 -0.4868 0.1748 -0.2700
-0.3775
V2 -0.4050 0.1531 -0.2109
-0.5047
V3 -0.6347 -0.2531 -0.2447
0.0672
V4 -0.2196 -0.3538 -0.5735
-0.0651
V5 -0.1892 -0.0661 -0.7549
-0.1136
V6 -0.0838 -0.1814 -0.2121
-0.6080
V7 -0.0546 -0.1309 -0.9169
-0.0167
V8 0.6836 0.2492
0.2067 -0.0857
V9 0.0872 0.7236
0.1033 0.1597
V10 -0.0759 -0.6491 -0.1190
-0.0399
V11 0.6094 0.0692 0.0887
0.3273
V12 0.0488 -0.1431 0.0146
-0.5887
V13 0.0128 -0.7362 -0.1294
-0.2354
V14 0.7866 -0.0208 -0.1537
-0.0452
V15 0.7218 -0.0361 0.1822
0.1689
V16 0.0720 0.3982 -0.1743
0.6378 |
Mit ALMO 6.4: Rechtwinklig Varimax-rotierte Faktorladungen
Faktor 1 Faktor 2 Faktor
3 Faktor 4
V1 0.4882 0.1739
0.2700 0.3761
V2 0.4066 0.1526
0.2109 0.5035
V3 0.6340 -0.2550
0.2443 -0.0684
V4 0.2190 -0.3545
0.5733 0.0648
V5 0.1897 -0.0668
0.7548 0.1130
V6 0.0848 -0.1808
0.2122 0.6080
V7 0.0547 -0.1314
0.9168 0.0164
V8 -0.6828 0.2512 -0.2062
0.0869
V9 -0.0857 0.7236 -0.1030
-0.1605
V10 0.0743 -0.6493 0.1187
0.0406
V11 -0.6100 0.0704 -0.0885
-0.3260
V12 -0.0479 -0.1421 -0.0144
0.5890
V13 -0.0142 -0.7359 0.1291
0.2364
V14 -0.7865 -0.0187 0.1541
0.0469
V15 -0.7224 -0.0343 -0.1820
-0.1672
V16 -0.0723 0.3974 0.1743
-0.6383 |
Zum Vergleich aus Revenstorf (1980, S. 115):
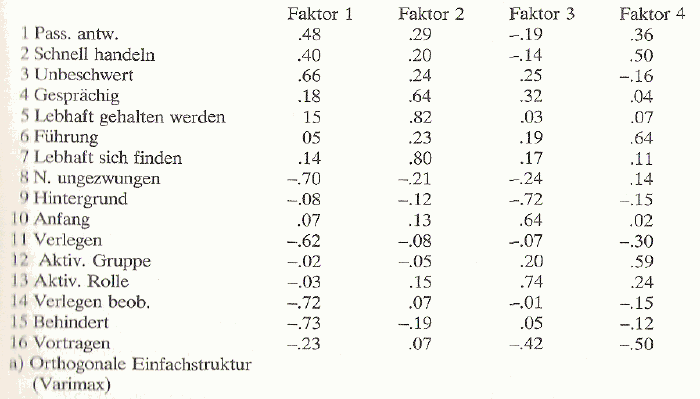
Anmerkung: Die Werte, auch wenn man Faktor 2 und 3 umbenennt,
unterscheiden sich zum Teil schon recht deutlich, wenn auch die grobe Größenordnung
meist stimmt. Die Rechnerprogramme waren aber zu den Zeiten als Revenstorfs
Buch erschien (1980) vielleicht noch nicht so ausgereift wie 20 Jahre später
oder heute, was bei Vergleichen der Werte auch berücksichtigt werden
muß.
___
Änderungen wird
gelegentlich überarbeitet, ergänzt und vertieft * Anregungen
und Kritik willkommen
05.06.06 Dimensionsanalyse
* Eindimensionale Extraversions
Konstruktion *
01.06.06 Anmerkung zu "ungefähr
replizieren". Ergänzung: Was
müßte und sollte eine Faktorenanalyse des Konstruktes Extraversion
leisten?
31.05.06 Exkurs:
Ist eine 4-Faktorenlösung angemessen? Anmerkung:
zu Revenstorfs Varimax Ergebnissen.
30.05.06 Ergänzung
zu "Reventorf nicht kritisch reflektiert". Endnote zu "phänotypisch".
Querverweise
Standort: Kollinearitätsanalyse des Extraversionsfragebogens
...
Zur Interpretation
der Faktorenladungen. * Dimensionsanalyse
* Eindimensionale Extraversions
Konstruktion *
Zum
Fast-Kollinearitätsbegriff.
* Korrelation
* Partielle
Korrelation *
Überblick Numerisch Instabile
Matrizen und Kollinearität in der Psychologie.
Überblick
der Dokumentationen zur Handhabung der Faktorenanalyse.
Überblick
Arbeiten
zur Definitionslehre, Methodologie, Meßproblematik, Statistik und
Wissenschaftstheorie.
*
*
Dienstleistungs-Info.
*
Zitierung
Sponsel, Rudolf (DAS).
Kollinearitäts-,
Eigenwert- und Faktorenanalysen einer Korrelationsmatrix von Revenstorf
der 16 Extraversionsfragen nach Brengelmann & Brengelmann.
Ist
Extraversion multifaktoriell bedingt oder die Faktorenanalyse ein falsches
Modell? IP-GIPT. Erlangen: https://www.sgipt.org/wisms/fa/analyse/extravBB.htm
Copyright & Nutzungsrechte
Diese Seite darf von jeder/m in nicht-kommerziellen
Verwertungen frei aber nur original bearbeitet und nicht inhaltlich
verändert und nur bei vollständiger Angabe der Zitierungs-Quelle
benutzt werden. Das Einbinden in fremde Seiten oder Rahmen, die die Urheberschaft
der IP-GIPT nicht jederzeit klar erkennen lassen, ist nicht gestattet.
Sofern die Rechte anderer berührt sind, sind diese dort zu erkunden.
Sollten wir die Rechte anderer unberechtigt genutzt haben, bitten wir um
Mitteilung. Soweit es um (längere) Zitate aus ... geht,
sind die Rechte bei/m ... zu erkunden oder eine Erlaubnis einzuholen.
Ende_Kollinearitätsanalyse
Extraversion_ Überblick
_ Relativ
Aktuelles _ Rel.
Beständiges _ Titelblatt
_ Konzept
_ Archiv
_ Region
_ Service
iec-verlag _ Mail:
sekretariat@sgipt.org
___Wichtige
Hinweise zu Links und Empfehlungen
kontrolliert am: 28.05.06
irs










