(ISSN 1430-6972)
IP-GIPTDAS=06.01.2006 Internet-Erstausgabe, letzte Änderung: 28.01.20
Impressum: Diplom-Psychologe Dr. phil. Rudolf Sponsel Stubenlohstr. 20 D-91052 Erlangen
E-Mail: sekretariat@sgipt.org _ Zitierung & Copyright
Anfang_Lobatschewski__Datenschutz_Überblick__Rel. Beständiges _Titelblatt_ Konzept_ Archiv_ Region_ English contents__ Service_iec-verlag_ Dienstleistungs-Info * Anmeldung _ Wichtige Hinweise zu Links und Empfehlungen
Nikolai Iwanowitsch Lobatschewski
20.11.1792 - 12.2.1856
Leben und Werk - Psychologie der
Forschungsleistung
|
|

Lobatschewski, Porträt und
Denkmal vor der Universität Kasan.
von Rudolf Sponsel, Erlangen
nach den mir zugänglichen biographischen
Werken
- Übersicht:
- Zusammenfassung.
- Herkunft und Kindheit.
- Jugend und heranwachsenden Zeit.
- Exkurs: Die Universität Kasan zur Zeit Lobatschewskis.
- Lobatschewski 1807 im Alter von 14 Jahren immatrikuliert.
- Kortaschewski von Jakowkin vertrieben - Kasans Uni ohne Mathematik.
- Johann Christian Martin Bartels durch Gauß nach Kasan empfohlen.
- Der junge Rebell.
- Akademische Karriere im Lebensverlauf.
- Dokumente aus Lobatschewskis Schriften:
- Negatives Gutachten zum Lehrbuch der Geometrie 1823 (1898 wieder gefunden und 1909 veröffentlicht).
- Fußnote über eine beleidigende Kritik 1834.
- Einleitung Imaginäre Geometrie 1835.
- Inhalt Imaginäre Geometrie und Anwendung der imaginären Geometrie auf einige Integrale.
- Inhaltsverzeichnis Pangeometrie (1856).
- Pangeometrie: Die ungenügende Begründung der gewöhnlichen Parallelentheorie.
- Lobatschewski als Lehrer und Pädagoge.
- Ausgangsbasis: 1919-1926 Restauration und geistige Inquisition in der Ära Magnizki.
- Aus der Rede vom 17. Juli 1828 "Über die wichtigsten Fragen der Erziehung".
- Einsicht in die enorme Bedeutung der Lehrer-Fort- und Weiterbildung.
- Vorlesungs- und Unterweisungskonzeption.
- Sokratische Methodik.
- Ehe, Familie und Kinder.
- Alter, Lebensende und Tod.
- Rätsel um Lobatschewskis letzte Jahre und Ende.
- Lobatschewskis Persönlichkeit.
- Würdigung.
- Auswahl 'Ahnengalerie' zur Geschichte der Parallellinien.
- Vorgeschichte und Geschichte der Anerkennung der nichteuklidischen Geometrie.
- Zum Verständnis des Parallelenaxioms und der nichteuklidischen Geometrie nach Meschkowski.
- Die fünf Postulate Euklids.
- Sätze der Nichteuklidischen Geometrie nach A. Filler.
- Psychologie der Forschungsleistung.
- Was 'ist' eigentlich ein 'Dreieck'?
- Wie kann man das fünfte Postulat Euklids in Zweifel ziehen und seine Nichtgültigkeit denken?
- Anschauungsargument 1: Müssen zwei geneigte Gerade im Unendlichen zusammentreffen?
- Anschauungsargument 2: Müssen Fortlaufende G1, G2 immer einen Anfang oder ein Ende haben?
- Die Forschungsleistung Lobatschewskis.
- Literatur (Auswahl):
- Werke von Lobatschewski.
- Werke von Lobatschewski in deutscher Sprache.
- Biographische Literatur.
- Literatur zur Geschichte des Parallelen-Postulats und der nichteuklidischen Geometrie.
- Einführungen in die nichteuklidische Geometrie von Lobatschewski.
- Links (Auswahl: beachte) zu den verschiedenen Geometrien und ihrer Bezeichnungen.
- Die verschiedenen Geometrien und ihre unterschiedlichen Bezeichnungen.
- Zusammenhänge in der Mathematik und ihrer Teilgebiete.
- Querverweise.
Nikolai Iwanowitsch Lobatschewski wurde am 20. November 1792 in Nishni-Nowgorod
(Sibirien), heute Gorki,
geboren. Sein Vater verließ die Familie als er fünf war. Hochbegabt
wird er nach kurzer rebellischer Entwicklung bereits 1812 mit 19 Magister
und Dozent für Mathematik (Titel 1814) und 1816 im Alter von 24 als
außerordentlicher Professor berufen, Dekan (1820) und Rektor (1827-1846)
der 1805 gegründeten Universität Kasan,
geadelt 1837, mit Gauß
und Bolyai einer der Begründer und
Erst-Veröffentlicher (1826) einer nichteuklidischen (hyperbolischen)
Geometrie, angewendet, ausgebaut und weiter entwickelt durch Beltrami,
Klein,
Riemann
, Poincaré und neben
anderen
Anwendungen in der
Relativitätstheorievon
Einstein
genutzt. Im letzten Lebensjahrzehnt Opfer von Intrigen und die letzten
Lebensjahre schwer erkrankt, erblindet und motorisch beeinträchtigt
starb er am 12.2.1856 in Kasan an einer Lungenparalyse,
die beantragten 1500 Silberrubel für eine Klinikbehandlung in Moskau
wurden zu spät bewilligt.
 |
Links: Die "Anfangsgründe ..." in deutscher Übersetzung 1840. Hieraus obiges Zitat. Kritik 1840. Rechts: Titelblatt Vorgestellte Geometrie 1835 (B1, S.33) |
 |
Die Kindheit von Nikolai Iwanowitsch Lobatschewski wird als freudlos
beschrieben. Der Vater, Registrator Iwan Maksimow Lobatschewski, habe wenig
gearbeitet und viel getrunken. Die Mutter Praskowja Aleksandrowna
wird von den Biographen (B1) - im Gegensatz zu Engel
- als eine junge, energische aber wenig gebildete
Frau geschildert, die nur schwer mit dem wenigen Geld zurechtgekommen sei
und ihre Ehe für unglücklich gehalten habe. Die Biographen [B1]
schreiben: "Eine unerwartete Unterstützung kam in dieser Situation
von Seiten des Nishni-Nowgoroder Landmessers Sergej Stepanowitsch Schebarschin.
Er hatte Praskowja Aleksandrowna mit ihrem zukünftigen Mann
bekannt gemacht und kannte die Familienverhältnisse.
Schebarschin
kaufte ein kleines Haus, das er Praskowja Aleksandrowna zum Geschenk
machte. Er siedelte sich in der Nachbarschaft an und nahm lebendigen Anteil
an der Erziehung der drei Kinder. Für einige Zeit war Praskowja
Aleksandrowna dadurch von der ständigen Sorge um ein Stück
Brot erlöst." Im Oktober 1797 verstarb Schebarschin und hinterließ
der Familie Lobatschewski eine kleine Erbschaft. Der Vater
Iwan Maksimowitsch habe zu dieser Zeit hunderte von Kilometern von Nishni-Nowgorod
entfernt in Ufa
gearbeitet und sich nicht mehr um seine Kinder und Familie gekümmert.
Aus dem Jahre 1811 stammt die letzte Nachricht über den Vater. Die
Familie habe von ihm keine Nachricht und kein Geld mehr erhalten. Praskowja
Aleksandrowna habe dann ihren bescheidenen Besitz verkauft und sei mit
ihren drei Kindern Aleksander, Nikolai und Aleksei zu ihren Eltern zurück
in die Kleinstadt Makarjew gekehrt.
Psychologisch fällt auf, daß die Biographen
sehr einseitig die Schuld an den Vater delegieren; mögliche Anteile
der Mutter bleiben im Dunkeln. Immerhin: sie hätte nicht mit Geld
umgehen können, wurde vom Landmesser vermittelt, dieser soll sich
sehr um die Kinder gekümmert haben und hat ihr auch eine kleine Erbschaft
gemacht.
Sodann habe, wie die Biographen [B1] etwas melodramatisch
berichten, Schebarschin, "bereits im Sterben liegend, Praskowja Aleksandrowna
gebeten, sich stets um die Erziehung der Kinder zu kümmern. Das Schulwesen
war im damaligen Rußland sehr schlecht entwickelt. Im Jahre 1802
brachte Praskowja Aleksandrowna ihre drei Söhne, den 11jährigen
Aleksander,
den 9jährigen Nikolai und den 7jährigen
Aleksei,
nach Kasan, wo kurz zuvor ein Gymnasium eröffnet worden war. Neben
den Kindern von Adeligen wurden damals in die Gymnasien auch schon. Kinder
von Beamten aufgenommen. Iwan Maksimowitsch Lobatschewski besaß
den staatlichen Rang eines Kollegienregistrators, der dem ersten Offiziersrang
entsprach. Damit hatten seine Kinder die Möglichkeit zum Schulbesuch."
Alle drei Brüder bestanden die Aufnahmeprüfungen
und sie wurden auf Beschluß des Rates des Kasaner Gymnasiums am 5.
November 1802 in das Gymnasium aufgenommen werden, "später sogar
auf Staatskosten und mit vollem Pensionat." Für die Gymnasiasten sollen
die Tage recht gleichförmig verlaufen sein: " Zum Gebet, zum Frühstück,
zum Unterricht — überallhin mußte in Reih und Glied marschiert
werden. Es war verboten, persönliche Sachen und Geld aufzubewahren,
Essen oder auch Süßigkeiten zu kaufen, Briefe an die eigenen
Verwandten zuzukleben, weil der Aufseher diese Briefe vor dem Abschicken
lesen mußte. Die Aufseher lasen aber nur jeden fünften oder
sechsten Brief, da sie zum Lesen aller Briefe zu bequem waren. Lobatschewski
hatte im Gymnasium hauptsächlich bei dem Tataren N. M. Ibragimow,
einem Absolventen der Moskauer Universität, Unterricht, und zwar in
Arithmetik, Algebra, altslawischer und russischer Sprache. Das war ein
in Kasan recht bekannter Dichter, ein Mensch mit einer hohen Kultur, der
mehrere Sprachen beherrschte und der die russische Literatur liebte. Später
arbeitete er als Adjunkt am Lehrstuhl für
russische Sprache. Die von Natur aus wißbegierigen Brüder Lobatschewski
lernten leidenschaftlich, sie fanden Gefallen am Prozeß des Erkennens.
Nikolai,
der mittlere Bruder, liebte besonders die Mathematik", was die Biographen
wie folgt erklären: "Sein Mathematiklehrer war in der Abschlußklasse"
- damals gab es nur drei Klassenstufen an russischen Gymnasien - "Grigori
Iwanowitsch Kortaschewski - ein junger, sehr talentierter und hochgebildeter
Absolvent der Moskauer Universität. Er war ein sehr erfahrener Pädagoge,
kannte Sprachen, die Literatur und — vor allem — die Geschichte seines
Faches. Kortaschewski unterrichtete seine Schüler nach einem
eigenen Lehrplan. Er machte sie nicht nur mit der Mathematik bekannt, sondern
auch mit der Geschichte ihrer Entstehung und Entwicklung. Kortaschewski
war der Auffassung, daß in der Geschichte jeder Wissenschaft ein
Augenblick komme, wo es erforderlich sei, einmal stehenzubleiben, alles
zu sammeln, das bereits Bekannte und Entdeckte zu systematisieren, und
erst danach die Entwicklung weiter voranzutreiben.
Solche Gedanken flossen natürlich auch in seinen Unterricht ein
und formten die Vorstellungen seiner Schüler von der Geschichte der
Mathematik.
Lobatschewski erhielt also bereits in der Abschlußklasse
des Gymnasiums einen guten Mathematikunterricht. Das sollte sich dann auch
in der Universität fortsetzen." (B1, S. 17f) Diese Ausführungen
zeigen doch sehr überzeugend, von welch kaum zu überschätzender
Bedeutung die richtigen LehrerInnen sind oder sein können
und bestätigen all die Mathematiker, die sich sehr für die Erziehung
und Schulbildung einsetzten, wie z.B. Felix Klein
und viele andere (aber).
Geschwister- und Familienkonstellation Lobatschewskis
Nikolai bekleidet innerhalb der Geschwisterreihe eine mittlere Position. Alle Brüder besuchten das Gymnasium in Kasan und waren dort, wie oben ausgeführt, in einer streng reglementierten 'Kadettenanstalt'. Die Trennung von der Mutter erfolgte für Nikolai im Alter von 9. Der Vater trennte sich 1897 von der Familie, Nikolai war damals 5 Jahre alt. Die Biographen (B1, S. 81) berichten, daß es 1811 die letzte Nachricht über den Vater, der in Ufa lebte, gegeben habe. Sein älterer Bruder Aleksander Iwanowitsch (1790 — 1807) studierte von 1805 an der Universität Kasan. Während des Studiums ertrank er im Sommer 1807 beim Baden im Fluß Kasanka, einem Nebenfluß der Wolga (nach Engel in dt. Lobatschewski, 1899, S. 352, nahm er sich das Leben). Sein jüngerer Bruder Aleksei Iwanowitsch (1795 — 1870) studierte ebenfalls und wurde sogar Adjunkt (1817). Nach den Biographen [B1, S. 87] habe er aber keine besonderen Neigungen zur Wissenschaft entwickelt; so habe er nicht den Professorentitel erhalten und sei im Jahre 1823 im Range eines Hofrates entlassen worden. Er habe später in der Industrie gearbeitet als Direktor einer Tuchfabrik. Die Beziehung zur Mutter Praskowja Aleksandrowna Lobatschewskaja (1773—1840) ist den Biographen zufolge zeit lebens gut gewesen, sie berichten nämlich (B1, S. 87): "Noch in der Zeit, als N. I. Lobatschewski bereits Rektor der Universität Kasan war, stand sie ihm mit Ratschlägen zur Seite, die sich auf ihre große Lebenserfahrungen gründeten.".
Jugend und heranwachsenden Zeit
Nach Beendigung des Gymnasiums 1806 bestand Lobatschewski die Aufnahmeprüfung
an der Universität, aber ihm wurde zunächst geraten, die Sprachen
mehr zu studieren. Das hatte damals besonders seine guten Gründe,
denn, so die Biographen in einer erläuternden Fußnote [B1, S.
19] , "zu Beginn des 19. Jahrhunderts arbeiteten an den russischen Universitäten
hauptsächlich ausländische Professoren, die ihre Vorlesungen
in Deutsch oder Latein, manchmal auch in Französisch hielten. Die
wissenschaftliche Literatur begann man damals erst in die russische Sprache
zu übersetzen. Deshalb mußten die Studenten mehrere Fremdsprachen
beherrschen."
| Exkurs:
Die Universität Kasan zur Zeit Lobatschewskis
Die Biographen Halameisär, Alexander & Seibt, Helmut (1978) führen aus: "Im Jahre 1803 wurde Stepan Jakowlewitsch Rumowski, der damalige Vizepräsident der Russischen Akademie der Wissenschaften in Petersburg, ein Schüler von Euler und Lomonossow und inzwischen ein bekannter Mathematiker und Astronom, zum Kurator des Kasaner Schulbezirkes ernannt. Der Kasaner Schulbezirk umfaßte damals die Gouvernemente Kasan, Nishni-Nowgorod (heute: Gorki), Simbirsk (heute: Uljanowsk), Pensa, Saratow, Wjalka (heute: Kirow), Perm und Orenburg. Zur damaligen Zeit gab es in Rußland nur drei Universitäten: die im Jahre 1755 auf Initiative von Lomonossowe eröffnete Mos-[<18] kauer Universität und die soeben erst gegründeten Universitäten in Dorpat und Wilno. Im Jahre 1804 erhielt Rumowski den Hohen Befehl in Kasan eine neue Universität zu eröffnen. Im Februar 1805 kam Rumowski nach Kasan und verkündete dort feierlich den Ukas des Zaren und die Verordnung des Unterrichtsministeriums über die Eröffnung der Kasaner Universität '... für den Unterricht und für die Verbreitung der Wissenschaften - besonders der experimentellen und der exakten, die sich, auf zuverlässige Grundlagen stützen ... und für die Vorbereitung der Jugend auf den Eintritt in den Staatsdienst.' An der neu gegründeten Kasaner Universität waren anfangs lediglich zwei neu ernannte Professoren und vier Adjunkte tätig, die zuvor Lehrer am Kasaner Gymnasium gewesen waren. Die Universität stellte deshalb auch in den ersten Jahren ihres Bestehens nur eine Art "Erweiterung" des Gymnasiums dar, in der die Ausbildung der Abiturienten fortgesetzt wurde. Die sechs Lehrkräfte hatten zu dieser Zeit lediglich 33 Studenten zwischen 13 und 20 Jahren." Engel (1899, S. 357) berichtet, daß zu dieser Zeit drei akademische
Grade von der Universität verliehen werden konnten: Kandidat, Magister
und Doktor. Bis 1819 habe es hierfür aber keinerlei Vorschriften gegeben
und der Senat wie auch der Kurator (oberster Bildungsbeauftragter der Region)
hätten völlig freie Hand gehabt.
|
Lobatschewski 1807 im Alter von 14 Jahren immatrikuliert
Nach einer zweiten erfolgreich bestandenen Aufnahmeprüfung wurde
der 14jährige Lobatschewski im Februar 1807 offiziell als Student
der gerade ein Jahr jungen Kasaner Universität immatrikuliert.
Kortaschewski von Jakowkin vertrieben - Kasans Uni ohne Mathematik
Die Biographen berichten, daß Kortaschewski, der an der Universität als Adjunkt und als der einzige Mathematiklehrer gearbeitet habe. Sein unabhängiger Charakter und die ständigen Auseinandersetzungen mit dem eigensinnigen und herrschsüchtigen Direktor Jakowkin sollen Kortaschewski bewogen haben, seine Stellung in Kasan aufzugeben und nach Petersburg zu gehen, wo er später Senator wurde.
"Unter dem Einfluß des in Kasan ansässigen
Arztes Karl Fuchs begann
sich Lobatschewski für die Naturwissenschaften zu interessieren,
unter anderem auch für die Chemie. Früher hatte er bereits
gelegentlich mit dem Mikroskop gearbeitet. Jetzt, in der Zeit seines Studiums,
in der er keinen Mathematiklehrer hatte" - Kortaschewski war vertrieben
- , "widmete sich Lobatschewski der
Chemie und der Pharmakologie.
Der Unterricht in diesen Fächern wurde von Adjunkt
Ewest durchgeführt. Viele Studenten studierten Chemie;
in Pharmakologie war Lobatschewski aber der einzige Schüler
seines Lehrers. Ewest ließ Lobatschewski selbständig
im Labor arbeiten und war mit ihm insgesamt sehr zufrieden, da sein Schüler
- wie üblich - ernsthaft und akkurat arbeitete und auch Ergebnisse
erzielte. Jakowkin hörte von Ewest das Lob über
Lobatschewski
und überlegte: Die mathematischen Vorlesungen besucht er nicht, dafür
beschäftigt er sich mit Chemie und Pharmakologie, d. h. er müßte
also Arzt werden. Das schrieb er auch an den Kurator Rumowski
nach Petersburg: 'Der Student Nikolai Lobatschewski bereitet sich
offensichtlich auf ein Studium an der Medizinischen Fakultät vor.'
Darin irrte er sich jedoch. Lobatschewski besuchte niemals die Medizin-Vorlesungen
von Professor Braun. ..." (B1, S. 20)
Johann
Christian Martin Bartels durch Gauß nach Kasan empfohlen
Ein mathematisch-naturwissenschaftliches Zentrum entsteht
Die Historiker und Biographen berichten: "Im Jahre 1801 hatte
Rumowski
vergeblich versucht, den deutschen Mathematiker Carl Friedrich Gauß
an die Russische Akademie der Wissenschaften nach Petersburg zu berufen.
Gauß
konnte sich von seiner bisherigen Tätigkeit in Braunschweig nicht
trennen und empfahl an seiner Stelle seinen Lehrer und Freund Johann
Christian Martin Bartels.
Von Rumowski wurde daraufhin Bartels im Jahre 1805 der Lehrstuhl
für reine Mathematik an der Universität Kasan angeboten, Bartels
kam erst Anfang 1808 nach Kasan. Er war ein talentierter Pädagoge
und ein für seine Zeit hoch gebildeter Mathematiker. Für die
Vorlesungen bei Bartels wollte sich auch Lobatschewski einschreiben
lassen. Das wurde ihm jedoch von Jakowkin verwehrt. Daraufhin setzte
Lobatschewski
seine Chemiestudien noch eine Zeit lang fort. Er fühlte sich jedoch
mehr zur Mathematik hingezogen. Es kam zu einem Gespräch mit Bartels,
in dem Lobatschewski diesem seine Absichten zur Fortsetzung seiner
mathematischen Studien erläuterte. Bartels war damit einverstanden,
zumal er bereits in Petersburg von Kortaschewski von diesem talentierten
Studenten gehört hatte. Nach dem Gespräch mit Bartels
zog sich Lobatschewski eine Erkältung zu und war längere
Zeit krank. Inzwischen traf in der Universität ein Brief von Rumowski
ein. Rumowski kümmerte sich sehr um die Ausbildung von russischen
Wissenschaftlern auf den verschiedensten Gebieten der exakten Wissenschaften.
Da er von der Ankunft Bartels in Kasan wußte, schrieb er:
'Ich. wünschte, daß es unter den Studenten und Kandidaten mehr
solche geben würde, die sich für die mathematischen, physikalischen
und philosophischen Wissenschaften entscheiden würden.' Nachdem Jakowkin
dieses Schreiben erhalten halle, entwickelte er eine ungewöhnliche
Fürsorge und besuchte sogar den kranken Lobatschewski. Er wünschte
ihm baldige Genesung, hob das von ihm selbst ausgesprochene Verbot wieder
auf und empfahl Lobatschewski, daß er unbedingt alle Vorlesungen
bei Professor Bartels besuchen solle. Um Bartels, den Astronomen
Littrow
und den Physiker Bronner, die später nach Kasan kamen, bildete
sich recht bald eine Gruppe talentierter und wißbegieriger Kasaner
Studenten. Zusammen mit seinem Freund Iwan Simonow begann Lobatschewski
das Studium der Mathematik, Physik und Astronomie.
Bartels
schrieb später über seine ersten Eindrücke nach seiner Ankunft
in Kasan: 'Mein Wirkungskreis ist hier angenehmer, als ich erwarten durfte.
Die meisten meiner Zuhörer sind in der Mathematik sehr gut vorbereitet.'
(Brief an Gauß
vom 6. Juli 1808)." (B1, S. 20f)
Der junge Rebell.
Bereits mit 16 Jahren gilt er als der talentierteste Student der jungen
Kasaner Universität. Jakowkin schrieb [B1, S. 22]: "Lobatschewski
führt sich oft sehr gut, wenn man von gelegentlichen Fehltritten absieht."
Er fiel auf als er am für Studenten verbotenen Neujahrsumzug teilnahm
und im Hof der Uni eine Rakete zündete. Im Stadtpark wurde er vom
Rektor auf einer Kuh reitend gesichtet. Die Klagen häuften sich, so
daß der Kurator Rumowski
an den Rektor schrieb [B1, S. 22]: "Dem Studenten Lobatschewski,
der im schlechten Benehmen den ersten Platz einnimmt, ist mein Bedauern
darüber mitzuteilen, daß er seine ausgezeichneten Fähigkeiten
durch unangemessenes Betragen trübt."
Die Biographen berichten, daß sich Lobatschewski
als Student in Jakowkins
Tochter Anna verliebt haben soll und daß sie sich öfter getroffen
hätten und er im Hause Jakowkins
verkehrt wäre. Der arme Student sei mit Mißfallen geduldet worden,
weil Jakowkin seine
Tochter für den reichen Baron E. W. Wrangel vorgesehen habe.
Lobatschewski habe die enge, gottesfürchtige Atmosphäre im Hause
von Jakowkin mit der Zeit immer weniger gefallen und es habe darüber
auch gelegentlich Auseinandersetzungen zwischen Jakowkin und Lobatschewski
gegeben. "Die 'gegen Gott gerichteten Gedanken' Lobatschewskis rüttelten
in den Augen von Jakowkin an den Grundfesten seiner Weltanschauung,
an seiner Ergebenheit gegenüber Gott und der zaristischen Bürokratie."
So soll Jakowkin
Rumowski gemeldet haben, daß Lobatschewski „in bedeutendem Maße
Anzeichen von Gottlosigkeit" zeige. "Das", so die Biographen, "stellte
im damaligen zaristischen Rußland eine schreckliche Beschuldigung
dar." Jakowkin
schickte seine Tochter Anna dann nach Petersburg, wo sie später einen
Fürsten, der ebenfalls Student der Kasaner Universität gewesen
war, geheiratet habe. Die Biographen vermuten, daß Lobatschewski
vom Abbruch dieser Verbindung tief betroffen gewesen sei.
Die Biographen berichten weiter (B1, S. 23) : "Wegen seines schlechten
Verhaltens und wegen der 'Bekundung von Anzeichen der Gottlosigkeit' erhielt
Lobatschewski
nach Beendigung der Universität nicht einmal den Titel eines Kandidaten.
An den russischen Universitäten war es zu dieser Zeit üblich,
daß die besten Studenten den Magistertitel erhielten und an der Universität
blieben, um unter der Leitung eines Professors ihre wissenschaftliche Ausbildung
weiter zu vervollkommnen. Die übrigen Studenten beendeten die Universität
mit dem Kandidatentitel [<23] Lobatschewski mußte mit seinem
Ehrenwort Besserung versprechen und erhielt dann, nach einem Monat, am
3. August 1811 den Magistertitel.
Lobatschewski wurde auch mit einem
besonderen Dankschreiben des Bildungsministers ausgezeichnet. Für
all das hatte sich Bartels
besonders eingesetzt."
Akademische
Karriere im Lebensverlauf.
nach den biographischen Quellen, hauptsächlich B1
| 1807 | Immatrikulation |
| 1811 | Magister, Abschluß des Studiums |
| Frühjahr 1812
Vorlesungen in russischer Sprache 1812
|
Assistent bei Bartels,
Magistertätigkeit, der sich in einer Woche mehrfach mit ihm beschäftigte.
Studium der „Disquisitiones arithmeticae" von Gauß
und die „Mecanique celeste" (Himmelsmechanik) von Laplace. Bei Littrow,
der neben Lobatschewski zwei weitere Studenten betreute, Vertiefung der
Kenntnisse in Astronomie „zur einstweiligen Vorbereitung auf die Durchführung
von Beobachtungen"
„Theorie der elliptischen Bewegung von Himmelskörpern". Bartels: "Viele Stellen dieses kleinen Werkes zeugen von einer herausragenden mathematischen Begabung, die in der Zukunft nicht unberühmt bleiben wird." [B1, S. 25] |
| 1814
|
26.4. Verleihung des Adjunkttitels. Ableistung des Eides "... ich verspreche und schwöre dem allmächtigen Gott vor dem heiligen Evangelium ... treu und ehrlich zu dienen, mich in allen stets zu fügen ... alle Geheimnisse fest zu bewahren ... und den mir bestimmten Rang ehrlich auszufüllen ... so wahr mir Gott helfe. Amen." (B1, S. 25) |
| 1816 | 7.7. Berufung zum außerordentlichen Professor. |
| 1819 | 16.12. mit der Reorganisation der Universitätsbibliothek beauftragt. |
| 1820 | Titel Hofrat. Bartels überträgt ihm die Vorlesung über reine Mathematik. Nachfolger von Bartels, der einen Ruf nach Dorpat annimmt, Dekan der Physikalisch-Mathematischen Fakultät. |
| 1821 | Bestätigung als Dekan der Physikalisch-Mathematischen Fakultät. |
| 1822 | 24.5. Bestätigung als ordentlicher Professor. Mitglied des Baukomitees. |
| 1823 | Negatives Gutachten zum vorgelegten Lehrbuch zur Geometrie durch N. Fuß, Sekretär Eulers, Mitglied und ständiger Sekretär der Petersburger Akademie der Wissenschaften. Das Buch wurde erst 1898 wieder gefunden und 1909 gedruckt. |
| 1824 | Verleihung erster Orden (Wladimir-Orden 4. Stufe.) |
| 1825 | Titel Kollegienrat. Vorsitzender Baukomitee. Leiter der Universitätsbibliothek. Abschluß Algebralehrbuches. |
| 1826 | 'Geburtsstunde' der nichteuklidischen Geometrie (offizielle): Vortrag am 12.2. vor dem Rat der Universität: Grundlagen der Geometrie mit einem strengen Beweis des Parallelentheorems. |
| 1827 | Ernennung zum Kurator des Kasaner Schulbezirks und am 30.7. Rektor bis 14.8.1846. |
| 1828 | Rede "Über die wichtigsten Fragen der Erziehung" (Immatrikulationsfeier), veröffentlicht . 1832 im Kasaner Boten. |
| 1829 | Alexander von Humbold in Kasan, Begegnung mit Lobatschewski. "Über die Anfangsgründe der Geometrie" im Kasaner Boten (dt. 1898) in fünf Teilen vom Februar / März 1829 bis Juli/August 1830. |
| 1830 | Cholera-Epidemie in Kasan. Hervorragende Einsicht in die erforderlichen und erfolgreichen Maßnahmen Ls., denen der Gouverneur nicht zu folgen vermochte. |
| 1832 | Heirat. Fertigstellung der Arbeit "Über die Anfangsgründe der Geometrie" Übergabe an die Akademie der Wissenschaften in Petersburg. Negatives Gutachten des Akademiemitgliedes Ostrogradski. (B1, S. 82) |
| 1833 | Titel Staatsrat. |
| 1834
|
Gründung "Wissenschaftliche Schriften der Kasaner Universität". Lehrbuch "Algebra oder die Berechnung des Finiten" u.a. Beleidigende Kritik in der Zeitschrift "Sohn des Vaterlandes". "Über die Anfangsgründe der Geometrie", Erwiderung Ls. auch nach fünf Monaten nicht abgedruckt [nach Fußnote in Lobatschewski, N. I. (dt. 1904, S. 4). Die Gutachter der Universität kommen nach bald 8 Jahren zu keiner Beurteilung seiner Arbeit. |
| 1835 | Imaginäre Geometrie. [Einleitung hier] Neue Strategie über die Analysis Verständnis und Anerkennung zu finden (S.4). |
| 1837 | Adelung (vererblich und mit Wappen). "Vorgestellte Geometrie" fr. (dt. 1904) |
| 1840 | Tod der Mutter. dt. "Geometrische Untersuchungen zur Theorie der Parallellinien". |
| 1841 | Titel "Verdienter Professor" |
| 1842
|
Wahl zum korrespondierenden Mitglied der Königlich wissenschaftlichen Gesellschaft in Göttingen; Initiative Gaußens, der ihn allerdings nicht in Schutz nahm als sein Werk Geometrische Untersuchungen zur Theorie der Parallellinien (Berlin 1840) negativ besprochen wurde. |
| 1845 | Übernahme der Aufgaben Kurator des Schulbezirks Kasan. |
| 1846 | Emeritierung. Intrigen. Stellvertretender Kurator. Krank, schwach. |
| 1852/53
|
Sein ältester Sohn Aleksei, der studierte, starb an Tuberkulose. Sein letzter, 1852 geborener Sohn, Aleksei, wird geboren (stirbt bereits 1883). Sein zweitältester Sohn muß die Universität verlassen, weil er 1853 zum Militärdienst eingezogen wird. |
| 1855
|
Pensionierung. Wahl zum Ehrenmitglied der Moskauer Universität. Materielle Probleme. Antrag auf finanzielle Unterstützung zur Behandlung in einer Moskauer Klinik beim im Sep. in Kasan weilenden Unterrichtsminister A. S. Norow, die 12 Tage vor seinem Tod zu spät bewilligt wurde. Französische Ausgabe (Faksimile): Pangeometrie. |
| 1856 | 12.2. Tod (Lungenparalyse). Gedenkrede am Grab. Pangeometrie zum 50jährigen Jubiläum der Universität Kasan. |
Dokumente aus Lobatschewskis Schriften
Negatives Gutachten zum Lehrbuch der Geometrie 1823 (1898 wieder gefunden und 1909 veröffentlicht).
Die Biographen Halameisär, Alexander & Seibt, Helmut (1978,
S. 28) berichten: "In dem 1823 vorgelegtem Geometrielehrbuch schreibt Lobatschewski
u. a. folgendes:
- 'Die Messung ebener Flächenräume gründet sich darauf,
daß zwei Linien zusammentreffen, wenn sie auf einer dritten
nach derselben Seite hin stehen und wenn die eine eine Senkrechte ist,
die andere aber unter einem spitzen Winkel geneigt ist, der sich der Senkrechten
zuwendet. Die Linien AB und CD müssen bei genügender
Verlängerung zusammentreffen, wenn die eine von ihnen AB auf
BC
senkrecht steht und die andere CD gegen BC unter einem spitzen
Winkel C geneigt ist, der sich der Senkrechten AB zuwendet.
Einen strengen Beweis für diese Wahrheit hat man bis jetzt nicht finden
können. Die Beweise, die man gegeben hat, kann man nur als Erläuterungen
bezeichnen, aber sie verdienen nicht im vollen Sinne als mathematische
Beweise geschätzt zu werden.'
Bei dem Versuch, über Euklid hinauszugehen, baut Lobatschewski
im ersten Teil seiner Arbeit eine „absolute Geometrie'' auf, die vom Parallelenpostulat
unabhängig ist. Er war inzwischen davon überzeugt, daß
eine Geometrie, in der alle Axiome von Euklid mit Ausnahme des Parallelenaxioms
erfüllt sind, in sich widerspruchsfrei sein könnte. Dabei spielte
Lobatschewskis
kritische Einstellung eine Rolle, die er zu der Auffassung vom Angeborensein
unserer geometrischen Kenntnisse hatte, aus der die Einzigkeit des bisherigen
geometrischen Systems folgen würde. Das Geometriebuch
Lobatschewskis
wurde vom Kurator der Kasaner Universität der Petersburger Akademie
der Wissenschaften zur [<28] Begutachtung als Lehrbuch, das für
Gymnasien geschrieben war, zugeschickt. Für den Anfangsunterricht
war dieses Werk tatsächlich nicht geeignet. Das Gutachten der Akademie
verfaßte N. Fuß,
ein Schüler und Mitarbeiter von Euler und damaliger ständiger
Sekretär der Akademie. Fuß erkannte nicht den sich andeutenden
revolutionierenden Gehalt dieser Arbeit. Sein Gutachten vorn 3. August
1823 war äußerst negativ. Er schrieb unter anderem:
- 'Wenn der Verfasser glaubt, seine Schrift könne als Lehrbuch dienen,
so zeigt er dadurch, daß er von den Ansprüchen, die man an ein
Lehrbuch stellen muß, keinen rechten Begriff hat, d. h. keinen Begriff
von der Fülle der geometrischen Wahrheiten, die den Inbegriff eines
Elementarkurses der Wissenschaft bilden, von der mathematischen Methode,
von der Notwendigkeit scharfer und deutlicher Erklärungen aller Begriffe,
von der logischen Ordnung und der methodischen Einteilung des Stoffs, von
der gehörigen Aufeinanderfolge der geometrischen Wahrheiten, von der
unerläßlichen Strenge und möglichst rein geometrischen
Fassung der Beweise. Von allen diesen notwendigen Eigenschaften ist in
der Geometrie, die ich durchgesehen habe, auch nicht eine Spur.'
Besonders empört zeigte sich Fuß über die
Einführung des Meters als Einheit der Längenmessung und die Teilung
des Kreises in 400 und nicht in 360 Grad. Er analysierte nicht das Wesen
des von Lobatschewski vorgenommenen Aufbaus der Geometrie auf der
Grundlage einer Axiomatik. Fuß schrieb sarkastisch:
- '. . . und es ist verwunderlich, daß der Verfasser das französische
Meter als Maßeinheit für die geraden Linien und den hundertsten
Teil eines Viertelkreises, den er als Grad bezeichnet, als Maßeinheit
für Kreisbogen benutzt. Diese Einteilung ist in der Zeit der französischen
Revolution erdacht worden, als die Raserei einer Nation alles bisherige
vernichtete und sich sogar auf den Kalender und auf die Teilung des Kreises
erstreckte; diese Neuheit wurde aber wegen ihrer Unbequemlichkeit nirgendwo
verwendet.'
Diese Rezension erwies sich in zweierlei Hinsicht als falsch: die
Genialität der Lobatschewskischen Idee entging nicht nur dem
damals 78jährigen Fuß, der als "alter Weiser" galt, sondern
auch vielen, talentierten Köpfen der damaligen Zeit; das Meter hatte
sich damals überall schnell eingebürgert. Das Gradmaß für
die
Winkel blieb jedoch auch in der Folgezeit unverändert.
Die Rezension von Fuß hatte natürlich zur Folge,
daß das Geo-[<29] metriebuch von Lobatschewski nicht gedruckt
wurde. Das Manuskript galt lange Zeit als verschollen, bis es im Jahre
1898 bei einer Durchsicht des Archivs des Kurators der Universität
wieder aufgefunden wurde. Die erste Auflage dieses Buches erschien im Jahre
1909 in Kasan, d. h. 86 Jahre nach Fertigstellung des Manuskripts durch
Lobatschewski."
Fußnote
über eine beleidigende Kritik 1834

Quelle: Lobatschewski, N.
I. (dt. 1904, russ. 1835). Imaginäre Geometrie Fußnote
S. 4. Leipzig: Teubner.
Einleitung Imaginäre
Geometrie 1835.
Übersetzt von Heinrich Liebmann

Inhalt Imaginäre Geometrie und Anwendung der imaginären Geometrie auf einige Integrale

Inhaltsverzeichnis
Pangeometrie (1856)
Übersetzt von Heinrich Liebmann

Anmerkung: Inhaltsverzeichnis, Zwischenüberschriften,
Querverweise und erläuternde Figuren fehlen im
russischen Original und wurden von Liebmann der deutschen
Übersetzung beigegeben.
Pangeometrie:
Die ungenügende Begründung der gewöhnlichen Parallelentheorie
Übersetzt von Heinrich Liebmann

Lobatschewski als Lehrer und Pädagoge
Lobatschewski war Mathematiker, Naturwissenschaftler und Materialist und alles andere als ein bigotter Frömmling, wie schon frühzeitig durch seine Auseinandersetzung mit Jakowkin, dem Vater seiner ersten Liebe (Anna) zum Ausdruck kam.
Ausgangsbasis:
1919-1926 Restauration und geistige Inquisition in der Ära Magnizki
Die Biographen (B1, S. 40f, fette Hervorhebung von RS) schildern eindrucksvoll:
"Infolge der ungünstigen Zustände im gesamten russischen Bildungssystem
der damaligen Zeit, die auch zur Folge hatten, daß manche der ausländischen
Professoren die Universität bald wieder verließen, verschlechterten
sich nach einigen Jahren die Arbeitsbedingungen an der Universität
sehr stark.
Im Jahre 1819 beauftragte der damalige Minister
für kirchliche Angelegenheiten und Bildung, Fürst Golizyn,
den äußerst reaktionären M. L. Magnizki
mit einer Revision der Tätigkeit des Kasaner Universität. In
der Universitätsbibliothek fand dieser Revisor Werke von Diderot,
Voltaire, Rousseau und anderen Vertretern der Aufklärung, aber
keine Bibel. Darüber war er schrecklich erzürnt. Er hielt das
ständige Erinnern an die Weisheit, Allwissenheit und Allmächtigkeit
Gottes für die wichtigste Aufgabe im Unterricht. Magnizki meinte,
daß die Universität strenggläubige Beamte und keine Philosophen
und
Freidenker ausbilden muß. Er schlug sogar vor, die Universität
zu schließen, weil in ihr ein unzu-[<40]lässiger 'Voltaireismus'
gedeihe und weil sie eine Brutstätte von revolutionären Gedanken
und von Gottlosigkeit sei. Dieser Vorschlag war aber selbst dem ebenfalls
reaktionär eingestellten Minister zu viel.
Vor seiner Abreise nach Petersburg erteilte Magnizki
in Kasan ausführliche Instruktionen. So ordnete er an, daß über
dem Haupteingang der Universität ein Kreuz mit der Inschrift „In Deinem
Lichte erblicken wir die Wahrheit" anzubringen sei. Außerdem sollte
auch eine Medaille mit diesem Text geprägt werden. Lobatschewski
erhielt auch schriftliche Instruktionen. Als Physiklehrer wurde er verpflichtet,
'auf die Allwissenheit Gottes und auf die Beschränktheit unserer Sinne
und Geräte für das Erkennen der uns umgebenden Wunder hinzuweisen'.
In der Astronomieausbildung sollte er 'mit flammenden Worten auf die Unveränderlichkeit
der Weisheit des Schöpfers und der Gesetze für die Himmelskörper
hinweisen'.
Es ist jedoch schwierig, mathematische und physikalische
Formeln mit Gott in Einklang zu bringen. Lobatschewski hielt
es auch nicht für erforderlich, diesen Instruktionen nachzukommen.
Bedeutend schlechter hatten es dagegen die Lehrkräfte für
Medizin: Magnizki verbot die Untersuchungen des menschlichen Körpers
und ordnete an, daß die Skelette, die bei den Anatomievorlesungen
benutzt worden waren, feierlich zu beerdigen seien, mit einer Totenmesse
und unter Teilnahme von Geistlichen. Ferner wurde die Benutzung von menschlichen
Knochen und Skeletten zu Lehrzwecken verboten.
Im selben Jahr 1819 wurde Magnizki zum Kurator
des Kasaner Schulbezirks ernannt. Damit war er faktisch unumschränkter
Herrscher in der Universität. Durch einen Erlaß des Ministers
Golizyn,
der vom Zar gebilligt worden war, wurde an der Kasaner Universität
der 'Unterricht in göttlicher Erkenntnis und Christenlehre' eingeführt.
Neun fortschrittliche Professoren wurden von der Universität vertrieben.
Einige der verbleibenden Lehrkräfte standen
fest auf den Positionen der göttlichen Erschaffung der Welt und sprachen
darüber auch in ihren Vorlesungen. So steht zum Beispiel in einem
Vorlesungsmanuskript aus der damaligen Zeit:
. . . Aus der heiligen Schrift geht hervor, daß das Sonnenlicht
ein schwacher Abglanz des Angesichts Gottes ist. Wie es sich ausbreitet,
[<41] ob durch Wellen oder auf andere Art, darüber sagt die heilige
Schrift nichts aus. In Übereinstimmung mit der heiligen Schrift stellen
wir uns das Licht als ein Organ vor, durch das der Herr, der unerreichbar
ist, seinen Geist auf die Erde schickt.
Der Mathematikprofessor Nikolski lehrte seinen
Studenten:
'So wie die Zahlen nicht ohne Einsen existieren können, so kann
die Welt auch nicht ohne Schöpfer existieren.'
Über dem Katheder des Professors für russische Literatur Gorodtschaninow
hing die Inschrift "Die Literatur ist ein Organ des Verstandes; der Verstand
ist die Literatur der Seele: die Seele, vernünftig und unsterblich,
ist ein kostbarer Funken der Gottheit."
Ein Verbot folgte nach dem anderen. Magnizki
annullierte den Unterricht in neuester Geschichte. Die praktischen Übungen
in russischer Literatur sollten an Hand der Bibel und der Psalmen durchgeführt
werden. Das Studium der Mythologie wurde verboten, da die Mythologie ein
Fach sei, 'das dem Christentum widerspricht'. Die Beschäftigung mit
der Geologie wurde ebenfalls verboten, da die Geologie eine Wissenschaft
sei, 'die der heiligen Schrift widerspricht'. Das Beziehen ausländischer
Zeitschriften war ebenfalls verboten ...
Magnizki erreichte durch die sieben Jahre
seiner 'Leitung' des Schulbezirks den Niedergang der Kasaner Universität.
Er wurde erst im Jahre 1826 als Kurator des Kasaner Schulbezirks abgelöst."
Von Mathematik verstand Magnizki
glücklicherweise wohl nichts, sonst hätte er sie gleich ganz
verboten.
Aus der Rede vom 17. Juli 1828 "Über die wichtigsten Fragen der Erziehung".
Die Biographen (B1, S. 43 ) berichten und zitieren: "'In die Erziehung,
in diese wichtige Sache, beziehen meine Gedanken erste Grundlagen der Sittlichkeit
mit ein; sie können dabei auf Regeln verweisen, die der Lehrer unbedingt
befolgen sollte. Die Erziehung nimmt in der Wiege ihren Anfang: zuerst
wird sie durch die bloße Nachahmung erworben, allmählich entwickeln
sich Verstand, Gedächtnis, Vorstellungskraft, Geschmack für das
Schöne, es erwacht die Liebe zu sich selbst und zum Nächsten,
das Ehrgefühl, der Wunsch, das Leben zu genießen ... und der
Mensch, als wäre er von neuem geboren, wird immer vollkommener ...
Die Weisheit wird dem Menschen nicht mit in die Wiege gelegt, sie wird
durch Lernen erworben.'
Lobatschewski wandte sich scharf gegen scholastische
und spekulative Überlegungen und erhob die Praxis und die Natur zum
Kriterium der Wahrheit.
Er führte in seiner Rede weiter aus:
'Bemüht Euch nicht vergebens, aus einer Einsieht die ganze Wahrheit
zu folgern. Befragt die Natur, sie enthält alle Wahrheiten. Auf
Eure Fragen wird sie Euch unbedingt und befriedigend Antwort geben ...
Die Jugend, die an dieser Einrichtung immatrikuliert wird, wird nicht leere
Worte hören, ohne jeglichen Sinn. Hier wird das gelehrt, was wirklich
existiert, und nicht das, was von einem untätigen Verstand erfunden
worden ist. Hier sind die Fächer unter den Lehrkräften so verteilt,
daß jeder das lehrt, womit er sich sein ganzes Leben, lang beschäftigt.
Wer seine Kinder zum Nutzen des Staates bilden will, der muß sie
in den staatlichen Lehranstalten bilden lassen.'
Lobatschewski war der Ansicht, daß
Müßiggang den menschlichen Verstand verdirbt. Eine wichtige
Aufgabe der Pädagogen sah er im Herausfinden und im Erziehen von Genies.
Er sagte dazu:
'Darin besteht die Kunst der Erzieher: ein Genie zu entdecken und es
mit Erkenntnissen auszustatten.'
Damals lernte man in den Schulen und auch an den Universitäten
nur solche Dinge, die bereits untersucht und bekannt waren, die sich herauskristallisiert
und gefestigt hatten.
Erst kürzlich entdeckte Fakten bzw. neue Entwicklungstendenzen
hielt man dagegen nicht für geeignet, daß sie zum Gegenstand
des allgemeinen Unterrichts gemacht wurden. [<43]
Aber die Wissenschaft kann nicht auf der Stelle treten. Es ist unmöglich,
über Jahrzehnte hinweg immer wieder dieselben Tatsachen zu wiederholen,
als ob sie stets unwidersprochen und ewig seien. Mit der Entwicklung und
der Erneuerung der Wissenschaft muß auch die Bildung weiterentwickelt
und erneuert werden, und zwar sowohl inhaltlich als auch methodisch.' sagte
Lobatschewski."
Einsicht
in die enorme Bedeutung der Lehrer-Fort- und Weiterbildung
Lobatschewski wirkte ganz im Sinne seiner Rede und tat sehr viel für
die Lehrer- Fort- und Weiterbildung, die gar nicht hoch genug eingeschätzt
werden kann. Dazu trug auch sehr bei, daß er seine Vorlesungen und
Unterweisungen in russischer Sprache hielt.
Vorlesungs-
und Unterweisungskonzeption
Die Biographen (B1, S. 51) berichten: "Lobatschewski war ein
vorzüglicher Lehrer, ein guter Methodiker. Er hielt fast jeden Vormittag
zwei zweistündige Vorlesungen. Professor A. F. Popow, sein
Schüler und sein späterer Nachfolger als Leiter des Mathematik-Lehrstuhls,
erinnert sich:
'Im Hörsaal bemühte er sich um große
Klarheit in seinen Darlegungen dadurch, daß er Aufgaben zunächst
mit der synthetischen Methode löste und erst danach allgemeine Sätze
mit der analytischen Methode bewies. Er kümmerte sich wenig um den
Mechanismus des Rechnens, sondern weitaus mehr um Klarheit in den Begriffen.
Er liebte es besonders, nach eigenen Gedanken zu unterrichten, anstatt
Lehrbüchern zu folgen. Seine Hörer sollten sich selbständig
mit der Literatur beschäftigen.'
Professor Laptew schreibt zu diesem Thema in seiner Biographie:
'Eine mechanische Aneignung des Stoffs durch die
Studenten wurde von Lobatschewski nicht gebilligt, er forderte eine
hohe Genauigkeit im Ausdruck und legte auf die Fähigkeit zum selbständigen
Überlegen besonderen Wert. Sein methodologisches Herangehen und seine
pädagogischen Auffassungen fanden keine offizielle Billigung und blieben
den Lehrkräften für Mathematik und Naturwissenschaften an den
anderen Universitäten unbekannt. An der Kasaner Universität wirkten
sie sich aber nicht nur auf den Verlauf des Unterrichts der anderen Kollegen
im Verlaufe der langjährigen eigenen pädagogischen Arbeit Lobatschewskis
praktisch aus, sondern auch noch später.'
Es sei dazu noch angemerkt, daß an der Kasaner Universität
viele jüngere Lehrkräfte ihre Vorlesungen nach Konspekten Lobatschewskis
hielten.'"
Sokratische Methodik in der Pädagogik
und Konfliktlösung
Die Biographen (B1, S. 44) berichten: "Lobatschewski unterhielt
sich gern mit begabten Studenten. Er interessierte sich für deren
Neigungen, stellte Fragen und gab Ratschläge - auch dann, wenn die
Studenten die Disziplin und die in der Universität geltenden Regeln
verletzt hatten. Er erinnerte sich gut an seine eigene Studentenzeit, als
er durch die Lebhaftigkeit seines Charakters und durch die überschäumende
Energie die Verwaltung der Universität außer sich brachte (vgl.
unter 2.2.). Wenn ein Student, der sich etwas hatte zuschulden kommen lassen,
zu Lobatschewski 'zu einem Gespräch' kommen mußte, gelang
es dem Rektor gewöhnlich, diesen Studenten 'selbständig' zu der
Einsicht von der Unwürdigkeit ähnlicher Handlungen zu bringen,
ihn sein Verhalten 'selbst' verurteilen zu lassen und ihn zu dem Versprechen
zu bewegen, sich von nun an vernünftiger zu führen. So wird zum
Beispiel berichtet, daß der überaus begabte Student Chlebnikow,
der aber gleichzeitig ein großer Bacchus-Jünger war und
der sich manchmal bis zur Bewußtlosigkeit betrank, nach einer [<44]
längeren Unterhaltung mit Lobatschewski diesem sein Ehrenwort
gab, in Zukunft nicht mehr zu trinken, was er in der Folgezeit auch
hielt."
Nach den Biographen (B1, S. 45) soll Lobatschewski
faule und gewissenlose Studenten nicht geliebt haben. Er soll der Auffassung
gewesen sein, "daß man schwache und schlechte Studenten an den ersten
Worten erkennen könne und daß es unnütz sei, sie mit vergeblichen
Fragen zu quälen."
Sokratische Methoden sollen Lobatschewski auch beim Schlichten von
Streiten im Rat der Universität geholfen haben: "Als er feststellte,
daß es nicht gelingen würde, für eine in einer offiziellen
Ratssitzung erörterte Frage Stimmenmehrheit zu erhalten, kündigte
er eine Pause an und schlug vor, für diese Zeit in seine Universitätswohnung
zu gehen. Dort wurden dann bei einem Becher guten Punsches des gastfreundlichen
Rektors alle Zweifel glücklich beseitigt.
Nur in seltenen Ausnahmefällen nahm Lobatschewski zu Druckmitteln
Zuflucht, indem er zum Beispiel erklärte, daß das der Wunsch
des Kurators sei - und der Streit hörte sofort auf."
Ehe, Familie und Kinder
Die Biographen [B1, S. 46f] teilen unter dem Titel "Familienangelegenheiten"
mit: "Im Oktober 1832 heiratete N. I. Lobatschewski die 19jährige
Warwara
Aleksejewna Moissejewa, die Tochter eines reichen Gutsbesitzers. Als
Mitgift erhielt die junge Frau einige Dörfer mit zahlreichen leibeigenen
Bauern und in Kasan selbst ein dreigeschossiges steinernes Haus. Obwohl
das Eigentum der Eheleute nach dem Heiratsvertrag als getrennt betrachtet
wurde, läßt sich feststellen, daß sich für Lobatschewski
die materiellen Lebensbedingungen wesentlich verbessert hatten. Sein ehemaliger
Lehrer, Professor Littrow, der inzwischen Direktor des Wiener Observatoriums
geworden war. schrieb damals an seinen Kollegen I. M. Simonow, der
nun an der Kasaner Universität die Professur für Astronomie innehatte
und der als guter Freund Lobatschewskis galt: 'Tausend Grüße
an Herrn Professor Lobatschewski. Ich gratuliere ihm aus vollem
Herzen zu seiner Heirat. Aber das kommt etwas spät: Ihm wird es schwerfallen,
Sie auf diesem Wege einzuholen, wo Sie bereits drei Kinder haben.' Littrow
dürfte mit seiner Sorge nur schwerlich recht behalten haben: Lobatschewski
hatte insgesamt 15 Kinder, manche Quellen sprechen von 18. M. N. Mussin-Puschkin,
der Kurator der Kasaner Universität, war ein Vetter der Frau von Lobatschewski.
Durch seine Hochzeit war also der Rektor der Universität ein Verwandter
des Kurators des Kasaner Schulbezirks geworden. Dadurch wurden die freundschaftlichen
Bande zwischen Lobatschewski und Mussin-Puschkin noch weiter
verlieft; die dienstlichen Beziehungen vereinfachten sich." Seine Frau
Warwara Aleksejewna (1812 — 1885) überlebte ihn um bald 30 Jahre.
Alter, Lebensende und Tod (12.2.1856).
Im Juli 1846 war Lobatschewski 53 Jahre alt und schon 30 Jahre Professor,
eine Zeitdauer, nach der man in Rußland zur damaligen Zeit gewöhnlich
emeritiert wurde. Bei ihm wie bei dem Physiker Simonow,
mit dem er sein Studium an der Uni Kasan begonnen hatte, machte man eine
Ausnahme und er durfte weitere 5 Jahre seinen Lehrstuhl behalten. Nachdem
im Frühjahr 1845 der Kurator des Kasaner Schulbezirks Mussin-Puschkin
nach Petersburg berufen wurde und Lobatschewski dieses Amt übernommen
hatte wurde ihm die vielen Verpflichtungen zu viel und er schlug Popow,
Doktor der Mathematik und Lehrer am Kasaner Gymnasium, für seinen
Lehrstuhl zur reinen Mathematik vor, fest damit rechnend, daß er
weiterhin Rektor und zum Kurator ernannt werden würde. Aufgrund von
Intrigen durch Mißgünstlinge kam es dann ganz anders: Die Abgabe
des Lehrstuhl wurde 'genehmigt', zugleich entband man ihm vom Rektorposten
und ernannte ihn lediglich zum stellvertretenden Kurator. Die Biographen
kommentieren (B1, S. 57):
"Bei Lobatschewski rief die Entfernung aus
der aktiven Lehr- und Verwaltungsarbeit einen starken Kräfteverfall
hervor. Mit 55 Jahren fühlte er sich schwach und krank.
Schließlich verlor er auch noch seine nominelle Stellung als
Stellvertreter von Molostwow. Das bedeutete gleichzeitig, daß
er von nun an kein Gehalt mehr erhielt, sondern nur noch seine Pension.
Es entstanden materielle Schwierigkeiten.
Lobatschewski erblindete allmählich.
Das war wohl auch ein Ausdruck für seine übermäßige
nächtliche wissenschaftliche Arbeit in seiner Jugend. In den letzten
Lebensjahren konnte er sich nicht mehr allein bewegen.
Trotzdem glaubte er auch in diesen Jahren fest an
eine große Zukunft seiner Entdeckung. Er verlor nie den Drang zur
wissenschaftlichen Arbeit. In diesem Zustand — schwach, krank und fast
erblindet — diktierte er seinen Schülern seine letzte wissenschaftliche
Arbeit, die berühmte „Pangeometrie", die 1855 in den „Wissenschaftlichen
Schriften der Kasaner Universität" erschienen und die ein Jahr später,
im Sterbejahr Lobatschewskis, in französischer Sprache in der
Festschrift zur 50-Jahrfeier der Universität Kasan noch einmal gedruckt
wurde.
Bis zuletzt verlor Lobatschewski nicht die
Hoffnung, doch wieder gesund zu werden. Er hatte aus der Rektoratswohnung
ausziehen müssen. Im Jahre 1852 verlor er seinen ältesten Sohn
Aleksei,
der Student war und an Tuberkulose starb. Sein zweiter Sohn Nikolai
mußte ein Jahr später die Universität verlassen und seinen
Militärdienst ableisten. Seine Gesundheit verschlechterte sich immer
mehr. Trotzdem nahm er noch am wissenschaftlichen Leben der Universität
teil. So beteiligte er sich zum Beispiel, wie Laptew berichtet,
noch an Prüfungen und an Promotionen. [<57]
Lobatschewski hatte den Plan, sich in einer
Moskauer Klinik behandeln zu lassen. Dazu brauchte er aber Geld. Deshalb
wandte er sich an den Unterrichtsminister A. S. Norow, der im September
1855 Kasan besuchte, mit der Bitte um eine einmalige finanzielle Unterstützung.
Zu Beginn des Jahres 1856, zwölf Tage vor seinem Tode, erhielt er
endlich eine Mitteilung über die Bewilligung von 1500 Silberrubeln.
Diese mögliche Hilfe kam zu spät. Lobatschewski
starb am 12. Februar 1856."
Aus
der Gedenkrede anläßlich seiner Beerdigung:
Die Biographen [B1, S. 58) schreiben: "Auf seinem letzten Weg zum Arskischen
Friedhof in Kasan folgten ihm Hunderte Professoren und Studenten der Universität,
Gymnasiasten und ehemalige Schüler. Am Grabe hielt Professor N.
N. Bulitsch eine kurze Rede, in der er u. a. ausführte: 'Als Wissenschaftler
war Lobatschewski seiner Sache treu ergeben. Er richtete seine Aufmerksamkeit
stets auf die führenden wissenschaftlichen Zentren in Europa und bemühte
sich, daß das Niveau der wissenschaftlichen Arbeit hier in Kasan
sich immer .mehr dem erreichten Entwicklungsstand angleicht. Als Erzieher
bildete er einige Generationen von Mathematiklehrern aus, die ihm für
ihre Entwicklung dankbar sind. Als Rektor vermehrte er die Mittel der Wissenschaft,
und die Universität ist ihm allein zu großem Dank verpflichtet.
Große gedankliche Leistungen sind uns teuerer als alle anderen Heldentaten,
denn nur die Wissenschaft, die Gedanken und die Kenntnisse sind die wahren
Grundlagen für den gesellschaftlichen Wohlstand.'"
Rätsel
um Lobatschewskis letzte Jahre und Ende
Bedenkt man, wie vielen Menschen Lobatschewski geholfen - und, denken
wir an sein umsichtiges und erfolgreiches Wirken bei der Choleraepidemie,
wo er wahrscheinlich viele Leben rettete, wie viele Studenten er ausgebildet
und gefördert und was er für den Schulbezirk Kasan und die Universität
getan hat, an seinen durch wahrhaften Verdienst erworbenen Adelsstand,
an den Reichtum, den die Ehegattin mit eingebracht hat, so kann ich seine
doch sehr bitteren und schweren letzten Lebensjahr nicht so recht verstehen
und nachvollziehen, was hier geschehen ist. Hier scheint die Biographieforschung
noch Aufklärungsbedarf zu haben.
Lobatschewskis Persönlichkeit.
Eine angemessene Persönlichkeitsbeurteilung ist sehr schwierig.
Erstens liegen bald 200 Jahre dazwischen. Zweitens geht es um eine Persönlichkeit
aus dem zaristischen Rußland in Kasan, Sibirien. Drittens sind wir
- wie bei allen posthumen Berühmtheiten - auf zumindest teilweise
hagiographisch-euphemistische
- Sekundärquellen angewiesen und ich auch noch auf Übersetzungen.
Viertens müßte auch das nähere Umfeld, Milieu, das Universitätswesen
und der Wissenschaftsbetrieb einbezogen werden. Die folgenden Ausführungen
sollten also mit Vorsicht und kritischer Distanz gelesen werden.
Lobatschweski wird als geistig frühreifer,
vielseitig
hochbegabter, begeisterungsfähiger und wissbegieriger Junge
geschildert, der in seiner Jugend ziemlich über die Stränge schlug
und eine kurze wild-rebellische Zeit hatte. Als Beamtensohn erhielten
er und seine beiden Brüder das Privileg, ein Gymnasium, sogar mit
vollem Pensionat, zu besuchen, also Finanzierung auf Kosten des zaristischen
Staates. Von Jugend an war er aufklärerisch-materialistisch
orientiert und geriet einerseits mit dem Bigott-Unterwürfigen (Jakowkin,
Magnizki)
und andererseits mit den konservativen Mathematikern (Fuß,
Ostrogradski)
aneinander, so daß seine geistige Unabhängigkeit, persönliche
Autonomie, Ausdauer und Konsequenz, Standvermögen und Unbeirrbarkeit
im besten Sinne sein ganzes Leben wie ein beständiger roter Faden
durchzog. Betrachtet man, was er alles gemacht hat, erscheint er, etwas
negativ gesehen, als eine Art 'workoholic', positiv betrachtet als
ein außerordentlich fähiger, vitaler (auch fruchtbarer:
15-18 Kinder) fleißiger und tüchtiger Mensch.
Daher war die relativ plötzliche Entbindung vom Rektorat, Kurator
und von der Professur für ihn ein ziemlicher Verlust und Schlag. In
der Psychotherapie erleben wir nicht selten, daß die Zusammenbrüche
erfolgen, wenn die Anspannung und Forderung nachläßt, z. B.
in Urlaub oder Freizeit. Mit einem Male fühlte er sich krank und schwach;
hier könnte sein Abwehrsystem einen ziemlichen Knacks bekommen haben
und er verlor in den letzten Lebensjahren zunehmend Funktionstüchtigkeit,
erblindete und konnte sich nicht mehr richtig bewegen. Dieses traurige
Kapitel seines Lebensendes ist noch nicht genügend aufgeklärt.
Hinweise erhalten wir von den Biographen (B1, S. 56, fette Hervorhebung
im Sinne einer Persönlichkeitscharakteristik durch RS): "Lobatschewski
hatte in Kasan aber auch zahlreiche Neider. Es begannen
Intrigen. Nicht jeder liebte offene Meinungen und einen geraden
und unabhängigen Charakter, wie ihn Lobatschewski in
hohem Maße besaß."
Lobatschweski bemühte sich sein Leben lang,
seine Geometrie verständlich zu machen und durchzusetzen. So zeigen
z.B. seine Ausführungen
in Lobatschewski (russ. 1835, dt. 1904, S. 4), wie sehr er
nach Wegen gesucht hat, sich den Fachkollegen verständlich zu machen
und so ersann er auch eine neue Strategie (1835), die nun darin bestand,
"daß die hauptsächlichen Gleichungen, die ich für die Abhängigkeit
der Seiten und Winkel eines Dreiecks in der imaginären Geometrie gefunden
habe, mit Nutzen in die Analysis aufgenommen werden können, und niemals
zu Schlüssen führen, die in irgendeiner Beziehung falsch sind."
Zu seinen besonders herausragenden Fähigkeiten
gehörte auch, mit Niederlagen und sich nicht Durchsetzen können,
fertig zu werden, nicht zu verzweifeln, nicht abzudriften und seltsame
Entwicklungen einzugehen. Souverän verarbeitet er die vernichtende
Kritik durch
Nikolaus Fuß
ebenso wie das negative Gutachten von Ostrogradski
1832
oder die beleidigende
Kritik in der Zeitschrift "Sohn des Vaterlandes" 1834. Man hatte ihn
eingeordnet und sein Lebenswerk "als verzeihliche Wahnidee eines sonst
verdienten Mannes" (Quelle)
angesehen.
Trotz aller kühnen und unverstandenen Abstraktionen
jenseits des 5. Postulats von Euklid war Lobatschewski kein entrückter,
abgehobener Mathematiker im Elfenbeinturm. Er hatte auch einen ausgesprochenen
Sinn für das Praktische auf fast allen Lebensgebieten. Eine seiner
herausragendsten Leistungen - bei der ihm sicher seine Kenntnisse in Chemie
und Pharmakologie sehr halfen - ist zweifellos sein integres und lebensrettendes
Verhalten angesichts der Choleraepidemie,
mit dem er, statistisch gesehen, über 200 Leben rettete.
Würdigung
Lobatschewski hat die angemessene Würdigung seiner eigentlichen großen mathematischen Leistung trotz vieler Ehrungen nicht mehr erlebt. Zu revolutionär, zu unverständlich und außergewöhnlich waren seine Überlegungen, die immerhin sogar Gauß im Alter von 63 Jahren veranlaßt haben sollen, noch russisch zu lernen, um Lobatschewski im Original lesen zu können. Doch Gaußens Mitgefühl, Verständnis im Geiste und Zivilcourage reichten bei aller Wertschätzung ("meisterhafte Art") leider nicht aus, um Lobatschewski fachwissenschaftlich öffentlich in Schutz zu nehmen, als seine Geometrie in einer Berliner Zeitschrift negativ besprochen wurde (war es wirklich nur die Sorge um das "Geschrei der Böotier"?). So berichtet Meschkowski [B2, S. 142]:
- "Der einzige Mathematiker von Rang, der die Arbeit Lobatschewskys würdigen
konnte, war Gauß. Er beschäftigte sich sogar in seinen späteren
Jahren mit der russischen Sprache, um einige Arbeiten Lobatschewskys im
Original lesen zu können. In einigen Briefen an Freunde äußerte
er sich lobend über die Leistungen des russischen Staatsrates, aber
er vermied es doch, die Idee einer nichteuklidischen Geometrie in der Öffentlichkeit
zu vertreten. So widersprach er auch der ablehnenden Besprechung in einer
Berliner Zeitschrift nicht, aber immerhin sorgte er dafür, daß
Lobatschewsky im Jahre 1842 zum auswärtigen Mitglied der Göttinger
Akademie gewählt wurde."
Die Biographen [B1, S. 59] werten wie folgt: "Die Gedanken von Lobatschewski
zu den Grundlagenfragen der Geometrie führten zu einer breiten und
vielschichtigen Entwicklung. Sie wirkten sich auf Ausgangspunkte und Formen
des Aufbaus der Mathematik aus. In der Folgezeit fanden sie auch Anwendung
in der Mechanik, in anderen Teilen der Physik und in der Astronomie. Sie
beeinflußten auch philosophische Überlegungen. In der Geschichte
der Mathematik, der exakten Wissenschaften und der Philosophie wird der
Name von Lobatschewski stets neben denen von Archimedes,
Galilei,
Kopernikus,
Newton
und anderen großen Wissenschaftlern stehen. Man sprach oft davon,
daß Lobatschewski der Kopernikus der Geometrie sei.
Auch Gauß hatte die Existenz einer solchen neuen Geometrie
lange nicht für möglich gehalten. Er hatte sich seit 1792 mit
Grundlagenfragen der Geometrie beschäftigt. In seinen Überlegungen
war er offenbar recht weit gekommen und hatte ähnliche Ergebnisse
wie
Lobatschewski erreicht.
| Lobatschewski, auf festen materialistischen Positionen stehend, entwickelte und publizierte seine Gedanken ungeachtet der Nichtanerkennung und des Hohns vieler Mathematiker der damaligen Zeit und setzte seine Arbeit durch viele Jahrzehnte seines Lebens konsequent fort. |
Bald nach dem Tode von Gauß begann man mit der Herausgabe seines Briefwechsels. Seine insbesondere in mehreren Briefen an Schumacher enthaltenen Äußerungen zur nichteuklidischen Geometrie richteten die Blicke vieler Mathematiker erneut auf die fast vergessenen Arbeiten von Bolyai und Lobatschewski. Damit rückte das Problem der Widerspruchslosigkeit der nichteuklidischen Geometrie wieder in den Mittelpunkt."
Die
Meinung der ihn umgebenden zeitgenössischen Wissenschaftler und Mathematiker
[fett
RS]
Nach den von mir eingesehenen Quellen gab es das negative Gutachten
von Nikolaus Fuß 1823
und das negative Gutachten von Ostrogradski
1832, Lobatschewski berichtet selbst in einer Fußnote von einem beleidigenden
Artikel in der Zeitschrift "Sohn des Vaterlandes". Ein auf seine Bitte
hin von der Fakultät 1826 in Auftrag gegebenes Gutachten kam bis 1834
nicht zustande und die Schrift wanderte ins Archiv. Im abc-fachlexikon
der forscher und erfinder (1992, S. 374) wird unter dem Eintrag Lobatschewski
u.a. berichtet: "... Das verdienstvolle Wirken von L. an der Univ. Kasan,
sein pädagogisches und organisatorisches Engagement (er führte
im Kasaner Schulbezirk erstmals eine Art Lehrerweiterbildung ein) hatten
ihm bald die hohe Wertschätzung vieler Vorgesetzter, Kollegen und
Studenten (aber natürlich auch viele Anfeindungen) und schließlich
zahlreiche staatliche Ehrungen (1837 erbliche Erhebung in den Adelsstand)
eingebracht.
Dies trug jedoch nicht zur Anerkennung seines wissenschaftlichen
Lebenswerkes bei, das vielmehr in seiner Umgebung zeitlebens als verzeihliche
Wahnidee eines sonst verdienten Mannes angesehen wurde. Nur GAUSS verfolgte
nach der Bekanntschaft mit L.s erster deutschsprachiger Veröffentlichung
(1840) dessen weitere Arbeiten mit großem Interesse (er lernte zu
diesem Zweck sogar Russisch). ..."
Gauß: "... auf eine meisterhafte Art in ächt geometrischem Geiste."

Die
Rezension 1840 in Gersdorfs' Repertorium der gesammten deutschen Literatur
und einem inoffiziellen Kommentar Gaussens vom 8.2.1844

Auswahl 'Ahnengalerie' zur Geschichte der Parallellinien

Euklid, Wallis,
Saccheri
(Titel), Lambert,
Legendre,
Schweikart,
Taurinus,
Gauß,
Lobatschewski,
Bolyai
[falsch],
Beltrami,
Klein,
Riemann,
Poincaré.
Vorgeschichte und Geschichte der Anerkennung der nichteuklidischen Geometrie
Die fünf Postulate
Euklids
Zitiert nach: Euklid (dt.
1969). Die Elemente. Buch I-XIII. Hrsg. u. übersetzt von C. Thaer.
Darmstadt: WBG, S. 2-3

Zum
Verständnis des Parallelenaxioms und der nichteuklidischen Geometrie
Um die Psychologie einer Forschungsleistung einschätzen zu können,
ist es eigentlich notwendig, die Forschungsleistung im Kern zumindest zu
verstehen und die Zeit, in der diese Forschungsleistung erbracht wurde,
zu kennen und zu berücksichtigen, weil sich im Nachhinein vieles anders
darstellt. Beides ist mir nur unzulänglich möglich, so daß
ich hier nur einen allerersten Versuch auf den Weg bringen kann.
Aus Meschkowski, Herbert (1966). Einführung in die moderne Mathematik. Mannheim: BI, S. 12f

Die ersten vier Axiome Euklids gelten auch in der nichteuklidischen Geometrie.
Sätze der Nichteuklidischen Geometrie nach A. Filler
[Quelle A. Filler; URL verändert] "Sätze der nichteuklidischen
Geometrie (1)
V'. (Lobatschewskisches Parallelenaxiom):
Es existiert eine Gerade g und ein nicht auf g liegender Punkt P, durch
den mindestens zwei Geraden verlaufen, die g nicht schneiden.
- Satz: Falls die Axiome der absoluten Geometrie und V' gelten, so existieren zu jeder Geraden g und zu jedem nicht auf g liegenden Punkt P mindestens zwei Geraden, die durch P verlaufen und g nicht schneiden.
- Satz: Zu jeder Geraden g und zu jedem nicht auf g liegenden Punkt P existieren unendlich viele Geraden, die durch P verlaufen und g nicht schneiden.
- Satz: (Kongruenzsatz "www"): Stimmen zwei Dreiecke in allen drei Winkelmaßen überein, so sind sie kongruent.
- Satz: (Innenwinkelsatz der Lobatschewski-Geometrie): Die Innenwinkelsumme eines jeden Dreiecks ist kleiner als zwei Rechte.
- Satz: (Außenwinkelsatz der Lobatschewski-Geometrie): Jeder Außenwinkel eines beliebigen Dreiecks ist größer als die Summe der beiden nichtanliegenden Innenwinkel."
Psychologie der Forschungsleistung.
Querverweise: Denken, Kreativität, Problemlösungen II. Ordnung.
Die Geschichte der Parallellinien gehört für mich zu den faszinierendsten Themen, mentalen Dramen und ihre Lösung zu den Großtaten der Geistesgeschichte. Über 2200 Jahre hat das 5. Postulat viele Mathematiker, mathematisch Interessierte (z.B. Schweikart) wie "Cranks" beschäftigt, fasziniert, irritiert, herausgefordert, gequält, genarrt und ich möchte nicht wissen, wie viele darüber sonderbar, depressiv (Kaestner?) oder gar verrückt (Bolyai?) wurden und ihre Beziehungen und Lebensqualität durch ihre leidenschaftliche Besessenheit für die Mathematik aufs Spiel setzten. So ist die Geschichte um das "Parellelenpostulat" nicht nur interessant für mathematisch Interessierte und die Denkpsychologie (die sich leider um 'die' Mathematik ganz wenig kümmert, sofern sie überhaupt noch existiert), sondern sie hat auch ihren besonderen Reiz für PsychopathologInnen. Ist die Mathematik wirklich so klar und exakt, wie sie sich immer gibt? Wieso gab es so viele 'Beweise', die alle falsch waren; und zwar 'Beweise' nicht von irgendwelchen "Cranks", sondern guten oder sogar hervorragenden Vertretern des Faches (z.B. Lindemann)? Klügel allein fand ja schon im Auftrag Kaestners in seiner meist wohl zu Recht gerühmten Dissertation 28 und ausschließlich fehlerhafte 'Beweise'. So mag man sich an dieser Stelle auch einmal fragen: Was heißt eigentlich Definition (was ist eine 'Gerade', ein 'Eck', ein 'Dreieck', eine 'Parellele') Satz (Theorem), Beweis und gültiger Schluß? Was bedeuten die Begriffe "Verlängerung ins unendliche" und "treffen"? "Parallel" kommt übrigens gar nicht vor, obwohl es in der letzten Definition zuvor schon eingeführt wurde.
In der Psychologie der nichteuklidischen Geometrie als Forschungsleistung stecken eine ganze Reihe spannender Fragen, so z. B.:
- Wie konnte das fünfte Postulat Euklids über 2200 Jahre so viel Verwirrung stiften und so viele fehlgeschlagene Beweisversuche hervorlocken?
- Wie kann man die dem gesunden Menschenverstand und der Anschauung völlig zuwiderlaufende Konstruktion einer euklidischen Geometrie jenseits des Parallelenaxioms verstehen?
- Wie konnten Menschen zu solchen un- und außergewöhnlichen geistigen Konstruktionen fähig sein?
- Wie kann man einen Menschen und Denker wie Lobatschewski verstehen, so lange, so konsequent und so alleine unbeirrt und unverstanden seinen Weg zu gehen? Wie hat er das ausgehalten, wie konnte er das verkraften?
- Was kann die Psychologie der Wissenschaft daraus lernen?
- Was können wir alle von Lobatschewskis Leben und Denken lernen?
Was 'ist'
eigentlich ein 'Dreieck' ?
In der technisch entwickelten Mathematik ist seit Entwicklung der Mengenlehre und der damit verbundenen Grundlagenkrise und ihrer mühseligen Behebung durch den Formalismus für Außenstehende so gut wie nichts mehr klar. Man kann und darf sich - weniger denn je - auf keinerlei Vorverständnis oder gesunden Menschenverstand verlassen. In diesem Zusammenhang muß man auch Fragen sehen wie: was ist eine 'Gerade', ein 'Eck', ein 'Dreieck', der 'kürzeste Abstand' zwischen zwei Punkten oder eine 'Parallele'?
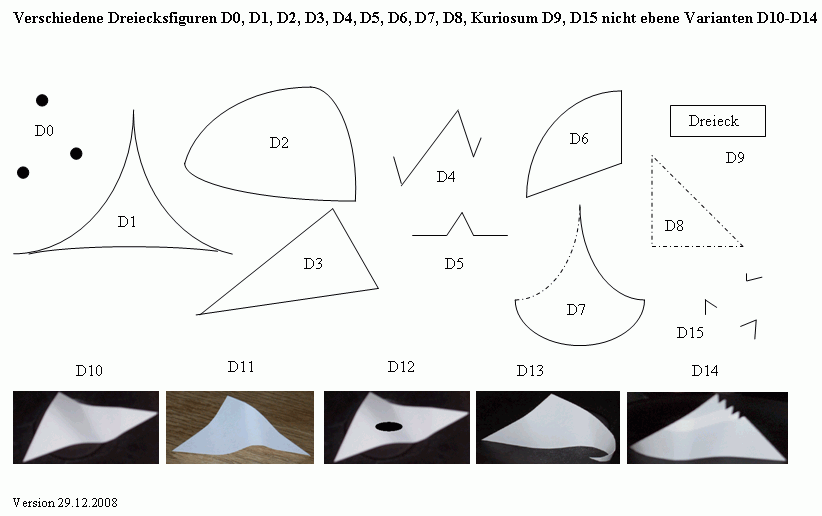
Anmerkung: D10 bis D14 wurde aus
dickerem Papier ausgeschnitten und mit der Hand "gewellt" und fotografiert;
"Loch" in D12 mit Malprogramm.
Wie selbstverständlich nimmt man gewöhnlich an, wenn man von
einem Dreieck spricht, daß es sich um ein Dreieck vom Typ D3 handelt.
Betrachtet man sich jedoch die anderen drei Figuren, D1, D2 und D4, wird
offensichtlich, daß es eigentlich überhaupt nicht so klar ist,
was ein Dreieck "ist".
Ja, es ist noch nicht einmal klar, was ein "Eck" ist,
und einige mathematische Lexika
und Wörterbücher enthalten "Eck/eckig/"Ecke" noch nicht einmal
als Eintrag. Bei D2 scheinen nur die beiden unteren Ecken Ecken zu sein,
die obere 'Ecke' wirkt ziemlich rund. Ebenso wenig selbstverständlich
oder klar ist, daß
die Verbindungen zwischen den Ecken Gerade sind.
Meist nimmt man auch an, daß die Dreiecksfiguren D1, D2 und D3 in
einer "Ebene" liegen (gilt nicht für D10-D14), so daß zu fragen
ist: was "ist" eine "Ebene"?
Weiter nimmt man gewöhnlich an, daß diese Ebene zweidimensional
überall gleich flach ist. Dies bringt die Vorstellung von Dimensionen
ins Spiel. Kein Mensch würde auch auf die Idee kommen, D4 oder
D5 ein Dreieck zu nennen, womit deutlich wird, daß mit dem üblichen
Dreiecksbegriff offenbar auch eine geschlossene Figur assoziiert wird.
Damit kommen wir zur Frage, wann ist eine Figur geschlossen, wann offen,
was heißt das? Und, man denkt sich die Verbindungen zwischen den
Ecken gewöhnlich auch dicht oder stetig, ohne jede Unterbrechung.
Das ist bei D7 und D8 nicht der Fall. D8 hat wahrnehmungspsychologisch
Dreiecksgestalt, aber das ist kein mathematischer Begriff, und es
wird durch "Schweizerkäse-Geraden verbunden". Noch deutlicher zeigt
D0, wie sehr wir allein durch unsere Wahrnehmung in die drei Punkte ein
Dreieck hineinsehen, was sich durch einfache wahrnehmungspsychologische
Experimente bestätigen läßt. Als doppelt paradox anmutendes
Kuriosum wurde D9 aufgenommen: die erste Paradoxie besteht darin, daß
in einem Viereck das Wort "Dreieck" steht. Das Wort "Dreieck" ist natürlich
selbst kein Dreieck, sondern ein Wort aus 7 Buchstaben, das Wort ist der
Name des Begriffs [Objekt
/ Metasprache]. Andere Kuriosa sind D12: trotz des "Loches" nimmt man
ein gewellt-geknicktes und nicht-ebenes Dreieck wahr. D14 zeigt ein gewelltes
"großes" Dreieck, das genau genommen aus 11 Ecken besteht. D15 besteht
ebenfalls aus merkwürdigen drei Ecken.
Nichts ist also bei genauer Betrachtung selbstverständlich,
sondern schlicht und einfach Gewohnheit, Erziehung oder Lernen in einer
bestimmten Kultur, manches einfach nur Vorurteil oder Meinung. Es gehört
zu den großen Leistungen der Mathematik, diese scheinbaren "Selbstverständlichkeiten"
gehörig in Frage zu stellen - manchmal sogar sie nachhaltig und tiefgreifend
zu erschüttern - und klar zu stellen, welche Voraussetzungen und Annahmen
jeweils für diese oder jene Auffassung und Deutung getroffen werden
müssen.
Damit habe ich Sie, werte LeserIn, hoffentlich genügend
kritisch sensibilisiert und wir können uns nun an die Hauptfrage heranmachen:
Wie kann man denken, daß die beiden Geraden in Euklids 5. Postulat
sich nicht treffen, wobei wir der Einfachheit halber erst mal annehmen
wollen, daß "treffen"
auch "schneiden" bedeutet, was keineswegs zwingend ist.
Wie kann man das fünfte Postulat Euklids in Zweifel ziehen und seine Nichtgültigkeit denken?
Zur Erinnerung, das 5. Postulat Euklids lautet wie bei den meisten
in der Übersetzung von Thaer, WBG 1969, S. 3:
| "Und daß, wenn eine gerade Linie beim Schnitt mit zwei geraden Linien bewirkt, daß innen auf derselben Seite entstehende Winkel zusammen kleiner als zwei Rechte werden, dann die zwei geraden Linien bei Verlängerung ins Unendliche sich treffen auf der Seite, auf der die Winkel liegen, die zusammen kleiner als zwei Rechte sind." |
Die denkpsychologische Sperre läßt sich gut darstellen an einer Ausführung, die Dudley in seinem Buch "Mathematik zwischen Wahn und Witz" im Kapitel "Euklids fünftes Axiom" macht (der Autor interpretiert Euklids "treffen", wie gewöhnlich, mit "schneiden"):

Der gesunde Menschenverstand, unsere Gewohnheit und Intuition sagen uns, daß zwei Gerade mit einem kleineren Innenwinkel von zusammen 180% irgendwann einander treffen müssen. Und die Nichtbeweisbarkeit des Parallelenaxioms sagt uns, daß das genau nicht der Fall sein muß. Man kann es denken und so einrichten, dann entsteht die euklidische Geometrie. Und wenn man darauf verzichtet entsteht nichteuklidische Geometrie. Daß man dies denken kann, wurde durch all jene Denker bewiesen, die bewußt versucht haben, eine Geometrie aufzubauen, die eben das 5. Postulat Euklids nicht verwenden bzw. dessen Negation. Denken, das ist klar, kann man es. Aber kann man es sich auch anschaulich vorstellen?
Anschauungsargument 1: Müssen zwei geneigte Gerade im Unendlichen zusammentreffen ?

Das ist eine verblüffend einfache Veranschaulichung, die zeigt,
daß man sich in der Tat anschaulich vorstellen kann, daß sich
zwei geneigte Gerade im Unendlichen
nicht treffen müssen. Sie sind sozusagen nicht 'lang'
genug für die 'Unendlichkeit'.
Anschauungsargument 2: Müssen Fortlaufende G1, G2 immer einen Anfang oder ein Ende haben ?

Das lineare Denken [1,2,]
geht meist davon aus, daß alles einen Anfang (Ursache) und ein Ende
(Wirkung) hat. Betrachtet man sich die Welt und das Leben genauer, kann
man feststellen, daß es zu vielen Phänomenen - natürlich
nicht unbedingt allen - nicht den einen "Anfang", sondern immer noch
einen früheren gibt. "Anfang" und "Ende". Darauf beruht z.B. die philosophische
Lehre des Determinismus, des Kausalprinzips und die Verneinung der Willensfreiheit.
In dem Anschauungsbeispielzylinder schneiden sich die "Mantelgeraden",
G1 ein Kreis, G2 eine Ellipse nicht. Das Beispiel Umkreis veranschaulicht,
daß jeder Punkt als Anfang oder als Ende betrachtetet werden könnte.
Im Kreis drehen ist daher auch eine Metapher für keine Lösung
finden. In der Psychotherapie der zwischenmenschliche Konflikte macht es
oft keinen Sinn, danach zu suchen, wer "angefangen" hat, weil damit nicht
selten nur ein Spiel ohne Ende, bzw. ein Henne-Ei-Problem,
das außer ewigen Debatten und wechselseitigen Vorwürfen zu nichts
führt, in Gang gesetzt wird. Eine Schwäche dieser Überlegungen
ist, daß hier der intuitive Geradenbegriff verlassen und verallgemeinert
wird.
Stellt man sich unter "Gerade" den kürzesten
Weg auf einem Objekt relativ zu einem Bezugssystem, z.B. dem Mittelpunkt
einer Kugel, vor so schneiden sich alle 'Großkreis-Geraden' und es
gibt unendlich viele.
So viel erst mal zum Thema, wie man über das
5. Postulat hinausdenken und sich andere Möglichkeiten
vorstellen kann. Zu den verschiedenen Modellen und ihren Deutungen siehe
auch die
Newsletter-Seite
von Jutta Gut zur nichteuklidischen Geometrie. Dort werden auch weitere
Links angegeben.
Die Forschungsleistung Lobatschewskis
kann nicht hoch genug eingeschätzt werden, weil er sehr viele Widerstände,
Ablehnung, Unverständnis, Kopfschütteln bis hin zu massiven Entwertungen
aushalten mußte und ganz alleine auf sich gestellt war. Umso erstaunlicher
wirkt, wie er das alles mit stoischer Gemütsruhe und trotz beleidigender
Äußerungen mit Gelassenheit und Beherrschung - im Gegensatz
zu Janos Bolyai, dem es weitaus schlechter
ging - souverän gemeistert zu haben scheint. Er wirkt an keiner Stelle
gebrochen, tief oder nachhaltig gekränkt; er wendet sich nicht ab
und läßt sein Werk liegen, nein, er setzt es konsequent fort,
vertieft es und baut es aus. So erscheint seine Haltung eine Meisterleistung
an unbeirrbarer Souveränität, ohne Überheblichkeit, ohne
Verzweiflung, ohne Zorn, ohne Rache oder reaktiver Entwertung der Verständnislosen
oder auch Mißgünstigen.
Literatur-Auswahl von und zu Nikolai Iwanowitsch Lobatschewski
hauptsächlich den biographischen Quellen B1, B2, B3 entnommen.
- Lobatschewski, N. I. (russ. 1828). Über die Resonanz oder wechselseitige Schwingung von Luftsäulen. Kasan: Kasaner Bote. Zeitschrift.
- Lobatschewski, N. I. (russ. 1829, 1830; dt. 1898). Über die Anfangsgründe der Geometrie (russ.). Kasan: Kasaner Bote. Zeitschrift.
- Lobatschewski, N. I. (russ. 1832). Über die wichtigsten Fragen der Erziehung, Rede vom 5. Juli 1828 (russ.). Kasan: Kasaner Bote. Zeitschrift.
- Lobatschewski, N. I. (russ. 1834). Algebra oder die Rechnung mit endlichen Größen. Kasan.
- Lobatschewski, N. I. (russ. 1834). Erniedrigung des Grades einer zweigliedrigen Gleichung, wenn der um eins verminderte Grad durch acht teilbar ist. Kasan: Wissenschaftliche Schriften der Universität Kasan, Zeitschrift .
- Lobatschewski, N. I. (russ. 1834). Über die Konvergenz der trigonometrischen Reihen (russ.). Kasan: Wissenschaftliche Schriften der Universität Kasan, Zeitschrift.
- Lobatschewski, N. I. (russ. 1835). Die Bedingungsgleichungen für die Bewegung und die Lage der Hauptdrehungsachsen eines starren Systems. Moskau: Wissenschaftliche Schriften der Universität Moskau, Zeitschrift.
- Lobatschewski, N. I. (russ. 1835, fr. 1837, dt. 1904). Vorgestellte Geometrie. Kasan: Wissenschaftliche Schriften der Universität Kasan, Zeitschrift. [fr. in Grelles Journal für reine und angewandte Mathematik]
- Lobatschewski, N. I. (russ. 1835). Ein Verfahren, um sich von der Konvergenz unendlicher Reihen zu überzeugen und sich dem Werte von Funktionen sehr großer Zahlen anzunähern. Kasan: Wissenschaftliche Schriften der Universität Kasan, Zeitschrift.
- Lobatschewski, N. I. (russ. 1835, engl. 1897, dt. 1898, fr. 1900). Neue Anfangsgründe der Geometrie mit einer vollständigen Theorie der Parallellinien. Kasan: Wissenschaftliche Schriften der Universität Kasan, Zeitschrift.
- Lobatschewski, N. I. (russ. 1836). Anwendung der vorgestellten Geometrie auf einige Integrale. Kasan: Wissenschaftliche Schriften der Universität Kasan, Zeitschrift.
- Lobatschewski, N. I. (1840). Geometrische Untersuchungen zur Theorie der Parallellinien. Berlin: Funcke.
- Lobatschewski, N. I. Über die Konvergenz der unendlichen Reihen (deutsch): In: Lobatschewski, N. I. (1841). Meteorologische Beobachtungen aus dem Lehrbezirk der Kaiserlich Russischen Universität Kasan, herausgegeben von E. Knorr, Kasan
- Lobatschewski, N. I. (russ. 1842). Die totale Sonnenfinsternis in Pensa am 26. Juni 1842 (russ.). Kasan: Wissenschaftliche Schriften der Universität Kasan, Zeitschrift..
- Lobatschewski, N. I. (russ. 1845). Ausführliche Analyse der von dem Magister A. Popow zur Erlangung des Doktorgrades in der Mathematik und Astronomie vorgelegten Dissertation, betitelt: „Über die Integration der Differentialgleichungen der Hydrodynamik, wenn diese auf lineare Form gebracht sind'' (russ.). In: Anhang der Dissertation. Kasan.
- Lobatschewski, N. I. (dt. 1855, russ. 1852). Der Wert einiger bestimmter Integrale. Kasan: Wissenschaftliche Schriften der Universität Kasan, Zeitschrift. Archiv für wissenschaftliche Kunde von Rußland.
- Lobatschewski, N. I. (russ. 1855, fr. 1856, dt. 1858, ital. 1867). Pangeometrie. Kasan: Wissenschaftliche Schriften der Universität Kasan, Zeitschrift.
Werke
von Lobatschewski in deutscher Sprache
- Lobatschewski, Nikolai Iwanowitsch (dt. 1899). Zwei geometrische Abhandlungen. Aus dem Russischen übersetzt mit Anmerkungen und einer Biographie des Verfassers von F. Engel. Reihe Urkunden zur Geschichte der Nichteuklidischen Geometrie. Hrsg. von Friedrich Engel und Paul Stäckel. I. Nikolaj Iwanowitsch Lobatschewskij. Leipzig: Teubner.
- Lobatschewski, N. I. (dt. 1904, russ. 1835). Imaginäre Geometrie und Anwendung der Imaginären Geometrie auf einige Integrale. Aus dem Russischen übersetzt und mit Anmerkungen versehen vor G. Liebmann. Leipzig: .
- Lobatschewski, N. I. (dt. 1840). Geometrische Untersuchungen zur Theorie der Parallellinien. Berlin 1840: Finck' sche Buchhandlung [1887 Famsimile davon]
- Lobatschewski, N. I. (1902). Pangeometrie. Deutsch ed. von H. Liebmann, Ostwalds Klassiker der exakten Wissenschaften, Nr. 130, Leipzig
- Alexandrow, P. S. (russ. 1956). N. I. Lobatschewski — ein großer russischer Mathematiker. Moskau:
- Autorenkollektiv (1989). Nikolai Iwanowitsch Lobatschewski. In: Wußing, Hans & Arnold, Wolfgang (1989, Hrsg.), 345-357. [B3]
- Engel, F. (1899). Biographie Lobatschewskis. In: Lobatschewski (dt. 1899). Zwei geometrische Abhandlungen.
- Engel, F. & Stäckel, P. (1898, Hrsg.). Nikolai Iwanowitsch Lobatschewski. In: Urkunden zur Geschichte der nichteuklidischen Geometrie, Bd. 1. Leipzig 1898.
- Halameisär, Alexander & Seibt, Helmut (1978). Nikolai Iwanowitsch Lobatschewski. Biographien hervorragender Naturwissenschaftler, Techniker und Mediziner. Bd. 34. Leipzig: Teubner. [B1]
- Istoriko - mathematiceskie issledovanija, Bd. IX. (1956). (Sammelband von Arbeiten über Leben und Wirken von N. I. Lobatschewski). Moskva 1956.
- Kagan, W. F. (russ. 1944). Nikolai Iwanowitsch Lobatschewski (russ.). Moskau:
- Laptew, B. L. (russ. 1976). Nikolai Iwanowitsch Lobatschewski. Kasan:
- Meschkowski, Herbert (1990). Bolyai und Lobatschweski: Nichteuklidische Geometrie. In (S. 133 - 147): Die Denkweisen großer Mathematiker. Braunschweig: Vieweg. [B2]
- Modsalevskij, L. B. (russ. 1948). Materialy k biografii N. I. Lobacevskogo. [Materialien für die Biographie von N. I. Lobatschewski.]. Moskva-Leningrad 1948.
- Sagoskin, N. P. (russ. 1902-1904). Geschichte der Kasaner Universität von 1804 bis 1904. 4 Bände. Kasan 1902-1904.
- Wußing, Hans & Arnold, Wolfgang (1989, Hrsg.). Biographien bedeutender Mathematiker. Eine Sammlung von Biographien. Darmstadt: WBG. [B3]
Geschichte
des Parallelen-Postulats und der nichteuklidischen Geometrie
- Bonola, R.: Die nichteuklidische Geometrie. Historisch-kritische Darstellung ihrer Entwicklung. Bearbeitet von H. Liebmann, 2. Auflage, Leipzig/Berlin 1919.
- Engel & Stäckel > Stäckel
- Engel, Friedrich & Stäckel, Paul (1899, Hrsg.). Urkunden zur Geschichte der Nichteuklidischen Geometrie. I. Nikolaj Iwanowitsch Lobatschewskij. Leipzig: Teubner. [= Lobatschewski, Nikolai Iwanowitsch (dt. 1899). Zwei geometrische Abhandlungen. 2 Tle. ]
- Gauß, C. F.: Werke, 12 Bände. Leipzig, Berlin, usw. 1863 bis 1933.
- Klügel, Georg S. (1763). Conatuum praecipuorum theoriam parallelarum demonstrandi recensio. [deutsch; URL verändert] Dissertation Göttingen.
- Klein, Felix (1928; Nachdruck 1968). Die Geschichte der nichteuklidischen Geometrie ; Beziehungen zur Axiomatik und zur Differentialgeometrie. In (S. 271-306): Vorlesungen über Nicht-Euklidische Geometrie. Reihe: Die Grundlehren der mathematischen Wissenschaften in Einzeldarstellungen, Bd. 26. Berlin: Springer.
- Kolman, E.: Velikii russkii myslitel' N. I. Lobacevskij. 2. Auflage, Moskva 1956.
- Lobacevskij, N. I.: Tri cocinenija geometrii. Ed. P. L Norden und V. F. Kagan, Moskva 1956.
- Reichardt, H.: Gauß und die Anfänge der nichteuklidischen Geometrie. Mit Originalarbeiten von J. Bolyai, N. I. Lobatschewski und F. Klein. Leipzig 1985.
- Stäckel, P. / Engel, F.: Die Theorie der Parallellinien von Euklid bis auf Gauß, eine Urkundensammlung zur Vorgeschichte der nichteuklidischen Geometrie. Herausgegeben von P. Stäckel. Leipzig 1895. [siehe auch: Engel]
Hierzu Meschkowski [B2, S. 133]: "l Die Dissertation von Klügel. Im Jahre 1763 legte der Göttinger Mathematiker Abraham Kästner (1719-1800) seiner Fakultät eine Dissertation {XIII 1] seines Schülers Georg Klügel (1739-1812) vor, in der er die wichtigsten Beweisversuche für das Euklidische Parallelenpostulat (Kap. II) kritisch untersucht hatte. Er kam zu dem Ergebnis, daß alle 28 Versuche unzulänglich waren. Es ist schon im Kap. II gesagt worden, daß viele Mathematiker meinten, das Parallelenpostulat sei überflüssig; es müsse beweisbar sein, da seine Umkehrung aus den übrigen Postulaten und Axiomen Euklids hergeleitet werden könne. Und man war gewöhnt, daß man in der Geometrie bei Vertauschung von Voraussetzung und Behauptung immer wieder zu einer richtigen Aussage kommt."
Einführungen
in die nichteuklidische Geometrie von Lobatschewski (Auswahl)
- Buchmann, G. (1975). Nichteuklidische Elementargeometrie. Reihe Mathematik Lehrerausbildung. Stuttgart: Teubner.
- Filler, A. (1993). Euklidische und nichteuklidische Geometrie. Mathematische Texte Band 7. Mannheim: BI.
Links (Auswahl: beachte) der verschiedenen Geometrien und ihrer Bezeichnungen
- Anwendungen nichteuklidische Geometrie: [1,2,3,4,] Aus [1].
- Google: Lobatschewski, Lobatschewski +Biographie, Lobatschewski +Leben, Lobatschewski +Nichteuklidische Geometrie.
- Cinderella Geometrieprogramm (euklidisch und nichteuklidisch): https://cinderella.de/tiki-index.php.
- Allgemeine Geometrie: [1, Filler; URL verändert]
- Minkowski Diagramme (Gauss-Lobatschewski-Geometrie: URL verändert).
- Nichteuklidische Geometrieseite von Jutta Gut.
- Geschichte des Parallelenproblems [URL verändert] von Klaus Volkert (Vorlesung, gehalten an der Universität Frankfurt im WS 02/03)
- Querverweis: Mathematikgeschichte-Links.
- Digitale Mathematik Bibliothek: https://www.mathematik.uni-bielefeld.de/~rehmann/DML/dml_links_title_Z.html.
- Digitalisierungszentrum Göttingen: https://gdz.sub.uni-goettingen.de/en/index.html. [URLs verändert]
- Hilbert (1892): Über die gerade Linie als kürzeste Verbindung zweier Punkte.
- Hilbert (1899): Neue Begründung der Bolyai-Lobatschefskyschen Geometrie.
- Hilbert (1901): Ueber die Grundlagen der Geometrie.
- Hilbert (1909): Ueber die Grundlagen der Geometrie.
- Hilbert (1932): Über anschauliche Geometrie.
- Mathematiker Biographien: [1,2,3,]
- Geschichte der russischen Akademie der Wissenschaften.
- Geschichte Rußlands [1,2,3,]
- Geschichte Kasans [Wikipedia, 2, 3,]

Die verschiedenen
Geometrien und ihre unterschiedlichen Bezeichnungen
Absolute Geometrie (Bolyai, Lobatschewski,
B1-S.28,) * Allgemeine Geometrie (B1-S.38) * Analytische Geometrie
* Antieuklidische Geometrie (Gauß)
* Astralgeometrie (Schweikart)
* Darstellende Geometrie * Differentialgeometrie [1,2,3,]
* Elliptische Geometrie (Riemann)
[1, 2,
3,]. * Euklidische Geometrie (Euklid,
Hilbert)
* Geometrie (allgemeine) * Grundlagen der Geometrie (Hilbert)
* Hyperbolische Geometrie [1,
2, 3,] * Imaginäre Geometrie (Lobatschewski) * Nichteuklidische Geometrie
[1,
2, 3,] * Projektive Geometrie * Pangeometrie (Lobatschewski) * Sphärische
Trigonometrie (Geometrie der Kugeloberfläche) * Vorgestellte Geometrie
(Lobatschewski) *
Zusammenhänge
in der Mathematik und ihrer Teilgebiete
Im dtv-Atlas Mathematik (1974 ff) wird im ersten Bd.
folgende systematische Übersicht und der Zusammenhänge gegeben:
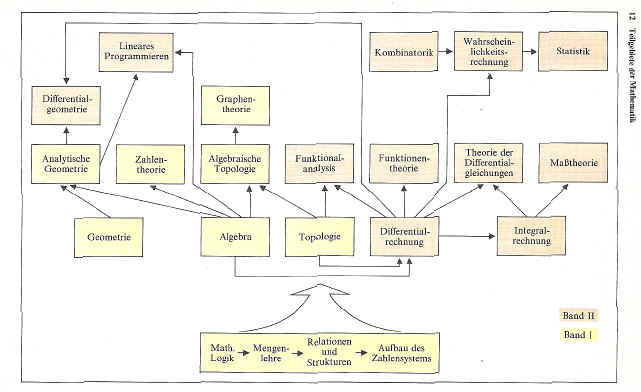
Anmerkungen und Endnoten:
1) GIPT= General and Integrative Psychotherapy, internationale Bezeichnung für Allgemeine und Integrative Psychotherapie.
___
Die folgenden Anmerkungen sind der leichteren Auffindbarkeit halber alphabetisch geordnet:
___
Adjunkte: In unserem Zusammenhang eine Bezeichnung für einen Dozenten im russischen Universitätswesen. [sonst: W]
___
Anwendungen nichteuklidischer Geometrie.
[1] Konforme Abbildungen und nichteuklidische Geometrie:
- "Da die Begriffe des Kurstitels in der Regel in der Schulmathematik
nicht vorkommen, zunächst einige Erläuterungen. Konforme Abbildungen
sind Abbildungen eines Teilgebiets der komplexen Ebene auf ein anderes
Teilgebiet derselben, die in gewissem Sinne winkelerhaltend sind; winkelerhaltend
bedeutet in diesem Zusammenhang, dass der Winkel zweier sich schneidender
Kurven im Ausgangsgebiet gleich dem Winkel der Bildkurven ist. In dem Kursabschnitt
über konforme Abbildungen sollen zumindest Teilantworten zu den folgenden
beiden essentiellen Fragen gegeben werden: Welche Gebiete können überhaupt
konform aufeinander abgebildet werden - z.B.: Halbebene-Kreis, Polygon-Kreis,
Mandelbrotmenge-Kreis, etc.? Kann man diese konformen Abbildungsfunktionen
- evtl. nur bei speziellen Gebieten - bestimmen? Unter nichteuklidischen
Geometrien versteht man, grob gesprochen, die Geometrien, die sich ergeben,
falls man das sogenannte Parallelenaxiom fallen lässt. Das Parallelenaxiom
besagt, dass es zu einer gegebenen Gerade und einem beliebigen Punkt außerhalb
der Geraden genau eine Gerade gibt, die diesen Punkt enthält und zur
gegebenen Gerade parallel liegt. Bei vergleichbar kleinen Abständen
sind euklidische und nichteuklidische Geometrien im wesentlichen äquivalent.
Hat man es jedoch mit Abständen im Weltraum oder mit Problemen der
modernen Physik wie der Relativitätstheorie zu tun, beschreiben die
nichteuklidischen Geometrien die beobachteten Phänomene meist genauer
als die euklidische."
- "Kugelzweieck
und Kugeldreieck
finden Aufmerksamkeit (Nepersche Regel) und es ergibt sich die Möglichkeit,
erste Anwendungen zu besprechen, z.B. die Untersuchung räumlicher
Kristalle ohne Verwendung der Vektorrechnung. Es schließen sich die
Sätze zur Berechnung allgemeiner, schiefwinkliger Kugeldreiecke an.
Ein Vergleich mit der Trigonometrie ebener Dreiecke soll diesen Teil abrunden.
Ein Schwerpunkt des Kurses wird die Anwendung auf Probleme der Geographie
und der Astronomie sein, wobei aufgrund der Vielfalt hier nur einige von
den Teilnehmenden untersucht werden können, beispielsweise im Flugwesen
bzw. der Schifffahrt (kürzeste Entfernung zwischen zwei Orten, Kurswinkel
und Loxodrome, Prinzip der Funkortung). Dabei muss man verschiedene Kartenentwürfe
der Erdkugel diskutieren. Eine besondere Bedeutung kommt dem Mercator-Entwurf
zu, die Ursache hierfür kann mit Hilfe des vermittelten Stoffes geklärt
werden. Im Bereich der Astronomie geht es hauptsächlich um das Kennenlernen
verschiedener Koordinatensysteme zur Orientierung an der Himmelskugel,
welche z.B. zur Berechnung des Auf- und Untergangs von Gestirnen dienen."
- "Die Kategorisierung von Objekten bis zur Basisebene
...
Die zentrale Hypothese des zweiten Kapitels lautet, dass die Kategorisierung von Objekten bis zur Basisebene ebenfalls transformational erklärt werden kann - und zwar einfach durch eine Erweiterung der zulässigen Transformationen auf nicht-Euklidische und insbesondere topologische (d.h. raumkrümmende) Transformationen. Topologische Transformationen lassen sich auf einfache Weise durch die Metapher eines Gummituchs veranschaulichen: Wenn man das Bild eines Schäferhundes auf ein Gummituch malt, dann kann durch ein Verformen des Gummituchs die Form des Schäferhundes in die Form eines anderen Hundes, wie z.B. eines Boxers transformiert werden. Nach dem transformationalen Modell erfolgt die Kategorisierung durch eine verformende Transformation der Kategorierepräsentation. Das Erkennen nach räumlichen Transformationen und das Kategorisieren von Objekten erfolgen somit auf Basis der gleichen Verarbeitungsprinzipien - nur die zugrundeliegenden Transformationen unterscheiden sich. Die verschiedenen Transformationen, die beim Erkennen und Kategorisieren eines Objekts eine Rolle spielen können, lassen sich anhand der Hierarchie geometrischer Transformationen klassifizieren, die Felix Klein im Jahr 1872 in seinem Erlanger Programm spezifiziert hat.
Es wird somit die Hypothese formuliert, dass die Kategorisierung von Objekten durch topologische Transformationen erfolgt. In Anlehnung an die im ersten Kapitel dargestellten Befunde wird postuliert, dass es sich - wie bei den Rotationen, Größenskalierungen und Translationen - auch bei den topologischen Transformationen um zweikonsumierende, fehleranfällige und analoge Transformationsprozesse handelt.
Dieses Modell kann nicht nur die Leistung beim Kategorisieren von Objekten erklären, sondern bietet auch einen Erklärungsansatz für die Ähnlichkeit von Formen. Nach dem vorliegenden Modell nimmt die Ähnlichkeit von Formen ab mit zunehmendem Umfang topologischer Transformation, die für eine räumliche Ausrichtung erforderlich ist."
Bartels, Johann Christian Martin (1769 — 1836)
Halameisär, Alexander & Seibt, Helmut (1978, S. 83) würdigen Bartels: "Sohn eines Zinngießers. Seit seiner Kindheit interessierte er sich für Mathematik. Als Gehilfe des Lehrers Büttner wurde er mit dem jungen Gauß bekannt und freundete sich mit diesem, trotz des Altersunterschiedes von 8 Jahren, durch gemeinsame Begeisterung für die Wissenschaft an. Bei Pfaff und Kästner hatte er gründliche mathematische Kenntnisse erworben. Von 1794 bis 1804 arbeitete er als Lehrer in der Schweiz. An der Universität Jena promovierte er zum Doktor der Philosophie.
Rumonowski berief Bartels nach Kasan, wo dieser an der Universität den Lehrstuhl für reine Mathematik bekam und bald Dekan der Physikalisch-Mathematischen Fakultät wurde. Bartels erkannte früh die große Begabung Lobatschewskis und nahm großen Einfluß auf dessen Entwicklung. Er setzte sich auch (gemeinsam mit Littrow) später dafür ein, daß Lobatschewski nicht als "Freidenker" die Universität verlassen mußte und zum Militär eingezogen wurde. Die Überlegungen von Lobatschewski zur nichteuklidischen Geometrie verstand Bartels nicht. Die Tätigkeit von Bartels an der Kasaner Universität führte zu einer bedeutenden Niveauerhöhung der dortigen mathematischen Ausbildung. Im Jahre 1820 folgte er einer Berufung an die Universität Dorpat." [1,2,3,]
___
Beltrami, Eugenio (1835-1900)
Halameisär, Alexander & Seibt, Helmut (1978, S. 83) würdigen Beltrami: "Italienischer Geometer, Professor an den Universitäten Bologna, Pavia und Rom. Beschäftigte sich mit Differentialgeometrie und entwickelte Gedanken von Gauß weiter. Im Zusammenhang mit kartographischen Aufgaben untersuchte er Flächen mit konstanter Krümmung, insbesondere die Pseudosphäre. Seine Arbeit "Versuch einer Interpretation der nichteuklidischen Geometrie" (1868) war bahnbrechend für die Anerkennung dieser Geometrie." [Anschauung, Wikipedia.en, ]
___
Bolyai (1802-1860)
Halameisär, Alexander & Seibt, Helmut (1978, S. 83) schreiben zu ihm: "Ungarischer Mathematiker. Sohn des Mathematikprofessors Farkas Bolyai. Bereits als Student der Militäringenieurakademie interessierte er sich für das 5. Postulat von Euklid. Nachdem er die Akademie absolviert hatte, schuf er die Grundlagen der nichteuklidischen Geometrie (1825), arbeitete weitere 6 Jahre daran und veröffentlichte seine Ergebnisse schließlich lediglich in einer Anlage zu einem Werk seines Vaters (Appendix, 1832). Im Jahre 1837 stellte er in Leipzig eine Arbeit vor, die die Schaffung der Quaternionen vorwegnahm, deren Theorie später von dem irischen Mathematiker W. R. Hamilton ausgearbeitet wurde. Beide Entdeckungen erhielten jedoch zu Lebzeiten Bolyais keine Anerkennung. Nachdem im Jahre 1840 Arbeiten von Lobatschewski in deutscher Sprache erschienen waren, meinte Bolyai, daß Gauß - unter Benutzung der Ideen und Methoden Bolyais - diese Arbeit unter fremdem Namen veröffentlicht hätte."
Anmerkung: Bolyai war psychisch krank (schizophren) - seine Mutter erkrankte psychotisch als er das Elternhaus verläßt und zur technischen Militärakademie (Genieakademie) nach Wien geht - und ist daher besonders schwierig zu beurteilen. An dieser Stelle erscheint daher auch der Hinweis angebracht, daß viele Menschen im Laufe ihres Lebens erkranken - auch psychisch - und Krisen durchmachen. In der Mathematik wie in der Wissenschaft überhaupt kommt es aber nicht darauf an, welche oder eine wie gestörte Persönlichkeit - zumal sich dies ja meist nur zeitweise und in begrenzten Bereichen entfaltet - diese oder jene Idee hat, sondern die Idee alleine ist von wissenschaftlicher Bedeutung (oder auch nicht). Ob eine Beweisidee also z.B. aus einer Schizophrenie, einer Eingebung Gottes, durch induzierte Drogenwirkung oder Plagiat zustande kommt, ist für die Stimmigkeit oder Nützlichkeit einer wissenschaftlichen Idee oder Beweisführung unerheblich: richtig sein muß sie, sonst nichts. Die Entwicklung seiner absoluten Geometrie ist wahrscheinlich auch unabhängig von seiner späteren, manifesten Erkrankung, nicht aber seine paranoid anmutende Verarbeitung, daß Gauß seine Idee Lobatschewski gesteckt haben könnte. Aber wie so oft bei den Paranoiden, sie argwöhnen vielfach auch zu Recht, womit ihr System auch 'objektive' Stützung erfährt. Und Gauß hat sich in der Tat merkwürdig verhalten, so daß bei Bolyai auf tragische Weise mehrere Faktoren zusammenkommen: die Einsamkeit und Verkennung seines Genies, das merkwürdige Verhalten von Gauß, die annähernd simultane Entwicklung bei Lobatschewski und die spätere geistige Erkrankung. [1,2,3,]
Bolyais Bild auf der Briefmarke.
 |
Meschkowski (1990, S. 139f) berichtet:
"3 Das Bild auf der Briefmarke
|
 |
| Dies ist sein Bericht (Brief vom 5.5.1972):
'Die Vorlage für die Marke war ein größeres Bild, das aus dem Besitz einer Budapester Mittelschule (Berzsényi Dániel Gymnasium) stammt und von dem Direktor dieser Schule vor etwa 15 bis 20 Jahren der ungarischen mathematischen Gesellschaft (Bolyai János Matematikai Társulat) übergeben wurde. So glaubte man zunächst, daß es tatsächlich ein Portrait von Johann Bolyai war, spätere Nachforschungen im Archiv dieser Mittelschule ergaben jedoch keinerlei Anhaltspunkte für diese Vermutung. Hingegen wurden Aufzeichnungen von Johann Bolyai aufgefunden, aus denen hervorgeht, daß es von ihm tatsächlich 2 Bilder gegeben hat. Das eine war ein großes Bild im Besitz seines Vaters, Wolfgang Bolyai, dieses hat Johann Bolyai selbst, anläßlich eines Streites mit seinem Vater vernichtet. Das zweite Bild war eine Miniatur im Besitze von Johann Bolyai. Mit dieser haben Kinder solange gespielt bis die Farbe abgewetzt war, und es wurde dann weggeworfen. Johann Bolyai sagt dann noch, daß es von ihm kein Bild gibt, und fügt noch hinzu, daß das gar nicht wichtig wäre, da man ja nicht auf diese Weise das Andenken verewigen soll.' Diese Information habe ich von einem ungarischen Mathematiker erhalten, der eine Biographie (in ungarischer Sprache) von Johann Bolyai geschrieben hat und diesen Dingen sehr gründlich nachgehen mußte. Dieser Bericht macht noch einmal deutlich, welche bitteren menschlichen Konsequenzen das harte Ringen um die wissenschaftliche Wahrheit hatte. Wir wissen, daß das Verhältnis zwischen Vater und Sohn zunächst ausgezeichnet war. Es gab herzliche Partnerschaft der Forschung, und (wir erwähnten es schon) Johann schätzte die wissenschaftliche Qualifikation seines Vaters höher ein als die Gaußens. In der Anspannung der späteren Jahre, in der Enttäuschung über die ausbleibende Anerkennung wurde das anders. Es dürften auch vermögensrechtliche Auseinandersetzungen dabei eine Rolle gespielt haben, als es zum Bruch zwischen Vater und Sohn kam. Johann von Bolyai ist zwar nicht in Vergessenheit geraten, aber ein Bild von ihm haben wir nicht. Es bleibt noch die Frage: Wer ist der junge Mann auf der Briefmarke? Wer mußte seinen Kopf dazu hergeben, um den Begründer der nichteuklidischen Geometrie zu ehren? ..." |
Braschman, Nikolai Dmitriewitsch (1796 — 1866)
Die Biographen Halameisär, Alexander & Seibt, Helmut (1978, S. 84) berichten: "Adjunkt an der Kasaner Universität (seit 1825), Professor an der Moskauer Universität (seit 1834), korrespondierendes Mitglied der Akademie der Wissenschaften (seit 1855). Er gehörte zu der Kommission, die mit der Einschätzung und Beurteilung der Entdeckung Lobatschewskis beauftragt worden war (1826), die aber kein Gutachten zustande brachte. Braschman ist Mitgründer der Moskauer Mathematischen Gesellschaft." Er war außerdem Lehrer von Tschebyschew. In den Biographien bedeutender Mathematiker (B3, S. 412) wird er als hervorragender Lehrer bezeichnet.
___
Bulitsch, Nikolai Nikititsch (1824 -1895)
Halameisär, Alexander & Seibt, Helmut (1978, S. 84) charakterisieren wie folgt: "Professor für russische Sprachen an der Universität Kasan, Wissenschaftshistoriker, Rektor der Kasaner Universität (1862—1864). In seiner Rede am Grabe Lobatschewskis rief er u. a. zu einer kritischen Haltung gegenüber der Regierung auf. Gegen ihn wurde Anklage wegen politischer Unzuverlässigkeit und Gottlosigkeit erhoben. Der heraufziehende Skandal konnte vertuscht werden. Im Jahre 1860 wurde er wegen „schädlicher Gedanken in den Vorlesungen" von der Lehrtätigkeit an der Universität suspendiert. Ein Jahr später durfte er wieder als Professor arbeiten." [1,2,3,]
___
Cholera-Epidemie in Kasan 1830. Der von Lobatschewski ausgearbeitete Plan zur Bekämpfung der Cholera fand beim Gouverneur kein Gehör, aber der Rat der Universität befolgte den Plan. Sämtliche zur Universität gehörenden Personen begaben sich in die über die Universität verhängte Quarantäne, insgesamt 560 Personen. Die Biographen [B1, S. 46] berichten: "Trotz aller getroffenen Vorsichtsmaßnahmen erkrankten und starben in den ersten vier Tagen zwölf Menschen. Auf Weisung des Rektors wurden die Leichen der Verstorbenen mit Chlorkalk übergossen und die Kleidung, das Bett und andere persönliche Sachen unverzüglich verbrannt. Am fünften Tag hörten die Erkrankungen auf. Das Beschaffen und das Chloren des Wassers beaufsichtigte Lobatschewski selbst. Obwohl die Cholera in der Stadt fast die Hälfte der Bevölkerung dahinraffte, gab es unter den 560 Menschen, die auf dem Territorium der Universität lebten, nur insgesamt 40 Cholerafälle, von denen insgesamt 16 tödlich verliefen. Die Vorlesungen konnten erst Ende November wieder aufgenommen werden. In der Presse erschien die folgende Notiz: 'Dem Herrn Rektor der Universität wurde für den gezeigten Eifer beim Schutz vor der Cholera das allerhöchste Wohlwollen Seiner Kaiserlichen Hoheit übermittelt.'" [1,2,3,]
___
Cranks. [,crank.net ,Dunham, Poessel [URL verändert], Dudley: Was sind Mathematik Cranks?,]
Literatur: Dudley, Underwood (dt. 1995, engl. 1993). Euklids fünftes Axiom. In (S. 98-121): Mathematik zwischen Wahn und Witz : Trugschlüsse, falsche Beweise und die Bedeutung der Zahl 57 für die amerikanische Geschichte / Underwood Dudley. Aus dem Amerikan. von Gisela Menzel. Basel: Birkhäuser.
Was sind Mathematik-Cranks ? "Handelt dieses Buch also von Spinnern? Keineswegs. Weder Kreisquadrierer, Winkeldreiteiler oder Fermatisten noch andere Amateurmathematiker, die sich großen ungelösten Problemen widmen, sind Spinner. Die meisten werden einfach von der Lust am Knobeln, vom mathematischen Erkenntnisdrang, manche auch vom Ehrgeiz angetrieben. Einige sind zwar komische Käuze, aber die meisten sind nicht verrückt. Viele sind Amateure - mathematische Amateure, die sich zwangsläufig nicht so gut in der Mathematik auskennen wie studierte Mathematiker. Wenn man sie nicht davon überzeugen kann, daß sie nicht das geleistet (d. h. bewiesen) haben, was sie glauben, werden die Eifrigen unter ihnen manchmal wunderlich. Wunderliche Leute sind aber keine Spinner, sie sind nur in einigen Bereichen blind. Ferner findet sich in diesem Buch vieles, was weder von Spinnern noch von wunderlichen Käuzen handelt. So gibt es ernsthafte Verfechter der Idee, die Zehn sei nicht die beste Basis für unser Zahlensystem. Und sie haben recht. Da wir aber niemals die Basis ändern werden, hält man es für exzentrisch, sich damit zu beschäftigen. Ich berichte auch von einem Priester, der mit Hilfe von Matrizen betet. Das mag zwar etwas ungewöhnlich sein, ist aber keineswegs verrückt. Wenn Sie diesen Zeitgenossen auf der Straße begegnen, werden Sie nichts Auffälliges bemerken.
Das Buch handelt also von Amateurmathematikern, wunderlichen Käuzen und Exzentrikern - doch es beschäftigt sich vor allem mit dem, was sie hervorgebracht haben. Und das sind die verschiedenartigsten Dinge. Es schildert, wie es ein Collegepräsident geschafft hat, Euklids fünftes Axiom zu beweisen, wie jemand den Umfang einer Ellipse ohne Verwendung von elliptischen Integralen gefunden hat, und wie jemand gezeigt hat, daß man eine Landkarte mit lediglich zwei Farben einfärben kann. Wenn Sie mit Hilfe eines Lineals, auf dem zwei Markierungen angebracht sind, einen Winkel dreiteilen oder einen Würfel verdoppeln möchten, können Sie in diesem Buch nachlesen, wie man dies bewerkstelligt. Interessieren Sie sich ein wenig für die Geschichte der Quadratur des Kreises, für eine Lösung dieses Problems mittels der Quadratrix des Hippias und ähnliche Dinge, so gönnen Sie sich ein paar unterhaltsame Stunden mit der Lektüre dieses Buches.
Denn: Ausgefallene Ideen und wunderliche Leute sind immer interessant. Man kann nie sicher sein, daß es einen nicht selbst trifft." (S.7/8).
___
Denken. In der allgemeinen und integrativen Psychotherapie charakterisieren wir: Denken nennen wir die Sprache des Geistes. Denken "ist" nicht sprechen und sprechen "ist" nicht denken. yDenken bedeutet geistige Modelle bilden und / oder zueinander in Beziehung setzen. Denken kann in oder mit einer Sprache kommuniziert werden. Denken und Sprechen. Definition: Denken und Sprechen sind zwei verschiedene psychologische Grundfunktionen. Denken ist eine notwendige, aber nicht hinreichende Bedingung für die Fähigkeit kommunikativ zu sprechen. Axiom: Denken ist grundsätzlich unabhängig von der Fähigkeit zu sprechen (es sei denn, man definiert Denken als Sprache des Geistes). Wollte man das Axiom beweisen und damit aus ihm einen Satz machen, würde man für die Versuche irgendeine Art der Sprache anwenden müssen und damit in einem logischen Zirkel landen - daher das Axiom. Taubstumme und oder Sprachzentrumgeschädigte können nicht sprechen, Mutisten (Schweiger) können es psychisch bedingt (elektiv oder selektiv teilweise) nicht. Daraus kann man natürlich nicht schließen, daß Taubstumme, Sprachzentrumsgeschädigte oder Mutisten nicht denken können. Man muß denken und sprechen genauso sorgfältig auseinanderhalten wie Intelligenz und Bildung. Es gibt viele intelligente, ja auch hochintelligente Ungebildete und es gibt nicht wenige Gebildete, deren Intelligenz guten Durchschnitt kaum überragt. Vom Denken, das auch abstrakt erfolgen kann (nicht muß), ist das Vorstellen oder auch das Phantasieren zu unterscheiden.
___
Denkpsychologie ... noch existiert. Mit der Amerikanisierung der Psychologie geht nicht nur ein allgemeiner Niedergang der klassischen Psychologie (bis etwa 1933) einher, sondern es scheint im Zuge der Kognitionswissenschaft und der Entwicklung der Neuroscience die Denkpsychologie in besonderem Maße vom Verschwinden (in die Bedeutungslosigkeit) bedroht zu sein.
___
Dorpat. Heute Tartu, zweitgrößte Stadt Estlands.
___
Engel (1899, S. 352) schreibt hingegen zur Bildung von Lobatschewskis Mutter: "Sehr bald nach der Eröffnung der Universität fragte man bei den Aeltern der Schüler des Gymnasiums an, ob sie bereit wären, ihre Söhne nach Beendigung des Gymnasialkurses in die Universität eintreten zu lassen; diese sollten da auf Staatskosten unterhalten werden, wenn sie sich verpflichteten, nachher sechs Jahre lang der Universität zu dienen. Unter denen, die auf dieses Anerbieten eingingen, war auch Lobatsecefskijs Mutter und zwar hatte sie ihr Antwortschreiben eigenhändig geschrieben, was als Beweis einer bei Frauen ihres Standes ungewöhnlichen Bildung gelten muss."
___
Euklid: Zur Geschichte und den Übersetzungen: [,Euklid im Mittelalter,] [Leben: Wikipedia,] [Zum Axiom Euklid 8: Das Ganze ist größer als der Teil]
___
Euler, Leonhard (1707 - 1783)
[ergänzern]
___
Fuchs, Karl (1776-1846)
Halameisär, Alexander & Seibt, Helmut (1978, S.85): "Absolvent der Universität Göttingen, promovierte in Marburg zum Doktor der Medizin (1798). Im Jahre 1800 siedelte er nach Petersburg über, wo er als praktischer Arzt tätig war. 1805 kam er nach Kasan und wurde Professor an der dortigen Universität, an der er als Arzt, als Dekan der Medizinischen Fakultät (1820—1823) und als Rektor (1823-1827) tätig war. Neben seiner wissenschaftlichen Arbeit an der Universität war Fuchs in Kasan auch als praktischer Arzt tätig und verfaßte eine Reihe von Arbeiten zur Geschichte, zur Etnographie, zur Statistik und zu ökonomischen Problemen Kasans und des Wolgagebiets. Sein Haus war ein Zentrum des kulturellen Lebens der Stadt." [1,2,3,]
___
Fuß, Nikolaus (1755 - 1826).
Nikolaus von Fuss 30.1.1755 - 23.12. 1825. 1773 - 1782 Sekretär von Leonhard Euler in Petersburg. 1776 Adjunkt. 1783 Ordentlicher Akademiker der Akademie der Wissenschaften in Petersburg. Professor für Mathematik am Adligen Landkadettenkorps 1790 Professor für Mathematik am Marinekorps in Petersburg. 1800 Beständiger Sekretär der Akademie der Wissenschaften in Petersburg. 1806 Wirklicher Staatsrat. Fuß verriß Lobatschewskis erstes Lehrbuch zur Geometrie. Möglicherweise wurde damals bereits ein negatives Vorurteil gegenüber Lobatschewski aufgebaut, das später seine Fortsetzung und Festigung durch Ostrogradski fand [Biographische Daten nach Quelle]
___
Gauß, Carl Friedrich (1777-1855)
Halameisär, Alexander & Seibt, Helmut (1978, S. 85) würdigen Gauß wie folgt: "Deutscher Mathematiker, studierte an der Universität Göttingen (1795 bis 1798). War Direktor der Sternwarte der Göttinger Universität (seit 1807 bis an sein Lebensende). Wegen seiner fundamentalen Arbeiten auf verschiedenen mathematischen Gebieten, in der Physik und in der Astronomie bezeichnete man ihn als den "Fürst der Mathematiker". Da er sich für Lobatschewskis Arbeiten interessierte, begann er im Alter von 63 Jahren die russische Sprache zu erlernen. Obwohl Lobatschewski auf Vorschlag von Gauß zum korrespondierenden Mitglied der Königlichen Wissenschaftlichen Gesellschaft in Göttingen gewählt wurde, konnte sich Gauß zu einer öffentlichen Anerkennung der Entdeckung von Lobatschewski in seinen Arbeiten nicht entschließen."
Engel & Stäckel (1895, S. 216) schätzen die Leistung von Gauß sehr hoch ein und kommen zu dem Ergebnis, "daß Gauß damals im Besitze einer weit ausgebildeten nicht-euklidischen Geometrie war", obwohl von Gauß - verglichen mit den Ausarbeitungen von Bolyai und Lobatschewski - nur spärliche Dokumente vorliegen.
Die Leistungen von Gauß werden von Felix Klein in seinen Vorlesungen über nicht-euklidische Geometrie (1927), S. 276, wie folgt zusammengefaßt (2. Absatz, ab Zeile 7):

Gauß würdigt
Lobatschewskis Arbeit als meisterhafte Leistung: In einem
Brief
von 1846 an Schumacher - im 5. Band des Briefwechsels - erwähnt
Gauß namentlich Lobatschewskis Geometrische Untersuchungen zur Theorie
der Parallellinien, die 1840 auf deutsch erschienen, und würdigt sie
als "meisterhafte Leistung" (nach Engel & Stäckel, 1895, S. 216).
Siehe auch: Gauß
an Taurinus am 8.11.1824. Und:
Brief
Nr. 396 von Gauss an Schumacher am 12.7.1831 zum Thema nichteuklidische
Geometrie mit einer Bewertung zum Unendlichen in der Mathematik.
Zu Gauss und Taurinus: https://www.ub.uni-heidelberg.de/helios/fachinfo/www/math/gif/taurinus-gauss.htm.
___
Geburtsstunde
der nichteuklidischen Geometrie. Meschkowski mutmaßt (B3, S.
354) "Uns fehlen Mitteilungen darüber, wie Lobatschewskis Vortrag
am 24. Februar 1826 von seinen Kollegen aufgenommen wurde, wir können
aber aus der Tatsache, daß die vorgelegte Arbeit nicht gedruckt wurde,
schlußfolgern, daß sie nicht die volle Anerkennung fand," was
möglicherweise zu weit geht. Eigentlich wissen wir nur sicher, daß
die Kollegenschaft Lobatschewskis Ideen nicht verstanden. Infolgedessen
war es folgerichtig, daß sich die um ein Urteil gebetenen Gutachter
der Universität eines ebensolchen enthielten. [1,2,3,]
___
Geschrei der Böotier (berühmter
und vielfach zitierter Ausspruch Gaußens 1829 in einem Brief an seinen
Freund F. W. Bessel).
"Böotier", Bewohner einer ebenso genannten Landschaft in Mittelgriechenland,
von Gauß metaphorisch für ungebildete Proleten und Dummköpfe
verwendet, was rein sachlich falsch ist: " Den Böotern wurden von
anderen Griechen Plumpheit und Unbildung nachgesagt. Dabei haben sie mit
HESIOD einen der größten Dichter, auch PINDAR und PLUTARCH stammten
hierher, HOMER erwähnt 29 böotische Staaten, die am Krieg gegen
Troja teilnahmen (Illias 2.494ff.)." [Quelle: URL verändert]. Siehe
auch Schlacht
von Delion und Böotien.
Zum 140 Geburtstag von Gauß heißt es
in [1]
euphemistisch-falsch und tendenziös: "Tatsächlich waren seine
mathematischen Neuentdeckungen mitunter so kühn, daß er diese
der Öffentlichkeit gar nicht mitzuteilen wagte, weil er das "Geschrei
der Böotier" fürchtete (wie es 1829 in einem Brief an seinen
Freund F. W. Bessel heißt); so mußte er es beispielsweise erleben,
daß ihm N. I. Lobatschewskij und J. Bólyai mit der Veröffentlichung
der Nichteuklidischen Geometrie zuvorkamen, obwohl er diese bereits 30
Jahre vorher durchdacht und die entsprechenden Aufzeichnungen im Schubfach
verwahrt hatte." Lobatschewski und Bolyai kamen Gauß nicht zuvor,
wie hier
hagiographisch-euphemistisch
gedeutet, sondern Gauß hatte Angst um seinen Ruf, nicht verstanden,
angefeindet und abgelehnt zu werden. Vielleicht ärgerte er sich aber
auch über seinen mutlosen, womöglich aber sehr lebensklugen Konformismus
und die hierdurch entgangene Chance. [1,2,3,]
___
Geschwister-
und Familienkonstellation
In der Psychologie der Familie wurden unter dem Begriff Familienkonstellationen
(Toman u.a.) Ideen entwickelt und
untersucht, die in der Position, die jemand in der Geburtenfolge und Familie
einnimmt, einen gewissen Einfluß sehen. Zur Problematik
dieser Hypothese.
___
Gutachter der Universität.
Nach den Biographen (B1, S. 31/32). Es waren dies die kollegialen Gutachter
Simonow,
Kupfer
und Adjunkt Braschmann.
Der Sekretär der Fakultät schreibt auf den Antrag (von 1826)
auf Beurteilung von Lobatschewski: "Diese Sache wird auf Beschluß
der Fakultät vom 13. Juli 1834 zur Aufbewahrung ins Archiv gegeben."
(S. 32) Diese Zurückhaltung der Kollegen kann man auch positiv
sehen. Fuß und Ostrogradski haben negativ geurteilt: sie haben sich
zurückgehalten. Man muß allerdings auch sehen, daß es
natürlich auch schwierig ist, gegen den eigenen Dekan und Rektor zu
urteilen.
___
hagiographisch-euphemistisch.
Wie so viele sonst neigen nicht wenige mathematische HistorikerInnen zu
einer hagiographisch-euphemistischen
Geschichtsschreibung und sind hierbei offenbar weniger an der Wahrheit
als an einem guten Marketing und Image ihrer Geisteshelden interessiert.
Das ist zwar verständlich, aber wenig aufklärend, nicht authentisch
und im Grunde Geschichtsklitterung bis zur Fälschung.
___
Hilbert, David (1862-1943)
Halameisär, Alexander & Seibt, Helmut (1978, S. 85f) würdigen
Hilbert wie folgt: "Deutscher Mathematiker, Professor an der Universität
Göttingen (seit 1902). Besaß einen großen Einfluß
auf die Entwicklung der Mathematik im 20. Jahrhundert. Hilbert formulierte
auf dem Internationalen Mathematikerkongreß in Paris (1900) in seinem
Vortrag "Mathematische Probleme" 23 Probleme, die als grundlegende Probleme
in der Folgezeit viele Mathematiker beschäftigten. Die Arbeiten Hilberts
zu den Grundlagen der Geometrie (1898—1902) und die Schaffung des ersten
vollständigen und widerspruchsfreien Axiomensystems für die Geometrie
durch ihn dienten nicht nur in der Geometrie, sondern auch in anderen Gebieten
der Mathematik (z. B. in Arbeiten von Weyl, Peano und Gödel)
als Grundlage für die Entwicklung der Axiomatik: [<85] Nach der
Machtergreifung der Faschisten (1933), als auch viele Mathematiker aus
Deutschland emigrieren mußten, aus Göttingen z. B. Weyl,
Courant,
Noether,
blieb Hilbert, schon in hohem Alter, vereinsamt zurück." [1,2,3,]
___
Jakowkin,
Ilja Fedorowitsch (1764 —1836)
Halameisär, Alexander & Seibt, Helmut (1978, S. 86) berichten:
"Direktor des Kasaner Gymnasiums, später Professor für Geschichte
und Geographie an der Universität Kasan, zeitweiliger Rektor. Egoistischer
und herrschsüchtiger Mensch, der den talentierten Mathematiklehrer
G.
I. Kortaschewski von der Universität vertrieb. Im Jahre 1819 wurde
Jakowkinvon
der Universität entlassen." S. 23: "... dieser überaus ehrgeizige
Direktor des Kasaner Gymnasiums und spätere Rektor der Universität
(bis 1813), war Lehrer für russische Sprache, Geographie und Statistik.
Er kümmerte sich sehr um das eigene Wohlergehen, sorgte sich aber
nur wenig um das Niveau der Ausbildung am Gymnasium und an der Universität."
[1,2,3,]
___
Kaestner,
Abraham Gotthelf (1719-1800). [1,2,3,]
Engel & Stäckel (1895, S. 140) führen aus: "Kaestners
Interesse für die Parallelentheorie zeigte sich jedoch nicht nur darin,
daß er die betreffenden Schriften sammelte - das 1801 veröffentlichte
Verzeichnis seiner Büchersammlung, die über 7000 Werke umfaßte,
enthält fast alles, was über diesen Gegenstand etwa bis 1770
erschienen
war - vielmehr entstand auch unter seiner Beihilfe eine noch heute wertvolle
Dissertation, in der zum ersten Male eine Geschichte der Parallelentheorie
gegeben wurde. Ihr Titel lautet:
- Conatuum praecipuorum theoriam parallelarum demonstrandi recensio,
quam publico examini submittent Abrah. Gotthelf Kaestner et auctor respondens
Georgius Simon Klügel,
Göttingen 1763. 4°. 34 Seiten, l Figurentafel.
Gegen dreißig Versuche, das Parallelenaxiom zu beweisen, unter ihnen auch, wie wir schon früher erwähnten, der Versuch Saccheris, werden hier mit sehr verständiger Kritik behandelt, und immer stellt sich heraus, daß sie als mißlungen anzusehen sind. Es ist daher erklärlich, daß Klügel (S. 16) zu der Ansicht gelangt: „Möglich wäre es freilich, daß Gerade, die sich nicht schneiden, von einander abweichen. Daß so etwas widersinnig ist, wissen wir nicht in Folge strenger Schlüsse oder vermöge deutlicher Begriffe von der geraden und der krummen Linie, vielmehr durch die Erfahrung und durch das Urteil unsrer Augen", und daß Kaestner in einem Nachworte sich dahin äußert, ein Beweis für das Parallelenaxiom sei nur zu erhoffen durch eine genauere Ausbildung der Lehre von der Lage, die mit Leibniz untergegangen sei. Gegenwärtig bleibe nur übrig, offen, wie es Hütern der reinsten Wahrheit gezieme, die Forderung Euklids als solche auszusprechen; niemand, der bei gesunden Sinnen sei, werde sie ja bestreiten wollen."
___
- Wurde Kaestner depressiv?
Engel und Stäckel berichten (1895, S. 141): "Dieser Skeptizismus Kaestners
scheint sich später fast noch verschärft zu haben, denn Schweikart
berichtet 1807, „daß Kaestner vor vielen Jahren schon, an der Möglichkeit
der Lösung verzweifelnd, mit unbegreiflicher Resignation, anstatt
nach der wahren Demonstration zu forschen, ein blindes Annehmen öffentlich
anrieth".
Kasan. [Wikipedia] Aus [2: URL verändert]: "Kazan ist das grösste historische, industrielle, kulturelle und wissenschaftliche Zentrum der mittleren Wolga, die Hauptstadt von Tatarstan. Die Stadt liegt am Linken Ufer des Flusses. In Kazan gibt es mehrere Meisterwerke der Architektur, islamische Moscheen und Minarette, wunderschöne orthodoxe Kirchen und Kathedralen, Denkmäler tatarischer, russischer und Weltkultur. Hier ist der berühmte "Fallende Turm", benannt nach der Zarin Sjujumbike, zu besichtigen. Kazan ist die Heimatstadt vieler berühmter Persönlichkeiten Russlands. Hier schuf Dichter G. R. Dershawin, sein grosser Schüler A. S. Puschkin schrieb hier ein Kapitel des Buches über den Pugatschow Aufstand. Hier ertönte der Bass des berühmten Kazaners Fjodor Schaljapin. Über die Strassen der alten Stadt spazierten Graf L. Tolstoj, Maxim Gorki. Hier lebten die tatarischen Schriftsteller Gabdulla Tukai, Musa Dshalil. Hier studierte V. I. Lenin. In Kazan leben über eine Million Einwohner. Das Klima ist gemässigt kontinental; Durchschnittstemperaturen im Januar -13°C, im Juni +20°C, ca. 272 Sonnentage im Jahr."
___
klar und exakt. Die Formalisten, so scheint es, fürchten nichts mehr als klare Definitionen (Hilberts Bierseidelmetapher), Inhalte und Interpretation, auch Didaktik und Pädagogik scheint für sie eine Praktik des Schreckens zu sein. Am liebsten sind ihnen - angeblich - bedeutungslose Zeichen bzw. Zeichenketten mit ein paar Spielregeln, was man mit diesen Zeichen bzw. Zeichenketten machen darf, etwa wenn man die natürlichen Zahlen mit Hilfe von Streichhölzern oder Zahnstochern einführt: 1 := |, 2 := ||, 3 := |||, ... . Aber bereits auf dieser Stufe ist sehr viel zu erklären: was ist ein Zeichen? Eine Zeichenkette? Eine zulässige Zeichenkette? Eine unzulässige Zeichenkette? Wie stellt 'man' das fest? Wie lautet die Konstruktionsregel? Warum? Was sind die Zeichen "1,2,3,...", " |, ||, ||| ", ... ? Was bedeutet " := "? Wie fängt man an? Wie hört man auf? Wie kann man es anwenden (Modelle) bilden? Manche flüchten sich dann in die absurde Aufforderung, um da mitreden zu können, müsse man erst mal richtig Mathematik studieren. Das ist natürlich alles Unsinn: Man kann keine Syntax aufbauen ohne jede Bedeutung, und man kann nicht kommunizieren, ohne Bedeutung und Interpretation. Die Verleugnung der Inhalts-, Bedeutungs- und Interpretationsklärungsbedürftigkeit verschiebt die Probleme lediglich und hilft nicht.
___
Klein, Felix 25.4.1849 Düsseldorf - 22.6.1925, Göttingen [Autobiographie: [URL verändert]
Aus der Quelle: "Er promovierte 1869 in Bonn als Schüler des kurz zuvor verstorbenen Julius Plücker mit einer Arbeit über quadratische Geradenkomplexe. Bei Karl Weierstrass* in Berlin lernte er Sophus Lie kennen, mit dem er 1870 bei einem gemeinsamen Aufenthalt in Paris die Bedeutung des Gruppenbegriffs für die Algebra durch Camille Jordan kennenlernte. Er wandte seine Kenntnisse sofort auf Fragen der Geometrie an und publizierte 1871 seinen ersten epochemachenden Artikel über nichteuklidische Geometrie. Bereits 1872 bekam er eine ordentliche Professur an der Universität Erlangen. "Zum Eintritt in die philosophische Facultät und den Senat der K. Friedrich-Alexander-Universität zu Erlangen" formulierte er sein Programm "Vergleichende Betrachtungen über neuere geometrische Forschungen". Es beruht wesentlich auf Vorarbeiten von Lie und erhob erstmals Gruppentheorie zu einem Ordnungsprinzip der Geometrie - dem bis heute wirkenden "Erlanger Programm". Seit 1876 war er Mitherausgeber der Mathematischen Annalen."
Die Meinung Felix Kleins, daß Gauß der eigentliche Urheber der nichteukleudischen Geometrie und Lobatschewski über Bartels und Bolyai direkt in seinem Studium bei ihm die Ideen erworben hätten, ist historisch kaum haltbar. Engel & Stäckel 1895, S. 242, zitieren die Vorlesungen Kleins Über Nicht-euklidische Geometrie von 1889/90: "Es ist keinem Zweifel unterworfen, daß Gauß durch seinen Einfluß die Untersuchungen von Lobatschewskij und Bolyai angeregt hat." In der Ausgabe von 1927 habe ich diese Textstelle nicht gefunden.
Anmerkung: Erst jüngst erschien eine wahrnehmungs- und kognitionspsychologische Arbeit von Graf, Marcus (2002). Form, Space and Object. Berlin: wvb, die nicht nur Felix Kleins Erlanger Programm nutzte, sondern auch die nichteuklidische Geometrie. Ich verdanke diesen Hinweis Hermann Kremer. [1,2,3,]
Exkurs Felix Klein und Erlangen. In seiner Autobiographie schreibt er zu seiner Berufung nach Erlangen (1872-1875):
Statt dessen erwartete mich der Druck und die anspornende Verantwortung eines schwierigen Amtes. Denn der mathematische Betrieb in Erlangen lag völlig darnieder. Offenbar hatte man eine ganz junge Kraft gerufen, damit sie einem tief im Schlendrian stecken gebliebenen Karren Vorspanndienste leistete. Auf der Bibliothek herrschten vorsintflutliche Verhältnisse. Mittel zur Anschaffung von Büchern oder gar Modellen, auf deren Vorhandensein ich großen Wert legte, standen zunächst nicht zur Verfügung. In meiner ersten Vorlesung, die nach ortsüblicher Sitte am 5. November stattfand, erschienen zwei Zuhörer, von denen ich den einen noch ein paar Mal, den anderen aber nie wieder gesehen habe, so daß eine Weiterführung der begonnenen Vorlesung sehr zweifelhaft gewesen wäre. Aber wieder trat das Schicksal dazwischen und schrieb mir durch eine unerwartete Wendung eine andere Bahn vor. Gleich am 7. November erlag Clebsch (damals Rektor der Universität) einem plötzlichen Anfall von Diphtheritis, wodurch mir meine wichtigste Stütze geraubt und dafür die Aufgabe zugewiesen wurde, das Werk meines verehrten Lehrers weiter fortzuführen. Denn eine Anzahl Spezialschüler Clebsch's, die teilweise älter waren als ich selbst, folgten mir nach Erlangen nach. Ihre weitere Förderung war meine nächstliegende Aufgabe, die alle meine Kräfte besonders auch nach organisatorischer Seite auf den Plan rief.
In Erlangen hatte jeder Dozent, der neu in Fakultät und Senat eintrat, eine wissenschaftliche Programmschrift einzureichen und außerdem in einer öffentlichen Antrittsrede die Ziele seiner Lehrtätigkeit vorzulegen, eine für den Neuling zwar unbequeme Vorschrift, die aber ihre großen Vorzüge besitzt. Als wissenschaftliche Arbeit hatte ich schon im Oktober eine Schrift angefertigt, in der ich die vorhandenen Richtungen der geometrischen Forschung einheitlich zusammenfaßte und in ein System einordnete. Hierbei ergab sich zugleich ein Ausblick auf zahlreiche neue Probleme, die sich der Bearbeitung darboten. Dieses "Erlanger Programm" ist für meine weiteren Untersuchungen immer die große Richtlinie geblieben und hat sein ordnendes Prinzip auch noch auf zahlreiche andere Gebiete wie Funktionentheorie, Mechanik und Physik ausgedehnt." So weit Felix Klein (Lebensbild].
Mathematik in Erlangen. Fraenkel, Abraham A. (1957, S. 79) in seiner Autobiographie' Lebenskreise' Jahre später über die Mathematik in Bayern und namentlich in Erlangen: "Dagegen [gegenüber München und Würzburg] hatte die dritte und kleinste bayerische Universität Erlangen, berühmt besonders für ihre Vertreter der protestantischen Theologie, auch in der mathematischen Welt einen internationalen Ruf, dank ihrer ausgezeichneten Forscher Paul Gordan und Max Noether [URL verändert]; Noether war Jude und der Vater der hervorragendsten weiblichen Mathematikerin Emmy Noether [URL verändert]." Merkwürdigerweise erwähnt Fraenkel Felix Klein nicht im Zusammenhang mit Erlangen. Die Erlanger Mathematik wirbt Heute [URL verändert].
*Weierstrass: Nach den Biographen (B1, S. 63) konnte Klein seine Ideen, daß eine Cayleysche Metrik nicht nur zur Euklidschen sondern auch auch zur Lobatschewskischen führen könnte, in einem Seminar von Weierstrass vortragen, er habe dort aber keine Anerkennung gefunden.
___
Klügel, Georg Simon (1739-1812).
Nach Meschkowski (1973, S. 156): "Schüler Kästners. Bekannt durch seine Dissertation, in der er 28 Beweisversuche für das Euklidsche Parallelenpostulat zusammenstellt und nachweist, daß sie alle unzulänglich seien. Verfasser eines mathematischen Wörterbuchs. Es gibt eine deutsche Übersetzung [URL verändert].
___
Kupfer, Adolf (1799-1865)
Kupfer, ein Baltischer Deutscher, erhielt seine Hochschulbildung in Deutschland, ging dann nach Rußland und war zunächst Professor an der Universität Kasan (1823 - 1828). B1, S. 87, weist ihn als Physikprofessor aus, eine andere Quelle ordnet ihm eine Chemieprofessur zu, eine dritte eine Professur für Physik, Mineralogie und Chemie in St. Petersburg. Auf einer Reise 1823 nach Paris, um Ausrüstung für die Universität zu kaufen, wurde Kupfer bekannt gemacht mit Francois Arago und Alexander Humboldt, der sein Interesse am Landmagnetismus und Meteorologie stimulierte. 1828 wurde Kupfer in die Akademie von Wissenschaften gewählt und ging nach St. Petersburg, wo er begann, seine meteorologischen Beobachtungsstationen überall in Russland zu organisieren, die durch eine Hauptsternwarte in der Hauptstadt beaufsichtigt wurden. 1849 wurde Kupfer zum Direktor dieser neuen Hauptsternwarte ernannt und wirkte dort bis zu seinem Tode. Kupfer war einer der von der Fakultät 1826 beauftragten Gutachter.
___
Lambert, Johann Heinrich (1728-1777).
Nach [URL verändert]: "Lambert stammte aus dem zu seiner Zeit der Eidgenossenschaft zugehörigen Mühlhausen (Elsaß), dem heutigen Mulhouse. Er war unter anderem als Schneider, Schreiber, Buchhalter und Privatlehrer tätig. 1765 ging Lambert auf Betreiben Friedrichs des Großen nach Berlin an die Akademie der Wissenschaften. Friedrich dem Großen war es nach seiner Thronbesteigung 1740 darum zu tun gewesen, aus Berlin ein mächtiges intellektuelles Zentrum zu formen, weshalb er neben Lambert auch zahlreiche andere Gelehrte wie Euler und Lagrange nach Berlin rief. Lambert war ein sehr vielseitiger Gelehrter; bekannt geblieben sind seine Beiträge zur Optik (u.a. Lambert - Beersches - Gesetz, Lambertsches Kosinusgesetz), seine Arbeiten zur Kartenprojektion (Lambert - Projektion), sein Beweis der Irrationalität der Kreiszahl sowie seine logisch - wissenschaftstheoretischen Untersuchungen. ... Lambert hat seine 1765 entstandene Theorie der Parallellinien nicht selbst veröffentlicht, vermutlich weil er mit ihr nicht zufrieden war. Sie wurde erst 1786 posthum von C. F. Hindenburg (1741-1808) ... publiziert". Mehr zu Lamberts Arbeit zu den Parallellinien an der Quelle [URL verändert].
___
Legendre, Adrien Marie (1752-1833).
Nach: "Andrien Marie Legendre (1752 - 1833) wirkte in Paris, wo er auch seine sehr gute wissenschaftliche Ausbildung erhielt. Er lehrte zunächst an der École Militaire, war ab 1783 eng mit der Pariser Akademie verbunden und wurde später Professor an der École Normale. Von 1813 bis 1833 gehörte er als Nachfolger von Lagrange dem Bureau des Longitudes an. Seine wichtigsten Arbeitsgebiete waren die elliptischen Integrale, die Zahlentheorie und die Grundlagen der Geometrie. Er leistete auch Beiträge zur Himmelsmechanik und Variationsrechnung. Seine 1794 erstmals erschienenen Eléments de géométrie erzielten mehr als 30 Auflagen und wurden in zahlreiche Sprachen (auch ins Deutsche) übertragen. Dabei handelt es sich um ein Lehrbuch der Geometrie, das sich allerdings von seinem antiken Vorgänger durch einen großzügigen Gebrauch von Algebra und Trigonometrie unterscheidet. In einem der vielen Anhänge (in der 11. Auflage ist es die Note IV) zu seinen Eléments äußerte Legendre übrigens wohl als Erster in der Mathematikgeschichte überhaupt klar die Vermutung, dass die Kreiszahl transzendent sei (Legendre 1817, 295). Die verschiedenen Auflagen der Eléments unterscheiden sich stark voneinander, wobei gerade bezüglich der Parallelentheorie immer wieder Änderungen vorgenommen wurden (die nachfolgend dargestellte Version der Parallelentheorie findet sich nach Legendres Angaben [Legendre 1833, 369 und 371] in den Auflagen drei bis acht). In seinem Todesjahr gab Legendre, der zeit seines Lebens davon überzeugt war, dass das PP ein beweisbarer Satz der absoluten Geometrie sei, eine Art Zusammenfassung seiner Ansichten in dem Vortrag Réflexions sur quelques manières de démonstrer la théorie des parallèles ou le théorème sur la somme des trois angles du triangle vor der Pariser Akademie (Legendre 1833)." Mehr an der Quelle [URL verändert].
___
Liebmann machte sich sehr verdient um das Werk Lobatschewskis in Deutschland, was ihm das dunkle Deutschland der Richter und Henker nicht dankte (Verfolgte MathematikerInnen. Mathematik im Dritten Reich):
"Der Mathematiker Karl Otto Heinrich Liebmann (geb. 22. Oktober 1874 in Straßburg, gest. 12. Juni 1939 Solln bei München) verbrachte seine Studienzeit in Leipzig, Göttingen und Jena, wo er auch promovierte. An der Leipziger Fakultät habilitierte er sich. 1910 kam er als etatm. ao Professor an die Technische Hochschule München. Fünf Jahre später übernahm er dort ein Ordinariat. Seit 1920 lehrte er in Heidelberg. Im April 1933 war auch seine Beurlaubung ausgesetzt worden. Ein Jahr später meinte das Kultusministerium, der (häufig kranke) Liebmann werde ohnehin in einigen Jahren von seinen Amtspflichten enthoben, deshalb bedürfe es keiner weiteren Maßnahme. Zur "Beseitigung der Schwierigkeiten" empfahl ihm das Reichserziehungsministerium die Emeritierung. Nach dem vergeblichen Kampf gegen den von der Fachschaft über ihn und seinen Kollegen Rosenthal ausgerufenen Boykott bat Liebmann selbst um seine Emeritierung und legte dazu ein ärztliches Gutachten Ludolf von Krehls vor. Zum 1. Oktober 1935 wurde er mit 61 Jahren entpflichtet. Er zog nach Solln (bei München) und starb dort 3 Jahre später." (Quelle)
___
Lindemann. Der Mathematiker Lindemann - promoviert von Felix Klein in Erlangen - wurde weltberühmt durch seinen Beweis von der Unmöglichkeit der Quadratur des Zirkels (Kreises; Pi ist eine transzendente Zahl). Der Autobiographie "Lebenskreise" Abraham A. Fraenkels (1957, S. 79/80) entnehmen wir zu Lindemann (fette Hervorhebung RS): "Ferdinand Lindemann, Hannoveraner, galt, was allerdings unter Mathe[>80]matikern oft vorkommt, als ein Sonderling. Er zählte keineswegs zu den großen Forschern seiner Zeit, war aber dadurch weltberühmt geworden, daß er eines der ältesten und bekanntesten mathematischen Probleme, das der Quadratur des Zirkels, endgültig gelöst hatte. Das Problem geht auf das vierte vorchristliche Jahrhundert zurück. Aufgrund der entscheidenden Vorarbeit des Franzosen C. Hermite, der 1873 mit großem Scharfsinn die Transzendenz der Zahl e (die Basis der natürlichen Logarithmen) bewiesen hatte, gelang es Lindemann 1882 zu zeigen, daß auch Pi, das Verhältnis des Kreisumfangs zu seinem Durchmesser, eine transzendente, also nicht algebraische Zahl darstellt, und um so weniger mit Lineal und Zirkel konstruiert werden kann, was schon vorher bekannt war [Fußnote 33]. Aufgrund dieser Entdeckung wurde er 1893, erst 41jährig, nach München berufen.
Wie sich in der Folge zeigte, war das eine Fehlberufung, wenigstens soweit es Forschung und Lehrtätigkeit betrifft. Die späteren Abhandlungen Lindemanns hatten nur beschränkte Bedeutung. Bekannt wurde er durch seine wiederholten, in Aufsätzen und einer Monographie niedergelegten, ausnahmslos fehlerhaften Versuche, den „Letzten Fermatischen Satz" zu beweisen." [Beleg, 2,3,]
___
Littrow, Josef (1781-1840)
Erster Professor für Astronomie an der Universität Kasan (1810—1816). Ab 1816 arbeitete er an der Sternwarte in Ofen und war später ein bekannter Astronom und Direktor der Wiener Sternwarte. [Wikipedia] [Bild]
___
Medizinischen Fakultät. Lobatschewski hat nach [B1] nie Medizin studiert. Diese Fehlinformation findet sich auch noch bei Meschkowski in [B2] (S. 141). Die Geschichte eignet sich womöglich gut dazu, zu untersuchen und zu erforschen, wie wissenschaftsbiographische Gerüchte entstehen und sich festsetzen. [1,2,3,]
___
Magnizki, Michail Leontjewitsch (1778 — 1844}
Die Biographen Halameisär, Alexander & Seibt, Helmut (1978, S. 88) berichten: "Revisor, danach Kurator des Kasaner Schulbezirks (1819—1826). Vertrieb die besten Professoren der Kasaner Universität und wollte die Universität wieder schließen lassen. Katastrophale Folgen seiner "Revision''. Die sich häufenden Klagen konnte der neue Unterrichtsminister nicht länger überhören, so daß vom Zaren Nikolaus I. Anfang 1826 eine erneute Revision an der Universität Kasan angeordnet wurde. Im Ergebnis dieser Revision wurde Magnizki seines Amtes enthoben und in Reval (heute Tallin) interniert."
___
Mitgift. Die Biographen [B1, S.87]. "Der Familie gehörte z.B. das Dorf Belowolshskaja Slohotka an der Wolga, wo sich Lobatschewski von seiner Arbeit zu erholen pflegte."
___
Modell. Allgemein eine Realisation bzw. Anwendung einer Theorie. In der mathematischen Logik ein eigener und ziemlich schwieriger Zweig: die Modell-Theorie. Ein wichtiger neuerer Begriff der Beweistheorie und Beweistechnik. Komplement zum Gegenbeispiel. Während idealiter ein einziges Gegenbeispiel eine allgemeine Behauptung widerlegt, beweist ein ausführbares Beispiel, ein "Modell", daß eine Theorie widerspruchsfrei ist. Potthoff (1981, S.1): "Modelltheorie handelt von den Beziehungen zwischen Aussagen einer formalen Sprache und Strukturen, in denen diese Aussagen vernünftig interpretiert werden können." Für die nicht-euklidische Geometrie bedeutet das: läßt sich ein Modell finden gilt sie als widerspruchsfrei bewiesen. Ein solcher Beweis gelang Felix Klein 1871.
Es ist allerdings sehr zweifelhaft, ob die mathematisch-logische Modelltheorie in der Lage ist, das Problem empirisch wissenschaftlicher Theorien lösen zu helfen, da dort im Grunde eine formale Welt in eine andere formale Welt abgebildet wird, ähnlich wie in der Meßtheorie (ein formales empirisches 'Relativ' in ein formales numerisches Relativ abbilden) oder auch in der Statistik [1,2], wenn man dort eine Hypothese gegen eine andere testet, denn meist will man nicht wissen, ob y gilt (z.B. die Nullhypothese beim Signifikanztest), wenn x gilt, sondern ob y gilt. [1,2,3,]
___
Neider. Es empfiehlt sich eine sorgfältige Trennung zwischen Neid und Mißgunst. Ich interpretiere die Biographen so, daß sie Neid und Mißgunst unter Neid zusammenfassen.
___
Ostrogradski, Michail Wassilowitsch (24.9.1801 - 1.1.1862).
Russisch-ukrainischer Mathematiker. Studierte in Charkow und Paris. Adjunkt an der Petersburger Akademie der Wissenschaften. Mehr bei: [Wikipedia,1,2,3]
___
Poincaré, Henri (1854 - 1912)
Bedeutender französischer Mathematiker, Physiker und Philosoph, Professor an der Universität Paris (seit 1886), Mitglied der Pariser Akademie der Wissenschaften (seit 1887). Das Modell von Poincaré wird ausführlich dargestellt von Filler, A. (1993, S. 174-195). [1,2,3,]. Poincaré gehört auch zu den Kritikern von Cantors aktual Unendlichem.
___
Psychologie der Wissenschaft. Leider bislang ein unterentwickeltes Gebiet der Psychologie, obgleich sehr spannend und fast alle Gebiete der Psychologie berührend: Entwicklungspsychologie: wie entwickeln sich WissenschaftlerInnen? Begabungspsychologie: Wie soll und kann Erkennen, Auslese und Förderung erfolgen? Differentielle Psychologie der Persönlichkeit: Was sind das für Menschen, unterscheiden sie sich von anderen und wie? Organisations- und Sozialpsychologie: wie funktioniert der Wissenschaftsbetrieb? Denkpsychologie: Wie denken Genies? [Wertheimer Studie zu Einstein]. Kreativitätsforschung: wie kann wissenschaftliche Kreativität gefördert werden?
- Maslow, Abraham H. (dt. 1977, engl. 1966). Die Psychologie der Wissenschaft. München: Goldmann.
- Müller-Freienfels, Richard (1936). Psychologie der Wissenschaft. Leipzig: Barth.
Riemann, Bernhard (1826 - 1866)
Die Biographen Halameisär, Alexander & Seibt, Helmut (1978, S. 88) würdigen: "Deutscher Mathematiker, Schüler von Gauß und Weber, Professor an der Universität Göttingen (seit 1857). Starb an Tuberkulose. Schuf eine neue (geometrische) Auffassung von der Theorie der analytischen Funktionen, entwickelte die Theorie der konformen Abbildungen weiter und beschäftigte sich mit der Flächentheorie; untersuchte die Zetafunktion, auf deren Grundlage später ein Gesetz über die Verteilung der Primzahlen aufgestellt worden ist. Seine wissenschaftlichen Hauptverdienste sind die Ausarbeitung einer Raumtheorie und die von ihm geschaffene elliptische nichteuklidische Geometrie." [1, 2, 3,] .
___
Rumowski, Stepan Jakowlewitsch (1734 — 1812)
Die Biographen Halameisär, Alexander & Seibt, Helmut (1978, S. 88): "Russischer Astronom, Schüler von Euler und Lomonossow, Vizepräsident der Petersburger Akademie der Wissenschaften, Kurator des Kasaner Schulbezirks (seit 1803), Gründer der Universität Kasan. Förderte die Berufung von westeuropäischen Wissenschaftlern an russische Universitäten." [1,2,3,]
___
Saccheri, Giralomo (1867-1733)
Zur Beweisidee siehe die Nichteukleudische Geometrieseite von Jutta Gut.
Eine englische Seite zu Saccheris Beweisideen.
___
Schweikart, Ferdinand Karl (1780-1857)
Ich bringe zu Schweikart ein wenig mehr Information, weil ich im deutschsprachigen Internet relativ wenig fand. Möglicherweise greift es ja Wikipedia mal auf. Eine eindrucksvolle niederländische Internetseite zur hyperbolischen Geometrie führt aus:

Und eine englische
Seite schreibt über einen Brief Gaussens an Schweikart, in dem
die Krümmung des Raumes, für den die euklidische Geometrie nicht
angemessen sein würde: "Gauss did not limit himself to thinking of
a curved two-dimensional surface floating in a flat three-dimensional universe.
In an 1824 letter to Ferdinand Karl Schweikart, he dared to conceive that
space itself is curved: "Indeed I have therefore from time to time in jest
expressed the desire that Euclidean geometry would not be correct." He
also wrote: "Although geometers have given much attention to general
investigations of curved surfaces and their results cover a significant
portion of the domain of higher geometry, this subject is still so far
from being exhausted, that it can well be said that, up to this time, but
a small portion of an exceedingly fruitful field has been cultivated" (Royal
Society of Göttingen, 8 October 1827). The inspiration of these thoughts,
dreams, and hopes passed from Gauss to his student, Bernhard Riemann."
___
Simonow, Iwan Michailowitsch
(1794—1855).
Die Biographen (B1) Halameisär, Alexander & Seibt, Helmut
(1978, S. 89): "Professor der Astronomie an der Universität Kasan.
Schüler von Littrow, Freund von N. I. Lobatschewski.
Absolvierte gemeinsam mit N. I. Lobatschewski die Universität
Kasan. Wurde mehrmals zum Dekan der Physikalisch-Mathematischen Fakultät
gewählt. Er gehörte zu der Kommission, die mit der Einschätzung
und der Beurteilung der Entdeckung Lobatschewskis beauftragt worden
war (1826), die aber kein Gutachten
zustande brachte." [1,2,3,]
___
Taurinus, Franz Adolph (1794-1874).
Engel & Stäckel schreiben (S. 246 ff, im Text gesperrt ist
hier kursiv geschrieben): "... Dagegen haben unsre Nachforschungen in Betreff
jenes Neffen Schweikarts, des Taurinus, zu dem überraschenden
Ergebnis geführt, daß auch Taurinus für die Vorgeschichte
der nichteuklidischen Geometrie von Bedeutung ist: zuerst angeregt durch
seinen Oheim Schweikart, dann beeinflußt durch Gauß
hat er bemerkenswerte selbständige Untersuchungen angestellt und in
den Jahren 1825 und 1826 veröffentlicht. Er ist darin schließlich
zur Entwickelung einer nichteuklidischen Trigonometrie gelangt und
hat somit einen wichtigen Teil der Ergebnisse von Lobatschefskij
und Bolyai vorweg genommen.
Über das Leben von Taurinus haben wir Folgendes
ermittelt: Franz Adolph Taurinus ist am 15. November 1794 zu König
im [>247] Odenwalde geboren: seine Eltern waren Julius Ephraim Taurinus,
gräflich Erbach- Schönbergischer Hofrat, und Luise Juliane, geborene
Schweikart.
Nachdem er in Heidelberg, Gießen und Göttingen
Rechtswissenschaften studiert hatte, lebte er von 1822 an in Köln
ohne Amt und Beruf und fand Muße, sich mannigfachen wissenschaftlichen
Interessen zu widmen. In Köln ist er auch hochbetagt am 13.
Februar 1874 gestorben.
Veröffentlicht hat Taurinus nur wenig: 1825 erschien seine
Theorie
der Parallellinien, Köln am Rhein, 102 S. 8°. 4 Tafeln und
im folgenden Jahre als Fortsetzung die Schrift: Geometriae prima elementa,
Coloniae Agrippinae, 76 S. 8°. 2 Tafeln.
In dem Vorwort zu den Elementa hat Taurinus auf Seite
IV—VI den Ursprung und Verlauf seiner Untersuchungen über die Parallelentheorie
folgendermaßen geschildert:
- „Der erste, der mich auf das neue System der Geometrie aufmerksam gemacht
hat, war ein mit mir verwandter und eng befreundeter Mann, Schweikart,
Professor der Rechte an der Universität zu Königsberg. Dieser
schrieb mir vor vier Jahren ungefähr folgendermaßeri: Durch
emsiges Studium der Geometrie sei er zu der Überzeugung gelangt, dass
es eine gewisse neue Geometrie gebe - er nannte sie Astralgeometrie -,
bei der die Winkelsumme im Dreieck kleiner als zwei Rechte sei, und er
habe zu seiner Freude erfahren, dass der berühmte Gauß,
dem seine Entdeckung mitgeteilt worden war, schon lange mit demselben Gegenstande
beschäftigt gewesen und darin noch weiter gekommen sei.
„Da jedoch unser Briefwechsel nicht fortgesetzt wurde, und da ich selbst damals keine Zeit zur Beschäftigung mit der Geometrie hatte, so kam es, dass ich meine Aufmerksamkeit diesem Gegenstande nicht eher wieder zuwendete, als bis mir die 1807 in Jena erschienene Schrift desselben Schweikart über die Parallellinien in die Hände fiel.
„Dieses Buch war mir deshalb höchst willkommen, weil ich daraus den Sinn und die Schwierigkeit des Problems gründlich kennen lernte, sowie auch alle die Methoden zum Beweise der Parallelentheorie, die bis dahin bekannt geworden waren.
„Bei der Ausarbeitung der von mir bereits herausgegebenen Theorie habe ich nämlich, wie ich gestehen muss, nur sehr wenige Bücher benutzt, hatte ich doch ausser der Ausgabe des Euklid von Lorenz *) [>248] kaum das eine oder andere Elementarbuch gelesen. Was ich daher aus Camerers Ausgabe der Elemente*) kennen lernte - einem Werke, das ich hochschätze -, das war mir zum Teil neu, besonders, dass ich, ohne es zu wissen, auf Gedanken gekommen war, welche denen, die man dem Italiener Saccheri und unseren Landsmanne Lambert zuschreibt, sehr ähnlich sind. Ich für meine Person hatte diese Beweismethode von vorn herein für die beste, ja für die einzige gehalten, die es ermöglicht, die Schwierigkeit zu überwinden, und habe deshalb kein Bedenken getragen, einige meiner Beweise Gauß selber mitzuteilen. Dieser hat mir sogleich aufs freundlichste geantwortet und einiges über den Gegenstand hinzugefügt, woraus ich freilich seine Ansicht über die Sache nicht vollständig habe erraten können. Möchte daher dieser ausgezeichnete Mann seine Gedanken über die ganze Frage, die bei einem solchen Geiste von unschätzbarem Werte sein müssen, baldigst veröffentlichen! Mit mir werden alle Geometer ihn immer von Neuem inständigst darum bitten.
„Zur Abfassung des vorliegenden Büchleins bin ich um so lieber geschritten, als meine Theorie, der ich nur ziemlich wenig Zeit gewidmet hatte, noch nicht öffentlich besprochen worden ist**), und ausserdem vieles enthält, was mir selbst bereits nicht mehr gefällt. Übrigens ging meine Absicht besonders dahin, die Analogien zwischen den verschiedenen Geometrien deutlicher hervortreten zu lassen. Ob mir das einigermassen gelungen ist, das zu entscheiden überlasse ich dem Urteile erfahrener Männer, die, wie ich zuversichtlich hoffe, wenigstens meine eifrigen Bemühungen, die Wissenschaft der Geometrie zu fördern, anerkennen und mir gewogen sein werden. "Köln am Rhein, den 1. December 1825."
Daß Taurinus zu seinen Untersuchungen über die Parallelentheorie
durch Schweikart angeregt worden ist, bestätigt einmal eine
Stelle seiner Theorie der Parallellinien, die wir S. 261 mitteilen
werden, noch deutlicher jedoch ein Brief, den Schweikart am 1. Oktober
1820 aus Marburg an Taurinus abgehen ließ, der damals
in
Göttingen Jura studierte. In diesem Briefe heißt es:
- „Was die Mathematik betrifft, so überzeugte mich das, was Du [>249]
schriebst, daß ich mich auch in diesem Punkte nicht in Dir geirrt
hatte. -
„Durch meine vieljährigen Studien bin ich zuletzt zu der Einsicht gelangt, daß unsere Geometrie nur eine relative Wahrheit habe, und daß es eine höhere, welche ich die Astralgeometrie nenne, gebe, nach welcher z. B. die Winkel im Dreyecke kleiner als 2 rechte sind und immer mehr abnehmen, jemehr der Inhalt wächst, ja daß mit der Größe der Winkel auch der Inhalt und umgekehrt gegeben ist.
„Zu meiner Freude erfuhr ich, dass der berühmte Gauß schon lange auf demselben Wege und darauf schon weit vorgeschritten ist. In kurzer Zeit würde ich Dich in diese Ansicht einführen können und Deinem Erfindungstriebe ein weites Feld eröffnen."
Erst seit dem Jahre 1824 scheint Taurinus sich eingehender mit der Parallelentheorie beschäftigt zu haben. Die Ergebnisse, zu denen er kam, hat er dann Schweikart und Gauß vorgelegt. Das Antwortschreiben Schweikarts vom 18. November 1824 ist schon auf Seite 245—246 mitgeteilt. Wir lassen nunmehr auch das Schreiben von Gauß folgen: "
- "„Ewr. Wohlgeboren
gefälliges Schreiben vom 30 Oct. nebst dem beigefügten kleinen Aufsatz habe ich nicht ohne Vergnügen gelesen, um so mehr, da ich sonst gewöhnt bin, bei der Mehrzahl der Personen, die neue Versuche über die sogenannte Theorie der Parallellinien [machen,] gar keine Spur von wahrem geometrischen Geiste anzutreffen.
„Gegen Ihren Versuch habe ich nichts (oder nicht viel) anderes zu erinnern als daß er unvollständig ist. Zwar lässt Ihre Darstellung des Beweises, daß die Summe der drei Winkel eines ebnen Dreiecks nicht grösser als 180° seyn kann in Rücksicht auf geometrische Schärfe noch zu desideriren übrig. Allein dies würde sich ergänzen lassen, und es leidet keinen Zweifel daß jene Unmöglichkeit sich auf das allerstrengste beweisen läßt. Ganz anders verhält es sich aber mit dem 2n. Theil, daß die Summe der Winkel nicht kleiner als 180° seyn kann; dies ist der eigentliche Knoten, die Klippe woran alles scheitert. Ich vermuthe, daß Sie sich noch nicht lange mit diesem Gegenstande beschäftigt haben. Bei mir ist es über 30 Jahr, und ich glaube nicht, daß jemand sich eben mit diesem 2n. Theil mehr beschäftigt haben könne als ich obgleich ich niemals etwas darüber bekannt gemacht habe. Die Annahme, daß die Summe der 3 Winkel kleiner sei als 180°, führt auf eine eigne von der unsrigen (Euclidi-[>250]schen) ganz verschiedene Geometrie, die in sich selbst durchaus consequent ist, und die ich für mich selbst ganz befriedigend ausgebildet habe, so daß ich jede Aufgabe in derselben auflösen kann mit Ausnahme der Bestimmung einer Constante, die sich a priori nicht ausmitteln läßt. Je grösser man diese Constante annimmt, desto mehr nähert man sich der Euclidischen Geometrie und ein unendlich großer Werth macht beide zusammenfallen. Die Sätze jener Geometrie scheinen zum Theil paradox, und dem Ungeübten ungereimt; bei genauerer ruhiger Überlegung findet man aber, daß sie an sich durchaus nichts unmögliches enthalten. So z. B. können die drei Winkel eines Dreiecks so klein werden als man nur will, wenn man nur die Seiten groß genug nehmen darf, dennoch kann der Flächeninhalt eines Dreiecks, wie groß auch die Seiten genommen werden, nie eine bestimmte Grenze überschreiten, ja sie nicht einmahl erreichen. Alle meine Bemühungen einen Widerspruch, eine Inconsequenz in dieser Nicht-Euclidischen Geometrie zu finden sind fruchtlos gewesen, und das Einzige was unserm Verstande darin widersteht, ist daß es, wäre sie wahr, im Raum eine an sich bestimmte (obwohl uns unbekannte) Lineargrösse geben müßte. Aber mir deucht, wir wissen, trotz der Nichts Sagenden Wort-Weisheit der Metaphysiker eigentlich zu wenig oder gar nichts über das wahre Wesen des Raumes, als daß wir etwas uns unnatürlich vorkommendes mit Absolut Unmöglich verwechseln dürfen. Wäre die Nicht-Euclidische Geometrie die wahre, und jene Constante in einigem Verhältniße zu solchen Grössen die im Bereich unsrer Messungen auf der Erde oder am Himmel liegen, so ließe sie sich a posteriori ausmitteln. Ich habe daher wohl zuweilen im Scherz den Wunsch geäußert, daß die Euclidische Geometrie nicht die Wahre wäre, weil wir dann ein absolutes Maass a priori haben würden.
„Von einem Manne, der sich mir als einen denkenden Mathematischen Kopf gezeigt hat, fürchte ich nicht, daß er das Vorstehende misverstehen werde: auf jeden Fall aber haben Sie es nur als eine Privat-Mittheilung anzusehen, von der auf keine Weise ein öffentlicher oder zur Oeffentlichkeit führenkönnender Gebrauch zu machen ist. Vielleicht werde ich, wenn ich einmahl mehr Muße gewinne, als in meinen gegenwärtigen Verhältnißen, selbst in Zukunft meine Untersuchungen bekannt machen.
„Mit Hochachtung verharre ich
Ewr Wohlgeboren
Göttingen den 8 November
ergebenster Diener
1824.
CFGauß""
Teilung des Kreises. [W.gon]
___
"treffen" (Euklid 5. Postulat). Für die meisten Menschen stellt sich die Frage nicht, was "treffen" bei Euklid bedeutet. Es scheint intuitiv klar. Und bevor ich mich nicht näher für bestimmte Gebiete der Mathematik interessierte, war es sicher bei mir auch so. Ich wäre früher nie auf die Idee gekommen, zu fragen, was Euklid - wenn die Übersetzung richtig ist - mit "treffen", nämlich schneiden, gemeint haben könnte. Taucht man aber ein wenig ein in die Geschichte der Parallellinien, der entstandenen nichteuklidischen Geometrie und der extremen und völlig abweichenden Bedeutungszuordnungen der neuen, sehr technisch orientierten und entwickelten Mathematik, dann ist eigentlich nichts mehr klar oder gar selbstverständlich. Mit dem Siegeszug der axiomatischen Formalisten ging eine extreme Flucht vor Inhalt und Interpretation einher, so daß Fragen nach der Bedeutung einen enormen Verweisungprozeß hervorrufen. Was also kann "treffen" bei Euklid bedeuten? Die Formulierung ausgehend von der Übersetzung Thaer, WBG 1969, S. 3. lautet: "'Und daß, wenn eine gerade Linie beim Schnitt mit zwei geraden Linien bewirkt, daß innen auf derselben Seite entstehende Winkel zusammen kleiner als zwei Rechte werden, dann die zwei geraden Linien bei Verlängerung ins Unendliche sich treffen auf der Seite, auf der die Winkel liegen, die zusammen kleiner als zwei Rechte sind." "Treffen" kann nun mehreres bedeuten: a) berühren und vereinigt in einer Linie weiter laufend; b) berühren und verschmelzen an dieser Stelle zu einem Endpunkt; c) schneiden und danach auseinanderlaufen wie bei einer Schere; d) ... ; e) letztlich unklar bleibend?
___
Ukas Persönlicher Befehl des Zaren. [Wikipedia]
___
Vater. Engel (1899, S. 351) läßt den Vater 1797 sterben. Nach den Biographen (B1) Halameisär & Seibt (B1) hat der Vater die Familie aber in diesem Jahr verlassen und es stirbt der Gönner der Mutter, der ihr eine kleine Erbschaft vermacht. Nach Engel (1899, S. 351) wurde Lobatschewski auch am 22. Oktober (2. November) 1993 geboren.
___
Wallis, John (1616-1703)
Studierte in Cambridge Philosophie und Theologie; bekleidete zunächst verschiedene Predigerstellen in London und wurde 1649 Professor für Mathematik (Geometrie) in Oxford. Seit 1660 Kaplan Karls II. Gründungsmitglied der Royal Society. Berühmt wurde seine Produktdarstellung Pi. Wallis fand: "Zu jedem Dreieck gibt es ein ähnliches Dreieck beliebiger Größe." Meschkowski (1973, S. 282): "Er zeigte weiter, daß das Parallelenpostulat aus der Existenz ähnlicher, nicht kongruenter Figuren abgeleitet werden kann." Eine ausführliche Darstellung der Arbeiten Wallis' zum Parallelenpostulat findet sich in Engel & Stäckel (1895). [ , Bio.en, Porträt, Wikipedia.de, ]
___
Werk. Hier im engeren Sinne als die Erfindung der nichteuklidischen Geometrie verstanden. Lobatschweski hat natürlich vielmehr Beiträge - Naas, J. & Schmid, H.L. erwähnen bedeutende Beiträge zur Algebra und Analysis - zur Mathematik geliefert, auf die hier aber nicht eingegangen wird. In russisch wurden 1948-1951 die vollständigen Werke in fünf Bdn. herausgegeben (Bd. IV Arbeiten zur Algebra, Bd. V. Arbeiten zur Analysis, Wahrscheinlichkeitsrechnung, Mechanik und Astronomie).
___
Wilno: Heute Vilnius bzw. Wilna, Hauptstadt Litauens.
___
Z. Ein denkwürdiges und interessant-paradox anmutendes Zitat aus seiner berühmten Rede "Über die wichtigsten Fragen der Erziehung" ein Jahr nach seiner Wahl zum Rektor, 1928, zur Immatrikulationsfeier. Wissenschaft wird hier scharf abgrenzt gegenüber Theologie und Philosophie, und auch die dazugehörige Mathematik wird hier offenbar sehr konstruktiv als Tätigkeit verstanden, wobei die wesentliche Tätigkeit eines Mathematikers das Beweisen ist. Die 'Wirklichkeit' - im empirischen Sinne - der nichteuklidischen Geometrie war damals nicht zu sehen, obwohl es nicht mehr lange dauerte. Lobatschewski hat aber hier in seiner Funktion als Rektor wahrscheinlich die naturwissenschaftliche Orientierung, also empirische Beobachtung, Erklärung und Vorhersage, Experiment und Beweis angesprochen.
__
Standort: Nikolai Iwanowitsch Lobatschewski.
*
Brief Nr. 396 von Gauss an Schumacher am 12.7.1831 zum Thema nichteuklidische Geometrie mit einer Bewertung zum Unendlichen in der Mathematik.
Überblick Wissenschaft in der IP-GIPT.
Biographie, Lebenslauf, Kritische Lebensereignisse, Entwicklung der Persönlichkeit, Psychographie, Pathographie, Psychopathographie.
Methodische Probleme, Fallstricke und Fehlschluß-Varianten in wissenschafts-geschichtlichen Fragestellungen und die Kunstfehler in der Wissenschaftsberichtserstattung. * Geschichte Rußlands in der IP-GIPT *
Literatur und Linkliste (LiLi): Irrtum, Betrug, Tricks, Täuschung, Fälschung, Risiko, Versagen und anderes Fehlverhalten in Forschung, Wissenschaft und Technik.
Übersicht Differentielle Psychologie und Psychopathologie der Persönlichkeit.
Axiome und Konstruktionsprinzipien Differentieller Psychologie der Persönlichkeit.
*
| Suchen in der IP-GIPT,
z.B. mit Hilfe von "google": <suchbegriff>
site:www.sgipt.org
z.B. Mathematik site:www.sgipt.org. * Biographie site:www.sgipt.org. * Russische Geschichte site:www.sgipt.org. |
Dienstleistungs-Info.
*
Sponsel, Rudolf (DAS). Nikolai Iwanowitsch Lobatschewski. Leben und Werk - Psychologie der Forschungsleistung. IP-GIPT. Erlangen: https://www.sgipt.org/biogr/matnat/lobat/Lobat.htm
Copyright & Nutzungsrechte
Diese Seite darf von jeder/m in nicht-kommerziellen
Verwertungen frei aber nur original bearbeitet und nicht inhaltlich
verändert und nur bei vollständiger Angabe der Zitierungs-Quelle
benutzt werden. Das direkte, zugriffsaneignende Einbinden in fremde Seiten
oder Rahmen ist nicht gestattet, Links und Zitate sind natürlich willkommen.
Sofern die Rechte anderer berührt sind, sind diese dort zu erkunden.
Sollten wir die Rechte anderer unberechtigt genutzt haben, bitten wir um
Mitteilung. Soweit es um (längere) Zitate aus ... geht,
sind die Rechte bei/m ... zu erkunden oder eine Erlaubnis einzuholen.
korrigiert: irs 04.01.06
Änderungen wird gelegentlich überarbeitet, ergänzt und vertieft * Anregungen und Kritik willkommen
15.09.15 Linkfehler geprüft und korrigiert.
29.12.08 Ergänzung "Dreiecke" um D15.
19.05.07 Ergänzung "Dreiecke".
17.01.06 Inhalt Imaginäre Geometrie und Anwendung der imaginären Geometrie auf einige Integrale.
15.01.06 Dreiecksbeispiele durch D0 ergänzt.
13.01.06 Briefmarke mit Anschauungsbeispiel.
11.01.06 Hinweis Engel, daß der Bruder 1807 Selbstmord verübt haben soll. Korrekturen Veröffentlichung Anfangsgründe 1829 ... Die Rezension 1840 in Gersdorfs' Repertorium der gesammten deutschen Literatur und einem inoffiziellen Kommentar Gaussens vom 8.2.1844.
10.01.06 Links zu der lateinisch und deutsch [URLs verändert] präsenten Dissertation von Klügel im Netz (Prof. Klaus Volkert, Universität Köln).
08.01.06 Fraenkel zur Mathematik in Erlangen. * Lindemanns zahlreiche Falschbeweise (nach Fraenkel).
07.01.06 1852/53, Tod, Verlust und Geburt einiger Söhne * Werk * Literaturergänzung * Neider.