Inhalt
Editorial.
Zusammenfassung Multivariate Analyse des Pilot-Fragenbogens zum Erleben-02.
Die Daten:
   Originale-Beurteilungsmatrix durch die Befragten.
   Skalierte-Rohwertebearbeitungen zur quantitativen Weiterverarbeitung.
   Zur Interpretation von Korrelationskoeffizienten.
   Skalierte-Rohwerte-Korrelationsmatrix als Basis der Eigenwertanalyse.
   Korrelationsmatrix der Mittelwerte.
Eigenwertanalysen (EWA):
   Eigenwertanalysen (EWA) der Korrelationsmatrix der skalierten Rohwerte.
      Fast-Kollinearitäten in der Korrelationsmatrix der skalierten Rohwerte.
   EWA der Korrelationsmatrix der Mittelwerte.
         Ausgangsdaten Mittelwerte mit zwei Nachkommastellen.
         Unterschiede der Mittelwerte, Korrelationen, Eigenwerte und Determinante bei Berechnung mit 2- und mit 14- Nachkommastellen.
         Unterschiede Rang, Determinante, Inversenbildung und Eigenwerte der Korrelationsmatrizen auf Basis von 2 und 14 Nachkommastellen.
         Korrelationsmatrix der Mittelwerte mit zwei Nachkommastellen.
         Eigenwerte der Korrelationsmatrix der 2stelligen Mittelwerte.
         Eigenwerte der Korrelationsmatrix der 2stelligen Mittelwerte .
           1 Fastkollinearität in Partitionen.
           12 Fast-Kollinearitäten in Paaren.
           2 Fastkollinearitäten in Partitionen.
           3 Fastkollinearitäten in Partitionen.
      FK-Register der erfassten, ausgewerteten und dargestellten Fast-Kollinearitäten.
         FK in der Korrelationsmatrix der skalierten Rohwerte: : FK_F05-F06-F08-F15u-F18
         FK in der  Korrelationsmatrix der Mittelwerte.
Vollständige partielle Korrelationsanalyse (zwei jeweils gegen den Rest von 18).
Systematische Untersuchung zu den Entgleisungen bei Auspartialisierung.
Multple Regressionsanalysen.
Rang-Folgen-Analysen der 11 Gruppen bei den 20 Fragen und ihren Mittelwerten:
   Zusammenfassung Ränge.
   Rangfolge-FB02-MW(MW)  Fragen 1-20.
   Rangfolge-FB02-F01 Grundbegriffsverständnis.
   Rangfolge-FB02-F02 16 Stunden am Tag erleben.
   Rangfolge-FB02-F03 Freunde.
   Rangfolge-FB02-F04 Sonnenuntergang.
   Rangfolge-FB02-F05 Musik.
   Rangfolge-FB02-F06 Blinzeln.
   Rangfolge-FB02-F07 Wetter.
   Rangfolge-FB02-F08 Gelingen.
   Rangfolge-FB02-F09 Gehen.
   Rangfolge-FB02-F10 Erste Tasse morgens.
   Rangfolge-FB02-F11 Quellen des Erlebens.
   Rangfolge-FB02-F12 Achten-1.
   Rangfolge-FB02-F13 Fühlen.
   Rangfolge-FB02-F14 Beeinflussen.
   Rangfolge-FB02-F15u Achten-2 (15 umgepolt).
   Rangfolge-FB02-F16 Merken.
   Rangfolge-FB02-F17 Störungen.
   Rangfolge-FB02-F18 Heilfaktor.
   Rangfolge-FB02-F19 Erlebnisfähigkeit.
   Rangfolge-FB02-F20 Sonstiges/Kritik.

Literatur, Links, Glossar, Anmerkungen und Endnoten, Querverweise, Copyright und Zitierung, Änderungen
 

Matrix der originalen Beurteilungen
Hier wurden die originalen Wahlen ++, +, ? und -  eingetragen. Bei 34 Befragten und 20 Fragen gibt es insgesamt 680 bearbeitete Wahlen in den Zellen. 359 (52.79%) wählten "++" (gute Nachvollziehbarkeit); 157 wählten "+" einigermaßen Nachvollziehbarkeit (23.9%); 17 (2.5%) wählten "?" (Weiß nicht); 46 ( 6.76%) wählten ein " -" (Nein, nicht) und 101 (14.85%) betrafen offene Fragen (OF)/Antworten (rein rechnerisch 102, aber ein OF erhielt ein "?"). Fasst man "++" und "+" zusammen, so wählten 75.88% gute oder einigermaßen Nachvollziehbarkeit zu den Erlebenssachverhalten in den 17 Fragen (ohne die drei offenen F11, F19, F20).

Scorierung der Rohwertwahlen ++, +, ?, -.
Damit die Wahlen rechnerisch und statistisch verarbeitet werden können, müssen sie Zahlen transformiert werden. Zahlenzuordnungen (Scorierungen)  sind in der Psychologie keine  Messungen, sondern quantitative Schätzungen.
    Für die Fragen 1-10 und  12-18 wurde wie folgt scoriert:
++  2 zugeordnet.
+    1 zugeordnet.
?     0.5 zugeordnet.
-     0  zugeordnet.
    Bei Frage 11, der Anzahl der genannten Quelle reicht der Zahlenbereich von 0-26.
    Bei Frage 19, der Erlebnisfähigkeit wurden die Angaben mit 6,5,4,3,2,1,0,-1,-2,-4,-6 scoriert.
    Bei Frage 20 wurde nur erfasst, ob Angaben gemacht wurden (Score 1) oder nicht (Score 0).

Matrix der scorierten Rohwertwahlen
Sie liefert die Grundlage für die rechnerische und statistische Weiterverarbeitung.

Korrelationen scorierter Rohdaten
Sie zeigen die linearen Zusammenhänge in Zahlen zwischen +1 und -1 an, wobei +1 den höchstmöglichen, -1 den geringstmöglichen und keinen Zusammenhang anzeigt, wobei man nicht den Fehler machen darf von 0 auf unabhängig zu schließen. Insgesamt erscheinen die Korrelationen wenig bis mäßig ausgeprägt und stärkere Zusammenhänge gab es gar nicht. Die Analyse von Korrelationen ist nicht einfach, sie birgt viele Tücken und Fallen.
Korrelationen > |0.40| wurden markiert. Lesebeispiele: Die höchste Korrelation mit 0.6018  besteht zwischen dem Erleben als Heilfaktor (heil) und den Störungen des Erlebens (stör). Keinen Zusammenhang gibt es zwischen angenehmes Erleben durch Freunde (Freu) treffen und Begriffsverständnis (2GrB) von erleben. Insgesamt erscheinen die Korrelationen wenig bis mäßig ausgeprägt und stärkere Zusammenhänge gibt es gar nicht.

Mittelwerte der Rohwertscorierungen (mit 2 Nachkommastellen)
Die Tabelle (Matrix) gibt die Mittelwerte für die 11 Gruppen an.

Eigenwerte der Rohwerte-Korrelationsmatrix
Die Korrelationsmatrix der Rohwerte zeigt mit vier Eigenwerten < 0.20 vier Fast-Kollinearitäten an, was man bei den nur mäßig ausgeprägten Korrelationskoeffizienten nicht vermutet hätte.

Fast-Kollinearitätsanalyse der Korrelationsmatrix der scorierten Rohwerte
Obwohl die Korrelationen je zweier Variablen nur mäßige Ausprägungen zeigen, zeigen die vier Eigenwerte < 0.20 vier Fast-Kollinearitäten an.

Korrelationen der Mittelwerte der Rohwertscorierungen
Die Korrelationsmatrix der Mittelwerte zeigt schon durch ihre hohen Koeffizienten 12 fast-kollineare 2er-Partitionen, also Paare
an, die die informativsten und einfachsten für die Interpretation sind. Im Zuge der Erkenntnis der hochgradig numerisch instabilen Korrelationsmatrix der Mittelwerte wurden zusätzlich zu den Mittelwerten mit zwei Nachkommastellen auch die Mittelwerte mit 14-Nachommastellen gerechnet.

Eigenwerte der Mittelwert-Korrelationsmatrix
Die hochgradig numerisch instabile Korrelationsmatrix der 2-stelligen Mittelwerte hat es in sich. Die Korrelationsmatrix mit Ordnung 20 der Mittelwerte zeigt 10 artefiziell echt lineare Abhängigkeiten (Kollinearitäten) und 4 Fast-Lineare Abhängigkeiten (Fast-Kollinearitäten). Die echten linearen Abhängigkeiten sind artefiziell, weil die Ausgangsmatrix 20 Spalten aber nur 11 Zeilen hat. Aber die vier fast-kollinearen werden dadurch nicht erklärt und sind ein empirisch-mathematisch außerordentlicher Befund.
Mit Hilfe einer vollständigen Partitionsanalyse, wenn die Anzahl der Variablen aus kombinatorischen Explosionsgründen nicht zu groß ist,  kann man sämtliche Partitionen aufspüren, die Eigenwerte < 0.20, also  Fast-Kollinearitäten  enthalten. Die kleinste mögliche - und interessanteste - Partition ist 2. Davon gibt es in einer 20er Matrix 190.
    Da die Korrelationsmatrix der Mittelwerte hochgradig kollinear und fast-kollinear ist, ist sie natürlich auch hochgradig numerisch instabil, was heißt, dass kleinste Veränderungen auf der Eingangsseite extreme Auswirkungen auf der Ausgangsseite haben können. Nur zwei Nachkommastellen sind eine potentielle Quelle für Entgleisungen korrelativer Kennwerte. Ich habe deshalb zur Kontrolle und Sicherheit die Mittelwerte noch einmal mit doppelter Genauigkeit auf 14 Nachkommastellen berechnet, um zu kontrollieren, wie Eigenwerte und Determinante der Korrelationsmatrix der 14stelligen-Mittelwerte sich gegenüber der 2stelligen Variante verhalten.

Fast-Kollinearitätsanalyse der Korrelationsmatrix der Mittelwerte der scorierten Rohwerte
In der Korrelationsmatrix der Mittelwerte fanden sich 12 Paare, also 6.3% (=(12/190)*100), die Eigenwerte < 0.20 hatten und damit  Fast-Kollinearität  (Fast-Gesetzmäßig- oder Regelhaftigkeit) anzeigen. > Fast-Kollinearitätregister.

Vergleich Korrelationsmatrix der Mittelwerte mit 2 und 14-Nachkommastellen
Man  sieht, es gibt zwar beachtliche Unterschiede schon ab der zweiten Nachkommastelle, etwa 0.0878 zwischen 6-blinz und 15u-nich, aber die meisten bewegen sich deutlich darunter, wie man direkt den Mittelwerten der absoluten Abweichungen entnehmen kann.

Unverständliche oder schwer nachvollziehbare Korrelationen
Wenn Korrelationen gänzlich unverständlich sind, drängen sich zwei Standardüberlegungen zur Interpretation von Korrelationskoeffizienten auf: (1) statistisch-zufälliger Zusammenhang ohne inhaltliche Bedeutung? (2) statistischer Zusammenhang durch verdeckte andere Variablen (Moderatorvariablen)?. Hier ist dann partielle Korrelationsanalyse angesagt, wobei man den gewöhnlich unbekannten relevanten Merkmalsraum kennen und auf positive Semidefinitheit achten sollte.

Vollständige partielle Korrelationsanalyse (zwei jeweils gegen den Rest von 18)
Man kann den gesamten Merkmalsraum in dieser Untersuchung durch die 20 Fragen (Variablen) als definiert ansehen. Man sollte aber an den Satz des Mathematikers Dr. Hain  denken: vollständig partialisierte Korrelationsmatrizen sind nicht notwendig positiv semidefit und können schwerwiegende Entgleisungen hervorrufen, wie es sich in dieser multivariaten Untersuchung auch tatsächlich ergeben und  gezeigt hat.

• Systematische Unterschungen zu Entgleisungen beu Auspartialisieren.
• Zusammenfassung Auspartialisierung der Korrelationsmatrix der Mittelwerte mit 14-Nachkommastellen.
• Weitere Einzellbeispiele.

Ende der Zusammenfassung multivariate Analyse

Die Daten

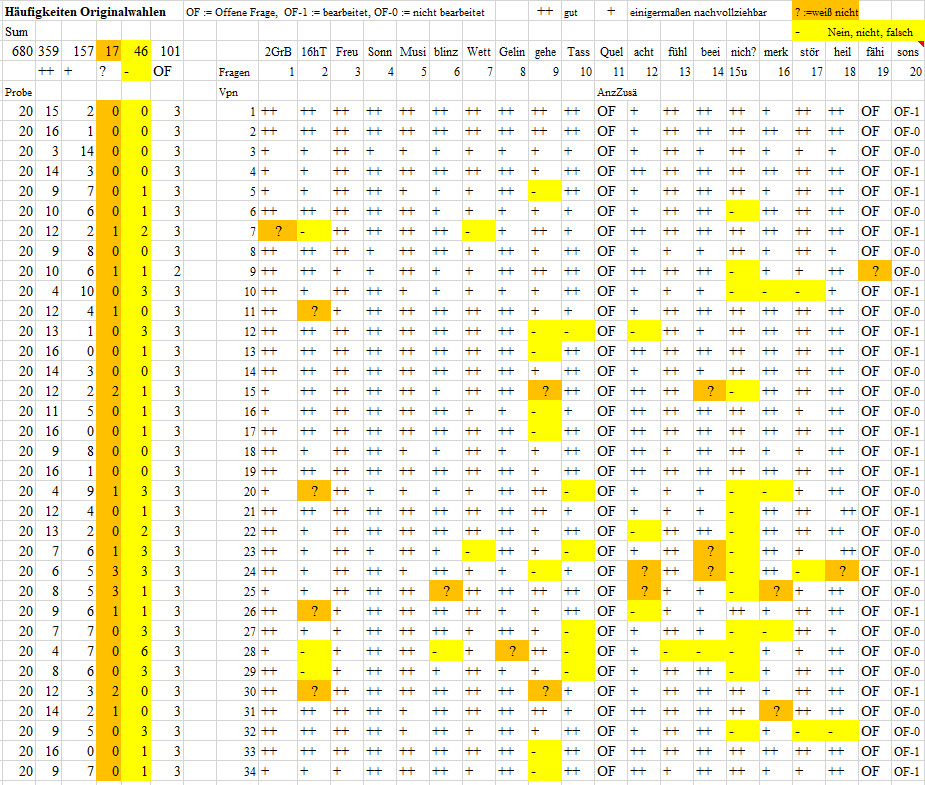
Originale-Beurteilungsmatrix durch die Befragten

Bei 34 Befragten und 20 Fragen gibt es insgesamt 680 bearbeitete Wahlen in den Zellen. 359 (52.79%) wählten "++" (gute Nachvollziehbarkeit); 157 wählten "+" einigermaßen Nachvollziehbarkeit (23.9%); 17 (2.5%) wählten "?" (Weiß nicht); 46 ( 6.76%) wählten ein " -" (Nein, nicht) und 101 (14.85%) betrafen offene Fragen (OF)/Antworten (rein rechnerisch 102, aber ein OF erhielt ein "?"). Fasst man "++" und "+" zusammen, so wählten 75.88% gute oder einigermaßen Nachvollziehbarkeit zu den Erlebenssachverhalten in den 17 Fragen (ohne die drei offenen F11, F19, F20).
    Die Häufigkeiten sind unabhängig von weiterverarbeitenden Skalierungen, aber nicht die weiterverarbeiteteten Größen wie z.B. Summen, Mittelwerte, Korrelationen, Eigenwerte.

Quartile der Wahlen
 

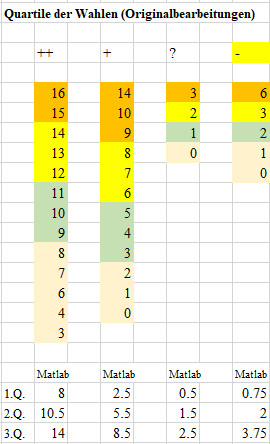
Zur Einschätzung der Häufigkeiten der Wahlen gut nachvollziehbar (++), einigermaßen nachvollziehbar (+),  ( ? ) unklar, weiß nicht und " - " Nein, nicht falsch wurden die Quartile berechnet (hier mit Matlab). Sie erlauben eine grobe Einschätzung mit wie viel Wahlen man sich in der Stichprobe wo befindet.  Mit 15 oder mehr " ++ " Wahlen (gute Nachvollziehbarkeit) gelangt man ins 4. Quartil. Mit 2 oder weniger " +" Wahlen (einigermaßen nachvollziehbar) befindet man sich im 1. Quartil, also bei den ersten 25%. Mit 1 ist man  mit " ? " (unklar, weiß nicht) am Median, der die Stichprobe teilt. Mit 3 " - "  (Verneinungen) befindet man sich im 3. Quartil, also den dritten 25% der Stichprobe.

Originale Bearbeitungen. Muster und Wahlen

Man beachte: Die Häufigkeitsverteilungen ändern sich nicht, wenn man die Skalierung der Originalbearbeitungen ändert.

Die Mittelwerte der Mittelwerte und die Mittelwerte der skalierten Rohwerte sind hier.

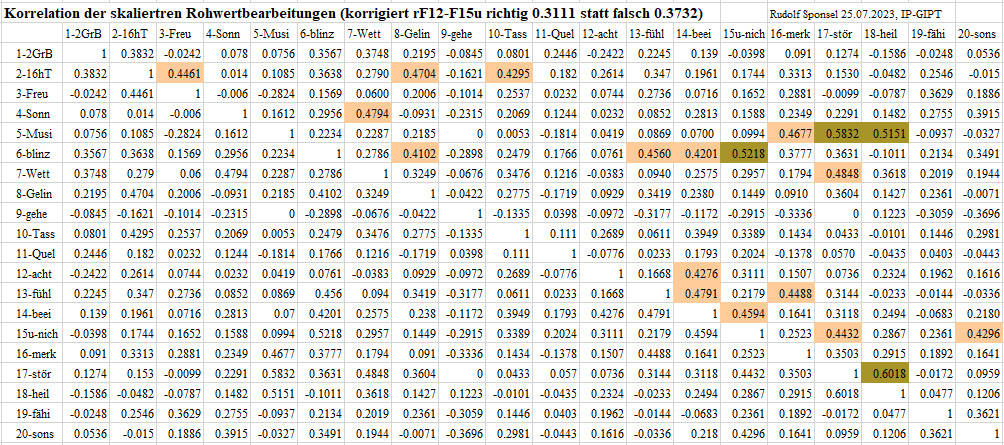
Korrigiert am 25.07.2023

Ziel von Eigenwertanalysen: aufspüren von Eigenwerten nahe 0, d.h. operational < 0.20 (entspricht einer Korrelation >= |0.80|). Ein Eigenwert nahe 0, operational < 0.20, zeigt eine Fast-Lineare Abhängigkeit oder  Fast-Kollinearität  an. Das bedeutet eine Gesetz- oder Regelhaftigkeit, also genau das, wonach man in der Wissenschaft sucht.

Die kleinste Partitionseinheit in einer Korrelationsmatrix besteht aus 2, gefolgt von 3, 4, ...n, mit n = Ordnung der Matrix = Anzahl der Variablen. Die kleinste Einheit ist auch die informativste. Allgemein gibt es in einer Korrelationsmatrix der Ordnung n  part=2^n-(n+2) + 1 Partitionen (Sponsel 2005, S.16 und tabelliert für n 2-50 S. 77).

über 2 Partitionen, n über 3 Dreier-Partitionen, ... bis n-2.  Bei den 20 Fragen des Pilot-Fragebogen sind das:

• 2 aus 20 = 190
• 3 aus 20 = 1140
• 4 aus 20 = 4845
• 5 aus 20 = 15504
• 6 aus 20 = 38760
• 7 aus 20 = 77520
• 8 aus 20 = 125.970
• 9 aus 20 = 167.960
• 10 aus 20 = 184.756
• 11 aus 20 = 167.960
• 12 aus 20 = 125.970
• 13 aus 20 = 77520
• 14 aus 20 = 38760
• 15 aus 20 =  15504
• 16 aus 20 = 4845
• 17 aus 20 = 1140
• 18 aus 20 = 190
• 19 aus 20 = 20
• 20 aus 20 =  1

Insgesamt, wollte man alle auswerten, gäbe es 1.048.555 Partitionen, das könnte bei meinem Rechner ungefähr 30 Stunden dauern. Größere Partitionen sind schwierig zu interpretieren. Für die Praxis sollte es reichen, wenn man sich auf sechs Partitionen beschränkt und damit der kombinatorischen Explosion aus dem Weg geht.

Am 11.07.2023 habe ich auf meinem Rechner (Intel(R) Core(TM) i7-3770K CPU @ 3.50GHz  3.90 GHz; Win10) um 1:30 Uhr einen Lauf mit Matlab (R2021a home use) gestartet um alle Partitionen in der 20*20 Korrelationsmatrix - das sind 1.048.555 - zu berechnen. Morgens um 7:30 Uhr brach ich  bei 196.000 ab.

EWA der Korrelationsmatrix der skalierten Rohwerte

Fast-Kollinearitäten in der Korrelationsmatrix der skalierten Rohwerte der 34 ProbandInnen
Eine Korrelationsmatrix der Ordnung n hat die Eigenwertsumme n, hier also 20. Die erste Spalte gibt die absoluten Eigenwerte an. Die zweite Spalte EigAnteil gibt den Anteil von 20 an, die dritte Spalte Ant% den Eigenwertanteil in % und die vierte Spalte summiert die  Prozentwerte der Eigenwertanteile auf,  so dass am Ende mit kleinen Rundungsfehlern 100% stehen sollten. Die letzten vier Eigenwerte sind < 0.20 und zeigen damit eine  Fast-Kollinearität  an:

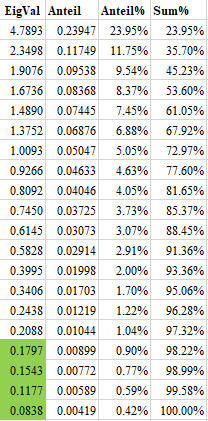
Anmerkung: korrigiert am 25.07.2023

Hier ist nun besonders interessant, zwischen welchen Variablen die Fast-Kollinearitäten  bestehen. Hierzu hat mir ein Mathematiker ein Programm geschrieben, das die Eigenwerte sämtlicher Partitionen berechnet.
_
Fast-Kollinearitäten Korrelationsmatrix skalierter Rohwerte
[Nach neuer Korrelationsrechnung 25.07.2023]

Zusammenfassung-Fast-Kollinearitäten-Korrelationsmatrix-skalierter-Rohwerte
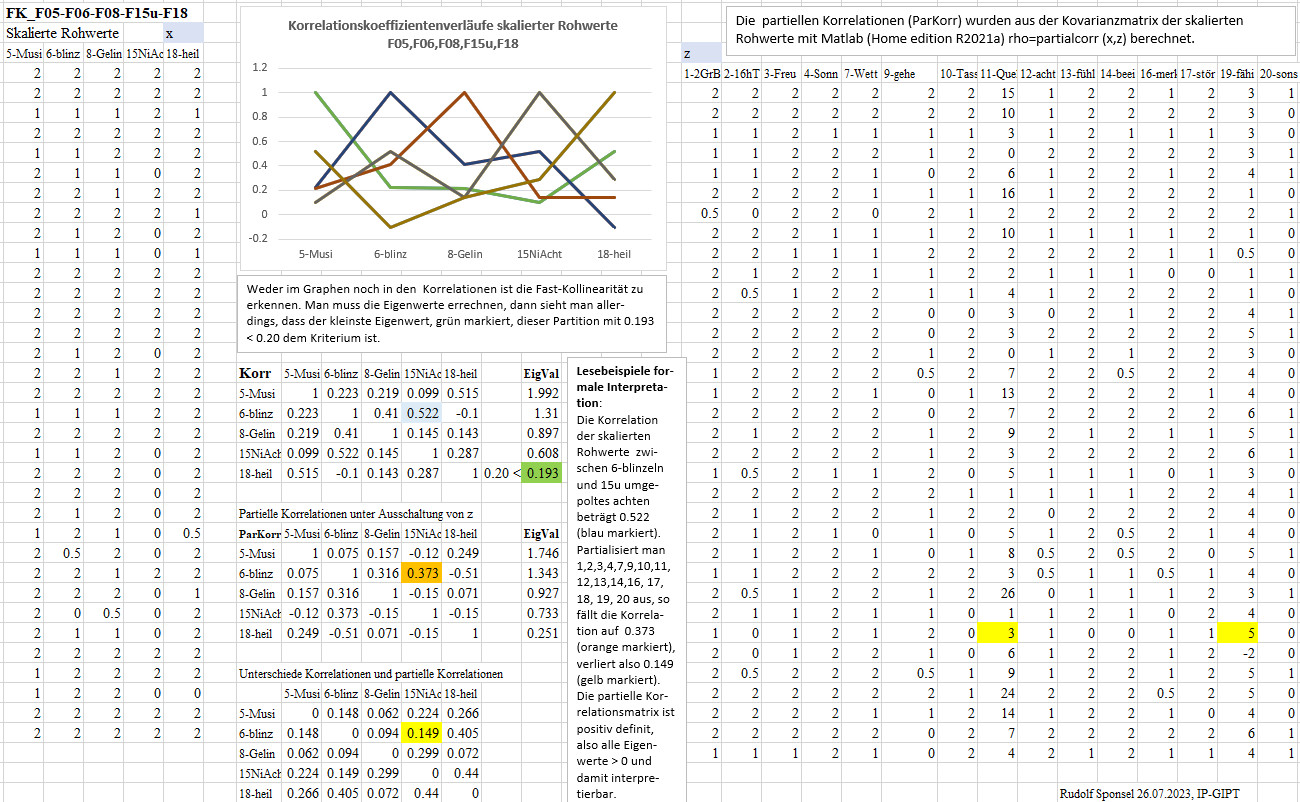
Es wurden alle Partitionen mit Eigenwerten < 0.20 gesucht. Die erste, die gefunden wurde, ist eine 5er-Partition: FK_F05-F06-F08-F15u-F18. Weder im Graphen noch in den  Korrelationen ist die Fast-Kollinearität zu erkennen. Man muss die Eigenwerte errechnen, dann sieht man allerdings, dass der kleinste Eigenwert dieser Partition mit 0.193 (grün markiert) < 0.20 (Kriterium) ist. Lesebeispiele formale Interpretation: Die Korrelation der skalierten Rohwerte  zwischen 6-blinzeln und 15u umgepoltes achten beträgt 0.522 (blau markiert). Partialisiert man 1,2,3,4,7,9,10,11,12,13,14,16, 17, 18, 19, 20 aus, so fällt die Korrelation auf  0.373 (orange markiert), verliert also 0.149 (gelb markiert). Die partielle Korrelationsmatrix ist positiv definit, also alle Eigenwerte > 0 und damit interpretierbar. Anmerkung: Die  partiellen Korrelationen (ParKorr) wurden aus der Kovarianzmatrix der skalierten Rohwerte mit Matlab (Home edition R2021a) rho=partialcorr (x,z) berechnet.

5er Partition: FK_F05-F06-F08-F15u-F18

FK-Register der erfassten, ausgewerteten und dargestellten Fast-Kollinearitäten:

Erfasst, analysiert und dargestellt in der Korrelationsmatrix der skalierten Rohwerte:
FK_F05-F06-F08-F15u-F18

Bislang nur erfasst (Auswahl: 27):
 

part:    6  14  17  18  19 part:    6  14  17  18  20  part:    1   3   5   6  15  18  part:    1   4   5   6  15  18  part:    1   4   6   7   8  15  part:    1   5   6   8  15  18  part:    1   5   6  14  15  18  part:    1   5   6  15  18  19  part:    1   6  14  17  18  19

part:    1   6  14  17  18  20  part:    2   5   6   8  15  18  part:    2   5   6  14  15  18  part:    2   6   8  11  16  18  part:    2   6   8  15  16  18  part:    2   6  14  17  18  19  part:    2   6  14  17  18  20  part:    3   4   5   6  15  18  part:    3   5   6   7  15  18

part:    3   5   6   8  15  18 part:    3   5   6  14  15  18  part:    3   5   8  13  16  17  part:    3   5   8  13  16  19  part:    3   6   8  15  16  18  part:    3   6  14  17  18  19 part:    3   6  14  17  18  20  part:    3   6  16  17  18  20  part:    4   5   6   8  15  18  .......................................

 Erfasst, analysiert und dargestellt aus der Korrelationsmatrix der Mittelwerte:

1. FK_F01-F02-F04  1 FK in 3er Part
2. FK_F01-F02-F04-F15u  3 Fast-Kollinearität in einer 4er Partition
3. FK_F01-F02-F04-F18   in F18 2 FK in 4er Part
4. FK_F01-F02-F13  von FK_F13  1 FK in 3er Part
5. FK_F01-F02-F15u  1 Fast-Kollinearität in einer 3er Partition
6. FK_F01-F02-F18  in F18
7. FK_F01-F02-F20  1 Fast-Kollinearität in  einer 3er-Partition
8. FK_F01-F03-F08  1 FK in 3er Part
9. FK_F01-F04-F07-F08-F11   in F11  3 Fast-Kollinearitäten in einer 5er-Partition
10. FK_F01-F04-F07-F08-F13   3 Fast-Kollinearitäten in zwei 5er-Partitionen.
11. FK_F01-F04-F07-F08-F14   in F14  3 Kollinearitäten in 5er Part
12. FK_F01-F04-F07-F08-F20   in F20   3-FK
13. FK_F01-F04-F07-F11-F13   3 Fast-Kollinearitäten in zwei 5er-Partitionen.
14. FK_F02-F03-F15u    in F15u  1 Fast-Kollinearität in einer 3er-Partition
15. FK_F02-F13     in F13 2-16hT - 13-fühl,   1 Fast-Kollinearität in Paaren
16. FK_F02-F15u   in F15u  2-16hT - 15u-achten (umgepolt)   1 Fast-Kollinearität in Paaren
17. FK_F06-F17:    in F17   1 Fast-Kollinearität in Paaren
18. FK_F07-F14    in F14    1 Fast-Kollinearität in Paaren
19. FK_F07-F20    in F20    1. Fast-Kollinearität in Paaren
20. FK_F09-F14    in F14   1 Fast-Kollinearität in Paaren
21. FK_F10-F18:   1 Fast-Kollinearität in Paaren
22. FK_F11-F13:   in F13   1 Fast-Kollinearität in Paaren
23. FK_F11-F14:   in F11   1 Fast-Kollinearität in Paaren
24. FK_F13-F15u  1 Fast-Kollinearität in Paaren
25. FK_F14-F20    1 Fast-Kollinearität in Paaren
26. FK_F16-F19:   1 Fast-Kollinearität in Paaren
27. FK-Befinden bei Bearbeitung. (4=gut - 3=befriedigend, 2=geht)
28. FK-Dauer der Bearbeitung (kurz und lang)
29. FK_SambistasNichtSambistas: Fast-Kollinearität der Mittelwertsverläufe.

Korrelationsmatrix der 2stelligen Mittelwerte als Basis der Eigenwertanalyse
Bildet man über alle 20 Fragen den Mittelwert erhält man eine Information, wie hoch die jeweiligen Gruppen die Nachvollziehbarkeit der Erlebenssachverhalte einschätzen. So kamen alle (n=34) bei Frage 01 zu den zwei Hauptbedeutungen des Erlebensbegriffs auf 1.69 (Wertebereich 0-2).
Lesebeispiel 05 Musik: Bei Frage 05 Musik als Erlebensverstärker kommt die Altersgruppe 20-55 auf den ersten Rang mit Mittelwert 1.89, Frauen und Berufsgruppe 3 Kaufmännisch-Sprache zugleich auf den 2. Rang mit Mittelwert 1.88 und die Sambistas auf Rang 3 mit Mittelwert 1.83. Der kleinste Mittelwert bei Musik mit 1.65 findet sich bei den Männern. Die Spanne Max-Min bei den Mittelwerten beträgt 1.89-1.65 = 0.24. Mehr und ausführlich bei den Rangfolgen nach Mittelwerten der 20 Fragen.

Ausgangsdaten 2stellige Mittelwerte
Vorbemerkung: Da die Korrelationsmatrix der Mittelwerte hochgradig kollinear und fast-kollinear ist, ist sie natürlich auch hochgradig numerisch instabil, was heißt, dass kleinste Veränderungen auf der Eingangsseite extreme Auswirkungen auf der Ausgangsseite haben können. Nur zwei Nachkommastellen sind eine potentielle Quelle für Entgleisungen korrelativer Kennwerte. Ich habe deshalb zur Kontrolle und Sicherheit die Mittelwerte noch einmal mit doppelter Genauigkeit auf 14 Nachkommastellen berechnet, um zu kontrollieren, wie Eigenwerte und Determinante der Korrelationsmatrix der 14stelligen-Mittelwerte sich gegenüber der 2stelligen Variante verhalten.

Korrelationsmatrix der Mittelwerte mit zwei Nachkommastellen

_

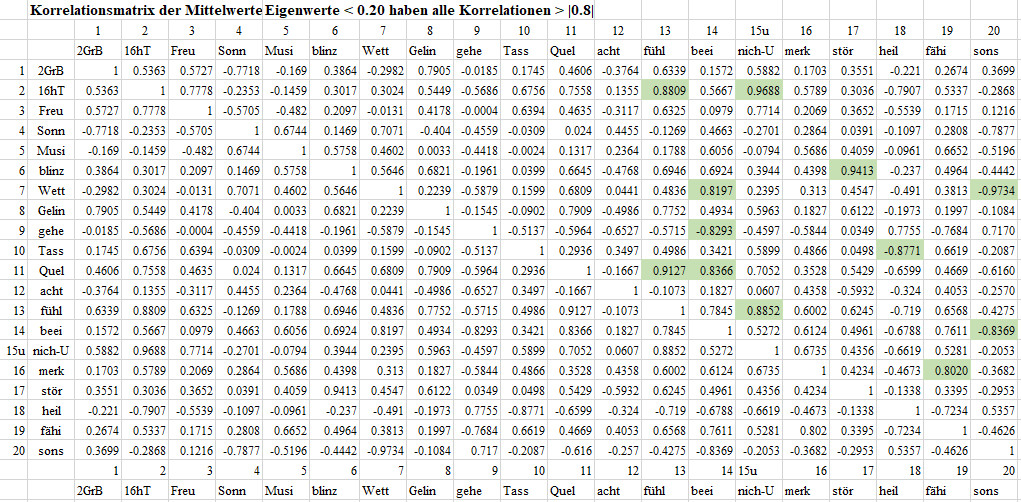
Eigenwerte der Korrelationsmatrix der 2stelligen Mittelwerte

Die hochgradig numerisch instabile Korrelationsmatrix der Mittelwerte mit zwei Nachkommastellen hat es in sich. Die Korrelationsmatrix mit Ordnung 20 der Mittelwerte zeigt 10 artefiziell echt lineare Abhängigkeiten (Kollinearitäten) und 4 Fast-Lineare Abhängigkeiten (Fast-Kollinearitäten). Die echten linearen Abhängigkeiten sind artefiziell, weil die Ausgangsmatrix 20 Spalten aber nur 11 Zeilen hat. Aber die vier fast-kollinearen werden dadurch nicht erklärt und sind ein empirisch-mathematisch außerordentlicher Befund.
Mit Hilfe einer vollständigen Partitionsanalyse, wenn die Anzahl der Variablen aus kombinatorischen Explosionsgründen nicht zu groß ist, kann man sämtliche Partitionen aufspüren, die Eigenwerte < 0.20, also  Fast-Kollinearitäten  enthalten. Die kleinste mögliche - und interessanteste - Partition ist 2. Davon gibt es in einer 20er Matrix 190. In der Korrelationsmatrix der Mittelwerte fanden sich 12 Paare, also 6.3% (=(12/190)*100), die Eigenwerte < 0.20 hatten und damit  Fast-Kollinearität  (Fast-Gesetzmäßig- oder Regelhaftigkeit) anzeigen.
 

Sucht man nach Partitionen mit Eigenwerten <0.20, findet man auf kleinster Ebene von 2er-Partitionen 12 Paare.

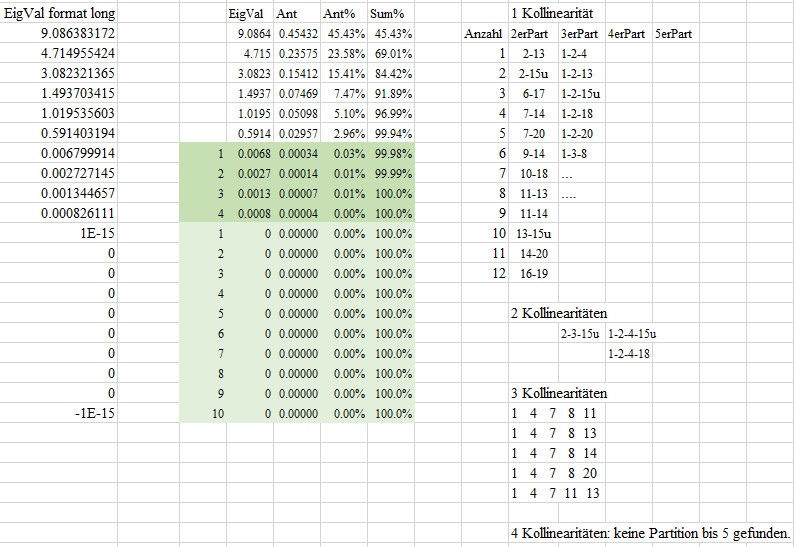
Fastkollinearitäten in der Korrelationsmatrix der 2stelligen-Mittelwerte
Man beachte, dass Mittelwerte Gruppen (Stichproben, Populationen) charakterisieren und nichts unmittelbar für den konkreten Einzelfall aussagen, es sei denn, es sind Mittelwerte eines Einzelfalles.

Partitionen in Korrelationsmatrizen
In Partitionen > 2 können mehrere Kollinearitäten vorkommen. Hier werden bis zu drei erfasst.

1 Fastkollinearität in Partitionen, hier zwei, drei, vier, der Korrelationsmatrix der 2stelligen-Mittelwerte

Fastkollinearitäten in den Paaren = Zweier Partitionen der Korrelationsmatrix der 2stelligen-Mittelwerte
Vorbemerkungen-Interpretation: (1) Die Eigenwerte in 2er-Partitionen von Korrelationsmatrizen lassen sich direkt aus den Korrelationskoeffizienten ablesen (Sponsel 30.06.2023). (2) > Zur Interpretation von Korrelationskoeffizienten. Die folgenden Interpretationen sind formal motiviert und man sollte sie erstmal nur als Zusammenhangshypothesen betrachten. Ob sich vernünftige inhaltliche Erklärungen finden lassen, erfordert vertiefte Betrachtungen, die hier (noch) nicht geboten werden.

Die hochgradig numerisch instabile Korrelationsmatrix aller 20 2stelligen-Mittelwerte  hat es in sich: sie zeigt allein 12 fast-lineare Abhängigkeiten oder Fast-Kollinearitäten zwischen Frage-Paaren (F02-F13;  F02-F15u; F06-F17; F07-F14; F07-F20; F09-F14; F10-F18; F11-F13, F11-F14; F13-F15u; F14-F20; F16-F19), also der kleinsten möglichen und informativsten Partition. Das sind von den 190 (20 über 2) möglichen Paaren immerhin 6.3%, was für empirische Daten schon sehr beachtlich ist.
 

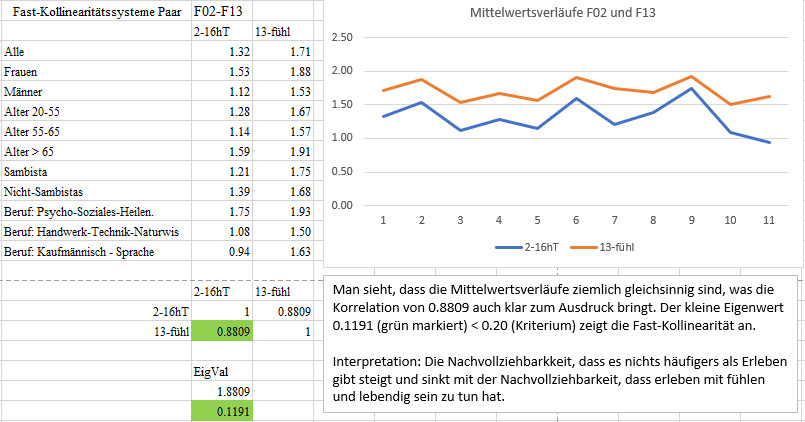
FK_F02-F13  16hT - fühl, r = 0.8809, Eigenwerte 1.8809, 0.1191 < 0.20. Gruppen, die 16 Stunden am Tag erleben als häufigstes psychisches Phänomen für nachvollziehbar halten, halten es auch für nachvollziehbar, fühlen und lebendig sein als wesentliches Element des Erleben anzusehen - und umgekehrt.
 

FK_F02-F15u  16hT - nich-U, r = 0.9688, Eigenwerte 1.9688, 0.0312 < 0.20. Gruppen, die 16 Stunden am Tag erleben als häufigstes psychisches Phänomen für nachvollziehbar halten, halten es für ebenso nachvollziehbar, auf sein Erleben zu achten- und umgekehrt.

FK_F06-F17  blinz  - stör, r = 0.9413, Eigenwerte 1.9413, 0.0587< 0.20. Gruppen, die es für nachvollziehbar halten, es angenehm zu erleben, auf einer Bank durch die Baumwipfel in die Sonne zu blinzeln, halten auch die Störungen des Erlebens für ebenso nachvollziehbar - und umgekehrt.

FK_F07-F14  Wett - beei, r = 0.8197, Eigenwerte 1.8197, 0.1803< 0.20. Gruppen, die das Erleben der Wettersituation für nachvollziehbar halten, halten  auch die Beeinflussbarkeit des Erlebens für nachvollziehbar - und umgekehrt.

FK_F07-F20  Wett - sons, r = - 0.9734, Eigenwerte 1.9734, 0.0266< 0.20. Achtung: negative Korrelation! Gruppen, die das Erleben der Wettersituation für nachvollziehbar halten, halten  Anmerkungen unter Sonstiges für wenig nachvollziehbar (negative Korrelation) - und umgekehrt.

FK_F09-F14  gehe - beei, r = - 0.8293, Eigenwerte 1.8293, 0.1707< 0.20. Achtung: negative Korrelation! Gruppen, die es für nachvollziehbar halten, ihr gehen nicht besonders zu beachten, sondern einfach zu gehen, halten auch für nachvollziehbar, dass man sein Erleben nicht (negative Korrelation) beeinflussen kann

FK_F10-F18 Tass - heil, r = - 0.8771, Eigenwerte 1.8771, 0.1229< 0.20. Achtung: negative Korrelation! Gruppen, die für nachvollziehbar halten, ihr erstes Morgengetränk als kleines Erlebnis anzusehen, halten es für wenig nachvollziehbar (negative Korrelation) dass einige Psychotherapieschulen meinen, erleben sei ein Heilfaktor - und umgekehrt.

FK_F11-F13 Quel - fühl, r = 0.9127, Eigenwerte 1.9127, 0.0873< 0.20. Gruppen, die viele Quellen des Erlebens für nachvollziehbar halten, halten es auch für nachvollziehbar, dass fühlen und lebendig  sein wesentliche Elemente des Erlebens sind.

FK_F11-F14 Quel - beei, r = 0.8366, Eigenwerte 1.8366, 0.1634 < 0.20. Gruppen, die viele Quellen des Erlebens für nachvollziehbar halten, halten es auch für nachvollziehbar, dass man sein Erleben beeinflussen kann.

FK_F13-F15u fühl - nich-U, r = 0.8852, Eigenwerte 1.8852, 0.1148< 0.20. Gruppen, die nachvollziehbar finden, dass fühlen und lebendig sein wesentliche Elemente für das Erleben sind,  halten es auch für nachvollziehbar, auf sein Erleben besonders zu achten. Die Frage 15 wurde zu 15u  umgepolt.

FK_F14-F20 gehe - sons, r = - 0.8369, Eigenwerte 1.8369, 0.1631< 0.20. Achtung: negative Korrelation! Gruppen, die es es für nachvollziehbar halten, auf ihr Gehen nicht besonders zu achten, sondern meist einfach gehen, halten Anmerkungen unter Sonstiges für wenig nachvollziehbar (negative Korrelation) - und umgekehrt.

FK_F16-F19 merk - fähi, r = 0.8020, Eigenwerte 1.8020, 0.1980< 0.20. Gruppen, die nachvollziehbar merken, wenn etwas im Erleben nicht so läuft, halten sich auch für erlebnisfähiger - und umgekehrt.

1 Fastkollinearität in Dreier-Partitionen der Korrelationsmatrix der Mittelwerte

FK_F01-F02-F04

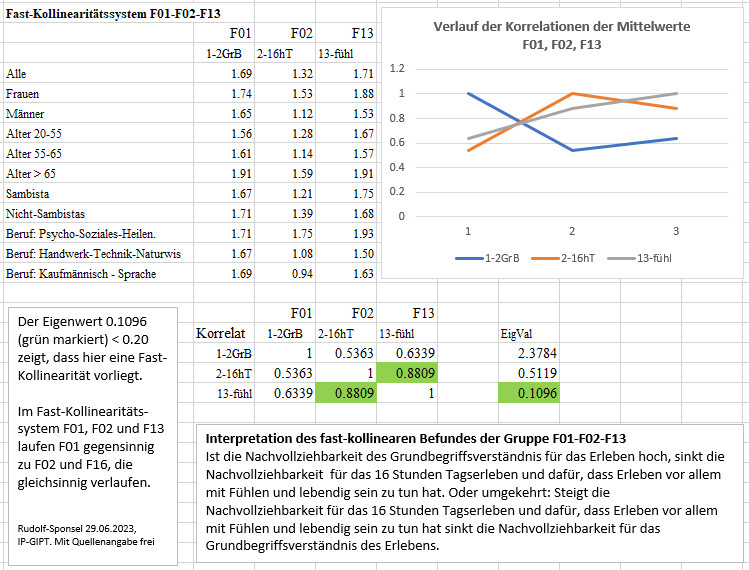
FK_F01-F02-F13  Der Eigenwert 0.1096 (grün markiert) < 0.20 zeigt, dass hier eine Fast-Kollinearität vorliegt. Im Fast-Kollinearitätssystem F01, F02 und F13 laufen F01 gegensinnig zu F02 und F16, die gleichsinnig verlaufen. Interpretation des fast-kollinearen Befundes der Gruppe F01-F02-F13. Ist die Nachvollziehbarkeit des Grundbegriffsverständnisses für das Erleben hoch, sinkt die Nachvollziehbarkeit  für das 16 Stunden Tagserleben und dafür, dass Erleben vor allem mit Fühlen und lebendig sein zu tun hat. Oder umgekehrt: Steigt die Nachvollziehbarkeit für das 16 Stunden Tagserleben und dafür, dass Erleben vor allem mit Fühlen und lebendig sein zu tun hat sinkt die Nachvollziehbarkeit für das Grundbegriffsverständnis des Erlebens.

FK_F01-F02-F15u
FK_F01-F02-F18
FK_F01-F02-F20
FK_F01-F03-F08
...
...

2 Fast-Kollinearitäten in Partitionen  der Korrelationsmatrix der Mittelwerte
FK_F02-F03-F15u

3 Fast-Kollinearitäten in Partitionen  der Korrelationsmatrix der Mittelwerte
FK_F01-F02-F04-F15u
FK_F01-F02-F04-F18
FK_F01-F04-F07-F08-F11

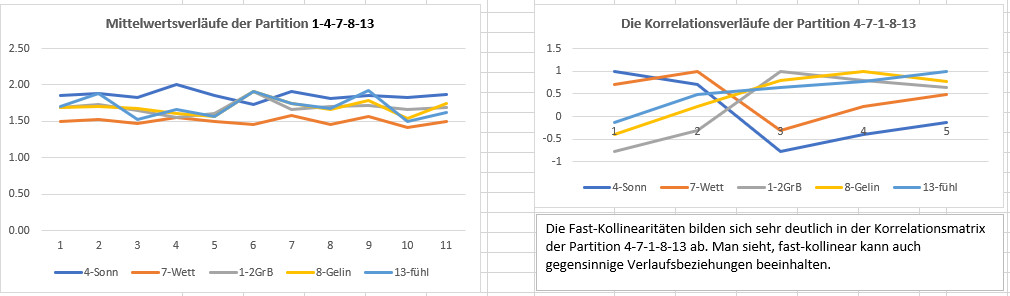
FK_F01-F04-F07-F08-F13  Die Fast-Kollinearitäten bilden sich sehr deutlich in der Korrelationsmatrix der Partition 4-7-1-8-13 ab. Man sieht, fast-kollinear kann auch gegensinnige Verlaufsbeziehungen beinhalten.
 

Unterschiede der Mittelwerte, Korrelationen, Eigenwerte und Determinante bei Berechnung mit 2- und mit 14- Nachkommastellen
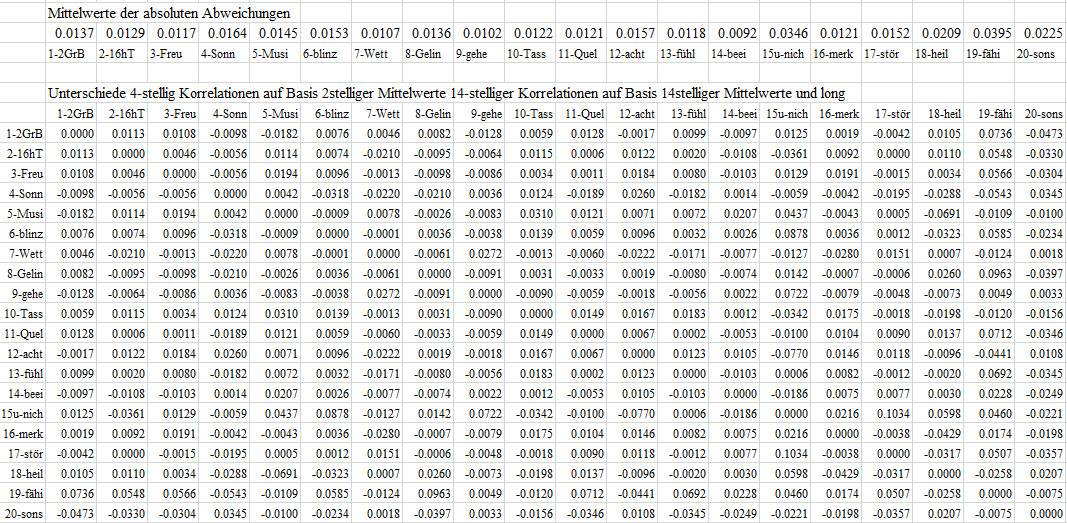
Man  sieht, es gibt zwar beachtliche Unterschiede schon ab der zweiten Nachkommastelle, etwa 0.0878 zwischen 6-blinz und 15u-nich, aber die meisten bewegen sich deutlich darunter, wie man direkt den Mittelwerten der absoluten Abweichungen entnehmen kann.

Unterschiede Rang, Determinante, Inversenbildung und Eigenwerte der Korrelationsmatrizen auf Basis von 2 und 14 Nachkommastellen
Die Korrelationsmatrix der Mittelwerte ist hochgradig kollinear und fast-kollinear und damit in höchstem Maß numerisch instabil, so dass man bei multivariaten Rechnungen auf allerlei gefasst sein muss und sehr aufpassen sollte (siehe bitte vollständige partielle Korrelationsanalyse). Es wurden Rang, Determinante, Inversenbildung und die Eigenwerte der Korrelationsmatrizen der Mittelwerte auf Basis von 2 und 14 Nachkommastellen miteinander verglichen.  Es müsste 10 Eigenwerte glatt 0 geben, was vermutlich aufgrund von kleinen Rundungsfehlern nicht der Fall ist. Matlab weist für r34NK14 Rang 7 und für r34NK2 Rang 10 aus. Die Determinante ist für r34NK14 mit 198 Nullen nach dem Komma praktisch 0. Trotzdem kann Matlab die Inverse bilden, wenn auch mit Warnung: "Warning: Matrix is close to singular or badly scaled. Results may be inaccurate. RCOND =  3.236109e-18."
 

Rechnung mit Matlab R2021a Home Edition durchgeführt (29.07.2023)	Korrelationsmatrix der Mittelwerte mit 2 Nachkomma	Korrmatrix Basi 14 Nachkomma	Bemerkungen
Rang	10	7	Numerisch mathematisch können in der 2-Nachkommastellenrechnung die 11 Gruppen auf 10, in der 14-Nachkommastellenrechnung auf 7 reduziert werden.
Determinante	5.610018331596747e-168	-1.878666478427723e-198	Da die Determinante u.a. das Produkt aus den Eigenwerten ist, und bei 2 Nachkommastellen vier negative Eigenwerte vorliegen, verschwinden die negativen Vorzeichen durch das geradzahlige Multiplizieren. Bei 14 Nachkommastellen ist die Determinante negativ, weil es fünf negative Eigenwerte gibt und durch die ungerade Anzahl das negative Vorzeichen erhalten bleibt.
Inversenbildung	Gelingt, aber mit Warnung: "Warning: Matrix is close to singular or badly scaled. Results may be inaccurate. RCOND =  .091418e-18."	Gelingt, aber mit Warnung: "Warning: Matrix is close to singular or badly scaled. Results may be inaccurate. RCOND = 3.236109e-18."	Nach der reinen Mathematik dürfte es gar keine Inversenbildung geben. Aber reine und numerische Mathematik sind eben zwei Welten. Vermutlich bewirken kleine Rundungsfehler die Fast-Kollinearitätsdiagnose von Matlab.
Eigenwerte	Eigenwerte 2 NK  9.086383172274570  4.714955424119610  3.082321364514860  1.493703415135060  1.019535602882060  0.591403193938404  0.006799913688422  0.002727145098223  0.001344656916989  0.000826111431777  0.000000000000001  0.000000000000000  0.000000000000000   0.000000000000000  0.000000000000000  0.000000000000000 -0.000000000000000 -0.000000000000000 -0.000000000000000 -0.000000000000001	Eigenwerte 14 NK  9.223911591068690  4.682088650324980  3.020823327807100  1.446199088826980  1.034025794135600  0.589927465372724  0.003024082463895  0.000000000000002  0.000000000000001  0.000000000000001  0.000000000000001  0.000000000000001  0.000000000000000  0.000000000000000  0.000000000000000 -0.000000000000001 -0.000000000000001 -0.000000000000001 -0.000000000000002 -0.000000000000002	Unterschiede 14 NK - 2 NK  0.137528418794121  -0.032866773794630 -0.061498036707760 -0.047504326308080  0.014490191253540 -0.001475728565680 -0.003775831224527 -0.002727145098221 -0.001344656916988 -0.000826111431776  0.000000000000000  0.000000000000001  0.000000000000000  0.000000000000000  0.000000000000000 -0.000000000000001 -0.000000000000001 -0.000000000000001 -0.000000000000002 -0.000000000000001

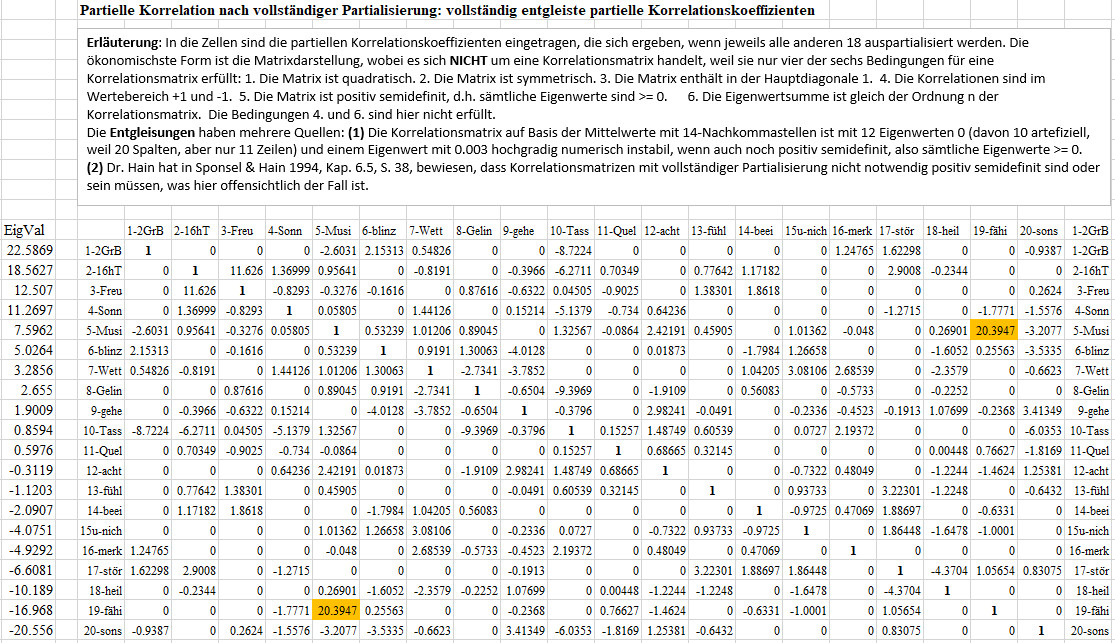
Erläuterung: In die Zellen sind die partiellen Korrelationskoeffizienten eingetragen, die sich ergeben, wenn jeweils alle anderen 18 auspartialisiert werden. Die ökonomischste Form ist die Matrixdarstellung, wobei es sich NICHT um eine Korrelationsmatrix handelt, weil sie nur vier der sechs Bedingungen für eine Korrelationsmatrix erfüllt: 1. Die Matrix ist quadratisch. 2. Die Matrix ist symmetrisch. 3. Die Matrix enthält in der Hauptdiagonale 1.  4. Die Korrelationen sind im Wertebereich +1 und -1.  5. Die Matrix ist positiv semidefinit, d.h. sämtliche Eigenwerte sind >= 0.  6. Die Eigenwertsumme ist gleich der Ordnung n der Korrelationsmatrix.  Die Bedingungen 4. und 6. sind hier nicht erfüllt, 5.ist davon abhängig, ab wie viel Nullen nach dem Komma ein Eigenwert mit 0 oder nicht bewertet wird.
    Die Entgleisungen haben mehrere Quellen: (1) Die Korrelationsmatrix auf Basis der Mittelwerte mit 14-Nachkommastellen ist mit 12 Eigenwerten 0 (davon 10 artefiziell, weil 20 Spalten, aber nur 11 Zeilen) und einem Eigenwert mit 0.003 hochgradig numerisch instabil, wenn auch - zumindest bis auf 15 Nachkommastellen - noch positiv semidefinit, also sämtliche Eigenwerte >= 0.  (2)  Dr. Hain hat in Sponsel & Hain 1994, Kap. 6.5, S. 38, bewiesen, dass Korrelationsmatrizen mit vollständiger Partialisierung nicht notwendig positiv semidefinit sind oder sein müssen, was hier offensichtlich der Fall ist.
    Weitere systematische Untersuchungen haben gezeigt, dass die Entgleisungen nicht erst mit vollständiger Partialisierung beginnen, sondern bereits viel früher.
    Lesebeispiel: pc5-19.1,2,3,4,6,7,8,9,10,11,12,13,14,15,16,17,18,20:  Der partielle Korrelationskoeffizient zwischen 5-Musik und 19-Erlebnisfähigkeit, wenn der Einfluss aller anderen 18 Variablen herausgerechnet wurde, beträgt, sage und schreibe, 20.3947 (orange markiert) - und schießt damit den Entgleisungs-Vogel ab!

Systematische Untersuchung zu den Entgleisungen bei Auspartialisierung
Im Auspartialisierungsprogramm wird "pcv" als Abkürzung für partielle correlation variable bzw. partielle Korrelationsvariable ausgegeben. Die Ziffern vor dem Punkt geben die Variablen (hier Fragen) an, deren partielle Korrelation betrachtet wird, wenn der Einfluss der Variablen nach dem Punkt herausgenommen wird.

Zusammenfassung Auspartialisierung der Korrelationsmatrix der Mittelwerte mit 14-Nachkommastellen. Die Matrix entgleist nicht erst bei vollständiger Partialisierung xy.18 aus 1 bis 20, sondern bereits bei 5 Auspartialisierungen treten deutliche Überschreitungen von |1| auf, die anzeigen, dass die partiellen Korrelationskoeffizienten problematisch sind oder sein können. Vertretbar erscheinen daher Auspartialisierungen von höchstens vier Variablen. Hier ist weitere Analyse und Forschung geboten.

Erste Entgleisungen bei der Auspartialisierung von nur 5 Variablen (von maximal 18 möglichen bei insgesamt  20)
Bei Auspartialisierung  von 5 Variablen wird der partielle Korrelationskoeffizient zwischen einem Paar des öfteren geringfügig an der 5. Nachkommastelle überschritten, z.B. pcv 1  8 .   4  7  9  10  14 = -1.00002. Deutlicher bereits bei pcv  4  9 .   1  7  8  11  14 =  -1.0149 oder pcv  1  9 .   4  7  8  11  14 =   -1.01517.

Massive Entgleisungen bei Auspartialisierung von 6 Variablen
pcv  9  18 .   3  7  12  14  16  17 =  1.43886
pcv  9  17 .   3  7  12  14  16  18 =  1.46781
pcv  9  16 .   3  7  12  14  17  18 = -1.66143

Massive Entgleisungen bei Auspartialisierung von 7 Variablen
pcv  11  12 .   1  5  9  10  14  15  16 = -1.31914
pcv    4  16 .   1  2  6  10  13  18  19 =  1.23043

Massive Entgleisungen bei Auspartialisierung von 8 Variablen
pcv  14  17 .   3  5  8  10  15  16  18  19 =  2.19055
pcv  14  18 .   3  5  8  10  15  16  17  19 = -1.09552
pcv    3  13 .   5  8  10  16  17  18  19  20 = 1.48158
pcv    3  10 .   5  8  13  16  17  18  19  20 = 1.62325
pcv    3  8 .     5  10  13  16  17  18  19  20 = 2.83134
 

Weitere Einzelbeispiele und Sonderstudien

pcvF01-F07
Die Korrelation zwischen F01 (Grundbegriffsverständnis) und F07 (Wettererleben) und den mit ihnen verbundenen Variablen betrug -0.2982. Partialisiert man F04 (Sonnenuntergang), F08 (Gelingen), F09 (Gehen), F13 (Gefühle) und F19 (Erlebnisfähigkeit) aus, verschwindet die negative Korrelation und wird pcv 1  7 .   4  8  9  13  19 =   0.00874174.

F07-F20 Partielle Studien zu F07 (Wettererleben) - F20 (Sonstig/Kritik)
Zwischen F07 (Wettererleben) und F20 (Sonstiges/Kritik) gab es eine sehr hohe, für mich überraschende und wenig verständliche negative Korrelation von -0.9734. Hier ist weitere Analyse und Aufklärung angesagt. Ein paar erste Sondierungen von Auspartialisierung der Fragen (Variablen) 1,2, ...19 und von einigen Paaren 1,2; 1,3; ... 1,19 erbrachten folgende Ergebnisse:
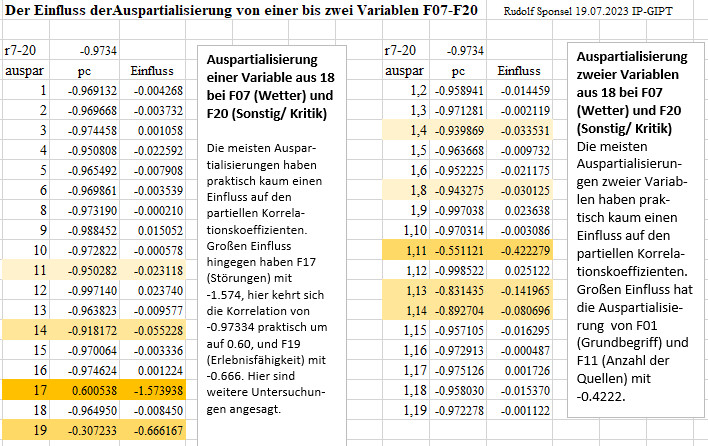
   Auspartialisierung einer Variable aus 18 bei F07 (Wetter) und F20 (Sonstig/ Kritik: Die meisten Auspartialisierungen haben praktisch kaum einen Einfluss auf den partiellen Korrelationskoeffizienten. Großen Einfluss hingegen haben F17 (Störungen) mit -1.574, hier kehrt sich die Korrelation von -0.97334 praktisch um auf 0.60, und F19 (Erlebnisfähigkeit) mit -0.666. Hier sind weitere Untersuchungen angesagt.
    Auspartialisierung zweier Variablen aus 18 bei F07 (Wetter) und F20 (Sonstig/ Kritik): Die meisten Auspartialisierungen zweier Variablen haben praktisch kaum einen Einfluss auf den partiellen Korrelationskoeffizienten. Beachtlichen Einfluss hat die Auspartialisierung  von F01 (Grundbegriff) und F11 (Anzahl der Quellen) mit  -0.4222.
 

_

Partielle Studien zu F12-F15u
Partielle Studien über die Matrix der Mittelwerte sind schwierig, weil die Korrelationsmatrix der Mittelwerte hochgradig kollinear bzw. fast-kollinear ist und bereits mit mehr als vier Auspartialisierungen entgleist, also partielle Korrelationskoeffizienten > |1| produziert. Hier ist weitere Analyse und partielle Korrelationsforschung angesagt, und zwar sowohl, wie man der kombinatorischen Explosion, als auch den Entgleisungen entgehen kann. Speziell den Fall F12-F15u habe ich mit einer vollständigen partiellen Korrelationsanalyse untersucht.

Multiple Regressionsanalysen (MRA)

Zusammenfassung Multiple Regressionsanalysen
Mit der multiplen Regressionsanalyse lassen sich Vorhersagen einer Variable (Frage) durch andere erfassen. Hier liegt mir leider kein systematisches Programm vor, das alle Partitionen bildet, so dass ich nur auf eine kleine Auswahl multipler Regressionsanalysen eingehen konnte.
MRA mit den skalierten Rohwerten: Es wurde die Vorhersage auf den skalierten Rohwert F19 (Erlebnisfähigkeit) durch alle anderen bestimmt. Dies ergab einen multiplen Korrelationskoeffizienten von 0.7422 (d.h. 55% Varianzaufklärung), also mittlerer Quantität.
MRA mit den Mittelwerten mit 14 Nachkommastellen: Hier genügen bereits vier bis fünf Variable (Fragen) um eine Vorhersage mit einem multiplen Korrelationskoeffizienten nahe 1 zu erzielen. Zwei Beispiele werden dargestellt: (1) Auf Basis der Fragen F12 (achten), F13 (fühlen), F14 (beeinflussen), F15u achten, F16 (merken) ist die multiple Korrelation zur Vorhersage F19 der Erlebnisfähigkeit 0.9847, also sehr hoch. (2) Auf Basis der Fragen F03 (Freunde), F05 (Musik), F12 (achten), F13 (fühlen), F16 (merken) ist die multiple Korrelation zur Vorhersage F19 der Erlebnisfähigkeit 0.9760, also sehr hoch, wenn auch etwas kleiner als im Beispiel (1).

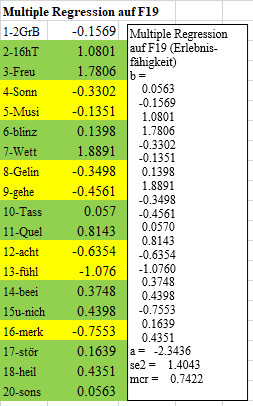
Multiple Regressionsanalysen (MRA) mit den skalierten Rohwerten
Es wurde die Vorhersage auf den skalierten Rohwert F19 (Erlebnisfähigkeit) durch alle anderen bestimmt. Dies ergab einen multiplen Korrelationskoeffizienten ist mit 0.7422 (d.h. 55% Varianzaufklärung), also mittlerer Quantität.
In der Tabelle sind die Steigungen der Regressionskoeffizienten b wiedergegeben (grün die positiven, gelb die negativen markiert).

Multiple Regressionsanalysen (MRA)  mit den Mittelwerten mit 14 Nachkommastellen
Ganz anders stellt die Lage bei den Mittelwerten dar. Hier genügen bereits vier bis fünf Variable (Fragen) um eine Vorhersage mit einem multiplen Korrelationskoeffizienten nahe 1 zu erzielen.

(1) MR auf F19 (Erlebnisfähigkeit) mit Basis F12, F13, F14, F15u, F16
Auf Basis der Fragen F12 (achten), F13 (fühlen), F14 (beeinflussen), F15u achten, F16 (merken) ist die multiple Korrelation zur Vorhersage F19 der Erlebnisfähigkeit 0.9847, also sehr hoch.
b =
F12    0.2542
F13    2.5330
F14   -1.5158
F15u  -1.2014
F16     1.3059
a =    0.7058
se2 =   8.1754e-04
mcr =    0.9847

(2) MR auf F19 (Erlebnisfähigkeit) mit Basis F03, F05, F12, F13, F16
Auf Basis der Fragen F03 (Freunde), F05 (Musik), F12 (achten), F13 (fühlen), F16 (merken) ist die multiple Korrelation zur Vorhersage F19 der Erlebnisfähigkeit 0.9760, also sehr hoch, wenn auch etwas kleiner als im Beispiel (1).

b =
F03-Freun     0.7494
F05-Musik    1.8241
F12-achten    0.5654
F13-Fühlen    0.4234
F16-merken  -0.3873
a =   -2.0042
se2 =    0.0013
mcr =   0.9760

Zusammenfassung Raenge

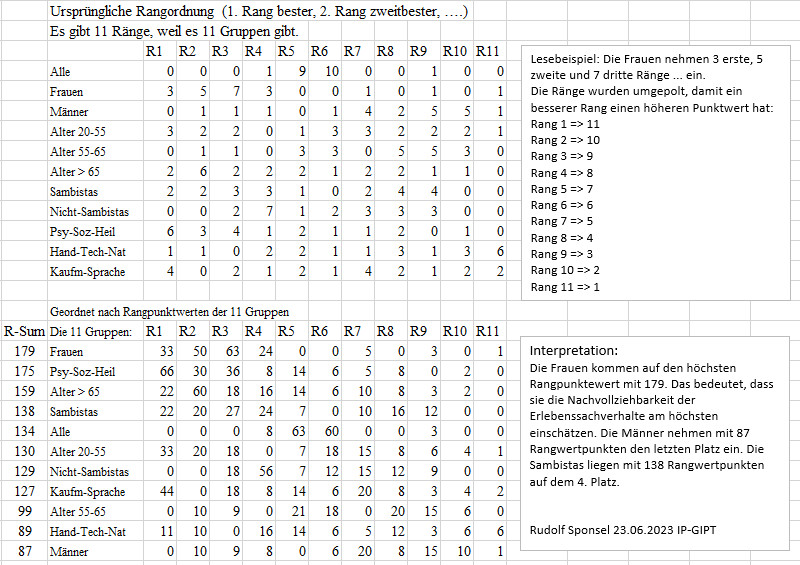
Rangfolge-FB02-MW(MW) Fragen 1-20
Von jeder Gruppe wurde über die 34 Wertzuweisungen zu den 20 Fragen der Mittelwert gebildet.
Lesebeispiel: Der Mittelwert Frage 1, Kürzel 2GrB (Zwei Grundbegriffe des Erlebens) in der Berufsgruppe 1 Psycho-Soziales-Heilen war mit 1.71 der höchste bei den 11 Gruppen, daher nimmt diese Berufsgruppe den ersten Platz ein.
Die Fragen 11 und 19 sind offene Fragen, deren Mittel 2 deutlich übersteigen kann (11: 4.33-9.5; 19: 3.12 - 3.77). Das ist der Grund, warum die Mittelwerte der 20 Mittelwerte 2 überschreiten können, wenn man sie nicht auf das Maximum 2 normiert (>Beispiel Partition-11-13). Die Fragen außer 11 und 19 können höchstens den Wert 2 zugeordnet bekommen.
Der Mittelwert ist eine Verdichtung der Einzelbewertungen, wobei deren Verteilung und Streuung nicht zum Ausdruck kommt. Ein höherer Mittelwert besagt bei diesem Pilot-Fragebogen und seinen Beurteilungsvorgaben, dass im Durchschnitt mehr gute oder einigermaßen Nachvollziehbarkeit zu den Erlebenssachverhalten bekundet wurde.

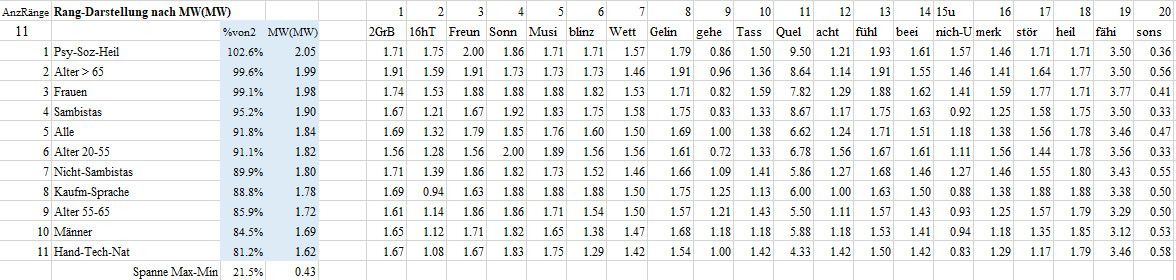
Von jeder Gruppe wurde über die 34 Wertzuweisungen zu den Fragen 1-20 der Mittelwert gebildet. Von diesen 20 Mittelwerten wurde ein Mittelwert der 20 Mittelwerte gebildet und anschließend absteigend ranggeordnet. Die Berufsgruppe-1 Psycho-Soziales-Heilen erzielte mit 2.05 den höchsten Mittelwert der 20 Mittelwerte und nimmt daher Platz (Rang) 1 bei den 11 Gruppen ein. Den letzten Platz nimmt die Berufsgruppe 2 Handwerk-Technik-Naturwissenschaft ein, was vielleicht etwas mit ihren wissenschaftlichen, kritisch-realistischen Ansprüchen zu tun haben kann. Man beachte: Letzter Platz heißt nicht schlechter Platz.

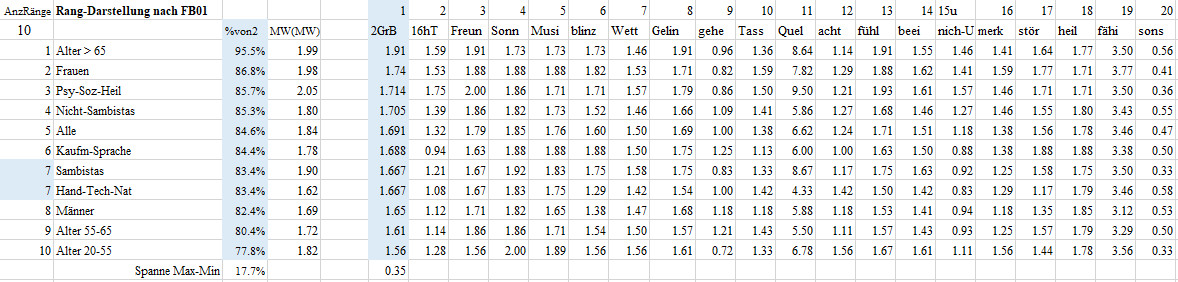
Diese Frage beantworteten die über 65jährigen im Mittel mit 1.91, das sind 95.5% des maximal möglichen Wertes von 2. Damit nimmt die Gruppe der über 65jährigen den ersten Platz bei den 11 Gruppen in der ersten Frage ein. Die 20-55jährigen erzielten mit einem Mittel von 1.56 oder von 77.8% des maximal möglichen Wertes von 2 den letzten Platz. Die Gruppen liegen mit einer Spanne von 17.7% auseinander, also eher wenig.

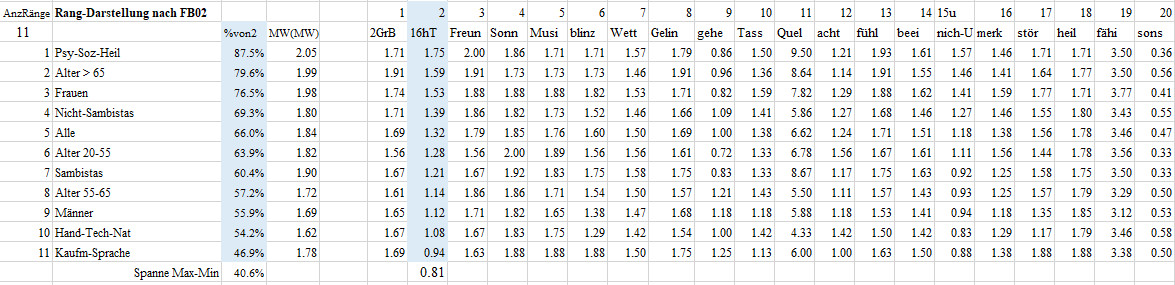
Diese Frage beantwortete die Berufsgruppe 1 Psycho-Soziales-Heilen im Mittel mit 1.75, das sind 87.5% des maximal möglichen Wertes von 2. Damit nimmt die Berufsgruppe-1 Psycho-Soziales-Heilen den ersten Platz bei den 11 Gruppen in der zweiten Frage ein. Die Berufsgruppe-3 Kaufmännisch-Sprache erzielte mit einem Mittel von 0.94 oder von 49.9% des maximal möglichen Werte von 2 den letzten Platz. Man beachte, dass letzter Platz nicht schlechter Platz bedeuten muss. Die Gruppen liegen mit einer Spanne von 40.9% deutlich auseinander..

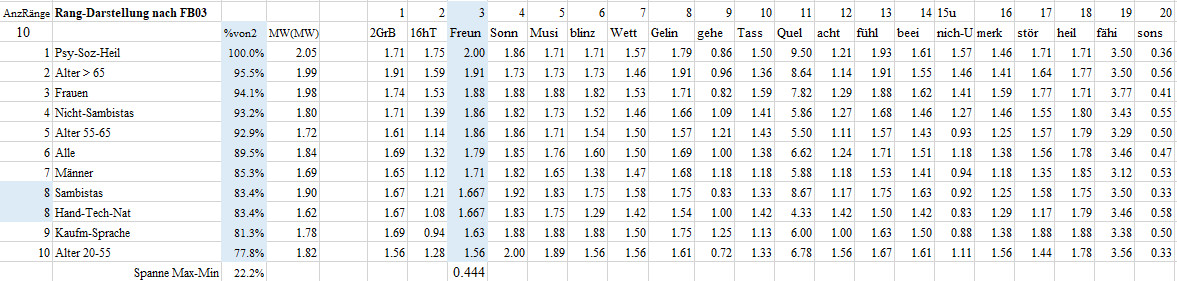
Diese Frage beantwortete die Berufsgruppe-1 Psycho-Soziales-Heilen im Mittel mit 2, das sind 100% des maximal möglichen Wertes von 2. Damit nimmt die Berufsgruppe-1 Psycho-Soziales-Heilen den ersten Platz bei den 11 Gruppen in der dritten Frage ein. Die Altersgruppe 20-55  erzielte mit einem Mittel von 1.56 oder von 77.8% des maximal möglichen Wertes von 2 den letzten Platz. Man beachte, dass letzter Platz nicht schlechter Platz bedeuten muss. Die Gruppen liegen mit einer Spanne von 22.2% auseinander.

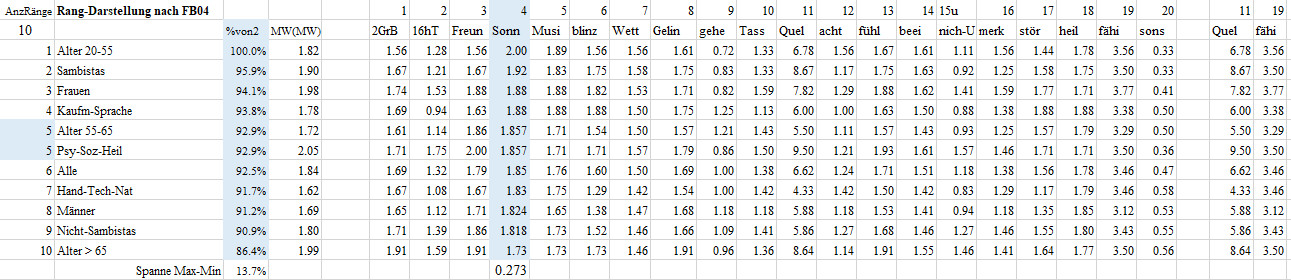
Diese Frage beantworteten die Befragten Altersklasse 20-55 im Mittel mit 2, das sind 100% des maximal möglichen Wertes von 2. Damit nimmt die Altersklasse 20-55 den ersten Platz bei den 11 Gruppen in der 4 Frage ein. Die Altersklasse > 65 erzielte mit einem Mittel von 1.73 oder von 86.4% des maximal möglichen Wertes von 2 den letzten Platz. Man beachte, dass letzter Platz nicht schlechter Platz bedeuten muss. Die Gruppen liegen mit einer Spanne von 13.7% auseinander, also nur wenig.

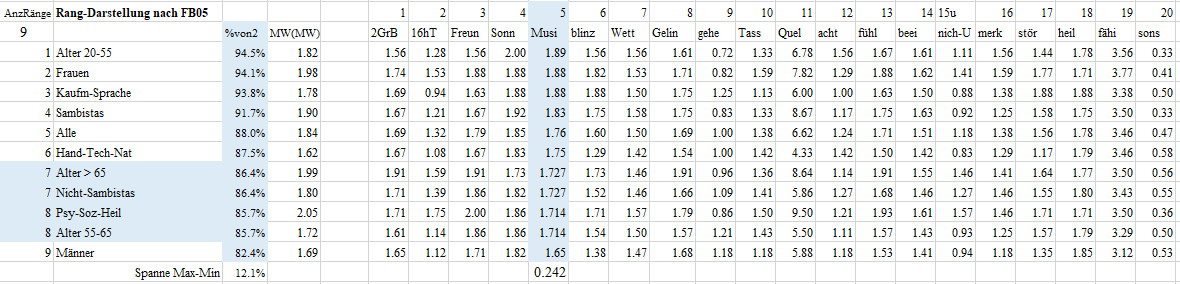
Diese Frage beantworteten die Befragten der Altersgruppe 20-55 im Mittel mit 1.88, das sind  94.5% des maximal möglichen Wertes von 2. Damit nimmt die Altersgruppe 20-55 den ersten Platz bei den 11 Gruppen in der Musik-Frage F05 ein. Die Gruppe der Männer erzielte mit einem Mittel von 1.65 oder von 82.4% des maximal möglichen Wertes von 2 den letzten Platz. Man beachte, dass letzter Platz nicht schlechter Platz bedeuten muss. Die Gruppen liegen mit einer Spanne von 12.1% nur wenig auseinander.

06 Auf der Bank im Park habe ich durch die Baumwipfel hindurch in die Sonne geblinzelt und diese Situation als angenehm erlebt.

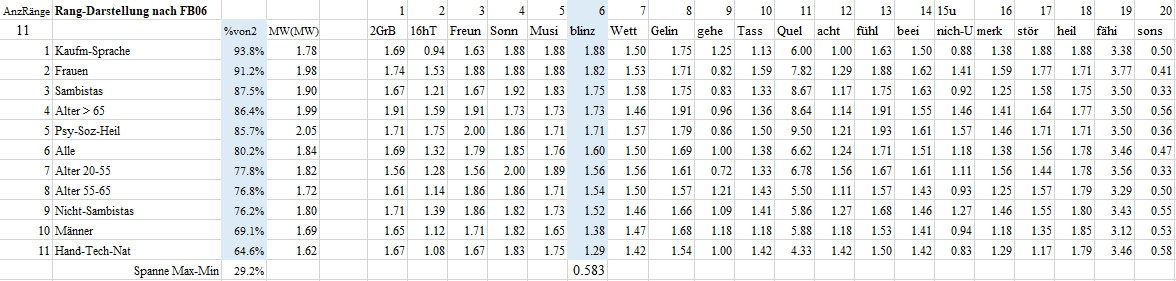
Diese Frage beantworteten die Befragten der Berufsgruppe-3 Kaufmännisch-Sprache im Mittel mit 1.88, das sind 93.8% des maximal möglichen Wertes von 2. Damit nehmen die Befragten der Berufsgruppe-3 Kaufmännisch-Sprache den ersten Platz bei den 11 Gruppen in der Frage 06 in die Sonne geblinzelt ein. Die Berufsgruppe-2 Handwerk-Technik-Naturwissenschaft erzielte mit einem Mittel von 1.29 oder von 64.6% des maximal möglichen Wertes von 2 den letzten Platz. Man beachte, dass letzter Platz nicht schlechter Platz bedeuten muss. Die Gruppen liegen mit einer Spanne von 29.2% deutlich auseinander.  gerichtet 1.7

7 Wett 07 Ich erlebe die Wettersituation, indem ich zum Fenster rausschaue, vielleicht auf den Balkon gehe, die Temperatur, Wolken und den Wind beachte.

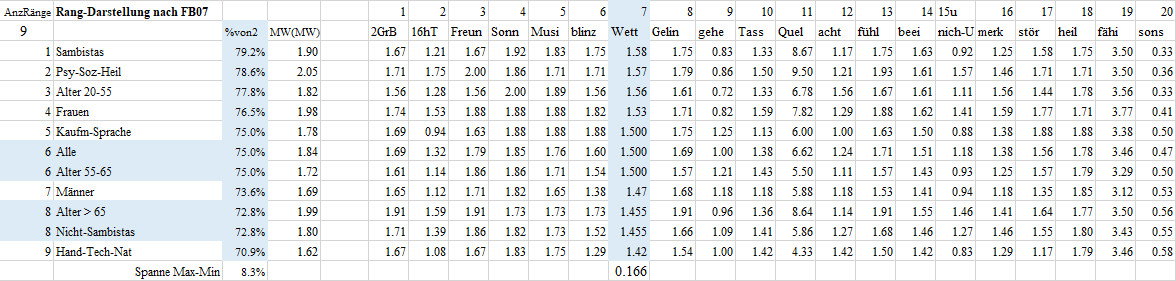
Diese Frage beantworteten die Sambistas im Mittel mit 1.58, das sind 79.2% des maximal möglichen Wertes von 2. Damit nehmen die Sambistas den ersten Platz bei den 11 Gruppen in der Wetter-Frage ein. Die Berufsklasse-2 Handwerk-Technik-Natuirwissenschaft erzielte mit einem Mittel von 1.42 oder von 70.9% des maximal möglichen Wertes von 2 den letzten Platz. Man beachte, dass letzter Platz nicht schlechter Platz bedeuten muss. Die Gruppen liegen mit einer Spanne von 8.3% nur wenig auseinander.

08 Ich erlebe Befriedigung, wenn mir etwas gelingt, was gar nicht so leicht ist

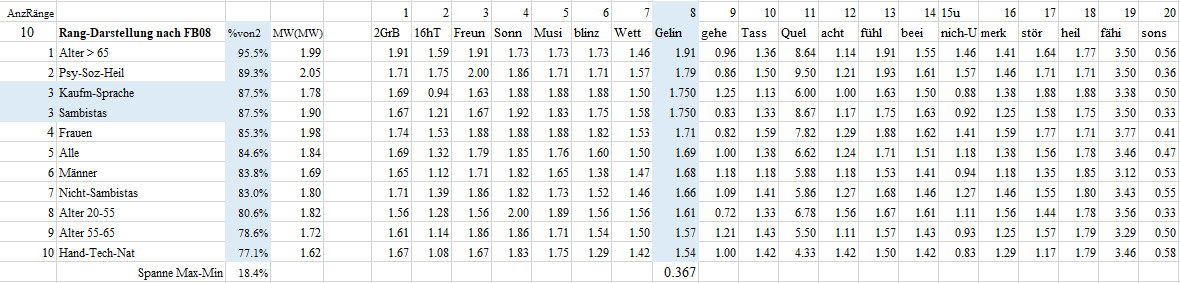
Diese Frage beantwortete die Altersgruppe > 65 im Mittel mit 1.91, das sind 95.5% des maximal möglichen Wertes von 2. Damit nimmt die Altersgruppe > 65 den ersten Platz bei den 11 Gruppen in der Frage 08 zum Erleben des Gelingens. Die Berufsklasse-2 Handwerk-Technik-Naturwissenschaft erzielte mit einem Mittel von 1.54 oder von 77.1% des maximal möglichen Wertes von 2 den letzten Platz. Man beachte, dass letzter Platz nicht schlechter Platz bedeuten muss. Die Gruppen liegen mit einer Spanne von 18.4% auseinander.

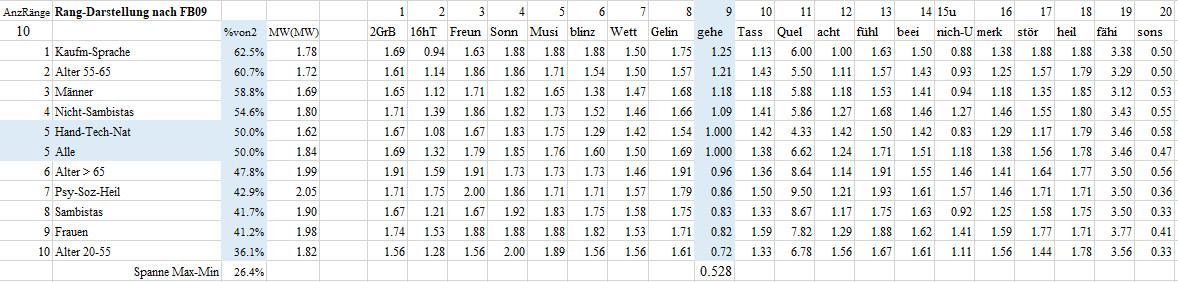
Diese Frage F09 beantwortete die Berufsgruppe-3 Kaufmännisch-Sprache im Mittel mit 1.25, das sind 62.5% des maximal möglichen Wertes von 2. Damit nimmt die Berufsgruppe-3 Kaufmännisch-Sprache den ersten Platz bei den 11 Gruppen in der Frage 09 des bewussten Gehens ein. Die Altersgruppe 20-55 erzielte mit einem Mittel von 0.72 oder von 36.1% des maximal möglichen Wertes von 2 den letzten Platz. Man beachte, dass letzter Platz nicht schlechter Platz bedeuten muss. Die Gruppen liegen mit einer Spanne von 26.4% auseinander, also schon deutlicher.

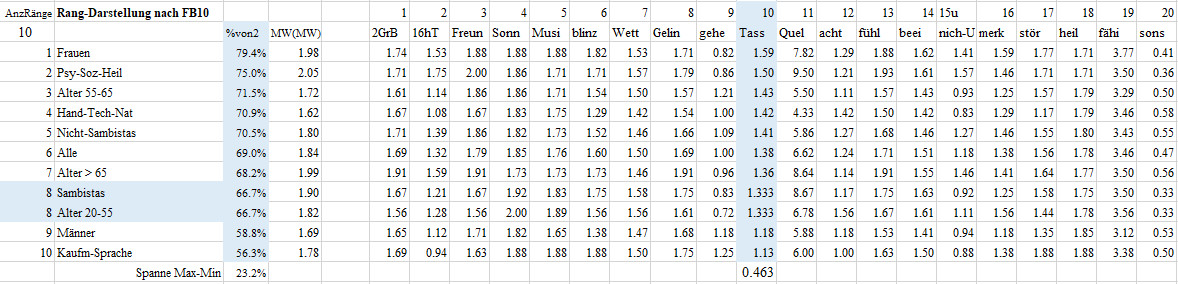
Diese Frage beantworteten die Frauen im Mittel mit 1.59, das sind 79.4% des maximal möglichen Wertes von 2. Damit nehmen die Frauen den ersten Platz bei den 11 Gruppen in der Frage 10 der ersten Tasse Morgengetränk ein. Die Berufsklasse-3 Kaufmännisch-Sprache erzielte mit einem Mittel von 1.13 oder von 56.3% des maximal möglichen Werte von 2 den letzten Platz. Man beachte, dass letzter Platz nicht schlechter Platz bedeuten muss. Die Gruppen liegen mit einer Spanne von 23.2% auseinander.

11 Es gibt viele Quellen und Möglichkeiten, sein Erleben zu aktivieren und auf Trab zu bringen (z.B. ausgehen, Bewegung, Film, Garten, Handwerkern, Kontakt, Kunst, Kultur, Sport, Natur, Musik, Singen, Spiel, Veranstaltungen, … ). Wie ist das bei Ihnen?

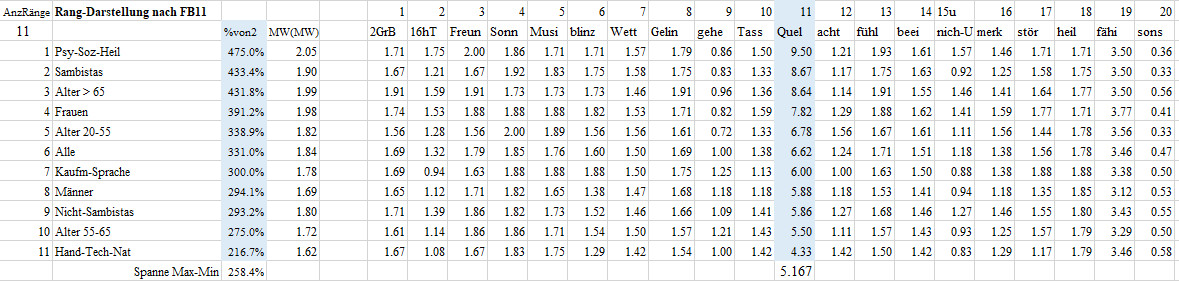
Diese Frage beantworteten die Berufsklasse-1 Psycho-Soziales-Heilen im Mittel mit 9.50, das sind 475.0% des sonst maximal möglichen Wertes von 2. Damit nimmt die Berufsklasse-1 Psycho-Soziales-Heilen den ersten Platz bei den 11 Gruppen in der Frage 11 Erlebnisquellen ein. Die Berufsklasse-2 Handwerk-Technik-Naturwissenschaft erzielte mit einem Mittel von 4.33 oder von 216.7% des sonst maximal möglichen Werte von 2 den letzten Platz. Man beachte, dass letzter Platz nicht schlechter Platz bedeuten muss. Die Gruppen liegen deutlich mit einer Spanne von 258.4% auseinander.

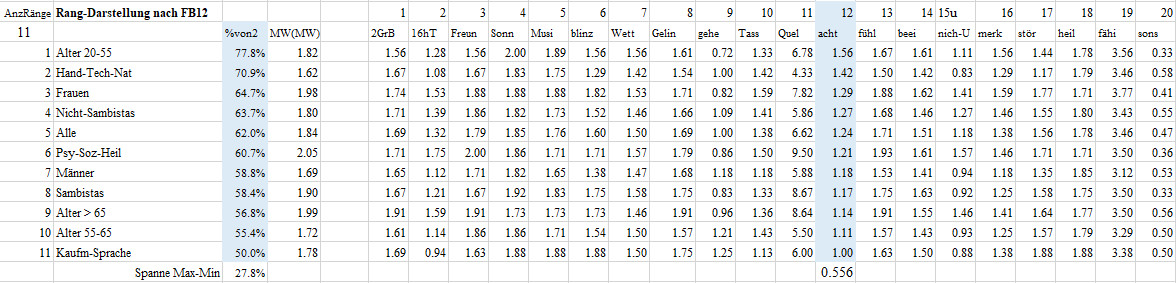
Diese Frage beantwortete die Altersgruppe 20-55 im Mittel mit 1.56, das sind 77.8% des maximal möglichen Wertes von 2. Damit nimmt die Altersgruppe 20-55 den ersten Platz bei den 11 Gruppen in der Frage 12 auf erleben achten ein. Die Berufsklasse-3 Kaufmännisch-Sprache erzielte mit einem Mittel von 1.0 oder von 50% des maximal möglichen Werte von 2 den letzten Platz. Man beachte, dass letzter Platz nicht schlechter Platz bedeuten muss. Die Gruppen liegen mit einer Spanne von 27.8% deutlich auseinander.

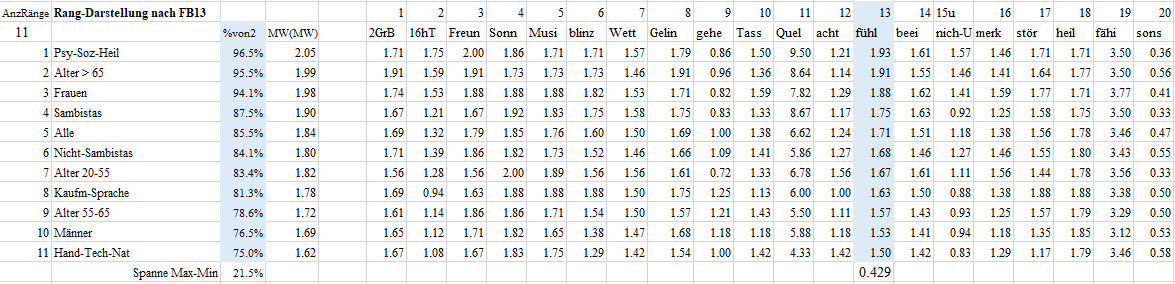
Diese Frage beantworteten die Berufklasse-1 Psycho-Soziales-Heilen im Mittel mit 1.93, das sind 96.5% des maximal möglichen Wertes von 2. Damit nimmt die Berufklasse-1 Psycho-Soziales-Heilen den ersten Platz bei den 11 Gruppen in der 13. Frage ein. Die Berufsklasse-2 Handwerk-Technik-Naturwissenschaft erzielte mit einem Mittel von 1.50 oder von 75% des maximal möglichen Werte von 2 den letzten Platz. Man beachte, dass letzter Platz nicht schlechter Platz bedeuten muss. Die Gruppen liegen mit einer Spanne von 21.5% deutlicher auseinander.

14 Ich kann mein Erleben beeinflussen (z.B. durch zuwenden oder abwenden, durch tun oder lassen).

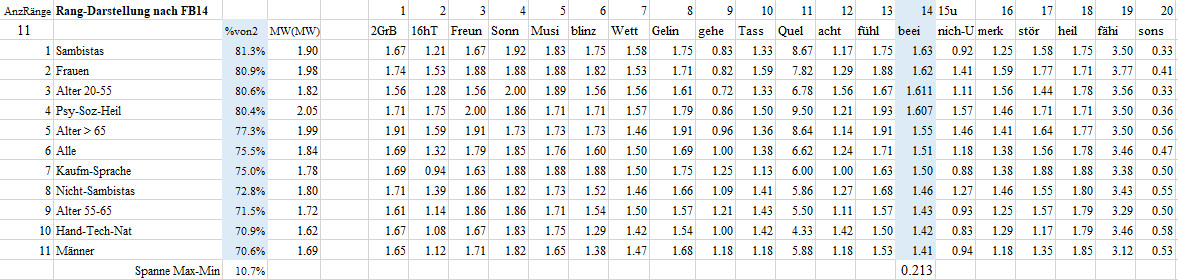
Diese Frage beantworteten die Sambistas im Mittel mit 1.63, das sind 81.3% des maximal möglichen Wertes von 2. Damit nehmen die Sambistas den ersten Platz bei den 11 Gruppen in der Frage 14 Erleben beeinflussbar ein. Die Männer erzielten mit einem Mittel von 1.41 oder von 70.6% des maximal möglichen Werte von 2 den letzten Platz. Man beachte, dass letzter Platz nicht schlechter Platz bedeuten muss. Die Gruppen liegen mit einer Spanne von 10.7% wenig auseinander.

15 Ich achte in meinem Leben nicht besonders auf mein erleben. Umgepolt: Ich achte besonders auf mein Erleben.
Aus "++" und "+" wird 0. Aus "?" wird 0.5 und aus "- " wird 2.

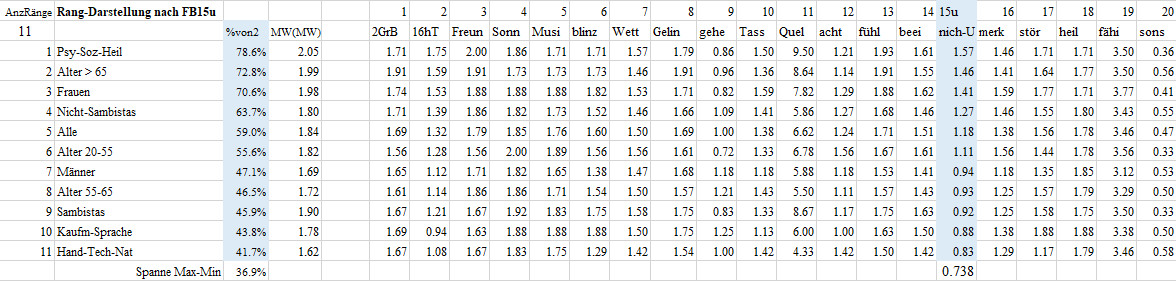
Diese Frage beantwortete die Berufklasse-1 Psycho-Soziales-Heilen im Mittel mit 1.57, das sind 78.6% des maximal möglichen Wertes von 2. Damit nimmt die Berufklasse-1 Psycho-Soziales-Heilen den ersten Platz bei den 11 Gruppen in der (umgepolten) Frage 15u besonders auf mein Erleben achten ein. Die Berufsklasse-2 Handwerk-Technik-Naturwissenschaft erzielte mit einem Mittel von 0.83 oder von 41.7% des maximal möglichen Werte von 2 den letzten Platz. Man beachte, dass letzter Platz nicht schlechter Platz bedeuten muss. Die Gruppen liegen mit einer beachtlichen Spanne von 36.9% auseinander.

Rangfolge-FB02-F16 Merken
16 Ich merke es, wenn es mit meinem Erleben nicht so gut läuft.

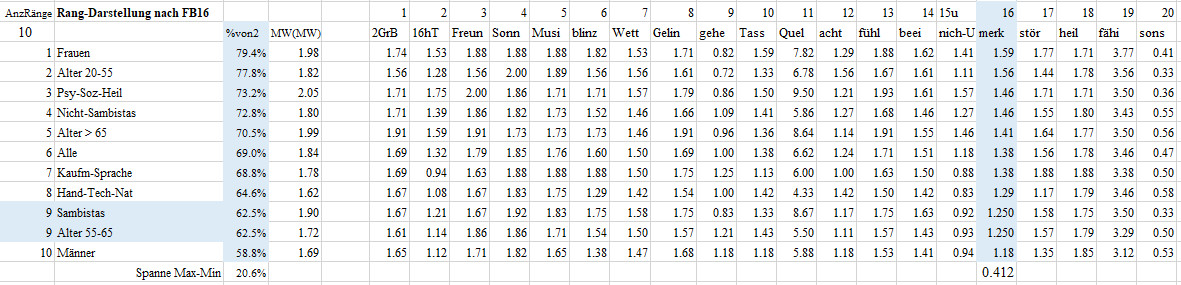
Diese Frage beantworteten die Frauen im Mittel mit 1.59, das sind 79.4% des maximal möglichen Wertes von 2. Damit nehmen die Frauen den ersten Platz bei den 11 Gruppen in der Frage 16 Merken, wenn Erleben nicht gut läuft ein. Die Männer erzielten mit einem Mittel von 1.18 oder von 58.8% des maximal möglichen Werte von 2 den letzten Platz. Man beachte, dass letzter Platz nicht schlechter Platz bedeuten muss. Die Gruppen liegen mit einer Spanne von 20.6% auseinander.

17 Erleben wird manchmal beeinträchtigt (z.B. durch Stress, Hektik, Druck, Alltag, Pflichten, Routinen, Gewöhnliches, Krankheit, Hindernisse). Wie sehen Sie das und wie ist das bei Ihnen:

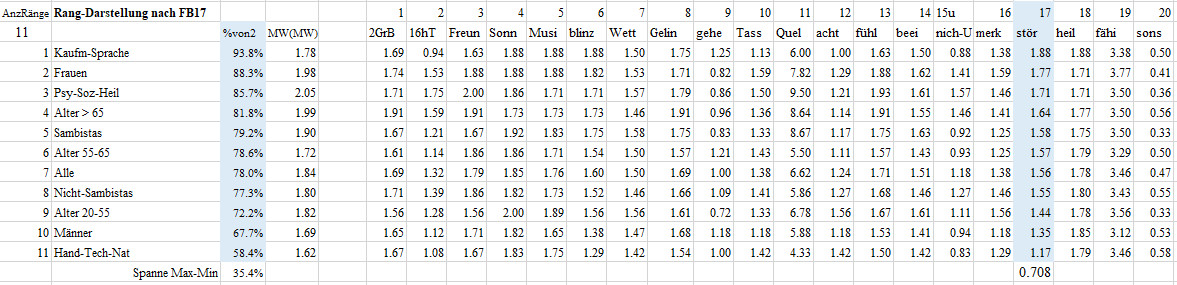
Diese Frage beantworteten die Berufsklasse-3 Kaufmännisch-Sprache im Mittel mit 1.88, das sind 93.8% des maximal möglichen Wertes von 2. Damit nimmt die Berufsklasse-3 Kaufmännisch-Sprache den ersten Platz bei den 11 Gruppen in der Frage 17 Erleben manchmal beeinträchtigt ein. Die Berufsklasse-2 Handwerk-Technik-Naturwissenschaft erzielte mit einem Mittel von 1.17 oder von 58.4% des maximal möglichen Werte von 2 den letzten Platz. Man beachte, dass letzter Platz nicht schlechter Platz bedeuten muss. Die Gruppen liegen mit einer beachtlichen Spanne von 35.4% auseinander.

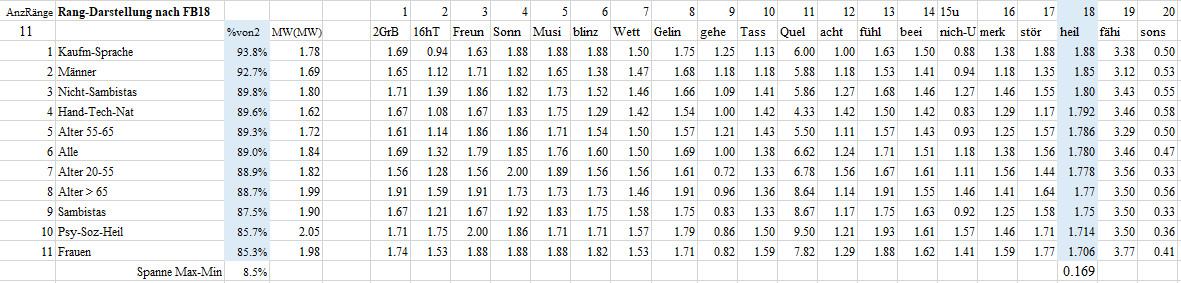
Diese Frage beantwortete die Berufsklasse-3 Kaufmännisch-Sprache im Mittel mit 1.88, das sind 93.8% des maximal möglichen Wertes von 2. Damit nimmt die Berufsklasse-3 Kaufmännisch-Sprache den ersten Platz bei den 11 Gruppen in der Frage 18 erleben wichtiger Heilfaktor ein. Die Frauen erzielten mit einem Mittel von 1.706 oder von 85.3% des maximal möglichen Werte von 2 den letzten Platz. Man beachte, dass letzter Platz nicht schlechter Platz bedeuten muss. Die Gruppen liegen nur mit einer kleinen Spanne von 8.5% auseinander.

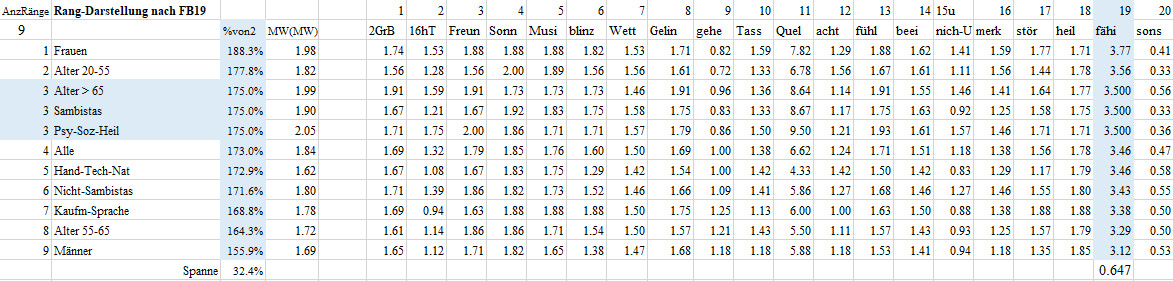
Diese Frage beantworteten die Frauen im Mittel mit 3.77, das sind 188.3% des maximal möglichen Wertes von 2. Damit nehmen die Frauen die den ersten Platz bei den 11 Gruppen in der Frage 19 Erlebnisfähigkeit ein. Die Männer erzielten mit einem Mittel von 3.12 oder von 155.9% des sonst maximal möglichen Werte von 2 den letzten Platz. Man beachte, dass letzter Platz nicht schlechter Platz bedeuten muss. Die Gruppen liegen mit einer Spanne von 32.4% auseinander.

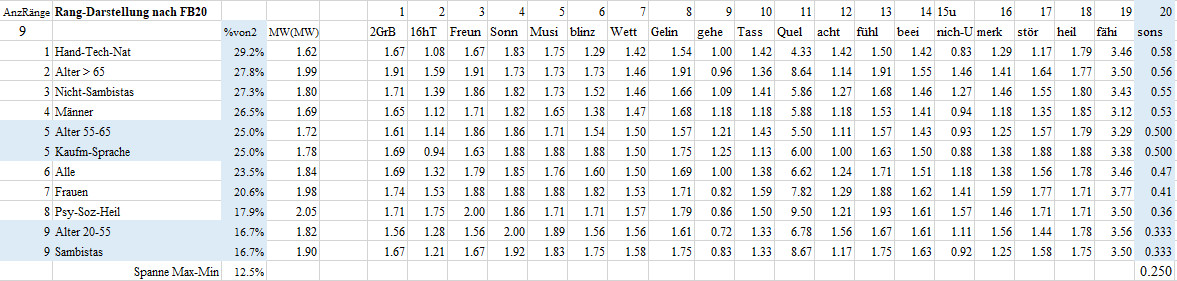
Diese Frage beantwortete die Berufsklasse-2 Handwerk-Technik-Naturwissenschaft im Mittel mit 0.58, das sind 29.2% des maximal möglichen Wertes von 2. Damit nimmt die Berufsklasse-2 Handwerk-Technik-Naturwissenschaft den ersten Platz bei den 11 Gruppen in der Frage 20 Sonst noch etwas zum Thema Erleben und Kritik ein. Die Sambistas erzielten mit einem Mittel von 0.333 oder von 16.7% des maximal möglichen Werte von 2 den letzten Platz. Man beachte, dass letzter Platz nicht schlechter Platz bedeuten muss. Die Gruppen liegen mit einer Spanne von 12.5% auseinander. Anmerkung: Die eigentlich offene Frage betrifft sehr Verschiedenes (>FB02-F20). Im Kern wird nur erfasst, ob es Anmerkungen gibt (1) oder nicht (0).
 

• Sponsel, Rudolf & Hain, Bernhard (1994) Numerisch instabile Matrizen und Kollinearität in der Psychologie. Diagnose, Relevanz & Utilität, Frequenz, Ätiologie, Therapie. Ill-Conditioned Matrices and Collinearity in Psychology. Deutsch-Englisch. Ins Englische übersetzt von Agnes Mehl. Kapitel 6 von Dr. Bernhard Hain: Bemerkungen über Korrelationsmatrizen. Erlangen: IEC-Verlag.
• Sponsel, Rudolf (2005)  Fast- Kollinearität in Korrelationsmatrizen mit Eigenwert-Analysen erkennen. Ergänzungsband - Band II zu Numerisch instabile Matrizen und Kollinearität in der Psychologie. Erlangen: IEC-Verlag.

• Eigenwert-Analysen von Korrelations-Matrizen im sozialwissenschaftlichen Bereich, in Psychologie und Psychotherapie. Darin:
• Fast-Kollinearitäts- über Eigenwertanalysen.
• Multivariate Links.
• Bedeutung der Eigenwerte einer Korrelationsmatrix.