(ISSN 1430-6972)
IP-GIPTDAS=20.01.2024 Internet-Erstausgabe, letzte Änderung: 25.05.24
Impressum: Diplom-Psychologe Dr. phil. Rudolf Sponsel Stubenlohstr. 20 D-91052 Erlangen
E-Mail: sekretariat@sgipt.org _ Zitierung & Copyright
Anfang_Numerische Therapie indefiniter Korrelationsmatrizen_Datenschutz_Überblick__Rel. Beständiges _Titelblatt_ Konzept_ Archiv_ Region_ English contents__ Service_iec-verlag__Dienstleistungs-Info * _ Wichtige Hinweise zu Links und Empfehlungen
Abteilung Wissenschaftstheorie in der Psychologie, Bereich Beweistheorie, und hier speziell zum Thema:
Numerische Therapie indefiniter
Korrelationsmatrizen
mit einer Beispielanwendung der indefiniten 11 Gefühle Matrix
von Burt 1915
Originalarbeit von Rudolf Sponsel, Erlangen
Hauptseiten: Korrelation und Eigenwertanalysen.
Warnung vor KI * Haupt- und Verteilerseite Definitions-Register Psychologie * Checkliste Definition, gpds-Regel * Definition und definieren: referenzieren; Hauptseite Referenzen in der psychologischen Forschung * Systematische Analyse Definition und definieren in der Psychologie. * Begriffscontainer (Containerbegriff) * Homonyme * Begriffsverschiebebahnhöfe * Sachverhalt * Wissenschaftliches Arbeiten, Regeln Grundbegriffe, Begriffsbasis, Zitieren * Aristoteles Zum Geleit * Sprachkritik und Sch^3-Syndrom * Methode der Textanalyse * Methodik-Beweissuche in der Psychologie * Beweissuchwortkürzel. * Signierung von Beweiserwähnungsbeurteilungen * Checkliste-Beweisen.: Beweisregister Psychologie * Beweis und beweisen in der Psychologie * natcode Register * Übersicht allgemeine Beweisseiten * Haupt- und Verteilerseite Die Erforschung des Erlebens und der Erlebnisse , Tabelle Fundstelleninformationen erleben, erlebt, Erlebnis * Hauptbedeutungen Erleben * Grunddimensionen des Erlebens * »«
Inhalt
Editorial.
Zusammenfassung-Numerische
Therapie indefiniter Korrelations-Matrizen.
Numerische Therapie der indefiniten
"Korrelationsmatrix" von Burt 1915.
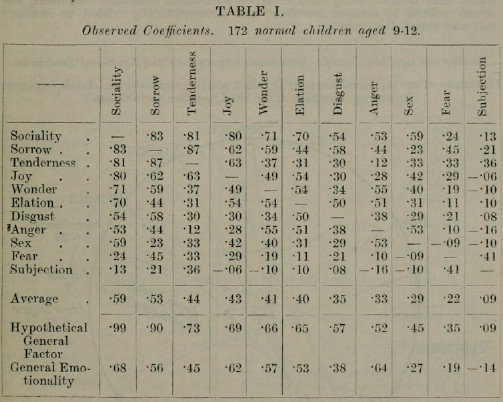
Die Ausgangsmatrix
Burt 1915.
Original
Table I.
I.
Angewandte numerische Therapiemethoden und ihre Ergebnisse. * Methodenkürzel.*
Gefühlskennungen.
- CR Faktorisieren.
CRn Faktorisieren und die Hauptdiagonale auf 1 skalieren ("normalisieren").
CR0 Den negativen Eigenwert durch 0 ersetzen.
CR0n Den negativen Eigenwert durch 0 ersetzen und die Hauptdiagonale auf 1 skalieren ("normalisieren").
CRs Die Eigenwerte durch die Singulärwerte ersetzen.
CRsn Die Eigenwerte durch die Singulärwerte ersetzen und die Hauptdiagonale auf 1 skalieren ("normalisieren").
CC Zentroidmethode.
- Vergleichende
vollständige partielle Matrix-Analysen der Originalmatrix mit den
verschiedenen numerischen Therapievarianten. * Zusammenfassung.
- R: Die Originalmatrix von Burt liefert bei den partiellen Korrelationen 7 Entgleisungen, 6 davon extrem.
- CR Fakorisierungsmethode.
- CR0 Die Methode setzt den negativen Eigenwert von -0.0245 glatt 0.
- CR0n Wie CR0, aber mit Normalisierung der Hauptdiagonalen zu 1.
- CRn Hier werden die erhöhten Hauptdiagonalwerte der faktorisierten Matrix CR auf 1 normalisiert.
- CRs Die Methode ersetzt die Eigenwerte durch die sämtlich positiven Singulärwerte.
- CRsn Normalisierung Hauptdiagonale der Singulärwert-Methode.
Hauptkomponentenanalyse mit der Gefühlsmatrix CRn. * Zusammenfassung.
Partielle Korrelationen mit der numerisch therapierten Korrelationsmatrix CRn.
- Zusammenfassung
Partielle Analysen nach numerischen Therapiemethoden.
IV. Kritik.
V. Burt 1940 zu seiner Arbeit 1915.
Numerische Therapie der indefiniten "Korrelations"matrix Berufsinteresse Mechanik der 5. bis 9. Klassen von Todt in Das Interesse (1978), S. 56.
Checkliste definieren.
Checkliste beweisen.
Zitierstil.
Literatur, Links, Glossar, Anmerkungen und Endnoten, Querverweise, Copyright und Zitierung, Änderungen
_
Editorial (von der Zusammenfassung Z0)
Eine indefinite Korrelationsmatrix hat irregulär mindestens einen negativen Eigenwert. Auch wenn dieser sehr klein ist, etwa erst bei der zweiten 0.0z .. oder dritten Nachkommastelle 0.00z ... oder noch weiter hinten aufscheint, kann er zu völlig entgleisten Ergebnissen bei multivariaten Verarbeitungen (partiellen, multiplen Korrelationskoeffizienten oder Faktorenladungen ("Heywoodfälle") z. B. > 1, 10, 20, 30, ... führen und jede vernünftige Interpretation unmöglich machen, falls die Programme überhaupt multivariate Verarbeitungen zulassen, wenn die Korrelationsmatrix ihre Positive-Semi-Definitheit (PSD) verloren hat und indefinit mit einem oder gar mehreren negativen Eigenwerten aufwartet (Matlab weist eine indefinite Matrix bei Faktorenanalysen zurück). Es ist daher wichtig, bevor man mit einer Korrelationsmatrix multivariate Verarbeitungen durchführt, zu prüfen, ob die Korrelationsmatrix überhaupt positiv semi definit ist, also alle Eigenwerte >= 0 sind. Das geht ganz einfach, indem man ihre Eigenwerte feststellt, was die meisten Statistikprogramme können.
Das Thema spielt seit Veröffentlichung 1994 meines ersten Bandes - zusammen mit dem Mathematiker Dr. B. Hain - Numerisch instabile Matrizen und Kollinearität in der Psychologie. Diagnose, Relevanz & Utilität, Frequenz, Ätiologie, Therapie wieder eine Rolle bei meinen Korrelationsmatrizenanalysen. Jüngst hat das Thema einen neuen Schub erhalten: Im Rahmen meiner Studien zur elementaren Dimension Fühlen bin ich bei Euler/Mandl (1983), S. 21 zufällig auf den Hinweis gestoßen, dass Burt 1915 eine Faktorenanalyse einer Korrelationsmatrix von 11 Gefühlen durchgeführt haben will. Das hat mich aus vier Gründen interessiert: Faktorenanalyse, Korrelationsmatrix, Gefühle und der Name Burt, der mir dunkel als bekannter Fälscher in der Psychologie in Erinnerung war. Also suchte ich die Korrelationsmatrix der 11 Gefühle (Online), wurde fündig und rechnete sie nach. Die vermeintliche Korrelationsmatrix zeigt einen relativ großen negativen Eigenwert mit -.0245, der sich kaum mit Rundungsfehlern der zweistelligen Korrrelationskoeffizientendarstellung erklären lässt. Das hat mich bewogen, mich noch einmal vertieft und verstärkt der Frage zu widmen, ob und wie man eine solche indefinite Korrelationsmatrix heilen kann, damit multivariate Weiterverarbeitungen möglich sind und nicht von Prgrammen wie z.B. Matlab zurückgewiesen werden. Diese Seite stellt sämtliche mir bekannten Methoden dar, wie man eine indefinite Korrelationsmatrix wieder positiv semi definit machen kann.
Zusammenfassung-Numerische Therapie indefiniter Korrelationsmatrizen
Z1 Eine indefinite
Korrelationsmatrix hat irregulär mindestens einen negativen Eigenwert.
Auch wenn dieser sehr klein ist, etwa erst bei der zweiten 0.0z .. oder
dritten Nachkommastelle 0.00z ... oder noch weiter hinten aufscheint, kann
er zu völlig entgleisten Ergebnissen bei multivariaten Verarbeitungen
(partiellen, multiplen Korrelationskoeffizienten oder Faktorenladungen
("Heywoodfälle") z. B. > 1, 10, 20, 30, ... führen und jede vernünftige
Interpretation unmöglich machen, falls die Programme überhaupt
multivariate Verarbeitungen zulassen, wenn die Korrelationsmatrix ihre
Positive-Semi-Definitheit (PSD) verloren hat und indefinit mit einem oder
gar mehreren negativen Eigenwerten aufwartet (Matlab
weist eine indefinite Matrix zurück). Es ist daher wichtig, bevor
man mit einer Korrelationsmatrix multivariate Verarbeitungen durchführt,
zu prüfen, ob die Korrelationsmatrix überhaupt positiv semi definit
ist, also alle Eigenwerte >= 0 sind. Das geht ganz einfach, indem man ihre
Eigenwerte feststellt, was die meisten Statistikprogramme können.
Das Thema spielt seit Veröffentlichung 1994
meines
ersten Bandes - zusammen mit dem Mathematiker Dr. B. Hain - Numerisch
instabile Matrizen und Kollinearität in der Psychologie. Diagnose,
Relevanz & Utilität, Frequenz, Ätiologie, Therapie wieder
eine Rolle bei meinen Korrelationsmatrizenanalysen. Jüngst hat das
Thema einen neuen Schub erhalten: Im Rahmen meiner
Studien zur elementaren Dimension
Fühlen bin ich bei Euler/Mandl (1983), S. 21 zufällig
auf den Hinweis gestoßen, dass Burt 1915 eine Faktorenanalyse einer
Korrelationsmatrix von 11 Gefühlen durchgeführt haben will. Das
hat mich aus vier Gründen interessiert: Faktorenanalyse,
Korrelationsmatrix,
Gefühle
und der Name Burt, der mir dunkel als bekannter Fälscher
in der Psychologie in Erinnerung war. Also suchte ich die Korrelationsmatrix
der 11 Gefühle (Online),
wurde fündig und rechnete sie nach. Die vermeintliche Korrelationsmatrix
zeigt einen relativ großen negativen Eigenwert mit -.0245, der sich
kaum mit Rundungsfehlern der zweistelligen Korrelationskoeffizientendarstellung
erklären lässt. Das hat mich bewogen, mich noch einmal vertieft
und verstärkt der Frage zu widmen, ob wie man eine solche indefinite
Korrelationsmatrix heilen kann, damit multivariate Weiterverarbeitungen
möglich sind und nicht von Prgrammen wie z.B. Matlab
zurückgewiesen werden. Diese Seite stellt sämtliche mir bekannten
Methoden dar, wie man eine indefinite Korrelationsmatrix wieder positiv
semi definit machen kann.
Z2 Dokumentation der Entgleisungen bei den partiellen Korrelationskoeffizienten der indefiniten Matrix von Burt 1915. Die Originalmatrix Burt 1915 mit einem negativen Eigenwert -0.0245 liefert bei den partiellen Korrelationen 7 Entgleisungen, 6 davon extrem, in der Spitze mit einem partiellen Korrelationskoeffizienten von 37! Sie ist damit für multivariate Analysen nicht zu gebrauchen.
Z3 Heilmethoden zur Wiederherstellung positiver Semidefinitheit. Es gibt im Wesentlichen zwei Wege: (1) die Ursachen für den Verlust der Semi-Positiven-Definitheit suchen, finden und beseitigen. (2) Falls (1) nicht möglich ist: Anwendung numerischer Therapiemethoden.
- Ursachen für den Verlust der Semi-Positiven-Definitheit Die Ursachen, manchmal sehr schwierig oder sehr aufwändig oder gar unmöglich mangels Informationen, für den Verlust der positiven Semi Definitheit suchen, finden und beseitigen, z.B.
- Wurden die Korrelationskoeffizienten mit unterschiedlichen Umfängen berechnet? Das ist eine theoretische Möglichkeit um Missing Data Lücken zu umgehen, was die numerische Mathematik gar nicht mag.
- Kollinearitäten können durch zentrieren entstehen oder aufbereitet werden
- Kollinearitäten können durch normieren entstehen oder aufbereitet werden
- Kollinearitäten können durch runden entstehen, am sichersten rechnet man mit maximalen Genauigkeiten
- Kollinearitäten können echt durch kollinearen Verlauf entstehen
- Mehrere Variable können einen kollinearen Verlauf bedingen oder nach sich ziehen
- bei fast kollinearen Verläufen genügen manchmal kleine Veränderungen zum Kippen
- unsymmetrische oder indefinite Korrelationsmatrizen können imaginäre Werte bewirken.
- Wurde mit Pearson oder mit anderen Formeln gerechnet?
- Wurden "Attenuitätskorrektoren" durchgeführt?
- Kritische Variable entfernen
- Falls man die Ursachen nicht findet oder beseitigen kann: Anwendung numerischer Therapiemethoden:
- Faktorisieren
- Negativen Eigenwert durch 0 ersetzen
- Eigenwerte durch Singulärwerte ersetzen
- Zentroidmethode mit allen n Faktoren durchführen; hilft nicht immer (es kann auch zu "Verschlimmbesserungen" kommen), aber manchmal (Beispiel Drinkmann-Matrix).
- Faktorisieren und nomalisieren, d.h. Hauptdiagonale auf 1 skalieren
- Negativen Eigenwert durch 0 ersetzen und normalisieren, d.h. Hauptdiagonale auf 1 skalieren
- Eigenwerte durch Singulärwerte ersetzen und normalisieren, d.h. Hauptdiagonale auf 1 skalieren
_
Z4 Demonstration der numerischen Therapiemethoden am Beispiel Burt 1915.
| Es wurden die verschiedenen numerischen Therapiemethoden angewendet und ziemlich vollständig und nachvollziehbar dokumentiert. Ergebniskontrolle anhand der Eigenwerte siehe bitte Tabelle rechts. Es zeigte sich, dass die indefinite Gefühlsmatrix leicht geheilt werden kann, wodurch die nun positiv semi definite Korrelationsmatrix der 11 Gefühle sowohl multivariater Verarbeitung zugänglich gemacht werden konnte als auch inhaltliche Interpretationen möglich wurden. |  |
Z5 Multivariate Verarbeitungen der numerisch therapierten Korrelationsmatrix CRn.
Z5.1 Hauptkomponentenanalyse Daten, die durch einen bestimmten Filter eines Modells betrachtet werden, werden durch diesen strukturiert und dargestellt. Bei der Hauptkomponentenanalyse (PCA) stehen die Vektoren orthogonal oder senkrecht aufeinander und sind damit voneinander unabhängig, eine in der Psychologie wohl öfter eine bedenkliche Annahme. In der Regel sucht man jedenfalls im faktorenanalytischen Umfeld vergeblich nach Begründungen, warum ein Modell gewählt wurde. Eigentlich sollte dies aus der gewählten Theorie folgen. Warum sollten ausgerechnet die Gefühle unabhängig von einander sein? Die Hauptkomponentenanalyse zeigt im Großen und Ganzen ein ein bifaktorielles Modell mit einem schwachen Generalfaktor (< 50%). Immerhin, die Generalfaktorvermutung von Burt 1915 wird hier im Wesentlichen bestätigt.
Z5.2 Fast-Kollinearitätsanalyse Fast-Kollinearitäten sind wissenschaftlich hochinteressant, weil sie Gesetzes- oder Regelhaftigkeiten anzeigen, also genau das, wonach man in der Wissenschaft immer sucht. Die Burt 1915 Matrix zeigt in allen Varianten, Original und nach 6 numerischen Therapien drei Eigenwerte < 0.20 (Kriterium für Fast-Kollinearität), also drei Fast-Kollinearitäten an. Schon erkennbar in den Korrelationsmatrizen mit Korrelationskoeffizienten > |0.80|.
Z5.3 Partielle Korrelationsanalysen sind sehr interessant, weil man mit ihnen verdeckte Beziehungen und Zusammenhänge zwischen den Variablen finden kann. Damit kann der relevante Merkmalsraum genauer bestimmt werden ein bislang kaum erkanntes und schon gar nicht gelöstes Problem der multivariaten Statistik. Im Wesentlichen interessiert jeweils, ob die Herausnahme von Variablen die partielle Korrelation dann erhöht oder senkt und wie sehr. Hierzu werden viele Beispiele dokumentiert, sortiert nach den Anzahlen der herausgenommenen Variablen. In der Burt Matrix 1915 sind 1, 2, 3, 4, 5, 6. 7, 8, 9 Herausnahmen möglich. Von allen werden Beispiele gebracht. Teilweise wurden sehr beachtliche Veränderungen gefunden: Bei vollständiger Auspartialisierung sinkt die ursprüngliche Korrelation zwischen 7 Ekel und 8 Wut von 0.349 auf -.051, das sind 86 Punkte, also erheblich. Selbst die Herausnahme von nur zwei Variablen 1 Sozialität und 2 Trauer aus 3 Zärtlichkeit und 8 Wut bewirkt, dass die ursprüngliche Korrelation von 0.12 auf -0.60 fällt, das sind 72 Punkte. Burt erklärt weder seine Methode noch die Herausnahmen für seine partiellen Korrelationen in Table II, ein miserabler Stil, den die Report-Redaktion so nicht hätte durchgehen lassen dürfen.
Z6 Kritik Veröffentlichungspraxis Burt 1915 und der Report-Redaktion . Die Arbeit ist völlig unzulänglich beschrieben.
- Z6.1 Die Daten der "Korrelationsmatrix der 11 Gefühle" sind mit keinem Beleg ausgewiesen. Die Stichproben und wie sie in die Matrix eingehen werden nicht ausgewiesen.
- Z6.2 Die Korrelationsmethode ist nicht benannt.
- Z6.3 Es bleibt unklar, ob alle Korrelationskoeffzienten auf der gleichen n-Umfangsbasis gerechnet wurden.
- Z6.4 Es bleibt unerwähnt, ob Missing Data vorlagen - was fast immer bei empirischen Untersuchungen der Fall ist - und wie sie behandelt wurden.
- Z6.5 Es bleibt unerwähnt, ob und wie die Eigenwerte berechnet wurden; und falls, weshalb der negative Eigenwert nicht erörtert und problematisiert wurde. Dieser Kritikpunkt entfällt, wenn Burt Eigenwerte und indefinite "Korrelations"matrizen noch nicht kannte.
- Z6.6 Es ist völlig unklar, weil nicht angegeben, welche Variablen in Tabelle II. auspartialisiert wurden.
- Z6.7 Die Kreisanordnung der positiven und negativen partiellen Korrelationen wird nicht erklärt und begründet.
- Z6.8 Die Faktorenanalyse, orthogonal oder oblique wird nicht angegeben, erörtert und begründet.
- Z6-Kritik-Fazit: Es ist eine miserable Darstellung, die mit einer wissenschaftlichen Veröffentlichung nichts zu tun hat. Das hätte die Report-Redaktion niemals durchgehen lassen dürfen.
Bei meinen Recherchen zu Burt stieß ich in seiner Arbeit THE FACTORS OF THE MIND (1940) auf das 1915 behandelte Thema. In dem Buch p.402-423 geht Burt an verschiedenen Stellen auf seine Arbeit 1915 ein und setzt sich mit seinen Kritikern auseinander. Im Wesentlichen geht es Burt um die Frage, wie man Typen feststellen kann. Er sieht hier in der Faktorenanalyse eine gute methodische Möglichkeit. Eine erste Sichtung hat einige Auffälligkeiten, Unklarheiten und Ungereimtheiten ergeben. Beim Vergleich der Merkmale der zwei Matrizen 1915 und 1940 fällt auf:
- Es scheint sich 1915 und 1940 um die gleichen oder ähnlichen 11 Merkmale zu handeln.
- Die Herkunft der Korrelationstabelle wird, wie schon 1915, nicht ausgewiesen.
- Die in 1915 als "emotions" bezeichneten Merkmale heißen nun "traits".
- Die Veränderung von emotions in traits wird nicht erklärt.
- Die Reihenfolge der Merkmale ist verändert.
- Vier Merkmalsnamen sind neu Assertiveness, Curiosity, Sociability, Submissiveness.
- Die Koeffizienten werden, sehr erfreulich, dreistellig angegeben, was die indefinite Fehlerquelle Rundung deutlich reduziert.
- Viele Korrelationskoeffizienten weichen unerklärt z.T. erheblich von einander ab, z.B.:
| Vergleiche | Burt 1915 Table I | Burt 1940 Table IV |
| Joy - Fear | 0.24 | 0.758 |
| Anger - Sex | 0.53 | 0.791 |
| Sorrow - Disgust | 0.58 | 0.339 |
Z-Fazit. 1. Es wird gezeigt, welche Auswirkungen indefinite Pseudo-Korrelationsmatrizen auf multivariate Verarbeitungen haben. 2. Beispielhaft wird das gezeigt anhand der indefiniten "Korrelations"-Matrix mit 11 Gefühlen von Burt 1915. 3. Aus der Matrix ergeben sich 7 entgleiste partielle Korrelationskoeffizienten, in der Spitze ein Wert von sage und schreibe 37.0111 (2 7 . 1 3 4 5 6 8 9 10 11). 4. Daraus kann man ersehen, dass multivariate Verarbeitungen mit einer solchen indefiniten Matrix nicht möglich sind, weil sie zu unsinnigen und unzuverlässigen Ergebnissen führen. 5. Es wird mit 6 von 7 numerischen Therapiemethoden gezeigt, wie man die indefinite Matrix so heilen kann, dass sie ihre positive (Semi) Definitheit wieder gewinnt und multivariat weiter verarbeitet werden kann. 6. Alle sechs durchgeführten numerischen Therapiemethoden fruchten und der Test mit der vollständigen partiellen Korrelationsanalyse 2 gegen den gesamten Rest zeigt keine Entgleisungen mehr. 7. Die Arbeit von Burt 1915 ist wissenschaftlich völlig unzulänglich dargestellt und im Wesentlichen unbrauchbar, was auch ein schlechtes Licht auf die Report-Redaktion wirft, die eine solche Veröffentlichung zugelassen hat.
Mildernd ist allerdings zu berücksichtigen, dass die 1915 zur Verfügung gestanden habenden Berechnungsmethoden, meist von Hand, nicht selten in wochenlanger Arbeit, mit den heutigen und hier angewandten überhaupt nicht vergleichbar sind. Heute gibt man seine Daten ein und mit wenigen Befehlen ist Sekunden später das Ergebnis da (so zumindest bei Matlab). Burt hat noch nicht, jedenfalls nicht explizit, auch nicht in seiner Arbeit 1940, mit Eigenwerten gearbeitet, obwohl er sie implizit durch die Quadratsummen der Faktoren haben konnte, wenn auch wahrscheinlich keine negativen. Letztlich muss oder kann man Burt zu Gute halten, dass er von indefiniten Pseudo-Korrelationsmatrizen noch nichts wusste.
_
_
Numerische Therapie
der indefiniten "Korrelationsmatrix" von Burt 1915
Zusammenfassung-Burt-1915: Die mit einem negativen Eigenwert von -0.0245
indefinite Matrix von Burt 1915 mit 11 Gefühlen ist einfach numerisch
zu therapieren, so dass sie ihre Positive-Semi-Definitheit zurückgewinnt,
multivariat verarbeitet und interpretiert werden kann.
Eine kausale Therapie ist nicht möglich, weil wir die Originaldaten
nicht zur Verfügung haben. Wir begnügen uns daher damit, die
pragmatisch-numerischen Therapiemethoden allesamt anzuwenden, auch zum
Vergleichen ihrer Ergebnisse.
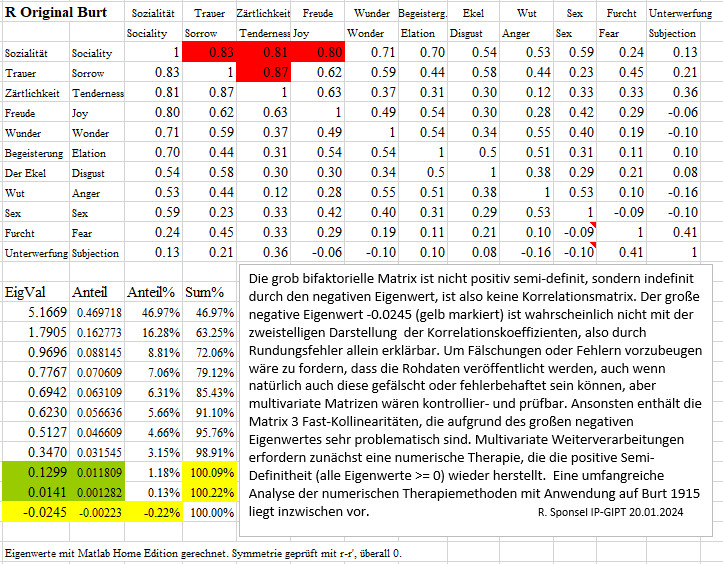
I. Angewandte numerische Therapiemethoden und ihre Ergebnisse
Methodenkürzel
:
1 CR Faktorisierung
2 CR0 Eigenwert 0 setzen
3 CR0n Eigenwert 0 normalisieren
4 CRn Faktorisierung normalisieren
5 CRs Singulärwert nehmen
6 CRsn Singulärwert normalisieren
7 CC Zentroid mit allen Faktoren,
aktuell nicht funktionsfähig
Gefühlskennungen (Google
Übersetzer)
Gefühlskennungen (Google Übers.)
1 Sociality - Sozialität
2 Sorrow - Trauer
3 Tenderness - Zärtlichkeit
4 Joy - Freude
5 Wonder - Wundern?
6 Elation - Begeisterung
7 Disgust - Ekel
8 Anger - Wut
9 Sex - Sex
10 Fear - Furcht
11 Subjection - Unterwerfung
_
CR Faktorisieren
Ergebnis: Nach Faktorisieren verschwindet der
negative Eigenwert und die positive Definitheit ist wieder hergestellt.
Die Korrelationsmatrix kann multivariat verarbeitet und interpretiert werden.

CRn
Faktorisieren und die Hauptdiagonale auf 1 skalieren ("normalisieren")
Ergebnis: Nach Faktorisieren und Skalieren der
Hauptdiagonalwerte auf 1 verschwindet der negative Eigenwert und die positive
Definitheit ist wieder hergestellt. Die Korrelationsmatrix kann multivariat
verarbeitet und interpretiert werden.

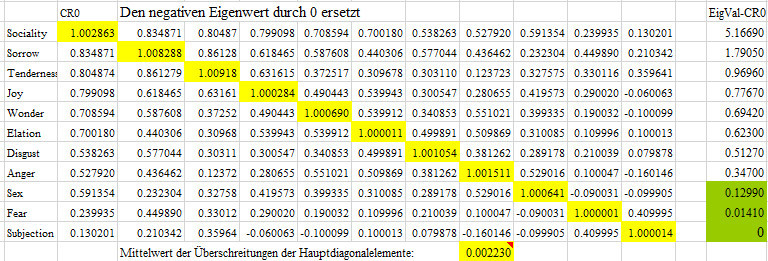
CR0
Den negativen Eigenwert durch 0 ersetzen
Ergebnis: Nach Setzen des negativen Eigenwerte
auf 0 ist der negative Eigenwert natürlich durch die Setzung verschwunden
und die Positive Semi-Definitheit ist wieder hergestellt. Die Korrelationsmatrix
ist dadurch kollinear oder linear abhängig und sie kann nur mit großer
Vorsicht und Skepsis multivariat verarbeitet und interpretiert werden.
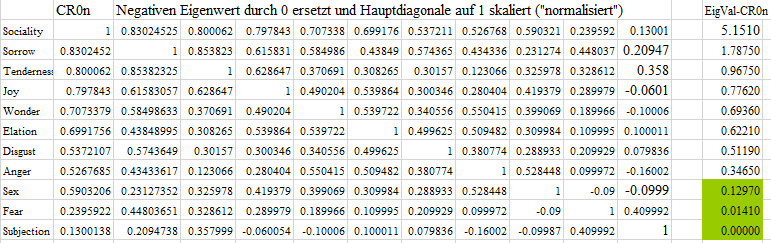
CR0n
Den negativen Eigenwert durch 0 ersetzen und die Hauptdiagonale auf 1 skalieren
("normalisieren")
Ergebnis: Nach Setzen des negativen Eigenwerte
auf 0 ist der negative Eigenwert natürlich durch die Setzung verschwunden
und die Positive Semi-Definitheit ist wieder hergestellt. Die Skalierung
der Hauptdiagonalelemente auf 1 hat keine Einfluss auf die Kollinearität.
Die Korrelationsmatrix ist dadurch kollinear oder linear abhängig
und sie kann nur mit großer Vorsicht und Skepsis multivariat verarbeitet
und interpretiert werden.
CRs
Die Eigenwerte durch die Singulärwerte ersetzen
Ergebnis: Nach Ersetzen der Eigenwerte durch
die Singulärwerte verschwindet der negative Eigenwert und die positive
Definitheit ist wieder hergestellt. Die Korrelationsmatrix kann multivariat
verarbeitet und interpretiert werden.
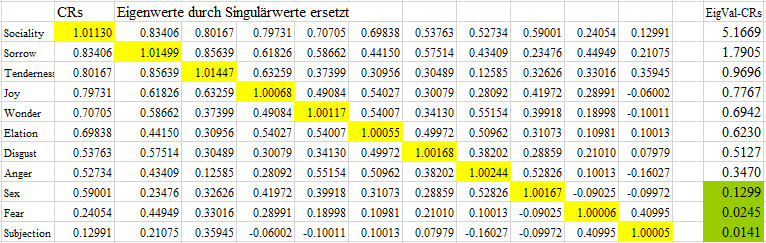
CRsn
Die Eigenwerte durch die Singulärwerte ersetzen und die Hauptdiagonale
auf 1 skalieren ("normalisieren")
Ergebnis: Nach Ersetzen der Eigenwerte durch
die Singulärwerte verschwindet der negative Eigenwert und die positive
Definitheit ist wieder hergestellt. Die Skalierung der Hauptdiagonalwerte
auf 1 hat wenig Einfluss. Die Korrelationsmatrix kann multivariat verarbeitet
und interpretiert werden.

CC Zentroidmethode
Nachdem aktuell die Zentroidmethode bei mir unter Win10 nicht zur Verfügung steht, habe ich ein früheres Beispiel aus 1994 herangezogen. Die Zentroidmethode kann aber auch zu "Verschlimmbesserungen" führen, wie hier gezeigt wird.

II. Multivariate Weiterverarbeitungen
- Vergleichende vollständige partielle Matrix-Analysen der Originalmatrix mit den verschiedenen numerischen Therapievarianten
- Hauptkomponentenanalyse mit der Gefühlsmatrix
- Partielle Korrelationen mit der numerisch therapierten Korrelationsmatrix CRn
1. Multivariate Verfahren und Analysen gehören zum Standard
der Psychologie und psychologischen Statistik. Die Kern- und Hauptfrage
der Wissenschaft ist einfach: was gibt es und wie hängt es zusammen?
Die strengen messtheoretischen (Intervallskalenniveau ) oder statistischen
Voraussetzungen (Zufallsauswahlen, Verteilungsannahmen, angemessene Verfahren,
einheitlicher Erhebungsraum, reguläre Erhebungen) werden hierbei meist
nicht beachtet. Das sind grundsätzliche Fragen und Probleme, die hier
ausgeklammert werden sollen.
2. Die ungeheure Vielfalt der Gefühle lassen sie für multivariate
Verfahren geradezu prädestiniert erscheinen, so dass gegen multivariate
Verfahren bei Gefühl nicht nur nichts einzuwenden ist, sondern sie
geradezu danach verlangen.
3. Grundsätzlich und konzeptionell gibt es gegen Burts Analyse
von 1915 also nichts einzuwenden.
4. Bei aller Kritik muss man mildernd auch berücksichtigen, dass
man 1915 über keine leistungsfähigen Rechner und Programme verfügte,
die multivariate Analysen so leicht und einfach wie heute machen. Die Alten
waren gegenüber uns Heutigen haushoch im Vorteil, weil sie mathematisch
und rechentechnisch auf der Höhe waren. Wer wochenlang rechnen musste,
um eine Faktorenanalyse zu erstellen, der wusste - in der Regel - wie es
geht, was man von uns heutigen KnöpfedrückerInnen nicht mehr
sagen kann (beim Knopfdruck "All" wird schon was dabei sein, was sich veröffentlichen
lässt).
Vergleichende vollständige partielle Matrix-Analysen der Originalmatrix mit den verschiedenen numerischen Therapievarianten
Zusammenfassung
Vergleichende vollständige partielle Matrix-Analysen der Originalmatrix
mit den verschiedenen numerischen Therapievarianten
1. Die Originalmatrix Burt 1915 mit einem negativen
Eigenwert -0.0245 liefert bei den partiellen Korrelationen 7 Entgleisungen,
6 davon extrem (mit einem partiellen Korrelationskoeffizienten von 37!).
Sie ist damit für multivariate Analysen nicht zu gebrauchen.
2. Die Ersetzung des negativen Eigenwertes -0.0245
durch 0 bedeutet die Einrichtung einer linearen Abhängigkeit und führt
zu unsicheren, wahrscheinlich unbrauchbaren Ergebnissen.
3. Die anderen vier numerischen Therapiemethoden
liefern interpretierbare Ergebnisses bei den partiellen Korrelation: Zwischen
CR, CRn, CRs und CRsn sind keine großen Unterschiede, die sich meist
ab der 2. Nachkommastelle bemerkbar machen.
4. Multivariate Verarbeitungen wie etwa eine
Hauptkomponentenanalyse sind daher möglich.
5. Interpretationen.
R:
Die Originalmatrix von Burt 1915 mit einem negativen Eigenwert -0.0245
liefert bei den partiellen Korrelationen 7 Entgleisungen, 6 davon extrem:
pcv : 7 8 .
1 2 3 4 5 6 9 10 11 corrmat:
-11.5931
pcv : 3 8 .
1 2 4 5 6 7 9 10 11 corrmat:
-3.7083
pcv : 3 7 .
1 2 4 5 6 8 9 10 11 corrmat:
-4.2176
pcv : 2 8 .
1 3 4 5 6 7 9 10 11 corrmat:
31.9130
pcv : 2 7 .
1 3 4 5 6 8 9 10 11 corrmat:
37.0111
pcv : 2 3 .
1 4 5 6 7 8 9 10 11 corrmat:
16.4418
pcv : 1 9 .
2 3 4 5 6 7 8 10 11 corrmat:
1.1618
CR Diese Methode faktorisiert die Originalmatrix von Burt, wobei sich die imaginären Werte von F bei Multiplikation von F mit der Transponierten wieder aufheben. Der negative Eigenwert ist verschwunden und die CR-Matrix ist positiv definit. Hier überschreiten die Hauptdiagonalen die 1 ab der 2. Nachkommastelle, was im Allgemeinen zu einer Erhöhung der numerischen Stabilität führt, was man bei der Ridge- bzw. Tikhonov-Methode gezielt anwendet. Will man die Auswirkungen auf die partielle Korrelation der Faktorisierungsmethode mit oder ohne Normalisierung der Hauptdiagonalen prüfen, muss man CR mit CRn vergleichen. Es gibt hier bis auf die 4. Nachkommastelle keinen Unterschied.
CR0 Die Methode setzt den negativen Eigenwert von -0.0245 glatt 0. Die Matrix wird dadurch positiv semi definit, enthält damit also eine Kollinearität oder lineare Abhängigkeit. Man sieht, dass den negativen Eigenwert einfach 0 zu setzen dazu führt, dass die partiellen Korrelationskoeffizienten 2 (1 Paar) gegen den ganzen Rest allesamt gegen 1 oder -1 tendieren, was verständlich ist, da ja mit der Eigenwertsetzung 0 eine lineare Abhängigkeit eingerichtet wurde. Der Mathematiker Dr. B. Hain hat gezeigt (1994, Kap. VI, S. 38 ff), daß die Korrelationsmatrix bei vollständiger Partialisierung - rij.n-2 - nicht notwendig positiv definit sein muß. Hier ist also größte Vorsicht geboten, wenn Verdacht auf lineare Abhängigkeit besteht, was Eigenwerte 'nahe' 0 anzeigen. Quelle: https://www.sgipt.org/wisms/statm/kor/partkor.htm.
CR0n Wie CR0, aber mit Normalisierung der Hauptdiagonalen zu 1. Die Normalisierung der Hauptdiagonalen auf 1 gelingt, wie man sieht bis zu 4. Nachkommastellen
CRn Hier werden die erhöhten Hauptdiagonalwerte der faktorisierten Matrix CR auf 1 normalisiert. Bei 4-stelliger Genauigkeit der Darstellung keine Unterschiede erkennbar.
CRs Die Methode ersetzt die Eigenwerte durch die sämtlich positiven Singulärwerte, was bei den Hauptdiagonalwerten ab der 2. Nachkommastelle zu geringfügig erhöhten Werten über 1 führt.
CRsn Diese Normalisierungs-Methode
beseitigt die über 1 erhöhten Hauptdiagonalwerte und bringt sie
auf 1 zurück.
Vergleichstabelle Partielle Korrelationskoeffizienten 2 gegen den ganzen Rest nach den verschiedenen numerischen Therapiemethoden.
Lesebeispiel Zeile 47: Die partielle Korrelation zwischen Gefühl 10 () und 11 () beträgt in der Originalmatrix Burt 1915 0.5533, in der faktorisierten Matrix CR 0.5538, in der Matrix CR0, Eigenwert gleich 0 gesetzt, 0.9907, in CR0n, Eigenwert gleich 0 gesetzt und Hauptdiagonale auf 1 skaliert 1.0004, in CRn der faktorisierten und Hauptdiagonale auf 1 skaliert 0.5538, in CRs, Eigenwerte durch Singulärwerte ersetzt, 0.5342 und CRsn, Eigenwerte durch Singulärwerte ersetzt und Hauptdiagonale auf 1 skaliert 0.5342. Centroid aktuell nicht verfügbar.

Hauptkomponentenanalyse mit der Gefühlsmatrix CRn
Zusammenfassung
Hauptkomponentenanalyse der numerisch therapierten CRn Korrelationsmatrix
Daten, die durch einen bestimmten Filter eines Modells betrachtet werden,
werden durch diesen strukturiert und dargestellt. Bei der Hauptkomponentenanalyse
(PCA) stehen die Vektoren orthogonal oder senkrecht aufeinander und sind
damit voneinander unabhängig, eine in der Psychologie wohl öfter
bedenkliche Annahme. In der Regel sucht man jedenfalls im faktorenanalytischen
Umfeld vergeblich nach Begründungen, warum ein Modell gewählt
wurde. Eigentlich sollte dies aus der gewählten Theorie folgen. Warum
sollten ausgerechnet die Gefühle unabhängig von einander sein?
Die Hauptkomponentenanalyse zeigt im Großen und Ganzen ein bifaktorielles
Modell mit einem schwachen Generalfaktor (< 50%). Immerhin, die Generalfaktorvermutung
von Burt 1915 wird hier im Wesentlichen bestätigt.

Ab welcher Größe sollen Faktorenladungen relevant sein? In der PCA Tabelle wurden alle markiert > = 0.50.
Fast-Kollinearitätsanalysen
Zusammenfassung: Fast-Kollinearitäten sind wissenschaftlich hochinteressant, weil sie Gesetzes- oder Regelhaftigkeiten anzeigen, also genau das, wonach man in der Wissenschaft immer sucht. Die Burt 1915 Matrix zeigt in allen Varianten, Original und nach 6 numerischen Therapien drei Eigenwerte < 0.20 (Kriterium für Fast-Kollinearität), also drei Fast-Kollinearitäten an. Schon erkennbar in den Korrelationsmatrizen mit Korrelationskoeffizienten > |0.80| wie im Folgenden auch dargestellt.
 _
_
_
Partielle
Korrelationen mit der numerisch therapierten Korrrelationsmatrix CRn
Nachdem keine Informationen vorliegen, wie die Partialisierungen gebildet
wurden, können die in Tabelle II. mitgeteilten partiellen Korrelationskoeffizienten
nicht nachgerechnet werden. Die Mitteilung "(Average for five groups.)"
lässt nichts Gutes ahnen. Wie die Report-Redaktion eine so miserabel
dokumentierte Arbeit aufnehmen konnte, ist mir rätselhaft.
Diskussionsbeispiel: Die partielle Korrelation zwischen Joy und Sex
wird mit 0.21 angegeben, in der Korrelationsmatrix oben mit 0.42. Partialisiert
man aus - was oder welche Variablen, also das Entscheidende, verrät
Burt nicht - fällt sie also um die Hälfte.

Ich kann deshalb nur eigene partielle Korrelationsrechnungen durchführen und einige Ergebnisse hier mitteilen und kurz kommentieren. Ich beschränke mich dabei auf einige besonders interessante Fälle, hier den Einfluss der anderen Variablen auf die Korrelation zwischen 1 Sozialität und 2 Trauer, die mit einem r=0.83 eine Fast-Kollinearität anzeigen. Die Kennungen 1...11 sind nach der Reihenfolge der Korrelationsmatrix gebildet.
Zusammenfassung Partielle Korrelationsanalysen sind sehr interessant, weil man mit ihnen verdeckte Beziehungen und Zusammenhänge zwischen den Variablen finden kann. Damit kann der relevante Merkmalsraum genauer bestimmt werden, ein bislang kaum erkanntes und schon gar nicht gelöstes Problem der multivariaten Statistik. Im Wesentlichen interessiert jeweils, ob die Herausnahme von Variablen die partielle Korrelation dann erhöht oder senkt und wie sehr. Hierzu werden viele Beispiele dokumentiert, sortiert nach den Anzahlen der herausgenommenen Variablen. In der Burt Matrix 1915 sind 1, 2, 3, 4, 5, 6. 7, 8, 9 Herausnahmen möglich. Von allen werden Beispiele gebracht. Teilweise wurden sehr beachtliche Veränderungen gefunden: Bei vollständiger Auspartialisierung sinkt die ursprüngliche Korrelation zwischen 7 Ekel und 8 Wut von 0.349 auf -.051, das sind 86 Punkte, also erheblich. Selbst die Herausnahme von nur zwei Variablen 1 Sozialität und 2 Trauer aus 3 Zärtlichkeit und 8 Wut bewirkt, dass die ursprüngliche Korrelation von 0.12 auf -0.60 fällt, das sind 72 Punkte. Burt erklärt weder seine Methode noch die Herausnahmen für seine partiellen Korrelationen in Table II, ein miserabler Stil, den die Report-Redaktion so nicht hätte durchgehen lassen dürfen.
1 Partielle Korrelation zwischen
1 und 2, ursprüngliche Korrelation 0.83, nach Auspartialisierung von
jeweils 3, 4, 5, 6, 7, 8, 9, 10, 11.
| pcv : 1 2 .
3 = 0.503287
pcv : 1 2 . 4 = 0.717429 pcv : 1 2 . 5 = 0.729719 pcv : 1 2 . 6 = 0.815968 pcv : 1 2 . 7 = 0.757387 pcv : 1 2 . 8 = 0.78734 pcv : 1 2 . 9 = 0.883198 pcv : 1 2 . 10 = 0.832898 pcv : 1 2 . 11= 0.828491 In abnehmender Reihenfolge
|
Partialisiert man den Einfluss von 3 Zärtlichkeit aus, sinkt die
Korrelation zwischen 1 Sozialität und 2 Trauer von 0.83 auf 0.50.
10 Furcht hat so gut wie keinen Einfluß. Partialisiert man sie
aus, bleibt die Korrelation mit 0.83 gleich.
|

_ _ _ _ _ _ _ |
2 auspartialisiert aus 1 2. mit
ursprünglicher Korrelation = 0.83
| Auswahl:
pcv : 1 2 . 3 10 = 0.54597 pcv : 1 2 . 5 7 = 0.657325 pcv : 1 2 . 5 8 = 0.721209 pcv : 1 2 . 5 9 = 0.828795 pcv : 1 2 . 5 10= 0.742638 pcv : 1 2 . 5 11= 0.702683 pcv : 1 2 . 6 7 = 0.799461 pcv : 1 2 . 6 8 = 0.801557 pcv : 1 2 . 6 9 = 0.908036 pcv : 1 2 . 6 10 = 0.81941 pcv : 1 2 . 6 11 = 0.817291 pcv : 1 2 . 7 8 = 0.734217 pcv : 1 2 . 7 9 = 0.846863 pcv : 1 2 . 7 10 = 0.769683 pcv : 1 2 . 7 11 = 0.75588 pcv : 1 2 . 8 11 = 0.770544 pcv : 1 2 . 8 9 = 0.870123 pcv : 1 2 . 9 11 = 0.876221 |

_ _ _ _ _ _ |
3 auspartialisiert aus 1 2. mit
ursprünglicher Korrelation = 0.83
| Auswahl
pcv : 1 2 . 5 7 9 = 0.78917 pcv : 1 2 . 5 7 10 = 0.67934 pcv : 1 2 . 5 7 11 = 0.628325 pcv : 1 2 . 5 8 9 = 0.834409 pcv : 1 2 . 5 8 10 = 0.732533 pcv : 1 2 . 5 8 11 = 0.685182 pcv : 1 2 . 5 9 10 = 0.817987 pcv : 1 2 . 5 9 11 = 0.806168 pcv : 1 2 . 5 10 11 = 0.732723 pcv : 1 2 . 6 7 8 = 0.788908 pcv : 1 2 . 6 7 9 = 0.9164 pcv : 1 2 . 6 7 10 = 0.807963 pcv : 1 2 . 6 7 11 = 0.80163 pcv : 1 2 . 6 8 9 = 0.928211 pcv : 1 2 . 6 8 10 = 0.805162 pcv : 1 2 . 6 8 11 = 0.797352 pcv : 1 2 . 6 9 10 = 0.896365 pcv : 1 2 . 6 9 11 = 0.904299 pcv : 1 2 . 6 10 11 = 0.819507 pcv : 1 2 . 7 8 9 = 0.839506 pcv : 1 2 . 7 8 10 = 0.744398 pcv : 1 2 . 7 8 11 = 0.719526 pcv : 1 2 . 7 9 10 = 0.835706 pcv : 1 2 . 7 9 11 = 0.839789 pcv : 1 2 . 7 10 11 = 0.769233 pcv : 1 2 . 8 9 10 = 0.856442 pcv : 1 2 . 8 9 11 = 0.857379 pcv : 1 2 . 8 10 11 = 0.784618 pcv : 1 2 . 9 10 11 = 0.86756 |

_ _ _ _ _ _ _ _ _ _ _ _ _ _ |
4 auspartialisiert aus 1 2.
mit ursprünglicher Korrelation = 0.83
| Auswahl
pcv : 1 2 . 5 7 9 11 = 0.765475 pcv : 1 2 . 5 7 10 11 = 0.667449 pcv : 1 2 . 5 8 9 10 = 0.82442 pcv : 1 2 . 5 8 9 11 = 0.809487 pcv : 1 2 . 5 8 10 11 = 0.718102 pcv : 1 2 . 5 9 10 11 = 0.813072 pcv : 1 2 . 6 7 8 9 = 0.937685 pcv : 1 2 . 6 7 8 10 = 0.797121 pcv : 1 2 . 6 7 8 11 = 0.785897 pcv : 1 2 . 6 7 9 10 = 0.908985 pcv : 1 2 . 6 7 9 11 = 0.913283 pcv : 1 2 . 6 7 10 11 = 0.808168 pcv : 1 2 . 6 8 9 10 = 0.919715 pcv : 1 2 . 6 8 9 11 = 0.92604 pcv : 1 2 . 6 9 10 11 = 0.89677 pcv : 1 2 . 7 8 9 10 = 0.829583 pcv : 1 2 . 7 8 9 11 = 0.827934 pcv : 1 2 . 8 9 10 11 = 0.85337 pcv : 1 2 . 7 8 10 11 = 0.739951 pcv : 1 2 . 7 9 10 11 = 0.835844 pcv : 1 2 . 6 8 10 11 = 0.803894 |
Die Herausnahme von 6 Begeisterung, 7 Ekel, 8 Wut und 9 Sex erhöht
die partielle Korrelation zwischen 1 Sozialität und 2 Trauer von 0.83
auf 0.937.
Am meisten wird die Korrelation zwischen 1 Sozialität und 2 Trauer
durch die Herausnahme von 5 wundern, 7 Ekel, 10 Furcht und 11 Unterwerfung
von 0.83 auf 0.667 gesenkt.
|

_ _ _ _ _ _ _ _ |
5 auspartialisiert aus 1 2.
aus 1 2. mit ursprünglicher Korrelation = 0.83
| Auswahl
pcv : 1 2 . 5 7 9 10 11 = 0.777217 pcv : 1 2 . 5 8 9 10 11 = 0.816169 pcv : 1 2 . 6 7 8 9 10 = 0.932699 pcv : 1 2 . 6 7 8 9 11 = 0.936742 pcv : 1 2 . 6 7 8 10 11 = 0.795769 pcv : 1 2 . 6 7 9 10 11 = 0.909126 pcv : 1 2 . 6 8 9 10 11 = 0.919728 pcv : 1 2 . 7 8 9 10 11 = 0.82693 |
Auch wenn man 5 Variable auspar- tialisiert, ändert sich an den
Größen- ordnungen der Korrelation zwischen 1 Sozialität
und 2 Trauer nicht sehr viel.
|
 |
6 auspartialisiert aus 1 2.
mit ursprünglicher Korrelation = 0.83
| Auswahl
pcv : 1 2 . 5 7 8 9 10 11 = 0.782578 pcv : 1 2 . 6 7 8 9 10 11 = 0.932957
|
 |
7 auspartialisiert aus 1 2.
mit ursprünglicher Korrelation = 0.83
| Auswahl
pcv : 1 2 . 5 6 7 8 9 10 11 = 0.918217
|
 |
8 auspartialisiert aus 1 2.
mit ursprünglicher Korrelation = 0.83
| Auswahl
pcv : 1 2 . 4 5 6 7 8 9 10 11 = 0.881886
|
 |
Alle 9 auspartialisiert
aus 1 2. mit ursprünglicher Korrelation = 0.83
| Auswahl
pcv : 1 2 . 3 4 5 6 7 8 9 10 11 = 0.440535
|
Partialisiert man alle 9 aus, fällt die ursprüngliche Korrelation
von 0.83 auf 0.44, also erheblich. Das scheint aber vor allem An Variable
3 Zärtlichkeit zu liegen, wie man aus den folgenden Auspartialisierungen
erschließen kann.
|
 |
Stark veränderte
Korrelationen durch Auspartionalisierungen
| Auswahl
pcv : 2 9 . 1 3 10 = -0.470999 von 0.21 pcv : 3 8 . 1 2 10 11 = -0.603377 von 0.12 pcv : 3 8 . 1 2 11 = -0.605709 von 0.12 pcv : 3 8 . 1 2 = -0.642702 von 0.12 pcv : 3 8 . 1 2 10 = -0.643432 von 0.12 pcv : 3 8 . 1 2 9 11 = -0.680831 von 0.12 pcv : 2 9 . 1 3 8 11 = -0.666924 pcv : 3 8 . 1 2 9 = -0.701682 von 0.12 pcv : 2 9 . 1 3 8 = -0.659481 pcv : 7 8 . 1 2 3 4 5 6 9 10 11 = -0.512249 |
Bei vollständiger Auspartialisierung sinkt die ursprüngliche
Korrelation zwischen 7 Ekel und 8 Wut von 0.349 auf -.051, das sind 86
Punkt, also erheblich.
Selbst die Herausnahme von nur zwei Variablen 1 Sozialität und 2 Trauer aus 3 Zärtlichkeit und 8 Wut bewirkt, dass die ursprüngliche Korrelation von 0.12 auf -0.60 fällt, das sind 72 Punkte. |
 |
III. Interpretationen der positiv semi definiten Gefühlsmatrix
Hier sollte es nicht mehr um die Analyse und Darstellung, sondern um
die Interpretationsmöglichkeiten multivariater Gefühlsforschung
gehen. Vernünftige und begründete Interpretationen sind mangels
Angaben und Dokumentation in Burt 1915 aber nicht möglich, so dass
es bei der Kenntnisnahme der formalen Zahlen und ihrer Beziehungen bleiben
muss.
IV. Zusammenfassung Kritik der Veröffentlichung Burt 1915 und der Report-Redaktion, die diese Arbeit offenbar völlig kritiklos angenommen hat. Die Arbeit ist völlig unzulänglich beschrieben. Mit Wissenschaft hat das nichts zu tun. "Z" ist das Kürzel aus der Zusammenfassung.
- Z6.1 Die Daten der "Korrelationsmatrix der 11 Gefühle" sind mit keinem Beleg ausgewiesen. Die Stichproben und wie sie in die Matrix eingehen werden nicht ausgewiesen. Auch zur Quelle von McDougall der primären Emotionen wird keine genaue Fundstelle angegeben.
- Z6.2 Die Korrelationsmethode ist nicht benannt.
- Z6.3 Es bleibt unklar, ob alle Korrelationskoeffzienten auf der gleichen n-Umfangsbasis gerechnet wurden.
- Z6.4 Es bleibt unerwähnt, ob Missing Data vorlagen - was fast immer bei empirischen Untersuchungen der Fall ist - und wie sie behandelt wurden.
- Z6.5 Es bleibt unerwähnt, ob und wie die Eigenwerte berechnet wurden; und falls, weshalb der negative Eigenwert nicht erörtert und problematisiert wurde.
- Z6.6 Es ist völlig unklar, weil nicht angegeben, welche Variablen in Tabelle II. auspartialisiert wurden.
- Z6.7 Die Kreisanordnung der positiven und negativen partiellen Korrelationen wird nicht erklärt und begründet.
- Z6.8 Die Faktorenanalyse, orthogonal oder oblique wird nicht angegeben, erörtert und begründet.
- Z6-Kritik-Fazit: Es ist eine miserable Darstellung, die mit einer wissenschaftlichen Veröffentlichung nichts zu tun hat. Das hätte die Report-Redaktion niemals durchgehen lassen dürfen.
V. Burt 1940 zu seiner Arbeit 1915
In seinem Buch 1940 "THE FACTORS OF THE MIND", p.402- geht Burt auf seine Arbeit 1915 ein und setzt sich mit seinen Kritikern auseinander. Eine erste Sichtung hat einige Auffälligkeiten, Unklarheiten und Ungereimtheiten ergeben.
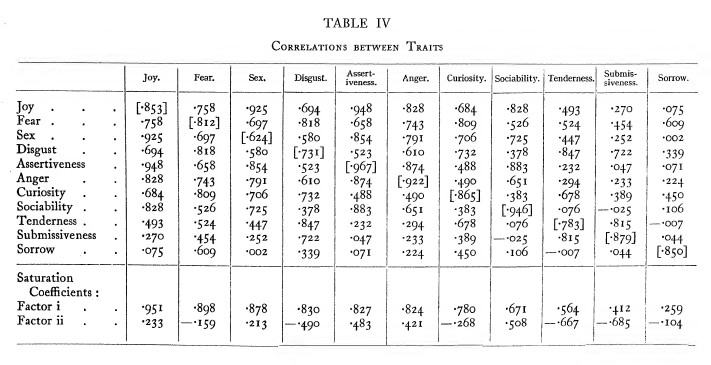
Im Wesentlichen geht es Burt um die Frage, wie man Typen feststellen kann. Er sieht hier in der Faktorenanalyse eine gute methodische Möglichkeit.
Zusammenfassung-Erstsichtung-Burt-1940
verglichen mit Burt 1915:
Im Wesentlichen geht es Burt um die Frage, wie
man Typen feststellen kann. Er sieht hier in der Faktorenanalyse eine gute
methodische Möglichkeit. Beim Vergleich der Merkmale der zwei Matrizen
1915 und 1940 fällt auf:
- Es scheint sich 1915 und 1940 um die gleichen oder ähnliche 11 Merkmale zu handeln.
- Die Herkunft der Korrelationstabelle wird, wie schon 1915, nicht ausgewiesen.
- Die in 1915 als "emotions" bezeichneten Merkmale heißen nun "traits".
- Die Veränderung von emotions in traits wird nicht erklärt.
- Die Reihenfolge der Merkmale ist verändert.
- Vier Merkmalsnamen sind neu Assertiveness, Curiosity, Sociability, Submissiveness.
- Die Koeffizienten werden, sehr erfreulich, dreistellig angegeben, was die indefinite Fehlerquelle Rundung deutlich reduziert.
- Viele Korrelationskoeffizienten weichen unerklärt z.T. erheblich von einander ab, z.B.:
| Vergleiche | Burt 1915 Table I | Burt 1940 Table IV |
| Joy - Fear | 0.24 | 0.758 |
| Anger - Sex | 0.53 | 0.791 |
| Sorrow - Disgust | 0.58 | 0.339 |
Soviel zu den Eindrücken meiner Erstsichtung. Bei Gelegenheit werde ich diese Arbeit genauer und gründlicher analysieren, sofern es die dort mitgeteilten Informationen zulassen und hergeben.
Münsterbergs 12-Werke-Matrix
Obwohl die Matrix regulär aus vollständigen empirischen Daten gewonnen wurde, zeigt sie sich im kaum sichtbaren Grenzbereich als indefinit. An dieser Matrix lässt sich sehr schön zeigen, was das Wesen und Kernproblem der Instabilität ist: kleine und hier sogar winzige Veränderungen auf der Eingangsseite (negativer Eigenwert an der 15. Nachkommastelle) und extreme Entgleisung auf der Ausgangsseite (z.B. partielle Korrelation von pcv : 6 9 . 1 2 3 4 5 7 8 10 11 12 = 7.18055. > Prüfung auf Entgleisungen .... Aber die Matrix ist aufgrund ihres Spalten-Zeilverhältnis vielfach kollinear und schon von daher, auch ohne den winzigen negativen Eigenwert, hochgradig numerisch instabil, Es ist daher Es ist daher bei multivariaten Verarbeitungen mit Entgleisungen zu rechnen. Das ist hier zwar nicht bei den multiplen Korrelationen zu sehen, aber massiv bei den den partiellen Korrelationen, z.B. bei pcv : 6 9 . 1 2 3 4 5 7 8 10 11 12 = 7.18055.
Prüfung auf Entgleisungen
bei multiplen und partiellen Korrelationen
Zusammenfassung
Prüfung auf multivariate Entgleisungen der Werke-Matrix : Die multiplen
Korrelationen zeigen nur unbedeutende Abweichungen mit Werten größer
1 ab der 4. Nachkommastelle (gefettet), die man vernachlässigen
kann. Von dieser Seite her, gibt es keine numerischen Therapiebedarf der
Matrix. Ganz anders stellt sich die Sachlage bei den partiellen Korrelationen
dar. Hier gibt es viele hochpathologische Entgleisungen, die eine numerische
Therapie nahelegen. Am 24.05.2025 (gerechnet am 24.05.2025 mit dem
Karl Wiesent Programm in Matlab).
- multiple
correlation coefficients
0.9991004867458424
0.9999780497833574
0.9991004867459061
0.9998746956217148
0.9997299823950333
1.000129683076549
1.000014290800755
1.000081966335072
1.000126370736338
0.999522181034878
0.9999525357462469
0.9999872810154017
- _
Partielle Korrelationen Werke: massive Entgleisungen.
Hier gibt es massive Entgleisungen - und nicht nur bei 2 gegen den Rest -, die anzeigen, dass die scheinbare Korrelationsmatrix bei partieller Weiterverarbeitung keine ist. Ich greife einige Entgleisungen heraus:
10 auspartialisiert also 2 gegen den Rest
pcv : 10 11 .
1 2 3 4 5 6 7 8 9
12 = 1.38077
pcv : 6 9 .
1 2 3 4 5 7 8 10 11
12 = 7.18055
pcv : 5 10 .
1 2 3 4 6 7 8 9 11
12 = 4.36702
pcv : 4 10 .
1 2 3 5 6 7 8 9 11
12 = 2.55928
9 auspartialisiert, also 2 gegen den Rest-1
pcv : 6 7 .
2 3 4 5 8 9 10 11 12 =
-1.94665
4 auspartialisiert
pcv : 8 11 .
7 9 10 12 = 1.80101
pcv : 8 11 .
6 9 10 12 = 1.78382
pcv : 6 11 .
8 9 10 12 = -2.40733
pcv : 7 8
. 6 9 10 11 = 2.797
3 auspartialisiert
pcv : 7 11 .
8 9 12 = 1.33105
pcv : 6 7 .
8 10 11 = -1.52153
2 auspartialisiert
pcv : 11 12 .
9 10 = -1.16731
pcv : 9 12
. 8 10 = -1.05712
Ich habe die bislang 6 entwickelten numerischen Therapiemethoden auf die Münsterberg Werke-Matrix angewandt und mit 3 von ihnen die positive Semidefinitheit wieder herstellen können. Die Prüfung der partiellen Korrelation bei CRn ergab, dass keine Entgleisungen pc >> |1|.
Originalmatrix mit 4 Nachkommastellen
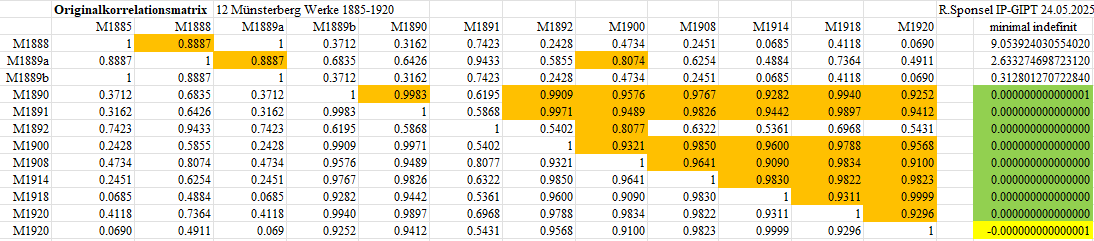

_
CRn
Faktorisieren und die Hauptdiagonale auf 1 skalieren ("normalisieren")

_
CR0 Den negativen Eigenwert durch 0
ersetzen

_
CR0n Den negativen Eigenwert durch 0
ersetzen und die Hauptdiagonale auf 1 skalieren ("normalisieren")

_
CRs Die Eigenwerte durch die Singulärwerte
ersetzen

_
CRsn Die Eigenwerte durch die Singulärwerte
ersetzen und die Hauptdiagonale auf 1 skalieren ("normalisieren")

_
Checkliste definieren
Checkliste-Beweisen
Methodik-Beweissuche in der Psychologie
Viele positive oder bejahende Feststellungen oder Aussagen haben kein Suchtextkriterium, so dass Fundstellen nur durch lesen, Zeile für Zeile, erfassbar sind. Negative Feststellungen oder Aussagen sind hingegen oft durch ein "nicht" zu finden.
Signierung von Beweiserwähnungsbeurteilungen [Stand 27.03.2023, 18:21 Uhr]
Beweissuchwortkürzel.
Hauptunterscheidungskriterien mit Kürzeln (In Entwicklung und Erprobung) siehe bitte Beweissignierungssystem.
Zitierstil
Burt beruft sich auf eine Liste von McDougall, ohne die genaue Fundstelle anzugeben.
Literatur (Auswahl)
- Burt, C. (1915) General and specific factors underlying the primary emotions. Report 85. Meeting of the British Association for the Advancement of Science. Manchester, 1915. REPORT Of THE EIGHTY-FIFTH MEETING OF THE BRITISH ASSOCIATION FOR THE ADVANCEMENT OF SCIENCE.
- Burt, Cyril (1940) THE FACTORS OF THE MIND. An Introduction to Factor-analysis in Psychology. London: University of London Press. [Online]
https://archives.bodleian.ox.ac.uk/repositories/2/resources/3195. Report of the British Association for the Advancement of Science. London, https://www.biodiversitylibrary.org/bibliography/2276
- Sponsel, Rudolf & Hain, Bernhard (1994) Numerisch instabile Matrizen und Kollinearität in der Psychologie. Diagnose, Relevanz & Utilität, Frequenz, Ätiologie, Therapie. Ill-Conditioned Matrices and Collinearity in Psychology. Deutsch-Englisch. Ins Englische übersetzt von Agnes Mehl. Kapitel 6 von Dr. Bernhard Hain: Bemerkungen über Korrelationsmatrizen. Erlangen: IEC-Verlag [ISSN-0944-5072 ISBN 3-923389-03-5]. Aktueller Preis: www.iec-verlag.de.
- Sponsel, R. (2005) Fast- Kollinearität in Korrelationsmatrizen mit Eigenwert-Analysen erkennen. Ergänzungsband - Band II zu Numerisch instabile Matrizen und Kollinearität in der Psychologie. Erlangen: IEC-Verlag.
- Todt, Eberhard (1978) Das Interesse. Empirische Untersuchungen zu einem Motivationskonzept. Bern: Huber.
Links (Auswahl: beachte)
- Erste Stellungnahme: "Faktorenanalyse" einer indefiniten "Korrelationsmatrix" mit 11 Emotionen von C. Burt 1915.
- Eigenwert-Analysen von Korrelations-Matrizen im sozialwissenschaftlichen Bereich, in Psychologie und Psychotherapie.
- Bereits 1994 habe ich Thurstone's Zentroidmethode zufällig als numerische Therapiemethode entdeckt: Zentroidmethode zur Heilung indefiniter Korrelationsmatrizen.
- Die 1994 im Matrizenhandbuch erstmals erfassten Methoden wurden 2019 erneut evaluiert.
- Singulär-indefinite Interkorrelationsmatrix der 10 allgemein-wissenschaftlichen Kategorien nach Auswertung von 10 rechtswissenschaftlichen Werken einer "Therapie" mit Thurstones Zentroidmethode unterzogen. Ergebnis: Verschlimmbesserung.
KI: Warnung vor KI.
- https://chat.deepseek.com/
- https://chat.openai.com/
- Qwen 2.5: https://qwen.readthedocs.io/en/latest/getting_started/quickstart.html
Glossar, Anmerkungen und Endnoten:
GIPT= General and Integrative Psychotherapy, internationale Bezeichnung für Allgemeine und Integrative Psychotherapie.
__
__
Standort: Numerische Therapie indefiniter Korrelationsmatrizen._
*
Hauptseiten: Korrelation und Eigenwertanalysen.
| Suchen in der IP-GIPT,
z.B. mit Hilfe von "google": <suchbegriff>
site:www.sgipt.org
z.B. Inhaltsverzeichnis site:www.sgipt.org. |
Dienstleistungs-Info.
*
Sponsel, Rudolf (DAS) Numerische Therapie indefiniter Korrelationsmatrizen mit einer Beispielanwendung auf die indefinite 11 Gefühle Matrix von Burt 1915 u.a.. IP-GIPT. Erlangen: https://www.sgipt.org/wisms/nis/NumTher/NumThInKM.htm
*
Copyright & Nutzungsrechte
Diese Seite darf von jeder/m in nicht-kommerziellen Verwertungen frei aber nur original bearbeitet und nicht inhaltlich verändert und nur bei vollständiger Angabe der Zitierungs-Quelle benutzt werden. Das direkte, zugriffsaneignende Einbinden in fremde Seiten oder Rahmen ist nicht gestattet, Links und Zitate sind natürlich willkommen. Sofern die Rechte anderer berührt sind, sind diese dort zu erkunden. Sollten wir die Rechte anderer unberechtigt genutzt haben, bitten wir um Mitteilung. Soweit es um (längere) Zitate aus ... geht, sind die Rechte bei/m ... zu erkunden oder eine Erlaubnis einzuholen.
korrigiert: 21.01.2024 + 20.01.2024 irs Rechtschreibprüfung und gelesen
Änderungen wird gelegentlich überarbeitet, ergänzt und vertieft * Anregungen und Kritik willkommen
25.05.2025 Münsterberg Werke.
04.03.2024 Numerische Therapie der indefiniten "Korrelations"matrix Berufsinteresse Mechanik der 5. bis 9. Klassen von Todt in Das Interesse (1978), S. 56 (ausgelagert auf eigene Seite).
21.01.2024 irs Erstsichtung Burt 1940 aufgenommen als V. und in der Zusammenfassung Rechtschreibprüfung und gelesen.
21.01.2024 Erstsichtung Burt 1940 aufgenommen als V. und in der Zusammenfassung.
20.01.2024 irs Rechtschreibprüfung und gelesen.
20.01.2024 Fertigstellung Ausarbeitungen und Analyse.
19.01.2024 Ausarbeitungen und Analyse.
18.01.2024 Angelegt. Ausarbeitungen und Analyse.
[intene Hilfen:
CR Faktorisieren
CRn Faktorisieren und die Hauptdiagonale auf
1 skalieren ("normalisieren")
CR0 Den negativen Eigenwert durch 0 ersetzen
CR0n Den negativen Eigenwert durch 0 ersetzen
und die Hauptdiagonale auf 1 skalieren ("normalisieren")
CRs Die Eigenwerte durch die Singulärwerte
ersetzen
CRsn Die Eigenwerte durch die Singulärwerte
ersetzen und die Hauptdiagonale auf 1 skalieren ("normalisieren")
]