(ISSN 1430-6972)
IP-GIPTDAS=04.03.2024 Internet-Erstausgabe, letzte Änderung: tt.mm.jj
Impressum: Diplom-Psychologe Dr. phil. Rudolf Sponsel Stubenlohstr. 20 D-91052 Erlangen
E-Mail: sekretariat@sgipt.org _ Zitierung & Copyright
Anfang_Numerische Therapie einer indefiniten "Korrelations"matrix bei Todt 1978, S.56_ Datenschutz_ Überblick__Rel. Beständiges _Titelblatt_ Konzept_ Archiv_ Region_ English contents__ Service_iec-verlag__Dienstleistungs-Info * _ Wichtige Hinweise zu Links und Empfehlungen
Numerische Therapie der indefiniten
"Korrelations"matrix
Berufsinteresse Mechanik der
5. bis 9. Klassen von Todt in Das Interesse (1978), S. 56
Originalarbeit von Rudolf Sponsel, Erlangen
| Eine Pseudokorraltionsmatrix sieht aus wie eine Korrelationsmatrix, ist aber keine, was man an mindestens einem negativen Eigenwert erkennen kann. Daher muss man rechnen (lassen). |
Hauptseiten: Numerische Therapie * Korrelation und Eigenwertanalysen.
Haupt- und Verteilerseite Definitions-Register Psychologie * Checkliste Definition, gpds-Regel * Definition und definieren: referenzieren; Hauptseite Referenzen in der psychologischen Forschung * Systematische Analyse Definition und definieren in der Psychologie. * Begriffscontainer (Containerbegriff) * Homonyme * Begriffsverschiebebahnhöfe * Sachverhalt * Wissenschaftliches Arbeiten, Regeln Grundbegriffe, Begriffsbasis, Zitieren * Aristoteles Zum Geleit * Sprachkritik und Sch^3-Syndrom * Methode der Textanalyse * Methodik-Beweissuche in der Psychologie * Beweissuchwortkürzel. * Signierung von Beweiserwähnungsbeurteilungen * Checkliste-Beweisen.: Beweisregister Psychologie * Beweis und beweisen in der Psychologie * natcode Register * Übersicht allgemeine Beweisseiten * Haupt- und Verteilerseite Die Erforschung des Erlebens und der Erlebnisse , Tabelle Fundstelleninformationen erleben, erlebt, Erlebnis * Hauptbedeutungen Erleben * Grunddimensionen des Erlebens * »«
Inhalt
- Editorial.
- Numerische (In)Stabilität der Matrix durch minimalen negativen Eigenwert -0.0005.
- 4 Fast-Kollinearitäten in der 5er-Matrix.
- Alle 6 angewandten numerischen Therapiemethoden erfolgreich.
- Ergebnisse des vollständigen Vergleichs aller 70 partiellen Korrelationskoeffizienten der original indefiniten Matrix mit der erfolgreichen numerisch therapierten CR Matrix (Faktorisierung).
- Fazit.
Zusammenfassung-Numerische Therapie indefiniter Korrelations-Matrizen.
Komplexe Faktorenladungen.
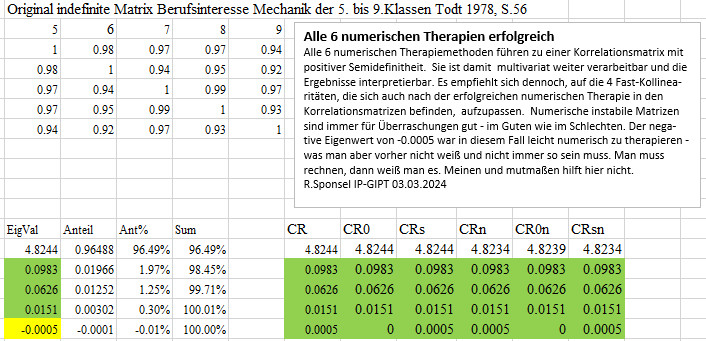
Ergebnisse der 6 numerischen Therapiemethoden im Vergleich.
Zwei vollständige partielle Korrelationsanalysen der indefiniten und numerisch therapierten Matrix.
Checkliste definieren.
Checkliste beweisen.
Zitierstil.
Literatur, Links, Glossar, Anmerkungen und Endnoten, Querverweise, Copyright und Zitierung, Änderungen
Editorial
Todt hat in seinem Werk Das Interesse viele interessante multivariate Befunde von seinem Berufsinteressentest mitgeteilt - u.a. mit vielen Generalfaktoren, die die psychologischen multivariaten Statistiker- und FaktorenanalytikerInnen gewöhnlich nicht erkannt haben.
Die Matrix Berufsinteresse an Mechanik korreliert die Ergebnisse der 5. bis zur 9. Klasse und gelangt zu durchweg sehr hohen Korrelationskoeffizienten. In der nur 5 Variablen fassenden Matrix gibt es 4 (!) Fast-Kollinearitäten und einen minimalen negativen Eigenwert -0.0005, der es aber in sich hat wie die Rechnung zeigt. Die Faktorenladungen werden komplex und 12 von 70 partiellen Korrelationskoeffizienten entgleisen, in der Spitze mit 1.27059! Wenn man von dem Abweichungsbetrag zu 0 beim Eigenwert mit 0.0005 ausgeht und diesen zur Abweichung mit dem höchsten entgleisten partiellen Korrelationskoeffizienten in Beziehung setzt, also zu 0.27059 (Betrag größer zulässigem Maximum 1), dann ergibt sich 0.27059 / 0.0005 = 541.18 als Faktor zum Verhältnis Eingangsgröße - Ausgangsgröße, ein eindrucksvolles Beispiel, was numerische Instabilität operational und handfest bedeutet. Vor multivariater Weiterverabeitung muss die Matrix also numerisch therapiert werden. Das wird auf dieser Seite durchgeführt und dokumentiert. Zudem wird ein vollständiger Vergleich aller 70 partiellen Korrelationen der indefiniten Originalmatrix mit der durch Faktorisierung numerisch therapierten Matrix gerechnet und dokumentiert, so dass man sehen kann, welche Unterschiede der minimale negative Eigenwert -0.0005 bewirkt.
Zusammenfassung-Todt-1978-56
Numerische Therapie der indefiniten "Korrelations"matrix
Todt1978.56-Z0 Man
kann an dem Beispiel eindrucksvoll sehen, was numerische (In)Stabilität
bedeutet. Der minimal negative Eigenwert von -0.0005 in der nur
5 Variablen fassenden Matrix hat extreme Auswirkungen, wie die multivariate
Rechnung zeigt. Die Faktorenladungen werden komplex und 12 von 70 partiellen
Korrelationskoeffizienten entgleisen, in der Spitze mit 1.27059! Wenn man
von dem Abweichungsbetrag zu 0 beim Eigenwert mit 0.0005 ausgeht und diesen
zur Abweichung mit höchsten entgleisten partiellen Korrelationskoeffizienten
in Beziehung setzt, also zu 0.27059 (Betrag größer zulässigem
Maximum 1), dann ergibt sich 0.27059 / 0.0005 = 541.18 als Faktor zum Verhältnis
Abweichung Eingangsgröße - Abweichung Ausgangsgröße,
ein eindrucksvolles Beispiel, was numerische Instabilität operational
und handfest bedeutet.
Todt1978.56-Z1 Die Korrelationen
der Interessen an Mechanik sind zwischen den 5. bis 9. Klassen sehr hoch
und zeigen für alle Paare r > |0.80| Fast-Kollinearitäten an.
Die kleine Matrix der Ordnung 5 enthält vier Fast-Kollinearitäten,
aber auch einen minimalen negativen Eigenwert mit -0.0005, der zu komplexen
Faktorenladungen führt und zu 12 entgleisten von 70 partiellen
Korrelationskoeffizienten führt, weshalb die indefinite Matrix vor
multivariater Weiterverarbeitung numerisch therapiert werden muss.
Todt1978.56-Z2 Alle angewandten
6 numerischen Therapiemethoden sind erfolgreich und stellen mindestens
eine positiv semidefinite (alle Eigenwerte >= 0), in vier von 6 Fällen
sogar eine positiv definite (alle Eigenwerte > 0) Matrix her, so dass einer
multivariaten Weiterverabeitung der numerisch therapierten Korrelationsmatrizen
nichts mehr im Weg steht. Die angewandten Methoden sind:
- CR Faktorisieren.
- CRn Faktorisieren und die Hauptdiagonale auf 1 skalieren ("normalisieren").
- CR0 Den negativen Eigenwert durch 0 ersetzen.
- CR0n Den negativen Eigenwert durch 0 ersetzen und die Hauptdiagonale auf 1 skalieren ("normalisieren").
- CRs Die Eigenwerte durch die Singulärwerte ersetzen.
- CRsn Die Eigenwerte durch die Singulärwerte ersetzen und die Hauptdiagonale auf 1 skalieren ("normalisieren").
- CC Zentroidmethode: hier wegen aktueller Nichtverfügbarkeit eines funktionsfähigen Programmes nicht angewandt.
- (1a) In einer Matrix der Ordnung 5 sind 3 Auspartialisierungen vollständige Partialisierungen. Davon gibt es in der 5er Original-Matrix 10, wovon 6, also 60%, sichtbar mit Werten > |1| entgleisen.
- (1b) Von 2 Auspartialisierungen gibt es 30, wovon in der indefiniten Original-Matrix sichtbar 6 mit Werten > |1| entgleisen, das sind 20%.
- (1c) Bei einer einzigen Auspartialisierung, wovon es in der 5er Matrix auch 30 gibt, entgleist in der indefiniten Originalmatrix sichtbar keine.
- (2) Die Korrelation der partiellen Korrelationen ist trotz der pathologischen Entgleisungen zwischen originalen und faktorisiert-therapierten mit 0.94 überraschend hoch und verleitet damit zu Falschinterpretationen.
- (3a) Die absoluten Abweichungen zwischen den partiellen Korrelationen der originalen und der faktorisiert-therapierten Matrix CR sind mit 0.4009 im Mittel am stärksten bei vollständiger Partialisierung.
- (3b) Die Abweichung sinken auf 0.0518 im Mittel, also auf rund 1/8, wenn nur 2 auspartialisiert werden.
- (3c) Sie sinken schließlich im Mittel auf 0.0078, wenn nur ein Item auspartialisiert wird.
- (4) Bei der erfolgreich numerisch therapierten Matrix CR gab es keine sichtbaren Entgleisungen mehr.
_
Ausgangsmatrix Korrelationen der 5.-9. Klassen am Berufs-Interesse für Mechanik Todt 1978, S. 56
Die Korrelationen der Interessen an Mechanik sind zwischen den 5. bis 9. Klassen sehr hoch und zeigen für alle Paare r > |0.80| Fast-Kollinea-ritäten an. Wie der kleine negative Eigenwert (gelb markiert) zeigt, hat die Matrix ihre positive Semidefinitheit verloren, wahrscheinlich auf-grund der hohen Fast-Kollinearitäten im Zusammenhang mit Rundungsfehlern, weil die Koeffizienten nur zweistellig angegeben sind. Es könnten aber auch noch unterschiedliche n bei den 5. bis 9. Klassen eine Rolle spielen. Damit können massive multivariate Entgleisungen eintreten, wie auch eine erste Prüfung der komplexen Faktorenladungen oder partiellen Korrela-tionen belegt. Obwohl der negative Eigenwert nur -0.0005 beträgt, entgleist der größte partielle Korrelationskoeffizient mit 0.27059 > 1, das ist der Faktor 0.27059/0.0005 = 541.18, wenn man beide Abweichungen zueinander in Beziehung setzt. Das eben ist das Wesen der numerischen Instabilität: kleine Veränderungen auf der Eingangsseite (Eigenwert -.0005) bewirken extreme Veränderungen auf der Ausgangsseite ) (partielle Korrelation pcv : 2 5 . 1 3 4 = 1.27059 oder komplexe Faktorenladungen) mit 0.27059 > 1.

_
_
komplexe Faktorenladungen
Gerechnet 1) [V,D] = seig(r), 2) F= V*sqrt(D) (in Matlab, Home Edition 2023b)
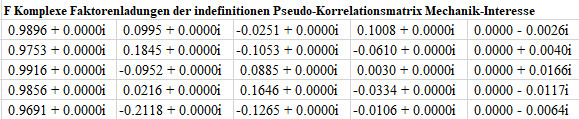
Ergebnisse der 6 numerischen Therapiemethoden im Vergleich > Beschreibung der num. Therapiemethoden.
Alle 6 numerischen Therapiemethoden führen zu einer Korrelationsmatrix mit positiver Semidefinitheit. Sie ist damit multivariat weiter verarbeitbar und die Ergebnisse interpretierbar. Es empfiehlt sich dennoch, auf die 4 Fast-Kollinearitäten, die sich auch nach der erfolgreichen numerischen Therapie in den Korrelationsmatrizen befinden, aufzupassen. Numerische instabile Matrizen sind immer für Überraschungen gut - im Guten wie im Schlechten. Der negative Eigenwert von -0.0005 war in diesem Fall leicht numerisch zu therapieren - was man aber vorher nicht weiß und nicht immer so sein muss. Man muss rechnen, dann weiß man es. Meinen und mutmaßen hilft hier nicht.
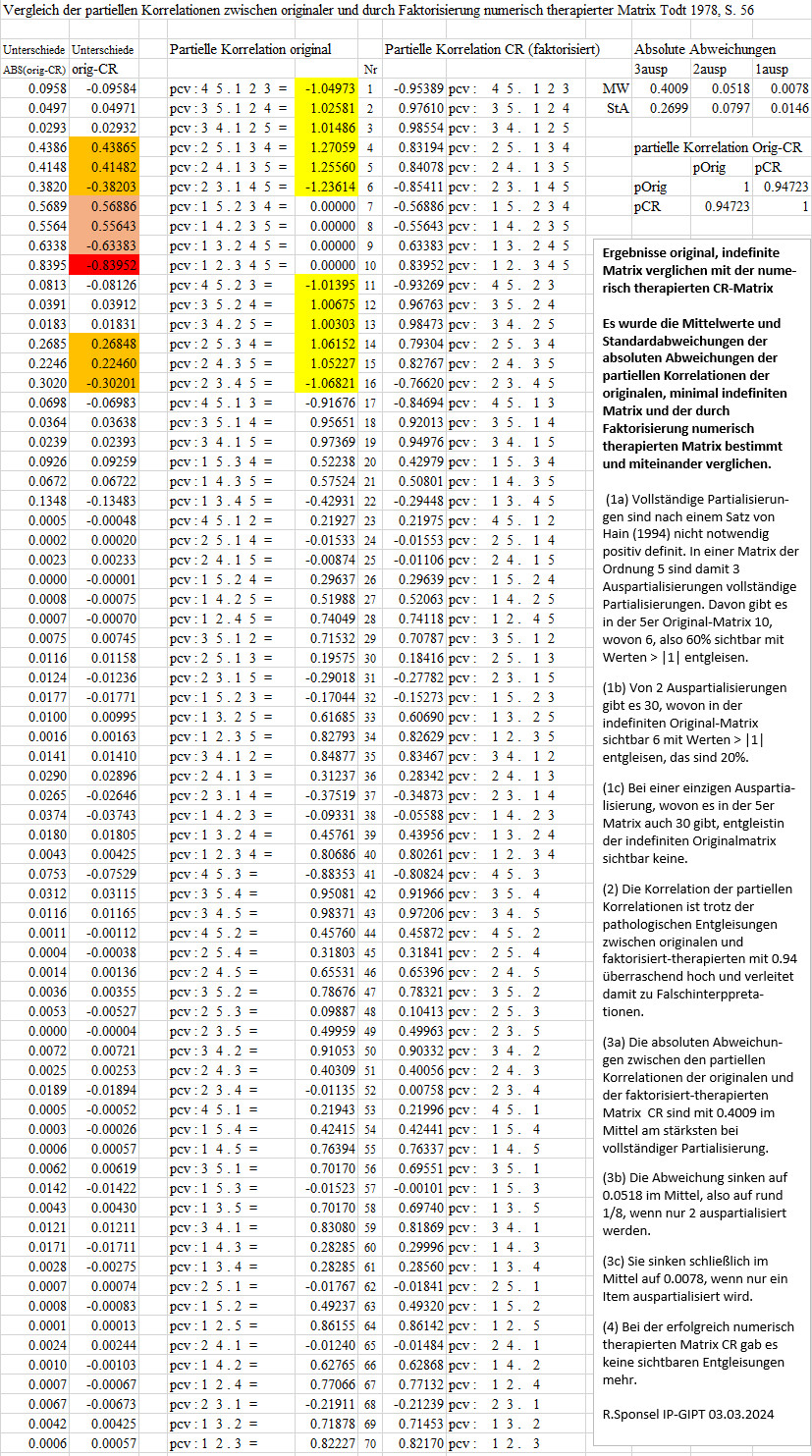
partielle Korrelationsanalysen
Sichtbar sind 12 deutliche Entgleisungen bei den partiellen Korrelationskoeffzienten, der größte bei pcv : 2 5 . 1 3 4 = 1.27059. Das sind 17% von allen 70. Man darf sich aber von den rein sichtbaren nicht täuschen lassen. Sämtliche partiellen Korrelationskoeffizienten sind aufgrund der Entgleisung durch den negativen Eigenwert -.0005 nicht zuverlässig und daher nicht interpretierbar. Setzt man die Größen der pathologischen Abweichungen zueinander in Beziehung, so ergibt sich als Auswirkung der Faktor 5400. Zu besseren Einschätzung und Beurteilung habe ich zum Vergleich die partiellen Korrelationen der numerisch-therapierten partiellen Korrelationskoeffizienten angeben.
Vergleich sämtlicher partiellen Korrelationen r und CR:
Es wurde die Mittelwerte und Standardabweichungen der absoluten Abweichungen
der partiellen Korrelationen der originalen, minimal indefiniten Matrix
und der durch Faktorisierung numerisch therapierten Matrix bestimmt und
miteinander verglichen.
(1a) Vollständige Partialisierungen sind nach einem Satz
von Hain (1994) nicht notwendig positiv definit. In einer Matrix der Ordnung
5 sind damit 3 Auspartialisierungen vollständige Partialisierungen.
Davon gibt es in der 5er Matrix 10, wovon 6, also 60% sichtbar mit Werten
> |1| entgleisen.
(1b) Von 2 Auspartialisierungen gibt es 30, wovon sichtbar 6 mit Werten
> |1| entgleisen, das sind 20%.
(1c) Bei einer einzigen Auspartia-lisierung, wovon es in der 5er Matrix
auch 30 gibt, entgleist sichtbar keine.
(2) Die Korrelation der partiellen Korrelationen ist trotz der pathologischen Entgleisungen zwischen originalen und faktorisiert-therapierten mit 0.94 überraschend hoch und verleitet damit zu Falschinterppretationen.
(3a) Die absoluten Abweichungen zwischen den partiellen Korrelationen
der originalen und der faktorisiert-therapierten Matrix CR sind mit
0.4009 im Mittel am stärksten bei vollständiger Partialisierung.
(3b) Die Abweichung sinken auf 0.0518 im Mittel, also auf rund 1/8,
wenn nur 2 auspartialisiert werden.
(3c) Sie sinken schließlich im Mittel auf 0.0078, wenn nur ein
Item auspartialisiert wird.
_
Checkliste definieren
Checkliste-Beweisen
Methodik-Beweissuche in der Psychologie
Viele positive oder bejahende Feststellungen oder Aussagen haben kein Suchtextkriterium, so dass Fundstellen nur durch lesen, Zeile für Zeile, erfassbar sind. Negative Feststellungen oder Aussagen sind hingegen oft durch ein "nicht" zu finden.
Signierung von Beweiserwähnungsbeurteilungen [Stand 27.03.2023, 18:21 Uhr]
Beweissuchwortkürzel.
Hauptunterscheidungskriterien mit Kürzeln (In Entwicklung und Erprobung) siehe bitte Beweissignierungssystem.
Zitierstil
Todt pflegt den in der Psychologie üblichen Hochstaplerzitierstil.
Literatur (Auswahl)
- Sponsel, Rudolf & Hain, Bernhard (1994) Numerisch instabile Matrizen und Kollinearität in der Psychologie. Diagnose, Relevanz & Utilität, Frequenz, Ätiologie, Therapie. Ill-Conditioned Matrices and Collinearity in Psychology. Deutsch-Englisch. Ins Englische übersetzt von Agnes Mehl. Kapitel 6 von Dr. Bernhard Hain: Bemerkungen über Korrelationsmatrizen. Erlangen: IEC-Verlag [ISSN-0944-5072 ISBN 3-923389-03-5]. Aktueller Preis: www.iec-verlag.de.
- Sponsel, R. (2005) Fast- Kollinearität in Korrelationsmatrizen mit Eigenwert-Analysen erkennen. Ergänzungsband - Band II zu Numerisch instabile Matrizen und Kollinearität in der Psychologie. Erlangen: IEC-Verlag.
- Todt, Eberhard (1978) Das Interesse. Empirische Untersuchungen zu einem Motivationskonzept. Bern: Huber.
Links (Auswahl: beachte)
- Die 1994 im Matrizenhandbuch erstmals erfassten Methoden wurden 2019 erneut evaluiert.
- Singulär-indefinite Interkorrelationsmatrix der 10 allgemein-wissenschaftlichen Kategorien nach Auswertung von 10 rechtswissenschaftlichen Werken einer "Therapie" mit Thurstones Zentroidmethode unterzogen. Ergebnis: Verschlimmbesserung.
ChatGPT:
- https://chat.openai.com/
- https://chatgpt.ch/
- https://talkai.info/de/chat/
Glossar, Anmerkungen und Endnoten:
GIPT= General and Integrative Psychotherapy, internationale Bezeichnung für Allgemeine und Integrative Psychotherapie.
__
__
Standort: Numerische Therapie einer indefinite "Korrelations"matrix bei Todt 1978, S.56
*
Hauptseiten: Korrelation und Eigenwertanalysen.
| Suchen in der IP-GIPT,
z.B. mit Hilfe von "google": <suchbegriff>
site:www.sgipt.org
z.B. Inhaltsverzeichnis site:www.sgipt.org. |
Dienstleistungs-Info.
*
Sponsel, Rudolf (DAS) Numerische Therapie der indefiniten "Korrelations"matrix
Berufsinteresse Mechanik der 5. bis 9. Klassen von Todt in Das Interesse (1978), S. 56. IP-GIPT. Erlangen: https://www.sgipt.org/wisms/nis/NumTher/Todt1978-56/Todt1978-56.htm
*
Copyright & Nutzungsrechte
Diese Seite darf von jeder/m in nicht-kommerziellen Verwertungen frei aber nur original bearbeitet und nicht inhaltlich verändert und nur bei vollständiger Angabe der Zitierungs-Quelle benutzt werden. Das direkte, zugriffsaneignende Einbinden in fremde Seiten oder Rahmen ist nicht gestattet, Links und Zitate sind natürlich willkommen. Sofern die Rechte anderer berührt sind, sind diese dort zu erkunden. Sollten wir die Rechte anderer unberechtigt genutzt haben, bitten wir um Mitteilung. Soweit es um (längere) Zitate aus ... geht, sind die Rechte bei/m ... zu erkunden oder eine Erlaubnis einzuholen.
korrigiert: 21.01.2024 + 20.01.2024 irs Rechtschreibprüfung und gelesen
Änderungen wird gelegentlich überarbeitet, ergänzt und vertieft * Anregungen und Kritik willkommen
04.03.2024 Abschluss.
03.03.2024 Rechnungen.
02.03.2024 Angelegt.