(ISSN 1430-6972)
IP-GIPTDAS=29.09.2019 Internet Erstausgabe, letzte Änderung: 08.10.19
Impressum: Diplom-Psychologe Dr. phil. Rudolf Sponsel Stubenlohstr. 20 D-91052 Erlangen
Mail:_sekretariat@sgipt.org_ Zitierung & Copyright
Anfang_Anlage "Zahlensalat" Datenschutz_ Rel. Aktuelles _Überblick_Überblick Wissenschaft _Rel. Beständiges_ Titelblatt_Konzept_Archiv_Region_Service iec-verlag__Wichtige Hinweise zu Links und Empfehlungen
Willkommen in unserer Internet-Publikation für Allgemeine und Integrative Psychotherapie, Abteilung Wissenschaft, Bereich Rechtswissenschaft und hier speziell zum Thema:
Anlage "Zahlensalat"
Rangfolgen, Verteilungen, Korrelations-
und Eigenwertanalysen
der ersten 10 Auswertungen zu
Recht und Rechtswissenschaft
Eine wissenschaftstheoretisch
empirisch operationale Analyse
mit Schwerpunkt Begriffswelt
und Methoden
aus interdisziplinärer Perspektive
Haupt- und Verteilerseite Auswertung
Originalarbeit von Rudolf
Sponsel, Erlangen
Darf mit Angabe der Quelle frei verwendet werden.
Aufgrund fortlaufender Ergänzungen und gelegentlicher
Korrekturen mit F5-Taste updaten empfohlen
__
Rangfolgen nach Mittelwerten der Kategorien und Kriterien
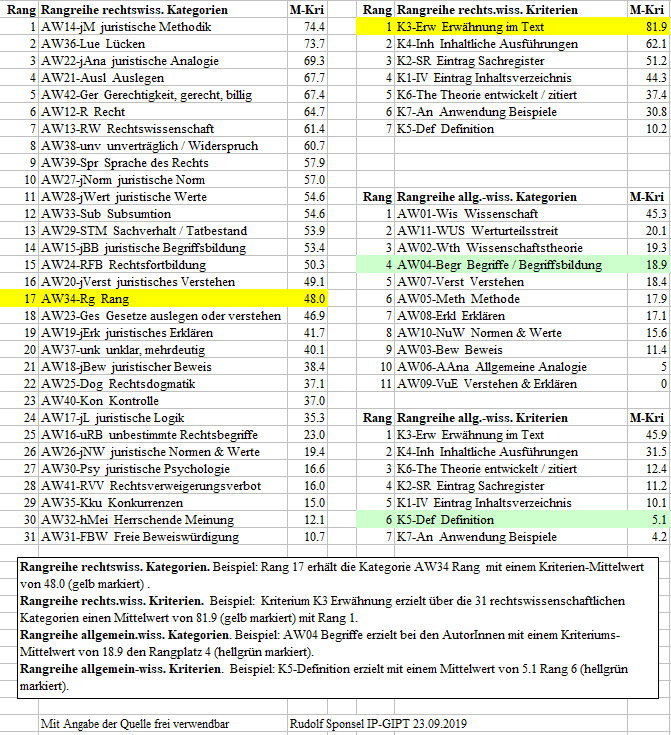
Interpretation der Rangfolgen: Die Ausprägung der Mittelwerte der Bearbeitungen repräsentiert die Intensität der Bearbeitungen in den Kriterien der Kategorien, die, je höher, umso mehr Bearbeitungsintensität anzeigen. Ordnet man die Mittelwerte nach Größe, hier absteigend, dann ergibt sich eine Rangreihe. Die höchste Bearbeitungsintensität mit 74.4 und Rang 1 zeigt die Kategorie juristische Methodik, gefolgt von Lücken mit 73.7. Die kleinste Bearbeitungsintensität mit 10.7 und Rang 31 zeigt die Kategorie Freie Beweiswürdigung, was mich sehr überraschte und was mir auch unverständlich ist.
Verteilung der Mittelwerte in den Kriterien und Kategorien
Die Verteilungen der Mittelwerte werden nur informatorisch mitgeteilt.
- Verteilung der 7-Kriterien-Mittelwerte
über 11 allgemein-wissenschaftliche Kategorien
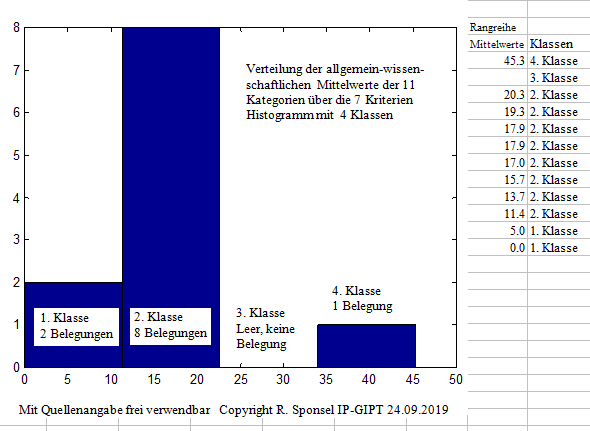
Verteilung der 11-Kategorien-Mittelwerte über 7 allgemein-wissenschaftliche Kriterien
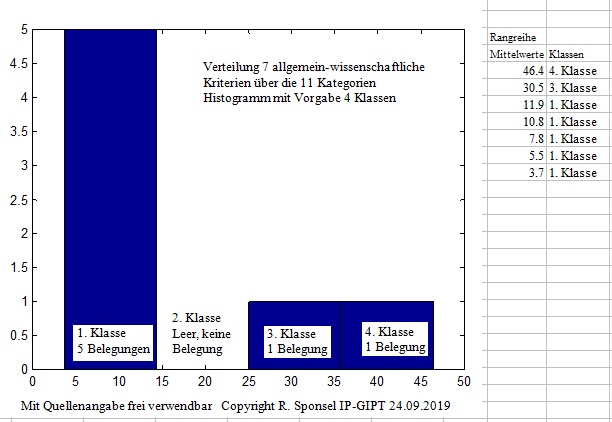
Verteilung der 7-Kriterien-Mittelwerte
über 31 rechtswissenschaftliche Kategorien
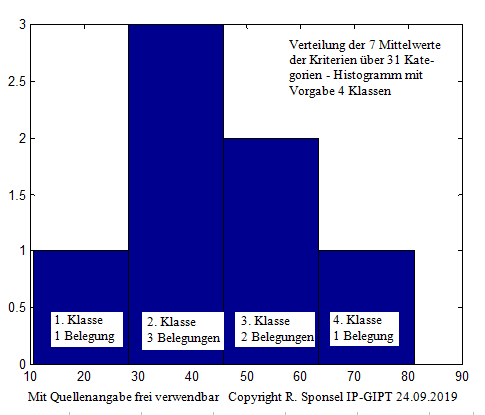 \
\
Verteilung der 31-Kategorien-Mittelwerte
über 7 rechtswissenschaftliche Kriterien
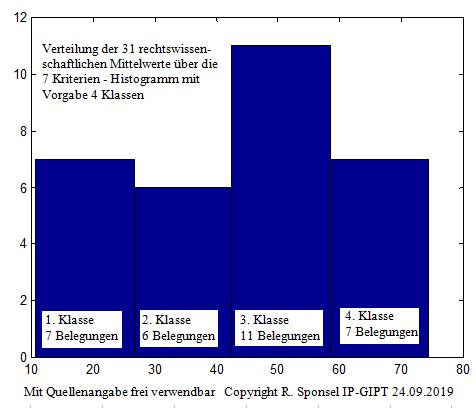
Interpretation: Knapp 1/4 der rechtswissenschaftlichen Kategorien erzielen
Bearbeitungsmittelwerte unter 27% (nämlich: AW16 unbestimmte Rechtsbegriffe,
AW26 Normen und Werte, AW30 juristische Psychologie, AW31 Freie
Beweiswürdigung, AW32 herrschende Meinung, AW35 Konkurrenzen und AW41
Rechtsverweigerungsverbot).
Gut ein Viertel der rechtswissenschaftlichen Kategorien
erzielen Bearbeitungsmittelwerte über 58% (nämlich: AW13 Rechtswissenschaft,
AW14 juristische Methodik, AW21 Auslegen, AW22 Analogie, AW36 Lücken,
AW38 Widersprüche und AW42 Gerechtigkeit), das sind sozusagen die
"Renner" unter den rechtswissenschaftlichen Kategorien.
Was bedeuten "geringe Bearbeitungsmittelwerte"?
Dazu fallen mir folgende Gründe ein: die Kategorie erscheint
den BearbeiterInnen a) nicht besonders interessant; b) nicht besonders
wichtig oder c) schwierig. Interesse kann man über die Anzahl
der Erwähnungen (K3) schätzen, die Wichtigkeit über K1,
K2 und K4. Die Schwierigkeit erfasst am besten K5, aber auch K6 und K7.
- Verteilung der 7-Kriterien-Mittelwerte
über alle 42 Mittelwerte
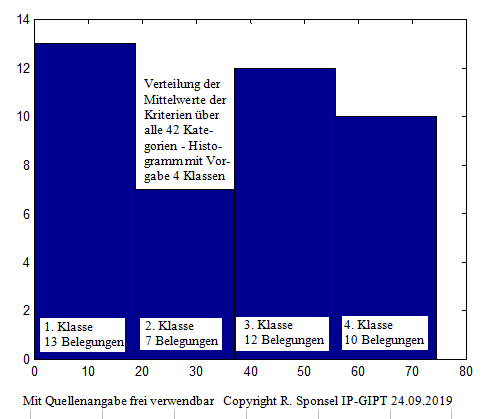
Korrelations-
und Eigenwertanalysen (EWA) - mit Vorsicht
zu genießen!
Information zu Korrelationen
und zu Eigenwerten.
Zur Interpretation der Größe der Korrelationskoeffizienten siehe
bitte hier.
Für die Interpretation gilt der wichtige Vieldeutigkeitssatz:
| Der Korrelationskoeffizient zwischen zwei Variablen gibt die Korrelation zwischen diesen beiden und der mit ihnen verbundenen Variablen an. Eine tragbare Interpretationsbasis erhält man daher erst, wenn man das System der vorliegenden Variablen einer partiellen Korrelationsanalyse unterzieht (allgemein hier, am Beispiel allgemein-wissenschaftliche Kriterien hier. |
Gegen Ende der ersten 10 Auswertungen ist mir bei
der Tabellendarstellung der Ergebnisse aufgefallen, dass die Werte
einer Korrelations- und damit auch Eigenwertanalyse (zur Information >
EWA)
zugänglich sind. Das hat mich sehr neugierig gemacht, was da wohl
rauskommen mag. Das Ergebnis mit den durchgängig dominanten Generalfaktoren
()hat mich dann sehr überrascht, weil solche Ergebnisse in den empirischen
Wissenschaften selten sind. Dabei handelt es sich um eine erste Pilotstudie,
deren Ergebnisse man nicht überbewerten sollte, schon die nächste
Auswertung kann andere Ergebnisse bringen. Sie liefern einen ersten Eindruck
- nicht mehr - aber auch nicht weniger. Wenn der zweite Teil, ebenfalls
10 rechtswissenschaftliche Werke, abgeschlossen ist, wird man die drei
Ergebnisse (erste 10, zweite 10, alle 20) vergleichen können und kann
zu deutlich unterschiedlichen Korrelationsergebnissen kommen. Für
verlässliche und stabile Aussagen werden mehrere Untersuchungen von
verschiedenen Untersuchern benötigt. Möglicherweise ist das Design
(11 Zeilen zu 7 Spalten, 7 Zeilen zu 11 Spalten, 31 Zeilen zu 7 Spalten,
7 Zeilen zu 31 Spalten, 41 Zeilen zu 7 Spalten, 7 Zeilen zu 41 Spalten)
zu dünn und instabil. Jede statistische oder multivariate Verarbeitung
ist höchstens so gut, wie die zugrunde liegenden Rohdaten, hier also,
ob meine Verstehens- und Subsumtionleistungen objektiv,
reliabel und valide sind, worüber man natürlich
streiten kann.
Verarbeitungsprobleme: Sind
in einer Zeile alle Werte gleich, wie z.B. bei Verstehen und Erklären
sämtlich 0 (siehe bitte hier in der Tabelle),
so lässt sich keine Korrelation berechnen, weil die Streuung 0 ist
und durch 0 nicht dividiert werden darf und kann (mathematische Norm).
Sowohl excel (weist "#DIV/0%!" aus) als auch z.B. Matlab (weist NaN für
unendlich aus) haben mit der Berechnung der anderen Werte kein Problem.
Will man Eigenwerte berechnen, muss man den Wert mit konstanten Belegungen
herausnehmen, weil sonst die Matrix entgleist und negative Eigenwerte produziert
(hier dokumentiert).
Singularität: Korrelationsmatrizen,
deren Datenbasis auf mehr Spalten als Zeilen beruht (Rang = Min(Zeilenrang,
Spaltenrang), sind notwendig singulär und können bei multivariaten
Weiterverarbeitungen entgleisen, selbst wenn ein Eigenwert auch nur minimal
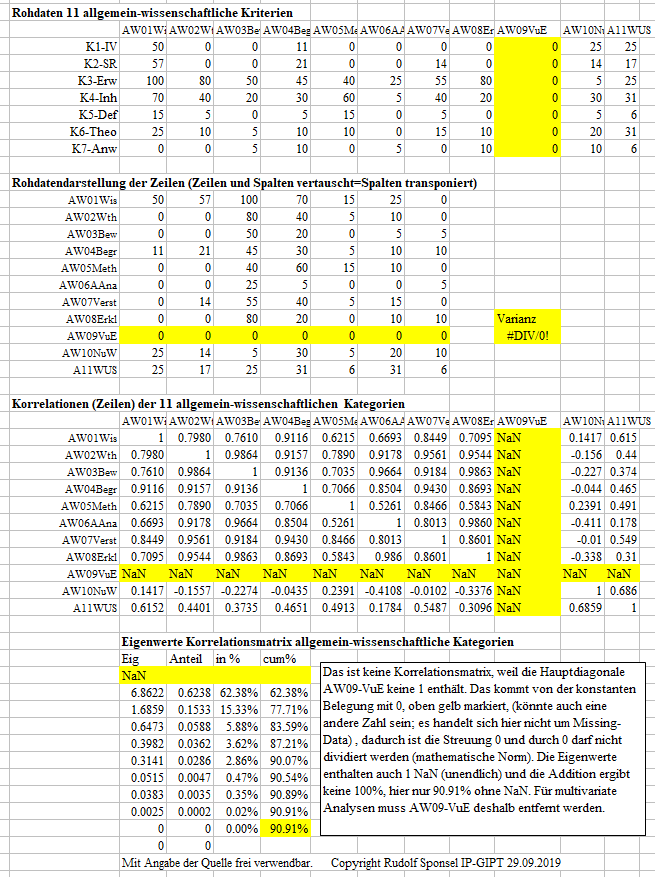
negativ ist, wie z.B. hier:
 |
Eigenwerte der Korrelation der 10 allgemein-wissenschaftlichen Kategorien nach Herausnahme der mit einer konstanten 0 belegten Variable AW09-VuE (Verstehen und erklären). Die "negative 0" des letzten Eigenwertes bringt multivariate Analysen, wie z.B. partielle Korrelationsanalysen, zum Entgleisen. Das eben ist das Wesen der numerischen Instabilität, dass kleinste Veränderungen auf der Eingangsseite, extreme Veränderungen auf der Ausgangsseite bewirken können. Man glaubt es kaum, aber es ist so, wie eine einfache Anwendung der partiellen Korrelationsanalyse zeigt. Korrelationsmatrizen müssen positiv-semidefinit sein, also die Eigenwerte müssen >= 0 sein. Am besten prüft man bei einer Korrelationsmatrix erst mal die Eigenwerte. |
Zur Beachtung Eigenwertbedeutung: Die Eigenwerte
dürfen nicht den Variablen (Kriterien oder Kategorien) zugeordnet
werden, denn: vertauschte man Zeilen oder Spalten, ergäben sich trotzdem
die gleichen Eigenwerte, und diese hätten dann andere Variablen-Zuordnungen,
womit Widersprüche entstünden.
Nachprüfung: Wer die Rechnungen
nachprüfen will und Zugang zu Matlab, eine alte Studentenversion genügt,
hat, kann die Rechnung mit ganzen vier Befehlen einfach und schnell durchführen:
ds=[Rohdaten einkopieren], rds=corrcoef(ds) ergibt die Korrelationen und
eig(rds) liefert die unsortierten Eigenwerte (wenn die Zeilen korreliert
werden sollen, muss die Datei lediglich transponiert, also Zeilen und Spalten
vertauscht werden: dz=ds'. Anmerkung: man beachte, dass die Dezimal-Trenner
("," oder ".") stimmen.
Korrelationen
zwischen den Kriterien
Zur Interpretation der Größe der Korrelationskoeffizienten
siehe bitte hier.
Für die Interpretation gilt der wichtige Vieldeutigkeitssatz:
| Der Korrelationskoeffizient zwischen zwei Variablen gibt die Korrelation zwischen diesen beiden und der mit ihnen verbundenen Variablen an. Eine tragbare Interpretationsbasis erhält man daher erst, wenn man das System der vorliegenden Variablen einer partiellen Korrelationsanalyse unterzieht (allgemein hier, am Beispiel allgemein-wissenschaftliche Kriterien hier. |
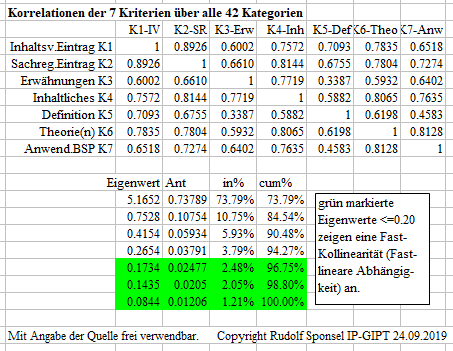
Korrelationen und Eigenwertanalysen der 7 Kriterien der 11 allgemein-wissenschaftlichen Kategorien
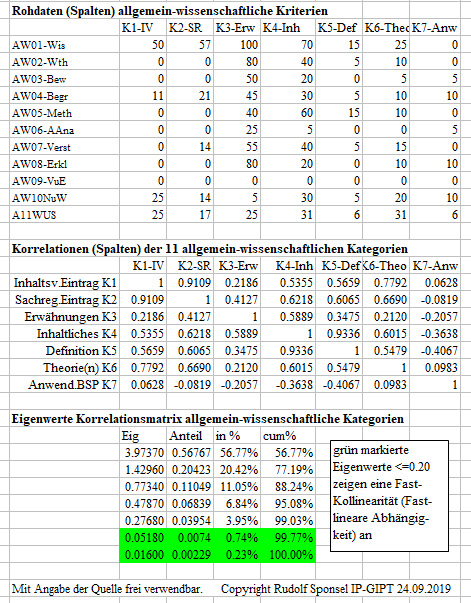
Lesebeispiele und Interpretation: Die Korrelation
zwischen Suchwort im Inhaltsverzeichnis und einem Eintrag im Sachregister
beträgt hohe r=0.9109, was plausibel und im Prinzip, wenn auch nicht
unbedingt in dieser Größenordnung, zu erwarten ist. Zwischen
Sachregistereintrag und Anwendung mit Beispielen beträgt die Korrelation
-.0819, also praktisch 0, d.h. es gibt keinen linearen Zusammenhang.
Die Eigenwertanalyse der
Korrelationsmatrix der allgemein-wissenschaftlichen Kriterien zeigt, es
gibt mit 56.77% Varianzaufklärung einen dominanten Generalfaktor,
den man als allgemein-wissenschaftlichen Generalfaktor bezeichnen
kann (aber).
Das spricht für den Zusammenhang der Kriterien und ist ein Bestätigungsindiz
für den gewählten Ansatz. Nach der Regel,
dass Eigenwerte < 0.20 praktische lineare Abhängigkeit (Fast-Kollinearität)
anzeigen, gibt es in der Matrix der 7 Kriterien über die 11 allgemein-wissenschaftlichen
Kategorien zwei lineare Abhängigkeiten (grün markiert). Eine
genauere Analyse (nach Sponsel
2005, S. 55) der Partitionen und ihrer Eigenwerte ergab, dass es sogar
zwei Paare von Kriterien gibt, nämlich K1-K2 und K4-K5, die eine Fast-Kollinearität
oder Fast-lineare Abhängigkeit anzeigen. Das kann man hier schon durch
die hohen Korrelationswerte vermuten, aber das ist nicht zwingend, denn
(fast) lineare Abhängigkeiten können auch in niedrigen Korrelationen
enthalten sein.
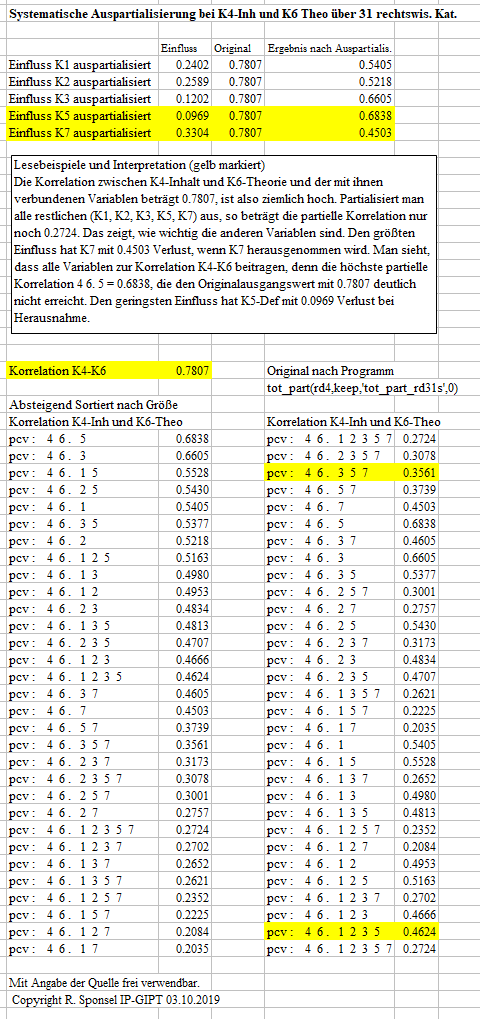
Partielle Korrelationsanalyse zur missglückten
Demonstration der Gültigkeit des Vieldeutigkeitssatzes.
| Der Korrelationskoeffizient zwischen zwei Variablen gibt die Korrelation zwischen diesen beiden und der mit ihnen verbundenen Variablen an. Eine tragbare Interpretationsbasis erhält man daher erst, wenn man das System der vorliegenden Variablen einer partiellen Korrelationsanalyse unterzieht (allgemein hier, am Beispiel allgemein-wissenschaftliche Kriterien hier: |
Vollstaendig
auspartialisierte Matrix 7 Kriterien über 11 allgemein.-wiss. Kategorien
ist keine Korrelationsmatrix mehr!

Nachdem die vollständig auspartialisierte Matrix keine Korrelationsmatrix mehr ist, kann bezweifelt werden, ob mit einer solchen Matrix der Vieldeutigkeitssatz durch Modellbildung bewiesen werden kann. Besser ist es daher, noch eine Auspartialiserung mit einer Restvariablen, also ein Modell i j. 1 2 3 4 von 7. Von den 5 möglichen werden nur 4 auspartialisiert.
Korrelation
zwischen Inhalts- und Sachverzeichnis nach Auspartialisierung über
die 11 allgemein-wissenschaftlichen Kategorien
| Die hohe fast kollineare Korrelation zwischen Einträgen im Inhaltsverzeichnis und im Sachregister ändert sich durch Auspartialisierung der anderen Kriterien und ihrer Kombination nur wenig. Daraus ist der Schluss zu ziehen, dass die Korrelation zwischen Einträgen im Inhaltsverzeichnis und im Sachregister weitgehend unabhängig sind. Man könnte daher einen eigenen Faktor vermuten und ihn mit der Eigenwertvarianz 20.42% identifizieren, so dass ein Bifaktormodell und kein Generalfaktor-Modell mehr vorliegt. Die hohe Korrelation ist stabil. wie die partielle Korrelationsanalyse unterstreicht. |
 |
Lesebeispiele und Interpretation
Vor dem Punkt stehen die zwei Kürzel 1=K1und 2=K2, für die Variablen, deren Korrelation nach Auspartialisierung errechnet wurde. Nach dem Punkt stehen die Variablen, die auspartialisiert (herausgenommen, konstant gehalten) wurden. Die originale Korrelation zwischen K1 und K2 und der mit ihnen verbundenen Variablen betrug 0.9109, also eine fast kollinare Beziehung. Das bedeutet: gibt es einen Eintrag im Inhaltsver- zeichnis, so gibt es fast immer auch einen Eintrag im Sachregister und umgekehrt. Die hohe Korrelation ändert sich auch nur geringfügig, wenn
man auspartialisert. Der kleinste Wert ergibt sich nach Auspartialisierung
von K5 und K2 mit 0.8252. Die höchste Korrelation klettert minimal
auf 0.9289, wenn man K3 und K7 auspartialisert.
Das mathematisch deskriptiv statistische Ergebnis ist inhaltlich nachvollziehbar und plausibel. |
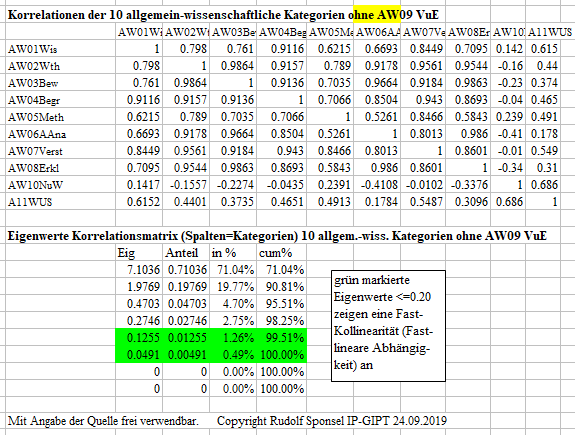
Korrelation und Eigenwertanalyse der Kriterien in den 10 allgemein-wissenschaftlichen Kategorien ohne AW09
Zur Interpretation der Größe der Korrelationskoeffizienten siehe bitte hier. Für die Interpretation gilt der wichtige Vieldeutigkeitssatz:
| Der Korrelationskoeffizient zwischen zwei Variablen gibt die Korrelation zwischen diesen beiden und der mit ihnen verbundenen Variablen an. Eine tragbare Interpretationsbasis erhält man daher erst, wenn man das System der vorliegenden Variablen einer partiellen Korrelationsanalyse unterzieht (allgemein hier, am Beispiel allgemein-wissenschaftliche Kriterien hier. |
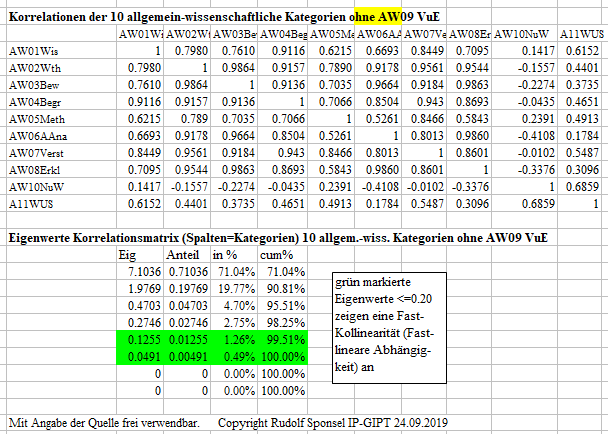
Lesebeispiel und Interpretation: Die Korrelation
zwischen der Kategorie AW02 Wissenschaftstheorie und AW03 Beweis beträgt
hohe fast-kollineare 0.984. Die geringste Korrelation gibt mit -0.3376
zwischen AW10 Normen und Werten und AW08 Erklären. Bei der Kategorie
AW10 Normen und Werte - und nur bei ihr - fällt auf, dass auffällig
viele negative Korrelationen auftreten. Dieses Ergebnis erfordert noch
nähere Exploration.
Die Eigenwertanalyse der Korrelationsmatrix der
10 allgemein-wissenschaftlichen Kategorien zeigt einen sehr hohen Eigenwert
mit 7.1036. Es gibt daher mit 71.04% Varianzaufklärung einen sehr
dominanten Generalfaktor,
den man als allgemein-wissenschaftlichen Generalfaktor
bezeichnen kann. Streng gesehen kann man auch von einem Bifaktormodell
sprechen, weil der zweitgröße Eigenwert immerhin noch 19.77%
Varianaufklärung bringt. Das spricht für den Zusammenhang der
Kriterien und bestätigt damit, quasi im Nachhinein, den gewählten
Ansatz, was aber so gar nicht geplant war. Nach der Regel,
dass Eigenwerte < 0.20 praktisch lineare Abhängigkeit (Fast-Kollinearität)
anzeigen, gibt es in der Matrix der Kriterien zwei lineare Abhängigkeiten.
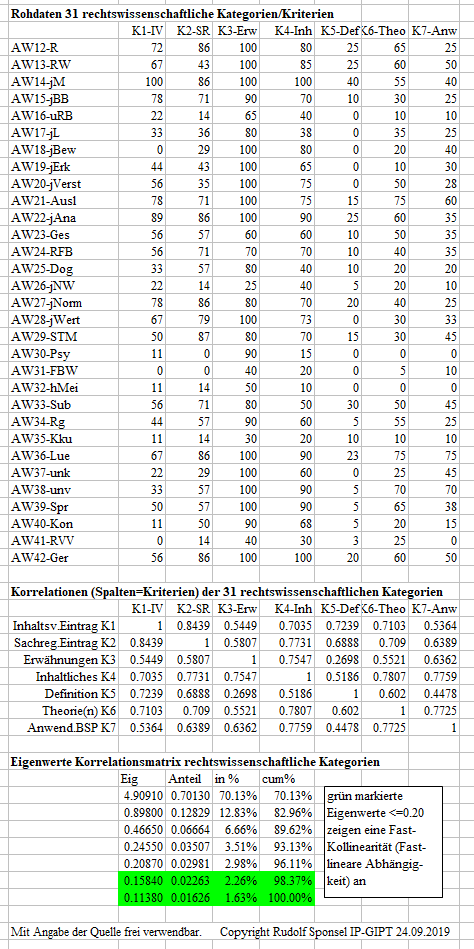
Korrelationen und Eigenwertanalysen der 7 Kriterien 31 rechts-wissenschaftlichen Kategorien
Zur Interpretation der Größe der Korrelationskoeffizienten siehe bitte hier. Für die Interpretation gilt der wichtige Vieldeutigkeitssatz:
| Der Korrelationskoeffizient zwischen zwei Variablen gibt die Korrelation zwischen diesen beiden und der mit ihnen verbundenen Variablen an. Eine tragbare Interpretationsbasis erhält man daher erst, wenn man das System der vorliegenden Variablen einer partiellen Korrelationsanalyse unterzieht (allgemein hier, am Beispiel allgemein-wissenschaftliche Kriterien hier. |