(ISSN 1430-6972)
IP-GIPTDAS=06.09.2018 Internet Erstausgabe, letzte Änderung: TT.MM.JJ
Impressum: Diplom-Psychologe Dr. phil. Rudolf Sponsel Stubenlohstr. 20 D-910Tes52 Erlangen
Mail:_sekretariat@sgipt.org_ Zitierung & Copyright
Anfang_ EWA Sprachstudie 01_ Rel. Aktuelles _Überblick_Überblick Wissenschaft _Rel. Beständiges_ Titelblatt_Konzept_Archiv_Region_Service iec-verlag___ _Wichtige Hinweise zu Links und Empfehlungen
Willkommen in unserer Internet-Publikation für Allgemeine und Integrative Psychotherapie, Abteilung Wissenschaft, Bereich Eigenwertanalysen, und hier speziell zum Thema:
Vollständige Eigenwert- und Kollinearitätsanalyse der Korrelationen der Realisierungsgrade der Sprachstudie 01 mit Gesamtschau nach der ABC-Methode
Originalarbeit von Rudolf Sponsel, Erlangen
Zusammenfassung - Abstract
- Summary
In der Sprachstudie-01 wurden I. 10 Sachverhalte, für die 8 Realisierungsbegriffe
- denkbar, undenkbar, möglich, unmöglich,
wahrscheinlich, unwahrscheinlich, realistisch, unrealistisch
- zuzuordnen waren und II. die Reihenfolge der Realisierungsgrade untersucht.
An der Pilotstudie beteiligten sich 37 TeilnehmerInnen (danke), wovon alle
37 die Aufgabe I. bearbeiten und 29 der 37 die Reihenfolgeaufgabe II.
Den kleinen Fragebogen finden Sie hier.
Außerdem wurden verschiedene, insgesamt vier
Skalierungsvarianten untersucht. Auf dieser Seite werden die Ergebnisse
der Skalierung 2 (S2) vorgestellt.
Die Variablenbezeichnungen und ihre Skalierung
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Die Skalierung (2. Variante S2)
| -9 b undenkbar (V2) | 2 a denkbar (V1) |
| -8 d unmöglich (V4) | 3 c möglich (V3) |
| -3 h unrealistisch (V8) | 8 e wahrscheinlich (V5) |
| -2 f unwahrscheinlich (V6) | 9 g realistisch (V7) |
1:=denkbar * 2:=undenkbar * 3:=möglich * 4:=unmöglich * 5:=wahrscheinlich * 6:=unwahrscheinlich * 7:=realistisch * 8:=unrealistisch
Korrelationsmatrix der Realisierungsgrade nach S2 skaliert

Interpretation
von Fast-Kollinearitaeten
| Man beachte beim inhaltlichen Interpretieren der Fast-Kollinearitäten das Vorzeichen der zugehörigen Korrelationskoeffizienten. |
Eigenwertanalyse der Korrelationsmatrix
der Realisierungsgrade nach S2 skaliert
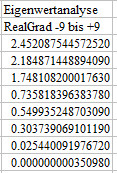 |
In der Sprachstudie der nach S2 skalierten Korrelationsmatrix
der Realisierungsgrade - denkbar, undenkbar,
möglich, unmöglich, wahrscheinlich, unwahrscheinlich, realistisch,
unrealistisch - fanden sich eine Kollinearität
(Eigenwert < 0.0001) und eine Fast-Kollinearität.(Eigenwert <
02) .
Das ist bei einer empirischen Stichprobe eher erstaunlich, so dass eine
besondere Untersuchung interessant und geboten war.
|
Eigenwertanalyse
der vier Skalierungsvarianten
Insgesamt wurden die Reihenfolgen der Realisierungsgrade mit vier verschiedenen
Skalierungen bewertet. Damit sollte untersucht werden, wie stabil die Korrelationen
und Eigenwerte gegenüber unterschiedlichen Skalierungen sind.
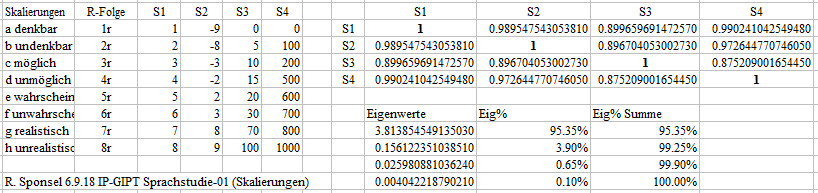
Die Eigenwertanalyse deer vier Skalierungen zeigt, dass die vier Skalierungen als eindimensional interpretiert werden dürfen, weil es nur einen einzigen großen Eigenwert, den wir Skalierungs-Faktor nennen, gibt, der 95.3% der Varianz ausschöpft.
Genauere
Bestimmung der Fast-Kollinearitaeten
Mit diesem Ergebnis stellte sich die Frage, ob sich die (Fast-) Kollinearitäten
genauer bestimmen ließen. Die geschieht auf dieser Seite nach zwei
Methoden, wie ich sie im Bd. 2 (2005) Fast-
Kollinearität in Korrelationsmatrizen mit Eigenwert-Analysen erkennen
entwickelt habe. Beide Methoden beruhen auf der Partitionierung der Korrelationsmatrix.
Die Idee der Partionierung
Die Idee ist sehr einfach: Man zerlegt die Korrelationsmatrix in alle
möglichen Teilmatrizen der Ordnung 2-7 und schaut, in welchen Partitionen
sich Eigenwerte < 0.20 oder gar gleich 0 finden. Allerdings geht
das derzeit nur mit relativ "kleinen" Korrelationsmatritzen, auf meinem
Notebook etwa bis zur Ordnung 16, weil man sich sonst in der kombinatorischen
Explosion verfängt und riesige Datensätze erzeugt, die den Arbeitsspeicher
sprengen können.
Die kleinste Partitionierung einer Korrelationsmatrix
ist ein Paar (Variablenpaar). Es folgen Dreier-, Vierer-, Fünfer-
Sechser und Siebener Partitionen in einer Korrelationsmatrix der Ordnung
8.
Im Idealfall findet man sogar ein Paar und könnte
dies dann in dieser Sprachstudie-01 als eigenwertanalytisch begründete
Synonymität bei positiver Korrelation oder Antonymität bei negativer
Korrelation interpretieren. Tatsächlich zeigt sich ein solcher Idealfall
in der Sprachstudie-01 zwischen Variable 3 (möglich) und 5 (wahrscheinlich)
mit einer negativen Korrelation r35-S2 = -0.8647,
was überrascht und nach besonderer Aufklärungs- und Interpretationsarbeit
verlangt.
Es gelangten zwei Methoden für die Fast-Kollinearitätsanalyse zur Anwendung:
Methode ABC-Gesamtanalyse der
Fast-Kollinearitaeten
Hier werden sämtliche Fastkollinearitäten in allen Partitionen
untersucht und gesamtverarbeitet. Aus den Gesamtmaßen lassen sich
Schlüsse ziehen, wie wichtig (unwichtig) die einzelnen Variablen für
Fast-Kollinearitäten sind.
Man kann der ABC-Gesamtschau entnehmen, dass die Variablen V3 mit 93, V5 mit 92, V8 mit 91 und V2 mit 87 Partitionen den größten Einfluss auf die Fastkollinearitäten haben, wenn auch alle anderen ebenfalls deutlichen Einfluss haben V1 und V7 mit 71, V6 mit 70 und V4 mit 64 Partitionen. Insgesamt kann man daher davon sprechen, dass alle Variablen für die Fast-Kollinearitäten eine Rolle spielen, die sich in zwei Einflussgruppen einteilen lassen (87-93) und (64-71).
Methode der
Fast-Kollinearitaetsbestimmung durch Eigenwertanalyse der Partitionen
Hier wird jede einzelne Partition auf Fast-Kollinearität untersucht.
| Für alle Partitionen, die eine fast-kollineare Partition ij enthalten, gilt, dass sie deshalb mindestens eine Fast-Kollinearität enthalten müssen, nämlich die durch ij bedingte. |
Methode ABC-Gesamtanalyse der Fast-Kollinearitaeten
Hier wird einerseits untersucht, wie viele Fast-Kollinearitäten es gibt, wenn die Variable V in (Ain) der Partition ist bzw. nicht (Aout) in der Partition ist. Andererseits wird untersucht, wie viele Nicht-Kollinearitäten es gibt, wenn die Variable V in der Partition ist (Bin) bzw. nicht (Bout) in der Partition ist.
A := Fast-Kollinear (Eigenwert < 0.2) einschließlich
kollinear (Eigenwert < 0.0001)
B := keine Kollinearität (Eigenwert > 0.2)
Ain Anzahl der Fastkollinearitäten (A), wenn die Variable V = 0, 1,..., 8 in der Partition ist
| Wenn Var. enthalten dann | A= 0 1 2 Fast-Kollinearitaeten (es gibt nur zwei) |
| 1:=denkbar (a)
2:=undenkbar (b) 3:=möglich (c) 4:=unmöglich (d) 5:=wahrscheinlich (e) 6:=unwahrscheinlich(f) 7:=realistisch (g) 8:=unrealistisch (h) |
62 57 7
62 Part. mit 0, 57 mit 1 und 7 mit 2 Fast-Kollin.
51 63 12 51 Part. mit 0, 63 mit 1 und 12 mit 2 Fast-Kollin. 45 69 12 ... 68 52 6 ... 46 68 12 ... 62 58 6 ... 62 57 7 ... 47 67 12 47 Part. mit 0, 67 mit 1 und 12 mit 2 Fast-Kollin. |
Bei einer Fast-Kollinearität hat die Variable 3 (möglich)
mit 69 Vorkommnissen den stärksten Einfluss und den schwächsten
mit 47 Partitionen die Variable 8 (unrealistisch).
Bei zwei Fast-Kollinearitäten - mehr gibt es in dieser Korrelationsmatrix
nicht - sind es vier Variable (undenkbar, möglich, wahrscheinlich,
unrealistisch), die bei 12 Partitionen zwei Kollinearitäten bewirken.
Aout Anzahl der Fastkollinearitäten (A), wenn die Variable V = 0, 1,..., 8 NICHT in der Partition ist
Wenn Var. nicht enth dann A= 0 1 2 3 4 5 6 7 8 Fast-Kollinearitaeten 1:=denkbar (a)
2:=undenkbar (b)
3:=möglich (c)
4:=unmöglich (d)
5:=wahrscheinlich (e)
6:=unwahrscheinlich(f)
7:=realistisch (g)
8:=unrealistisch (h)70 45 5 0 0 0 0 0
81 39 0 0 0 0 0 0
87 33 0 0 0 0 0 0
64 50 6 0 0 0 0 0
86 34 0 0 0 0 0 0
70 44 6 0 0 0 0 0
70 45 5 0 0 0 0 0
85 35 0 0 0 0 0 0
Bin Anzahl der NICHTkollinearitaeten (B), wenn
die Variable V = 1, 2, ..., 8 in de Partition ist
| Wenn Var. enthalten dann | B= 0 1 2 3 4 5 6 7 8 NICHTKollinearitaeten |
| 1:=denkbar (a)
2:=undenkbar (b) 3:=möglich (c) 4:=unmöglich (d) 5:=wahrscheinlich (e) 6:=unwahrscheinlich(f) 7:=realistisch (g) 8:=unrealistisch (h) |
0 0 9
31 49 33 4 0
0 0 11 36 48 28 3 0 0 1 12 35 49 26 3 0 0 0 8 28 51 35 4 0 0 1 12 35 48 27 3 0 0 0 9 30 50 33 4 0 0 0 9 31 49 33 4 0 0 0 11 37 50 25 3 0 |
| Wenn Var. nicht enth.dann | B= 0 1 2 3 4 5 6 7 8 NICHTKollinearitaeten |
| 1:=denkbar (a)
2:=undenkbar (b) 3:=möglich (c) 4:=unmöglich (d) 5:=wahrscheinlich (e) 6:=unwahrscheinlich(f) 7:=realistisch (g) 8:=unrealistisch (h) |
0 1 27
46 37 9 0 0
0 1 25 41 38 14 1 0 0 0 24 42 37 16 1 0 0 1 28 49 35 7 0 0 0 0 24 42 38 15 1 0 0 1 27 47 36 9 0 0 0 1 27 46 37 9 0 0 0 1 25 40 36 17 1 0 |
- In aller Kürze (ausführlich):
sAi= gewichtete Summe A=1,2,..., Amax, wenn Variable in Partition.
sAin= (Summe [A>0])/(Summe [A=0]) wenn Variable in Partition.
SBi= gewichtete Summe B=1,2, .., Bmax, wenn Variable in Partition
sAo= gewichtete Summe A=1,2,..., Amax, wenn Variable nicht in Partition.
sAon= (Summe [A>0])/(Summe [A=0]), wenn Variable nicht in Partition.
sBo= Summe B=1,2, ..., Bmax, wenn die Variable nicht in Partition
Man kann der ABC-Gesamtschau entnehmen, dass die Variablen V3 mit 93, V5 mit 92, V8 mit 91 und V2 mit 87 den größten Einfluss auf die Fastkollinearitäten haben, wenn auch alle anderen ebenfalls deutlichen Einfluss haben V1 und V7 mit 71, V6 mit 70 und V4 mit 64 Partitionen. Insgesamt kann man daher davon sprechen, dass alle Variablen für die Fast-Kollinearitäten eine Rolle spielen, die sich in zwei Einflussgruppen einteilen lassen (87-93) und (64-71).
ABC-Gesamtschau V1 V2 V3 V4 V5 V6 V7 V8 sAi
sAin
sBi
sAo
sAon
sBo71 87 93 64 92 70 71 91
1.145 1.705 2.066 0.941 2 1.129 1.145 1.936
496 480 474 503 475 497 496 476
55 39 33 62 34 56 55 35
0.785 0.481 0.379 0.968 0.395 0.8 0.785 0.411
386 402 408 379 407 385 386 406
Methode
der Fast-Kollinearitaetsbestimmung durch Eigenwertanalyse der Partitionen
Gruppierte Ausgabe der Ergebnisse der Eigenwertanalysen der Partitionen
der Korrelationsmatrix der Realisierungsgrade mit Skalierungsvariante S2
von -9 bis +9.
Kommentierte Programmausgabe
# Korrelationsmatrix aus Datei SS_K2.dat
Informativ werden die multiplen Korrelationskoeffizienten der Partitionen
mit ausgegeben.
Eigenwerte kleiner 0.2 oder um 0 fettmarkiert.
Rechts vom " . " befinden sich die herausgenommenen Variablen.
Kommentiert werden die ersten 10 Ergebnisse, die mindestens eine Fast-Kollinearität
enthalten.
Sämtlich Partitionen, die Fast-Kollinearität enthalten, werden
voran gestellt.
part: 1 2 3 4
5 6 7 8 . 0 (die komplette
Korrelationsmatrix enthält eine Kollinearität und eine Fast-Kollinearität)
eig: 0.549935 0.303739 0.0254401
-0.000000000337228 0.735818 1.74811 2.18487
2.45209
mcor:
1 1
1 1
1 1
1 1
part: 2 3 4 5
6 7 8 . 1
eig: 0.362195 0.125382 0.0217111
0.642343 1.60503 2.00265 2.24069
mcor: 0.90922504 0.97052617 0.86715759
0.97173103 0.90419937 0.78921974 0.92386992
Erläuterung: Nimmt man Variable 1 = denkbar heraus,
gibt es immer noch 2 Fast-Kollinearitäten. Das heißt, die Variable
denkbar
beeinflusst die Fast-Kollinearitäten nicht, hat aber die Kollinearität
mit 9 Nachkomma-Nullen zum Verschwinden gebracht..
Alle Paare mit einer Fast-Kollinearitaet
Da gibt es tatsächlich eines:
Partition 35 mit Fast-Kollinearitaet
part: 3 5 . 1
2 4 6 7 8
eig: 1.86474 0.135261
mcor: 0.86473853 0.86473853
Kommentar: Zwischen dem Variablenpaar 3 = möglich und 5
= wahrscheinlich gibt es eine Fast-Kollinearität, d.h. überall,
wo die Variable 3 und 5 enthalten sind, gibt es mindestens eine Fast-Kollinearität.
Berücksichtigt man das Vorzeichen des Korrelationskoeffizienten, r35-S2
=
-
0.8647,
so schließen sich in dieser Stichprobe (n=29) die Wahl
möglich
und wahrscheinlich weitgehend aus. Möglich
und wahrscheinlich haben hier keine synonyme,
sondern antonyme, also gegensätzliche Bedeutung! Das ist ein überraschendes
Ergebnis und wird unter Sprachstudie-01 inhaltlich diskutiert. Daher soll
diese Diskussion hier nicht weiter verfolgt werden. Hier soll es ausschließlich
um das Aufspüren von Fast-Kollinearitäten in Partitionen gehen
und wie man die Einflüsse über Eigenwertbetrachtungen erkennen
kann.
Für alle Partitionen, die die Partition 35 enthalten, gilt, dass
sie deshalb mindestens eine Fast-Kollinearität enthalten müssen.
Allgemein:
| Für alle Partionen, die eine fast-kollineare Partition ij enthalten, gilt, dass sie deshalb mindestens eine Fast-Kollinearität enthalten müssen, nämlich die durch ij bedingte. |
- Dreier-Partitionen mit Variable 3 und 5 und einer
Fast-Kollinearität
- part: 3 5
8 . 1 2 4 6
7
eig: 0.135241 0.916683 1.94808
mcor: 0.86501535 0.86536701 0.2061479
part: 3 5
7 . 1 2 4 6
8
eig: 0.127636 0.989748
1.88262
mcor: 0.87289254 0.87005386 0.23894865
part: 3 4 5
. 1 2 6 7 8
eig: 1.01262 1.91259 0.0747893
mcor: 0.91635841 0.65248011 0.92471424
part: 3 5
6 . 1 2 4 7
8
eig: 0.132169 0.986125
1.88171
mcor: 0.86840926 0.86659637 0.16630178
part: 2 3
5 . 1 4 6 7
8
eig: 0.904867 0.127622
1.96751
mcor: 0.31493743 0.87537975 0.86816016
part: 1 3 5
. 2 4 6 7 8
eig: 0.996633 0.135258
1.86811
mcor: 0.039855024 0.86474381
0.8647696
- Vierer-Partitionen mit Variable 3 und 5 und einer
Fast-Kollinearität
- part: 3 4 5
7 . 1 2 6 8
eig: 0.0740402 0.769654 1.23719 1.91912
mcor: 0.91796304 0.65657737 0.92527614 0.25671574
part: 3 5
7 8 . 1 2 4
6
eig: 0.126763 0.645308
1.27821 1.94972
mcor: 0.8750164 0.87005499
0.39482342 0.37790956
part: 3 5
6 8 . 1 2 4
7
eig: 0.131647 0.710115
1.16888 1.98936
mcor: 0.86840927 0.86801613 0.31606593
0.33709901
part: 3 4 5
6 . 1 2 7 8
eig: 0.059735 0.785032
1.2066 1.94863
mcor: 0.93166404 0.74190919 0.93737974
0.48866598
part: 3 5
6 7 . 1 2 4
8
eig: 1.88482 1.648 0.0978456
0.369336
mcor: 0.89708628 0.88569826
0.726645 0.73641263
part: 3 4 5
8 . 1 2 6 7
eig: 0.0693993 0.719512
1.24207 1.96901
mcor: 0.91925849 0.70309411 0.93090481
0.39609961
- part: 2 3 5
8 . 1 4 6 7
eig: 0.114242 0.314799 1.35693 2.21403
mcor: 0.74339151 0.88116522 0.87625574 0.7242084
part: 2 3 5
7 . 1 4 6 8
eig: 0.123333 0.728266
1.14005 2.00835
mcor: 0.3678051 0.87975547
0.87191795 0.30802264
part: 2 3 5
6 . 1 4 7 8
eig: 1.96973 1.2107
0.699151 0.12042
mcor: 0.4258457 0.88309562
0.8719729 0.34108519
part: 2 3 4
5 . 1 6 7 8
eig: 0.525108 1.42788 0.0732338
1.97378
mcor: 0.50175542 0.91641944 0.72318436
0.92680122
part: 1 3 5
8 . 2 4 6 7
eig: 0.135238 0.416711
1.44014 2.00791
mcor: 0.57029715 0.86509136 0.86547869
0.59404229
part: 1 3 5
7 . 2 4 6 8
eig: 0.126702 0.692499
1.29802 1.88278
mcor: 0.31365075 0.87384311 0.87036907
0.38536184
part: 1 3 5
6 . 2 4 7 8
eig: 0.1288 0.386966
1.56621 1.91803
mcor: 0.62410616 0.87038365 0.86826847
0.63674801
part: 1 3 4
5 . 2 6 7 8
eig: 1.12164 0.891151
1.91345 0.0737589
mcor: 0.16145864 0.91707427 0.66318252
0.9257297
part: 1 2 3
5 . 4 6 7 8
eig: 1.02068 0.882518 0.127613
1.96919
mcor: 0.061224529 0.31801644
0.87542501 0.86816772
Fünfer-Partitionen mit Variable 3 und 5 und
einer Fast-Kollinearität
- part: 3 4 5
6 7 . 1 2 8
eig: 1.95957 1.75635 0.880508 0.36469 0.0388769
mcor: 0.95418248 0.78564324 0.95424309 0.82610124 0.78122793
- part: 2 3 5
6 8 . 1 4 7
eig: 1.13662 1.36509 0.210966 0.0622466 2.22508
mcor: 0.88963091 0.91187149 0.90123256 0.76183043 0.87988293
part: 2 3 5
6 7 . 1 4 8
eig: 0.36924 0.0906152
0.782302 1.7316 2.02624
mcor: 0.42643616 0.90690954 0.89005225
0.74392916 0.73660364
part: 2 3 4
5 8 . 1 6 7
eig: 0.0689694 0.262881
0.749741 1.68791 2.2305
mcor: 0.76218647 0.92059118 0.72548301
0.93100444 0.72649669
- part: 2 3 4
5 7 . 1 6 8
eig: 0.524745 0.0720509 0.820283 1.57446 2.00846
mcor: 0.52455059 0.91818488 0.72326848 0.92778606 0.3083972
part: 2 3 4
5 6 . 1 7 8
eig: 0.519718 0.812361
0.0594847
1.62639 1.98205
mcor: 0.51549872 0.93174467 0.77251217
0.93798545 0.50300805
part: 1 3 5
6 8 . 2 4 7
eig: 0.128412 0.282647
0.710164 1.68653 2.19225
mcor: 0.74940216 0.87113681 0.86861658
0.64435865 0.60290816
part: 1 3 5
6 7 . 2 4 8
eig: 0.275361 0.0867372
0.693316 1.87934 2.06525
mcor: 0.6537834 0.90237125
0.89030588 0.83682083 0.75547074
part: 1 3 5
7 8 . 2 4 6
eig: 0.12651 0.415877
0.743526 1.69567 2.01842
mcor: 0.58587129 0.87507643 0.87051466
0.42238743 0.61287441
part: 1 3 4
5 8 . 2 6 7
eig: 0.921223 0.0691512
0.401833 1.59479 2.013
mcor: 0.57190238 0.91927597 0.70407054
0.93112876 0.64611548
part: 1 3 4
5 7 . 2 6 8
eig: 1.11885 1.32975
1.91914 0.558779 0.0734821
mcor: 0.36537344 0.9181578
0.67324176 0.92591802 0.41102063
part: 1 3 4
5 6 . 2 7 8
eig: 1.08195 1.56674
1.98131 0.335166 0.034831
mcor: 0.8027389 0.95425658
0.85914248 0.95864552 0.84974229
part: 1 2 3
5 7 . 4 6 8
eig: 0.887485 0.625866
0.122587
1.35515 2.00892
mcor: 0.31406502 0.36814398 0.88052913
0.87219937 0.4255428
part: 1 2 3
5 6 . 4 7 8
eig: 0.882606 0.113849
0.356074 1.6685 1.97897
mcor: 0.64154324 0.45928085 0.88688774
0.87483686 0.69143174
Sechser-Partitionen mit Variable 3 und 5 und einer
Fast-Kollinearität
- part: 3 4 5
6 7 8 . 1 2
eig: 0.349597 0.520386 0.0314965 1.24354 1.78068 2.0743
mcor: 0.9603952 0.85172587 0.96350708 0.854269 0.78144915 0.62244313
Erläuterung: Nimmt man Variable 1 = denkbar und 2 = undenkbar heraus, gibt es immer noch eine 1 Fast-Kollinearität. Das heißt, die Herausnahme der Variablen 2 = undenkbar senkt die Fast-Kollinearität von 2 auf 1, ist also für die Fast-Kollinearität bedeutungsvoll.
part: 2 3 4
5 6 7 . 1 8
eig: 0.526418 0.362032
0.0383634
1.05699 1.95787 2.05833
mcor: 0.52455553 0.95424551
0.8129513 0.95517463 0.82610262 0.78442092
part: 1 3 5
6 7 8 . 2 4
eig: 0.213354 0.0748515
0.556425 0.853437 1.88526 2.41667
mcor: 0.79972282 0.90970907 0.89197501
0.86135573 0.79839988 0.6800064
part: 1 3 4
5 6 8 . 2 7
eig: 0.0325109 0.278725
0.521982 1.23773 1.72932 2.19973
mcor: 0.81887324 0.95657819 0.87539102
0.96244239 0.85381317 0.65726734
part: 1 3 4
5 6 7 . 2 8
eig: 0.27467 0.0109098
0.55979 1.12337 1.89529 2.13597
mcor: 0.90688924 0.98435613 0.93877871
0.98434739 0.96691808 0.89746088
part: 1 2 3
5 7 8 . 4 6
eig: 0.130741 0.0179185
0.647729 1.2256 1.6957 2.28231
mcor: 0.93003839 0.97274976 0.90488437
0.9055766 0.8662169 0.98039381
part: 1 2 3
5 6 7 . 4 8
eig: 0.62681 0.893389
0.274246 0.0772019 1.97435 2.154
mcor: 0.6715462 0.46420555
0.91412519 0.89630912 0.85322441 0.75710645
part: 1 2 3
4 5 7 . 6 8
eig: 0.0713454 0.486929
0.626856 1.21527 1.59057 2.00903
mcor: 0.37105962 0.52787901
0.9184094 0.73741207 0.92856606 0.43180059
part: 1 2 3
4 5 6 . 7 8
eig: 0.521113 0.335056
0.0346928
1.34946 1.76217 1.99751
mcor: 0.8028662 0.51590791
0.95426598 0.86974304 0.95900993 0.8504153
Siebener-Partitionen mit Variable 3 und 5 und einer
Fast-Kollinearität
- part: 1 3
4 5 6 7 8 .
2
eig: 0.0108612 0.201588 0.566458 0.520246 1.89534 1.3748 2.43071
mcor: 0.91908846 0.9844121 0.93899959 0.98434836 0.96752144 0.90360149 0.68138627
- part: 1 2 3
4 5 6 7 . 8
eig: 0.490481 0.628141 0.274189 0.0105346 1.35716 1.99457 2.24492
mcor: 0.90903985 0.53953849 0.98467228 0.94485226 0.98498976 0.96749844 0.90113741
- Hier enden die Partitionen, die die Variablen 3 und 5 enthalten,
die für eine Fast-Kollinearität verantwortlich sind.
P128
part: 1 2 8
. 3 4 5 6 7
eig: 1.03508 1.88524 0.0796772
mcor: 0.83173339 0.87843974 0.91886828
P268 Partitionen mit den Variablen 2, 6 und 8
und einer Fast-Kollinearität
1:=denkbar * 2:=undenkbar * 3:=möglich * 4:=unmöglich
* 5:=wahrscheinlich * 6:=unwahrscheinlich * 7:=realistisch * 8:=unrealistisch
Dreier-Partitionen mit Variable 2, 6 und 8 und einer Fast-Kollinearität
- part: 2 6 8
. 1 3 4 5 7
eig: 1.15109 1.70583 0.143084
mcor: 0.83377096 0.66561687 0.83849518
- Zur genaueren Analyse empfiehlt sich immer eine Betrachtung der Korrelationskoeffizienten
der Partition, hier also der Korrelationen der drei Paare aus 2, 6 und
8:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Informationen aus den Zweier-Partitionen
part: 2 6 .
1 3 4 5 7 8
eig: 0.768066 1.23193
mcor: 0.23193405 0.23193405
part: 2 8 .
1 3 4 5 6 7
eig: 1.70396 0.296044
mcor: 0.70395612 0.70395612
part: 6 8 .
1 2 3 4 5 7
eig: 0.72015 1.27985
mcor: 0.27985019 0.27985019
- Ergebnis-268: Man sieht, dass der
stärkste Anteil zwischen Variable 2 (undenkbar) und 8 (unrealistisch)
mit einem Eigenwert von 0.296044 besteht. Die Korrelation zwischen 2 (undenkbar)
und 8 (unrealistisch) betrug -0.703956 und ist negativ, also besteht inhaltlich
eine gegensinnige Beziehung wie auch zwischen Variable 2 (undenkbar) und
6 (unwahrscheinlich). P26 (0.768066 1.23193) und P68 (0.72015
1.27985) liefern annähernd gleich große Eigenwerte, so dass
man schätzen darf, dass ihr Anteil 0.296044 - 0.143084 = 0.15296
beträgt, also jeweils ungefähr die Hälfte 0.07648.
- Anmerkung zur Rechnung Einfluss des 28 auf 268:
part: 2 8 . 1 3 4 5 6 7 enthält 0.296044
part: 2 6 8 . 1 3 4 5 7 enthält 0.143084.
P278 Partitionen mit den Variablen 2, 7 und 8 und einer Fast-Kollinearität
1:=denkbar * 2:=undenkbar * 3:=möglich * 4:=unmöglich * 5:=wahrscheinlich * 6:=unwahrscheinlich * 7:=realistisch * 8:=unrealistisch
Dreier-Partitionen mit Variable 2, 7 und 8 und einer Fast-Kollinearität
- part: 2 7 8
. 1 3 4 5 6
eig: 1.16835 1.70517 0.126482
mcor: 0.851282 0.70744454 0.85486155
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Informationen aus den Zweier-Partitionen
part: 2 7 .
1 3 4 5 6 8
eig: 1.25298 0.747016
mcor: 0.25298442 0.25298442
part: 2 8 .
1 3 4 5 6 7
eig: 1.70396 0.296044
mcor: 0.70395612 0.70395612
part: 7 8 .
1 2 3 4 5 6
eig: 1.29114 0.708858
mcor: 0.29114222 0.29114222
- Vierer-Partitionen mit Variable 2, 7 und 8 und einer
Fast-Kollinearität
- part: 2 5 7
8 . 1 3 4 6
eig: 0.913256 1.17151 1.79039 0.124837
mcor: 0.85153465 0.22584676 0.7107942 0.85858969
part: 2 4 7
8 . 1 3 5 6
eig: 0.691475 1.26289 0.124884
1.92075
mcor: 0.85984441 0.41074741 0.70876055
0.85498293
part: 2 4 5
7 8 . 1 3 6
eig: 1.11911 1.38386
0.440792 0.124332 1.93191
mcor: 0.86046084 0.56062588 0.46605724
0.71509261 0.85884353
part: 2 4 6
8 . 1 3 5 7
eig: 0.633621 1.29673 0.143008
1.92665
mcor: 0.8394185 0.4407289
0.67982638 0.8388807
part: 2 4 5
6 8 . 1 3 7
eig: 0.434335 1.01717 0.143004
1.47079 1.9347
mcor: 0.84205732 0.57608619 0.45372753
0.68136405 0.84095757
part: 2 3 7
8 . 1 4 5 6
eig: 0.800558 1.23294
1.8401 0.126404
mcor: 0.85225344 0.29815389 0.71179257
0.85577065
- part: 2 4 6
7 8 . 1 3 5
eig: 0.345903 0.697807 0.112988 1.80961 2.03369
mcor: 0.87615042 0.44073007 0.72169948 0.74608562 0.8770054
part: 2 3 6
7 8 . 1 4 5
eig: 0.295098 0.111359
0.918949 1.81256 1.86203
mcor: 0.87804075 0.42634676 0.74569413
0.76016727 0.8771426
part: 2 4 5 6 7 8 . 1 3
eig: 0.345851 0.441239 0.112433 1.21648 1.84968 2.03431
mcor: 0.87653642 0.57749318 0.46636549 0.72182136 0.75042363 0.88006285
part: 2 5 6
7 8 . 1 3 4
eig: 0.34819 0.112433
0.919522 1.76083 1.85902
mcor: 0.87284265 0.23238894 0.71220107
0.74971445 0.87876869
- Nachdem die Partition 2,6,8 eine Fast-Kollinearität enthält,
werden alle Partitionen, die die Variablen 2,6 und 8 enthalten, ebenfalls
eine Fastkollinearität enthalten.
- part: 2 5 6
8 . 1 3 4 7
eig: 1.15698 0.906529 1.79344 0.143047
mcor: 0.83406756 0.20561624 0.66578417 0.83962598
part: 2 6 7
8 . 1 3 4 5
eig: 0.353203 0.113178
1.69206 1.84155
mcor: 0.87280689 0.71110392 0.74608525
0.87678736
part: 2 3 6
8 . 1 4 5 7
eig: 1.16485 0.859074
1.84533 0.130745
mcor: 0.85215761 0.37504528
0.6936699 0.84368477
part: 2 3 4
6 8 . 1 5 7
eig: 0.623386 0.867247
1.36392 0.130492 2.01495
mcor: 0.85764474 0.37888767 0.44379977
0.7037502 0.84390743
part: 1 2 7
8 . 3 4 5 6
eig: 0.645706 1.39081
1.93825 0.0252334
mcor: 0.90867556 0.96301447 0.84705553
0.97383568
part: 1 2 6
8 . 3 4 5 7
eig: 0.352754 0.0750246
1.51479 2.05744
mcor: 0.84049096 0.89563175 0.68520707
0.9254232
part: 1 2 5
8 . 3 4 6 7
eig: 1.07008 0.898592 0.0785737
1.95276
mcor: 0.83350821 0.87874696 0.22601356
0.92071813
part: 1 2 4
8 . 3 5 6 7
eig: 1.11352 0.76479 0.0629165
2.05878
mcor: 0.85902604 0.91096019 0.53900184
0.93078745
part: 1 2 3
8 . 4 5 6 7
eig: 1.11972 0.817448 0.0783429
1.98449
mcor: 0.83318724 0.88366437
0.2911087 0.91933064
- part: 2 3 4
7 8 . 1 5 6
eig: 0.981267 0.597626 1.27074 0.124876 2.02549
mcor: 0.86140251 0.31649364 0.42308201 0.71365917 0.85582925
part: 1 2 6
7 8 . 3 4 5
eig: 0.646167 0.271157
0.0190114
1.69602 2.36765
mcor: 0.94478356 0.96863148 0.83394485
0.91532981 0.97884836
part: 1 5 6
7 8 . 2 3 4
eig: 0.804403 0.539445
1.10308 0.17612 2.37695
mcor: 0.77138166 0.27368073
0.8058679 0.7021461 0.64880884
part: 1 6 7
8 . 2 3 4 5
eig: 0.185742 0.546797
0.90136 2.3661
mcor: 0.76535842 0.80122198 0.69313575
0.61644428
part: 1 4 6
7 8 . 2 3 5
eig: 0.592548 0.513713
0.173574
1.34755 2.37261
mcor: 0.78033008 0.46916193 0.82560728
0.69317151 0.62880331
part: 1 3 6
7 8 . 2 4 5
eig: 0.544251 0.785405
1.15152 0.144662 2.37417
mcor: 0.78745481 0.4685333
0.83317147 0.75132547 0.6742283
part: 1 3 4
6 7 . 2 5 8
eig: 1.02125 1.13535
0.558014 0.180331 2.10505
mcor: 0.69917155 0.34777591 0.45563698
0.83731838 0.70186644
part: 1 2 5
7 8 . 3 4 6
eig: 1.42477 0.914007
0.645461 1.99204 0.0237245
mcor: 0.9131694 0.96462425
0.30916003 0.85483932 0.9756297
part: 1 2 5
6 8 . 3 4 7
eig: 0.349096 0.925828
0.0742594
1.54793 2.10289
mcor: 0.84240776 0.89572963 0.22978566
0.68590809 0.92674744
part: 1 2 4
7 8 . 3 5 6
eig: 0.589876 0.772965
1.55074 0.0196561 2.06676
mcor: 0.92890888 0.97255563 0.58824202
0.8600024 0.97881883
part: 1 2 4
5 8 . 3 6 7
eig: 1.06751 1.31218
0.484468 0.0621678 2.07367
mcor: 0.85981813 0.91381764 0.63798832
0.45487119 0.93080426
part: 1 2 3
7 8 . 4 5 6
eig: 0.637357 0.820688
1.51161 0.0252309 2.00511
mcor: 0.90871606 0.96313902
0.2987984 0.84788159 0.97384158
part: 1 2 3
4 8 . 5 6 7
eig: 0.981134 1.13617
0.681808 0.0606696 2.14022
mcor: 0.86202382 0.91666892 0.32458676
0.5536253 0.93191828
part: 1 2 3
4 5 . 6 7 8
eig: 0.502391 1.0166
1.4343 0.0718558 1.97485
mcor: 0.20215577 0.51295945 0.91719767
0.73536924 0.92814703
part: 1 2 3
6 8 . 4 5 7
eig: 0.324893 0.0719869
0.908555 1.56337 2.13119
mcor: 0.84068728 0.90421821 0.37633109
0.70885641 0.92702389
Sechser Partitionen mit einer Fast-Kollinearitaet
- part: 1 4 5
6 7 8 . 2 3
eig: 0.367771 0.565538 0.171781 1.10245 1.40478 2.38767
mcor: 0.78118998 0.58367002 0.46680433 0.82561765 0.7042714 0.67998434
part: 1 2 5
6 7 8 . 3 4
eig: 0.646039 0.926023
0.268066 0.0168691 1.76213 2.38087
mcor: 0.9506212 0.97126656
0.38920264 0.84515456 0.92451249 0.98132528
part: 1 3 4
6 7 8 . 2 5
eig: 0.560505 0.503465
1.02659 0.137063 1.39239 2.37998
mcor: 0.80110202 0.4701771
0.4708023 0.85232702 0.75134868 0.68136219
- part: 1 2 4
6 7 8 . 3 5
eig: 0.592503 0.773911 0.254155 0.00887819 1.99793 2.37262
mcor: 0.97526008 0.98537584 0.79581423 0.91063034 0.9528484 0.98910003
part: 1 2 4
5 7 8 . 3 6
eig: 1.24632 1.5653
0.657259 0.428975 0.0196127 2.08253
mcor: 0.92897139 0.97255592 0.65913301
0.46676798 0.86209287 0.97898879
part: 1 2 4
5 6 8 . 3 7
eig: 0.285284 0.504596
0.0620026
1.24046 1.77203 2.13563
mcor: 0.87574769 0.91660297 0.68094791
0.46193885 0.72185097 0.93265689
part: 1 2 4
5 6 7 . 3 8
eig: 1.16742 1.36334
0.623997 0.406275 0.196471 2.24249
mcor: 0.69971259 0.52592321 0.64842821
0.46277844 0.81912846 0.66917313
part: 1 2 3
6 7 8 . 4 5
eig: 0.638936 0.919375
0.22313 0.0181765 1.82116 2.37922
mcor: 0.94800649 0.96898799 0.47775939
0.86135675 0.92422688 0.97966504
part: 1 2 3
4 7 8 . 5 6
eig: 0.98436 0.717627
0.54579 1.59128 0.0195427 2.1414
mcor: 0.92940015 0.97294734 0.32582028
0.59845528 0.86013815 0.9788642
part: 1 2 3
4 6 7 8 . 5
eig: 0.54977 0.735815
1.02959 0.216175 0.00822181 2.07928 2.38115
mcor: 0.97735022 0.98597471 0.50273151
0.80309017 0.92587749 0.95880257 0.98985199
part: 1 2 3
4 6 8 . 5 7
eig: 1.013 0.686758
0.281445 0.0598903 1.76707 2.19183
mcor: 0.8750689 0.92178627
0.38384749 0.59875017 0.73469943 0.93447724
part: 1 2 3
4 6 7 . 5 8
eig: 1.43841 1.02153
0.627845 0.487534 0.17976 2.24492
mcor: 0.69944602 0.51088475 0.44460183
0.54054373 0.83924181 0.702466
Siebener Partitionen mit einer Fast-Kollinearität
- part: 1 2 4
5 6 7 8 . 3
eig: 0.432292 0.252621 0.658895 0.00886725 1.25785 2.00163 2.38785
mcor: 0.97527334 0.98537593 0.81365119 0.46680922 0.91063495 0.95312621 0.98915229
Alle Partitionen mit 2 Fast-Kollinearitäten
Alle siebener Partitionen mit 2 Fast-Kollinearitäten
- part: 1 2 3
5 6 7 8 . 4
eig: 0.0772204 0.0157867 0.307675 0.648462 1.38243 2.11723 2.45119
mcor: 0.95137371 0.97442107 0.91992131 0.91157022 0.87037704 0.92482647 0.98254374
part: 1 2 3
4 5 7 8 . 6
eig: 0.072156 0.0175152
0.547681 0.721832 1.56523 1.76523 2.31036
mcor: 0.93404832 0.97474571 0.92630132
0.74623829 0.9358297 0.86758194 0.98096203
part: 1 2 3
4 5 6 8 . 7
eig: 0.066882 0.0238137
0.35055 0.688987 1.77404 1.72908 2.36664
mcor: 0.87698815 0.93520338 0.96610031
0.87660285 0.96876863 0.88513523 0.95023321
- part: 2 3
5 6 7 8 . 1
4
eig: 0.372355 0.143009 0.0620573 1.36445 1.83273 2.2254
mcor: 0.89897513 0.91865999 0.90529923 0.80931769 0.77095395 0.89429191
Hier ist eine Fast-Kolinearität durch die Variablke 3 und 5 bedingt, die andere wahrscheinlich durch die Variablen 2 und 8.
part: 2 3 4
5 7 8 . 1 6
eig: 0.0678608 0.127056
0.602175 1.27044 1.6918 2.24067
mcor: 0.86213435 0.92060145 0.72863128
0.93131186 0.71513496 0.86315789
part: 2 3 4
5 6 8 . 1 7
eig: 0.173443 0.0238404
0.635137 1.1673 1.76509 2.23519
mcor: 0.90613542 0.96577544 0.85628234
0.96830634 0.87388034 0.92228133
part: 1 2 3
4 5 8 . 6 7
eig: 0.0782547 0.0527861
0.687199 1.12787 1.74355 2.31034
mcor: 0.86486885 0.91818493 0.92335466
0.74339141 0.93237175 0.93591339
- part: 2 3 5
7 8 . 1 4 6
eig: 1.13312 1.39697 0.1448190.104722 2.22036
mcor: 0.8593784 0.88152959 0.87625607 0.71179344 0.86070299
part: 1 2 3
5 8 . 4 6 7
eig: 1.00446 0.1580290.0529673
1.50248 2.28206
mcor: 0.85625959 0.90724732 0.89699803
0.89298323 0.93415417
part: 1 2 3
5 6 8 . 4 7
eig: 0.358129 0.152238
0.0398415 1.35708 1.73562 2.35709
mcor: 0.85673674 0.93458851 0.91958591
0.91085952 0.76267361 0.94758753
Vollständige und Schlussmatrix (wie Anfang)
- part: 1 2 3
4 5 6 7 8 . -1
(Schluss = wie Anfang)
eig: 0.549935 0.303739 0.0254401-0.000000000337228 0.735818 1.74811 2.18487 2.45209
mcor: 1 1 1 1 1 1 1 1
Alle Partitionen ohne Fast-Kollinearitäten (alle Eigenwerte > 0.2)
- Alle Paare ohne Fast-Kollinearitäten
- part: 7 8 .
1 2 3 4 5 6
eig: 1.29114 0.708858
mcor: 0.29114222 0.29114222
part: 6 8 .
1 2 3 4 5 7
eig: 0.72015 1.27985
mcor: 0.27985019 0.27985019
part: 6 7 .
1 2 3 4 5 8
eig: 1.64773 0.35227
mcor: 0.64773043 0.64773043
part: 4 5 .
1 2 3 6 7 8
eig: 1.31037 0.689626
mcor: 0.31037377 0.31037377
part: 5 8 .
1 2 3 4 6 7
eig: 0.798318 1.20168
mcor: 0.20168237 0.20168237
part: 5 7 .
1 2 3 4 6 8
eig: 0.968741 1.03126
mcor: 0.03125933 0.03125933
part: 5 6 .
1 2 3 4 7 8
eig: 0.950037 1.04996
mcor: 0.04996274 0.04996274
part: 4 8 .
1 2 3 5 6 7
eig: 0.781793 1.21821
mcor: 0.2182067 0.2182067
part: 4 7 .
1 2 3 5 6 8
eig: 0.802625 1.19737
mcor: 0.19737452 0.19737452
part: 4 6 .
1 2 3 5 7 8
eig: 1.27268 0.727319
mcor: 0.27268057 0.27268057
part: 3 8 .
1 2 4 5 6 7
eig: 1.19583 0.804165
mcor: 0.19583499 0.19583499
part: 3 7 .
1 2 4 5 6 8
eig: 1.14601 0.853995
mcor: 0.14600518 0.14600518
part: 3 6 .
1 2 4 5 7 8
eig: 1.12287 0.877133
mcor: 0.12286674 0.12286674
part: 3 4 .
1 2 5 6 7 8
eig: 1.01985 0.98015
mcor: 0.01984952 0.01984952
part: 2 8 .
1 3 4 5 6 7
eig: 1.70396 0.296044
mcor: 0.70395612 0.70395612
part: 2 7 .
1 3 4 5 6 8
eig: 1.25298 0.747016
mcor: 0.25298442 0.25298442
part: 2 6 .
1 3 4 5 7 8
eig: 0.768066 1.23193
mcor: 0.23193405 0.23193405
part: 2 5 .
1 3 4 6 7 8
eig: 1.16677 0.833226
mcor: 0.16677409 0.16677409
part: 2 4 .
1 3 5 6 7 8
eig: 1.39757 0.60243
mcor: 0.3975702 0.3975702
part: 2 3 .
1 4 5 6 7 8
eig: 0.721613 1.27839
mcor: 0.27838737 0.27838737
part: 1 8 .
2 3 4 5 6 7
eig: 1.56489 0.435114
mcor: 0.56488593 0.56488593
part: 1 7 .
2 3 4 5 6 8
eig: 0.70056 1.29944
mcor: 0.29943993 0.29943993
part: 1 6 .
2 3 4 5 7 8
eig: 1.61708 0.382918
mcor: 0.61708169 0.61708169
part: 1 5 .
2 3 4 6 7 8
eig: 1.0394 0.960601
mcor: 0.03939868 0.03939868
part: 1 4 .
2 3 5 6 7 8
eig: 1.10979 0.890209
mcor: 0.10979134 0.10979134
part: 1 3 .
2 4 5 6 7 8
eig: 0.96291 1.03709
mcor: 0.03708987 0.03708987
part: 1 2 .
3 4 5 6 7 8
eig: 1.03593 0.964066
mcor: 0.03593364 0.03593364
- part: 6 7 8
. 1 2 3 4 5
eig: 0.352147 0.806384 1.84147
mcor: 0.65471835 0.65776361 0.31482494
part: 5 7 8
. 1 2 3 4 6
eig: 1.02924 1.34003
0.630733
mcor: 0.22253437 0.30529171 0.35949526
- part: 5 6 8
. 1 2 3 4 7
eig: 0.952706 0.67751 1.36978
mcor: 0.20179522 0.27992834 0.33709894
part: 5 6 7
. 1 2 3 4 8
eig: 1.00478 1.648
0.347216
mcor: 0.097312662 0.65152822
0.65085525
part: 4 7 8
. 1 2 3 5 6
eig: 1.18095 1.29264
0.52641
mcor: 0.34926955 0.39526916 0.40476988
part: 4 6 8
. 1 2 3 5 7
eig: 1.29675 1.21801
0.485238
mcor: 0.41044483 0.44189486 0.41475732
part: 4 6 7
. 1 2 3 5 8
eig: 0.864487 0.347275
1.78824
mcor: 0.27403749 0.66436604 0.64808943
part: 4 5 8
. 1 2 3 6 7
eig: 1.31118 1.17907
0.50975
mcor: 0.4225232 0.41538078
0.35767584
part: 4 5 7
. 1 2 3 6 8
eig: 1.35419 1.02827
0.617535
mcor: 0.37316824 0.32440508 0.22006587
part: 4 5 6
. 1 2 3 7 8
eig: 0.610832 0.950466
1.4387
mcor: 0.40328101 0.31245872
0.2751088
part: 3 7 8
. 1 2 4 5 6
eig: 1.13075 1.29741
0.571843
mcor: 0.28876669 0.35724657 0.37790035
part: 3 6 8
. 1 2 4 5 7
eig: 0.886776 0.707114
1.40611
mcor: 0.20827252 0.28832854 0.32370047
part: 3 6 7
. 1 2 4 5 8
eig: 1.05126 1.64816
0.300575
mcor: 0.32058 0.68400596
0.68645864
part: 3 4 8
. 1 2 5 6 7
eig: 0.980267 0.716494
1.30324
mcor: 0.19723375 0.21945086 0.29034855
part: 3 4 7
. 1 2 5 6 8
eig: 0.98103 0.763724
1.25525
mcor: 0.14629149 0.19758259
0.2432149
part: 3 4 6
. 1 2 5 7 8
eig: 1.01484 1.29205
0.693114
mcor: 0.13480141 0.27792959
0.3013582
part: 2 6 7
. 1 3 4 5 8
eig: 0.85258 0.351872
1.79555
mcor: 0.26829729 0.65154035
0.6562875
part: 2 5 8
. 1 3 4 6 7
eig: 0.914952 0.295116
1.78993
mcor: 0.70441129 0.20468238
0.7091267
part: 2 5 7
. 1 3 4 6 8
eig: 0.971319 0.710737
1.31794
mcor: 0.29877115 0.16715644 0.25322725
part: 2 5 6
. 1 3 4 7 8
eig: 1.04721 1.26351
0.689286
mcor: 0.29272184 0.19004725 0.24874856
part: 2 4 8
. 1 3 5 6 7
eig: 0.817095 0.269176
1.91373
mcor: 0.74702568 0.40694011 0.70715678
part: 2 4 7
. 1 3 5 6 8
eig: 0.596838 0.8286
1.57456
mcor: 0.43560509 0.40996594 0.27409751
part: 2 4 6
. 1 3 5 7 8
eig: 0.598993 0.793557
1.60745
mcor: 0.41778702 0.43872919 0.30410112
part: 2 4 5
. 1 3 6 7 8
eig: 1.43248 1.16049
0.407027
mcor: 0.50123447 0.55136901 0.44309959
part: 2 3 8
. 1 4 5 6 7
eig: 0.870943 0.290634
1.83842
mcor: 0.71839401 0.27838744 0.70395613
part: 2 3 7
. 1 4 5 6 8
eig: 0.689074 0.854944
1.45598
mcor: 0.35152415 0.2891402
0.2649395
part: 2 3 6
. 1 4 5 7 8
eig: 1.30802 1.12027
0.571707
mcor: 0.38654228 0.33856818 0.30311123
part: 2 3 4
. 1 5 6 7 8
eig: 0.981351 0.52384
1.49481
mcor: 0.48089383 0.29546276 0.40866251
part: 1 7 8
. 2 3 4 5 6
eig: 0.778371 0.43503
1.7866
mcor: 0.58223917 0.33394742 0.57917545
part: 1 6 8
. 2 3 4 5 7
eig: 0.290666 0.72155
1.98778
mcor: 0.74005209 0.62267768 0.57159865
part: 1 6 7
. 2 3 4 5 8
eig: 0.24232 0.701013
2.05667
mcor: 0.63095847 0.78499934 0.66014337
part: 1 5 8
. 2 3 4 6 7
eig: 0.975112 0.411728
1.61316
mcor: 0.56998788 0.22098278 0.59273946
part: 1 5 7
. 2 3 4 6 8
eig: 1.00801 1.29955
0.692442
mcor: 0.3033876 0.059906182
0.30252446
part: 1 4 5
. 2 3 6 7 8
eig: 1.02456 1.31861
0.656834
mcor: 0.13426918 0.33353234 0.31905537
part: 1 3 7
. 2 4 5 6 8
eig: 1.02908 1.31971
0.651208
mcor: 0.31038156 0.1687925
0.33820446
part: 1 3 6
. 2 4 5 7 8
eig: 0.985835 0.376915
1.63725
mcor: 0.61831443 0.13235772 0.62513953
part: 1 5 6
. 2 3 4 7 8
eig: 0.993687 0.382827
1.62349
mcor: 0.61714131 0.051135303
0.6176154
part: 1 4 8
. 2 3 5 6 7
eig: 0.927536 0.424001
1.64846
mcor: 0.56505455 0.21881649 0.58633452
part: 1 4 7
. 2 3 5 6 8
eig: 1.09919 1.3155
0.585307
mcor: 0.34546411 0.26512484 0.37858471
part: 1 4 6
. 2 3 5 7 8
eig: 1.08019 1.63989
0.279923
mcor: 0.68140766 0.44633727 0.70575986
part: 1 3 8
. 2 4 5 6 7
eig: 0.977097 0.412761
1.61014
mcor: 0.56984129 0.21515749 0.59137337
part: 1 2 7
. 3 4 5 6 8
eig: 0.964579 0.625262
1.41016
mcor: 0.3022554 0.25640384
0.38524384
part: 1 2 6
. 3 4 5 7 8
eig: 0.976372 0.351923
1.6717
mcor: 0.6268432 0.26897645
0.6518021
part: 1 3 4
. 2 5 6 7 8
eig: 0.988186 0.888778
1.12304
mcor: 0.1152101 0.040343787
0.11092072
part: 1 2 5
. 3 4 6 7 8
eig: 1.01553 1.16681
0.817663
mcor: 0.058399993 0.1721134
0.17284863
part: 1 2 4
. 3 5 6 7 8
eig: 1.01834 1.40454
0.577122
mcor: 0.13991671 0.40555254 0.41650593
part: 1 2 3
. 4 5 6 7 8
eig: 1.00927 1.27839
0.712344
mcor: 0.060789192 0.2822098
0.28234762
part: 4 6 7 8 . 1 2 3 5
eig: 0.345887 0.540996 1.21814 1.89498
mcor: 0.41709106 0.68005739 0.66060999 0.44205848
part: 4 5 7
8 . 1 2 3 6
eig: 1.38482 1.26196
0.987063 0.366155
mcor: 0.52339104 0.46261409
0.4455619 0.51525526
part: 4 5 6
8 . 1 2 3 7
eig: 0.937416 1.22592
1.47118 0.365483
mcor: 0.54874563 0.44017879 0.46465519
0.51012317
- part: 4 5 6
7 . 1 2 3 8
eig: 0.634606 0.345602 1.20691 1.81289
mcor: 0.40665338 0.32579954 0.66479192 0.652298
part: 3 6 7
8 . 1 2 4 5
eig: 0.293794 0.719921
1.13871 1.84758
mcor: 0.38605132 0.68525669 0.70378689
0.38153294
part: 3 4 7
8 . 1 2 5 6
eig: 1.2544 1.31334
0.979494 0.452761
mcor: 0.3013538 0.35931088
0.44923583 0.4723858
part: 3 4 6
8 . 1 2 5 7
eig: 1.2424 1.40666
0.86715 0.48379
mcor: 0.20828149 0.41044879 0.44611904
0.43963966
part: 3 4 6
7 . 1 2 5 8
eig: 1.05132 0.864294
0.295622 1.78876
mcor: 0.32402017 0.27817707 0.69935475
0.68651608
part: 2 5 6
7 . 1 3 4 8
eig: 1.102 0.751437
0.347216 1.79935
mcor: 0.31650058 0.19889151 0.65679697
0.65783352
part: 2 4 6
7 . 1 3 5 8
eig: 0.611214 0.342532
1.02982 2.01643
mcor: 0.43610981 0.43921332 0.66459429
0.65651575
part: 2 4 5
8 . 1 3 6 7
eig: 1.30087 0.510706
0.262221 1.9262
mcor: 0.75775375 0.55290205
0.4502956 0.70997879
part: 2 4 5
7 . 1 3 6 8
eig: 0.407018 1.20324
0.805383 1.58436
mcor: 0.52275423 0.5596089
0.44437647 0.27646619
part: 2 4 5
6 . 1 3 7 8
eig: 1.16783 0.406314
0.791976 1.63388
mcor: 0.51468653 0.57163688 0.44317722
0.30422884
part: 2 3 6
7 . 1 4 5 8
eig: 1.19925 0.689138
0.294241 1.81737
mcor: 0.38911166 0.42374636 0.69625192
0.68736045
part: 5 6 7
8 . 1 2 3 4
eig: 0.345858 0.703505
1.09723 1.85341
mcor: 0.23185492 0.65665967 0.66359815
0.37335457
part: 2 3 4
8 . 1 5 6 7
eig: 0.982225 0.745288
0.260849 2.01164
mcor: 0.7618036 0.29561878
0.41778768 0.7071925
part: 2 3 4
7 . 1 5 6 8
eig: 0.981391 0.523619
0.81699 1.678
mcor: 0.50093569 0.30870493 0.42271811
0.28850755
part: 2 3 4
6 . 1 5 7 8
eig: 0.512288 0.693145
1.16201 1.63256
mcor: 0.50872286 0.34407167 0.44261703
0.35126651
part: 1 5 7
8 . 2 3 4 6
eig: 1.0418 0.736929
0.41134 1.80993
mcor: 0.58561988 0.23494432
0.3427343 0.60816569
part: 1 5 6
8 . 2 3 4 7
eig: 1.02578 0.679344
0.281734 2.01314
mcor: 0.74362423 0.22795011 0.62429233
0.60002986
part: 1 4 6
8 . 2 3 5 7
eig: 0.255892 0.51534
1.2396 1.98917
mcor: 0.75876947 0.46908262 0.70599985
0.58671216
part: 1 5 6
7 . 2 3 4 8
eig: 1.0083 0.693215
0.24058 2.05791
mcor: 0.63096316 0.097362727
0.78644315 0.66307808
part: 1 4 7
8 . 2 3 5 6
eig: 0.591331 0.419783
1.18486 1.80403
mcor: 0.58285049 0.35062131
0.4260972 0.61079801
part: 1 4 6
7 . 2 3 5 8
eig: 1.0992 0.591887
0.204025 2.10489
mcor: 0.69250333 0.44750546
0.8184586 0.66070036
part: 1 4 5
8 . 2 3 6 7
eig: 1.30687 0.674072
0.363747 1.65531
mcor: 0.5717803 0.42545982
0.42642183 0.63424241
part: 1 4 5
6 . 2 3 7 8
eig: 1.30281 0.765488
1.66804 0.263662
mcor: 0.68912729 0.53834239 0.33978333
0.71114553
part: 1 3 7
8 . 2 4 5 6
eig: 0.665121 1.13078
0.409567 1.79453
mcor: 0.58401687 0.29370259 0.38568864
0.61234115
part: 1 3 6
8 . 2 4 5 7
eig: 0.994511 0.708075
0.272187 2.02523
mcor: 0.74815875 0.26247408 0.63422113
0.60160672
part: 1 3 6
7 . 2 4 5 8
eig: 1.06832 0.661396
0.213253 2.05703
mcor: 0.6362678 0.33585864
0.80593366 0.70036221
part: 1 4 5
7 . 2 3 6 8
eig: 1.26638 1.36984
0.867562 0.49622
mcor: 0.36266236 0.42033519 0.34294647
0.39800886
part: 1 3 4
8 . 2 5 6 7
eig: 0.988985 0.921007
0.401825 1.68818
mcor: 0.5700548 0.21659838
0.22023109 0.61119117
part: 1 3 4
7 . 2 5 6 8
eig: 1.12158 0.978838
1.34174 0.557839
mcor: 0.35536079 0.17061193 0.26623698
0.40854234
part: 1 3 4
6 . 2 5 7 8
eig: 0.984404 1.08374
1.65822 0.27363
mcor: 0.6836447 0.15416996
0.45200768 0.71360185
part: 1 2 6
7 . 3 4 5 8
eig: 0.992432 0.626903
0.239944 2.14072
mcor: 0.6377527 0.292017
0.790093 0.66607116
part: 1 2 5
7 . 3 4 6 8
eig: 0.825933 1.12478
0.622453 1.42683
mcor: 0.30524263 0.30066041 0.17286604
0.3852507
part: 1 2 5
6 . 3 4 7 8
eig: 0.817825 1.16166
0.348463 1.67205
mcor: 0.62695527 0.32205054
0.1906333 0.65473545
part: 1 2 4
7 . 3 5 6 8
eig: 0.561926 0.63102
1.21074 1.59632
mcor: 0.34627157 0.43619456 0.44069006
0.41203399
part: 1 2 4
6 . 3 5 7 8
eig: 0.621753 1.33039
0.279846 1.76801
mcor: 0.68144827 0.41788908 0.53620087
0.71006983
part: 1 2 4
5 . 3 6 7 8
eig: 1.01452 1.16049
1.43829 0.386695
mcor: 0.17957021 0.51193437 0.56933763
0.45466687
part: 1 2 3
7 . 4 5 6 8
eig: 0.714914 0.625166
1.14184 1.51808
mcor: 0.31110739 0.35214589 0.29845918
0.39632314
part: 1 2 3
4 . 5 6 7 8
eig: 1.03422 0.963051
1.50077 0.501957
mcor: 0.15357161 0.48917471 0.30171009
0.42852522
part: 1 2 3
6 . 4 5 7 8
eig: 1.27424 0.727594
1.67372 0.324443
mcor: 0.6316906 0.41525842
0.35146235 0.67247564
- part: 3 5 6
7 8 . 1 2 4
eig: 0.0975677 0.36635 0.752767 1.76613 2.01719
mcor: 0.89792524 0.8857644 0.72786255 0.7476845 0.38214117
- part: 3 4 6
7 8 . 1 2 5
eig: 1.00708 1.29577 0.292895 0.506354 1.8979
mcor: 0.38683331 0.41779377 0.70516427 0.70640514 0.48534047
- part: 3 4 5
7 8 . 1 2 6
eig: 1.22839 1.27919 0.453679 0.0693748 1.96937
mcor: 0.91967096 0.72265785 0.93096187 0.44994266 0.52928179
part: 3 4 5
6 8 . 1 2 7
eig: 1.24747 1.16725
0.51748 0.0443368 2.02346
mcor: 0.94371585 0.83007632 0.95278374
0.66816849 0.62200607
part: 2 4 5
6 7 . 1 3 8
eig: 0.410073 0.342246
1.00761 1.21812 2.02196
mcor: 0.52362529 0.57163831 0.44593065
0.66531813 0.65783457
part: 2 3 4
6 7 8 . 1 5
eig: 0.293632 0.640888
1.00924 0.111099 1.86004 2.0851
mcor: 0.88159195 0.42970213 0.44392744
0.75221836 0.76020645 0.87732851
part: 4 5 6
7 8 . 1 2 3
eig: 0.345601 0.368058
1.0841 1.27652 1.92572
mcor: 0.56116772 0.46390924 0.68066049
0.67186533 0.54183904
part: 2 3 4
6 7 . 1 5 8
eig: 0.526387 0.936111
1.20738 0.293231 2.03689
mcor: 0.51034089 0.42736052
0.4426447 0.70397747 0.68737214
part: 1 4 5
7 8 . 2 3 6
eig: 1.3447 0.987353
0.521675 0.329864 1.8164
mcor: 0.5856202 0.52339142
0.46675929 0.4664758 0.66655983
part: 1 4 5
6 8 . 2 3 7
eig: 0.254145 0.381954
0.975203 1.37542 2.01327
mcor: 0.75879677 0.58031064 0.44026821
0.71119093 0.63430398
part: 1 4 5
6 7 . 2 3 8
eig: 1.30751 0.868731
0.507922 0.201452 2.11438
mcor: 0.69849557 0.53839281
0.347075 0.81910945 0.66311038
part: 1 3 4
7 8 . 2 5 6
eig: 0.558094 0.984359
1.26023 0.382955 1.81436
mcor: 0.58445713 0.30560845 0.36025578
0.47061019 0.64388387
part: 1 3 4
6 8 . 2 5 7
eig: 0.984615 1.24289
0.503779 0.241804 2.02692
mcor: 0.76672577 0.26598446 0.47073608
0.7148272 0.61301617
part: 1 2 5
6 7 . 3 4 8
eig: 0.827708 0.623778
1.17063 0.237069 2.14082
mcor: 0.63803282 0.33702367 0.20034066
0.79260236 0.66771397
part: 1 2 4
6 8 . 3 5 7
eig: 0.2986 0.0626545
0.765316 1.76161 2.11182
mcor: 0.87447485 0.91443325 0.59514956
0.71911309 0.93265687
part: 1 2 4
6 7 . 3 5 8
eig: 0.64139 0.583031
0.202528 1.3341 2.23895
mcor: 0.69257057 0.43627593 0.54047831
0.81847628 0.66876525
part: 1 2 4
5 7 . 3 6 8
eig: 1.1239 1.27076
1.60375 0.622896 0.378692
mcor: 0.36798583 0.52585809 0.58749929
0.46001423 0.41819967
part: 1 2 4
5 6 . 3 7 8
eig: 1.15845 1.35168
0.451547 0.255369 1.78295
mcor: 0.68970315 0.51576523 0.64684763
0.46193862 0.7129972
part: 1 2 3
6 7 . 4 5 8
eig: 0.728026 0.62676
1.29967 0.201693 2.14385
mcor: 0.64789352 0.41556503 0.44451167
0.8179292 0.70047417
part: 1 2 3
4 7 . 5 6 8
eig: 0.979 1.21587
0.626855 0.486202 1.69207
mcor: 0.35863923 0.50293479 0.32289405
0.45567332 0.42644738
part: 1 2 3
4 6 . 5 7 8
eig: 1.00758 0.51313
1.43782 0.272479 1.76899
mcor: 0.68415743 0.50968115 0.35280975
0.5369197 0.72280166
- part: 1 3 4
5 7 8 . 2 6
eig: 0.558919 0.383035 0.0691443 1.23095 1.73481 2.02314
mcor: 0.58598668 0.91972574 0.72272591 0.93115653 0.47093169 0.6741681
Literatur (Auswahl)
- Sponsel, Rudolf & Hain, Bernhard (1994). Numerisch instabile Matrizen und Kollinearität in der Psychologie. Diagnose, Relevanz & Utilität, Frequenz, Ätiologie, Therapie. Ill-Conditioned Matrices and Collinearity in Psychology. Deutsch-Englisch. Ins Englische übersetzt von Agnes Mehl. Kapitel 6 von Dr. Bernhard Hain: Bemerkungen über Korrelationsmatrizen. Erlangen: IEC-Verlag [ISSN-0944-5072 ISBN 3-923389-03-5]. Aktueller Preis: www.iec-verlag.de.
- Sponsel, R. (2005). Fast- Kollinearität in Korrelationsmatrizen mit Eigenwert-Analysen erkennen. Ergänzungsband - Band II zu Numerisch instabile Matrizen und Kollinearität in der Psychologie. Erlangen: IEC-Verlag.