(ISSN 1430-6972)
IP-GIPTDAS=12.10.2012 Internet Erstausgabe, letzte Änderung 13.10.12
Impressum: Diplom-Psychologe Dr. phil. Rudolf Sponsel Stubenlohstr. 20 D-91052 Erlangen
Mail:_sekretariat@sgipt.org_ Zitierung & Copyright
Anfang_ Fast-Kollinearitätsanalyse einer Emotions- & Persönlichkeitsmatrix Rel. Aktuelles _Überblick_Überblick Wissenschaft _Rel. Beständiges_ Titelblatt_Konzept_Archiv_Region_Service iec-verlag___Wichtige Hinweise zu Links und Empfehlungen
Willkommen in unserer Internet-Publikation für Allgemeine und Integrative Psychotherapie, Abteilung Wissenschaft, Bereich Eigenwertanalysen, und hier speziell zum Thema:
Fast-Kollinearitätsanalyse
einer Korrelationsmatrix
zu Emotions- und Persönlichkeitseigenschaften
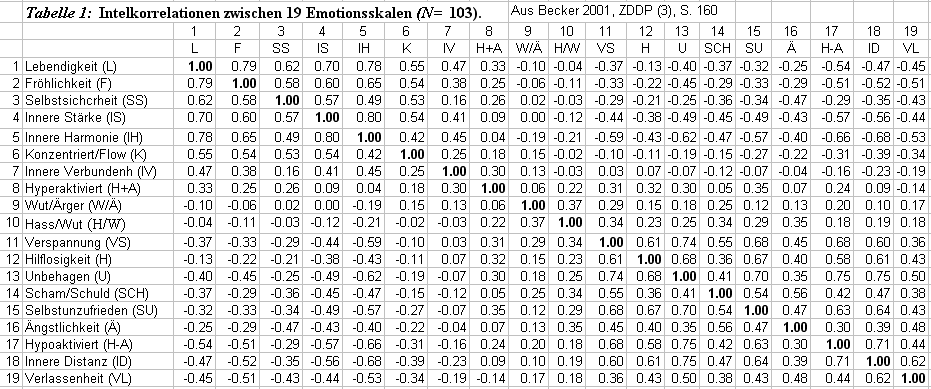
nach Peter Becker, ZDDP 22 (3), 2001, S. 160
von Rudolf Sponsel, Erlangen
Abstract
- Zusammenfassung - Summary
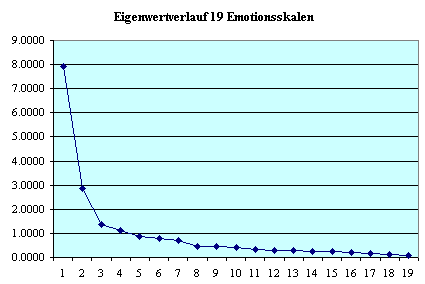
Die Eigenwerte
einer Korrelationsmatrix geben direkt
und unmittelbar Auskunft, ob und wie viele Fast-Kollinearitäten,
d.h. fast-lineare Abhängigkeiten und damit Gesetzes-
oder Regelhaftigkeiten in den Daten vorhanden sind (Sponsel
2005). Die Fast-Kollinearitäten lassen sich in der Korrelations-
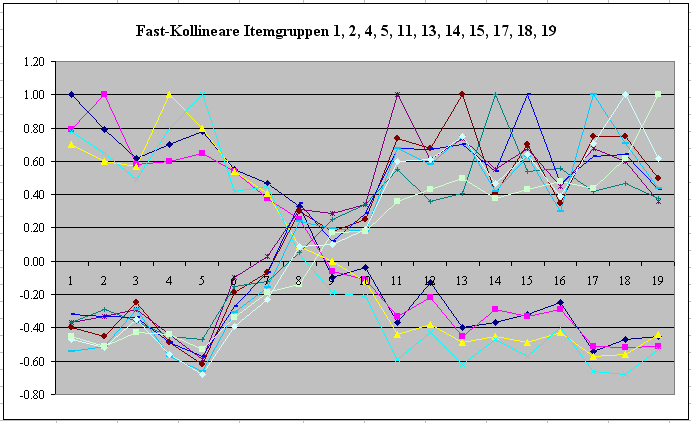
im Gegensatz zur Datenmatrix auch leicht graphisch darstellen, wie
man z.B. der Eingangsgraphik entnehmen kann. Als Fast-Kollinearität
werte ich Eigenwerte < 0.20, weniger streng und erweitert Eigenwerte
< 0.30. Fast-Kollinearitäten können Matrizen im Grenzbereich
der numerischen Genauigkeit allein durch Rundungsfehler zum Entgleisen
bringen, es resultieren dann pathologische Werte, die eine sinnvolle Interpretation
multivariater Kennwerte nicht mehr zulassen (Sponsel
1994).
Fast-Kollinearität kann im Regelfall vier Hauptgründe haben: Neben artifiziellen, wenn z.B. ein Gesamtwert in die Korrelationsmatrix aufgenommen wird, können auch die mathematischen Prozeduren selbst, z.B. durch das Zentrieren, Fast-Kollinearitäten erzeugen oder inhaltliche Redundanzen dahinter stecken. Der die WissenschaftlerIn am meisten interessierende Grund ist natürlich das Finden einer echten Gesetzes- oder Regelhaftigkeit. Leider hat der Datenreduktionsfuror der FaktorenanalytikerInnen den Blick für die kaum zu überschätzende Bedeutung kleiner Eigenwerte völlig vernebelt: man wirft dort die Juwelen weg, ohne es zu bemerken.
Literatur (Auswahl)
- Sponsel, Rudolf & Hain, Bernhard (1994). Numerisch instabile Matrizen und Kollinearität in der Psychologie. Diagnose, Relevanz & Utilität, Frequenz, Ätiologie, Therapie. Ill-Conditioned Matrices and Collinearity in Psychology. Deutsch-Englisch. Ins Englische übersetzt von Agnes Mehl. Kapitel 6 von Dr. Bernhard Hain: Bemerkungen über Korrelationsmatrizen. Erlangen: IEC-Verlag [ISSN-0944-5072 ISBN 3-923389-03-5]. Aktueller Preis: www.iec-verlag.de.
- Sponsel, R. (2005). Fast- Kollinearität in Korrelationsmatrizen mit Eigenwert-Analysen erkennen. Ergänzungsband - Band II zu Numerisch instabile Matrizen und Kollinearität in der Psychologie. Erlangen: IEC-Verlag.
- Becker, Peter (2001). Struktur- und Zusammenhangsanalysen von Emotionen und Persönlichkeitseigenschaften. Universität Trier. Zeitschrift für Differentielle und Diagnostische Psychologie, 22 (3), 2001,155-172
Links (Auswahl: beachte)
- Eigenwertanalysen in der IP-GIPT. * Fast- Kollinearität in Korrelationsmatrizen mit Eigenwert-Analysen erkennen.
- Überblick: "Ätiologie", Ursachen, Bedingungen und Quellen numerischer Instabilität - und Fast-Kollinearität.
- Überblicks- und Verteilerseite: Numerisch instabile Matrizen und Kollinearität in der Psychologie - Ill-Conditioned Matrices and Collinearity in Psychology - Diagnose, Relevanz & Utilität, Frequenz, Ätiologie, Therapie.
- Einführung und Überblick. Kritik der Handhabung der Faktorenanalyse, Kommunalität.
- Korrelation. Was bedeutet der lineare Korrelationskoeffizient? Probleme, Kurioses, Paradoxes, Ungereimtheiten und Widersprüchliches in der Korrelationsrechnung und wie man dem begegnen kann, Partielle Korrelation.
- Pseudo-Korrelationsmatrizen.
- Vollständig Partielle Korrelationsmatrix nicht notwendig positiv definit. Der Beweis von Dr. Bernhard Hain (1994).
- Systematische Veränderungs-Paradoxie beim linearen Produkt- Moment- Korrelationskoeffizienten und Effekten von Lernen, Üben, Vergessen, Entwicklung, Fortschritt, Rückschritt und ganz allgemein bei systematischen Veränderungen relativ konstanter Zunahmen oder Abnahmen.
- Beweis und beweisen in Wissenschaft und Leben.
- Überblick Arbeiten zur Theorie, Definitionslehre, Methodologie, Meßproblematik, Statistik und Wissenschaftstheorie besonders in Psychologie, Psychotherapie und Psychotherapieforschung.
Glossar, Anmerkungen und Fußnoten
1) GIPT= General and Integrative Psychotherapy, internationale Bezeichnung für Allgemeine und Integrative Psychotherapie.
___
Standort: Fast-Kollinearitätsanalyse einer Emotions- & Persönlichkeitsmatrix.
*
Links.
*
| Suchen in der IP-GIPT,
z.B. mit Hilfe von "google": <suchbegriff>
site: www.sgipt.org
z.B. Wissenschaft site: www.sgipt.org. |
Dienstleistungs-Info.
*
Zitierung
Sponsel, R. (DAS). Fast-Kollinearitätsanalyse einer Emotions- & Persönlichkeitsmatrix nach Becker. Internet Publikation für Allgemeine und Integrative Psychotherapie IP-GIPT. Erlangen: https://www.sgipt.org/wisms/EWA/Becker01.htm
Copyright & Nutzungsrechte
Diese Seite darf von jeder/m in nicht-kommerziellen Verwertungen frei aber nur original bearbeitet und nicht inhaltlich verändert und nur bei vollständiger Angabe der Zitierungs-Quelle benutzt werden. Das direkte Einbinden in fremde Seiten oder Rahmen ist nicht gestattet - Links sind natürlich willkommen. Sofern die Rechte anderer berührt sind, sind diese dort zu erkunden. Sollten wir die Rechte anderer unberechtigt genutzt haben, bitten wir um Mitteilung. Soweit es um (längere) Zitate aus ... geht, sind die Rechte bei/m ... zu erkunden oder eine Erlaubnis einzuholen.
Ende_Fast-Kollinearitätsanalyse einer Emotions- & Persönlichkeitsmatrix __Rel. Aktuelles_Überblick_Überblick Wissenschaft _Rel. Beständiges_Titelblatt_Konzept_Archiv_Region_Service iec-verlag___Wichtige Hinweise zu Links und Empfehlungen_ Mail: sekretariat@sgipt.org_
korrigiert: irs 13.10.12
Änderungen Kleinere Änderungen werden nicht extra ausgewiesen; wird gelegentlich überarbeitet und ergänzt.
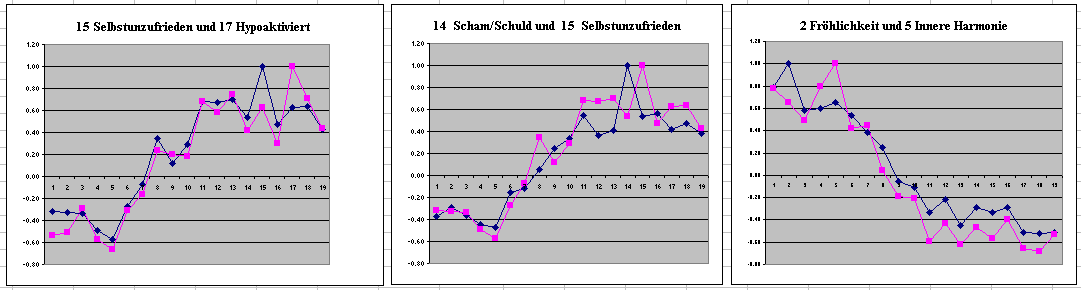
13.10.12 Drei Einzelpaarbeispiele.