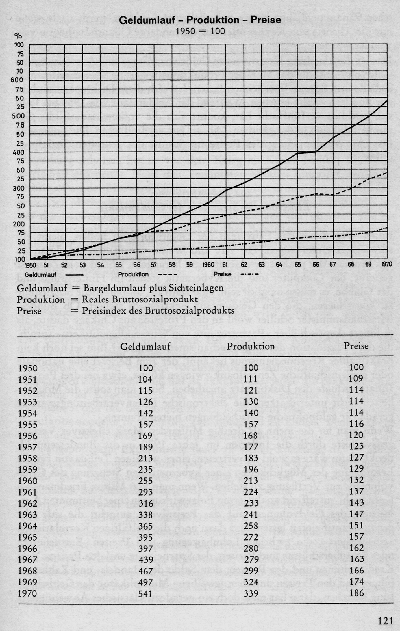Index-Rohdaten nach Slotosch (1971, S. 121)
Jahr     Geldumlauf Produktion Preise
1950     100         100         100
1951     104         111         109
1952     115         121         114
1953     126         130         114
1954     142         140         114
1955     157         157         116
1956     169         168         120
1957     189         177         123
1958     213         183         127
1959     235         196         129
1960     255         213         132
1961     293         224         137
1962     316         233         143
1963     338         241         147
1964     365         258         151
1965     395         272         157
1966     397         280         162
1967     439         279         163
1968     467         299         166
1969     497         324         174
1970     541         339         186
 

Korreliert man die Rohdaten, ergibt sich folgende Korrelationsmatrix:

             Geldumlauf Produktion Preise
Geldumlauf    1.0000     0.9920    0.9937
Produktion    0.9920     1.0000    0.9896
Preise        0.9937     0.9896    1.0000

Interpretation Korrelation: Die drei Variablen Geldumlauf, Produktion und Preise korrelieren extrem hoch, d.h. man die Werte einer jeden Variable ziemlich gut aus den Werten der jeweils anderen gut vorhersagen: ein Wert enthält die wesentliche Information aller drei. Solche Phänomene gibt es in der Ökonomie oft (Belsley et al.), so dass sich verschärft die Frage der Bedeutung und Interpretation stellt.

Eigenwert-Analyse der Korrelationsmatrix:
2.9836    in%    99.45333 %
0.0106    in%     0.35333 %
0.0058    in%     0.19333 %

Die Korrelationsmatrix der drei ökonomischen Variablen Geldumlauf, Produktion und Preise zeigt einen ungewöhnlich eindeutigen und großen Generalfaktor an, weil ein einziger Eigenwert mit 99.45333 % fast die gesamte Varianz (100%) ausschöpft. Man kann auch sagen: Die Matrix ist hochgradig "fast kollinear" ("multilinear"). Und man kann sagen: in den drei Variablen Geldumlauf, Produktion und Preise steckt nur eine einzige Dimension, ein einziger Faktor. Man könnte diese einzige Dimension als wirtschaftliche Entwicklung 1950-1970 interpretieren, die sich hier - in dieser Datenbasis - im Geldumlauf, in der Produktion und in den Preisen ausdrückt .

Ergänzung: partielle Korrelationsanalyse:

Partiell korreliert simuliert die experimentelle Technik des Konstanthaltens. Die auspartialisierte Variable steht bei den folgenden Ergebnissen nach dem Punkt " . " und die beiden  Ziffern vor dem Punkt geben die Korrelation zwischen den Variablen hat, wenn die rechts vom Punkt stehende Variable auspartialisiert ("konstant gehalten") wurde.

r12.3 = 0.535595
r13.2 = 0.661759
r23.1 = 0.272098

Ergebnisse in Worten:
r12.3: Partialisiert man die 3=Preise aus, fällt die Korrelation zwischen 1=Geldumlauf und 2=Produktion von 0.9937 auf 0.535595.
r13.2: Partialisiert man die 2=Produktion aus, fällt die Korrelation zwischen 1=Geldumlauf und 3=Preisen von 0.9920 auf 0.661759.
r23.1: Partialisiert man den 1=Geldumlauf aus, fällt die Korrelation zwischen 2=Produktion und 3=Preisen von 0.9896 auf 0.272098.

Hieraus könnte man die Hypothese gewinnen: Die Korrelation fällt am stärksten, wenn der Geldumlauf auspartialisiert wird. Er könnte damit die wichtigste Variable in diesem Trio sein.

ParKor Marix  1=Geldumlauf 2=Produktion 3=Preise     Eigenwerte    in Prozent
1=Geldumlauf     1         0.535595     0.661759      1.9962        66.54%
2=Produktion 0.535595        1         0.272098      0.7353        24.51%
3=Preise     0.661759      0.272098        1          0.2685         8.95%

Bemerkung: wie Dr. Hain gezeigt hat, ist die partielle Korrelationsmatrix alle gegen den Rest nicht notwendig positiv definit. Diese hier ist es zwar, das muss aber nicht so sein. Es empfiehlt sich daher aufpassen.
 

Anmerkungen in Bezug zur Quantitätstheorie
W120907 schreibt: "Die Quantitätstheorie des Geldes besagt, dass eine Veränderung des Geldangebots (M) eine proportionale Veränderung des Preises zur Folge hat. Es kann darauf geschlossen werden, dass eine Verdopplung der Geldmenge eine Verdopplung des Preises nach sich zieht." Diese Behauptung wird durch die Slotosch-Daten nicht gestützt.
Betrachtet man die Slotosch-Daten für Deutschland 1950-1970, so stimmt diese Behauptung für diese nicht. Die Preise hinken dem Geldumlauf zunehmend mehr hinterher:
 

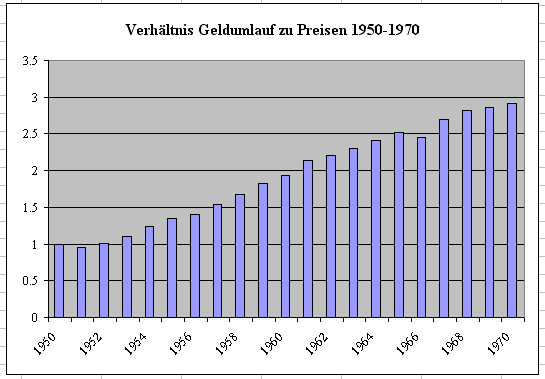Erläuterungen: Während der Geldumlauf von 1950-1970 auf den Indexwert 541 steigt, entwickelt sich der Index der Preise auf 186. Beide wachsen also keineswegs im gleichen Maße, das müßte nämlich eine waagrechte Gerade, die auf der y-Achse durch 1 geht, ergeben. Die Daten enthalten zwar eine hochgradige lineare Fast-Abhängigkeit (extreme Multikollinearität), aber nicht im Verhältnis 1 :1.

• Belsley, David A.; Kuh, Edwin & Welsch, Roy E. (1980). Regression Diagnostics: Identifying Influential Data and Sources of Collinearity. New York: Wiley. [Den Ökonomen sind die Probleme mit der (Multi-) Kollinearität im Gegensatz zu den meisten PsychologInnen wohlvertraut]
• Slotosch, Walter (1971). Das Geld mit dem wir leben müssen. Panorama der Weltinflation. München: Desch.
• Sponsel, Rudolf & Hain, Bernhard (1994). Numerisch instabile Matrizen und Kollinearität in der Psychologie. Diagnose, Relevanz & Utilität, Frequenz, Ätiologie, Therapie.  Ill-Conditioned Matrices and Collinearity in Psychology. Deutsch-Englisch. Ins Englische übersetzt von Agnes Mehl. Kapitel 6 von Dr. Bernhard Hain: Bemerkungen über Korrelationsmatrizen. Erlangen: IEC-Verlag [ISSN-0944-5072  ISBN 3-923389-03-5]. Aktueller Preis: www.iec-verlag.de.
• Sponsel, R. (2005). Fast- Kollinearität in Korrelationsmatrizen mit Eigenwert-Analysen erkennen. Ergänzungsband - Band II zu Numerisch instabile Matrizen und Kollinearität in der Psychologie. Erlangen: IEC-Verlag.

• Überblicks- und Verteilerseite: Numerisch instabile Matrizen und Kollinearität in der Psychologie - Ill-Conditioned Matrices and Collinearity in Psychology -   Diagnose, Relevanz & Utilität, Frequenz, Ätiologie, Therapie.
• Eigenwertbedeutung, Fast-Kollinearitätsanalyse,
• Einführung und Überblick. Kritik der Handhabung der Faktorenanalyse, Kommunalität.
• Korrelation. Was bedeutet der lineare Korrelationskoeffizient? Probleme, Kurioses, Paradoxes, Ungereimtheiten und Widersprüchliches in der Korrelationsrechnung und wie man dem begegnen kann,  Partielle Korrelation.
• Pseudo-Korrelationsmatrizen.
• Vollständig Partielle Korrelationsmatrix nicht notwendig positiv definit. Der Beweis von Dr. Bernhard Hain (1994).
• Systematische Veränderungs-Paradoxie beim linearen Produkt- Moment- Korrelationskoeffizienten und Effekten von Lernen, Üben, Vergessen, Entwicklung, Fortschritt, Rückschritt und ganz allgemein bei systematischen Veränderungen relativ konstanter Zunahmen oder Abnahmen.
• Beweis und beweisen in Wissenschaft und Leben.
• Überblick Arbeiten zur Theorie, Definitionslehre, Methodologie, Meßproblematik, Statistik und Wissenschaftstheorie besonders in Psychologie, Psychotherapie und Psychotherapieforschung.