Internet Publikation für Allgemeine und Integrative Psychotherapie
    IP-GIPT DAS=30.10.2002 Internet-Erstausgabe, Letze Änderung 29.4.06
    Impressum: Diplom-PsychologInnen Irmgard Rathsmann-Sponsel und Dr. phil. Rudolf Sponsel *
    Stubenlohstr. 20     * D-91052 Erlangen * Mail: sekretariat@sgipt.org_Zitierung  &  Copyright
    Anfang  NVZZ-Versuche_Übersicht Wissenschaft__Überblick-Gesamt_Rel. Aktuelles _ Rel. Beständiges_ Titelblatt_Konzept_Archiv_Region_Service iec-verlag  _ __Wichtiger Hinweis zu Links und Empfehlungen
    Willkommen in der Abteilung Wissenschaft,     Methodologie, Meßproblematik, Statistik und Wissenschaftstheorie, besonders in Psychologie, Psychotherapie und Psychotherapieforschung  unserer Internet-Publikation IP-GIPT1), hier speziell angewandte Mathematik zum Thema:

    (Entwicklungs- und Diskussionsversion)

    Normalverteilte Zufallsfehler Versuche
    Zwischenprüfungen, Hilfs- und Dokumentationsseite zum Quaderversuch

    von Rudolf Sponsel, Erlangen

    Für den Quaderversuch zur Überprüfung der Auswirkungen von Fehlern auf Eigenwerte und Faktoren sollen 50*30*100*8 Zufallswerte, die innerhalb gewisser Grenzen um definierte wahre Werte schwanken, erzeugt werden. Die "wahren Werte" wurden im Basisversuch festgelegt.

    Die Versuche wurden auf einem Pentium 3, Betriebssystem Win98, auf dem die Atari Emulation MagiC PC von der Firma Applications Systems Heidelberg implementiert wurde, durchgeführt, und zwar mit dem von Jörn Wilms für die Statistik Library für Omikron.Basic programmierten normalverteilten Zufallsgenerator. [Zum Hintergrund] [Warum Atari u. Omikron.Basic].

    Wilms Zufallsgenerator erwartet bei der Parameterübergabe Mittelwert und Varianz. Da unsere "ProbandInnen" im Quaderversuch innerhalb fester Fehlergrenzen 1%, 2% ,..., 50% Werte produzieren sollen, habe ich ein kleines Programm geschrieben, das die Produktionsgüte der vom Zufallsgenerator erzeugten Zahlen um die wahren Werte prüft.

    Zur Prüfung, ob die Zufallswert-Produktionen im Rahmen der Erwartungen liegen, habe ich den Mittelwert über die N Versuche (hier 100), Minimum und Maximum erhoben. Für den 1%-Fehlerfall sollten sich die Werte, wenn 1 der wahre Wert und Mittelwert ist, im Bereich  zwischen 0.995 und 1,005 ergeben, also

    MIN >= .995  und MAX <= 1,005.

    Graphischer Zufallsgenerator-Test, N=100, Var3 aus Sig3




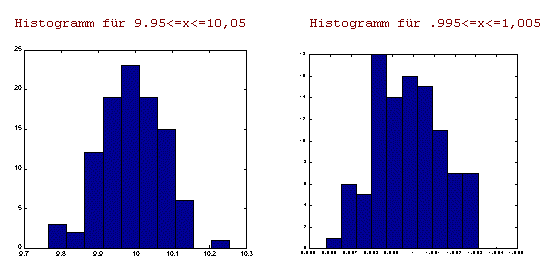
    Zufallsversuch vom 10/30/02 10:08:16 mit nv_rand.BAS vom 27.10.2002 zum Ueberpruefen in Datei C:\NIM\ZUFALL\Z1_100b.TXT
    Parameter Anzahl der Versuche = 100
    Parameter Fehlerspanne UG-OG  = 1%
    Parameter Mittelwert ........ = 1
    Parameter Sigma ............. = 0.005
    Parameter Sigma2 ............ = 0.0025
    Parameter Sigma3 ............ = 0.0016666666666666667

        Var aus Sig     Var2 aus Sig2     Var3 aus Sig3
        Sig=Mit*F/200   Sig2=Sig/2        Sig3=Sig/3

    Mit 1Sig=.9999     Mit 2Sig= .9996   Mit 3Sig= .9998
    Min =    .989      Min2=     .9926   Min3 =    .9958
    Max=    1.0107     Max2=    1.0049   Max3=    1.0031

     1    .9989            .9977            .9991
     2    .9909            .9992            .9997
     3   1.0008            .9987           1.0006
     4    .9992           1.0007            .9979
     5   1.0036           1.0007            .9999
     6    .9973           1.0013            .999
     7   1.0011            .9987            .9966
     8   1.0019           1.0011           1.0016
     9   1.0008           .9986             .9994
     10  1.0041           1.0046           1.0014
     11  1.0044           1.0003            .9996
     12  1.0107            .9971            .9982
     13   .9949            .9975            .9987
     14  1                 .996             .9969
     15   .9964            .998             .9991
     16  1.0039            .9992           1.0031
     17   .9932            .9978            .9974
     18   .9918            .9983            .9995
     19  1.0066           1.0003           1.0007
     20  1.0009           1.0007           1.0004
     21  1.0013            .9995            .9987
     22   .9946            .9942           1.0026
     23   .9933            .9969            .9968
     24   .9962            .9966            .9997
     25  1.0016           1.003            1.0013
     26  1.0008            .9976            .9984
     27  1.0018           1.0004            .9983
     28  1.0042            .9991           1.0002
     29  1.0019           1.0002            .9999
     30  1.0066            .9997            .9972
     31  1.005            1.0004            .9989
     32  1.0039            .9996           1.0029
     33   .9908           1.0012           1.001
     34   .9992           1.0007           1.0024
     35   .9919            .9973            .998
     36  1.0077            .9973           1.0001
     37   .9963            .9982            .9996
     38  1.0016            .9985           1.0002
     39   .9932           1.0043           1.0015
     40   .9983            .9984            .9958
     41   .9993           1.0015            .9998
     42  1.0012           1.002            1.0016
     43  1                 .9997            .9995
     44  1.0033           1.0007            .9986
     45   .9994           1.0027           1.0004
     46   .997            1.0004            .9972
     47  1.0039           1.0016           1.0006
     48  1.003             .9974            .9991
     49  1.0012           1.0024            .9991
     50  1.0019            .997             .9972
     51   .9988           1.0019           1.0011
     52   .9959            .9998           1.0009
     53   .992             .9983            .9999
     54  1.0095            .9937           1.0016
     55  1.0051            .9966            .9976
     56   .9991           1.0031            .9998
     57   .9979            .9971            .9984
     58  1.002             .9997            .9984
     59  1.001             .9952           1.0017
     60  1.0003            .9988           1.0018
     61   .9951           1.0009            .9997
     62  1.0067           1.0012           1.0023
     63   .9893           1.003             .9974
     64   .9977           1.001            1.0014
     65  1.0067           1.0021           1.0019
     66   .994            1.0049           1.0018
     67  1.0043            .999             .9984
     68  1.0048            .9976           1.0015
     69   .989            1.0014           1.0014
     70   .9981           1.0021            .9991
     71   .9994           1.0032            .9986
     72   .9988            .9966            .9999
     73   .9966            .9994           1.0009
     74  1.0061           1.0027            .9989
     75  1.0034            .9994            .9981
     76  1.0019           1.0048            .9996
     77  1.0073            .9982           1.0009
     78   .99             1.0014            .9976
     79  1.0023            .9972            .9992
     80   .9925           1.0002           1.0017
     81   .9996           1.0036            .9987
     82   .9982            .9996           1.0001
     83   .9955            .9986            .9989
     84   .9961           1.0018           1.0019
     85   .9986           1.0001            .9984
     86  1.0017            .9991            .9985
     87  1.0041            .9999           1.0031
     88  1.0025           1.0013           1.0008
     89  1.0013            .9926            .9982
     90   .9937           1.002             .9989
     91   .9999           1.0037           1.0005
     92  1.0015            .9943            .9993
     93  1.0014            .9978            .9992
     94  1.0021            .9993            .998
     95  1.0036            .9932           1.0005
     96  1.0103           1.0037           1.0026
     97  1.0012            .9996           1.0004
     98   .9946           1.0004            .9981
     99  1.0015            .9999           1.0008
     100  .9964            .998            1.0029

    Anmerkung: Spalte 1 wendet für die Varianz ein  Sigma, Spalte 2 zwei  Sigma und Spalte 3 drei 3 Sigma an.
     
    Ergebnis: Die gewünschten normalverteilt fehlerbehafteten Testwerte sind mit dem Zufallsgenerator von Wilms erzeugbar. Parameterübergabe: Mittelwert = Wahrer Wert = MWW, Var = (MWW * F/ 200)/3)^2. 


    Geschichte der numerisch-statistischen Versuche: Ich erhielt im Jahre 1984  (Dissertation) u.a. nach vollständiger Partialisierung einen Korrelationskoeffizienten der Größe 1.388, der nicht erklärbar war und damals auch nicht restolos aufgeklärt, nur richtig dokumentiert werden konnte. Langwieriges Suchen führte mich zur Numerik und dem numerisch-empirischen Studum indefiniter Matrizen, also letztlich zu Pseudo-Korrelationsmatrizen. In Zusammenarbeit mit dem Mathematiker Dr. B. Hain, Erlangen, konnten die Probleme der seltsamen numerischen und mathematischen Phänomene schließlich nach 11 Jahren weitgehend aufgeklärt werden und mündeten in ein Buch, in dem über 1000 phänotypische Korrelationsmatrizen untersucht wurden, wobei sich unter 769 angeblichen Korrelationsmatrizen 17,9% indefinite, also rund 138 mit negativen Eigenwerten fanden: Sponsel, Rudolf & Hain, Bernhard (1994). Numerisch instabile Matrizen und Kollinearität in der Psychologie. Diagnose, Relevanz & Utilität, Frequenz, Ätiologie, Therapie.  Ill-Conditioned Matrices and Collinearity in Psychology. Deutsch-Englisch. Übersetzt von Agnes Mehl. Kapitel 6 von Dr. Bernhard Hain: Bemerkungen über Korrelationsmatrizen. Erlangen: IEC-Verlag [ISSN-0944-5072  ISBN 3-923389-03-5]
    Aktueller Preis: https://ww.iec-verlag.de. Internet-Informationen zu diesem Projekt hier. Zur genaueren Hintergrundgeschichte hier.
    ___
    Atari und Omikron.Basic. Mitte der 80iger Jahre wurde mir das Geld knapp, um meine wissenschaftlichen Hobbies durch bezahlte Programmierer weiterhin so zu pflegen, so daß ich mich entschloß, selbst ein wenig das Programmieren zu lernen, was mir für die Denkpsychologie und zum Verständnis künstlicher Intelligenz auch sehr nützlich schien. Im Zuge der Matrixanalysen enstanden dann viele Programme in Omikron.Basic auf dem Atari. Als die Firma dann den Atari nicht weiter pflegte, entstand das Problem: erneut neu programmieren - und vor allem sehr zeitaufwendig und nervig alles erneut durchzutesten - oder den Atari und die Omikron.Basic Programme durch Emulation auf ein Windwos System zu retten? Ich entschied mich für die Emulation und bin bislang damit sehr gut gefahren. Programmieren, EDV und Computer sind für mich nur Werkzeuge, mehr nicht. Ich bin daher nicht motiviert, den Hauptteil meiner Zeit in immer neue Anpassungsarbeit zu investieren, damit Bill Gates & Co sich noch eine Milliarde mehr einverleiben, da ich sozusagen mit Leib und Seele Psychologe und Psychotherapeut bin. Ich beherrsche weder die angewandte Mathematik so wie ich mir das wünsche noch das Programmieren. Doch reichte es so weit, daß ich immerhin nicht abhängig von Statistikpaketen bin und viele wichtige und notwendige Kontrollen, Versuche und Entwicklungen selbst durchführen und daher auch ungewöhnlich und gut dokumentieren und kontrollieren kann, so daß meine eigene Arbeit ebenfalls sehr gut kontrollier- und kritisierbar ist, wie erst kürzlich beim Thurstone'schen [Biographie] Trapezversuch [1. Version *  berichtigte Version] offenbar wurde.
    ____
    Jörn Wilms hat auch die Numerik-Library für Omikron.Basic programmiert u.a. mit einem Eigenwertunterprogramm auf der Basis der Jacobirotation, das für unsere Matrixanalyse integriert wurde.

    Fußnoten
    1) GIPT= General and Integrative Psychotherapy, internationale Bezeichnung für Allgemeine und Integrative Psychotherapie.
     


    Änderungen - wird unregelmäßig überarbeitet, kleine Änderungen werden nicht extra dokumentiert
    29.04.06    Layout, Links.
    14.12.05    Zielmarken eingebaut.

    Querverweise
    Standort: Normalverteilte Zufallsfehler Versuche. Zwischenprüfungen, Hilfs- und Dokumentationsseite zum Quaderversuch.
    Überblick Statistik in der IP-GIPT. * Vorläufige Hauptergebnisse Quaderversuch *
    * Beweis und beweisen in Wissenschaft und Leben * Beweis und beweisen in Mathematik *
    Materialien zur Mathematik: Lexika, Wörterbücher, Glossare.
    Materialien zur Kontroverse um "das" Unendliche.
    Unendlich. Vorstellungen, Metaphern, Analogien, Begriffe, Kennzeichnungen, Definitionen.
    Cantor Diagonalverfahren I Probleme. Unklarheiten, Paradoxes, Widersprüchliches mit Zählen, Anzahlen und den Mächtigkeiten im Endlich-Unendlichen aus der Sicht eines mathematischen Laien.
    Wissenschaft in der IP-GIPT.
    *
    Suchen in der IP-GIPT, z.B. mit Hilfe von "google": <suchbegriff> site:www.sgipt.org
    z.B. Quaderversuch site:www.sgipt.org. * Faktorenanalyse site:www.sgipt.org
    *
    Dienstleistungs-Info.
    *
    Zitierung
    Sponsel, R.  (DAS). Normalverteilte Zufallsfehler Versuche. Zwischenprüfungen, Hilfs- und Dokumentationsseite zum Quaderversuch. Abteilung Arbeiten zur Definitionslehre, Methodologie, Meßproblematik, Statistik und Wissenschaftstheorie besonders in Psychologie, Psychotherapie und Psychotherapieforschung. Internet Publikation  für Allgemeine und Integrative Psychotherapie  IP-GIPT. Erlangen:  https://www.sgipt.org/wisms/mathe/zufall/nvzz01.htm
    Copyright & Nutzungsrechte
    Diese Seite darf von jeder/m in nicht-kommerziellen Verwertungen frei aber nur original bearbeitet und nicht  inhaltlich verändert und nur bei vollständiger Angabe der Zitierungs-Quelle benutzt werden. Das Einbinden in fremde Seiten oder Rahmen, die die Urheberschaft der IP-GIPT nicht jederzeit klar erkennen lassen, ist nicht gestattet. Sofern die Rechte anderer berührt sind, sind diese dort zu erkunden. Sollten wir die Rechte anderer unberechtigt genutzt haben, bitten wir um Mitteilung. Soweit es um (längere) Zitate aus  ...  geht, sind die Rechte bei/m ... zu erkunden oder eine Erlaubnis einzuholen.
    Ende  NVZZ-Versuche_Überblick_ Rel. Aktuelles _Rel. Beständiges_ Titelblatt_ Konzept_ Archiv_ Region_Service iec-verlag  _Mail: sekretariat@sgipt.org_ _Wichtiger Hinweis zu Links und Empfehlungen_