Original-Text Thurstone
"trapezoid
population
In previous studies of factorial theory it has been found
useful to illustrate the principles by means of a population of simple
physical objects or geometrical figures. The box population was used to
illustrate three correlated factors and their physical interpretation.
In the present case we want four factors in the first-order domain, which,
by their correlations of unit rank, determine a general second-order factor.
The correlations of three variables can nearly always be accounted for
by a single factor, and hence it seems better to choose a four-dimensional
system in which the existence of a second-order general factor is more
clearly indicated by the unit rank of the correlations of four primary
factors. For the present physical illustration we have chosen a population
of trapezoids whose shapes are determined by four primary parameters or
factors.
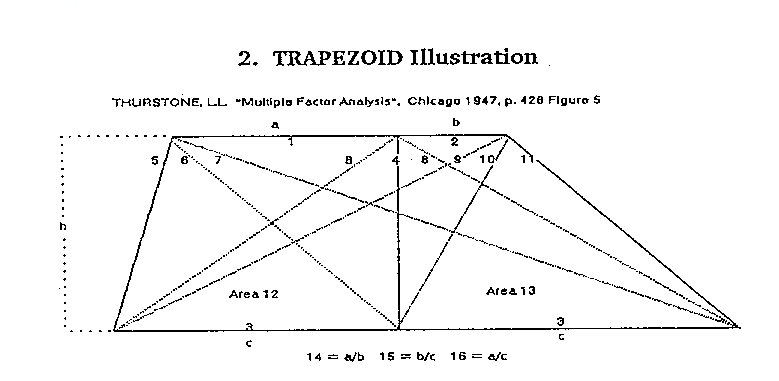
The measurements on the trapezoids are indicated in Figure
5. The base line is bisected, and the length of esch half is denoted by
the parameter c. An ordinate is erected at this mid-point, and its length
is h. This ordinate divides the top section into two parts, which are denoted
a and b as shown. These four parameters, a, b, c, and h, completely determine
the figure. The test battery was represented by sixteen measurements, wEich
are drawn in the figure. The parameters a, b, c, and h are given code numbers
1, 2, 3, and 4, respectively. Variables (12) and (13) are the two areas
as shown. The sum of (12) and (13) equals the total area of the trapezoid.
In general, each of these measurements is a function of two or three of
the parameters but not of all four of them, and hence we should expect
a simple structure in this [p. 428] set of measurements. There is a rather
general impression that a simple structure is necessarily confined to the
positive manifold. In order to offset this impression we included here
three additional measures, which extend the simple structure beyond the
positive manifold. These three additional measures are as follows:
14 = (1)/(2) = a/b, 15 = (2)/(3) = b/c, 16 = (1)/(3) = a/c .
These three measures will necessarily introduce negative
saturations on some of the basic factors.
In Table 6 we have a list of dimensions for a set of thirty-two
trapezoids. These will constitute the trapezoid population. Each figure
was drawn to
FIGURE 5
scale on cross-section paper, and then the sixteen measurements
were made on each figure. These constituted the test scores for the present
example. In setting up the dimensions of Table 6 the numbers were not distributed
entirely at random. To do so would tend to make the correlations between
the four basic parameters, a, b, c, and h, approach zero, and this would
lead to an orthogonal simple structure in which there would be no provocation
to investigate a second-order domain. The manner in which the generating
conditions of the objects determine the factorial results will be discussed
in a later section. Table 6 was so constructed that, in addition to the
four basic parameters, there was also a size factor, which functioned as
a second-order parameter in determining correlation between the four primary
factors in generating the figures.
The product-moment correlations between the sixteen measurements
for the thirty-two objects were computed, and these are listed in Table
7. This [p. 429] correlation matrix was factored by the group centroid
method, and the resulting factor matrix F is shown in Table 8. The fourth-factor
residuals are listed in Table 9, which indicates that the residuals are
vanishingly small." |
3.
Übersicht der Ergebnisse und bibliographische Hinweise
THURSTONE, L. L. (USA: University Of Chicago) "Multiple
Factor Analysis" Chicago 1947, p.427-436 "A trapezoid
population", p. 431 Table 7 'Correlation Matrix' a n d THURSTONE,
L. L. "SECOND-ORDER FACTORS" Psychometrika 9.2,1944, p.96 Table
7 Correlation Matrix. Bemerkung: Die Matrix enthält zwei Druckfehler:
r14,16 und r15,16 müssen positiv sein.
(1=12a) TH43116.K16 raw scores measured with 2-digit input
accuray read
Samp__Ord__MD__NumS__Condition__Determinant__HaInRatio__R_OutIn__K_Norm__C_Norm
32 16 0 --4
2992 6.36 D-21 1.43 D-13
79208 2D-3(9) -1(-1)
(2=12b) TH429R17.D16 raw scores are computed and not measured
with 17-digit-input-accuracy calculated and read
Samp__Ord__MD__NumS__Condition__Determinant__HaInRatio__R_OutIn__K_Norm__C_Norm
32 16 0 -
343457 1.08 D-29 8.94 D-30
16479 0(9) 6D-3(8)
(3=12c) TH429R4.D16 raw scores are computed and not measured
with 4-digit-input-accuracy read
Samp__Ord__MD__NumS__Condition__Determinant__HaInRatio__R_OutIn__K_Norm__C_Norm
32 16 0 --1
331205 -1.86 D-29 3.53 D-29 33770
0(9) -1(-1)
(4=12d) TH429R3.D16 raw scores are computed and not measured with
3-digit-input-accuracy read
Samp__Ord__MD__NumS__Condition__Determinant__HaInRatio__R_OutIn__K_Norm__C_Norm
32 16 0 --1
257081 -5.84 D-28 5.56 D-30 10090
0(9) -1(-1)
(5=12e) TH429R2.D16 raw scores are computed and not measured with
2-digit-input-accuracy read
Samp__Ord__MD__NumS__Condition__Determinant__HaInRatio__R_OutIn__K_Norm__C_Norm
32 16 0 --4
7450 4.83 D-22 6.20 D-16
16479 1D-3(9) -1(-1)
(6=12f) THPMF16.K16 raw scores measured with 2-digit input
accuray read
Samp__Ord__MD__NumS__Condition__Determinant__HaInRatio__R_OutIn__K_Norm__C_Norm
32 16 0 --4
3711 -3.67 D-20 3.12 D-23
347573 0(8) -1(-1)
4. Detail Analysen
(1)
values measured with 2-digit input accuray calculed
********** Summary of standard correlation
matrix analysis ***********File = TH431_16.K16 N-order=
16 N-sample= 32 Rank= 16 Missing data = 0
Positiv Definit=Cholesky successful________= No with
4 negative eigenvalue/s
HEVA: Highest eigenvalue abs.value_________= 10.288
LEVA: Lowest eigenvalue absolute value_____= 0.003438778
CON: Condition number HEVA/LEVA___________~= 2991.69
DET: Determinant original matrix___________= D-21 6.359
HAC: HADAMARD condition number_____________= D-27 1.481
HCN: Heuristic condition |DET|CON__________= D-24 2.125
D_I: Determinant Inverse absolute value____= 1.5724911329896272D+20
HDA: HADAMARD Inequation absolute value___<= 1.0988050960598554D+33
HIR: HADAMARD RATIO: D_I / HDA ____________= 1.4310919549138755D-13
Highest inverse positive diagonal value____= 60.001125634
thus multiple r( 7.rest)_________________= .99163181
and 1 multiple r > .99
Highest inverse negative diagonal value____= -1.762489944
thus multiple r( 12.rest)_________________= 1.251950128
(!)
and there are 5 multiple r > 1 (!)
Maximum range (upp-low) multip-r( 1.rest)_= .257
LES: Numerical stability analysis:
Maximum range input x(upper)-x(lower)____=
0.009
Maximum range output x(upper)-x(lower)____= 712.87197
Ratio maximum range output / input _______= D +4
7.9
Mean absolute value of ranges output _____= 335.51821
Ratio mean range output/ mean range input_= D +4
3.7
Sigma of mean (abs. value range output)___= 244.66269
Ncor L1-Norm L2-Norm Max
Min m|c| s|c|
Ncomp M-S S-S
256 156 10.79
1 -.84 .61
.527 120 .218 .244
class boundaries and distribution of the correlation-coefficients
-1 -.8 -.6 -.4 -.2 0
.2 .4 .6 .8 1
2 8 12
20 12 18 24 32
46 82
Original input data with 2-digit-accuracy and read with 2-digit-accuracy
(for control here the analysed original matrix):
1 .5 .5 .32
.29 .58 .72 .49 .58 .45 .31 .66
.53 .76 -.35 .11
.5 1 .5 .32
.36 .42 .57 .49 .74 .67 .33 .54
.64 -.16 -.14 -.23
.5 .5 1 .32
.52 .42 .88 .82 .9 .45 .3
.78 .75 .19 -.84 -.72
.32 .32 .32 1 .95
.96 .65 .8 .61 .91 .98 .78
.82 .12 -.22 -.15
.29 .36 .52 .95 1
.9 .75 .9 .75 .9 .94
.84 .89 .05 -.37 -.31
.58 .42 .42 .96 .9 1
.78 .83 .7 .92 .94 .86 .86
.34 -.29 -.09
.72 .57 .88 .65 .75 .78
1 .95 .95 .74 .64 .95 .91
.39 -.69 -.46
.49 .49 .82 .8 .9
.83 .95 1 .93 .83 .78 .94
.95 .19 -.64 -.52
.58 .74 .9 .61 .75 .7
.95 .93 1 .79 .6 .9
.93 .11 -.64 -.57
.45 .67 .45 .91 .9 .92
.74 .83 .79 1 .9 .83
.9 .01 -.22 -.21
.31 .33 .3 .98 .94 .94
.64 .78 .6 .9 1 .77
.8 .11 -.12 -.09
.66 .54 .78 .78 .84 .86
.95 .94 .9 .83 .77 1
.97 .34 -.59 -.39
.53 .64 .75 .82 .89 .86
.91 .95 .93 .9 .8 .97 1
.12 -.52 -.44
.76 -.16 .19 .12 .05 .34 .39
.19 .11 .01 .11 .34 .12 1
-.28 .34
-.35 -.14 -.84 -.22 -.37 -.29 -.69 -.64 -.64 -.22 -.12 -.59 -.52
-.28 1 .76
.11 -.23 -.72 -.15 -.31 -.09 -.46 -.52 -.57 -.21 -.09 -.39
-.44 .34 .76 1
i.Eigenvalue Cholesky i.Eigenvalue
Cholesky i.Eigenvalue Cholesky
1. 10.28775 1
2. 2.36742 .866
3. 1.89721 .8165
4. 1.12211 .92
5. .16865 .1697
6. .07716 -5.6D-3
7. .06717 -.5981
8. .01777 -1.5864 9.
.01327 -2.2646
10. 9.35D-3 -2.7013 11. 4.55D-3
-3.0387 12. 3.44D-3 -4.5821
13.-3.69D-3 -5.6998 14.-7.39D-3
-.4257 15.-.01038 -1.9947
16.-.01438 -1.8594
The matrix is not positive definit. Cholesky decomposition
is not successful (for detailed information Cholesky's diagonalvalues are
presented).
(2)
Values are computed and not measured with 17-digit-input-accuracy
& calculed
********** Summary of standard correlation matrix
analysis ***********
File = TH429R17.D16 N-order= 16 N-sample= 32
Rank= 16 Missing data = 0
Positiv Definit=Cholesky successful________= Yes with
0 negative eigenvalue/s
HEVA: Highest eigenvalue abs.value_________= 9.602
LEVA: Lowest eigenvalue absolute value_____= 0.000027957
CON: Condition number HEVA/LEVA___________~= 343456.58
DET: Determinant original matrix___________= D-29 1.084
HAC: HADAMARD condition number_____________= D-36 5.014
HCN: Heuristic condition |DET|CON__________= D-35 3.158
D_I: Determinant Inverse absolute value____= 9.2189364602807023D+28
HDA: HADAMARD Inequation absolute value___<= 1.0306084087129445D+58
HIR: HADAMARD RATIO: D_I / HDA ____________= 8.9451399603789321D-30
Highest inverse positive diagonal value____= 25362.029045018
thus multiple r( 9.rest)_________________= .999980285
and 15 multiple r > .99
There are no negative inverse diagonal values.
Maximum range (upp-low) multip-r( 11.rest)_= .361
LES: Numerical stability analysis:
Maximum range input x(upper)-x(lower)____=
0.009
Maximum range output x(upper)-x(lower)____= 148.30955
Ratio maximum range output / input _______= D +4
1.6
Mean absolute value of ranges output _____=
51.16785
Ratio mean range output/ mean range input_= 5685.31686
Sigma of mean (abs. value range output)___=
40.82624
Ncor L1-Norm L2-Norm Max
Min m|c| s|c|
Ncomp M-S S-S
256 146.9 10.26
1 -.83 .574
.523 120 .217 .238
class boundaries and distribution of the correlation-coefficients
-1 -.8 -.6 -.4 -.2 0
.2 .4 .6 .8 1
2 12 10
18 14 16 32 46
36 70
Original input data with 17-digit-accuracy and read 17-digit-accuracy
(for control here the analysed original matrix):
1 .5 .5 .316 .286
.583 .725 .5 .576 .456 .308 .598 .52 .729-.338 .095
.5 1 .5 .316 .361
.424 .572 .5 .736 .672 .313 .507 .609-.199-.123-.238
.5 .5 1 .316 .52
.424 .88 .816 .897 .456 .295 .948 .951 .166-.83 -.713
.316 .316 .316 1 .95 .953 .65
.798 .611 .913 .978 .255 .329 .105-.214-.15
.286 .361 .52 .95 1 .899 .749
.904 .743 .893 .936 .458 .537 .041-.368-.309
.583 .424 .424 .953 .899 1 .783 .837 .701
.922 .932 .402 .442 .318-.287-.099
.725 .572 .88 .65 .749 .783 1
.946 .949 .747 .629 .867 .872 .36 -.68 -.462
.5 .5 .816 .798 .904 .837 .946 1
.932 .833 .777 .766 .812 .166-.629-.521
.576 .736 .897 .611 .743 .701 .949 .932 1
.789 .589 .854 .911 .075-.634-.575
.456 .672 .456 .913 .893 .922 .747 .833 .789 1
.895 .411 .511-6D-3-.216-.217
.308 .313 .295 .978 .936 .932 .629 .777 .589 .895 1
.27 .342 .096-.115-.09
.598 .507 .948 .255 .458 .402 .867 .766 .854 .411 .27
1 .979 .268-.677-.518
.52 .609 .951 .329 .537 .442 .872 .812 .911 .511 .342
.979 1 .108-.642-.573
.729-.199 .166 .105 .041 .318 .36 .166 .075-6D-3 .096
.268 .108 1 -.275 .325
-.338-.123-.83 -.214-.368-.287-.68 -.629-.634-.216-.115-.677-.642-.275
1 .76
.095-.238-.713-.15 -.309-.099-.462-.521-.575-.217-.09 -.518-.573
.325 .76 1
i.Eigenvalue Cholesky i.Eigenvalue
Cholesky i.Eigenvalue Cholesky
1. 9.60228 1
2. 2.8399 .866
3. 1.87505 .8165
4. 1.18439 .922 5.
.37067 .164
6. .08016 .0535
7. .01835 .0597
8. .01318 .0158
9. 4.85D-3 .0257
10. 4.3D-3 .0343
11. 3.54D-3 .0976 12. 2.25D-3
.1358
13. 8.8D-4 .0328
14. 1.3D-4 .1588
15. 5D-5 .0986
16. 3D-5 .1014
Cholesky decomposition successful, thus the matrix is (semi)
positive definit.
(3)
Values are computed and not measured with 4-digit-input-accuracy calculed
********** Summary of standard correlation matrix
analysis ***********
File = TH429_R4.D16 N-order= 16 N-sample= 32
Rank= 16 Missing data = 0
Positiv Definit=Cholesky successful________= No with
1 negative eigenvalue/s
HEVA: Highest eigenvalue abs.value_________= 9.602
LEVA: Lowest eigenvalue absolute value_____= 0.000028991
CON: Condition number HEVA/LEVA___________~= 331204.46
DET: Determinant original matrix___________= D-29 -1.861
HAC: HADAMARD condition number_____________= D-36 8.607
HCN: Heuristic condition |DET|CON__________= D-35 5.621
D_I: Determinant Inverse absolute value____= 5.3710384638007393D+28
HDA: HADAMARD Inequation absolute value___<= 1.5207913243518122D+57
HIR: HADAMARD RATIO: D_I / HDA ____________= 3.5317392845398889D-29
Highest inverse positive diagonal value____= 3482.152767664
thus multiple r( 8.rest)_________________= .9998564
and 10 multiple r > .99
Highest inverse negative diagonal value____= -333.4295839
thus multiple r( 10.rest)_________________= 1.001498444
(!)
and there are 3 multiple r > 1 (!)
Maximum range (upp-low) multip-r( 11.rest)_= .151
LES: Numerical stability analysis:
Maximum range input x(upper)-x(lower)____=
0.009
Maximum range output x(upper)-x(lower)____= 303.93217
Ratio maximum range output / input _______= D +4
3.3
Mean absolute value of ranges output _____= 106.84911
Ratio mean range output/ mean range input_= D +4
1.1
Sigma of mean (abs. value range output)___=
96.49423
Ncor L1-Norm L2-Norm Max
Min m|c| s|c|
Ncomp M-S S-S
256 146.9 10.26
1 -.83 .574
.523 120 .217 .238
i.Eigenvalue Cholesky i.Eigenvalue Cholesky
i.Eigenvalue Cholesky
1. 9.60228 1
2. 2.83986 .866
3. 1.87503 .8165
4. 1.1844 .922
5. .3707 .1638
6. .08013 .054
7. .01836 .0611
8. .01321 .0165
9. 4.79D-3 .025
10. 4.31D-3 .029
11. 3.62D-3 -1.4D-3 12. 2.29D-3 -.0554
13. 8.6D-4 -1.0567 14. 1.1D-4
-.053 15. 9D-5
-.9549
16.-3D-5 -1.2285
The matrix is not positive definit. Cholesky decomposition
is not successful (for detailed information Cholesky's diagonalvalues are
presented).
(4)
Values are computed and not measured with 3-digit-input-accuracy read
********** Summary of standard correlation matrix
analysis ***********
File = TH429_R3.D16 N-order= 16 N-sample= 32
Rank= 16 Missing data = 0
Positiv Definit=Cholesky successful________= No with
1 negative eigenvalue/s
HEVA: Highest eigenvalue abs.value_________= 9.601
LEVA: Lowest eigenvalue absolute value_____= 0.000037347
CON: Condition number HEVA/LEVA___________~= 257080.91
DET: Determinant original matrix___________= D-28 -5.836
HAC: HADAMARD condition number_____________= D-34 2.701
HCN: Heuristic condition |DET|CON__________= D-33 2.270
D_I: Determinant Inverse absolute value____= 1.713470565278007D+27
HDA: HADAMARD Inequation absolute value___<= 3.0792420801426819D+56
HIR: HADAMARD RATIO: D_I / HDA ____________= 5.5645854423975996D-30
Highest inverse positive diagonal value____= 6139.822157645
thus multiple r( 6.rest)_________________= .999918561
and 15 multiple r > .99
There are no negative inverse diagonal values.
Maximum range (upp-low) multip-r( 4.rest)_= .277
LES: Numerical stability analysis:
Maximum range input x(upper)-x(lower)____=
0.009
Maximum range output x(upper)-x(lower)____=
90.81287
Ratio maximum range output / input _______= D +4
1.0
Mean absolute value of ranges output _____=
30.84446
Ratio mean range output/ mean range input_= 3427.16331
Sigma of mean (abs. value range output)___=
22.03785
Ncor L1-Norm L2-Norm Max
Min æ|c| å|c|
Ncomp æ-S å-S
256 146.9 10.26
1 -.83 .574
.523 120 .217 .238
i.Eigenvalue Cholesky i.Eigenvalue
Cholesky i.Eigenvalue Cholesky
1. 9.60145 1
2. 2.83953 .866
3. 1.87509 .8165
4. 1.18407 .9221
5. .36997 .1627
6. .08079 .059
7. .01866 .0585
8. .01319 .0273
9. 5.15D-3 .0257
10. 4.74D-3 -2D-3 11.
3.54D-3 -.7772 12. 2.37D-3 -.2299
13. 1.45D-3 -1.3261 14. 3.3D-4
-.0537 15. 4D-5 -.927
16.-3.6D-4 -1.2721
The matrix is not positive definit. Cholesky decomposition
is not successful (for detailed information Cholesky's diagonalvalues are
presented).
(5)
Values are computed and not measured with 2-digit-input-accuracy read
********** Summary of standard correlation matrix
analysis ***********
File = TH429_R2.D16 N-order= 16 N-sample= 32
Rank= 14 Missing data = 0
Positiv Definit=Cholesky successful________= No with
4 negative eigenvalue/s
HEVA: Highest eigenvalue abs.value_________= 9.605
LEVA: Lowest eigenvalue absolute value_____= 0.001289180
CON: Condition number HEVA/LEVA___________~= 7450.29
DET: Determinant original matrix___________= D-22 4.835
HAC: HADAMARD condition number_____________= D-28 2.224
HCN: Heuristic condition |DET|CON__________= D-26 6.490
D_I: Determinant Inverse absolute value____= 2.0679229830898941D+21
HDA: HADAMARD Inequation absolute value___<= 3.3333973491181176D+36
HIR: HADAMARD RATIO: D_I / HDA ____________= 6.2036498098163515D-16
Highest inverse positive diagonal value____= 177.548875466
thus multiple r( 10.rest)_________________= .997179898
and 4 multiple r > .99
Highest inverse negative diagonal value____= -13.074879701
thus multiple r( 15.rest)_________________= 1.037536765
(!)
and there are 8 multiple r > 1 (!)
Maximum range (upp-low) multip-r( 11.rest)_= .361
LES: Numerical stability analysis:
Maximum range input x(upper)-x(lower)____=
0.009
Maximum range output x(upper)-x(lower)____= 148.30955
Ratio maximum range output / input _______= D +4
1.6
Mean absolute value of ranges output _____=
51.16785
Ratio mean range output/ mean range input_= 5685.31686
Sigma of mean (abs. value range output)___=
40.82624
Ncor L1-Norm L2-Norm Max
Min m|c| s|c|
Ncomp M-S S-S
256 147 10.27
1 -.83 .574
.523 120 .217 .239
i.Eigenvalue Cholesky i.Eigenvalue
Cholesky i.Eigenvalue Cholesky
1. 9.60477 1
2. 2.83809 .866
3. 1.87558 .8165
4. 1.18944 .92
5. .37127 .1697
6. .07919 .1099
7. .02196 .0399
8. .01767 -.0188
9. .01135 -.8712
10. 9.08D-3 -1.3064 11. 5.23D-3
-1.7335 12. 1.98D-3 -1.5587
13.-1.29D-3 -2.8004 14.-6.35D-3
-.1904 15.-8.22D-3 -1.721
16.-9.73D-3 -1.8826
The matrix is not positive definit. Cholesky decomposition
is not successful (for detailed information Cholesky's diagonalvalues are
presented).
(6)
Values measured with 2-digit input accuracy read
********** Summary of standard correlation matrix
analysis ***********
File = THPMF16.K16 N-order= 16 N-sample= 32
Rank= 16 Missing data = 0
Positiv Definit=Cholesky successful________= No with
4 negative eigenvalue/s
HEVA: Highest eigenvalue abs.value_________= 10.261
LEVA: Lowest eigenvalue absolute value_____= 0.002764723
CON: Condition number HEVA/LEVA___________~= 3711.28
DET: Determinant original matrix___________= D-20 -3.670
HAC: HADAMARD condition number_____________= D-27 8.551
HCN: Heuristic condition |DET|CON__________= D-24 9.890
D_I: Determinant Inverse absolute value____= 2.7243326243127375D+19
HDA: HADAMARD Inequation absolute value___<= 8.7270894616169875D+41
HIR: HADAMARD RATIO: D_I / HDA ____________= 3.1216966851259516D-23
Highest inverse positive diagonal value____= 637.130010907
thus multiple r( 6.rest)_________________= .999214923
and 10 multiple r > .99
Highest inverse negative diagonal value____= -9.745219835
thus multiple r( 12.rest)_________________= 1.05005448
(!)
and there are 2 multiple r > 1 (!)
Maximum range (upp-low) multip-r( 15.rest)_= .454
LES: Numerical stability analysis:
Maximum range input x(upper)-x(lower)____=
0.009
Maximum range output x(upper)-x(lower)____= 3128.15835
Ratio maximum range output / input _______= D +5
3.4
Mean absolute value of ranges output _____= 1118.18184
Ratio mean range output/ mean range input_= D +5
1.2
Sigma of mean (abs. value range output)___= 984.60139
Ncor L1-Norm L2-Norm Max
Min m|c| s|c|
Ncomp M-S S-S
256 156 10.79
1 -.84 .61
.537 120 .218 .244
class boundaries and distribution of the correlation-coefficients
-1 -.8 -.6 -.4 -.2 0
.2 .4 .6 .8 1
2 9 12
21 12 18 23 32
45 82
REMARK: The table contents two print errors (r14,16 and r15,16 have
to be positive)
Original input data with 2-digit-accuracy and read with 2-digit-accuracy
(for control here the analysed original matrix):
1 .5 .5 .32
.29 .58 .72 .49 .58 .45 .31 .66
.53 .76 -.35 .11
.5 1 .5 .32
.36 .42 .57 .49 .74 .67 .33 .54
.64 -.16 -.14 -.23
.5 .5 1 .32
.52 .42 .88 .82 .9 .45 .3
.78 .75 .19 -.84 -.72
.32 .32 .32 1 .95
.96 .65 .8 .61 .91 .98 .78
.82 .12 -.22 -.15
.29 .36 .52 .95 1
.9 .75 .9 .75 .9 .94
.84 .89 .05 -.37 -.31
.58 .42 .42 .96 .9 1
.78 .83 .7 .92 .94 .86 .86
.34 -.29 -.09
.72 .57 .88 .65 .75 .78
1 .95 .95 .74 .64 .95 .91
.39 -.69 -.46
.49 .49 .82 .8 .9
.83 .95 1 .93 .83 .78 .94
.95 .19 -.64 -.52
.58 .74 .9 .61 .75 .7
.95 .93 1 .79 .6 .9
.93 .11 -.64 -.57
.45 .67 .45 .91 .9 .92
.74 .83 .79 1 .9 .83
.9 .01 -.22 -.21
.31 .33 .3 .98 .94 .94
.64 .78 .6 .9 1 .77
.8 .11 -.12 -.09
.66 .54 .78 .78 .84 .86
.95 .94 .9 .83 .77 1
.97 .34 -.59 -.39
.53 .64 .75 .82 .89 .86
.91 .95 .93 .9 .8 .97 1
.12 -.52 -.44
.76 -.16 .19 .12 .05 .34 .39
.19 .11 .01 .11 .34 .12 1
-.28 -.34
-.35 -.14 -.84 -.22 -.37 -.29 -.69 -.64 -.64 -.22 -.12 -.59 -.52
-.28 1 -.76
.11 -.23 -.72 -.15 -.31 -.09 -.46 -.52 -.57 -.21 -.09 -.39
-.44 .34 .76 1
i.Eigenvalue Cholesky i.Eigenvalue
Cholesky i.Eigenvalue Cholesky
1. 10.26065 1
2. 2.17133 .866
3. 1.75624 .8165
4. 1.0651 .92
5. .88599 .1697
6. .07148 -5.6D-3
7. .0514 -.5981
8. .02466 -1.5864 9.
.014 -2.2646
10. 9.28D-3 -2.7013 11. 5.2D-3
-3.0387 12. 2.76D-3 -4.5821
13.-4.57D-3 -5.6998 14.-8.45D-3
-.4257 15.-.01274 -1.9947
16.-.22922 -1.8594
The matrix is not positive definit. Cholesky decomposition
is not successful (for detailed information Cholesky's diagonalvalues are
presented).
5.
Überblick der berechneten Trapezoid-Parameter
Hinweis 23.10.2002: Parameterberechnung für 12 und 13 wurde falsch
interpretiert. Der Fehler hat aber glücklicherwiese keinerlei
Auswirkungen auf die grundlegenden Aussagen oder Interpretationen. Die
korrigierte Version finden Sie hier.
Thurstone's trapezoid raw scores with 3-digit-accuracy for view:
1 2 1 2 2 2.24 2.83 2.24
3.61 2.83 2.24 1 2
.5 2 1
1 2 1 4 4 4.12 4.47 4.12
5 4.47 4.12 1 3
.5 2 1
1 2 3 2 2.83 2.24 4.47 3.61 5.39
2.83 2.24 7 8 .5
.67 .33
1 2 3 4 4.47 4.12 5.66 5
6.4 4.47 4.12 5 7
.5 .67 .33
1 3 1 2 2 2.24 2.83 2.24
4.47 3.61 2.83 1 3
.33 3 1
1 3 1 4 4 4.12 4.47 4.12
5.66 5 4.47 1 5
.33 3 1
1 3 3 2 2.83 2.24 4.47 3.61 6.32
3.61 2 7 9
.33 1 .33
1 3 3 4 4.47 4.12 5.66 5
7.21 5 4 5
9 .33 1 .33
2 2 1 2 2.24 2.83 3.61 2.24 3.61
2.83 2.24 2 2 1
2 2
2 2 1 4 4.12 4.47 5 4.12
5 4.47 4.12 3 3
1 2 2
2 2 3 2 2.24 2.83 5.39 3.61 5.39
2.83 2.24 8 8 1
.67 .67
2 2 3 4 4.12 4.47 6.4 5
6.4 4.47 4.12 7 7
1 .67 .67
2 3 1 2 2.24 2.83 3.61 2.24 4.47
3.61 2.83 2 3 .67
3 2
2 3 1 4 4.12 4.47 5 4.12
5.66 5 4.47 3 5
.67 3 2
2 3 3 2 2.24 2.83 5.39 3.61 6.32
3.61 2 8 9
.67 1 .67
2 3 3 4 4.12 4.47 6.4 5
7.21 5 4 7
9 .67 1 .67
2 3 3 3 3.16 3.61 5.83 4.24 6.71
4.24 3 7.5 9 .67
1 .67
2 3 3 5 5.1 5.39 7.07 5.83 7.81
5.83 5 6.5 9 .67
1 .67
2 3 5 3 4.24 3.61 7.62 5.83 8.54
4.24 3.61 20.5 22 .67 .6
.4
2 3 5 5 5.83 5.39 8.6 7.07 9.43
5.83 5.39 17.5 20 .67 .6
.4
2 4 3 3 3.16 3.61 5.83 4.24 7.62
5 3.16 7.5 10.5 .5
1.33 .67
2 4 3 5 5.1 5.39 7.07 5.83 8.6
6.4 5.1 6.5 11.5 .5 1.33
.67
2 4 5 3 4.24 3.61 7.62 5.83 9.49
5 3.16 20.5 23.5 .5 .8
.4
2 4 5 5 5.83 5.39 8.6 7.07 10.3
6.4 5.1 17.5 22.5 .5 .8
.4
3 3 3 3 3 4.24 6.71 4.24
6.71 4.24 3 9 9
1 1 1
3 3 3 5 5 5.83 7.81 5.83
7.81 5.83 5 9 9
1 1 1
3 3 5 3 3.61 4.24 8.54 5.83 8.54
4.24 3.61 22 22 1
.6 .6
3 3 5 5 5.39 5.83 9.43 7.07 9.43
5.83 5.39 20 20 1
.6 .6
3 4 3 3 3 4.24 6.71 4.24
7.62 5 3.16 9 10.5
.75 1.33 1
3 4 3 5 5 5.83 7.81 5.83
8.6 6.4 5.1 9 11.5
.75 1.33 1
3 4 5 3 3.61 4.24 8.54 5.83 9.49
5 3.16 22 23.5 .75
.8 .6
3 4 5 5 5.39 5.83 9.43 7.07 10.3
6.4 5.1 20 22.5 .75 .8
.6
6.
OMIKRON-Basic-Programm zur Berechnung der Parameter des THURSTONEschen
Trapezoids
Hinweis 23.10.2002: Parameterberechnung für 12 und 13 wurde falsch
interpretiert. Der Fehler hat aber glücklicherwiese keinerlei
Auswirkungen auf die grundlegenden Aussagen oder Interpretationen. Die
korrigierte Version finden Sie hier.
REM TRAPEZ.BAS (THURSTONE's trapezoid)
' 20.11.93 R.Sponsel D-91052 Erlangen
COMPILER "TRACE ON"
DEFDBL "X"
S=16:Z=32: DIM Xd#(S,Z)
OPEN "I",1,"C:\OMI\NUMERIK\MATRIX\URDAT\THURS\TH429_4.N32"
FOR I=1 TO 4'
trapezoid parameter a,b,c,h read
FOR J=1 TO Z
INPUT #1,Xd#(I,J)
NEXT J
NEXT I: CLOSE 1
OPEN "O",1,"C:\OMI\NUMERIK\MATRIX\URDAT\THURS\TH429_32.N16"
OPEN "O",2,"C:\OMI\NUMERIK\MATRIX\URDAT\THURS\TH429_32.TAB"
FOR I=5 TO S
FOR J=1 TO Z
A#=Xd#(1,J):B#=Xd#(2,J):C#=Xd#(3,J):H#=Xd#(4,J)
IF I=5 THEN Xd#(I,J)= SQR((C#-A#)^2+H#^2)
IF I=6 THEN Xd#(I,J)= SQR(A#^2+H#^2)
IF I=7 THEN Xd#(I,J)= SQR((A#+C#)^2+H#^2)
IF I=8 THEN Xd#(I,J)= SQR(C#^2+H#^2)
IF I=9 THEN Xd#(I,J)= SQR((C#+B#)^2+H#^2)
IF I=10 THEN Xd#(I,J)= SQR(B#^2+H#^2)
IF I=11 THEN Xd#(I,J)= SQR((C#-B#)^2+H#^2)
IF I=12 THEN Xd#(I,J)=C#*H#-(C#-A#)*H#/2
IF I=13 THEN Xd#(I,J)=C#*H#-(C#-B#)*H#/2
IF I=14 THEN Xd#(I,J)=A#/B#
IF I=15 THEN Xd#(I,J)=B#/C#
IF I=16 THEN Xd#(I,J)=A#/C#
NEXT J
NEXT I
FOR I=1 TO S
FOR J=1 TO Z
PRINT #1,Xd#(I,J)
NEXT J
NEXT I: CLOSE 1
PRINT #2,"Thurstone's trapezoid raw scores with 3-digit-accuracy
for view:"
FOR I=1 TO Z
FOR J=1 TO S
PRINT #2, TAB (7*(J-1)); INT(Xd#(J,I)*10^2+.5)/10^2;
NEXT J: PRINT #2
NEXT I
CLOSE 2
END
Querverweise:
Wird im Laufe der Zeit fortgesetzt, ergänzt und erweitert
FN01
Sponsel, Rudolf & Hain, Bernhard (1994). Numerisch instabile Matrizen
und Kollinearität in der Psychologie. Diagnose, Relevanz & Utilität,
Frequenz, Ätiologie, Therapie. Ill-Conditioned Matrices and
Collinearity in Psychology. Deutsch-Englisch. Übersetzt von Agnes
Mehl. Kapitel 6 von Dr. Bernhard Hain: Bemerkungen über Korrelationsmatrizen.
Erlangen: IEC-Verlag [ISSN-0944-5072 ISBN 3-923389-03-5]. Aktueller
Preis:
www.iec-verlag.de
Zitierung
Sponsel, Rudolf (DAS).
Dokumentation
Rundungsfehler & Kollinearität am THURSTONEschen
Trapezoid- Beispiel. Abteilung: Numerisch instabile Matrizen und Kollinearität
in der Psychologie - Ill-Conditioned Matrices and Collinearity in Psychology
- Diagnose, Relevanz & Utilität, Frequenz, Ätiologie,
Therapie. IP-GIPT. Erlangen: https://www.sgipt.org/wisms/nis/k7/K7_3.htm
Copyright & Nutzungsrechte
Diese Seite darf von jeder/m in nicht-kommerziellen
Verwertungen frei aber nur original bearbeitet und nicht inhaltlich
verändert und nur bei vollständiger Angabe der Zitierungs-Quelle
benutzt werden. Das direkte, zugriffsaneignende Einbinden in fremde Seiten
oder Rahmen ist nicht gestattet. Zitate und Links sind natürlich erwünscht.
Sofern die Rechte anderer berührt sind, sind diese dort zu erkunden.
Sollten wir die Rechte anderer unberechtigt genutzt haben, bitten wir um
Mitteilung. Soweit es um (längere) Zitate aus ... geht,
sind die Rechte bei/m ... zu erkunden oder eine Erlaubnis einzuholen.
Ende_
Trapezoid
(7.3) _Überblick
_ Relativ
Aktuelles _ Rel.
Beständiges _ Titelblatt
_ Konzept
_ Archiv
_ Region
_ Service
iec-verlag _ Mail:
_ Sekretariat@sgipt.org
_ _
Änderungen
wird fortlaufend überarbeitet, ergänzt und vertieft *
Anregungen und Kritik willkommen
14.05.2015 Linkfehler geprüft und korrigiert,
Layout-Anpassung.