Polya zur Organisation seines Werks
Aus dem Vorwort ergibt sich zur Orientierung die Organisation des zweibändigen Werkes, wobei der 2. Bd. die Fortsetzung des 1. Bds. ist. Die 2. Auflage 1969 des 1. Bandes ist nur ein Nachdruck der 1. Auflage von 1962:
 

"5. Diese Arbeit über Mathematik und ₂₆plausibles Schließen, die ich immer als Einheit angesehen habe, zerfällt auf natürliche Weise in zwei Teile: Induktion und Analogie in der Mathematik (Band I) und Typen und Strukturen ₂₇plausibler Folgerung (Band II). Im Interesse des Lesers erscheinen diese Teile in zwei getrennten Bänden. Band I ist unabhängig von Band II, aber ich glaube, die meisten Leser sollten diesen ersten Band erst sorgfältig durchsehen, ehe sie an den zweiten herangehen. Der erste Band enthält hauptsächlich die mathematische Substanz des Werkes und liefert Daten für die induktive Untersuchung der Induktion im zweiten Band." (S.15)

Auswertungsmethode
Gemäß der Empfehlung Polyas habe ich mir zunächst den ersten Band vorgenommen und systematisch nach dem Suchtext "plausib" durchsucht. Der Suchtext "plausib" wird 91 mal gefunden. In den Titelseiten 2x, im Inhaltsverzeichnis 1x, in den Kopfzeilen 27x S. 284-310, Titel Kapitel XV 1x,  in der Bibliographie 3x, ergibt 34, so dass 91-34 = 57 textliche Fundstellen bleiben, in denen der Plausibilitätsbegriff erklärt, begründet oder gar definiert sein könnte. Zur leichteren Bezugnahme und Verständigung habe ich jede Fundstelle von 1,2,...57  indiziert.

Inhaltliche Ergebnisse der Auswertung des 1. Bandes
Nachdem die Zusammenfassung natürlich auf den einzelnen Fundstellen beruht, sind Wiederholungen unvermeidlich, wofür ich um Verständnis bitte.

• Nach Polya gibt es keine Theorie plausiblen Schließens (Fundstelle 6) und daher auch keine allgemein Definition. Die Normen für plausibles Schließen seien fließend (Fundstelle 5). Die Anwendung plausiblen Schließen sei eine Kunstfertigkeit (Fundstelle 15), die man durch Beispiele bzw. Gegenbeispiele, Nachahmung und Übung erlernen muss, also praktisch mit Durcharbeiten beider Bände, vor allem des ersten, wie S. 15 ausführt.
• Es gibt nach Polya absolut sicheres Wissen, das mit demonstrativem Schließen operiert, in Mathematik und Logik, wobei Polya die Logik als Teil der Mathematik ansieht. Alles Nicht-Mathematisch-Logische, genauer alles Empirische muss sich nach Polya mit Vermutungen begnügen für die das plausible Schließen zuständig ist. Nach Polya ist damit ein wichtiges Kriterium für Plausibilität die Unsicherheit.
• Alles Empirische gehört nach Polya zum plausiblen Schließen. Damit sind die beiden Pole des Schließens sehr allgemein und sehr weit (un)bestimmt. Vergegenwärtigt man sich den  Grundlagenstreit der Mathematik  erscheint sehr fraglich, ob die Auffassung Polyas "sicher, unbestreitbar und endgültig" wirklich für das demonstrative Schließen in Mathematik und Logik gilt. Jeder Beweis beruht auf Voraussetzungen und gilt auch nur relativ zu diesen. So betrachtet gibt es womöglich keinen grundsätzlichen Unterschied zwischen mathematischem und nicht-mathematischem  Beweis, was der mainstream der Wissenschaftler- und insbesondere der MathematikerInnen allerdings anders sieht.
• In Polya1962-1-S.283 wird eine wichtige Grundidee zur Plausibilität formuliert, das es nämlich Argumente für und gegen eine Vermutung gibt (wie in meiner Plausibilitätsformel).
• In Polya1962-1-S.295f (47 bis 52) spielen Gründe eine ganz zentrale Rolle (wie in meinem Definitionsvorschlag zur Plausibilität).

Gesamtergebnis 1. Band: Der Plausibilitätsbegriff bleibt ungeklärt.
Im gesamten 1. Band wird in allen 57 Fundstellen weder der Plausibilitätsbegriff noch plausibles Schließen erklärt. Was Plausibilität bei Polya bedeutet ist durch Nachahmung und Übung seiner Beispiele, sozusagen learning by doing im wahrsten Sinne des Wortes herauszufinden, wie sich aus dem Vorwort plausibel ;-) ergibt. Das bestätigt auch die Schlussbemerkung Polya1962-1-S.311-55:
 

"Der Leser, welcher sich der Lektüre der vorstehenden Kapitel unterzogen und einige der vorstehenden Aufgaben selbst bearbeitet hat, hatte gute Gelegenheit, gewisse Aspekte plausiblen Schließens kennenzulernen. Es ist das Ziel der verbleibenden fünf Kapitel dieses Werks, die in Band II zusammengestellt sind, einen allgemeinen Begriff von der Natur ₅₅plausiblen Schließens zu geben."

Ende der Zusammenfassung Polya 1. Bd.

Zur besseren Einordnung der Fundstellen habe ich die Inhaltsverzeichnisse sozusagen als Kontextrahmen der entsprechenden Kapitel beigegeben. Manche enthalten gar keine Fundstellen (II, IV, V, VI), was aber auch interessant sein kann. Es werden sämtliche Erwähnungen erfasst und auf ihren Gehalt hin untersucht. Die Fundstellen werden fortlaufend numeriert und links am Begriff indiziert. Wichtiger objekt- oder metasprachliche Ausdrücke werden rechts am Begriff indiziert. So bedeutet

        Vorwort
 

    Polya1962-1-Vorwort-S9-1,2,3: "1. Streng genommen besteht unser ganzes Wissen außerhalb der Mathematik und der demonstrativen Logik (die ja in der Tat ein Zweig der Mathematik ist) aus Vermutungen. Es gibt natürlich Vermutungen und Vermutungen. Es gibt höchst respektable und zuverlässige Vermutungen wie die in gewissen allgemeinen Gesetzen der Naturwissenschaften niedergelegten. Es gibt andere Vermutungen, die weder respektabel noch zuverlässig sind, und die einen zuweilen ärgern können, wenn man sie in der Zeitung liest. Und zwischen diesen beiden Extremen stehen alle möglichen Arten und Schattierungen von Vermuten, instinktivem Vorausfühlen und Erraten.
Wir sichern die Gültigkeit unseres mathematischen Wissens durch demonstratives Schließen, aber wir stützen unsere Vermutungen durch ₁plausibles Schließen, Ein mathematischer Beweis besteht aus demonstrativem Schließen, aber der Induktionsbeweis des Physikers, der Indizienbeweis des Juristen, der dokumentarische Beweis des Historikers, der statistische Beweis des Nationalökonomen gehören zum ₂plausiblen Schließen. Der Unterschied zwischen den beiden Schlußweisen ist groß und mannigfaltig. Demonstratives Schließen ist sicher, unbestreitbar und endgültig. ₃Plausibles Schließen ist gewagt, strittig und provisorisch."
 

Kommentar-Polya1962-1-Vorwort-S9-1,2,3:  Bei den ersten drei Erwähnungen "plausiblen Schließens" erfahren wir nicht, was darunter zu verstehen ist, nur, dass es "gewagt, strittig und provisorisch" sein soll, womit allerdings drei (metasprachliche) Polya-Kriterien für Plausibilität genannt sind. Angemerkt sei, dass Polya das Thema Objekt- und Metasprache im 1. und auch im 2. Band nicht behandelt (keine Fundstelle für "Objektsprache" oder "Metasprache". Alles Empirische gehört nach Polya zum unsicheren plausiblen Schließen. Damit sind die beiden Pole des Schließens sehr allgemein und sehr weit (un)bestimmt. Vergegenwärtigt man sich jedoch den  Grundlagenstreit der Mathematik  erscheint sehr fraglich, ob die Auffassung Polyas "sicher, unbestreitbar und endgültig" wirklich für das demonstrative Schließen in Mathematik und Logik gilt. Jeder Beweis beruht auf Voraussetzungen und gilt auch nur relativ zu diesen. So betrachtet gibt es womöglich keinen grundsätzlichen Unterschied zwischen mathematischem und nicht-mathematischem  Beweis, was der mathematische und wissenschaftliche mainstream anders sieht. Anmerkung Sprachstufen. Ein Schluss ist kein Sachverhalt der Wirklichkeit, sondern eine Konstruktion des menschlichen Geistes und ein logischer Ausdruck mindestens der Metastufe 1. Spricht man über die Qualität oder Güte eines Schlusses, befindet man sich mindestens auf Metastufe 2. Ein plausibler Schluss ist auf der gleichen metasprachlichen Ebene wie ein demonstrativer Schluss. Sie gehören unterschiedlichen Kategorien der gleichen Ebene an. Eine interessante Frage ist die Beziehung zwischen logischen Schlüssen und ihrer Bedeutung für die Wirklichkeit.

    Polya1962-1-Vorwort-S10f-4 bis 6: "... Was immer wir Neues über die Welt erfahren, involviert ₄plausibles Schließen, die einzige Art des Schließens, die uns im Alltag interessiert. Demonstratives Schließen hat starre, von der Logik (der demonstrativen oder formalen Logik), welche ja die Theorie des demonstrativen Schließens ist, niedergelegte und erläuterte Normen. Die Normen des ₅plausiblen Schließens sind fließend, und es gibt keine Theorie des ₆plausiblen Schließens, die sich an Klarheit mit der demonstrativen Logik vergleichen läßt oder in ähnlichem Maß auf ungeteilte Zustimmung Anspruch erheben kann.
 

Kommentar-Polya1962-1-Vorwort-S10f-4 bis 6: Bei den Erwähnungen  "plausiblen Schließens"  4, 5, 6 erfahren wir nicht, was darunter zu verstehen ist, nur dass die Grenzen fließend sind und es nach Polya keine der Klarheit der Logik vergleichbare Theorie des plausiblen Schließens gibt.Wie kann er das alles wissen, wo er doch gar nicht weiß, was plausiblen Schließen ist.  Bisheriger Stand: von 1-6 keine Erklärung zur Plausibilität und zum plausiblen Schließen.

    2. Ein weiterer, die beiden Schlußweisen betreffender Punkt verdient unsere Aufmerksamkeit. Jeder weiß, daß die Mathematik eine ausgezeichnete Gelegenheit bietet, um demonstratives Schließen zu lernen, aber ich behaupte, daß es in den üblichen Schullehrplänen keinen Gegenstand gibt, der eine auch nur annähernd so gute Gelegenheit gewährt, um ₇plausibles Schließen zu lernen. Ich wende mich an alle, die sich für die Mathematik interessieren, ganz gleich auf welcher Stufe, und ich sage: Gewiß, laßt uns beweisen lernen, laßt uns aber auch erraten lernen. Dies klingt etwas paradox, und ich muß einige Punkte erwähnen, um etwaigen Mißverständnissen vorzubeugen.
    Die Mathematik wird als demonstrative Wissenschaft angesehen. Doch ist das nur einer ihrer Aspekte. Die fertige Mathematik, in fertiger Form dargestellt, erscheint als rein demonstrativ. Sie besteht nur aus Beweisen. Aber die im Entstehen begriffene Mathematik gleicht jeder anderen Art menschlichen Wissens, das im Entstehen ist. Man muß einen mathematischen Satz erraten, ehe man ihn beweist; man muß die Idee eines Beweises erraten, ehe man die Details ausführt. Man muß Beobachtungen kombinieren und Analogien verfolgen; man muß immer und immer wieder probieren. Das Resultat der schöpferischen Tätigkeit des Mathematikers ist demonstratives Schließen, ist ein Beweis; aber entdeckt wird der Beweis durch ₈plausibles Schließen, durch Erraten. Wenn das Erlernen der Mathematik einigermaßen ihre Erfindung widerspiegeln soll, so muß es einen Platz für Erraten, für ₉plausibles Schließen haben.
 

Kommentar-Polya1962-1-Vorwort-S10f-7 bis 9: Bei den Erwähnungen  "plausiblen Schließens"  7 und 8 erfahren wir nicht, was darunter zu verstehen ist; kein Beweis, aber anscheinend eine wichtige Vorstufe zum Beweis.  Bisheriger Stand: von 1-9 keine Erklärung zur Plausibilität und zum plausiblen Schließen.

    Wie wir sagten, gibt es zwei Arten des Schließens, demonstratives Schließen und ₁₀plausibles Schließen. Ich möchte bemerken, daß sich ]>11] die beiden nicht widersprechen; im Gegenteil, sie ergänzen sich. Im strengen Schließen ist es Hauptsache, Beweis von Vermutung zu unterscheiden, eine gültige Beweisführung von einem ungültigen Versuch. Im ₁₁plausiblen Schließen ist es Hauptsache, Vermutung von Vermutung, eine vernünftigere von einer weniger vernünftigen zu unterscheiden. Wenn Sie Ihre Aufmerksamkeit auf beide Unterscheidungen richten, werden beide vielleicht klarer.
    Wer sich ernsthaft mit der Mathematik befaßt und sich ihr ganz widmet, muß demonstratives Schließen lernen; das ist sein Beruf und ist das auszeichnende Merkmal seiner Wissenschaft. Wenn er jedoch wirklich Erfolg haben will, muß er auch ₁₂plausibles Schließen lernen; das ist die Schlußweise, von der seine schöpferische Tätigkeit abhängen wird. Auch wer sich nicht als Fachmann mit der Mathematik befaßt, sollte mit demonstrativem Schließen bekannt werden; er mag wenig Gelegenheit haben, es direkt zu gebrauchen, aber er sollte sich eine Norm aneignen, mit der er angebliche Beweise aller Art vergleichen kann, die im modernen Leben auf ihn losgelassen werden. Dagegen wird er ₁₃plausibles Schließen brauchen bei allem, was immer er anfängt. Jedenfalls sollte jeder, der das Studium der Mathematik mit einigem Ehrgeiz betreibt, versuchen, was auch seine anderen Interessen sein mögen, beide Schlußweisen, die demonstrative und die ₁₄plausible, zu lernen.
 

Kommentar-Polya1962-1-Vorwort-S10f-10 bis 14: Bei den Erwähnungen 10-14 erfahren wir nicht, was unter "plausiblem Schließen" zu verstehen ist. Bisheriger Stand: von 1-14 keine Erklärung zur Plausibilität und zum plausiblen Schließen.

        3. Ich glaube nicht, daß es eine unfehlbare Methode gibt, das Erraten zu lernen. Jedenfalls kenne ich sie nicht, wenn es eine solche gibt, und maße mir ganz gewiß nicht an, sie auf den folgenden Seiten darzustellen. Die zweckmäßige Anwendung ₁₅plausiblen Schließens ist eine praktische Kunstfertigkeit und wird wie jede andere praktische Kunstfertigkeit durch Nachahmung und Übung erlernt. Ich werde mein Bestes für den Leser tun, dem daran liegt, ₁₆plausibles Schließen zu lernen, aber was ich zu bieten habe, sind nur Beispiele zur Nachahmung und Gelegenheit zur Übung." \g
 

Kommentar-Polya1962-1-Vorwort-S12f-15 und 16: Bei den Erwähnungen 15, 16 erfahren wir nicht, was unter "plausiblem Schließen" zu verstehen ist. Ploya postuliert die Hypothese, dass man Regeln und Prinzipien zwar (implizit) lernen kann, wenn man Beispiele bearbeitet, aber man kann sie nicht ausdrücklich formulieren. Das ist eine interessante Hypothese, die in der Psychologie des Alltagslebens als gut bestätigt anzusehen ist, wobei wir hier aber in der Mathematik und Wissenschaft sind. Ob diese Hypothese  richtig ist, dass man keine Regeln und Prinzipien ausdrücklich formulieren kann, lässt sich durch eine Analyse der Beispiele feststellen. Aber diese Arbeit hätte Polya selber machen müssen und im 2. Band macht er ja auch welche, was seiner Aussage hier im Grunde wiederspricht.    Bisheriger Stand: von 1-16 keine Erklärung zur Plausibilität und zum plausiblen Schließen.

 
    Polya1962-1-Vorwort-S12f-17 bis 18: "zustande kommen können. Ich werde versuchen, die Motive, die der Entdeckung zugrunde lagen, die ₁₇plausiblen Folgerungen, die dazu führten, kurzum alles, was Nachahmung verdient, hervorzuheben. Natürlich werde ich versuchen, den Leser zu beeindrucken; das ist meine Pflicht als Lehrer und Autor. Ich werde jedoch in dem Punkt, auf den es wirklich ankommt, absolut ehrlich mit dem Leser sein: Ich werde versuchen, nur mit solchen Dingen, die mir selbst echt und zweckdienlich erscheinen, einen Eindruck auf ihn zu machen.
    Jedem Kapitel folgen Aufgaben und Bemerkungen. Die Bemerkungen behandeln Punkte, die technisch zu fortgeschritten oder zu subtil für den Text des Kapitels sind, oder Punkte, die etwas abseits von der Hauptdiskussionslinie liegen. Manche Aufgaben geben dem Leser Gelegenheit, im Text nur angedeutete Einzelheiten noch einmal durchzugehen. Aber die Mehrzahl der Aufgaben gibt ihm Gelegenheit, eigene ₁₈plausible Schlüsse zu ziehen. Ehe er eine schwierigere am Ende eines Kapitels gestellte Aufgabe in Angriff nimmt, sollte der Leser sorgfältig die einschlägigen Teile des Kapitels lesen und sollte auch einen Blick auf die benachbarten Aufgaben werfen; die eine oder andere mag ihm einen Anhaltspunkt geben. Um das Präsentieren (oder Verstecken) solcher Anhaltspunkte möglichst nutzbringend und belehrend zu gestalten, ist große Sorgfalt nicht nur auf den Inhalt und die Form der gestellten Aufgaben verwendet worden, sondern auch auf ihre Disposition. In der Tat hat die Anordnung dieser Aufgaben viel mehr Zeit und Sorgfalt beansprucht, als ein Außenstehender vermuten oder für nötig halten würde.
 

Kommentar-Polya1962-1-Vorwort-S12f-17 bis 18: Bei den Erwähnungen 17, 18 erfahren wir nicht, was unter "plausiblem Folgern" oder "plausible Schlüsse zu ziehen" zu verstehen ist. Es soll sich ein Verständnis durch das Bearbeiten und Lösen der Aufgabe einstellen. An dieser Stelle scheint es, als ob plausibel sei, was zur Lösung der Aufgabe führt. Bisheriger Stand: von 1-18 keine Erklärung zur Plausibilität und zum plausiblen Schließen.

 
    Um einen weiten Leserkreis zu erreichen, habe ich versucht, jeden wichtigen Punkt durch ein möglichst elementares Beispiel zu erläutern. In verschiedenen Fällen habe ich mich jedoch gezwungen gesehen, ein nicht zu elementares Beispiel heranzuziehen, um den fraglichen Punkt mit genügender Eindrücklichkeit zu stützen. In der Tat hatte ich das Gefühl, ich sollte auch Beispiele von historischem Interesse anführen, Beispiele von echter mathematischer Schönheit und Beispiele, welche erläutern, wie Verfahren in anderen Wissenschaften und im täglichen Leben denen in der Mathematik parallel laufen.
    Ich möchte hinzufügen, daß bei vielen der erzählten Geschichten die endgültige Form aus einer Art von improvisiertem psychologischem [>13] Experiment hervorgegangen ist. Ich besprach den Gegenstand in verschiedenen Vorlesungen und unterbrach dabei häufig meine Darstellungen mit Fragen wie: 'Nun, was würden Sie in einer solchen Lage tun?' Verschiedene, in den folgenden Text aufgenommene Stellen sind durch die Antworten meiner Studenten angeregt worden, oder meine ursprüngliche Fassung ist auf irgendeine andere Weise durch die Reaktion meiner Zuhörerschaft beeinflußt und modifiziert worden.
    Kurzum, ich habe versucht, meine ganze Erfahrung als Forscher und Lehrer aufzubieten, um dem Leser passende Gelegenheit für intelligentes Nachahmen und selbständiges Arbeiten zu geben.

    4. Die in diesem Buch zusammengestellten Beispiele von ₁₉plausiblem Schließen können noch einem anderen Zweck dienlich gemacht werden: Sie können ein viel umstrittenes philosophisches Problem erhellen, nämlich das Problem der Induktion. Die kritische Frage ist diese: Gibt es Induktionsregeln ? Manche Philosophen sagen Ja, die meisten Naturwissenschaftler Nein. Um diese Frage nutzbringend zu besprechen, sollte man sie anders stellen. Auch sollte man sie anders behandeln, mit weniger Berufung auf herkömmliche schablonenhafte Ausdruckweisen oder neumodische Formalismen, dafür in engerer Berührung mit der Praxis des Naturwissenschaftlers. Man beachte nun, daß induktives Schließen ein Sonderfall von ₂₀plausiblem Schließen ist. Man beachte ferner (was moderne Autoren fast vergessen, aber ältere Autoren wie EULER und LAPLACE klar erkannt haben), daß induktive Beweisstützen in der Mathematik eine ähnliche Rolle spielen wie in der physikalischen Forschung. Man wird dann vielleicht die Möglichkeit gewahr, durch das Studieren und Vergleichen von Beispielen ₂₁plausiblen Schließens bei mathematischen Gegenständen Aufschluß über induktives Schließen überhaupt zu erlangen. Und so öffnet sich das Tor für die Untersuchung der Induktion auf induktive Weise.
 

Kommentar-Polya1962-1-Vorwort-S13-19 bis 21: Die Erwähnungen 19, 20 und 21 erklären nicht, worin plausibles Schließen besteht, was unter Plausibilität zu verstehen ist. Ohne zu wissen, was plausibles Schließen ist, erfährt man hier, dass induktives Schließen, das auch nicht erklärt wird, jedenfalls ein Sonderfall plausiblen Schließens ist. Bisheriger Stand: von 1-21 keine Erklärung zur Plausibilität und zum plausiblen Schließen.

        Wenn ein Biologe es unternimmt, irgendein allgemeines Problem, sagen wir aus der Genetik, zu untersuchen, so ist es sehr wichtig, daß er als Untersuchungsmaterial solche Pflanzen und Tiere wählt, die sich für die experimentelle Erforschung seines Problems eignen. Wenn ein Chemiker sich vornimmt, irgendein allgemeines Problem, sagen wir chemische Reaktionsgeschwindigkeiten, zu untersuchen, so ist es [>14] sehr wichtig, daß er als Material für die in bezug auf sein Problem einschlägigen Experimente solche Substanzen wählt, mit denen sich diese Experimente leicht ausführen lassen. Die Wahl von geeignetem Versuchsmaterial ist in der induktiven Untersuchung jedes Problems von großer Bedeutung. Es scheint mir, daß die Mathematik in mehr als einer Hinsicht das geeignetste Versuchsmaterial für die wissenschaftliche Untersuchung des induktiven Schließens ist. Diese Untersuchung schließt Experimente gewissermaßen psychologischen Charakters ein. Man muß es erleben, wie das Vertrauen zu einer Vermutung durch verschiedene Arten von Beweisgründen beeinflußt wird. Mathematische Gegenstände eignen sich, dank der ihnen innewohnenden Einfachheit und Klarheit, viel besser zu einem psychologischen Experiment dieser Art als Gegenstände aus irgendeinem anderen Gebiet. Auf den folgenden Seiten wird der Leser reichlich Gelegenheit finden, sich hiervon zu überzeugen.
    Ich finde es philosophischer, die allgemeinere Idee des ₂₂plausiblen Schließens zu untersuchen anstatt des Sonderfalls, den induktives Schließen darstellt. Ich glaube, daß die in diesem Buch zusammengestellten Beispiele sich zu einer scharf umrissenen und einigermaßen zufriedenstellenden Ansieht von ₂₃plausiblem Schließen zusammenfügen. Ich will jedoch dem Leser meine Ansichten nicht aufdrängen. In der Tat teile ich sie im ersten Band nicht einmal mit; die Beispiele sollen selbst sprechen. Die ersten vier Kapitel des zweiten Bandes sind jedoch einer ausführlicheren allgemeinen Besprechung des ₂₄plausiblen Schließens gewidmet. Dort gebe ich formell die Struktur der durch die vorangegangenen Beispiele nahegelegten ₂₅plausiblenFolgerungsweisen an. Ich versuche, sie auf eine systematische Form zu bringen und gebe eine teilweise Übersicht über ihre Beziehungen zueinander und zu dem Begriff der Wahrscheinlichkeit. Ich weiß nicht, ob der Inhalt dieser vier Kapitel es verdient, als Philosophie bezeichnet zu werden. Wenn das Philosophie ist, ist es jedenfalls eine ziemlich erdnahe Art von Philosophie, der mehr daran gelegen ist, konkrete Beispiele und konkretes menschliches Verhalten zu verstehen als Allgemeinheiten breitzutreten. Ich weiß natürlich noch weniger, wie das endgültige Urteil über meine Ansichten ausfallen wird. Ich habe aber das zuversichtliche Gefühl, daß meine Bei-[>15] spiele jedem nützlich sein können, der leidlich unvoreingenommen an das Studium der Induktion herangeht, und dem daran gelegen ist, seine Ansichten in enger Berührung mit den beobachtbaren Tatsachen zu bilden.
 

Kommentar-Polya1962-1-Vorwort-S14-22 bis 25: Die Erwähnungen 22, 23, 24 und 25 erklären nicht, worin plausibles Schließen und plausible Folgerungsweise bestehen und was unter Plausibilität zu verstehen ist. Bisheriger Stand: von 1-25 keine Erklärung zur Plausibilität und zum plausiblen Schließen.

    5. Diese Arbeit über Mathematik und ₂₆plausibles Schließen, die ich immer als Einheit angesehen habe, zerfällt auf natürliche Weise in zwei Teile: Induktion und Analogie in der Mathematik (Band I) und Typen und Strukturen ₂₇plausibler Folgerung (Band II). Im Interesse des Lesers erscheinen diese Teile in zwei getrennten Bänden. Band I ist unabhängig von Band II, aber ich glaube, die meisten Leser sollten diesen ersten Band erst sorgfältig durchsehen, ehe sie an den zweiten herangehen. Der erste Band enthält hauptsächlich die mathematische Substanz des Werkes und liefert Daten für die induktive Untersuchung der Induktion im zweiten Band. Mancher Leser, der in der Mathematik vorgerückt und erfahren ist, wird vielleicht gleich zum zweiten Band greifen wollen; auch für diesen wird es eine Annehmlichkeit sein, ihn getrennt zu haben. Im Interesse bequemer Bezugnahme auf den Text sind die Kapitel beider Bände durchgehend numeriert. Ich habe das Werk nicht mit einem Index ausgestattet, da ein solcher dazu verleiten konnte, die Terminologie starrer zu machen, als es dem Autor in einem Werk dieser Art wünschenswert erscheint. Ich glaube, daß das Inhaltsverzeichnis ein zufriedenstellender Führer durch das Buch sein wird.
    Das vorliegende Werk bildet eine Fortsetzung meines früheren Buches How to Solve ItFN1). Der Leser, der sich für den Gegenstand interessiert, sollte beide lesen. Die Reihenfolge, in welcher er sie liest, ist unwichtig. Das vorliegende Werk ist so abgefaßt, daß es unabhängig von dem früheren gelesen werden kann. In der Tat finden sich in diesen Bänden nur wenige direkte Hinweise auf das frühere Werk, und sie können bei einer ersten Lektüre außer acht gelassen werden. Doch finden sich auf fast jeder Seite indirekte Hinweise auf das frühere Buch, auf manchen Seiten in fast jedem Satz. Wiederum liefert das [>16] gegenwärtige Buch zahlreiche Aufgaben und einige fortgeschrittenere Beispiele für das frühere Werk, in welchem sie in Anbetracht seines geringen Umfangs und seines elementaren Charakters keinen Platz gefunden hatten.
    Ebenso besteht ein gewisser Zusammenhang zwischen dem vorliegenden Buch und einer Sammlung von Aufgaben aus der Analysis von G. SZEGÖ und dem Verfasser (siehe die Bibliographie). Die Aufgaben in dieser Sammlung sind sorgfältig in Serien angeordnet, so daß sie sich gegenseitig stützen, sich gegenseitig Anhaltspunkte liefern, einen gewissen Gegenstand gemeinsam behandeln und dem Leser die Gelegenheit geben, sich in verschiedenen beim Aufgabenlösen wichtigen Griffen zu üben. In der Behandlung der Aufgaben folgt das gegenwärtige Werk der von dem früheren eingeführten Methode. Dieser Zusammenhang ist nicht ohne Bedeutung.
    Zwei Kapitel in Band II befassen sich mit der Wahrscheinlichkeitslehre. Das erste dieser Kapitel hängt in gewissem Sinne mit einer elementaren Darstellung der Wahrscheinlichkeitsrechnung zusammen, die der Autor vor mehreren Jahren geschrieben hat (siehe die Bibliographie). Die zugrunde liegenden Ansichten über Wahrscheinlichkeit und die Ausgangspunkte sind die gleichen, aber sonst liegen wenig Berührungspunkte vor.
    Einige von den in diesem Buch dargebotenen Ansichten habe ich schon in früheren, in der Bibliographie zitierten Arbeiten zum Ausdruck gebracht. Längere Stellen aus Arbeiten Nr. 4, 6, 8, 9 und l0 sind dem folgenden Text einverleibt worden. Meine Anerkennung und mein bester Dank richten sich an die Herausgeber des American Mathematical Monthly, der Etudes de Philosophie des Sciences en Hommage a Ferdinand Gonseth und der Proceedings of the International Congress of Mathematicians 1950, die mir freundlicherweise die Erlaubnis gaben, diese Stellen abzudrucken.
    Ich habe den Inhalt dieses Buches in der Hauptsache in meinen Vorlesungen vorgetragen, Teile davon sogar mehrmals. In manchen Abschnitten habe ich den Ton der mündlichen Darstellung gewahrt. Ich glaube nicht, daß ein solcher Ton im allgemeinen in einer gedruckten Darstellung der Mathematik ratsam ist, aber im gegenwärtigen Fall mag er geeignet, oder zum mindesten entschuldbar sein.[>17]
 

Kommentar-Polya1962-1-Vorwort-S15-26 bis 27: Die Erwähnungen 26 und 27 erklären nicht, worin plausibles Schließen und Folgern besteht, was unter Plausibilität zu verstehen ist. Bisheriger Stand: von 1-27 keine Erklärung zur Plausibilität und zum plausiblen Schließen.

    6. Das letzte Kapitel von Band II, das von Entdeckung und Unterricht handelt, verbindet den Inhalt des gegenwärtigen Buchs ausdrücklicher mit dem verwandten früheren Werk des Autors (Schule des Denkens) und deutet auf eine eventuelle Folge hin.
    Die zweckmäßige Anwendung von ₂₈plausiblem Schließen spielt beim Aufgabenlösen eine wesentliche Rolle, und das vorliegende Buch sucht diese Rolle an vielen Beispielen zu erläutern. Aber es gibt noch andere Aspekte des Aufgabenlösens, die eine ähnliche Erläuterung brauchen. Viele Punkte, die hier nur gestreift worden sind, erfordern weitere Bearbeitung. Meine Ansichten über ₂₉plausibles Schließen sollten denen anderer Autoren gegenübergestellt werden, die historischen Beispiele sollten gründlicher ausgewertet, die Ansichten über Entdeckung und Lehren soweit wie möglich mit den Methoden der Experimentalpsychologie untersucht werdenFN2) und so weiter. Verschiedene solche Aufgaben bleiben offen, auch möchten einige davon undankbar sein.
    Das vorliegende Buch ist kein Lehrbuch. Ich hoffe aber, daß es im Lauf der Zeit die übliche Darstellung der Mathematik in den Lehrbüchern und deren Aufgabenauswahl beeinflussen wird. Die Lehrbücher der geläufigeren Unterrichtsfächer in diesem Sinn umzuarbeiten braucht keine undankbare Aufgabe zu sein.
 

Kommentar-Polya1962-1-Vorwort-S17-28 bis 29: Die Erwähnungen 28 und 29 erklären nicht, worin plausibles Schließen besteht, was unter Plausibilität zu verstehen ist. Bisheriger Stand: von 1-29 keine Erklärung zur Plausibilität und zum plausiblen Schließen.

    7. Ich möchte der Princeton University Press meinen Dank ausdrücken für ihre sorgfältige Drucklegung und besonders Herrn HERBERT S. BAILEY jr., dem Leiter des Verlags, für seine verständnisvolle Hilfe in so mancher Hinsicht. Ich bin auch Frau PRISCILLA FEIGEN für die Herstellung der Maschinenschrift und Herrn JULIUS G. BARON für seine freundliche Hilfe beim Korrekturlesen sehr verpflichtet.
Stanford University                                                               Georg Pólya
Mai 1953
 

   Info/Inhaltsverzeichnis Kapitel I Induktion  1 Fundstelle "plausib"
    Kapitel I. Induktion    21

1. Erfahrung und Ansichten    21
2. Suggestive Beobachtungen    22
3. Stützende Beobachtungen    24
4. Die induktive Einstellung    27
Aufgaben und Bemerkungen zu Kapitel I, 1-14. [12. Ja und Nein. 13. Erfahrung und Verhalten. 14. Der Logiker, der Mathematiker, der
Physiker und der Ingenieur.]    28


Polya1962-1-S.26: "Die Vermutung verifiziert sich in allen hier untersuchten Fällen. Jede Verifizierung, die unsere Tabelle verlängert, stärkt die Vermutung, Macht sie glaubhafter, erhöht ihre ₃₀Plausibilität. Natürlich kann aber kein noch so großes Ausmaß an Verifizierungen die Vermutung beweisen."
 

Kommentar-Polya1962-1-S.26: Die Erwähnung 30 erkläret nicht, was unter Plausibilität zu verstehen ist. Behauptet wird die mainstream Auffassung, dass keine noch so große Anzahl an Verifizierungen (mathematische) Beweiskraft hat (kritisch siehe bitte hier). Bisheriger Stand: von 1-31 keine Erklärung zur Plausibilität und zum plausiblen Schließen.

       Kapitel II. Verallgemeinerung, Spezialisierung, Analogie    33
1. Verallgemeinerung, Spezialisierung, Analogie und Induktion    33
2. Verallgemeinerung    33
3. Spezialisierung    34
4. Analogie    34
5. Verallgemeinerung, Spezialisierung und Analogie    38
6. Entdeckung durch Analogie    41
7. Analogie und Induktion    46
Aufgaben und Bemerkungen zu Kapitel II, 1-46; [Erster Teil, 1-20; Zweiter Teil, 21-46]. [1. Die richtige Verallgemeinerung. 5. Ein extremer Spezialfall. 7. Ein führender Spezialfall. 10. Ein repräsentativer Spezialfall. 11. Ein analoger Fall. 18. Große Analogien. 19. Geklärte Analogien. 20. Zitate. 21. Die Vermutung E. 44. Ein Einwand und ein erster Zugang zu einem Beweis. 45. Ein zweiter Zugang zu einem Beweis. 46. Gefahren der Analogie.]    48

    Info/InhaltsverzeichnisKapitel III. Induktion in der Geometrie des Raumes  3 Fundstellen

1. Polyeder  66
2. Erste stiitzende Beobachtungen.  69
3. Weitere stiitzende Beobachtungen 70
4. Eine strenge Probe  71
5. Es gibt Verifikationen und Verifikationen 73
6. Ein ganz anderer Fall 75
7. Analogie. 75
8. Raumteilungen. 77
9. Modifizierung der Aufgabe 78
10. Verallgemeinerung, Spezialisierung, Analogie 79
11. Eine weitere analoge Aufgabe   79
12. Zusammenstellung von analogen Aufgaben    81
13. Viele Aufgaben sind manchmal leichter als nur eine    82
14. Eine Vermutung    83
15. Voraussage und Verifikation    84
16. Noch einmal und besser    85
17. Induktion legt Deduktion, der Spezialfall den allgemeinen Beweis nahe    86
18. Weitere Vermutungen    88
Aufgaben und Bemerkungen zu Kapitel III, 1-41. [21. Induktion: Anpassung der Gedanken, Anpassung der Sprache. 31. Descartes' Untersuchung über Polyeder. 36. Supplementäre Raumwinkel, supplementäre sphärische Polygone.]    89
     _
Polya1962-1-S.69-31: "2. Erste stützende Beobachtungen. Ein erfahrener Naturforscher erkennt nicht leicht eine Vermutung als gültig an. Selbst wenn die Vermutung ₃₁plausibel erscheint und sich in verschiedenen Fällen bestätigt hat, wird er sie in Frage ziehen und neue Beobachtungen sammeln oder sich neue Experimente ausdenken, um sie zu prüfen. Wir werden genau dasselbe tun. Wir werden noch weitere Polyeder untersuchen, ihre Flächen, Ecken und Kanten zählen und F + E mit K + 2 vergleichen. Vielleicht sind diese Zahlen einander gleich, vielleicht aber auch nicht. Es wird interessant sein zu sehen, wie die Entscheidung ausfällt."
 

Kommentar-Polya1962-1-S.69-31: Hier wird die Idee thematisiert, dass eine Vermutung nur  plausibel erscheinen kann, ohne es tatsächlich zu sein, wobei wiederum offen bleibt, was unter plausibel zu verstehen ist.     Bisheriger Stand: von 1-31 keine Erklärung zur Plausibilität und zum plausiblen Schließen.

Polya1962-1-S.70-32: "3. Weitere stützende Beobachtungen. Dank den vorangegangenen Verifizierungen ist unsere Vermutung merklich ₃₂plausibler geworden; ist sie aber jetzt bewiesen? Keineswegs. ..."
 

Kommentar-Polya1962-1-S.70:  Hier formuliert Polya ein wichtiges Plausibilitätskriterium, nämlich die Anzahl der Verifizierungen (weitere stützende Beobachtungen). Hier hätte er eigentlich auch die Anzahl der Falsifizierungen berücksichtigen müssen, zumal er den allgemeinen Gedanken S. 73 formuliert: "Ein Fall, der im Einklang mit der Vermutung steht, macht diese wahrscheinlicher, ein im Widerspruch damit stehender Fall widerlegt sie, und hier beginnt der Unterschied."     Bisheriger Stand: von 1-32 keine Erklärung zur Plausibilität und zum plausiblen Schließen, aber ein positives Kriterium.

Polya1962-1-S.84: "... Wir scheinen die gestellte Aufgabe gelöst zu haben. Oder es ist uns wenigstens gelungen, auf eine ₃₃plausible Vermutung zu kommen, die von allem bisher gesammelten Beweismaterial gestützt wird."
 

Kommentar-Polya1962-1-S.84-33: =Plausible Vermutung wird nicht erklärt.    Bisheriger Stand: von 1-33 keine Erklärung zur Plausibilität und zum plausiblen Schließen.

Kapitel IV. Induktion in der Zahlentheorie *** keine Fundstelle "plausib"
Kapitel IV. Induktion in der Zahlentheorie    100

1. Pythagoreische Dreiecke    100
2. Quadratsummen    103
3. Über die Summe von vier ungeraden Quadratzahlen    105
4. Untersuchung eines Beispiels    106
5. Tabellarisierung der Beobachtungen    109
6. Wie lautet die Regel?    109
7. Von der Natur induktiver Entdeckung    112
8. Von der Natur induktiver Beweisgründe    113
Aufgaben und Bemerkungen zu Kapitel IV., 1-26. [1. Bezeichnung 26. Gefahren der Induktion]    116


Info/Inhaltsverzeichnis Kapitel V. Diverse Induktionsbeispiele. 123-143  *** keine Fundstelle "plausib"
Kapitel V. Diverse Induktionsbeispiele    123

1. Reihenentwicklung    123
2. Annäherung    125
3. Grenzwerte    128
4. Wir versuchen zu widerlegen    129
5. Wir versuchen zu beweisen    131
6. Die Rolle der induktiven Phase    133
Aufgaben und Bemerkungen zu Kapitel V, 1-18. [15. Man erkläre die beobachteten Regelmäßigkeiten. 16. Man klassifiziere die beobachteten Tatsachen. 18. Worauf beruht die Unterscheidung ?]    134


Info/Inhaltsverzeichnis Kapitel VI  1. Eine allgemeinere Formulierung 143-167 *** keine Fundstelle "plausib"
Kapitel V 1. Eine allgemeinere Formulierung    143

1. Euler    143
2. Eulers Schrift    144
3. Übergang zu einem allgemeineren Gesichtspunkt    155
4. Schematischer Umriß von Eulers Schrift    156
Aufgaben und Bemerkungen zu Kapitel VI, 1-25. [1. Erzeugende Funktionen. 7. Eine kombinatorische Aufgabe in der Geometrie der Ebene. 10. Quadratsummen. 19. Noch eine Rekursionsformel. 20. Noch ein ganz außergewöhnliches Gesetz der ganzen Zahlen betreffend die Summe ihrer Teiler. 24. Wie Euler eine Entdeckung entging. 25. Eine Verallgemeinerung des Eulerschen Satzes über a
(n).]    157


Info/Inhaltsverzeichnis Kapitel VII. Vollständige Induktion  1 Fundstelle "plausib"
Kapitel VII. Vollständige Induktion    167

1. Die induktive Phase    167
2. Die beweisende Phase    169
3. Untersuchung von Übergängen    170
4. Die Technik der vollständigen Induktion    172
Aufgaben und Bemerkungen zu Kapitel VII, 1-18. [12. Manchmal ist es weniger Mühe, mehr zu beweisen. 14. Man solI den Satz ausbalancieren. 15. Ausblick. 17. Sind n beliebige Zahlen gleich ?]    178


    Polya-1962-1-S.170-34: "Wir haben hier ein grundsätzlich wichtiges Beweisverfahren. Es wird der «Schluß von n auf n + 1» oder auch «vollständige Induktion» genannt. Die letztere Bezeichnung ist ein sehr unangebrachter Name für ein Beweisverfahren, da Induktion (in dem Sinn, in dem der Ausdruck meistens, und auch hier, gebraucht wird) nur einen ₃₄Plausibilitätsschluß, nicht einen Beweisschluß liefert."
 

Kommentar-Polya1962-1-S.170-34: "nur" ein Plausibilitätsschluss wird nicht erklärt.    Bisheriger Stand: von 1-34 keine Erklärung zur Plausibilität und zum plausiblen Schließen.

Info/Inhaltsverzeichnis Kapitel VIII. Maxima und Minima 185-214   Eine Fundstelle "plausib"
Kapitel VIII. Maxima und Minima    185

1. Lösungsschemata    185
2. Beispiel    186
3. Das Schema der berührenden Niveaulinie    188
4. Beispiele    192
5. Das Schema der partiellen Variation    195
6. Der Satz von dem arithmetischen und geometrischen Mittel und seine ersten Konsequenzen    198
Aufgaben und Bemerkungen zu Kapitel VIII, 1-63; [Erster Teil, 1-32; Zweiter Teil, 33-63.]. [1. Entfernungsminima und -maxima in der ebenen Geometrie. 2. Entfernungsminima und -maxima in der räumlichen Geometrie. 3. Niveaulinien in einer Ebene. 4. Niveauflächen im Raum. 11. Das Prinzip der kreuzenden Niveaulinie. 22. Das Prinzip der partiellen Variation. 23. Existenz des Extremums. 24. Eine Modifizierung des Schemas der partiellen Variation: ein unendlicher Prozeß. 25. Eine weitere Modifizierung des Schemas der partiellen Variation: ein endlicher Prozeß. 26. Graphischer Vergleich. 33. Polygone und Polyeder. Flächeninhalt und Umfang. Volumen und Oberfläche. 34. Das gerade Prisma mit quadratischer Grundfläche. 35. Der gerade Zylinder. 36. Das allgemeine gerade Prisma. 37. Die gerade Doppelpyramide mit quadratischer Grundfläche. 38. Der gerade Doppelkegel. 39. Die allgemeine gerade Doppelpyramide. 43. Eine Anwendung von Geometrie auf Algebra. 45. Eine Anwendung von Algebra auf Geometrie. 51. Die gerade Pyramide mit quadratischer Grundfläche. 52. Der gerade Kegel. 53. Die allgemeine gerade Pyramide. 55. Die Schachtel ohne Deckel. 56. Der Trog. 57. Ein Fragment. 62. Eine Postamtsaufgabe. 63. Eine Aufgabe von Kepler.]    200


    Polya1962-1-S.187-35,36: "Die Lösung unserer Aufgabe ist nicht unmittelbar ersichtlich. Aber selbst, wenn wir noch nicht wissen, wo das Maximum erreicht wird, zweifeln wir nicht daran, daß es irgendwo erreicht wird. Warum ist das so ₃₅plausibel ?
Wir können uns Rechenschaft über diese ₃₆Plausibilität geben, wenn wir uns die Variation des Sehwinkels vergegenwärtigen, dessen Maximalwert wir zu finden suchen.


"
_

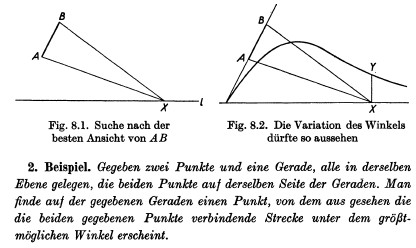
Kommentar-Polya1962-1-S.187-35,36: Auch hier wird "so plausibel" nicht erklärt, aber auf ein Beispiel verwiesen, aus dem sich das Begriffsverständnis erhellen solle.      Auch wenn es die Analogie nicht ganz trifft, so mag sie doch eine Hintergrundrolle spielen: Aus der Alltagswahrnehmung weiß man, die Gegenstände erscheinen größer, wenn man sich auf sie zubewegt und kleiner, wenn man sich weg bewegt. Warum können wir eine solche Erfahrung als plausibel beurteilen? Ich denke, weil es eben eine Erfahrung jedermans ist. Aber diese Erfahrung trifft es nicht richtig, weil das Maximumn nicht dazwischen liegt, sondern am Gegenstandspunkt. Man kann kann sich aber ein Tor vorstellen durch das man gehen kann. Je mehr man sich ihm nähert, desto größer erscheint es und je mehr man sich nach Durschreiten von ihm entfernt, desto kleiner erscheint es. Das trifft es schon ganz gut, aber auch noch nicht völlig wie die Beispielzeichnung zeigt. Die Grunderfahrung für das Beispiel konnte lauten: vor-größer, zurück-kleiner oder umgeklehrt. So könnte man es experimentell angehen, obwohl das genaue Maximum so wahrscheinlich gefunden werden kann, weil man in der engeren Maximumsumgebung keine Wahrnehmungsunterschiede mehr feststellen kann, es dann vielleicht 5, 10 oder 20 Maximapunkte gibt. Ist die Maximumsbehauptung nur plausibel oder nicht einfach richtig?    Aber wenn ein Maximum gesucht wird, denke ich zunächst an folgende drei Möglichkeiten: es gibt ein Maximum, es gibt mehrere Maxima, es gibt kein Maximum. Man könnte die Extreme prüfen: X als Verlängerung von AB, Polya spricht hier vermutlich  von "Ausgangspunkt" Von der Schule her dämmert mir noch, dass die Kurve stetig sein muss, um differenzierbar zu sein und ein Maximum zu finden.     Bisheriger Stand: von 1-35 keine Erklärung zur Plausibilität und zum plausiblen Schließen; Verweis auf ein Beispiel (den größten Sehwinkel suchen).

Info/Inhaltsverzeichnis Kapitel IX. Physikalische Mathematik 215-252   2 Fundstellen "plausib"
Kapitel IX. Physikalische Mathematik    215

1. Optische Interpretation    215
2. Mechanische Interpretation    221
3. Neuinterpretierung    224
4. Johann Bernoullis Entdeckung der Brachistochrone    229
5. Archimedes' Entdeckung der Integralrechnung    233
Aufgaben und Bemerkungen zu Kapitel IX, 1-38. [3. In ein gegebenes Dreieck einbeschriebenes Dreieck kleinsten Umfangs. 9. Verkehrszentrum für vier Punkte im Raum. 10. Verkehrszentrum für vier Punkte in einer Ebene. 11. Verkehrsnetz für vier Punkte. 12. Auffalten und ausziehen. 13. Billard. 14. Geophysikalische Forschungsmethode. 23. Kürzeste Linien auf einer Polyederfläche. 24. Kürzeste (geodatische) Linien auf einer gekrümmten Fläche. 26. Eine Konstruktion durch Papierfalten. 27. Der Würfel ist gefallen. 28. Die Sintflut. 29. Stille Wasser sind tief. 30. Ein nützlicher Extremfall. 32. Die Variationsrechnung. 33. Vom Gleichgewicht des Querschnitts zum Gleichgewicht des Körpers. 38. Rückblick auf Archimedes' Methode.]    238


    Polya1962-1-S. 226-37: "... Diese Gewichte können nicht gleich sein: Wären sie es, so wäre A X B in der Gleichgewichtsstellung eine gerade Linie (dies scheint wenigstens ₃₇plausibel), und A X B wäre nicht dazu geeignet, die Bahn des gebrochenen Lichtes darzustellen. ..."
 

Kommentar-Polya1962-1-S.226-37: Plausibel wird nicht erklärt. Bisheriger Stand: von 1-37 keine Erklärung zur Plausibilität und zum plausiblen Schließen.

    Polya1962-1-S.237f-38,39: "... Aber dieser Schritt beruht nur auf einer heuristischen Grundlage, auf physikalisch [>238] ingenieurhafter Intuition; er ist nicht logisch gerechtfertigt.  Er ist ₃₈plausibel, sogar sehr ₃₉plausibel, aber er ist kein Beweis. ..."
 

Kommentar-Polya1962-1-S.237f-38,39: Plausibel wird so wenig erklärt wie sehr plausibel Bisheriger Stand: von 1-39 keine Erklärung zur Plausibilität und zum plausiblen Schließen.

Info/Inhaltsverzeichnis Kapitel X. Das isoperimetrische Problem. 252-283   5 Fundstellen "plausib"
Kapitel X. Das isoperimetrische Problem    252

1. Descartes' induktive Gründe    252
2. Latente Gründe    253
3. Physikalische Gründe    254
4. Lord Rayleighs induktive Gründe    255
5. Wir leiten Konsequenzen ab    257
6. Wir verifizieren Konsequenzen    260
7. Sehr nahe dran    265
8. Drei Formen des isoperimetrischen Satzes    267
9. Anwendungen und Fragen    269
Aufgaben und Bemerkungen zu Kapitel X, 1-43; [Erster Teil 1-15; Zweiter Teil 16-43]. [1. Rückblick. 2. Ließe sich irgendein Teil des Resultats anders ableiten? 3. Man entwickle mit größerer Ausführlichkeit. 7. Läßt sich die Methode für irgendein anderes Problem benützen? 8. Schärfere Form des isoperimetrischen Satzes. 16. Der Stock und die Schnur. 21. Zwei Stöcke und zwei Schnüre. 25. Didos Problem in der Geometrie des Raumes. 27. Halbierungslinien eines ebenen Bereichs. 34. Halbierungslinien einer geschlossenen Fläche. 40. Eine Figur vielseitiger Vollkommenheit. 41. Ein analoger Fall. 42. Die regelmäßigen Körper. 43. Induktive Gründe.]    271


    Polya1962-1-S.254-40: "Was ist der Unterschied zum Fall des Kreises? Wir sind zugunsten des Kreises voreingenommen. Der Kreis ist die vollkommenste Figur; wir glauben gerne, daß der Kreis neben seinen anderen Vollkommenheiten bei gegebenem Inhalt den kürzesten Umfang hat. Das induktive Argument, auf welches DESCARTES hinweist, erscheint so überzeugend, weil es eine von vornherein ₄₀plausible Vermutung bekräftigt."
 

Kommentar-Polya-1962-1-S.254-40: Was eine von "vornherein plausible Vermutung" ist, wird nicht erklärt.    Bisheriger Stand: von 1-40 keine Erklärung zur Plausibilität und zum plausiblen Schließen.

    Polya1962-1-S.265-41: "7. Sehr nahe daran. Die Konsequenzen, deren Ableitung uns gelungen ist, machen den isoperimetrischen Satz höchst ₄₁plausibel. Aber sie leisten noch mehr. Sie erwecken in uns das Gefühl, daß «sehr viel in ihnen steckt», daß wir «sehr nahe» an der endgültigen Lösung, dem vollständigen Beweis, sind."
 

Kommentar-Polya-1962-1-S.265-41: "sehr nahe dran", "höchst plausibel". Bisheriger Stand: von 1-41 keine Erklärung zu plausibel und "höchst plausibel."

    Polya1962-1-S. 280-42: "Wenden wir uns dem folgenden einfacheren Fall zu, um eine ₄₂plausible Antwort zu finden. Betrachten wir zwei symmetrische Funktionen, f(x_l, x₂, ... ,x_n) und g(x_l, x₂, ... ,x_n), von n Veränderlichen, und suchen wir die Extremwerte von f(x_l, x₂, ... ,x_n), wenn g(x_l, x₂, ... ,x_n) = 1 vorgeschrieben ist. Es gibt Fälle, in denen kein Maximum existiert, andere Fälle, in denen kein Minimum existiert, und wiederum andere Fälle, in denen weder ein Maximum noch ein Minimum existiert. Die Bedingung x_l, x₂, ... ,x_n spielt eine wichtige RolleFN10), sie braucht jedoch nicht erfüllt zu sein, damit ein Maximum oder ein Minimum angenommen wird. ..."
 

Kommentar-Poly1962-1-S.280-42: plausibel wird nicht erklärt. Bisheriger Stand: von 1-42 keine Erklärung zur Plausibilität und zum plausiblen Schließen.

    Polya1962-1-S.281-43: "Dieses sehr schwierige Problem wird durch das analoge Problem von § 7 (1) nahegelegt, und dieses analoge Problem legt gleichzeitig eine Vermutung nahe: Wenn es einen regelmäßigen Körper von n Flächen gibt, liefert er das Maximalvolumen. So ₄₃plausibel diese Vermutung auch erscheinen mag, sie stellt sich in zwei von fünf Fällen als falsch heraus. ..."
 

Kommentar-Poly1962-1-S.281-43: plausibel wird nicht erklärt. Hier wird mitgeteilt, dass die so plausibel erscheinende Vermutung in zwei von fünf Fällen falsch sei.    Bisheriger Stand: von 1-43 keine Erklärung zur Plausibilität.

    Polya1962-1-S.283-44: "... Unsere Beispiele gaben Gelegenheit, uns mit zwei Arten ₄₄plausibler Argumente vertraut zu machen, die für oder gegen eine aufgestellte Vermutung sprechen. Wir besprachen induktive Argumente, die sich auf die Verifizierung von Konsequenzen, und solche, die sich auf Analogie gründen.
 

Kommentar-Polya1962-1-S.283-44: Obwohl auch hier plausibel nicht erklärt wird, formuliert  Polya eine wichtige Grundidee zur Plausibilität, das es nämlich Argumente für und gegen eine Vermutung gibt (wie in meiner Plausibilitätsformel). Allerdings kommt diese Idee in seinen sonstigen Ausführungen nicht zum Tragen.     Bisheriger Stand: von 1-44 keine Erklärung zur Plausibilität.

    Polya1962-1-S.286-45: "... Man darf jedoch nicht vergessen, daß der Schluß, zu dem man durch ein solches Verfahren gelangt, nur provisorisch und nicht endgültig, nur ₄₅plausibel, aber nicht mit Gewißheit wahr ist."
 

Kommentar-Poly1962-1-S.286-45: Eine Widerholung, wobei auch hier "nur plausibel" nicht erklärt wird.     Bisheriger Stand: von 1-45 keine Erklärung zur Plausibilität und zum plausiblen Schließen.

Info/Inhaltsverzeichnis Kapitel XI. Weitere Arten plausibler Argumente 283-310   9 Fundstellen "plausib"
Kapitel XI. Weitere Arten plausibler Argumente    283

1. Vermutungen verschiedener Art    283
2. Wir richten uns nach einem verwandten Fall    283
3. Wir richten uns nach dem allgemeinen Fall    286
4. Ist die einfachere Vermutung vorzuziehen?    288
5. Kultureller Hintergrund    291
6. Unerschöpflich    295
7. Geläufige heuristische Annahmen    296
Aufgaben und Bemerkungen zu Kapitel XI, 1-23 [16. Der allgemeine Fall. 19. Keine Idee ist wirklich schlecht. 20. Einige geläufige heuristische Annahmen. 21. Optimismus wird gelegentlich belohnt. 23. Numerische Berechnung und der Ingenieur.]    297


    Poly1962-1-S.295f-47 bis 53 : "6. Unerschöpflich. Das vorstehende Beispiel stellt klar einen wesentlichen Grundzug ₄₆plausiblen Schließens heraus. Versuchen wir, ihn mit einiger Allgemeinheit zu beschreiben.
Wir haben eine gewisse Vermutung, sagen wir A. Das heißt, A ist eine klar formulierte, aber nicht bewiesene Behauptung. Wir haben das Gefühl, daß A wahr ist; aber wir wissen es nicht. Und doch haben wir ein gewisses Vertrauen zu unserer Vermutung A. Ein solches Vertrauen kann auf einer gedanklich klar gefaßten Grundlage beruhen, aber das muß nicht der Fall sein. Die Vermutung A war nach längerer und scheinbar erfolgloser Arbeit an einem Problem ganz unvermutet aufgetaucht. Sie mag als der einzig mögliche Ausweg aus einer verworrenen Situation erscheinen; sie mag als fast sicher wahr scheinen, obgleich wir nicht sagen können, warum.
Nach einer Weile werden uns jedoch klarer faßbare Gründe bewußt, die entschieden zugunsten von A sprechen, wenn sie A auch nicht beweisen: Gründe, die der Analogie, der Induktion, verwandten Fällen, der allgemeinen Erfahrung oder der A selbst innewohnenden Einfachheit entstammen. Solche Gründe können Asehr ₄₇plausibel machen, ohne einen strengen Beweis zu liefern. (Dabei sollte es uns zur Warnung dienen, daß wir ursprünglich dieser Vermutung getraut haben ohne irgendwelche dieser klarer gefaßten Gründe.)
Wir entdecken diese Beweggründe einen nach dem anderen. Es gelingt uns zunächst einmal, einen ersten klaren Punkt aus dem dunklen Hintergrund, auf dem die Vermutung steht, abzulösen. Aber der Hintergrund enthält mehr, denn später fordern wir aus ihm ein weiteres klares Argument ans Licht. Und so mag hinter jedem geklärten Punkt immer noch mehr liegen. Der Hintergrund ist vielleicht unerschöpflich. Vielleicht beruht unser Vertrauen zu einer Vermutung nie allein auf geklärten Gründen; ein solches Vertrauen benötigt vielleicht unsere ganze Erfahrung als Grundlage.
Jedenfalls sind ₄₈plausible Begründungen wichtig, besonders geklärte ₄₉plausible Begründungen. Wenn wir mit der beobachtbaren Wirklich-[>296] keit zu tun haben, können wir nie auf dem Beweisweg zu einer Wahrheit gelangen, wir müssen uns immer auf irgendwelche ₅₀plausiblen Begründungen verlassen. Wenn wir mit rein mathematischen Fragen zu tun haben, können wir zu einem strengen Beweis gelangen. Dies kann jedoch sehr schwierig sein, und das Heranziehen von vorläufigen ₅₁plausiblen Gründen kann uns als provisorische Stütze dienen und kann uns schließlich zu der Entdeckung des endgültigen Beweisschlusses führen.
    Heuristische Argumente sind wichtig, obgleich sie nichts beweisen. Ebenso ist es wichtig, unsere heuristischen Gründe zu klären, wenn auch hinter jedem so geklärten Grund etwas Weiteres stecken mag - vielleicht ein zur Zeit noch dunkler, aber noch wichtigerer GrundFN5) ^{[=Schule des Denkens, S. 252.).}
    Dies legt eine weitere Bemerkung nahe: Wenn wir in jedem konkreten Fall nur ein paar unserer ₅₂plausiblen Gründe klären und sie in keinem konkreten Fall erschöpfen können, wie können wir dann hoffen, die verschiedenen Arten ₅₃plausibler Gründe in abstracto erschöpfend zu beschreiben?"
 

Kommentar-Polya1962-1-S.295f-47 bis 53:  Kommentar-Polya1962-1-S.295f (47 bis 52): In diesem Abschnitt spielen Gründe eine ganz zentrale Rolle (wie in meinem  Definitionsvorschlag  für Plausibilität).    Bisheriger Stand: von 1-52 keine Erklärung zur Plausibilität und was plausible Gründe sind.

    Polya1962-1-S.303-54: "Enthält eine Aufgabe ebenso viele «Bedingungen wie verfügbare Parameter, so ist es vernünftig, von der Annahme auszugehen, daß die Aufgabe eine Lösung hat. Eine quadratische Form in n Veränderlichen hat zum Beispiel n(n + 1)/2 Koeffizienten, und eine orthogonale Substitution in n Veränderlichen hängt von n(n - 1)/2 Parametern ab. Darum ist es von vornherein ziemlich ₅₄plausibel, daß eine beliebige quadratische Form in n Veränderlichen durch eine passende orthogonale Substitution auf den Ausdruck



gebracht werden kann; ..."
 

Kommentar-Polya1962-1-S.303-54: "von vorneherein ziemlich plausibel" wird auch hier nicht erklärt - wie schon nicht in Polya-1962-1-S.254-40.    Bisheriger Stand: von 1-54 keine Erklärung zur Plausibilität und zu von vornherein plausibel .

Schlussbemerkung  2 Fundstellen "plausib"

    Polya1962-1-S.311-55,56: "SCHLUSSBEMERKUNG
    Der Leser, welcher sich der Lektüre der vorstehenden Kapitel unterzogen und einige der vorstehenden Aufgaben selbst bearbeitet hat, hatte gute Gelegenheit, gewisse Aspekte plausiblen Schließens kennenzulernen. Es ist das Ziel der verbleibenden fünf Kapitel dieses Werks, die in Band II zusammengestellt sind, einen allgemeinen Begriff von der Natur ₅₅plausiblen Schließens zu geben. Diesem Ziel kommt, glaube ich, erhebliches theoretisches Interesse zu; vielleicht hat es auch praktischen Wert: Wir werden eine konkrete Aufgabe vielleicht besser erfüllen, wenn wir mehr von der zugrunde liegenden abstrakten Idee verstehen.
Die Formulierung gewisser Formen ₅₆plausiblen Schließens ist der Hauptzweck des nächsten Bandes. Diese Formen werden jedoch konkreten Beispielen entnommen und in enger Berührung damit besprochen. Somit wird Band II eine Reihe von mathematischen Beispielen zu den in diesem ersten Band dargelegten hinzufügen und sie auf gleiche Weise behandeln."
 

Kommentar-Polya1962-1-S.311-55,56: Das klingt verheißungsvoll und macht mich gespannt auf den 2. Band. Es ist darüberhinaus ein Eingeständnis, dass bis hierher kein Begriff von der Natur plausiblen Schließens vorliegt.     Bisheriger Stand: von 1-56 keine Erklärung zur Plausibilität und zum plausiblen Schließen.

---




---


Lösungen  1 Fundstelle "plausib"

    Polya1962-1-S.363-57 (Lösungen): "40. Es gibt eine ₅₇plausible Vermutung: Das gleichseitige Dreieck hat bei gegebenem Flächeninhalt den kleinsten Umfang, oder bei gegebenem Umfang den größten Flächeninhalt.
 

Kommentar-Polya1962-1-S.363-57 (Lösungen): Wie zu erwarten wird auch im Abschnitt Lösung plausible Vermutung nicht erklärt.      Bisheriger Stand: von 1- keine Erklärung zur Plausibilität und zum plausiblen Schließen.