wie man unnötigerweise faktor-rückgerechnete Matrizen schönt
Aus: PAWLIK, K. (1968) Dimensionen des Verhaltens. Eine Einführung in Methodik und Ergebnisse faktorenanalytischer psychologischer Forschung. Bern: Huber. p.287-289
- Abstract und Zusammenfassung
- Einführung.
- Pawlik zu Rahmen und Hintergrund.
- Interkorrelationstabelle 10.1 von acht Lernabschnitten
- Tabellen 10.2 (Faktoren) und 10.3 (rückgerechnete Matrix)
- Matrixanalyse der Original Korrelationsmatrix: Die Matrixanalyse ergibt einen einzigen Eigenwert mit 86 % Varianzaufklärung, was für eine Generalfaktorlösung spricht.
- Exkurs: Generalfaktorprobe
- Rückgerechnete Matrix aus einem Generalfaktor
- Residualanalyse Original-Korrelationsmatrix und aus dem Generalfaktor rückgerechnete Matrix
- Von Sponsel richtig rückgerechnete Matrix aus den 2 Faktoren
- Matrixanalyse der aus den 2 Faktoren richtig rückgerechneten Matrix
- Residualanalyse zwischen originaler Korrelationsmatrix und der faktorrückgerechneten Matrix
- Matrixanalyse der aus den Faktoren rückgerechneten Korrelationsmatrix mit Hauptdiagonale gleich 1 gesetzt: wieder positiv definit.
- Diskussion
- Glosse zu den sieben goldenen Hauptspielregeln des "PSYCHOMETRIKERINNEN-Spiels"
- Vorschau und Querverweise
Abstract - Zusammenfassung
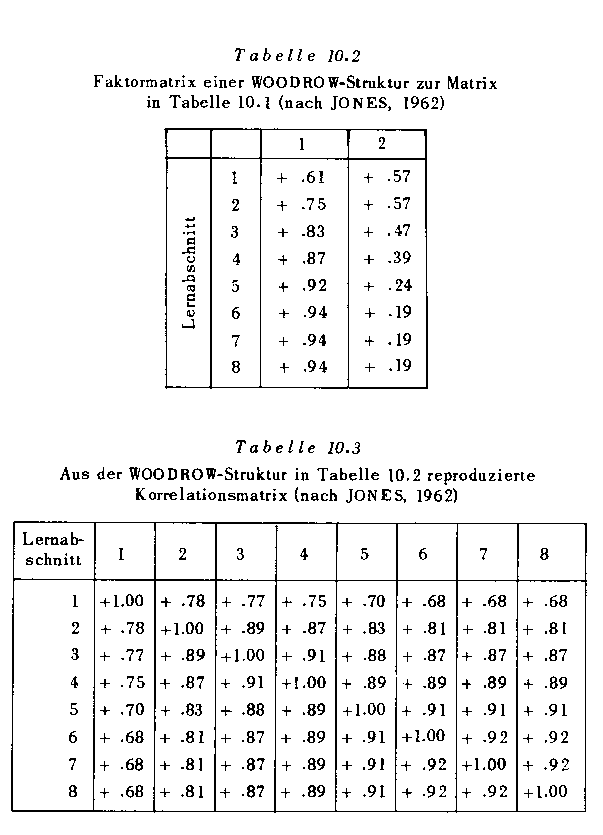
| Abstract - Zusammenfassung: PAWLIK (1968, S. 289) gibt in Tab.10.3 unter Berufung auf JONES (1962) eine 'Korrelationsmatrix' wieder, die aus der 2-Faktoren WOODROW- Struktur in Tab. 10.2 entstanden sein soll. Der Ausdruck 'Korrelationsmatrix' ist so nicht richtig und einer der häufigen Täuschungen faktorenanalytischer Veröffentlichungen, weil die Hauptdiagonalelemente nicht der korrekten Rechnung entsprechen, sondern einfach 1 gesetzt wurden ohne dies zu erwähnen. Das kann man tun, aber dann muß man es sagen. Die Tabelle ist auch entsprechend suggestiv überschrieben mit dem Titel "Aus der WOODROW- Struktur in Tabelle 10.2 reproduzierte Korrelationsmatrix (nach JONES, 1962)". Tatsächlich ergibt sich durch Rückrechnung der Faktormatrix eine vor allem in der Hauptdiagonalen phänotypisch wenig ähnliche Matrix im Vergleich zur ursprünglichen Korrelationsmatrix. Aber das täuscht - und nun echt ;-). Diese Matrix hat es wirklich in sich: Tatsächlich sind die vier negativen Eigenwerte nämlich sehr klein und daher ohne Probleme reparierbar. Daher zeigt auch eine genaue Analyse und Vergleich, daß die ursprüngliche Korrelationsmatrix für faktorenanalytische Verhältnisse ungewöhnlich und sehr gut reproduziert werden kann (wie im Verlauf dieser Gesamt- Dokumentation noch drastisch gezeigt wird), obwohl die Hauptdiagonalelemente teilweise recht erheblich von 1 abweichen. Das ist ein sehr interessanter Befund: Obwohl die aus den Faktoren reproduzierte Matrix mit einer Korrelationsmatrix in der Hauptdiagonalen wenig gemein hat (maximale Abweichung 0.30), also der Phänotyp sehr abweicht, ist der mathematisch entscheidende Genotyp tatsächlich sehr ähnlich [Zur Ähnlichkeit bei Matrizen], wie ein genauer Eigenwertvergleich zeigt. Inhaltlich überrascht, daß hier nicht von einer Generalfaktorstruktur ausgegangen wird, obwohl es nur einen großen Eigenwert mit 86 % (!) Varianzaufklärung gibt. Hier liegt es doch nun wirklich auf der Hand von einem einzigen General-Faktor, den wir Übungslernen nennen könnten, auszugehen. Wie kommt es, daß die FaktorenanalytikerInnen hier vor lauter Wald den nächstliegenden 1-General- Faktor- Baum nicht sehen? Merkwürdigerweise liefert Pawlik (p.93) eine Matrix für das Generalfaktormodell, das nicht die entfernteste Ähnlichkeit mit einer Generalfaktorlösung aufweist. Pawlik äußert sich nicht zur Problematik numerisch instabiler Matrizen, auch nicht dazu, wie man phänotypische und genotypische Matrizen unterscheidet und auch nicht dazu, wie man bösartig entgleiste Pseudo- Korrelations- Matrizen erkennt und behandelt, obwohl er eine solche Monster- Pseudo- Korrelationsmatrix in seinem Buch publiziert (Beleg: Simps14). |
Einführung.
Kurt
Pawliks Hauptwerk ist insofern außergewöhnlich als es die Faktorenanalyse
sehr eng mit ihren Ergebnissen für die Psychologie referiert. Allerdings
ist aufgrund meiner Ergebnisse und Kritik am faktorenanalytischen Gebaren
die Validität der referierten Studien sehr in Frage zu stellen. Ungeachtet
dessen kann Pawlik als bedeutender Faktorenanalytiker der Nachkriegspsychologie
in Deutschland betrachtet werden - den großen Alten (Spearman, Thurstone,
Cattell) verpflichtet und nahe. Trotzdem - oder vielleicht gerade deswegen
- übersah er wesentliche Probleme oder ignorierte sie in seinem Werk.
Positiv interpretiert, weil er wohl fasziniert und gebannt war von den
Möglichkeiten der Faktorenanalyse und weniger positiv, aber
nach Nietzsche sozusagen allzumenschlich wohl auch motiviert blind für
die grundlegende Aporie des faktorenanalytischen Ansatzes: wo keine Eigenwerte
gegen 0 gehen, ist Datenreduktion verantwortlich nicht möglich. Wie
im Laufe dieser Dokmentation aber immer wieder eindringlich dargelegt wird,
ist bereits die Fixierung auf die Datenreduktion ein grundlegendes Mißverständnis
und man verschenkt das wichtigste Implikat der Faktorenanalyse.
Die positiven Möglichkeiten und die Bedeutung, Eigenwerte nahe 0 zu
entdecken, hat Pawlik ebenso wenig erkannt, wie die meisten anderen FaktorenanalytikerInnen
auch.
Sie zogen es stattdessen wissenschaftsfremd vor, Eigenwerte mit 0 zu definieren
und haben damit das Wesen wissenschaftlichen Arbeitens auf den Kopf gestellt:
man muß Gesetzmäßigkeiten suchen, Hypothesen aufstellen
und sie erweisen oder widerlegen, aber kann sie nicht durch methodologischen
Beschluß am Schreibtisch definitorisch beschließen. Pawlik
erkannte wie seine klassischen Vorbilder auch nicht, daß Daten-Reduktion
nur in dem Maße möglich ist, wie die orignären Daten schon
Kollinearitäten - und d. h. Gesetzmäßigkeiten vom Typ lineare
Abhängigkeiten - enthalten.
Das andere grundlegende Problem, zu dem Pawlik sich nicht äußerte,
ist das tückische Problem der Positiven Definitheit. Damit ignorierte
Pawlik auch die notwendige Unterscheidung zwischen nur phänotypischen
(Schein-) und genotypischen (echten) Korrelationsmatrizen. Der Begriff
"positiv definit" - eine mathematisch notwendige Eigenschaft von rechenfähigen
Korrelationsmatrizen - kommt in seinem Sachregister nicht einmal vor, obwohl
er die Eigenschaft auf S. 455 zu den drei wichtigen Eigenwertsätzen
zählt und als erste aufführt. Pawlik erkennt nicht, daß
diese wichtige Eigenschaft nicht von Natur aus gegeben ist, sondern erfüllt
sein und die Erfüllung auch geprüft werden muß [Beleg:
Simps14].
Dafür entschädigt die Matrix mit der geheimnisvollen "Woodrow"-Struktur
ein wenig, denn diese hat es wirklich in sich.
Die tückischen numerischen Probleme, die Computerrechnen, Runden und
zahlreiche andere Prozeduren mit sich bringen, waren zu seiner Zeit (1968)
noch nicht so bekannt, obschon sie natürlich im Prinzip selbst Thurstone,
als noch mit Tischrechenmaschinen gerechnet wurde, hätte herausfinden
müssen. Während man aber zu Thurstones Zeiten Monate an einer
Faktorenanalyse rechnete, macht dies heute ein Computer in einer Sekunde.
Im folgenden werde ich einen seltsamen Befund zeigen. Nämlich, daß
die aus den Faktoren der Woodrow-Struktur rückgerechnete Matrix wenig
phänotypische und zugleich viel genotypische Ähnlichkeit
mit einer Korrelationsmatrix hat, obwohl sie ihre positive Definitheit
verliert und vier - allerdings sehr kleine und daher reparierbare - negative
Eigenwerte produziert. Dafür sind die Eigenwerte der originären
Korrelations- und der aus den Faktoren rückgerechneten Matrix sehr
ähnlich, so daß die faktor- rückgerechnete Matrix auch
ohne die illegitim und nicht ausgewiesene - hier ausnahmsweise unnötige
- Besetzung der Hauptdiagonalen mit 1 eine gute Repräsentation der
originären Korrelationsmatrix liefert.
|
|
Obwohl die Woodrow-Struktur, wenn sie denn empirisch gesichert sein sollte, ein interessantes lernpsychologisches Phänomen vorstellt, was gar nicht bestritten werden soll, geht es uns hier in erster Linie darum, zu zeigen, was genau für Matrizen entstehen, wenn man sie aus ihren Faktoren korrekt zurückrechnet. Zunächst aber, damit die Angelegenheit nicht so inhaltslos und trocken ist, wollen wir uns mit dem Hintergrund und Rahmen unserer Matrixanalyse beschäftigen. Zur Einführung in den Problemkreis lassen wir den Autor am besten selbst zu Wort kommen (Seite 287 - 289):
"10.2 "Molare Korrelationsanalyse" von Lerndaten
In der "molaren Korrelationsanalyse" ("molar correlational analysis"; M.B. JONES, 1959, 1960, 1962) wird die Korrelationsmatrix vor der Faktorenextraktion auf Besonderheiten in der Verteilung der Korrelationskoeffizienten untersucht. Daraus wird versucht, eine spezielle Faktorstruktur der Variablen im voraus anzugeben, deren Parameter (Faktorenladungen, Kommunalitäten) anschließend geschätzt werden.
Besondere Korrelationsstrukturen, wie sie die molare Korrelationsanalyse vor Augen hat, wurden bisher vor allem für Übungsmatrizen bestätigt, d.h. für die Interkorrelationen der aufeinanderfolgenden Prüfungen (Durchgänge) in einem Lernexperiment. In allen untersuchten Übungsmatrizen (s. die Literaturhinweise bei JONES, 1962; ferner auch: HUMPHREYS, 1960; PAWLIK, 1965b) stehen die höchsten Korrelationen unmittelbar neben der Hauptdiagonale und die Höhe der Korrelationen nimmt von da gegen die rechte obere (linke untere) Ecke der Korrelationsmatrix ab. JONES (1962) nannte diese Korrelationsstruktur Supradiagonalform. Tabelle. 10.1 [> S. 288] zeigt dazu ein Beispiel (aus JONES, 1962; nach einer Untersuchung von A. BILODEAU). Die Variablen sind acht aufeinanderfolgende Prüfungen in einem schwierigen Reaktionsversuch. Wie man sieht, korrelieren zwei Versuchsdurchgänge um so höher, je näher sie zeitlich beieinander liegen, je weniger zusätzliche Übung dazwischen liegt.
Tabelle 10.1 Interkorrelationen von acht Lernabschnitten
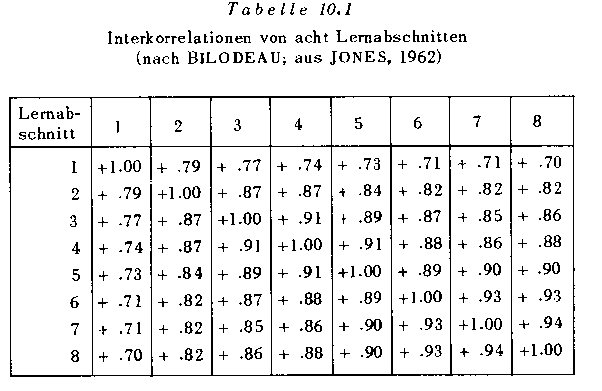
Bereits Ende der Dreißigerjahre hat der amerikanische Psychologe H. WOODROW (1939) für eine solche Supradiagonalform ein Zweifaktoren-Modell vorgeschlagen, aus dem viele Übungsmatrizen eine sehr einfache Erklärung finden. Sämtliche Faktorenladungen dieser WOODROW-Struktur sind nichtnegativ. Wurden die Übungsabschnitte in Übereinstimmung mit ihrer zeitlichen Aufeinanderfolge gereiht und ist g < i, so gilt für die Ladungen im ersten WOODROW- Faktor:
Für die Ladungen im zweiten WOODROW-Faktor:
ag2 >= ai2 ,
Tabelle 10.2 (nach JONES, l962) zeigt eine solche WOODROW-Lösung zur Übungsmatrix in Tabelle 10.1. Die daraus repro- [> S. 289] duzierte Korrelationsmatrix ist in Tabelle 10.3 angeführt; wie man sieht, gibt die WOODROW-Lösung bereits eine sehr gute Annäherung der Interkorrelationen. Übung kann als ein zweifaktorieller Prozeß verstanden werden, in dessen Verlauf die Bedeutung des einen Faktors zu-, die des anderen abnimmt.
Tabellen 10.2 (Faktoren) und 10.3 ('rückgerechnete' Matrix)
Matrixanalyse
der Original Korrelationsmatrix
|
Numerische Laien hier und Professionell Interessierte hier Bemerkung: Diese SMA enthält noch nicht alle erklärten Kriterien, da Prg-Version 6, nicht 9. Samp Or MD NumS Condit Determinant
HaInRatio R_OutIn K_Norm C_Norm
Datenquelle: PAWLIK,K. (GER: University Hamburg. Dimensionen des Verhaltens. Bern 1968, p.288 BIL8.K08 (from BILODEAU from JONES) Die Original Korrrelationsmatrix ist positiv definit und daher multivariat und auch faktorenanalytisch behandelbar. Wichtiges Nebenergebnis: Die Matrixanalyse zeigt einen einzigen großen Eigenwert mit 86% Varianzaufklärung, was für eine Generalfaktorlösung spricht. Weshalb dieser Hypothese nicht nachgegangen wurde, obwohl sie doch wirklich auf der Hand liegt, ist mir unklar geblieben. |
**********
Summary of standard
correlation matrix analysis ***********
File =
BIL8.K08 N-order= 8 N-sample=-1
Rank= 8 Missing data = ?
Positiv Definit=Cholesky successful________=
Yes with 0 negat. eigenvalue/s
HEVA: Highest eigenvalue abs.value_________=
6.9104764217122781
LEVA: Lowest eigenvalue absolute value_____=
.05485181505676583
CON: Condition number HEVA/LEVA___________~=
125.98446221990404
DET: Determinant original matrix___________=
2.8205583733505296D-6
HAC: HADAMARD condition number_____________=
2.2019696395939921D-9
HCN: Heuristic condition |DET|CON__________=
2.2388144725555808D-8
D_I: Determinant Inverse absolute value____=
354540
HDA: HADAMARD Inequality absolute value___<=
46437522
HIR: HADAMARD RATIO: D_I / HDA ____________=
7.6347684945572082D-3
Highest inverse positive diagonal value____=
11.809356557
thus multiple r( 8.rest)________________=
.956724297
There are no negative inverse diagonal values.
Maximum range (upp-low) multip-r( 1.rest)_=
7E-3
LES: Numerical stability analysis:
Ratio maximum range output / input
_______= 1.0396657943969279
PESO-Analysis correlation least Ratio RN/ON=
.02889 (<-> Angle = 1.66 )
Number of Ratios correlation RN/ON < .01__
= 0
PESO-Analysis Cholesky least Ratio RN/ON__
= .290996 (<-> Angle = 16.92 )
Number of Ratios Cholesky RN/ON < .1 _____
= 0
Ncor L1-Norm L2-Norm
Max Min m|c| s|c|
N_comp M-S S-S
64 55.2
6.93 1 .7
.842 .07 378
.081 .061
class
boundaries and distribution of the correlation-coefficients
-1 -.8 -.6 -.4
-.2 0 .2 .4 .6
.8 1
0 0
0 0 0 0
0 0 14 50
Original
input data with 2-digit-accuracy and read with
2-digit-accuracy
(for control here the analysed original matrix):
1 .79 .77
.74 .73 .71 .71 .7
.79 1 .87
.87 .84 .82 .82 .82
.77 .87 1
.91 .89 .87 .85 .86
.74 .87 .91 1
.91 .88 .86 .88
.73 .84 .89 .91
1 .89 .9 .9
.71 .82 .87 .88
.89 1 .93 .93
.71 .82 .85 .86
.9 .93 1 .94
.7 .82 .86
.88 .9 .93 .94 1
i.Eigenvalue Cholesky
i.Eigenvalue Cholesky i.Eigenvalue Cholesky
1. 6.91048 1
2. .42623 .6131
3. .21394 .4742
4. .14038
.383 5. .10278 .3837
6. .08404 .4112
7. .06729
.3284 8. .05485 .291
Cholesky decomposition successful,
thus the matrix is (semi) positive definit.
Faktormatrix
F:
.778 0
0 0 0
0 0 0
.908 0
0 0 0
0 0 0
.947 0
0 0 0
0 0 0
.952 0
0 0 0
0 0 0
.943 0
0 0 0
0 0 0
.942 0
0 0 0
0 0 0
.942 0
0 0 0
0 0 0
.942 0
0 0 0
0 0 0
Transpose
Factor Matrix F' :
.778 .908 .947
.952 .943 .942 .942 .942
0 0
0 0 0
0 0 0
0 0
0 0 0
0 0 0
0 0
0 0 0
0 0 0
0 0
0 0 0
0 0 0
0 0
0 0 0
0 0 0
0 0
0 0 0
0 0 0
0 0
0 0 0
0 0 0
Reproduction
Matrix F * F' with DET= 0
.605 .706 .737
.74 .734 .733 .733 .733
.706 .824 .859
.864 .856 .855 .855 .855
.737 .859 .896
.901 .893 .892 .892 .892
.74 .864 .901
.905 .898 .897 .897 .897
.734 .856 .893
.898 .89 .889 .889 .889
.733 .855 .892
.897 .889 .888 .888 .888
.733 .855 .892
.897 .889 .888 .888 .888
.733 .855 .892
.897 .889 .888 .888 .888
Interne
Belege und Quelldaten:
Analysis from 05/01/01 23:03:12
with KORFAK1.BAS (08/31/94)
8 Factors data from file C:\OMI\NUMERIK\MATRIX\SMA\PAW289FD\PAW289F1.FAK
Reproduction matrix in C:\OMI\NUMERIK\MATRIX\FAK\NEU\PAW289F1.IMA
Reproduction correlations in C:\OMI\NUMERIK\MATRIX\FAK\NEU\PAW289FD.F08
Residualanalyse
Original-Korrelationsmatrix und aus dem Generalfaktor rückgerechnete
Matrix
*******************
Residual analysis *********************
Matrix residuals (whole matrix inclusive
diagonal):
Mean absolute values of residuals
= .040561766812846954
Sigma absolute values of residuals
= .056449675043972028
Maximum range absolute values =
.39487229169233095 (r1.1)
Matrix residuals upper triangular matrix without
diagonal:
Mean absolute values of residuals
= .024657598760838306
Sigma absolute values of residuals
= .01833573
Maximum range absolute values =
.083974827327747389 (r1.2)
Residual-Analysis: Mean= .04056177 Sigma= .05644968 Maximum range= .39487229 (r1.1)
Matrix A:
1 .79
.77 .74 .73 .71 .71
.7
.79 1
.87 .87 .84 .82 .82
.82
.77 .87 1
.91 .89 .87 .85 .86
.74 .87 .91
1 .91 .88 .86
.88
.73 .84 .89
.91 1 .89 .9
.9
.71 .82 .87
.88 .89 1 .93
.93
.71 .82 .85
.86 .9 .93 1
.94
.7 .82
.86 .88 .9 .93 .94
1
Matrix B:
.605 .706 .737 .74
.734 .733 .733 .733
.706 .824 .859 .864
.856 .855 .855 .855
.737 .859 .896 .901
.893 .892 .892 .892
.74 .864 .901
.905 .898 .897 .897 .897
.734 .856 .893 .898
.89 .889 .889 .889
.733 .855 .892 .897
.889 .888 .888 .888
.733 .855 .892 .897
.889 .888 .888 .888
.733 .855 .892 .897
.889 .888 .888 .888
Matrix of residuals:
.395 .084 .033 0
-4E-3 -.023 -.023 -.033
.084 .176 .011 6E-3
-.016 -.035 -.035 -.035
.033 .011 .104 9E-3
-3E-3 -.022 -.042 -.032
0 6E-3
9E-3 .095 .012 -.017 -.037 -.017
-4E-3 -.016 -3E-3 .012 .11
1E-3 .011 .011
-.023 -.035 -.022 -.017 1E-3
.112 .042 .042
-.023 -.035 -.042 -.037 .011
.042 .112 .052
-.033 -.035 -.032 -.017 .011
.042 .052 .112
[Interne Datenquellen: Matrix RES(iduals)
in C:\OMI\NUMERIK\MATRIX\K\B\BIL8.RES
Analysis
from 05/01/01 23:09:52]
Matrixanalyse
der aus einem einzigen Faktor rückgerechneten Matrix
|
Numerische Laien hier und Professionell Interessierte hier Bemerkung: Diese SMA enthält noch nicht alle erklärten Kriterien, da Prg-Version 6, nicht 9. Samp Or MD NumS Condit Determinant
HaInRatio R_OutIn K_Norm C_Norm
Primär-Datenquelle: PAWLIK,K. (GER: University Hamburg. Dimensionen des Verhaltens. Bern 1968, p.288 BIL8.K08 (from BILODEAU from JONES) Matrizen sind von Haus aus numerisch sehr
sensible, d. h. instabile Gebilde und sie werden umso instabiler je näher
Eigenwerte in die "Nähe"
von 0 und damit in die Nähe der Singularität gelangen. Das kann
man hier sehr schön sehen. Faktorenanalytische Datenreduktion gelingt
nur um den Preis der Singularität und das heißt numerische
Instabilität im Maximalbereich - ein paradox anmutender Sachverhalt.
|
**********
Summary of standard
correlation matrix analysis ***********
File
= PAW289FO.F08 N-order= 8 N-sample=?
Rank= 6 Missing data = ?
Positiv Definit=Cholesky successful________=
No with 5 negat. eigenvalue/s
HEVA: Highest eigenvalue abs.value_________=
6.7848724545847401
LEVA: Lowest eigenvalue absolute value______=
0
CON: Condition number HEVA/LEVA____________~=
>>>>>>>>
DET: Determinant original matrix___________=
0
HAC: HADAMARD condition number_____________=
0
HCN: Heuristic condition |DET|CON__________=
0
D_I: Determinant Inverse absolute value____=
>>>>>>>>
HDA: HADAMARD Inequat.Amount 1/DET________<=
0
HIR: HADAMARD RATIO: D_I / HDA ____________=
>>>>>>>>
LES: Numerical stability analysis:
Linear Equation Solution not possible
thus matrix (on 3-digit accuracy)
singular.
PESO-Analysis correlation least Ratio RN/ON=
0 (<-> Angle = 0 )
Number of Ratios correlation RN/ON < .01__
= 7
PESO-Analysis Cholesky least Ratio RN/ON__
= (Not positiv definit)
Ncor L1-Norm L2-Norm
Max Min m|c| s|c|
N_comp M-S S-S
64 54.1
6.78 .905 .605 .845
.067 378 .069 .068
class boundaries and distribution of
the correlation coefficients
-1 -.8 -.6 -.4
-.2 0 .2 .4 .6
.8 1
0 0
0 0 0 0
0 0 15 49
Original data with 17, input read with
17, computet with 19,
and showed with 4 digit accuracy
(for control here the analysed original matrix):
.6051 .706 .7365
.7402 .7337 .7331 .7331 .7331
.706 .8237 .8593
.8636 .8561 .8553 .8553 .8553
.7365 .8593 .8965
.901 .893 .8923 .8923 .8923
.7402 .8636 .901
.9055 .8975 .8968 .8968 .8968
.7337 .8561 .893
.8975 .8897 .8889 .8889 .8889
.7331 .8553 .8923
.8968 .8889 .8881 .8881 .8881
.7331 .8553 .8923
.8968 .8889 .8881 .8881 .8881
.7331 .8553 .8923
.8968 .8889 .8881 .8881 .8881
i.Eigenvalue Cholesky
i.Eigenvalue Cholesky i.Eigenvalue Cholesky
1. 6.78487 .7779
2. 0 0
3. 0 0
4. 0
-.8117 5. 0
-1.6031 6. 0
-2.3905
7. 0
-3.1793 8. 0
-3.9681
The matrix is not positive definit.
Cholesky decomposition is not successful.
Eigenvalues in per cent of trace =
6.7848724545847401
1 100 2 0
3 0 4 0
5 0 6 0
7 0
8 0
analysed: 05/01/01 23:04:48 PRG
version 05/24/94 MA9.BAS
Gesamtzeit_____________ 47.205
Rang_____________
.25
Determinante_____
5E-3
Eigenwerte/Vekt__
0
Peso Kor+Chol____
.37
NuStabAnalyse____ nicht
ausgefuehrbar
Statistik________
.08
File = C:\OMI\NUMERIK\MATRIX\SMA\PAW289FO\PAW289FO.SMA
with data from C:\OMI\NUMERIK\MATRIX\SMA\PAW289FO\PAW289FO.F08
Date: 05/01/01 Time:23:04:48
Von Sponsel richtig rückgerechnete Matrix aus den 2 Faktoren
Auswertung vom 11.04.94 23:18:14
.61 .57
.75 .57
.83 .47
.87 .39
.92 .24
.94 .19
.94 .19
.94 .19
Ursprungsmatrix B
.61 .75 .83
.87 .92 .94 .94 .94
.57 .57 .47
.39 .24 .19 .19 .19
Produkt-Matrix A * B mit Determinante=
0
.7 .78
.77 .75 .7 .68 .68
.68
.78 .89 .89
.87 .83 .81 .81 .81
.77 .89 .91
.91 .88 .87 .87 .87
.75 .87 .91
.91 .89 .89 .89 .89
.7 .83
.88 .89 .90 .91 .91
.91
.68 .81 .87
.89 .91 .92 .92 .92
.68 .81 .87
.89 .91 .92 .92 .92
.68 .81 .87
.89 .91 .92 .92 .92
[Interne Datenquellen: Daten in C:\OMI\NUMERIK\MATRIX\FAK\PAW289FD.IMA
Ursprungsmatrix A von C:\OMI\NUMERIK\MATRIX\FAK\PAW289FD.FAK
Faktorrückgerechnete Korrelationen mit
ohne HD=h in:
C:\OMI\NUMERIK\MATRIX\FAK\PAW289FD.F08
Matrixanalyse der aus den 2 Faktoren richtig rückgerechneten Matrix
PAWLIK,K.
(GER: University Hamburg). "Dimensionen des Verhaltens" Bern 1968
(3b')
p.289 Richtige (Sponsel rueckgerechnete) Tabelle 10.3
(Data
from JONES "Practice as a process of simplification",
Psychol.
Review, 1962, 69, 274-294)
|
Numerische Laien hier und Professionell Interessierte hier Bemerkung: Diese SMA enthält noch nicht alle erklärten Kriterien, da Prg-Version 6, nicht 9. Samp Or MD NumS Condit Determinant HaInRatio R_OutIn K_Norm C_Norm -1 8 -1 --4 1.1D+18 0, Rank= 6! infinite impos. 0(6) -1(-1) Residual-Analysis: Mean= .026 Sigma= .043 Maximum range= .3 (r1.1) Primär-Datenquelle: PAWLIK,K. (GER: University Hamburg. Dimensionen des Verhaltens. Bern 1968, p.288 BIL8.K08 (from BILODEAU from JONES)
|
************
Summary of the
correlation matrix analysis ***************
calculated backword from factors
File = PAW289FD.F08 N-order= 8
N-sample=-1 Rank= 6 Missing data = ?
Positiv Definit=Cholesky successful________=
No with 4 negat. eigenvalue/s
HEVA: Highest eigenvalue abs.value_________=
6.7848724545847401
LEVA: Lowest eigenvalue absolute value______=
0
CON: Condition number HEVA/LEVA____________~=
>>>>>>>>
DET: Determinant original matrix___________=
0
HAC: HADAMARD condition number_____________=
0
HCN: Heuristic condition |DET|CON__________=
0
D_I: Determinant Inverse absolute value____=
>>>>>>>>
HDA: HADAMARD Inequat.Amount 1/DET________<=
0
HIR: HADAMARD RATIO: D_I / HDA ____________=
>>>>>>>>
LES: Numerical stability analysis:
Linear Equation Solution not possible
thus matrix (on 3-digit accuracy)
singular.
PESO-Analysis correlation least Ratio RN/ON=
0 (<-> Angle = 0 )
Number of Ratios correlation RN/ON < .01__
= 6
PESO-Analysis Cholesky least Ratio RN/ON__
= (Not positiv definit)
Ncor L1-Norm L2-Norm
Max Min m|c| s|c|
N_comp M-S S-S
64 54.1
6.79 .92 .68 .84
.078 378 .087 .072
class boundaries and distribution of
the correlation-coefficients
-1 -.8 -.6 -.4
-.2 0 .2 .4 .6
.8 1
0 0
0 0 0 0
0 0 15 49
Original input data with 2-digit-accuracy
and read with
2-digit-accuracy (for control here
the analysed original matrix):
.7 .78 .77 .75
.7 .68 .68 .68
.78 .89 .89 .87
.83 .81 .81 .81
.77 .89 .91 .91
.88 .87 .87 .87
.75 .87 .91 .91
.89 .89 .89 .89
.7 .83 .88
.89 .9 .91 .91 .91
.68 .81 .87 .89
.91 .92 .92 .92
.68 .81 .87 .89
.91 .92 .92 .92
.68 .81 .87 .89
.91 .92 .92 .92
i.Eigenvalue Cholesky
i.Eigenvalue Cholesky i.Eigenvalue Cholesky
1. 6.78487 .8367
2. .27827 .1444
3. 9.14D-3 .1179
4. 6.65D-3 -.0254
5. 0 -.7917
6. 0 -1.6174
7. -2.76D-3 -2.4638
8. -6.17D-3 -3.3102
The matrix is not positive definit.
Cholesky decomposition is not success-
ful (for detailed information Cholesky's
diagonalvalues are presented).
analysed: 11.04.94 23:32:08 PRG version
04/04/94 MA6.BAS
Gesamtzeit_____________ 53
Residualanalyse zwischen originaler Korrelationsmatrix und der faktorrückgerechneten Matrix
Matrix A:
.7 .78 .77
.75 .7 .68 .68 .68
.78 .89 .89 .87
.83 .81 .81 .81
.77 .89 .91 .91
.88 .87 .87 .87
.75 .87 .91 .91
.89 .89 .89 .89
.7 .83 .88
.89 .9 .91 .91 .91
.68 .81 .87 .89
.91 .92 .92 .92
.68 .81 .87 .89
.91 .92 .92 .92
.68 .81 .87 .89
.91 .92 .92 .92
Matrix B:
1 .79 .77
.74 .73 .71 .71 .7
.79 1 .87
.87 .84 .82 .82 .82
.77 .87 1
.91 .89 .87 .85 .86
.74 .87 .91 1
.91 .88 .86 .88
.73 .84 .89 .91
1 .89 .9 .9
.71 .82 .87 .88
.89 1 .93 .93
.71 .82 .85 .86
.9 .93 1 .94
.7 .82 .86
.88 .9 .93 .94 1
*******************
Residual analysis *********************
Matrix residuals (whole matrix inclusive
diagonal):
Mean absolute values of residuals
= .026
Sigma absolute values of residuals
= .043
Maximum range absolute values =
.3 (r1.1)
Matrix residuals upper triangular matrix without
diagonal:
Mean absolute values of residuals
= .014
Sigma absolute values of residuals
= 9D-3
Maximum range absolute values =
.03 (r1.5)
Residual-Analysis: Mean= .026 Sigma= .043 Maximum range= .3 (r1.1)
Matrix of residuals:
-.3 -.01 0
.01 -.03 -.03 -.03 -.02
-.01 -.11 .02
0 -.01 -.01 -.01 -.01
0 .02
-.09 0 -.01 0
.02 .01
.01 0
0 -.09 -.02 .01 .03
.01
-.03 -.01 -.01 -.02
-.1 .02 .01 .01
-.03 -.01 0
.01 .02 -.08 -.01 -.01
-.03 -.01 .02
.03 .01 -.01 -.08 -.02
-.02 -.01 .01
.01 .01 -.01 -.02 -.08
[Interne Quelldaten: Matrix A von C:\OMI\NUMERIK\MATRIX\FAK\PAW289FD.F08
Matrix B von C:\OMI\NUMERIK\MATRIX\K\B\BIL8.K08
Matrix RES in C:\OMI\NUMERIK\MATRIX\FAK\PAW289FD.RES
Auswertung vom 11.04.94 23:25:14]
Matrixanalyse
der aus den Faktoren rückgerechneten Korrelationsmatrix mit Hauptdiagonale
gleich 1 gesetzt.
|
Numerische Laien hier und Professionell Interessierte hier Bemerkung: Diese SMA enthält noch nicht alle erklärten Kriterien, da Prg-Version 6, nicht 9. Result abstract PAW289_1.F08 Result abstract
Residual-Analysis: Mean= .026 Sigma= .043 Maximum range= .3 (r1.1) Primär-Datenquelle: PAWLIK,K. (GER: University Hamburg. Dimensionen des Verhaltens. Bern 1968, p.288 BIL8.K08 (from BILODEAU from JONES) S. 289 Reproduzierte Korrelationsmatrix nach Jones 1962 wobei in
die Hauptdiagonale 1 eingesetzt wurde. Die Matrix wird durch die Ersetzung
der Hauptdiagonalen wieder positiv definit.
|
**********
Summary of standard
correlation matrix analysis ***********
File = PAW289_1.F08 N-order= 8
N-sample=? Rank= 8 Missing data = ?
Positiv Definit=Cholesky successful________=
Yes with 0 negat. eigenvalue/s
HEVA: Highest eigenvalue abs.value_________=
6.8939838452974744
LEVA: Lowest eigenvalue absolute value_____=
.079999999999999997
CON: Condition number HEVA/LEVA___________~=
86.174798066218433
DET: Determinant original matrix (OMIKRON)_=
3.3293883456D-6
DET: Determinant (CHOLESKY-Diagonal^2)_____=
3.3293883456D-6
DET: Determinant (PESO-CHOLESKY)___________=
3.3293883456D-6
DET: Determinant (product eigenvalues)_____=
3.3293883455999993D-6
DET: Determ.abs.val.(PESO prod.red.norms)__=
3.3293883456D-6
HAC: HADAMARD condition number_____________=
2.6531101087143035D-9
HCN: Heuristic condition |DET|CON__________=
3.8635290366931079D-8
D_I: Determinant Inverse absolute value____=
300355
HDA: HADAMARD Inequality absolute value___<=
25029543
HIR: HADAMARD RATIO: D_I / HDA ____________=
.012000037982558444
Highest inverse positive diagonal value____=
9.65369444
thus multiple r( 6.rest)_________________=
.946790745
There are no negative inverse diagonal values.
Maximum range (upp-low) multip-r( 1.rest)_=
7E-3
LES: Numerical stability analysis:
Ratio maximum range output / input
_______= 1.9541240933876713
PESO-Analysis correlation least Ratio RN/ON=
.037365 (<-> Angle = 2.14 )
Number of Ratios correlation RN/ON < .01__
= 0
PESO-Analysis Cholesky least Ratio RN/ON__
= .32185 (<-> Angle = 18.77 )
Number of Ratios Cholesky RN/ON < .1 _____
= 0
Ncor L1-Norm L2-Norm
Max Min m|c| s|c|
N_comp M-S S-S
64 55
6.92 1 .68
.84 .078 378
.087 .072
class boundaries and distribution of
the correlation coefficients
-1 -.8 -.6 -.4
-.2 0 .2 .4 .6
.8 1
0 0
0 0 0 0
0 0 14 50
Original data with 2, input read with
2, computet with 19,
and showed with 2 digit accuracy
(for control here the analysed original matrix):
1 .78 .77
.75 .7 .68 .68 .68
.78 1 .89
.87 .83 .81 .81 .81
.77 .89 1
.91 .88 .87 .87 .87
.75 .87 .91 1
.89 .89 .89 .89
.7 .83 .88
.89 1 .91 .91 .91
.68 .81 .87 .89
.91 1 .92 .92
.68 .81 .87 .89
.91 .92 1 .92
.68 .81 .87 .89
.91 .92 .92 1
i.Eigenvalue Cholesky
i.Eigenvalue Cholesky i.Eigenvalue Cholesky
1. 6.89398 1
2. .46958 .6258
3. .19325 .4396
4. .10521
.3914 5. .09289 .4216
6. .08508 .3708
7. .08
.3368 8. .08
.3218
Cholesky decomposition successful,
thus the matrix is (semi) positive definit.
Eigenvalues in per cent of trace =
8
1 .8617 2 .0587
3 .0242 4 .0132 5 .0116 6 .0106
7 .01 8 .01
analysed: 05/01/01 20:02:54 PRG
version 05/24/94 MA9.BAS
Gesamtzeit_____________ 53.735
Rang_____________
0
Determinante_____
.01
Eigenwerte/Vekt__
0
Peso Kor+Chol____
1.585
NuStabAnalyse____
.165
Statistik________
.08
File = C:\OMI\NUMERIK\MATRIX\SMA\PAW289_1\PAW289_1.SMA
with data from C:\OMI\NUMERIK\MATRIX\SMA\PAW289_1\PAW289_1.F08
Date: 05/01/01 Time:20:02:54
Eigenwertvergleiche Original Korrelationsmatrix und faktorrückgerechnete Matrix
Man beachte,
daß sich bei den faktorrückgerechneten Matrizen die Eigenwerte
bei praktisch 0 durch eben diese Vorgabe erklären. Eine solche Vorgabe
ist nur gerechtfertigt, wenn die Original Korrelations-Matrix das von ihrer
Eigenwertstruktur hergibt, was hier der Fall ist. Zum
intuitiven und mathematischen Begriff der Ähnlichkeit von Matrizen
siehe bitte hier. So grob aus der Anschauung heraus meine ich, daß
hier eine Faktorenanalyse wirklich gerechtfertigt ist. Im Gegensatz zu
Jones und Pawlik meine ich, daß diese Eigenwertstruktur für
eine Generalfaktorlösung und nicht für eine zweifaktorielle,
sog. "Woodrow"-Struktur spricht:
| Originalmatrix nach Tabelle 10.1 (von
Bilodeau nach Jones)
6.9104764217122781
|
Eigenwerte der aus den zwei Faktoren von
mir reproduzierten Woodrow- Matrix (6 EW=0 Vorgabe)
6.7848724545847401
|
Eigenwerte der 1-Generalfaktorlösung
(7 EW=0 Vorgabe) 6.7848724545847401
|
Während das Beispiel der angeblich zweifaktoriellen Woodrow-Struktur viel besser als einfaktorielles Generalfaktor Modell paßt, zeigt das Beispiel Pawliks für das Generalfaktor Modell genau das Gegenteil und ist als Beispiel für ein Generalfaktor Modell völlig ungeeignet (Eigenwerte: 2.387, .894, .795, .585, .337; hier klärt der größte Eigenwert und "Generalfaktor" noch nicht einmal 50 % der Varianz auf, also weit weniger als der - echte - Generalfaktor in der angeblichen zweifaktoriellen Woodrow-Struktur mit 86 %). Obwohl Pawlik (S. 95) schreibt: "Satz 4.1 Das Generalfaktormodell setzt Variable voraus, deren Interkorrelationen aus einem einzigen Faktor erklärbar sind;". Und S. 98: "Satz 4.2: Im Generalfaktormodell wird vorausgesetzt, daß der reduzierte Rang der Korrelationsmatrix Eins ist." Die Formulierung "wird vorausgesetzt" ist mehrdeutig und kritisch zu beleuchten. Korrekt muß das meiner Meinung nach lauten: Eine Generalfaktorlösung setzt einen Rang 1 voraus, was zu zeigenist. Man kann nicht voraussetzen, was zu zeigen ist, was ein circulus vitiosus wäre. Auch an dieser Formulierung sieht man wieder, wie die Wissenschaft von vielen FaktorenanalytikerInnen auf den Kopf gestellt wird.
Wir schließen diese 3. Dokumentation daher mit etwas bissigem schwarzen Humor: