Internet Publikation für Allgemeine und Integrative Psychotherapie
    IP-GIPT DAS=06.12.2005 Internet-Erstausgabe, letzte Änderung TMJ
    Impressum: Diplom-PsychologInnen Irmgard Rathsmann-Sponsel und Dr. phil. Rudolf Sponsel
    Stubenlohstr. 20     D-91052 Erlangen Mail:_sekretariat@sgipt.org_
    Anfang_ Coombs 1941 _ Überblick _Relativ Aktuelles  _Rel. Beständiges  _Titelblatt  _ Konzept  _ Archiv _ Region _ Service iec-verlag  _Mail: Sekretariat@sgipt.org  _ Zitierung & Copyright _ _ Wichtige Hinweise zu Links und Empfehlungen
    Willkommen in der Abteilung Wissenschaftstheorie, Methodologie und Statistisch-Mathematische Methoden in der Allgemeinen und Integrativen Psychologie, Psychodiagnostik und Psychotherapie hier zum Thema Numerisch instabile Matrizen imd Kollinearität in der Psychologie und Psychotherapie:
    Standard-Matrix-Analyse
    Coombs, C.H. (1941). A criterion for significant common factor variance. Psychometrika 6, 267-272.
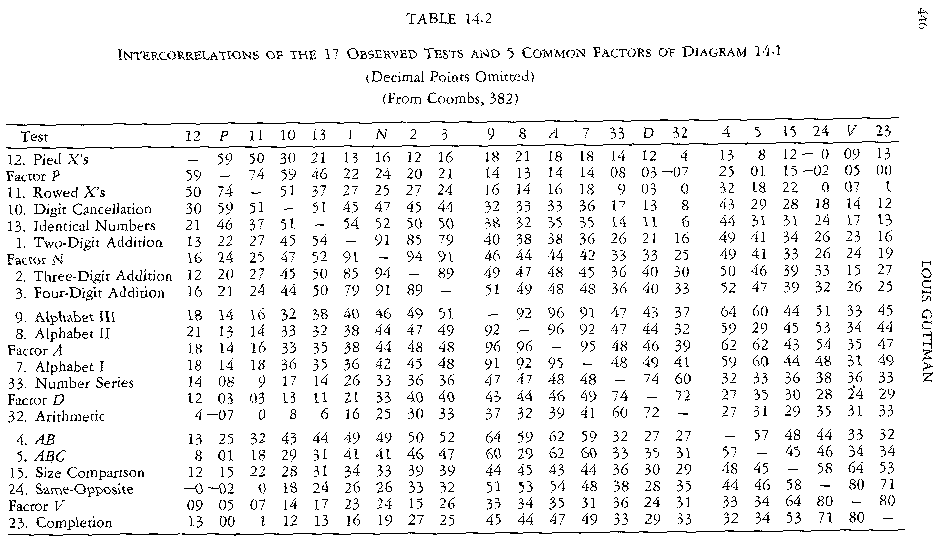
    In: Guttman, Louis (1966). Order Analysis Of Correlation Matrices, p. 446.
    In: Cattell, Raymond B. (1966, Ed.). Handbook Of Multivariate Experimental Psychology. Chicago: Rand & McNally.

    Permutation und Determinanten Graphik 4 k

    von Rudolf Sponsel, Erlangen
    Zusammenfassung - Summary - Abstract: Die Matrix vom Coombs ist nicht positiv semidefinit, sie ist indefinit mit zwei größeren negativen negativen Eigenwerten (-.02013 und -.07025) entgleist, die durch Rundungsfehler nicht erklärbar sind. Das heißt, die Korrelationen müssen in unzulässiger Weise gewonnen  worden sein. Damit ist die phänomenologisch erscheinende Matrix  im mathematischen Sinne keine "genotypische" (echte) Korrelationsmatrix (Produkt-Moment oder Bravais Pearson). Die Entgleisung zeigt sich sehr drastisch durch einen multiplen Korrelationskoeffizienten von 1.5715 (!) und insgesamt 5 multiplen Korrelationskoeffizienten > 1. 
    Samp _Ord_ MD_ NumS_ Condition_Determinant_HaInRatioR_ OutInK_ Norm_  C Norm 
     ?    22   -1  --2    452.8       0         8.34D-11   44.8   .013(0)  -1(-1)
    Erläuterungen zur Matrixanalyse:  Numerische Laien hier    und      Professionell Interessierte hier

    **********    Summary of standard correlation matrix analysis  ***********
    File = coombs41.k22  N-order= 22  N-sample=?     Rank= 22  Missing data = ?
    Positiv Definit=Cholesky successful________= No with  2 negat. eigenvalue/s
    HEVA: Highest eigenvalue abs.value_________=    9.1144109647408429
    LEVA: Lowest eigenvalue absolute value_____=    .020127036090946055
    CON: Condition number HEVA/LEVA___________~=    452.84417057516329
    DET: Determinant original matrix (OMIKRON)_=    6.0403604739505258D-11
    DET: Determinant (CHOLESKY-Diagonal^2)_____=   -999 (not positive definit)
    DET: Determinant (PESO-CHOLESKY)___________=   -999 (not positive definit)
    DET: Determinant (product eigenvalues)_____=    6.0403604739505181D-11
    DET: Determ.abs.val.(PESO prod.red.norms)__=    6.0403604739505258D-11
    HAC: HADAMARD condition number_____________=    4.1650445190459257D-18
    HCN: Heuristic condition |DET|CON__________=    1.3338717524570506D-13
    D_I: Determinant Inverse absolute value____=    16555303352
    HDA: HADAMARD Inequality absolute value___<=    1.9843086250570484D+20
    HIR: HADAMARD RATIO: D_I / HDA ____________=    8.3431091024188185D-11
    Highest inverse positive diagonal value____=    14.081193508
      thus multiple r( 10.rest)_________________=   .963837794
    Highest inverse negative diagonal value____=   -.680449043
      thus multiple r( 22.rest)_________________=   1.571501754 (!)
      and there are  5 multiple r > 1 (!)
     Maximum range (upp-low) multip-r( 22.rest)_=   2.509
    LES: Numerical stability analysis:
     Ratio maximum range output / input _______=    44.751549794654189
    PESO-Analysis correlation least Ratio RN/ON=    .013422 (<-> Angle = .77 )
    Number of Ratios correlation RN/ON < .01__ =    0
    PESO-Analysis Cholesky least Ratio RN/ON__ = (Not positiv definit)

     Ncor  L1-Norm  L2-Norm  Max  Min    m|c|   s|c|  N_comp   M-S   S-S
      484    190.2      10.17        1   -.07    .364     .209     26565     .231  .186

     class boundaries and distribution of the correlation coefficients
     -1  -.8  -.6  -.4  -.2   0    .2   .4   .6   .8   1
        0    0    0    0    12   98   170  138  22   44

    Original data with  2, input read with  2, computet with 19,
     and showed with  2 digit accuracy (for control here the analysed original matrix):
     1    .59  .5   .3   .21  .13  .16  .12  .16  .18  .21  .18  .18  .14  .12  .04
     .59  1    .74  .59  .46  .22  .24  .2   .21  .14  .13  .14  .14  .08  .03 -.07
     .5   .74  1    .51  .37  .27  .25  .27  .24  .16  .14  .16  .18  .09  .03  0
     .3   .59  .51  1    .51  .45  .47  .45  .44  .32  .33  .33  .36  .17  .13  .08
     .21  .46  .37  .51  1    .54  .52  .5   .5   .38  .32  .35  .35  .14  .11  .06
     .13  .22  .27  .45  .54  1    .91  .85  .79  .4   .38  .38  .36  .26  .21  .16
     .16  .24  .25  .47  .52  .91  1    .94  .91  .46  .44  .44  .42  .33  .33  .25
     .12  .2   .27  .45  .5   .85  .94  1    .89  .49  .47  .48  .45  .36  .4   .3
     .16  .21  .24  .44  .5   .79  .91  .89  1    .51  .49  .48  .48  .36  .4   .33
     .18  .14  .16  .32  .38  .4   .46  .49  .51  1    .92  .96  .91  .47  .43  .37
     .21  .13  .14  .33  .32  .38  .44  .47  .49  .92  1    .96  .92  .47  .44  .32
     .18  .14  .16  .33  .35  .38  .44  .48  .48  .96  .96  1    .95  .48  .46  .39
     .18  .14  .18  .36  .35  .36  .42  .45  .48  .91  .92  .95  1    .48  .49  .41
     .14  .08  .09  .17  .14  .26  .33  .36  .36  .47  .47  .48  .48  1    .74  .6
     .12  .03  .03  .13  .11  .21  .33  .4   .4   .43  .44  .46  .49  .74  1    .72
     .04 -.07  0    .08  .06  .16  .25  .3   .33  .37  .32  .39  .41  .6   .72  1
     .13  .25  .32  .43  .44  .49  .49  .5   .52  .64  .59  .62  .59  .32  .27  .27
     .08  .01  .18  .29  .31  .41  .41  .46  .47  .6   .29  .62  .6   .33  .35  .31
     .12  .15  .22  .28  .31  .34  .33  .39  .39  .44  .45  .43  .44  .36  .3   .29
     0   -.02  0    .18  .24  .26  .26  .33  .32  .51  .53  .54  .48  .38  .28  .35
     .09  .05  .07  .14  .17  .23  .24  .15  .26  .33  .34  .35  .31  .36  .24  .31
     .13  0    .01  .12  .13  .16  .19  .27  .25  .45  .44  .47  .49  .33  .29  .33

     .13  .08  .12  0    .09  .13
     .25  .01  .15 -.02  .05  0
     .32  .18  .22  0    .07  .01
     .43  .29  .28  .18  .14  .12
     .44  .31  .31  .24  .17  .13
     .49  .41  .34  .26  .23  .16
     .49  .41  .33  .26  .24  .19
     .5   .46  .39  .33  .15  .27
     .52  .47  .39  .32  .26  .25
     .64  .6   .44  .51  .33  .45
     .59  .29  .45  .53  .34  .44
     .62  .62  .43  .54  .35  .47
     .59  .6   .44  .48  .31  .49
     .32  .33  .36  .38  .36  .33
     .27  .35  .3   .28  .24  .29
     .27  .31  .29  .35  .31  .33
     1    .57  .48  .44  .33  .32
     .57  1    .45  .46  .34  .34
     .48  .45  1    .58  .64  .53
     .44  .46  .58  1    .8   .71
     .33  .34  .64  .8   1    .8
     .32  .34  .53  .71  .8   1

     i.Eigenvalue  Cholesky   i.Eigenvalue  Cholesky   i.Eigenvalue  Cholesky
      1.  9.11441   1         2.  3.05858   .8074       3.  1.95686  .668
      4.  1.65374   .7967     5.  1.46789   .8355       6.  .81712   .7963
      7.  .65813    .4056     8.  .51057    .3266       9.  .48039   .3872
      10. .41222    .8242     11. .3872     .3799       12. .36244   .1931
      13. .27688    .2961     14. .2338     .8485       15. .20248   .5943
      16. .17469    .6333     17. .16373    .6816       18. .07963  -1.0387
      19. .05279    .6538     20. .02683    .5897       21.-.02013  -.0641
      22.-.07025   -.2761
     The matrix is not positive definit. Cholesky decomposition is not successful.

     Eigenvalues in per cent of trace =  21.999999999999999
      1 .4143   2 .139    3 .0889   4 .0752   5 .0667   6 .0371
      7 .0299   8 .0232   9 .0218   10 .0187  11 .0176  12 .0165
      13 .0126  14 .0106  15 9.2D-3 16 7.9D-3 17 7.4D-3 18 3.6D-3
      19 2.4D-3 20 1.2D-3 21-9D-4   22-3.2D-3

     analysed: 12/05/05 22:04:36  PRG version 05/24/94  MA9.BAS
     

    [Interne Verwaltung: File = C:\OMI\NUMERIK\MATRIX\SMA\coombs41\coombs41.SMA
     with data from C:\OMI\NUMERIK\MATRIX\SMA\coombs41\coombs41.k22
    Date: 12/05/05  Time:22:04:36]


    Multiple correlations of original matrix
       r1.rest  =  .60830421637969243
       r2.rest  =  .83150244686471082
       r3.rest  =  .72255511914761746
       r4.rest  =  .72499976754739536
       r5.rest  =  .69677119296304202
       r6.rest  =  .92744703638335478
       r7.rest  = imaginary with radicand -1.1840834886631961
       r8.rest  = 1.0333091726902099
       r9.rest  =  .92863322400750881
       r10.rest =  .96383779368842841
       r11.rest = 1.0757284750945087
       r12.rest =  .96331337753423112
       r13.rest =  .9413174325563095
       r14.rest =  .78431383745618764
       r15.rest =  .83369212519929888
       r16.rest =  .73175565639119942
       r17.rest =  .74144383636336374
       r18.rest = 1.4981160629242179
       r19.rest =  .45026634182605156
       r20.rest =  .707070626062042
       r21.rest = 1.0673517927832424
       r22.rest = 1.5715017536363515


    GIF-Faksimile aus Guttman in Cattell (1966)

    Anmerkungen und Endnoten
    ___
    FN01  Sponsel, Rudolf & Hain, Bernhard (1994). Numerisch instabile Matrizen und Kollinearität in der Psychologie. Diagnose, Relevanz & Utilität, Frequenz, Ätiologie, Therapie.  Ill-Conditioned Matrices and Collinearity in Psychology. Deutsch-Englisch. Übersetzt von Agnes Mehl. Kapitel 6 von Dr. Bernhard Hain: Bemerkungen über Korrelationsmatrizen. Erlangen: IEC-Verlag [ISSN-0944-5072  ISBN 3-923389-03-5]. Aktueller Preis: www.iec-verlag.de.
    Bd. 2.: Sponsel, R. (2005). Fast- Kollinearität in Korrelationsmatrizen mit Eigenwert-Analysen erkennen Ergänzungsband - Band II zu
    Numerisch instabile Matrizen und Kollinearität in der Psychologie.

    Änderungen wird gelegentlich überarbeitet, ergänzt und vertieft * Anregungen und Kritik willkommen
    00.00.00
    Querverweise
    Standort: Vorlage SMA
    Überblicks- und Verteilerseite: Numerisch instabile Matrizen und Kollinearität in der Psychologie - Ill-Conditioned Matrices and Collinearity in Psychology -   Diagnose, Relevanz & Utilität, Frequenz, Ätiologie, Therapie.
    * Überblick Statistik in der IP-GIPT * Überblick Wissenschaft in der IP-GIPT. * Überblick Faktorenananlyse *
    *
    Suchen in der IP-GIPT, z.B. mit Hilfe von "google": <suchbegriff> site:www.sgipt.org
    z.B. Numerisch instabile Matrizen site:www.sgipt.org. * Korrelation site:www.sgipt.org
    *
    Dienstleistungs-Info.
    *

    Zitierung
    Sponsel, Rudolf  (DAS). Eine indefinite Korrelationsmatrix von Coombs, C.H. (1941). A criterion for significant common factor variance. Psychometrika 6, 267-272. Aus der Abteilung Numerisch instabile Matrizen und Kollinearität in der Psychologie - Ill-Conditioned Matrices and Collinearity in Psychology -   Diagnose, Relevanz & Utilität, Frequenz, Ätiologie, Therapie.  IP-GIPT. Erlangen: https://www.sgipt.org/wisms/nis/sma/coombs41.htm
    Copyright & Nutzungsrechte
    Diese Seite darf von jeder/m in nicht-kommerziellen Verwertungen frei aber nur original bearbeitet und nicht  inhaltlich verändert und nur bei vollständiger Angabe der Zitierungs-Quelle benutzt werden. Das Einbinden in fremde Seiten oder Rahmen, die die Urheberschaft der IP-GIPT nicht jederzeit klar erkennen lassen, ist nicht gestattet. Sofern die Rechte anderer berührt sind, sind diese dort zu erkunden. Sollten wir die Rechte anderer unberechtigt genutzt haben, bitten wir um Mitteilung. Soweit es um (längere) Zitate aus  ...  geht, sind die Rechte bei/m ... zu erkunden oder eine Erlaubnis einzuholen.


      Ende_ Coombs 1941   _Überblick _Relativ Aktuelles  _Rel. Beständiges  _Titelblatt  _ Konzept  _Archiv _Region _Service iec-verlag  _Mail: Sekretariat@sgipt.org  _ _ Wichtige Hinweise zu Links und Empfehlungen