Zusammenfassung: Die allgemeine Idee der Kommutativität ist einfach erklärt: bei einer Operation dürfen die Operanden vertauscht werden, ohne dass das Ergebnis verändert wird. Die Operation ist invariant gegenüber der Reihenfolge der Ausführung. Ob Operationen kommutativ sind, ist nicht selbstverständlich und muss im jeweiligen Betrachtungsfall besonders untersucht, begründet, gezeigt oder vorausgesetzt werden.
    Kommutativität kann nun in sehr verschiedenen Bedeutungen, z.B. als Bedingung, Rechenregel, Axiom, Definition, Gesetz, Eigenschaft, Voraussetzung, Erklärung u.a.m. gebraucht werden. Sind diese verschiedenen Verwendungen allesamt in Ordnung? Um die Verwendungsweisen zu belegen und zu klären wird auf dieser Seite nun Material rund um den Begriff Kommutativität aus verschiedenen mathematischen Quellen zusammengetragen. Die Zielmarken bzw. Links zu den Fundstellen werden zur leichteren Bezugnahme der Reihe nach mit Bxx (B:=Beleg ) gekennzeichnet (unsystematische Anordnung nach Nachschlagen).
Ergebnisse der Auswertung im einzelnen
    B01-01   Unklarer Status, insbesondere "ist".
    B01-02   Notwendige Bedingung.
    B01-03   Satz
    B01-04   Rechenregel
    B02 ....   Unklarer Status, insbesondere "ist".
    B03 ....   Definition
    B04 ....   Definition
    B05 ....   Eigenschaft
    B06 ....   Eigenschaft
    B07 ....   Eigenschaft
    B08 ....   Bedingung an eine Mengenverknüpfung, Definition
    B09-01   Kommutatives Gesetz (Addition)
    B09-02   Kommutatives Gesetz (Arithmetik)
    B09-03   Kommutatives Gesetz (allgemein)
    B10-01   Axiom (Gruppe)?
    B10-02   5. Axiom (Abelsche Gruppe)
    B11-01   Eigenschaftsaspekt [Ausdruck Kommutatives Gesetz nicht gefunden]
    B11-02   Kommutativität als Verbandsaxiom
    B11-03   Definition (kommutatives Diagramm)
    B11-04   Definition kommutativ für abelsche Gruppe.
    B11-05   Bedingung, Eigenschaft und Definition.
    B11-06   Kommutatives Gesetz und Satz.

    Anmerkung Helmholtz (1887).
 

B01-1 Fundstelle: S. 16 Unter dem Stichwort "Algebra" wird ausgeführt, dass bei endlich erzeugten abelschen Gruppen die Verknüpfung kommutativ "ist".
    Anmerkung S. 16 Es bleibt hier offen, was die Kommutativität hier für einen  Status  hat.
 
B01-2 Fundstelle: S. 92 Unter dem Stichwort Gleichungen (fett kursiv RS) "... Dieser so selbstverständlich scheinende Sachverhalt beruht aber wesentlich auf der Kommutativität von K, d. h. auf der für beliebige a, b € K stets gültigen Beziehung b • a == a • b. Das eingangs angeführte Beispiel einer algebraischen Gleichung [RS S.79: x^5+x^4-x^3-x^2-2x-2], die im System der Quaternionen unendlich viele Lösungen besitzt, zeigt, daß für die Gültigkeit dieses Satzes die Kommutativität von K notwendig ist: die Quaternionen bilden nämlich einen Schiefkörper, in dem also die Beziehung b • a = a • b nicht ausnahmslos richtig ist, während die übrigen Rechenregeln, die für Körper charakteristisch sind, bestehen."
    Anmerkung S. 92  Die Kommutativität scheint hier den Status einer notwendigen  Bedingung  zu haben.
 
B01-3 Fundstelle: S. 249 Stichwort Mengen, Abbildungen, Strukturen: Hier wird von Rechenregeln gesprochen, die sich beweisen lassen:



    Anmerkung S. 249 Damit wird hier die Kommutativitätsregel zum Satz, weil beweisbar.

B01-4 Fundstelle: S. 311  Unter dem Stichwort "Zahlen". Auch hier wird von  Rechenregeln  gesprochen:



    Anmerkung: Das Kommutativgesetz wird durch Angabe der  Rechenregeln  erklärt mit dem
    ausdrücklichen Zusatz der Nicht-Trivialität. Interessant ist der entwicklungspsychologische Hinweis.
 

Fundstelle S. 237: "kommutativ, svw. vertauschbar; bezeichnet auch Verknüpfungen, bei denen das Ergebnis unabhängig von der Reihenfolge der verknüpften Elemente ist. Addition und Multiplikation von Zahlen sind kommutative Verknüpfungen; Subtraktion und Division sind nicht kommutativ.
Ist eine Verknüpfung kommutativ, so sagt man, sie erfüllt das Kommutativgesetz. Z. B. lautet das Kommutativgesetz der Multiplikation: Für alle Zahlen a, b gilt a • b = b • a. Ein Verknüpfungsgebilde mit einer kommutativen Verknüpfung bezeichnet man auch als kommutatives Verknüpfungsgebilde.
Kommutativgesetz >  kommutativ."

Anmerkung: Unklarer Status, insbesondere "ist... erfüllt", darüber hinaus aber eine Erklärung für den Ausdruck "Kommutativgesetz".

"Kommutativ > Algebraische Verknüpfung", darin:



    Anmerkung: Hier handelt es, wie das "heißt" nahelegt, um eine Definition.

    Anmerkung: Hier handelt es, wie das "heißt" nahelegt, um eine Definition.

 
S. 42: "II. Eigenschaften
Erste Frage: Ist die Operation kommutativ, d.h. ist die Reihenfolge der Elemente beliebig?"

    Anmerkung: Hier handelt es sich, wie die Überschrift "II. Eigenschaften" nahelegt, um eine Eigenschaft.

B06 Duden Rechnen und Mathematik 1994, S. 324
 

        Anmerkung: Hiernach handelt es sich ganz klar um eine bedingte  Eigenschaft.
        Beispiele in W.
 

        Anmerkung: Hiernach handelt es sich um eine  Eigenschaft.

    Anmerkung: Hier für das Kommutativgesetz von einer Bedingung an eine Mengenverknüpfung gesprochen und erklärt, was unter dem Kommunikationsgesetz in einer Mengenverknüpfung zu verstehen ist, was man unter der Efüllung des des Kommutativgesetzes zu verstehen hat (Definition).
 

B09-1 Fundstelle S. 117 (Addition):   "Man kann die Summanden vertauschen (kommutatives Gesetz):
a + b = b + a"

 
B09-2 Fundstelle S. 127 (Arithmetik): "... Für Addieren und Multiplizieren gelten folgende allg. Gesetze: 1) Kommutatives Gesetz: Es ist a + b = b + a ; p  • q = q  • p, d. h., es ergibt sich derselbe Wert, ob man a zu b hinzuzählt oder b zu a; bzw. ob man q mal p oder p mal q nimmt, wobei a, b; p, q beliebige Zahlen sind. ..."

B09-3 Fundstelle S. 274 (Kommutatives Gesetz):


 

    Anmerkung: Hier ist durchweg vom kommutativen Gesetz  die Rede. Zur Literaturangabe "L 9":
    v. Mangoldt-Knopp, Einführung in die höhere Mathematik, Verl. S. Hirzel, Leipzig, 1963.

B10-1 Fundstelle S. 58: "Beispiel: Das Axiomensystem der Gruppe ist nicht vollständig, denn es kann weder die Aussage der Kommutativität noch die Aussage der Nichtkommutativität aus ihm hergeleitet werden. Es gibt Modelle für Gruppen, in denen das Kommutativgesetz gilt, und solche, in denen das Kommutativgesetz nicht gilt."

Anmerkung: Aus diesem Zitat kann sich der Eindruck ergeben, als fehlte für die Vollständigkeit der Gruppenaxiome ein  Axiom  der Kommutativität.

B10-2 Fundstelle S. 227:

 
Anmerkung: Für die abelsche Gruppe ist Kommutativität offenbar das 5. Axiom.

B11-01 Fundstelle S. 25  Kommutatives Gesetz



Anmerkung: Auf der Seite 25 konnte ich den Ausdruck "Kommutatives Gesetz" nicht finden, wohl aber Ausführungen zur Kommutativität im Hinblick auf Mengenverknüpfungen, wobei hier der Eigenschaftsaspekt betont wird.

 
B11-02 Fundstelle S. 26  Kommutativität als Verbandsaxiom



Anmerkung: Hier ist Kommutativität offenbar ein Axiom.
 

B11-03 Fundstelle S. 33  kommutatives Diagramm

 
Anmerkung: Definition.

B11-04 Fundstelle S. 39  kommutativ



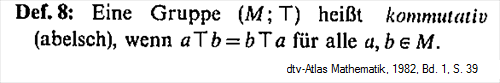
Anmerkung: Definition, wie aus "heißt" hervorgeht.
 

B11-05 Fundstelle S. 41  kommutativ



Anmerkung: Bedingung, Eigenschaft und Definition.
 

B11-06 Fundstelle S. 52, 53  Kommutatives Gesetz
Geltung der Kommutativgesetze S. 52: Rechengesetze im Halbring der natürlichen Zahlen: n + m = m + n, nm = mn.
Beweis S. 53, damit Satz.

• Behnke, H.; Remmert, R.; Steiner, H.G. & Tietz, H. (1964, Hrsg.). Mathematik 1. Frankfurt a.M.: Das Fischer Lexikon.  [ISBN keine Angabe].
• Beutelspacher, Albrecht (1992) "Das ist o.B.d.A. trivial" Tips und Tricks zur Formulierung mathematischer Gedanken. Braunschweig: Vieweg.
• Bibliographisches Institut Mannheim (1966) Schüler-Rechenduden. Ein Helfer für Schulaufgaben. Gekürzte Ausgabe von MEYERS Großem Rechenduden Bd. I. Mannheim: BI.
• Engesser, Hermann (1986). Der kleine Duden Mathematik. Mannheim: PI.
• Engesser, Hermann & Scheid, Harald (1994, 5.A.). Duden. Rechnen und Mathematik. Das Lexikon für Schule und Praxis. Mannheim: Duden-Verlag.
• Gellert, W.; Kästner, H. & Neuber, S. (1978, Hrsg.). Fachlexikon ABC Mathematik. Frankfurt: Deutsch.  Kramer, Jürg & Pippich, Anna-Maria von (2013) Von den natürlichen Zahlen zu den Quaternionen. Basiswissen Zahlbereiche und Algebra. Wiesbaden: Springer.
• Naas, J. & Schmid, H.L. (1972-74, Hrsg.). Mathematisches Wörterbuch mit Einbeziehung der theoretischen Physik  Bd. I A-K, Bd. II. L-Z. Berlin und Leipzig: Akademie und Teubner.
• Reinhardt, Fritz & Soeder, Heinrich (1982 f). dtv-Atlas zur Mathematik. 2 Bde. München: dtv.