Internet Publikation für Allgemeine und Integrative Psychotherapie
(ISSN 1430-6972)
IP-GIPT DAS=13.02.2006 Internet-Erstausgabe, letzte Änderung: 19.01.20
Impressum: Diplom-PsychologInnen Irmgard Rathsmann-Sponsel und Dr. phil. Rudolf Sponsel
Stubenlohstr. 20     D-91052 Erlangen * Mail: sekretariat@sgipt.org.
Anfang_Eigenwertsortierung in Matlab__Datenschutz_Überblick  _ Relativ Aktuelles  _ Rel. Beständiges  _ Titelblatt  _ Konzept  _  Archiv  _ Region _ Service iec-verlag _Zitierung & Copyright___Wichtige Hinweise zu Links und Empfehlungen
Willkommen in der Abteilung Wissenschaftstheorie, Methodologie und Statistisch-Mathematische Methodenin der Allgemeinen und Integrativen Psychologie, Psychodiagnostik und Psychotherapie, hier:
Tücken und Fallen bei der Interpretation von Faktorenanalysen bei unterschiedlichen Eigenwert- und Eigenvektor-Sortierungen
Hier mit Matlab angewendet auf Harry H. Harmans
First Ten Principal Components for Twenty-Four Psychological Tests

mitgeteilt von Rudolf Sponsel, Erlangen
Kritik und Anregungen bitte an sekretariat@sgipt.org.

Abstract - Zusammenfassung - Summary: Rechnet man Faktorenanalysen (Faktorisierungen) nach der Hauptkomponentenmethode in Matlab, erscheinen womöglich überraschende Ergebnisse, weil die Ergebnisse auf den ersten Blick nicht zu den Darstellungen passen, die man in der Literatur findet. Das liegt daran, daß in Matlab (hier Studendenversion 5.3) die Eigenwerte durcheinander absteigend sortiert in die Diagonalmatrix eingetragen werden (größter Eigenwert am Ende der Diagonalmatrix). Mit Matlab berechnete Faktoren (Hauptkomponenten) muß man also, wenn man sie mit aufsteigend sortiert gerechneten (größter Eigenwert am Anfang) vergleicht, von hinten lesen, aber auch da kann es noch Zuordnungs-, Lese oder Verständnisprobleme geben, weil Matlab nur eine "tendenziell" absteigende Ordnung einhält, wobei aber einige Eigenwerte in der Größenanordnung auch durcheinander geraten können. Das muß man wissen und berücksichtigen, sonst denkt man, die so bestimmten Faktoren stimmen mit anders dargestellten Ergebnissen nicht überein. In diese Falle beim interpretativen Vergleich der Daten bin ich kürzlich gestolpert und ich teile sie hier mit, damit diejenigen, die das noch nicht bemerkt haben, auch darauf achten und diese Tücke vermeiden können. Die Darstellung dieser Falle erfolgt am Beispiel der Hauptkomponentenanalyse von Harmann (1970, p. 168). 

In Harman, H.H. (1970, 3. edit.). Modern Factor Analysis. Chicago: The University of Chicago Press p. 168 findet sich:

"Table 8.20 First Ten Principal Components for Twenty Four Psychological Tests"

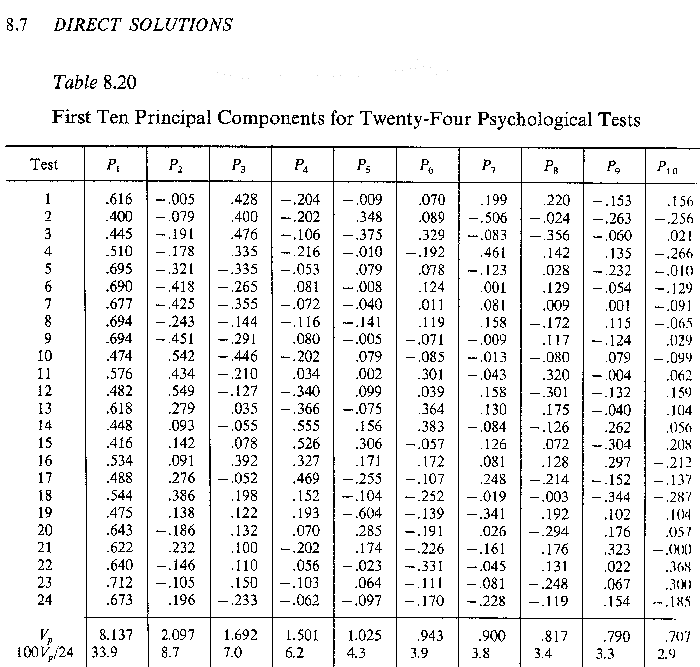
In dieser Tabelle sind die Faktoren aufsteigend sortiert geordnet, d.h.zum ersten und stärksten Faktor gehört der größte Eigenwert, zum zweiten Faktor der zweitgrößte Eigenwert usw.

Die bei Harman ausgewiesenen Hauptfaktoren ergeben sich aus der Faktorisierung der Korrelationstabelle p. 125:

"Table 7.4 Intercorrelations of Twenty-Four Psychological Tests for 145 Children"

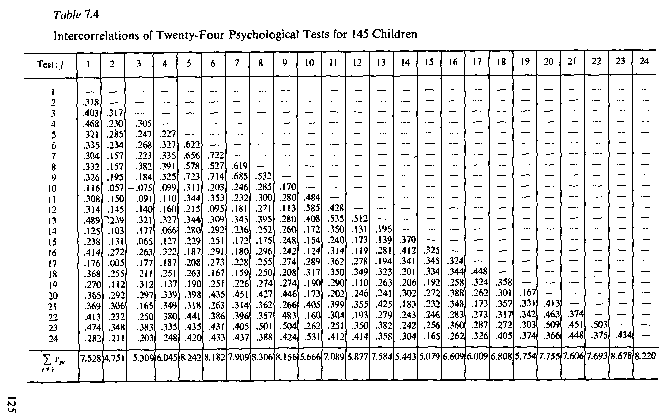
Führt man die Hauptkomponentenanalyse mit Matlab durch, beginnt man mit der Faktorisierung der Korrelationsmatrix und gelangt hier zu den Eigenvektoren und Eigenwerten mit [V,D]=eig(C), wobei V:= Eigenvektoren, D:=Diagonalatrix der Eigenwerte.

Eigenvektoren der Korrelationsmatrix

                01                    02                    03                        04                    05                    06                    07
01  0.0903   -0.4590   -0.3332    0.2310    0.0262   -0.0734   -0.0174
02 -0.2385    0.0107   -0.1560    0.0023   -0.1207   -0.0366   -0.0204
03  0.4058    0.2813    0.1324    0.2049    0.1210   -0.0661   -0.1692
04 -0.0324    0.0941   -0.1086   -0.0724    0.1196    0.0304    0.2627
05  0.1017   -0.0917    0.0812    0.3773    0.2174    0.3115    0.4288
06  0.0955   -0.0553   -0.1050   -0.1479    0.0750   -0.3597   -0.3299
07 -0.2763   -0.1506    0.1067    0.1217   -0.2552   -0.2260   -0.2972
08  0.0197    0.0012   -0.3634   -0.2599   -0.2409    0.3631   -0.0836
09 -0.0030    0.2150    0.1785    0.0232   -0.0483    0.1177    0.2289
10 -0.0529    0.1199   -0.2394    0.2475    0.5565    0.1337   -0.3372
11  0.3601    0.1373   -0.2567   -0.2400   -0.0794   -0.1218    0.1634
12 -0.1766    0.1590   -0.0949    0.1873   -0.4863   -0.0297    0.1135
13 -0.3525    0.0956    0.5133   -0.2252    0.1981   -0.1009    0.0182
14 -0.1892   -0.2921   -0.0293    0.0058    0.0255    0.1084    0.0392
15  0.1370    0.1296   -0.0602   -0.0833    0.0157   -0.1472   -0.1070
16 -0.0747    0.2400    0.0896    0.1928   -0.1073    0.2897   -0.1392
17 -0.0113   -0.2205    0.1542    0.2178   -0.0452   -0.1743    0.0860
18 -0.0263   -0.1096    0.1255   -0.2960    0.0612    0.1918   -0.1441
19 -0.3640    0.0850   -0.2467    0.0698    0.0296   -0.1137    0.2104
20 -0.1185    0.2645   -0.1440   -0.0670    0.2358   -0.4433    0.2379
21  0.2919   -0.2598    0.2798    0.2416   -0.1449   -0.1705   -0.0413
22 -0.0359    0.2460    0.0568    0.0802   -0.1112    0.2475   -0.3489
23  0.0129   -0.3531    0.0944   -0.3907    0.1974    0.1914    0.0319
24  0.3016    0.0540    0.1502   -0.2041   -0.1969   -0.0103    0.1477

                 08                    09                    10                        11                    12                    13                    14
01 -0.2349    0.3963    0.0071    0.1592    0.1055    0.0385    0.1613
02 -0.1695   -0.3209   -0.1324    0.0579    0.0796   -0.0041   -0.3191
03  0.0929    0.0080   -0.0951   -0.1030   -0.1060   -0.1503    0.0521
04  0.1800   -0.2099   -0.4487   -0.1509    0.0492   -0.1037   -0.3254
05  0.0650    0.0287    0.1192   -0.1729    0.1051    0.0936   -0.0336
06  0.3848   -0.0176   -0.0515    0.1844    0.0764    0.5104   -0.1695
07 -0.0456    0.0889    0.0166   -0.0912   -0.0347   -0.6086   -0.1111
08 -0.3146   -0.1589    0.2426   -0.2427   -0.2948    0.2253   -0.0487
09  0.0676    0.0411   -0.0168    0.2093   -0.1228   -0.0582    0.0490
10 -0.0662   -0.0444   -0.1162    0.0997   -0.1273   -0.0926   -0.0980
11  0.0668   -0.2096    0.2040   -0.0030    0.3178   -0.3514    0.0363
12  0.3870    0.0765   -0.0836    0.0799   -0.0404    0.1275    0.2021
13 -0.2569   -0.0039    0.0169   -0.0812   -0.0036    0.1859    0.1181
14  0.1237    0.1224   -0.3286   -0.3143    0.1494    0.0221    0.0581
15 -0.1671   -0.0435   -0.2538   -0.2004   -0.3853   -0.0270    0.2544
16  0.0505    0.1203    0.2463    0.3973   -0.1451   -0.0207   -0.2275
17 -0.2541   -0.4403    0.1014    0.2169    0.1886    0.0973   -0.1794
18  0.2753    0.3074    0.2597   -0.2819    0.0798   -0.0600   -0.3650
19  0.1042   -0.0010   -0.0321    0.0073   -0.2451    0.0178    0.1485
20 -0.1118    0.2118    0.3716   -0.1060    0.0996    0.0116    0.0686
21  0.0942   -0.2089    0.1476   -0.2935   -0.2901    0.1172    0.0207
22 -0.0888   -0.0968   -0.0800   -0.1302    0.5720    0.1062    0.3910
23  0.2137   -0.2085    0.0071    0.3909   -0.1205   -0.2115    0.3814
24 -0.3473    0.3834   -0.3940    0.2227    0.0203    0.0594   -0.2004

                 15                   16                    17                        18                    19                    20                     21
01  0.0795    0.2406   -0.2541    0.0635    0.1402    0.0349   -0.0943
02  0.2844    0.0685    0.5186    0.1548    0.0782    0.3398   -0.1025
03  0.2087   -0.2803    0.0737    0.3184    0.0904   -0.3976   -0.0456
04 -0.2223    0.0262   -0.4670   -0.2294   -0.0705    0.0195   -0.1353
05  0.2375    0.0898    0.1224    0.0867   -0.4004    0.0516   -0.1248
06  0.0073    0.1229   -0.0049    0.1183   -0.1013   -0.0468   -0.0224
07 -0.0015   -0.0045   -0.0658   -0.0115   -0.1516   -0.0792   -0.1608
08 -0.0490   -0.1952   -0.1432    0.0882    0.0622   -0.1783   -0.1535
09  0.1086    0.2118   -0.0611   -0.0527    0.7030    0.1027    0.1017
10 -0.0443   -0.0835    0.0315   -0.0886    0.1527    0.0817   -0.1913
11 -0.1225    0.2994   -0.0057    0.3183   -0.0107    0.0020    0.0222
12  0.2414   -0.2690   -0.1592    0.0369   -0.0262    0.1208   -0.2459
13 -0.0085    0.2046   -0.1997    0.3585   -0.0395   -0.0480   -0.2639
14 -0.2836   -0.2830    0.1232    0.4202    0.1862    0.0592    0.4133
15  0.3270    0.1710   -0.1476   -0.0578   -0.2673    0.3246    0.4548
16 -0.3583    0.0447   -0.0932    0.1802   -0.2672    0.1675    0.3302
17  0.1965   -0.2438   -0.2352   -0.1286    0.0463   -0.2652    0.3693
18  0.3522    0.0701    0.0135   -0.2510    0.0914   -0.0665    0.1779
19 -0.1070    0.3080    0.3173   -0.1603   -0.0734   -0.5759    0.1708
20 -0.1241   -0.4212    0.0591   -0.1774    0.0098    0.2347    0.0457
21 -0.3855    0.1147    0.1916   -0.2160    0.1313    0.1838   -0.1314
22 -0.0890    0.0890    0.0716   -0.3336   -0.0282   -0.0181    0.0414
23  0.0255   -0.2412    0.1166   -0.1049   -0.1257    0.0556   -0.0735
24 -0.1068   -0.1182    0.2692   -0.1695   -0.1281   -0.1103   -0.0826

       22        23       24
01  0.3539   -0.0088    0.2149
02  0.3285   -0.0600    0.1394
03  0.3796   -0.1370    0.1550
04  0.2786   -0.1243    0.1781
05 -0.2591   -0.2062    0.2427
06 -0.2273   -0.2810    0.2413
07 -0.2756   -0.2761    0.2363
08 -0.1016   -0.1553    0.2422
09 -0.2269   -0.2976    0.2514
10 -0.2966    0.3990    0.1651
11 -0.1486    0.3085    0.2010
12 -0.0332    0.3989    0.1679
13  0.0861    0.2088    0.2154
14 -0.1140    0.0449    0.1567
15 -0.0538    0.0300    0.1531
16  0.2258    0.0059    0.1923
17 -0.0858    0.1793    0.1704
18  0.1501    0.2589    0.1897
19  0.0851    0.0923    0.1659
20  0.0844   -0.1343    0.2246
21  0.1096    0.1664    0.2168
22  0.0780   -0.1013    0.2233
23  0.1267   -0.0701    0.2484
24 -0.1569    0.1520    0.2346
Ende Eigenvektoren nach Faktoisierung der Korrelationsmatrix
 

Eigenwerte der Korrelationsmatrix

                01                     02                    03                        04                    05                    06                    07
01  0.3854         0         0         0         0         0         0
02       0    0.3943         0         0         0         0         0
03       0         0    0.3541         0         0         0         0
04       0         0         0    0.3368         0         0         0
05       0         0         0         0    0.3117         0         0
06       0         0         0         0         0    0.4830         0
07       0         0         0         0         0         0    0.2756

                 08                    09                    10                        11                    12                    13                    14
08  0.2676         0         0         0         0         0         0
09       0    0.5105         0         0         0         0         0
10       0         0    0.5341         0         0         0         0
11       0         0         0    0.5584         0         0         0
12       0         0         0         0    0.6455         0         0
13       0         0         0         0         0    0.1898         0
14       0         0         0         0         0         0    0.7081
 

                 15                   16                    17                        18                    19                    20                     21
15  0.7943         0         0         0         0         0         0
16       0    0.8324         0         0         0         0         0
17       0         0    0.9036         0         0         0         0
18       0         0         0    0.9406         0         0         0
19       0         0         0         0    0.0875         0         0
20       0         0         0         0         0    1.0352         0
21       0         0         0         0         0         0    1.5282

       22        23       24
22  1.6706         0         0
23       0    2.0834         0
24       0         0    8.1693

Vergleich der Anordnung der Eigenwerte bei Harman und Matlab

Die Anordnung dieser Eigenwerte mutet seltsam an. Da es 24 Eigenwerte gibt, gibt es im Prinzip drei Anordnungsmöglichkeiten: aufsteigend, absteigend, durcheinander. Matlab wählt die Variante "durcheinander", die manchmal gar nicht so leicht zu erkennen ist. Im vorliegenden Fall stellt sich die Anordnung wie folgt dar:
 
Richtige abstei- gende Ordnung den Eigenwert- größen nach  Anordnung 
in Matlab 
Z=Zeile, 
S=Spalte		 "Tendenziell" absteigende 
"Un/Ordnung"
in Matlab		 Ordnungs-
Zahl nach
der richti-
gen Größe		 Richtige auf- 
steigende 
Ordnung		 Tatsächliche
Position in 
Matlab
0,3854 
0,3943 
0,3541 
0,3368 
0,3117 
0,483 
0,2756 
0,2676 
0,5105 
0,5341 
0,5584 
0,6455 
0,1898 
0,7081 
0,7943 
0,8324 
0,9036 
0,9406 
0,0875 
1,0352 
1,5282 
1,6706 
2,0834 
8,1693 		 Z1-S1
Z2-S2
Z3-S3
Z4-S4
Z5-S5
Z6-S6
Z7-S7
Z8-S8
Z9-S9
Z10-S10
Z11-S11
Z12-S12
Z13-S13
Z14-S14
Z15-S15
Z16-S16
Z17-S17
Z18-S18
Z19-S19
Z20-S20
Z21-S21
Z22-S22
Z23-S23
Z24-S24		 0,0875
0,1898
0,2676 
0,2756 
0,3117 
0,3368 
0,3541 
0,3854 
0,3943 
0,483 
0,5105 
0,5341
0,5584 
0,6455 
0,7081 
0,7943 
0,8324 
0,9036 
0,9406 
1,0352 
1,5282 
1,6706 
2,0834 
8,1693 		 19
13
8
7
5
4
3
1
2
6
9
10
11
12
14
15
16
17
18
20
21
22
23
24		 8,1693 
2,0834 
1,6706 
1,5282 
1,0352 
0,9406 
0,9036 
0,8324 
0,7943 
0,7081 
0,6455 
0,5584 
0,5341 
0,5105 
0,483 
0,3943 
0,3854 
0,3541 
0,3368 
0,3117 
0,2756 
0,2676 
0,1898 
0,0875 		 24
23
22
21
20
18
17
16
15
14
12
11
10
9
6
2
1
3
4
5
7
8
13
19

Faktoren (Hauptkomponenten) der Korrelationsmatrix nach  F = Vektoren * Sqrt(Eigenwerte)

                01                    02                    03                        04                    05                    06                    07
01  0.0561   -0.2883   -0.1983    0.1341    0.0146   -0.0510   -0.0092
02 -0.1481    0.0067   -0.0928    0.0013   -0.0674   -0.0254   -0.0107
03  0.2519    0.1766    0.0788    0.1189    0.0676   -0.0459   -0.0888
04 -0.0201    0.0591   -0.0646   -0.0420    0.0667    0.0211    0.1379
05  0.0631   -0.0576    0.0483    0.2189    0.1214    0.2165    0.2251
06  0.0593   -0.0347   -0.0625   -0.0858    0.0419   -0.2500   -0.1732
07 -0.1715   -0.0946    0.0635    0.0706   -0.1425   -0.1571   -0.1560
08  0.0123    0.0008   -0.2163   -0.1509   -0.1345    0.2523   -0.0439
09 -0.0019    0.1350    0.1062    0.0135   -0.0270    0.0818    0.1202
10 -0.0329    0.0753   -0.1425    0.1436    0.3107    0.0929   -0.1770
11  0.2236    0.0862   -0.1528   -0.1393   -0.0443   -0.0846    0.0858
12 -0.1097    0.0999   -0.0565    0.1087   -0.2715   -0.0206    0.0596
13 -0.2189    0.0600    0.3054   -0.1307    0.1106   -0.0701    0.0095
14 -0.1175   -0.1834   -0.0174    0.0034    0.0142    0.0753    0.0206
15  0.0850    0.0814   -0.0358   -0.0483    0.0088   -0.1023   -0.0562
16 -0.0464    0.1507    0.0533    0.1119   -0.0599    0.2014   -0.0731
17 -0.0070   -0.1385    0.0918    0.1264   -0.0252   -0.1211    0.0451
18 -0.0163   -0.0688    0.0747   -0.1718    0.0342    0.1333   -0.0756
19 -0.2260    0.0534   -0.1468    0.0405    0.0165   -0.0790    0.1104
20 -0.0736    0.1661   -0.0857   -0.0389    0.1316   -0.3081    0.1249
21  0.1812   -0.1632    0.1665    0.1402   -0.0809   -0.1185   -0.0217
22 -0.0223    0.1545    0.0338    0.0466   -0.0621    0.1720   -0.1832
23  0.0080   -0.2217    0.0562   -0.2267    0.1102    0.1330    0.0168
24  0.1872    0.0339    0.0894   -0.1185   -0.1099   -0.0072    0.0775

                 08                    09                    10                        11                    12                    13                    14
01 -0.1215    0.2832    0.0052    0.1190    0.0848    0.0168    0.1357
02 -0.0877   -0.2293   -0.0967    0.0433    0.0640   -0.0018   -0.2685
03  0.0480    0.0057   -0.0695   -0.0770   -0.0851   -0.0655    0.0438
04  0.0931   -0.1500   -0.3279   -0.1127    0.0395   -0.0452   -0.2738
05  0.0336    0.0205    0.0871   -0.1292    0.0844    0.0408   -0.0283
06  0.1990   -0.0126   -0.0376    0.1378    0.0614    0.2224   -0.1426
07 -0.0236    0.0635    0.0122   -0.0681   -0.0279   -0.2652   -0.0935
08 -0.1627   -0.1135    0.1773   -0.1814   -0.2369    0.0982   -0.0410
09  0.0350    0.0294   -0.0123    0.1564   -0.0987   -0.0253    0.0412
10 -0.0342   -0.0317   -0.0849    0.0745   -0.1023   -0.0403   -0.0824
11  0.0346   -0.1498    0.1491   -0.0022    0.2554   -0.1531    0.0306
12  0.2002    0.0547   -0.0611    0.0597   -0.0325    0.0556    0.1701
13 -0.1329   -0.0028    0.0123   -0.0607   -0.0029    0.0810    0.0994
14  0.0640    0.0875   -0.2402   -0.2349    0.1200    0.0096    0.0489
15 -0.0864   -0.0311   -0.1855   -0.1497   -0.3096   -0.0117    0.2141
16  0.0261    0.0859    0.1800    0.2969   -0.1166   -0.0090   -0.1915
17 -0.1314   -0.3146    0.0741    0.1621    0.1515    0.0424   -0.1510
18  0.1424    0.2197    0.1898   -0.2107    0.0641   -0.0262   -0.3071
19  0.0539   -0.0007   -0.0234    0.0055   -0.1969    0.0077    0.1250
20 -0.0578    0.1514    0.2716   -0.0792    0.0801    0.0051    0.0577
21  0.0487   -0.1493    0.1078   -0.2193   -0.2331    0.0510    0.0174
22 -0.0459   -0.0692   -0.0585   -0.0973    0.4595    0.0463    0.3290
23  0.1105   -0.1490    0.0052    0.2921   -0.0968   -0.0921    0.3209
24 -0.1797    0.2739   -0.2879    0.1664    0.0163    0.0259   -0.1686

                 15                   16                    17                        18                    19                    20                     21
01  0.0708    0.2196   -0.2416    0.0616    0.0415    0.0355   -0.1166
02  0.2534    0.0625    0.4929    0.1502    0.0231    0.3458   -0.1267
03  0.1860   -0.2557    0.0701    0.3088    0.0267   -0.4046   -0.0563
04 -0.1981    0.0239   -0.4439   -0.2225   -0.0209    0.0199   -0.1673
05  0.2117    0.0819    0.1164    0.0841   -0.1184    0.0525   -0.1543
06  0.0065    0.1122   -0.0047    0.1148   -0.0300   -0.0477   -0.0277
07 -0.0013   -0.0041   -0.0625   -0.0111   -0.0449   -0.0806   -0.1988
08 -0.0437   -0.1781   -0.1361    0.0855    0.0184   -0.1814   -0.1898
09  0.0968    0.1932   -0.0581   -0.0511    0.2080    0.1045    0.1257
10 -0.0395   -0.0761    0.0299   -0.0860    0.0452    0.0832   -0.2365
11 -0.1092    0.2732   -0.0054    0.3087   -0.0032    0.0020    0.0274
12  0.2151   -0.2454   -0.1513    0.0357   -0.0078    0.1229   -0.3040
13 -0.0076    0.1867   -0.1899    0.3477   -0.0117   -0.0488   -0.3262
14 -0.2527   -0.2582    0.1171    0.4076    0.0551    0.0602    0.5109
15  0.2915    0.1561   -0.1403   -0.0561   -0.0791    0.3302    0.5622
16 -0.3193    0.0408   -0.0885    0.1747   -0.0790    0.1704    0.4082
17  0.1751   -0.2225   -0.2236   -0.1248    0.0137   -0.2698    0.4565
18  0.3139    0.0639    0.0128   -0.2434    0.0270   -0.0677    0.2199
19 -0.0954    0.2810    0.3016   -0.1554   -0.0217   -0.5859    0.2111
20 -0.1106   -0.3843    0.0562   -0.1720    0.0029    0.2388    0.0565
21 -0.3436    0.1047    0.1821   -0.2095    0.0388    0.1870   -0.1624
22 -0.0793    0.0812    0.0681   -0.3235   -0.0083   -0.0184    0.0512
23  0.0227   -0.2200    0.1108   -0.1018   -0.0372    0.0566   -0.0909
24 -0.0952   -0.1078    0.2559   -0.1644   -0.0379   -0.1122   -0.1021

       22        23       24
01  0.4575   -0.0127    0.6142
02  0.4246   -0.0866    0.3985
03  0.4907   -0.1978    0.4429
04  0.3601   -0.1794    0.5092
05 -0.3349   -0.2976    0.6937
06 -0.2938   -0.4055    0.6896
07 -0.3563   -0.3985    0.6755
08 -0.1313   -0.2242    0.6923
09 -0.2932   -0.4296    0.7187
10 -0.3834    0.5759    0.4720
11 -0.1921    0.4453    0.5746
12 -0.0429    0.5757    0.4799
13  0.1113    0.3013    0.6156
14 -0.1474    0.0648    0.4478
15 -0.0695    0.0433    0.4376
16  0.2919    0.0086    0.5497
17 -0.1109    0.2588    0.4870
18  0.1941    0.3737    0.5423
19  0.1100    0.1332    0.4742
20  0.1090   -0.1938    0.6418
21  0.1417    0.2402    0.6195
22  0.1008   -0.1462    0.6382
23  0.1637   -0.1012    0.7100
24 -0.2028    0.2194    0.6704
Ende Faktoren (Hauptkomponenten) F = Eigenvektoren * Wurzel(Eigenwerte)
 

Probe: Korrelationsmatrix = F * F'

                01                    02                    03                        04                    05                    06                    07
01  1.0000    0.3180    0.4030    0.4680    0.3210    0.3350    0.3040
02  0.3180    1.0000    0.3170    0.2300    0.2850    0.2340    0.1570
03  0.4030    0.3170    1.0000    0.3050    0.2470    0.2680    0.2230
04  0.4680    0.2300    0.3050    1.0000    0.2270    0.3270    0.3350
05  0.3210    0.2850    0.2470    0.2270    1.0000    0.6220    0.6560
06  0.3350    0.2340    0.2680    0.3270    0.6220    1.0000    0.7220
07  0.3040    0.1570    0.2230    0.3350    0.6560    0.7220    1.0000
08  0.3320    0.1570    0.3820    0.3910    0.5780    0.5270    0.6190
09  0.3260    0.1950    0.1840    0.3250    0.7230    0.7140    0.6850
10  0.1160    0.0570   -0.0750    0.0990    0.3110    0.2030    0.2460
11  0.3080    0.1500    0.0910    0.1100    0.3440    0.3530    0.2320
12  0.3140    0.1450    0.1400    0.1600    0.2150    0.0950    0.1810
13  0.4890    0.2390    0.3210    0.3270    0.3440    0.3090    0.3450
14  0.1250    0.1030    0.1770    0.0660    0.2800    0.2920    0.2360
15  0.2380    0.1310    0.0650    0.1270    0.2290    0.2510    0.1720
16  0.4140    0.2720    0.2630    0.3220    0.1870    0.2910    0.1800
17  0.1760    0.0050    0.1770    0.1870    0.2080    0.2730    0.2280
18  0.3680    0.2550    0.2110    0.2510    0.2630    0.1670    0.1590
19  0.2700    0.1120    0.3120    0.1370    0.1900    0.2510    0.2260
20  0.3650    0.2920    0.2970    0.3390    0.3980    0.4350    0.4510
21  0.3690    0.3060    0.1650    0.3490    0.3180    0.2630    0.3140
22  0.4130    0.2320    0.2500    0.3800    0.4410    0.3860    0.3960
23  0.4740    0.3480    0.3830    0.3350    0.4350    0.4310    0.4050
24  0.2820    0.2110    0.2030    0.2480    0.4200    0.4330    0.4370

                 08                    09                    10                        11                    12                    13                    14
01  0.3320    0.3260    0.1160    0.3080    0.3140    0.4890    0.1250
02  0.1570    0.1950    0.0570    0.1500    0.1450    0.2390    0.1030
03  0.3820    0.1840   -0.0750    0.0910    0.1400    0.3210    0.1770
04  0.3910    0.3250    0.0990    0.1100    0.1600    0.3270    0.0660
05  0.5780    0.7230    0.3110    0.3440    0.2150    0.3440    0.2800
06  0.5270    0.7140    0.2030    0.3530    0.0950    0.3090    0.2920
07  0.6190    0.6850    0.2460    0.2320    0.1810    0.3450    0.2360
08  1.0000    0.5320    0.2850    0.3000    0.2710    0.3950    0.2520
09  0.5320    1.0000    0.1700    0.2800    0.1130    0.2800    0.2600
10  0.2850    0.1700    1.0000    0.4840    0.5850    0.4080    0.1720
11  0.3000    0.2800    0.4840    1.0000    0.4280    0.5350    0.3500
12  0.2710    0.1130    0.5850    0.4280    1.0000    0.5120    0.1310
13  0.3950    0.2800    0.4080    0.5350    0.5120    1.0000    0.1950
14  0.2520    0.2600    0.1720    0.3500    0.1310    0.1950    1.0000
15  0.1750    0.4800    0.1540    0.2400    0.1730    0.1390    0.3700
16  0.2960    0.4200    0.1240    0.3140    0.1190    0.2810    0.4120
17  0.2550    0.2740    0.2890    0.3620    0.2780    0.1940    0.3410
18  0.2500    0.2080    0.3170    0.3500    0.3490    0.3230    0.2010
19  0.2740    0.2740    0.1900    0.2900    0.1100    0.2630    0.2060
20  0.4270    0.4460    0.1730    0.2020    0.2460    0.2410    0.3020
21  0.3620    0.2660    0.4050    0.3990    0.3550    0.4250    0.1830
22  0.3570    0.4830    0.1600    0.3040    0.1930    0.2790    0.2430
23  0.5010    0.5040    0.2620    0.2510    0.3500    0.3820    0.2420
24  0.3880    0.4240    0.5310    0.4120    0.4140    0.3580    0.3040

                 15                   16                    17                        18                    19                    20                     21
01  0.2380    0.4140    0.1760    0.3680    0.2700    0.3650    0.3690
02  0.1310    0.2720    0.0050    0.2550    0.1120    0.2920    0.3060
03  0.0650    0.2630    0.1770    0.2110    0.3120    0.2970    0.1650
04  0.1270    0.3220    0.1870    0.2510    0.1370    0.3390    0.3490
05  0.2290    0.1870    0.2080    0.2630    0.1900    0.3980    0.3180
06  0.2510    0.2910    0.2730    0.1670    0.2510    0.4350    0.2630
07  0.1720    0.1800    0.2280    0.1590    0.2260    0.4510    0.3140
08  0.1750    0.2960    0.2550    0.2500    0.2740    0.4270    0.3620
09  0.4800    0.4200    0.2740    0.2080    0.2740    0.4460    0.2660
10  0.1540    0.1240    0.2890    0.3170    0.1900    0.1730    0.4050
11  0.2400    0.3140    0.3620    0.3500    0.2900    0.2020    0.3990
12  0.1730    0.1190    0.2780    0.3490    0.1100    0.2460    0.3550
13  0.1390    0.2810    0.1940    0.3230    0.2630    0.2410    0.4250
14  0.3700    0.4120    0.3410    0.2010    0.2060    0.3020    0.1830
15  1.0000    0.3250    0.3450    0.3340    0.1920    0.2720    0.2320
16  0.3250    1.0000    0.3240    0.3440    0.2580    0.3880    0.3480
17  0.3450    0.3240    1.0000    0.4480    0.3240    0.2620    0.1730
18  0.3340    0.3440    0.4480    1.0000    0.3580    0.3010    0.3570
19  0.1920    0.2580    0.3240    0.3580    1.0000    0.1670    0.3310
20  0.2720    0.3880    0.2620    0.3010    0.1670    1.0000    0.4130
21  0.2320    0.3480    0.1730    0.3570    0.3310    0.4130    1.0000
22  0.2460    0.2830    0.2730    0.3170    0.3420    0.4630    0.3740
23  0.2560    0.3600    0.2870    0.2720    0.3030    0.5090    0.4510
24  0.1650    0.2620    0.3260    0.4050    0.3740    0.3660    0.4480

       22        23       24
01  0.4130    0.4740    0.2820
02  0.2320    0.3480    0.2110
03  0.2500    0.3830    0.2030
04  0.3800    0.3350    0.2480
05  0.4410    0.4350    0.4200
06  0.3860    0.4310    0.4330
07  0.3960    0.4050    0.4370
08  0.3570    0.5010    0.3880
09  0.4830    0.5040    0.4240
10  0.1600    0.2620    0.5310
11  0.3040    0.2510    0.4120
12  0.1930    0.3500    0.4140
13  0.2790    0.3820    0.3580
14  0.2430    0.2420    0.3040
15  0.2460    0.2560    0.1650
16  0.2830    0.3600    0.2620
17  0.2730    0.2870    0.3260
18  0.3170    0.2720    0.4050
19  0.3420    0.3030    0.3740
20  0.4630    0.5090    0.3660
21  0.3740    0.4510    0.4480
22  1.0000    0.5030    0.3750
23  0.5030    1.0000    0.4340
24  0.3750    0.4340    1.0000
Ende Probe reproduzierte Korrelationsmatrix aus den Faktoren F * F'
 

Vergleich der Hauptkomponentenwerte von Harman und Matlab
 
1 Principal Factor Harman 24. Faktor Matlab Absolute Abstände
0,61600
0,40000
0,44500
0,51000
0,69500
0,69000
0,67700
0,69400
0,69400 <- vermutlich ein 
0,47400 Druckfehler.
0,57600
0,48200
0,61800
0,44800
0,41600
0,53400
0,48800
0,54400
0,47500
0,64300
0,62200
0,64000
0,71200
0,67300		 0,61420
0,39850
0,44290
0,50920
0,69370
0,68960
0,67550
0,69230
0,71870
0,47200
0,57460
0,47990
0,61560
0,44780
0,43760
0,54970
0,48700
0,54230
0,47420
0,64180
0,61950
0,63820
0,71000
0,67040		 0,00180
0,00150
0,00210
0,00080
0,00130
0,00040
0,00150
0,00170
0,02470 
0,00200
0,00140
0,00210
0,00240
0,00020
0,02160
0,01570
0,00100
0,00170
0,00080
0,00120
0,00250
0,00180
0,00200
0,00260
Mittel der Abs-Abstände = 
Standardabweichung =
 0,00395
0,00662

Die Werte stimmen selbst mit dem mutmaßlichen Druckfehler in Harman ziemlich gut überein.
Die Matlabwerte sind aufgrund präsziserer Algorithmen genauer. Bedenkt man, daß eine einfache, alte
Studentenversion von Matlab auf einem PC in Sekundenschnelle fertig ist, während man 1940 noch
ca. 100 Stunden mit Handmethoden rechnete und eine IBM 704 rund 8 Minuten im Jahre 1958
brauchte, kann man ermessen, welch extremer Rechnungsleistungs- und Preisleistungsfortschritt
bei den PCs inzwischen erreicht worden ist. Ein Hoch auf die Computertechnik.


Literatur (Auswahl)
Harman, H.H. (1970, 3. edit.). Modern Factor Analysis. Chicago: The University of Chicago Press.


Links (Auswahl: beachte)
Harry H. Harman in Google.


Anmerkungen und Endnoten:
1) GIPT= General and Integrative Psychotherapy, internationale Bezeichnung für Allgemeine und Integrative Psychotherapie.


Änderungen wird gelegentlich überarbeitet, ergänzt und vertieft * Anregungen und Kritik willkommen
13.02.06    Password-Sperre aufgehoben.

Querverweise
Standort: Eigenwertsortierung in Matlab.
Überblick der Dokumentationen zur Handhabung der Faktorenanalyse
Kritik der Handhabung der Faktorenanalyse
Was für ein Typ Matrix entsteht durch Faktorenanalysen?
Überblick Numerisch Instabile Matrizen und Kollinearität in der Psychologie
Zahlenmystik und numerologische Esoterik in Statistik und Testtheorie
Überblick Arbeiten zur Definitionslehre, Methodologie, Meßproblematik, Statistik und Wissenschaftstheorie
*
Suchen in der IP-GIPT, z.B. mit Hilfe von "google": <suchbegriff> site:www.sgipt.org
z.B. Faktorenanalyse site:www.sgipt.org
*
Dienstleistungs-Info.
*

Zitierung
Sponsel, Rudolf  (DAS). Tücken und Fallen bei der Interpretation von Faktorenanalysen bei unterschiedlichen Eigenwert- und Eigenvektor-Sortierungen Hier mit Matlab angewendet auf Harry H. Harmans First Ten Principal Components for Twenty-Four Psychological Tests. IP-GIPT. Erlangen: https://www.sgipt.org/wisms/fa/Harm168.htm
Copyright & Nutzungsrechte
Diese Seite darf von jeder/m in nicht-kommerziellen Verwertungen frei aber nur original bearbeitet und nicht  inhaltlich verändert und nur bei vollständiger Angabe der Zitierungs-Quelle benutzt werden. Das Einbinden in fremde Seiten oder Rahmen, die die Urheberschaft der IP-GIPT nicht jederzeit klar erkennen lassen, ist nicht gestattet. Sofern die Rechte anderer berührt sind, sind diese dort zu erkunden. Sollten wir die Rechte anderer unberechtigt genutzt haben, bitten wir um Mitteilung. Soweit es um (längere) Zitate aus  ...  geht, sind die Rechte bei/m ... zu erkunden oder eine Erlaubnis einzuholen.


  Ende_Eigenwertsortierung in Matlab__Datenschutz_Überblick  _ Relativ Aktuelles  _ Rel. Beständiges   _ Titelblatt  _ Konzept  _  Archiv  _ Region _ Service iec-verlag _ Mail:sekretariat@sgipt.org  ___Wichtige Hinweise zu Links und Empfehlungen
kontrolliert am: